41
3
INSTABILITÀ ROTODINAMICHE
È comunemente accettato che l’affidabilità e l’accettabilità delle turbomacchine moderne dipenda fortemente dal grado di vibrazione e di rumore da esse prodotto (Makay and Szamody 1978, [27]), e che una delle sorgenti di vibrazione più comuni è associata con la dinamica dell’albero e dei componenti ad esso collegati (Duncan 1966-67 [13], Doyle 1980 [12], Ehrich and Childs 1984 [14]).
È chiaro che i moderni progettisti devono prestare particolare attenzione alla rotodinamica dell’albero per assicurare che, non solo le velocità critiche avvengano ai valori aspettati, ma che anche i livelli di vibrazione siano minimizzati.
È importante osservare, comunque, che non tutte le vibrazioni dell’albero sono causate da instabilità rotodinamiche; ad esempio Rosenmann [29] riporta forze radiali oscillanti, su induttori cavitanti, che sono prodotte da oscillazioni del flusso.
In questo capitolo verrà effettuata una rapida panoramica sulle attuali conoscenze in tema di fenomeni rotodinamici ed, in particolare, saranno presentati i principali risultati sperimentali ottenuti finora, nei pochi impianti esistenti in grado di monitorare questi tipi di fenomeni.
42
3.1 Aspetti generali
Una turbomacchina funziona in condizioni ideali quando, indipendentemente dalla velocità di rotazione o dalle condizioni di carico, l’asse del rotore coincide con l’asse di rotazione della macchina. Ciò avviene se tutti i componenti, sia quelli rotorici che statorici, sono perfettamente rigidi ed allineati, o se tutti i carichi sono distribuiti in maniera esattamente simmetrica. In pratica, però, nessuna di queste due condizioni è mai realmente verificata: ci sarà comunque una certa inflessione del rotore, dalla quale si origina il moto di whirl.
Questo fenomeno, teoricamente, è accettabile fino a che non viene raggiunta una inflessione del rotore tale da provocare malfunzionamenti strutturali o danneggiamenti delle parti interne per annullamento dei giochi radiali. Il fatto che, in una certa applicazione pratica, si raggiunga o meno questa inflessione limite, dipende soltanto dal valore del rapporto tra velocità di rotazione dell’albero e velocità critica, oltre che dal bilancio tra forze eccitatrici e forze smorzatrici.
Il concetto di “velocità critica” è spesso introdotto attraverso lo studio del semplice sistema fisico rappresentato in figura 3.1.
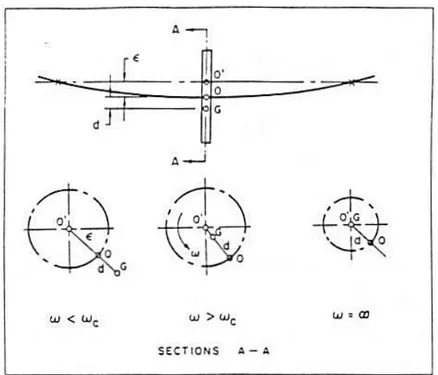
Figura 3.1: Sistema ideale contenente un rotore con centro di massa sbilanciato rispetto all’asse di rotazione (Jery, 1987).
Un rotore di massa (supposta concentrata nel suo centro di gravità G) è portato in rotazione da un albero privo di massa, in modo tale che il baricentro G si trovi ad una distanza d dall’asse dell’albero. Supponendo che l’albero ruoti con velocità costante, il rotore è in equilibrio sotto l’azione di due forze radiali:
43 1. La forza centrifuga, pari a:
in cui si è indicata con l’inflessione laterale dell’albero rispetto alla sua posizione nominale (si veda la figura 3.1);
2. La forza di richiamo elastico, data dal prodotto di per la rigidezza dell’albero, che nel semplice caso di figura 3.1 è uguale a:
essendo il modulo di Young del materiale costituente l’albero, il suo momento d’inerzia trasversale ed la sua lunghezza.
Se si impone l’equilibrio tra queste due forze, è possibile ottenere la relazione che lega ad :
La relazione (3.3) mette in evidenza che esiste un particolare valore di per cui tende a infinito (e quindi l’albero, almeno teoricamente, tende a rompersi). Questo valore, indicato in genere con , è detto “velocità critica” del particolare sistema preso in considerazione; chiaramente, per il sistema di figura 3.1, si ottiene:
Si noti che il periodo di rotazione dell’albero, alla velocità di rotazione critica, coincide con quello della sua vibrazione flessionale libera.
Dalla (3.3) è possibile dedurre che, per , l’inflessione cambia segno, ed il suo modulo tende a diminuire all’aumentare di . Ciò è illustrato bene dalla figura 3.1, nella quale si può anche vedere che, per , la forza centrifuga è in fase con l’inflessione, mentre ha verso opposto ad essa per .
Supponiamo ora di prevedere che, nel modello finora considerato, vi sia la presenza di uno smorzatore esterno: le cose si modificano come indicato in figura 3.2.
44
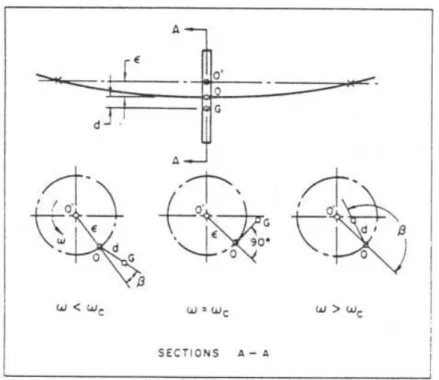
Figura 3.2: Sistema ideale contenente un rotore con centro di massa sbilanciato rispetto all’asse di rotazione, in presenza di smorzamento (Jery, 1987).
Lo smorzatore causa uno sfasamento, indicato in figura con , tra il vettore forza centrifuga ed il vettore spostamento; quando =C, il valore di è uguale a 90, e la
forza centrifuga ha direzione puramente tangenziale. In breve, la presenza di uno smorzatore permette di ridurre l’ampiezza di picco della vibrazione, ma non ne varia la frequenza.
Se a questo punto ci si sposta da un sistema ideale, come quello di figura 3.1 e 3.2, ad un sistema reale (quale è, per esempio, una turbomacchina), le cose cambiano in maniera significativa. Molte delle ipotesi semplificative fatte, infatti, non possono più essere considerate valide: ad esempio, il peso proprio dell’albero non può essere trascurato, e tutte le masse ed i carichi devono essere considerati distribuiti. Calcolare le velocità critiche di un sistema reale non è affatto semplice; possono però essere focalizzati alcuni aspetti di validità del tutto generale.
In primo luogo, ogni sistema fisico reale ha un numero infinito di velocità critiche, ciascuna delle quali corrisponde ad uno dei suoi modi di vibrazione flessionale. In pratica, un calcolo preciso di tutte le velocità critiche è impossibile: la cosa migliore che si può fare è una stima delle prime frequenze modali, che sono anche quelle predominanti, operando una discretizzazione del sistema tramite un insieme di masse, molle e smorzatori. L’informazione più importante che si ottiene da tale calcolo è rappresentata dal valore della prima velocità critica, che è anche, per definizione, quella a cui corrispondono le maggiori inflessioni.
Da un punto di vista progettuale, devono essere previsti sufficienti margini tra le velocità di rotazione previste e quelle critiche, in modo da tener conto delle incertezze di
45
calcolo e dei possibili transitori di velocità e di carico; inoltre, si deve fare in modo che i componenti del rotore abbiano abbastanza smorzamento da mantenere i principali modi vibratori sotto livelli accettabili. È anche possibile far attraversare al rotore una delle sue velocità critiche, a patto che ciò avvenga in modo sufficientemente rapido, per non dare tempo alla massima inflessione di svilupparsi completamente.
In letteratura si distingue spesso tra whirl “forzato” e whirl “autoeccitato”. Il primo è una forma di whirl sincrono, la cui ampiezza, come in tutti i fenomeni di vibrazione forzata, è massima in condizioni di risonanza (cioè quando la frequenza della forzante è uguale alla frequenza propria del sistema). Il whirl autoeccitato ha invece una frequenza non sincrona (in genere, vicina ad una delle frequenze critiche del rotore), e la sua ampiezza non assume valori percettibili fino a quando la velocità del rotore non raggiunge un valore ben preciso, denominato “velocità di inizio instabilità” (Onset Speed
of Instability, OSI). Il whirl forzato, inoltre, è sempre positivo, mentre quello
autoeccitato, pur essendo positivo nella maggior parte dei casi, può anche essere negativo.
Il whirl forzato, essendo sostanzialmente un caso di vibrazione forzata classica, è molto più semplice da predire: è possibile evitare che esso provochi vibrazioni eccessive, a patto di scegliere opportunamente le velocità di funzionamento e la procedura di avviamento. I meccanismi che causano il whirl autoeccitato, invece, non sono ancora stati del tutto chiariti: esso, comunque, deve essere considerato notevolmente più pericoloso, sia perché è inerentemente instabile, sia perché, non essendo sincrono, impone continue inversioni del verso della sollecitazione a cui è soggetto il rotore.
3.2 Attuali conoscenze teoriche e sperimentali
La risultante delle forze idrodinamiche che il fluido impartisce al rotore, in un piano perpendicolare all’asse di rotazione, può essere schematizzata assumendo un modello di perturbazione lineare:
Il termine , comunemente chiamato “forza radiale” o “spinta radiale”, è la media temporale della forza e rappresenta l’unica forza presente nel caso di rotore perfettamente centrato.
Il termine , chiamato “forza rotodinamica”, rappresenta la forza causata dallo spostamento dell’asse di rotazione rispetto alla sua posizione ideale. È proprio questo termine ad essere alla base della rotodinamica in quanto rappresenta, tramite la matrice
46
La matrice , conosciuta come “matrice di forza rotodinamica”, è indipendente dal tempo ed oltre ad essere funzione della geometria della turbomacchina e delle condizioni operative è funzione della frequenza di whirl .
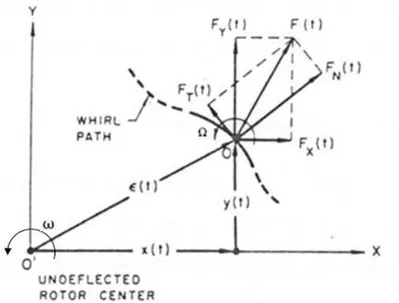
Figura 3.3: Forze laterali agenti sul centro di un rotore dotato di moto di whirl (modificato da Jery, 1987).
In un sistema di riferimento fisso la forza idrodinamica può essere rappresentata come:
dove lo spostamento è dato da e .
In aggiunta alle forze ed , solitamente vengono considerati anche i momenti flettenti indotti dal fluido, ed :
dove è conosciuta come “matrice di momento rotodinamico”.
Una particolare caratteristica delle matrici rotodinamiche, e , merita un’osservazione: entrambe sono operatori il cui compito consiste nel trasformare il vettore nel vettore o . Poiché entrambi i vettori sono nello stesso piano, la matrice che li lega ha le seguenti caratteristiche, proprie di una matrice di rototraslazione:
47
Come indicato in figura 3.3, una notazione alternativa per definire le forze rotodinamiche è tramite ed , le quali sono, istante per istante, la componenti normale e la componente tangente all’orbita di whirl. Osserva che è definita positiva se diretta verso l’esterno, mentre è definita positiva se diretta nel senso di rotazione della pompa.
L’importanza di questa notazione è giustificata dal fatto che i versi delle componenti ed permettono di determinare la stabilità locale del moto di whirl: la componente normale è instabile se è diretta verso l’esterno dell’orbita, cioè se tende a far aumentare il modulo del vettore , mentre la componente tangenziale è instabile se è diretta nello stesso verso della velocità , cioè se tende ad “alimentare” il moto di precessione.
In molti modelli utilizzati per lo studio dei fenomeni rotodinamici, è abitudine decomporre la matrice nelle matrici di “massa aggiunta”, di “smorzamento” e di “rigidezza”, in accordo a:
dove il punto denota la differenziazione rispetto al tempo, così che la matrice di massa aggiunta, , moltiplica il vettore accelerazione, la matrice di smorzamento, , moltiplica il vettore velocità e la matrice di rigidezza, , moltiplica il vettore spostamento. Osserva che sopra è stata assunta l’invarianza alla rotazione di , , , e ; M ed m denotano rispettivamente la massa aggiunta diretta e cross-accoppiata, C e c lo smorzamento diretto e cross-accoppiato, ed K e k la rigidezza diretta e cross-accoppiata.
Per capire il ruolo giocato dai coefficienti rotodinamici (cioè i coefficienti delle matrici , e ), si supponga di essere in un caso particolarmente semplice, in cui il centro del rotore si muove solamente lungo l’asse X. Se si suppone che, ad un certo istante, il moto di tale punto sia caratterizzato da posizione, velocità ed accelerazione unitarie e si trascurano i termini di ordine superiore al secondo, le forze indotte dal fluido diventano:
Si noti come la forza non agisca solo nella direzione del moto, ma anche in direzione perpendicolare ad esso: questa seconda componente è strettamente imparentata con la forza tangenziale agente su un rotore dotato di moto di whirl. Per esempio, può
48
accadere che un rotore che opera con una leggera inflessione statica (anche, semplicemente, quella dovuta al suo peso proprio) sia soggetto ad una forza laterale, perpendicolare al piano della deflessione, capace di innescare un moto di precessione; affinché ciò si verifichi, è sufficiente che la matrice abbia qualche elemento non nullo al di fuori della sua diagonale principale. Una volta innescato il whirl, però, la storia successiva del moto dipenderà non solo da , ma anche da ed .
La rappresentazione dell’equazione 3.10 è equivalente ad assumere una dipendenza quadratica degli elementi di (e delle forze , ) dalla frequenza di whirl, o dal rapporto .
Dovrebbe essere enfatizzato che le forze indotte dal fluido non sempre seguono tale dipendenza quadratica; gran parte dei risultati sperimentali, infatti, hanno dimostrato che ciò non si verifica.
Studiare le instabilità rotodinamiche di una macchina, quindi, significa studiare i meccanismi attraverso cui si originano le forze trasversali, ed il modo in cui i coefficienti rotodinamici influenzano la stabilità complessiva del moto del rotore.
Alcuni dei principali meccanismi finora scoperti sono elencati da Ehrich e Childs [14] e da Greitzer [19]. Da sempre, le maggiori attenzioni sono state date a quelli dovuti a cause puramente meccaniche, quali ad esempio: lo smorzamento interno e l’isteresi del rotore e dell’albero (si veda Kimball *24+); l’anisotropia della rigidezza dell’albero o dell’inerzia del rotore (Grabowski *18+); lo sbilanciamento delle masse del rotore (Gunter et al. *20+); le non linearità del sistema, come l’accoppiamento tra vibrazioni flessionali e torsionali (Wachel et al. [34]); lo strisciamento tra componenti rotorici e componenti statorici (Goggin [17]; Matsushita et al. [28]).
Sui meccanismi di origine fluidodinamica, invece, la letteratura presenta ancora ben poche certezze. Alcune informazioni esistono sui seguenti meccanismi: forze trasversali nei cuscinetti di strisciamento e nelle tenute (si vedano Brown et al. [7], Childs [8], Iwatsubo et al. [22], Lee et al. [25], Lund [26]) ; effetto di Alford-Thomas nelle turbopompe assiali (Alford [2], Thomas [30], Urlichs [32], Vance et al. [33], Wohlrab [35]); trascinamento del fluido da parte del rotore (Ehrich [15]); forze trasversali nelle pompe e nei compressori centrifughi (Agostinelli et al. [1], Biheller [4], Black [5], Colding-Jorgensen [9], Csanady [10], Domm et al. [11], Hergt et al. [21], Thompson [33]).
Lo studio dei fenomeni rotodinamici, attualmente, viene effettuato in apparati sperimentali nei quali si tende ad imporre dall’esterno un moto di precessione circolare alla girante, in modo da studiarne gli effetti. Nelle turbopompe reali, però, l’orbita effettivamente seguita dal centro della girante è ben lontana dall’essere una circonferenza perfetta.
Da un punto di vista pratico, imporre un moto di whirl circolare al rotore della pompa, misurando le forze che ne conseguono, permette di correlare tali forze alla posizione ed alla velocità del rotore lungo l’orbita; è inoltre possibile, almeno teoricamente, determinare completamente le forze radiali e la matrice di forza rotodinamica relative alle particolari condizioni di funzionamento scelte. Imporre un
49
moto ad orbita circolare equivale ad eseguire un esperimento di vibrazione forzata in un sistema meccanico; ne consegue che i coefficienti rotodinamici ottenuti possono essere impiegati anche per una analisi dinamica più generale del sistema, finalizzata ad esempio alla determinazione delle velocità critiche e della OSI.
Alternativamente, è anche possibile usare l’approccio della vibrazione libera, che consiste nel misurare le forze indotte dal moto di whirl direttamente sulla turbomacchina che ne è affetta, o su un suo modello scalato. L’approccio della vibrazione libera, non ponendo imposizioni di alcun genere sul moto del rotore, fornisce informazioni sicuramente più veritiere; esso, però, non permette di tenere continuamente sotto controllo la posizione del rotore, in modo da correlarla ai corrispondenti valori delle forze.
3.3 Alcuni risultati sperimentali
Generalmente, i dati sperimentali vengono forniti sotto forma di forze adimensionali. Per quanto riguarda la forza , per le macchine centrifughe essa viene normalmente adimensionalizzata nel modo seguente:
essendo il raggio esterno della girante, e la larghezza della girante al bordo d’uscita.
Le componenti ed vengono invece adimensionalizzate come segue:
Le figure 3.4 e 3.5 mostrano, rispettivamente, i valori adimensionali di ed e di ed per la girante “X”, in condizioni non cavitanti, in funzione del rapporto .
50
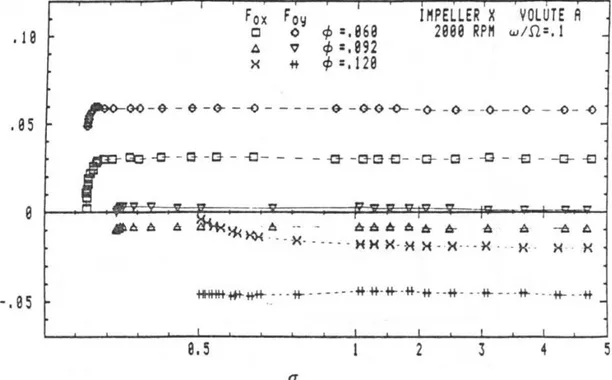
Figura 3.4: Componenti della forza radiale agente sulla girante “X” in condizioni non cavitanti (modificato da Jery, 1987).
51
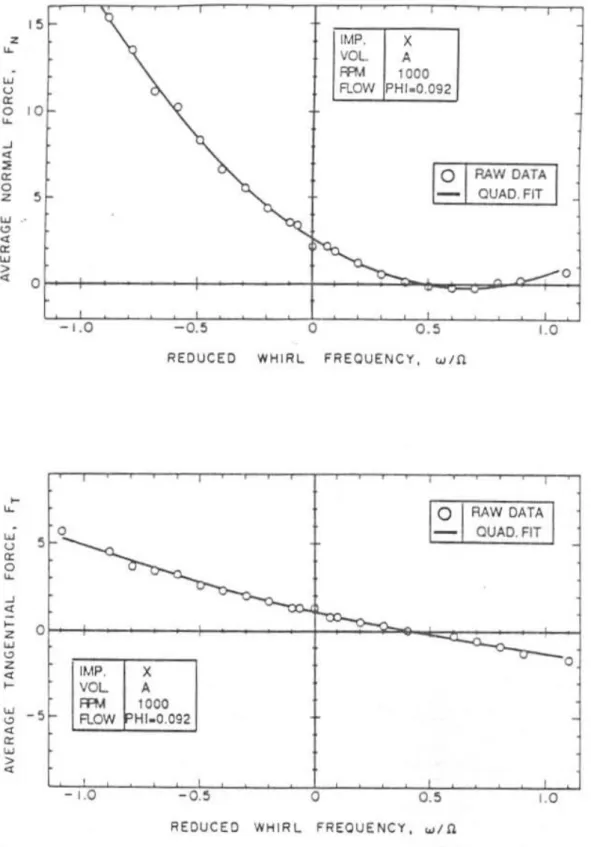
Figura 3.5: Componenti normale e tangenziale della forza rotodinamica trasversale agente sulla girante “X” in condizioni non cavitanti (modificato da Jery, 1987).
52
Per quanto riguarda la forza radiale , si nota che essa non dipende dal rapporto , ma solo dal valore del coefficiente di flusso a cui lavora la pompa. Teoricamente, una turbomacchina dovrebbe essere disegnata in modo che sia nulla per il valore di corrispondente alle condizioni nominali di funzionamento; ciò permette di ridurre al minimo le sollecitazioni affaticanti agenti sugli organi della macchina.
La componente normale della forza rotodinamica trasversale, , è praticamente sempre positiva: ciò significa che è diretta verso l’esterno, ed è quindi destabilizzante.
Quanto alla componente tangenziale , essa è destabilizzante (ha, cioè, lo stesso verso di ) per i valori di compresi tra 0 e 0.4.
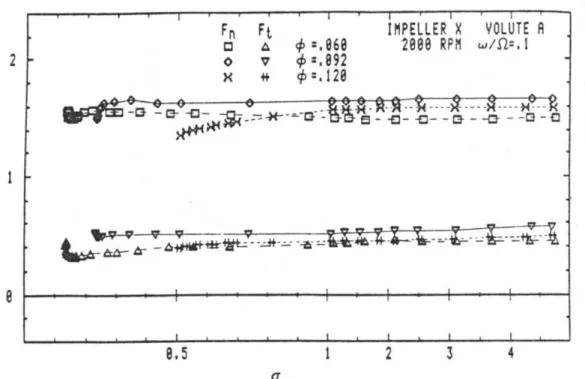
Per capire come variano le cose quando la pompa lavora in condizioni cavitanti, si può fare riferimento alle successive figure 3.6 e 3.7: esse mostrano l’andamento di , , ed , per un valore del rapporto fissato uguale a 0.1, in funzione del numero di cavitazione .
Figura 3.6: Componente della forza radiale agente sulla girante “X” in condizioni cavitanti (Franz, 1989).
53
Figura 3.7: Componenti normale e tangenziale della forza rotodinamica agente sulla girante “X” in condizioni cavitanti (modificato da Franz, 1989).
Passando ora a macchine a flusso assiale, verranno di seguito illustrati i dati relativi alle forze radiali e rotodinamiche agenti sull’induttore “VII”, così come presentati da Bhattacharyya [3].
Per gli induttori, la forza viene così adimensionalizzata:
essendo la lunghezza assiale delle pale e il raggio della pala alla sezione di uscita. Per quanto riguarda ed , valgono invece le seguenti:
Le tre figure che seguono illustrano, rispettivamente, i valori del modulo della forza e delle componenti ed , per l’induttore “VII”, in condizioni non cavitanti.
54
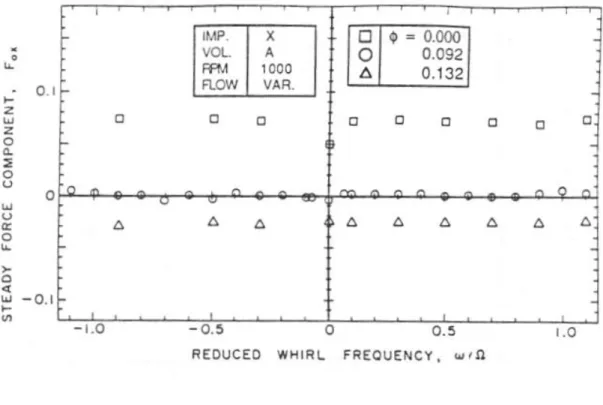
Figura 3.8: Forza radiale agente sull’induttore “VII” in condizioni non cavitanti per Ω=2000 rpm;
□ – φ=0.074, • - φ=0.059; (modificato da Bhattacharyya, 1994).
Figura 3.9: Componente normale della forza rotodinamica agente sull’induttore “VII” in condizioni non cavitanti per Ω=2000 rpm; □ – φ=0.037, - φ=0.015, ▲ - φ=0.0;
55
Figura 3.10: Componente tangenziale della forza rotodinamica agente sull’induttore “VII” in condizioni non cavitanti per Ω=2000 rpm; □ – φ=0.037, - φ=0.015, ▲ - φ=0.0;
(modificato da Bhattacharyya, 1994).
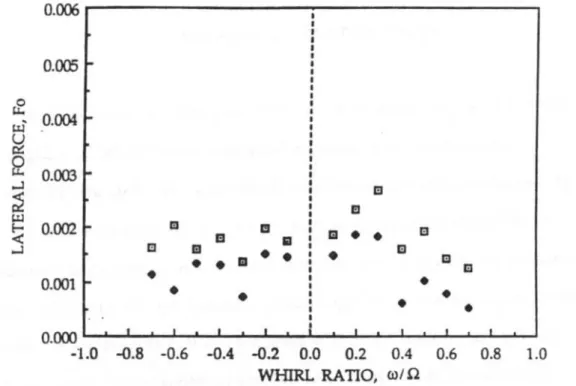
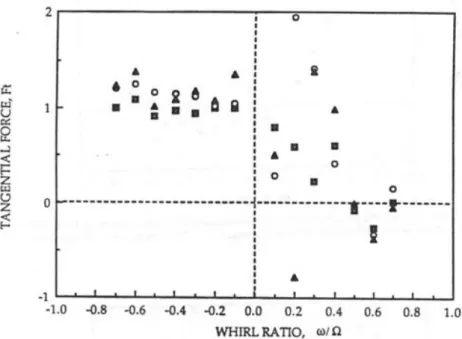
In condizioni cavitanti, le principali differenze che si notano sono relative alla componente tangenziale e sono messe bene in evidenza nella successiva figura 3.11. La figura mostra che, a differenza di quanto accade nel caso non cavitante, la assume un valore negativo (cioè destabilizzante) per quasi tutti i valori negativi del rapporto
; inoltre essa ha un evidente “picco” positivo per valori di prossimi a 0.2.
Figura 3.11: Componente tangenziale della forza rotodinamica agente sull’induttore “VII” in condizioni cavitanti per Ω=3000 rpm (modificato da Bhattacharyya, 1994).
56
3.4 Bibliografia
[1] A.Agostinelli, D.Nobels, C.R.Mockridge, “An Experimental Investigation of Radial
Thrust in Centrifugal Pumps”, Transactions of the ASME, pag. 120-126, Aprile 1960
[2] J.S.Alford, “Protecting Turbomachinery From Self-Excited Rotor Whirl”, Journal of Engineering for Power, pag. 333-344, Ottobre 1965
[3] A.Bhattacharyya, “Internal Flows and Force Matrices in Axial Flow Inducers”, Ph.D. Thesis, California Institute of Technology, 1994
[4] H.F.Biheller, “Radial Force on the Impeller of Centrifugal Pumps with Volute,
Semivolute, and Fully Concentric Casings”, Journal of Engineering for Power, pag.
319-323, Luglio 1965
[5] H.F.Black, “Lateral Stability and Vibrations of High Speed Centrifugal Pump Rotors”, International Union of Theoretical and Applied Mechanics, Dynamics of Rotors Symposium, 1974
[6] C.E. Brennen, “Hydrodynamics of Pumps”, Oxford University Press, 1994
[7] D.R.Brown, H.F.Black, “Limit Cycles of a Flexible Shaft with Hydrodynamic Bearings
in Unstable Regimes”, First workshop on Rotordynamic Instability Problems in
High-Performance Turbomachinery, 1980
[8] D.W.Childs, “Finite-Length Solutions for Rotordynamic Coefficients of Turbulent
Annular Seals”, ASME Journal of Lubrication Technology, Vol.105, pag. 437-444,
Luglio 1983
[9] J.Colding-Jorgensen, “Effect of Fluid Forces on Rotor Stability of Centrifugal
Compressors and Pumps”, First workshop on Rotordynamic Instability Problems in
High-Performance Turbomachinery, 1980
[10] G.T.Csanady, “Radial Forces in a Pump Caused by Volute Casing”, ASME Journal of
Engineering for Power, Vol.84, pag. 337-340, Ottobre 1962
[11] U.Domm, P.Hergt, “Radial Forces on Impeller of Volute Casing Pumps, Flow
Research on Blading”, Elsevier Pub.Co., pag. 305-321, 1970
[12] H.E.Doyle, “Field Experiences with Rotordynamic Instability in High-Performance
Turbomachine”, First workshop on Rotordynamic Instability Problems in
High-Performance Turbomachinery, NASA Conf. Pub. 2133, 1980
[13] A.B.Duncan, “Vibrations in Boiler Feed Pumps: a Critical Review of Experimental
and Service Experience”, Mechanical Engineering., pag. 55-64, 1966
[14] F.Ehrich, S.D.Childs, “Self-Excited Vibrations in High Performance Turbomachinery”, Mechanical Engineering, pag. 66-79, Maggio 1984
57
[15] F.F.Ehrich, “The Influence of Trapped Fluids on High Speed Rotor Vibration”, ASME Journal of Engineering for Industry, pag. 806-812, Novembre 1967
[16] R.J.Franz, “Experimental Investigation of the Effect of Cavitation on the
Rotordynamic Forces on a Whirling Centrifugal Pump Impeller”, Ph.D. Thesis,
California Institute of Technology, 1989
[17] D.C.Goggin, “Field Experiences with Rub Induced Instabilities in Turbo-machinery”, Second workshop on Rotordynamic Instability Problems in High-Performance Turbomachinery, NASA Conf. Pub. 2250, 1982
[18] B.Grabowski, “Shaft Vibrations in Turbomachinery Excited by Cracks”, Second workshop on Rotordynamic Instability Problems in High-Performance Turbomachinery, NASA Conf. Pub. 2250, 1982
[19] E.M.Greitzer, “The Stability of Pumping Systems – The 1980 Freeman Scholar
Lecture”, ASME Journal of Fluids Engineering, , Vol.103, pag. 193-242, Giugno 1981
[20] E.J.Gunter, H.Springer, R.Humphris, “Influence of Unbalance on the Stability
Characteristics of Flexible Rotor Bearing Systems”, ASME Applied Mechanics,
Bioengineering and Fluids Engineering Conference, 1983
[21] P.Hergt, P.Krieger, “Radial Forces in Centrifugal Pumps with Guide Vanes”, Proc.Inst. of Mechanical Engineers, Vol.184, pag. 101-107, 1969-1970
[22] T.Iwatsubo, R.Kawai, N.Kagawa, T.Kakiuchi, K.Takahara, “Analysis of Dynamic
Characteristics of Fluid Force Induced by Labyrinth Seal”, Third workshop on
Rotordynamic Instability Problems in High-Performance Turbomachinery, NASA Conf. Pub. 2338, 1984
[23] B.Jery, “Experimental Study of Unsteady Hydrodynamic Force Matrices on Whirling
Centrifugal Pump Impellers”, Ph.D. Thesis, California Institute of Technology, 1987
[24] A.L.Kimball Jr., “Internal Friction Theory of Shaft Whirling”, General Electric Review, Vol.27, pag. 244-251, Aprile 1924
[25] O.W.K.Lee, M.Martinez-Sanchez, E.Czajkowski, “Prediction of Force Coefficients for
Labyrinth Seals”, Third workshop on Rotordynamic Instability Problems in
High-Performance Turbomachinery, NASA Conf. Pub. 2338, 1984
[26] J.W.Lund, “Stability and Damped Critical Speeds of a Flexible Rotor in Fluid-Film
Bearings”, Journal of Engineering for Industry, pag. 509-517, Maggio 1974
[27] E.Makay, O.Szamody, “Survey of Feed Pump Outages”, Electric Power Research Institute, Report FP-754, 1978
[28] O.Matsushita, M.Takagi, K.Kikuchi, M.Kaga, “Rotor Vibration Caused by External
Excitation and Rub”, Second workshop on Rotordynamic Instability Problems in
58
[29] W.Rosenmann, “Experimental Investigations of Hydrodynamically Induced Shaft
Forces with a Tree Bladed Inducer”, ASME Symp. on Cavitation in Fluid Machinary,
pag. 172-195, 1965
[30] H.J.Thomas, “Unstable Oscillations of Turbine Rotors Due to Steam Leakage in the
Clearance of the Sealing Glands and the Buckets”, Bulletin Scientifique, A.J.M.,
Vol.71, 1958
[31] W.E.Thompson, “Fluid Dynamic Excitation of Centrifugal Compressor Rotor
Vibrations”, Journal of Fluid Engineering, Vol.100, pag. 73-78, Marzo 1978
[32] K.Urlichs, “Clearance-Flow Generated Transverse Forces at the Rotors of Thermal
Turbomachines”, NASA TM-77292, Translation of Doctoral Dissertation, Technical
University of Munich, 1975
[33] J.M.Vance, F.J.Laudadio, “Experimental Measurement of Alford’s Force in Axial
Flow Turbomachinery”, Second workshop on Rotordynamic Instability Problems in
High-Performance Turbomachinery, NASA Conf. Pub. 2250, 1982
[34] J.C.Wachel, F.R.Szenasi, “Field Verification of Lateral-Torsional Coupling Effects on
Rotor Instabilities in Centrifugal Compressors”, First workshop on Rotordynamic
Instability Problems in High-Performance Turbomachinery, 1980
[35] R.Wohlrab, “Experimental Determination of Gap Flow-Induced Forces at Turbine
Stages and Their Effect on the Running Stability of Simple Rotors”, NASA