4. ANALISI STRUTTURALE

135

4. ANALISI STRUTTURALE

4.1

Studio agli elementi finiti del pannello

L’analisi strutturale dello scudo, come previsto dalla specifica di progetto, è mirata alla determinazione dello stato di deformazione e, introdotte le caratteristiche meccaniche dei materiali, di quello tensionale della struttura, allo scopo di verificare il rispetto di tutti i requisiti imposti dalla specifica. Lo scudo, come descritto nella proposta, è costituito da dodici pannelli (paragrafo 3.2) di identiche proprietà meccaniche e geometriche; tutte le analisi verranno quindi condotte solo su un singolo pannello.

Analizzando la geometria della struttura introdotta, sono state eseguite, applicando le opportune condizioni di vincolo e di carico, le analisi statiche e dinamiche dei componenti strutturali costituenti lo scudo. Inoltre, dovendo considerare la schermatura come facente parte dello stadio superiore del lanciatore, è stato necessario progettare l’interfaccia con le strutture adiacenti, le cui geometrie sono opportunamente descritte nella specifica di progetto trattata nel capitolo precedente.

Tutte le analisi sono state effettuate utilizzando il metodo risolutivo degli elementi finiti o semplicemente FEM (Finite Element Method). Il metodo permette di risolvere in maniera approssimata problemi complessi, per la determinazione dello stato di tensione e deformazione di una struttura continua. Poiché il problema presenterebbe un numero infinito di incognite, il dominio in esame viene discretizzato in un numero finito di sottodomini detti elementi, tali che il loro assemblaggio dia poi luogo ad una rappresentazione della struttura di partenza, attraverso la creazione di una griglia (mesh) composta da primitive di forma codificata, triangoli e quadrilateri per domini 2D, esaedri e tetraedri per domini 3D (Figura 4.1).

136 Figura 4.1 Rappresentazione delle diverse tipologie di elementi

Gli elementi sopra raffigurati sono caratterizzati dalla presenza di nodi (nodes) localizzati agli angoli o lungo i lati (nel caso di elementi di ordine superiore al primo), che definiscono la geometria dell'elemento e rappresentano i punti di connessione fra gli elementi stessi (continuità). Nei nodi sono concentrati i gradi di libertà (DOF, Degrees of Freedom) mediante i quali vengono risolti gli spostamenti (lo spostamento di ciascun nodo è quantificato in termini di traslazione e rotazioni, rispetto ad un opportuno sistema di riferimento), le forze esterne e i vincoli (condizioni al contorno). Il problema originario diviene quindi un problema approssimato e descritto da un numero finito di incognite tra loro interconnesse nei nodi. La rappresentazione grafica di quanto esposto finora è illustrata in Figura 4.2.

137 Figura 4.2 Raffigurazione della discretizzazione di un elemento

Pertanto il metodo FEM ci consente di determinare lo stato di sforzo e di deformazione di ciascun elemento, utilizzando funzioni che legano gli spostamenti nel generico punto interno all’elemento con gli spostamenti nodali. Infatti, ad ogni elemento finito è associata una matrice di rigidezza che, assemblata con quelle di tutti gli elementi che descrivono la struttura, forma la matrice di rigidezza totale. La matrice di rigidezza dell’elemento lega gli spostamenti e le forze relative a tutti i gradi di libertà relativi ad esso mediante un’equazione matriciale fondamentale, che deriva direttamente dalla legge di Hooke:

{ }

[ ]

{ }

138 {f} è il vettore degli spostamenti incognito;

[K] è la matrice di rigidezza del modello matematico della struttura oggetto di studio.

Per la corretta gestione del metodo degli elementi finiti su modelli complessi si rende indispensabile l’utilizzo di software che consentano sia di generare il modello matematico che approssima la struttura reale oggetto di studio (generare la griglia degli elementi e definizione delle proprietà), sia di visualizzare i dati prodotti dal calcolo operato sul modello matematico, al fine di valutarne la correttezza (fase di analisi critica ed elaborazione dei risultati). Questi software vengono comunemente indicati con i termini pre-processing e post-processing: il primo è utilizzato in fase di caratterizzazione della struttura al fine di generare il modello matematico che la riproduce e che ne consente uno studio numerico, il secondo, invece, è utilizzato nella fase di valutazione dei risultati ottenuti con un calcolo numerico effettuato mediante l’uso del modello matematico. In genere i software pre/post-processing, oltre a possedere sufficienti strumenti per l’elaborazione dei dati geometrici a supporto della creazione del modello matematico, consentono di interfacciarsi con i software CAD; questo fa sì che le informazioni geometriche della struttura possono essere importate in ambiente CAE (Computer Aided Engineering), direttamente dall’ambiente CAD. Insieme ai software sopra citati va impiegato quello del codice di calcolo vero e proprio, che è in grado di risolvere, mediante l’uso di appropriati algoritmi, i sistemi di equazioni ai quali sono riconducibili le rappresentazioni dei vari fenomeni fisici. A tale codice bisogna fornire dei dati strutturali, secondo regole sintattiche ben precise (file di input), in modo da ottenere dei risultati scritti anch’essi secondo regole sintattiche (file output) che dipendono dal tipo di codice usato. È quindi il codice di calcolo che risolve il sistema visto in precedenza in modo da ricavare il vettore degli spostamenti incognito invertendo la matrice di rigidezza:

{ }

[ ]

{ }

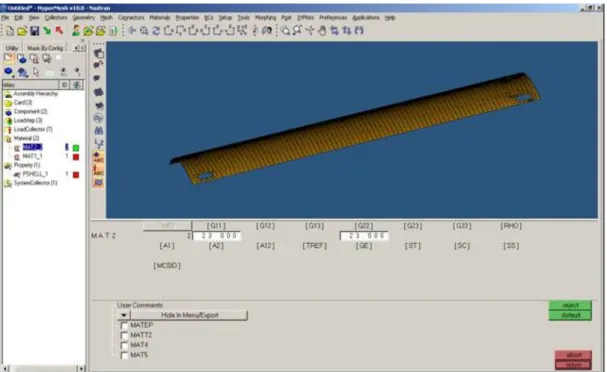
139 nella versione distribuita dalla MSC. Software Corporation; in particolare per la soluzione statica lineare è stato utilizzato l’algoritmo risolutivo SOL 101, mentre per l’analisi lineare dinamica il SOL 103 con il metodo di estrazione degli autovalori di tipo Lanczos. Tutte le operazioni di pre-processing e post-processing sono invece state eseguite con l’utilizzo del pacchetto HyperWorks 10.0® prodotto dall’Altair Engineering. In particolare per il processo di creazione e controllo della mesh, per la creazione ed assegnazione dei casi di carico, delle condizioni a contorno e dei materiali ai diversi componenti è stato utilizzato HyperMesh®. Infine per la visualizzazioni dei risultati ottenuti si è utilizzato il programma HyperView®.

140

4.1.1

Discretizzazione del modello

Il nostro sistema “pannello”, come analizzato nel paragrafo precedente, è stato suddiviso in elementi, a ciascuno dei quali sono state successivamente assegnate tutte le proprietà fisico meccaniche necessarie, come ad esempio la densità, il modulo elastico, il modulo di Poisson, ecc.

La geometria del pannello sandwich creata in ambiente CAD, utilizzando il SW Catia® V5 e mostrata in Figura 4.3, dovrà essere importata nell’ambiente Hyperworks per effettuare la discretizzazione del sistema.

Figura 4.3 Rappresentazione CAD del pannello

Il primo passo da fare è quello di modificare la geometria, la quale verrà semplificata in modo da considerare le sole parti del pannello che contribuiscono alla struttura meccanica. Infatti verranno eliminate le appendici aerodinamiche all’estremità e la geometria del pannello verrà ricondotta ad un caso perfettamente bidimensionale. In pratica, verrà estratta

141 mostrato in Figura 4.4.

Figura 4.4 Pannello ridotto al caso bidimensionale

Nei successivi paragrafi si mostrerà come si riescano a creare, attraverso opportune card image, file di input per l’assegnazione dei materiali e delle proprietà della struttura reale a sandwich (skin e core), pur considerando, in fase di analisi, la geometria sopra esposta priva di spessore.

In HyperMesh®, la discretizzazione del pannello è stata eseguita utilizzando elementi piani a quattro nodi (QUAD4 shell) e a tre nodi (TRIA3 shell), cercando di ridurre il numero di questi ultimi al minimo poiché meno precisi degli altri. La generazione della mesh è stata ottenuta utilizzando un processo semi-automatico. La griglia è stata generata seguendo delle linee guida, ad esempio su simmetrie e nell’intorno dei fori; variando i parametri di controllo della qualità degli elementi (Figura 4.5), variando la densità delle linee perimetrali, la griglia è stata generata mediante il comando di creazione automatica di HyperMesh®. Successivamente la mesh creata è stata

142 migliorata manualmente nelle zone di maggiore interesse per il sistema, ossia le zone in cui ci si aspettano maggiori deformazioni e quelle in prossimità dei fori (Figura 4.6).

Figura 4.5 Visualizzazione della discretizzazione del pannello

143

4.2

Definizione dei materiali

La realizzazione del pannello è stata immaginata inizialmente come costituita da pelli esterne di materiale composito in fibre di vetro, annegate in matrice di resine fenoliche, mentre il core del pannello è stato concepito in Airex R82. Le principali caratteristiche dei materiali scelti sono rappresentate rispettivamente in Tabella 4.1, per la skin [17] e nella Tabella 4.2 per il core [18].

144 Tabella 4.2 Principali proprietà dell’Airex R82

145

4.2.1

Creazione delle proprietà dei materiali

Le caratteristiche, definite nel paragrafo precedente, sono state introdotte nel modello matematico di analisi attraverso la creazione di opportune schede di proprietà dei materiali previsti da NASTRAN®.

Con l’utilizzo di HyperMesh sono state quindi create delle cards MAT22_,

utilizzate per la definizione dei materiali. Per le strutture di tipo sandwich si utilizzata la scheda dei materiali MAT8, la quale prevede l’inserimento delle proprietà meccaniche nelle due direzioni dell’elemento sia per la skin che per il core, in Figura 4.7 è rappresentata una scheda tipo MAT8.

Figura 4.7 Esempio per la definizione della scheda del materiali MAT8

146 Per lo studio di avamprogetto si è preferito adoperare le più semplici card, MAT1, utilizzata per i materiali omogenei, e MAT2, utilizzata omogenei o ortotropi (Figura 4.8), pre-calcolando le proprietà del pannello sandwich attraverso un foglio di calcolo che tiene conto di tutte le proprietà di skin e core. Questo metodo considera anche la distanza delle skin dal piano neutro attraverso i codici Z1 e Z2, i quali indicano le quote in cui si va a calcolare lo stato tensionale massimo.

Figura 4.8 Esempio delle schede MAT1 e MAT2

Di seguito è rappresentato un esempio di uno dei fogli di calcolo MathCad creato per la determinazione della cosiddetta equivalent pshell.

147

EQ UIV AL EN T P SHEL L CALCU L AT ION FOR A SA NDW ICH

F ibe rgla s s P h enolic S KINS + AIRE X R8 2 CORE

IN PUT M P a N mm2 ts k 0 .3 mm. Sk in Thic kne ss T s 25. 4 mm. Ho n eycom b Th i cknes s Z 1 T s 2 tsk Z 1 fo r stres s re covery Z 2 fo r stres s re covery Z 2 Z1 S kin

ν 0 .26 Sk in P ois son M o dulus

E skin 2 1235 .8 5M Pa. S kin Y oung M odulu s

ρsk in 1 80 0 1 0. 9 kg mm3

. S kin De n sity: E CD E-1 /0 -A 11 00

C OR E

G 1 1 23 M Pa. H on eyc om b S h e ar Mo dulus

G 2 2 23 M Pa. H on eyc om b S h e ar Mo dulus

ρh c 8 0 1 0. 9 k g m m3

. H on eyc om b D ens ity

Equiva lent M e m bra n e Thick ness

T 2 t sk. T=0 .6 mm INS ER T IN P SHE L L

Bendin g S tiffn es s P a ram ete r

I 2 tsk 3 1 2 tsk t sk 2 Ts 2 2 . . I =9 9.0 78 mm3 1 2 I T3 . _{=5.50 4 1 0}3 I NS ER T IN PS HE LL

Tra nve rse S h ear Th ick nes s

Ts T

4 2.3 33

148 Equivalent Density ρeq ρskin ρhc Ts T . ρeq 5.187 10 6 kg mm3 = INSERT IN MAT1 Mass

Area 3.446 10. 6.mm2 Area Pannello VTI

Mass Area.ρeq.T Mass =10.724 kg PROPERTIES

PSHELL PID MID1 T MID2 1 2I/T3 MID3 TS/T NSM

10 10 20 1 T=0.6 mm 12 I T3 . _{=5.504 10}3 Ts T 42.333 = Z1 Z2 Z1=13 mm Z2= 13 mm

MAT1 MID E G NU RHO

10 Eskin=2.124 104 MPa ν=0.26 ρeq 5.187 106 kg mm3 =

MAT2 MID G11 G12 G13 G22 G23 G33

20 G11 23 MPa= G22 23 MPa= Come si può notare, gli spessori della skin e del core e le relative proprietà sono definiti come degli input inseriti dall’utente e che quindi possono essere variati di volta in volta durante lo studio (Figura 4.9).

149 Figura 4.9 Spessori caratteristici del pannello

L’algoritmo creato ci fornisce in output le proprietà equivalenti (come momento d’inerzia, densità e massa) da inserire nelle cards MAT1 e 2 di HyperMesh® insieme ai valori delle quote Z1 e Z2. Le rappresentazioni della compilazione delle cards MAT1 e MAT2 sono illustrate rispettivamente in Figura 4.10 e Figura 4.11.

150 Figura 4.11 Assegnazione delle grandezza alla MAT2

Tale materiale è stato applicato al modello attraverso l’apposito menù “PROPERTIES”, presente nel software di pre-processing, ottenendo cosi la distribuzione del materiale rappresentato in Figura 4.12.

151

4.2.2

Definizione delle proprietà degli elementi

Agli elementi costituenti il dominio, in cui è stato discretizzato il modello CAD del pannello, sono state assegnate le caratteristiche meccaniche proprie del componente, attraverso l’utilizzo dell’apposito menù presente in HyperMesh®, illustrato in Figura 4.13.

Figura 4.13 Visualizzazione del menù PROPERTIES

In particolare, attraverso il campo “card image” è stata definita la tipologia del componente (PSHELL), mentre dal campo “material” si sono scelte le schede degli stessi preventivamente create da assegnare all’elemento. Dopo aver selezionato la tipologia di elemento e assegnato il materiale, è necessario inserire le caratteristiche mancanti per la definizione completa. Nel caso della PSHELL, i campi caratteristici, rappresentati in Figura 4.14, sono stati riempiti per ciascuna analisi presa in esame con i valori ottenuti dai rispettivi fogli di calcolo, di cui un esempio è menzionato nel paragrafo precedente; in riferimento a tale caso la Figura 4.15 riporta la “card edit” utilizzata nel pre-processing per l’assegnazione dei dati alla PSHELL.

152 Figura 4.15 Visualizzazione della card edit tipo pshell

153

4.3

Condizioni di carico

Dopo aver definito il dominio di calcolo e tutte le proprietà meccaniche degli elementi costituenti la discretizzazione del modello, è stato necessario definire le condizioni di carico alle quali la struttura dovrà resistere. I carichi di progetto, come definiti nei requisiti del capitolo 3, possono essere suddivisi in: • carichi aerodinamici;

• carico acustico;

• carichi indotti dalle accelerazioni dinamiche del lanciatore.

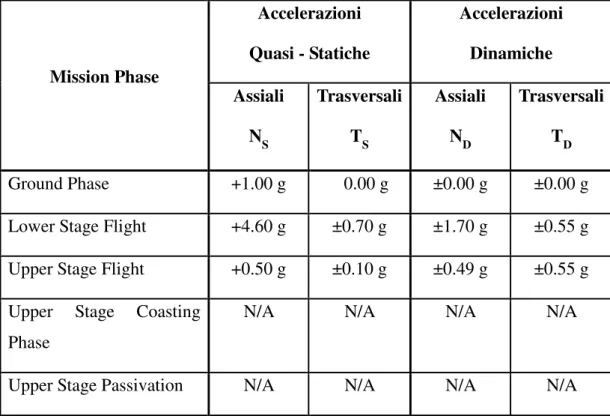
Questi ultimi vengono determinati prendendo come accelerazioni di riferimento quelle tipiche del lanciatore Ariane5, riportate in Tabella 4.3, nella quale sono elencate le accelerazioni gravitazionali quasi statiche e quelle dinamiche indotte dalle varie fasi della missione.

Mission Phase Accelerazioni Quasi - Statiche Accelerazioni Dinamiche Assiali N_S Trasversali T_S Assiali N_D Trasversali T_D Ground Phase +1.00 g 0.00 g ±0.00 g ±0.00 g

Lower Stage Flight +4.60 g ±0.70 g ±1.70 g ±0.55 g

Upper Stage Flight +0.50 g ±0.10 g ±0.49 g ±0.55 g

Upper Stage Coasting Phase

N/A N/A N/A N/A

Upper Stage Passivation N/A N/A N/A N/A

154 Tali accelerazioni agiscono in direzione assiale e trasversale come percentuale dell’accelerazione gravitazionale23 _{e dovranno essere considerate per mezzo}

di un’opportuna combinazione lineare prima di essere inserite nel software di pre-processing.

La determinazione dei carichi dinamici ed acustici, in termini di pressione applicata alla superficie del pannello, è stata effettuata utilizzando dei fogli di calcolo Mathcad, prendendo come grandezze caratteristiche quelle fornite da specifica; tale procedimento è stato di seguito riportato.

23_{g = 9.806 [m/s}2

156 Attraverso l’utilizzo del comando “create”, presente nel software di pre-processing, e la scelta di opportune schede di carico, è stato possibile applicare agli elementi tutti i tipi di carico elencati in precedenza. In particolare, per l’applicazione della pressione, si sono utilizzate le schede di carico PLOAD mentre per i carichi dovuti all’accelerazione si è utilizzata la scheda di carico GRAV.

157

4.4

Condizioni di vincolo

In un’analisi statica agli elementi finiti è sempre necessario imporre dei vincoli tali per cui siano annullati tutti i possibili movimenti di corpo rigido (se il corpo è uno solo, come nel presente caso, i vincoli devono annullare 3 traslazioni e 3 rotazioni). Infatti, per raggiungere la soluzione del modello FEM, è necessario rendere invertibile la matrice di rigidezza del sistema, trattata nel paragrafo 4.1, passaggio possibile solo eliminando le labilità della struttura in esame.

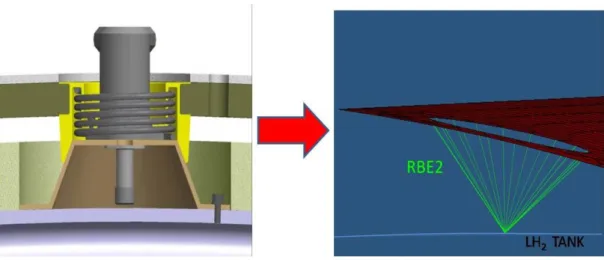
Le condizioni di vincolo sono state quindi pensate in quest’ottica ed in modo da essere coerenti con il comportamento reale della struttura. Per simulare il sistema di aggancio che collega il pannello alla superficie del serbatoio, sono state create delle connessioni RIGIDS di tipo RBE2 (Figura 4.16), le quali uniscono in modo rigido, bloccando quindi tutti i gradi di libertà, i nodi del foro con i punti di aggancio al serbatoio.

Figura 4.16 Rappresentazione delle RIGIDS RBE2

Tale condizione di vincolo permette di rispettare la realtà geometrica della struttura e quindi la distanza fra pannello e superficie di giunzione del serbatoio (31,19 [mm]).

158 In Figura 4.17 viene rappresentato come dalla geometria reale si è passati alla sua schematizzazione.

Figura 4.17 Rappresentazione della riproduzione del sistema di aggancio tramite RBE2 Una volta creato il modello del sistema di aggancio, per considerare i gradi di libertà di ogni foro rispetto ad esso, le connessioni RBE2 sono state vincolate attraverso il comando CONTRAINS (Figura 4.18), il quale consente di definire uguali a zero, quindi bloccare, le traslazioni e le rotazioni attorno agli assi del sistema di riferimento, scelto in fase di creazione del vincolo.

159 origine coincide con il centro del lanciatore e l’asse z, orientato lungo la direzione longitudinale del lanciatore stesso (asse di simmetria cilindrico). Con numeri che vanno da 1 a 3 si bloccano, rispettivamente, la traslazione lungo l’asse radiale (r), tangenziale (t), e z; invece con numeri che vanno da 4 a 6 si bloccano rispettivamente le rotazioni attorno ad r,t e z. In Figura 4.19 vengono rappresentate le traslazioni e le rotazioni impedite dai vincoli.

160

4.5

Analisi dinamica (Modale)

La prima tipologia di analisi strutturale eseguita sul modello è stata la modale. L'analisi modale è una metodologia di calcolo che si occupa della determinazione del comportamento dinamico di una struttura vincolata o libera. Essa prevede di studiare la struttura, schematizzata con il metodo degli elementi finiti (paragrafo 4.1.1), attraverso la valutazione di frequenze naturali e modi propri associati. Lo scopo di tale analisi è quello di studiare la risposta della struttura in progetto per evitare che si verifichino fenomeni di risonanza meccanica, dovuti alle frequenze eccitanti provenienti dal lanciatore e prodotte principalmente dal motore e dall’aerodinamica esterna. La risonanza è una condizione fisica che si verifica quando un sistema oscillante viene sottoposto a sollecitazione periodica di frequenza pari all'oscillazione propria del sistema stesso. Un fenomeno di risonanza provoca, in genere, un aumento significativo dell'ampiezza delle oscillazioni rispetto alla forzante che corrisponde ad un notevole accumulo di energia all'interno del sistema sollecitato e quindi può provocare il danneggiamento o la rottura della struttura stessa.

L’analisi dinamica è governata dalla seguente espressione:

[ ]

{ }

[ ]

{ }

[ ]

{ } { }

{ }

161

{ }

L’analisi modale è stata utilizzata per determinare le frequenze naturali e le forme modali della struttura. Nella nostra analisi il codice di calcolo, Nastran, considera vibrazioni libere non smorzate {F(t)}={0} e [C]= 0.

L’equazione che governa il sistema quindi si riduce a:

[ ]

{ }

[ ]

{ }

Se indichiamo, rispettivamente, con ω_ne φ_n le frequenze e i modi propri di vibrare, si può scrivere la relazione che ci fornisce la dinamica delle strutture come:

[ ] [ ]

(

)

La risoluzione dell’equazione scritta sopra è un problema agli autovalori, la cui soluzione fornisce gli autovalori e i corrispondenti autovettori. Gli autovalori rappresentano le frequenze proprie del sistema, mentre gli autovettori le corrispondenti forme modali. Il metodo utilizzato dal codice di calcolo per l’estrazione degli autovalori è quello di Lanczos; si sceglie di estrarne dieci che corrispondono ai primi dieci modi di vibrare della struttura e che saranno quindi oggetto di analisi (a partire dalla più bassa).

Per l’inserimento dei dati in HyperMesh® è stata utilizzo il comando EIGRL (Figura 4.20), in cui è stato inserito il numero di autovalori da estrarre (10) ed è stato richiesto di fornire come dato in output la quantità della massa partecipante rispetto a quella totale.

Figura 4.20 Scheda EIGRL per l’estrazione del numero degli autovalori

Sapendo che lo spettro di frequenze tipiche del lanciatore si concentra tra 9 e 10 [Hz], è importante verificare che le prime frequenze naturali del sistema

162 pannello siano sufficientemente lontane da questo spettro, in modo tale da essere sicuri che non si verifichi mai una risonanza meccanica. Nella prassi si considera una differenza pari a 5 [Hz] tra la massima frequenza del lanciatore e la minima del pannello per ottenere un efficace disaccoppiamento dinamico delle due strutture. In questo caso, la specifica del sistema pannello richiede che la prima frequenza propria sia superiore a 15 [Hz].

Di seguito vengono raffigurati solo i primi tre modi di vibrazione, cioè quelli con frequenza più bassa e quindi critici per la risonanza.

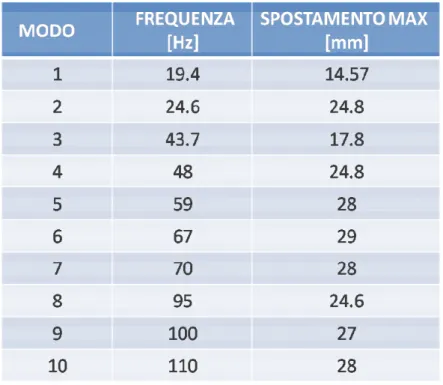
163 In Tabella 4.4 si riportano tutte le frequenze ed i relativi spostamenti massimi ottenuti dall’analisi modale.

164 Tabella 4.4 Frequenze e spostamenti dei dieci modi di vibrare del pannello

Dai risultati delle frequenze sopra esposte si può notare che i modi propri di vibrare del pannello avvengono a frequenze più elevate del valore di sicurezza richiesto (maggiore di 15 [Hz]).

165

4.6

Analisi statica

Dopo aver eseguito l’analisi dinamica, applicando sia le condizioni di vincolo esposte al paragrafo 4.4 che tutte le combinazioni di carico definite al 4.3, è stata effettuata un’analisi statica lineare volta a definire i valori delle tensione e il campo di spostamento del pannello. Per la definizione delle tensioni ammissibili (σ_amm) si è deciso di essere cauti, considerando un elevato valore del coefficiente di sicurezza (Cs) ed un valore di tensione a rottura del materiale relativamente basso. Il σamm rappresenta il valore con cui verranno

confrontati gli stress massimi estratti dal modello FEM della struttura per capirne lo stato di “salute”. La cautela adottata deriva da due considerazioni fondamentali: la prima è dovuta alla limitata disponibilità di dati di caratterizzazione termo-meccanica circa i materiali utilizzati (soprattutto per quelli costituenti le skin), la seconda deriva dall’aver considerato una laminazione quasi-isotropa per le skin del pannello sandwich. Quest’ultima ipotesi giustifica il fatto che, nelle analisi di seguito effettuate, si considereranno, nell’ottica di un’analisi preliminare, gli stress secondo il criterio di Von Mises (concepito rigorosamente per materiali quasi duttili ed isotropi). Da tutto ciò ne consegue che: scelto un valore di Cs pari a 1,5 e considerato il valore della tensione a rottura del materiale, pari ad 280 [MPa], si ottiene il seguente valore delle tensioni ammissibili.

[

]

Durante l’analisi sarà verificato il peso del pannello, che in questo caso non dovrà eccedere i 20.8 [Kg] (ottenuti da 250[Kg]/12 pannelli, come descritto dalla specifica PR2), e lo spostamento massimo, che non dovrà superare i 20 [mm]. Analizzando la missione del lanciatore e quindi la tipologia di carico agente in ogni sua fase, si è scelto di dividere lo studio in due differenti fasi: la fase di decollo e la fase iniziale di crociera.

166 Nella prima si considerano solo la pressione acustica, dovuta soprattutto all’azione del motore, e le accelerazioni. Nella seconda fase, invece, si valutano le due componenti del carico dinamico dovute, rispettivamente, alla pressione dinamica (q), data da specifica, e alle relative azioni tangenziali; una schematizzazione della condizione di carico complessiva è riportata nella Tabella 4.5.

Tabella 4.5 Tabella riassuntiva dei carichi applicati nelle due fasi di missione Durante la prima fase della missione (lift off), per simulare le combinazioni fra le accelerazioni, sono state create, nella load Collector, tre differenti “Cards Load”ed in esse vengono inserite le accelerazioni attraverso le opportune schede Grav 1 e Grav 3 rappresentate in Figura 4.21.

Figura 4.21 Rappresentazione delle schede GRAV

Ricordando che i valori di accelerazione (tabella 4.5) sono espressi in percentuale dell’accelerazione gravitazionale (g), nelle schede sopra esposte viene inserito il valore di g, mentre le loro direzioni vengono aggiunte al sistema di riferimento cilindrico attraverso i comandi N1, N2,e N3, che rappresentano rispettivamente la direzione radiale (Trasversale), la rotazione

167 richiamate nelle tre “Cards Load” (Figura 4.22) attraverso il loro “ID” dai comandi L1(1) ed L1(2), mentre in S1(1) e S1(2) verranno inseriti i valori dell’accelerazione; anche la pressione acustica, verrà richiamata tramite il proprio “ID” dal comando L1(3) ed inserita in S1(3).

Tale procedimento sarà ripetuto per altre due combinazioni di accelerazione, creando i tre casi di carico agenti nella fase lift-off e denominati rispettivamente SUBCASE 1, 2 e 3. Tali carichi vengono applicati attraverso l’utilizzo del comando “create”, presente nel software di pre-processing al pannello; nella Figura 4.23 viene rappresentata l’applicazione del carico di pressione acustica.

168 Figura 4.23 Applicazione dei carichi di pressione acustica

Inserite tutte le grandezze si può ritenere conclusa la fase di pre-processing; i dati vengono, quindi, immessi nel codice di calcolo Nastran che fornisce la soluzione numerica disponibile attraverso l’utilizzo del programma HyperView®.

La logica con la quale sono state effettuate le prime analisi è la seguente: sono stati considerati invariabili i carichi, le condizioni di vincolo ed i materiali scelti, come dati variabili gli spessori delle skin e del core, senza considerare le restrizioni dello spessore (requisito gr1). Per ogni caso analizzato viene verificato se i valori di stress, deformazione e peso della struttura rientrano nei limiti massimi previsti da specifica e riassunti all’inizio del paragrafo. Durante la prima fase di analisi, sono stati studiati valori minimi di 25,4 [mm] per lo spessore del core e 0,3 [mm] per quello delle skin per poi arrivare ad analizzare spessori di 80 [mm] per il primo e di 1,2 [mm] per il secondo; nella Tabella 4.6 sono riportati alcune delle analisi effettuate.

169 Tabella 4.6 Spessori analizzati relativi risultati ottenuti.

Di seguito verranno rappresentati, per il caso XII, la distribuzione degli stress e le deformazioni del pannello nelle tre combinazioni di carico applicato. STRESS

172 Analizzando le raffigurazioni sopra esposte, il comportamento del pannello è coerente con quanto atteso: le zone del pannello maggiormente sollecitate sono quelle in prossimità dei fori, mentre quella centrale è la zona in cui si registrano le maggiori deformazioni.

Gli elementi in prossimità dei fori, anche se risultano maggiormente sollecitati, non verranno analizzati in dettaglio, in quanto i vincoli e la mesh introducono dei livelli di carico concentrato elevati: tali zone andranno pertanto specificatamente studiate con dei modelli FEM locali eventualmente facenti ricorso ad elementi solidi; inoltre, le soluzioni costruttive dovranno prevedere degli ispessimenti ed irrigidimenti in corrispondenza dei punti di aggancio volti ad aumentare le prestazioni strutturali locali, contribuendo a ridurre lo stato tensionale e distribuire in maniera ottimale i carichi concentrati. Nel presente studio di avamprogetto non vengono considerate le possibili giunzioni longitudinali derivanti dalla eventuale sovrapposizione a “tegola” di pannelli adiacenti, che da un lato andrebbero ad abbassare notevolmente le deformazioni locali ma per contro imporrebbero una sequenza nella procedura di separazione dei pannelli dal lanciatore.

173 elevati (core 80 [mm]), sotto l’azione delle tre condizioni di carico (subcase1, 2, e 3) la struttura non riesce a soddisfare i requisiti imposti dalla specifica in termine di stress, ma soprattutto di deformazioni massime. Le analisi hanno però dimostrato che l’aumento dello spessore del core, quindi la distanza delle pelli dall’asse neutro, ha ridotto in modo significativo il valore degli spostamenti e degli stress. Tale riduzione è dovuta all’aumento della rigidezza flessionale (D), la quale dipende principalmente dalla distanza tra l’asse neutro del sandwich ed il piano medio delle skin.

Considerata la struttura esposta in Figura 4.24, per quest’ultima la rigidezza flessione sarà data da:

(

)

E E si indicano rispettivamente il modulo elastico del core e delle skin ,

c s

I I momenti d’inerzia del core e dello skin.

Figura 4.24 Tipica struttura sandwich

Considerando la larghezza del pannello unitaria, i momenti d’inerzia valgono rispettivamente: 3 12 s c T I =

174 2 3 12 2 sk s sk s sk T T T I = +T _ + _  

ponendo d =Ts+Tsk e sostituendo alla prima equazione, otteniamo la rigidità

flessionale della struttura a sandwich

3 3 2

12 6 2

c s s sk s sk

E T E T E T d

D= + +

Se le pelli sono relativamente sottili rispetto al core (d/Tsk>6) e considerando che Ec <Esk (Tskd2_/Ts3 _{Es/Ec>17), l’equazione può essere ridotta in:}

2

2

s sk

E T d D=EI =

Da tale relazione si deduce che la distanza delle pelli, più di ogni altra grandezza, contribuisce in modo determinante alla variazione della rigidezza della struttura e ciò risulta coerente con i risultati ottenuti nelle analisi sopra esposte.

Considerato che le prime analisi hanno dimostrato l’incapacità della struttura di soddisfare i requisiti imposti, si è deciso di modificare l’architettura del sistema.

Per le analisi successive, oltre alle modifiche all’architettura, è stata considerata solo la seconda fase della missione, in cui agiscono i carichi più gravosi. Per applicare la nuova condizione di carico, si modificano in HyperMesh solo le cards Load, inserendo i versi ed i valori delle pressioni normale e tangenziale al pannello; in Figura 4.25 vengono raffigurate tali pressioni.

175 Figura 4.25 Distribuzione delle pressioni

Le prime analisi con la nuova condizione di carico sono state effettuate senza alcuna modifica alla struttura, in modo da avere dei risultati di confronto che giustifichino o meno la presenza delle modifiche stesse; in Tabella 4.7 vengono riportati alcuni dei risultati ottenuti.

Tabella 4.7 Risultati caratteristici della porzione critica del pannello

176 Figura 4.26Visualizzazione del campo di spostamento e delle tensioni per il caso 6 Dai risultati sopra esposti si nota che, applicando la seconda condizione di carico, stress e deformazioni assumono valori ben lontani da quelli massimi ammissibili. Per diminuire tali valori, si modifica la struttura interna del pannello aumentando la rigidezza flessionale attraverso l’inserimento di

177 lo stesso materiale dello skin e vengono annegate all’interno del core. La creazione della Beam in HyperMesh avviene attraverso il comando elem types dove, fra le possibili tipologie, si sceglie la geometria CBEAM, la cui card image è rappresentata in Figura 4.27.

Figura 4.27 Card image per la creazione della trave a doppio T

La Beam, a doppio T, verrà creata inserendo le sei grandezze richieste dalla card sopra esposta che corrispondono alle dimensioni rappresentate nella Figura 4.28.

Figura 4.28 Dimensioni caratteristiche della CBEAM in HyperMesh

Create le Beam, sono state inserite nel pannello e collegate ai nodi del foro ed ai rispettivi RBE2. Si è scelto di analizzare due differenti soluzioni progettuali: la prima delle due è rappresentata in Figura 4.29 e prevede che vengano inserite tre Beam.

178 Figura 4.29 Soluzione con tre Beam

Nella soluzione di Figura 4.30 vengono utilizzate quattro Beam, aggiungendo però nei due fori centrali, fino a questo momento liberi, un vincolo che impedisce la traslazione radiale (blocca la direzione 1, paragrafo 4.4). Tale condizione di vincolo richiede che nella progettazione della parete del serbatoio vengano aggiunti due ulteriori punti di aggancio; per questa ragione tale soluzione verrà presa in considerazione solo se i risultati delle analisi seguenti si dimostreranno estremamente soddisfacenti; entrambe le soluzioni mirano all’irrigidimento della zona centrale del pannello.

179 Figura 4.30 Soluzione con quattro Beam

Partendo da valori di spessore per il core e per le skin uguali a quelli del caso 6, vengono inserite le tre beam e fatte variare le sei dimensioni caratteristiche delle stesse; si ottengono cosi le combinazioni esposte in Tabella 4.8 con i relativi risultati delle analisi effettuate.

Tabella 4.8 Dimensioni e risultati nel caso a tre beam

Nelle rappresentazioni esposte di seguito, relative al caso (7), vengono visualizzate la distribuzione degli stress ed il campo degli spostamenti del componente.

180 Figura 4.31 Visualizzazione del campo di spostamento e delle tensioni per il caso 7 Confrontando i risultati ottenuti per i casi 6 e 7 e le relative rappresentazioni (Figura 4.26 e Figura 4.31) si nota che l’inserimento delle beam ha portato ad

181 ancora a soddisfare i requisiti previsti.

Inserita la quarta beam centrale lungo la direzione longitudinale e aggiunti i vincoli ai due fori (Figura 4.30), vengono effettuate diverse analisi, i cui risultati confermano il trend relativo alla prima soluzione con tre beam.

Considerando tutte le combinazioni analizzate si nota che solo con spessori di core molto elevati (160 [mm]) si ottengono spostamenti e stress prossimi a quelli richiesti, con un peso che però supera di tre volte quello massimo previsto.

Mantenendo la configurazione a quattro beam, è stato fatto un ulteriore tentativo di ispessimento locale dello strato delle skin; per far ciò è stato modificato il modello in HyperMesh, inserendo le nuove proprietà (Doublers) agli elementi interessati (zone perimetrali contrassegnate in giallo) (Figura 4.32); inoltre si è allungata la beam centrale, diretta lungo la direzione trasversale del pannello, fino ai bordi della struttura in modo da collegarsi ai Doublers.

182 Di seguito vengono riportati alcune analisi ed i relativi risultati per la nuova soluzione progettuale (Tabella 4.9).

Tabella 4.9 Casi di analisi con ispessimenti locali (Doublers)

Le ultime modifiche strutturali riescono ad abbassare i valori di spostamento e stress, rientrando nei limiti imposti dalla specifica, a spese però dell’aumento del peso.

La soluzione con quattro beam, ma soprattutto l’aggiunta del vincolo ai fori centrali, non è riuscita ad apportare i miglioramenti che ne giustifichino il loro utilizzo.

Per mantenere la soluzione iniziale dello scudo con dodici pannelli separabili, si è cercato di irrigidire il singolo pannello aggiungendo un ulteriore vincolo centrale, il quale blocca la traslazione radiale della struttura nei punti di intersezione delle due beam (Figura 4.33). Queste modifiche, come nel caso dell’aggiunta dei due vincoli precedenti, sebbene non presenti nella proposta TAS-I, sono state analizzate come soluzione alternativa da presentare al cliente (ESA).

183 Figura 4.33 Rappresentazione della nuova condizione di vincolo

Partendo dagli spessori del caso 20, si effettuano diverse combinazioni (Tabella 4.10) in cui si riduce via via lo spessore del pannello, in modo da abbassare il peso della struttura.

184 Tabella 4.10 Casi di analisi con l’aggiunta del vincolo centrale

Applicando la nuova condizione di vincolo, come mostrato ad esempio per il caso 29 di seguito esposto, la distribuzione degli stress e la deformazione variano rispetto ai casi precedenti, spostando i punti di massimo stress e massima deformazione, rispettivamente, nella zona centrale ed ai lati del pannello.

185 Dai risultati in Tabella 4.10 e dalla visualizzazione sopra esposta, si nota che gli spostamenti assumono valori che rientrano nei limiti richiesti, tranne per la due zone laterali, le quali, come già detto in precedenza, non vengono prese in esame in questa fase di studio; anche i valori degli stress, ad eccezione della

186 parte in prossimità del vincolo, rientrano nei limiti massimi previsti da specifica.

Da ciò risulta che solo quest’ultima soluzione costruttiva, con vincolo centrale, riesce a soddisfare tutti i requisiti imposti dalla specifica; tale soluzione, però, impone la riprogettazione della parte centrale del serbatoio per consentire l’aggancio del pannello.

Per motivi legati alle modifiche consentite alle interfacce del lanciatore, la proposta alternativa di porre un vincolo centrale è stata scartata da ESA. Il lavoro di analisi e di studio svolto in questa fase ha dimostrato che la soluzione proposta da TAS-I (dodici pannelli singoli agganciati ai quattro angoli) non riesce a soddisfare i requisiti previsti. Per questo motivo è stato necessario modificare l’architettura del sistema.

La logica seguita per rivedere l’architettura del sistema è stata di tipo incrementale: partendo da un’architettura ipotetica di cilindro unico (Figura 4.34), che non permetterebbe la separazione, si è suddiviso il sistema dapprima in due e poi sei pannelli.

187 la labilità del sistema (Figura 4.35) ed applicazione della condizione di carico più gravosa (Figura 4.36), vengono ripetute per il nuovo design in esame.

Figura 4.35 Discretizzazione della struttura e applicazione dei vincoli

188 Per il caso in esame in Tabella 4.11 vengono riportati gli spessori analizzati ed i relativi risultati, mentre la visualizzazione delle analisi è stata riportata solo per il caso “c” (Figura 4.37). Come si nota dai risultati, il nuovo design riesce a soddisfare tutti requisiti imposti in specifica, tranne per ciò che riguarda la separazione della stessa.

Tabella 4.11 Spessori e risultati delle analisi per il caso cilindrico

189 soluzioni che prevedono la divisione del cilindro prima in due parti e successivamente in sei. Nel primo caso i due semicilindri verranno collegati tra loro lungo la direzione longitudinale attraverso l’introduzione di tre RBE2 i quali bloccano tutti i possibili gradi di libertà del sistema (Figura 4.38).

Figura 4.38 Rappresentazione della soluzione a due semicilindri

Le analisi vengono effettuate partendo da valori minimi di 25,4 [mm] per lo spessore del core e di 0,3 [mm] per quello delle skin; per tali spessori si riportano di seguito il campo degli spostamenti e delle tensioni interne del componente.

190 Osservando le prime analisi si nota che il nuovo design, con la soluzione a due semicilindri, riesce a soddisfare tutti i requisiti imposti dalla specifica con spessore del pannello relativamente piccolo; nonostante ciò, in un’ottica di futuri sviluppi commerciali, si prevede di modificare ulteriormente l’architettura suddividendo la struttura in 6 pannelli, al fine di ridurre i costi di produzione e garantire l’innovazione tecnologica prevista per l’Upper Stage. Saranno, quindi, gli studi tuttora in atto ed i futuri a stabilire se la soluzione progettuale da scegliere per la realizzazione del dimostratore in scala 1:1 debba essere quella sopra esposta a due pannelli o quella a sei.