CAPITOLO 3 3.1 IRRIGIDIMENTO ROTTO

CAPITOLO 3

3.1 IRRIGIDIMENTO

ROTTO

L’analisi con il metodo agli elementi finiti per le casistiche correlate all’irrigidimento rotto partono dai modelli utilizzati per l’irrigidimento integro nei quali si “svincola” la mezzeria dell’irrigidimento stesso. L’assenza di vincoli simula la rottura dell’irrigidimento nella zona corrispondente alla formazione della fessura nel pannello.

3.1.1 Corrente a doppia striscia

Lo studio del caso corrente a doppia striscia, come nel caso del corrente integro, è fondamentale perché a questo caso si vuole in definitiva ricondurre lo studio del corrente di sezione generica. E’ sui dati della geometria a doppia striscia che si formula l’espressione analitica previsionale.

Ancora una volta è studiato il caso per 3 valori di area equivalente e per 5 valori di dimensione di fessura, al variare della posizione assunta dal corrente rispetto alla mezzeria della fessura stessa

In tabella 3.1 i dati ottenuti per il caso generale di corrente a doppia striscia. L’andamento dei dati al variare della posizione del corrente rispetto alla mezzeria della fessura è del tipo mostrato in figura 3.1, ottenuto nel caso particolare A_eq = a6, =24

Figura 3.1:

0 K K_B

La curva può essere approssimata da una quadratica pesata da un esponenziale negativo che ne corregga l’andamento all’infinito. L’esponenziale, analogamente al caso integro, potrà essere strutturato in modo da valere circa 1 a ridosso della mezzeria e circa zero a distanza tendente all’infinito dalla mezzeria stessa.

Per semplicità di calcolo e coerentemente con l’assunzione che, ad una certa distanza dalla mezzeria della fessura, l’effetto del corrente è comunque noto, la funzione che viene proposta è a meno dell’esponenziale e strutturata come una quadratica di terzo grado.

Sarà allora

[

( )

]

)

(x a₁ x3 a₂ x2 a₃ x a₄

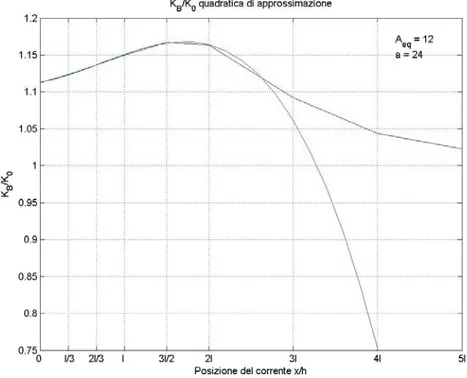
Figura 3.2: quadratica di approssimazione

Come si può notare, nel caso di figura 3.2, A_eq =12,a =24, l’approssimazione è ottima fino a x= 3⋅l, ovvero ben oltre l’apice della fessura (x=2l), più che

accettabile per i propositi di questa tesi per quanto detto sopra.

I coefficienti ai del procedimento di approssimazione sono riportati in Appendice IV, tabella 3.2.

La dipendenza dei coefficienti ai dalla dimensione di fessura è di tipo quadratico, ma è ben approssimata, salvo per il coefficiente a3, da funzioni

lineari.

Per ottenere la formula analitica si è deciso di procedere come segue: 1. Formulazione analitica per A_eq =6

2. Implementazione di una f

(

Aeq,a

)

a moltiplicare la relazione ottenuta al

primo step.

Basta allora risolvere l’interpolazione per i coefficienti ai ottenuti nel caso 6

= eq

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ + ⋅ − = − ⋅ + ⋅ − = − ⋅ = + ⋅ − = 1445 , 1 0037 , 0 0077 , 0 006 , 0 0002 , 0 0824 , 0 0068 , 0 0331 , 0 0045 , 0 4 2 3 2 1 a a a a a a a a a 6 = eq A (3.2) E’ allora:

(

)

(

)

(

)

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⋅ − ⋅ − ⋅ + ⋅ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⋅ − ⋅ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⋅ + ⋅ − ⋅ = = 45 , 114 37 , 0 77 , 0 6 , 0 02 , 0 24 , 8 68 , 0 31 , 3 45 , 0 01 , 0 2 2 3 6 0 a h x a a h x a h x a K K A B (3.3) che risolve il punto 1.

Per valutare la f

(

Aeq,a

)

che, moltiplicata alla relazione (3.3), valida per Aeq =6, risolve i casi A_eq =9 e A_eq =12 basta calcolare il rapporto tra i

0 K KB

corrispondenti ed interpolarli in un’unica espressione analitica funzione di Aeq e di a.

Procedendo in questa direzione si ottiene:

(

)

2 10

(

55

)

1 3 1 , ⎟⋅ 3⋅ − + ⎠ ⎞ ⎜ ⎝ ⎛_{− ⋅ +} = − a A a A f _{eq eq} (3.4)

3.1.2 Valutazione dell’errore

Come valutato per il caso integro, si passa al calcolo dell’errore commesso ricavando il valore del fattore di intensità degli sforzi con la formula individuata, rispetto al valore in output dal metodo FEM. In Appendice IV,

tabella 3.3 è riportato l’errore calcolato fino a x= 4⋅l, avendo poco senso

spingersi all’infinito.

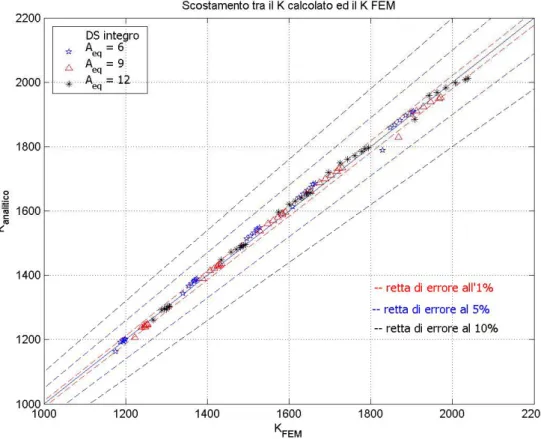
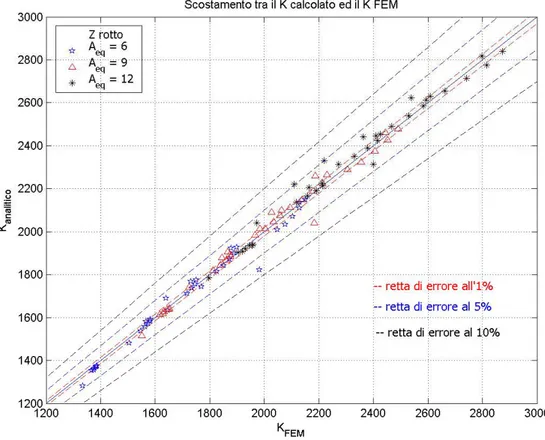
Figura 3.3: scostamento dei valori del K calcolati con la relazione (3.3) rispetto al valore

ottenuto con metodo FEM

La figura 3.3 bene evidenzia l’ottimo funzionamento della relazione (3.3).

Coerentemente con le limitazioni proposte la formula individuata per il corrente di geometria a doppia striscia rotto ben si comporta rispetto ai dati ottenuti con il metodo FEM.

3.2 IRRIGIDIMENTO DI FORMA REALE:

INAPPLICABILITA’ DEL CRITERIO DI AREA

EQUIVALENTE

Analogamente a quanto proposto per la configurazione integra si introduce il corrente di geometria reale. La forma della sezione ricalca quanto correntemente in uso nelle strutture aeronautiche, la dimensione è scelta secondo il criterio di equivalenza con il corrente a doppia striscia illustrato per la configurazione integra.

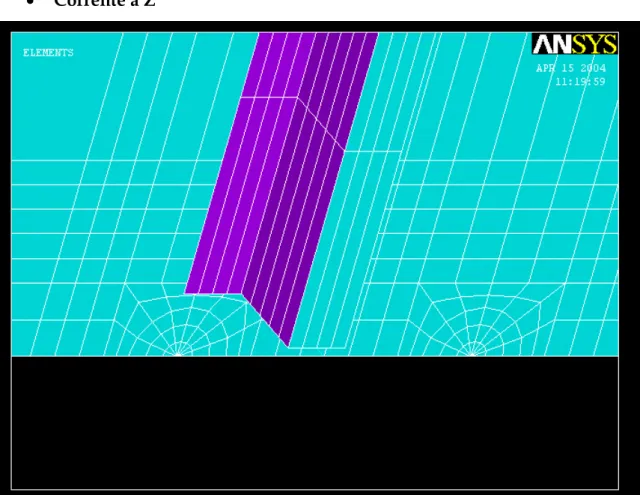
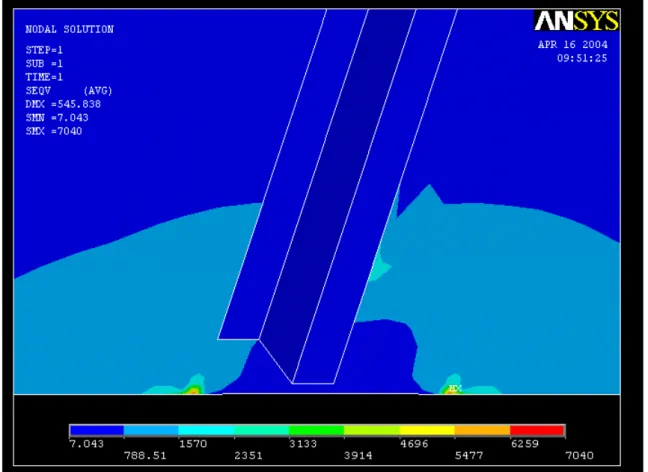
• Corrente a Z

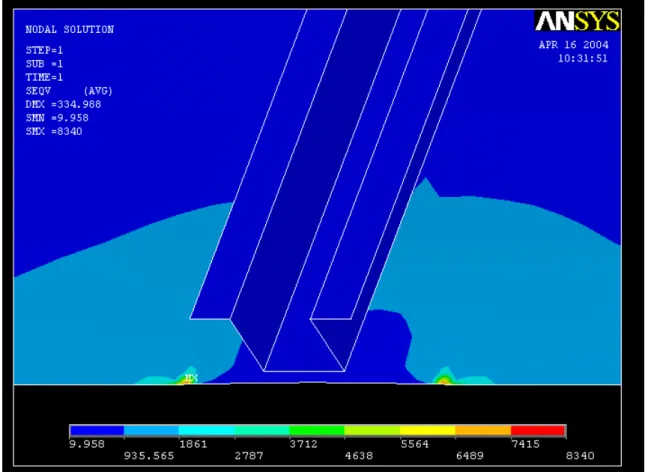
Figura 3.5: Andamento delle tensioni per corrente a Z

• Corrente ad Ω

Figura 3.7: Andamento delle tensioni per corrente a Ω

Figura 3.8: andamento di

0 K K_B

In figura 3.8 sono rappresentati i valori di KB K0calcolati nel caso Aeq =9, 18

= a

Appare evidente come l’equivalenza proposta sulla base delle considerazioni del modello integro non sia applicabile nel caso di corrente rotto.

Per meglio valutare l’inapplicabilità della equivalenza così come definita per il corrente integro è stata applicata la (3.3), ricavata con i dati della doppia striscia, alle configurazioni (Aeq, semidimensione di fessura a) in esame per il corrente a Z.

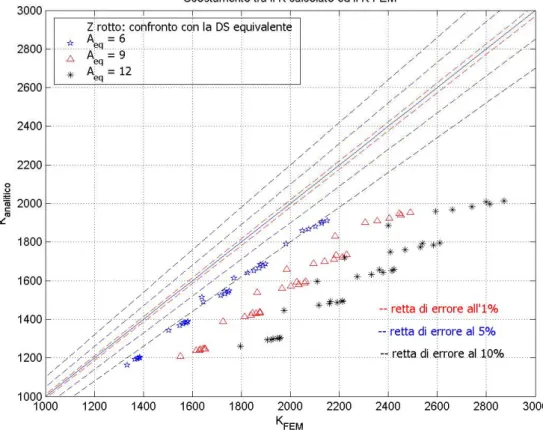
Figura 3.9: Scostamento dei valori del K calcolati con la relazione (3.3) rispetto al

valore ottenuto con metodo FEM, corrente a Z.

Lo scostamento dei dati calcolati analiticamente con la formula della Doppia Striscia equivalente rispetto a quelli ottenuti con il metodo FEM per il corrente di geometria reale (in figura 3.9 corrente a Z) dimostra come il criterio di equivalenza, così come definito in 2.1.1, non è applicabile alla configurazione rotta del corrente.

Si è deciso comunque di ricavare una formulazione analitica mutuata dal corrente a doppia striscia rotto e corretta con fattori di scala per renderla valida nei casi di geometria reale. Il procedimento è affrontato nel seguente capitolo, mentre uno studio più approfondito sulla non validità del criterio di equivalenza finora accettato è proposto in 3.4

3.3 FORMULAZIONE ANALITICA PER

IRRIGIDIMENTO ROTTO

Graficando i valori di K ottenuti con irrigidimento rotto di geometria reale in funzione dei K con irrigidimento rotto a doppia striscia (geometria di riferimento), si vuole valutare la possibilità di ridurre il caso di geometria reale alla doppia striscia stessa. I risultati sono in questo senso confortanti.

Il grafico che segue, disegnato per a=9, individua chiaramente un fattore di

scala fra i risultati con geometria reale ed i corrispettivi ottenuti con corrente a doppia striscia, dati ovviamente ottenuti con metodologia FEM.

Figura 3.10: a=9

I grafici sono ottenuti scalando l’origine di K₀ =1063,2. Rispetto a

0 K K_B

i coefficienti angolari delle rette individuate sono gli stessi, mentre l’origine è scalata di 1.

Tabella 3.7

La tabella 3.7 riassume per le due tipologie di correnti selezionate i coefficienti angolari delle rette di miglior approssimazione per i 3 valori di area considerati e per a = semidimensione di fessura = 9.

Ripetendo il medesimo procedimento per le altre dimensioni di fessura si ottengono i relativi coefficienti angolari riassunti in tabella 3.8

Figura 3.11: a=12 2,4113 3,1478 Corrente a Z 3,7125 3,0013 3,4094 Corrente a Ω 4,0624

Figura 3.12: a=15

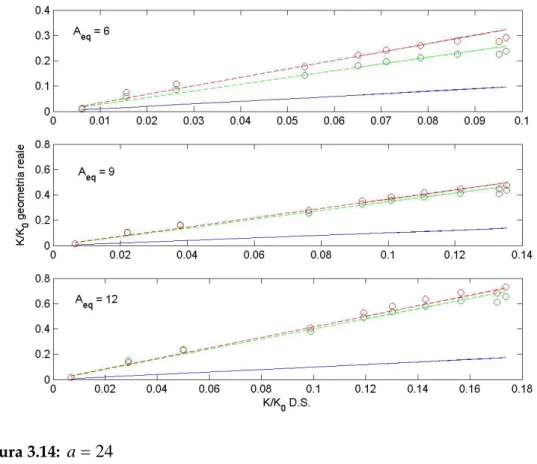
Figura 3.14: a=24 eq A a = 9 a = 12 a = 15 a = 18 a = 24 6 = eq A 2.4113 2.4801 2.5214 2.6235 2.6755 9 = eq A 3.1478 3.2233 3.3501 3.4157 3.4535 Corrente a Z 12 = eq A 3.7125 3.7849 3.8507 3.9225 3.9977 6 = eq A 3.0013 3.0922 3.0572 3.0949 3.3479 9 = eq A 3.4094 3.4770 3.4145 3.4842 3.6525 Corrente ad Ω 12 = eq A 4.0624 4.1023 4.1301 4.1608 4.1608 0 K 1063.2 1227.68 1372.59 1503.6 1736.2 Tabella 3.8

(

C

)

K K C K K DS B reale B = ⋅ + − 1 0 0 (3.5) La (3.5) esprime il concetto espresso al termine del paragrafo 3.2, ovvero il

reale, a Z o ad Ω, moltiplicando per un fattore di scala la relativa formulazione valida per la doppia striscia.

Rimane da esprimere C, funzione dei coefficienti angolari, in funzione di a e eq

A

Si esprime la dipendenza dei coefficienti angolari da a con una legge lineare valutata per Aeq =6 per poi estenderla ai casi Aeq =9 e Aeq =12 con un moltiplicatore.

Figura 3.15

La retta in figura 3.15, leggasi 2595 , 2 0181 , 0 ⋅ + = a C (3.6)

approssima i coefficienti moltiplicatori della geometria a Z rispetto alla doppia striscia per il caso di A_eq =6.

La dipendenza da Aeq si valuta ancora con approssimazione lineare, considerando che i coefficienti per Aeq =9 sono mediamente 1,3053 volte più

grandi dei corrispettivi per A_eq =6, mentre quelli per A_eq =12 sono mediamente più grandi di 1,5165 volte. Questa dipendenza è racchiusa nell’espressione lineare: M =0,0861⋅A_eq +0,4992.

E’ infine, per la geometria a Z:

(

A ,a

)

=

(

−0,0052⋅A2 +0,1802⋅A +0,1069

)

⋅

(

0,0181⋅a+2,2595

)

C_{Z eq eq eq} (3.7)

Ripetendo per la geometria ad Ω si ottiene:

(

,

)

=

(

0,0059⋅ 2 −0,0554⋅ +1,1405

)

⋅

(

0,0208⋅ +2,7937

)

Ω A a A A a

3.3.1 Valutazione dell’errore

• Corrente a Z

Figura 3.16

Come evidenziato dai dati riportati in tabella 3.9 e dalla figura 3.16 proposta, la formulazione individuata approssima il dato ottenuto con la metodologia FEM in modo soddisfacente. Chiaramente il dato è profondamente inattendibile allontanandosi dalla mezzeria della fessura (nell’origine del grafico), laddove il comportamento quadratico della funzione stessa non è stato corretto da un esponenziale di comodo come per il caso di corrente integro. La formula è quindi valida se il corrente è interno alla fessura stessa o esternamente nelle immediate vicinanze (la posizione 3l corrisponde al

corrente posizionato esternamente alla fessura ad una distanza pari ad 14della

dimensione di fessura stessa dall’apice B).

La figura 3.17 riporta lo scostamento dei valori del K ottenuti con la (3.3) corretta dalla relazione (3.5)

Figura 3.17: Scostamento dei valori del K calcolati con la relazione (3.3) corretta

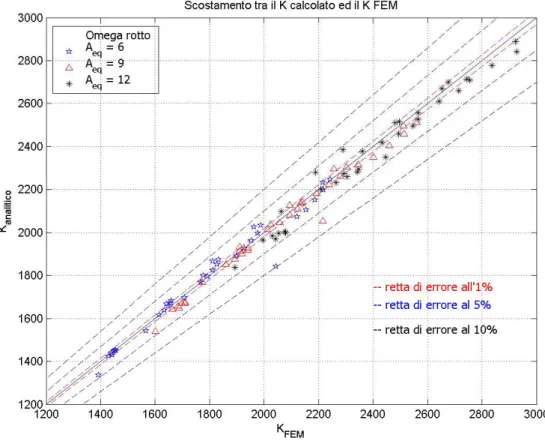
• Corrente ad Ω

Figura 3.18

L’errore commesso “correggendo” la formula individuata per la doppia striscia in funzione della geometria ad Ω è sicuramente più penalizzante rispetto a quanto trovato per il corrente a Z. Si può comunque contemplare un fattore 1,03 correttivo (3%) per mantenere un buon margine sul dato ottenuto al calcolatore in senso conservativo.

La figura 3.19 riporta lo scostamento dei valori del K ottenuti con la (3.3) corretta dalla relazione (3.5) per il corrente di forma ad Ω.

Figura 3.19: Scostamento dei valori del K calcolati con la relazione (3.3) corretta