4 Elementi della Rete Ferroviaria e metodologia di verifica

4 Elementi della Rete Ferroviaria e

metodologia di verifica

4.1 Premesse

Nel presente studio la Rete Ferroviaria è stata considerata come suddivisa negli elementi semplici archi, nodi e stazioni. Poiché i problemi di circolazione che riguardano tali elementi sono differenti, per ognuno di essi è stato utilizzato un metodo di analisi specifico:

- per gli archi l’elemento critico è la differente velocità di percorrenza, per cui è stata valutata la

Capacità di Linea;

- per i nodi l’elemento critico è il Taglio tra Flussi; in questo caso è stato utilizzato il Metodo

Sintetico di Potthoff per valutare la capacità di circolazione di un nodo;

- nel caso delle stazioni è necessario considerare la possibilità che il treno in arrivo possa trovare utenti in coda; si è quindi valutata la Capacità di Stazionamento per mezzo della Teoria delle

Code.

4.2 La capacità di circolazione di un nodo

Il problema generale da risolvere per quanto riguarda la circolazione ferroviaria è far si che una data quantità di treni possa circolare nell’ambito di un impianto durante un determinato intervallo di tempo. Per scegliere la metodologia bisogna considerare il valore che assumono tre parametri principali:

- l’arco temporale entro il quale la soluzione deve essere valida;

- i gradi di libertà a disposizione per la ricerca della o delle soluzioni cercate; - modalità che descrivono le caratteristiche aleatorie della circolazione.

Sulla base di tali considerazioni è possibile definire le due formulazioni estreme che il problema generale può assumere.

Quando la prospettiva è breve, l’impianto è definito ed i gradi di libertà topologica vengono soppressi, quanto meno in linea di principio; gli elementi aleatori a loro volta si riducono drasticamente essendo ipotizzabile la disponibilità di un orario di servizio, completo di tutti gli elementi accessori ed avvalorato da risultati di osservazioni sperimentali.

La forma risolutiva, più semplice e al tempo stesso più rozza, di questo problema è rappresentata dal diagramma di piazzamento dei treni nei binari di sosta di stazione; tale diagramma nelle ferrovie italiane assume la denominazione di M53.

In questo diagramma vengono disegnati tanti assi temporali quanti sono i binari di sosta, e su tali assi viene evidenziata, mediante ispessimenti convenzionali dell’asse, la presenza di un treno definita dai sui istanti di arrivo e partenza. Il fatto che un dato binario non sia accessibile in determinati periodi, perché gli itinerari che conducono ad esso sono sbarrati da itinerari incompatibili non viene evidenziato. La bontà di una soluzione è fortemente condizionata dal livello di esperienza e capacità, maturate per via empirica, di chi la elabora assegnando i vari treni ai binari disponibili.

Il primo rilevante passo sulla strada della razionalizzazione di questo metodo è stata compiuta da Műller. La novità è costituita dal fatto che i vari assi, corrispondenti ai binari di sosta, sono riuniti alle estremità dagli alberi ramificati che corrispondono ai fasci di deviatoi che collegano i binari di sosta alle linee di entrata e uscita dell’impianto. In questo modo è possibile vedere abbastanza agevolmente che l’assegnazione di un treno ad un dato binario comporta l’interdizione di altri binari per incompatibilità di ingresso o di uscita; pertanto tali binari anche se liberi non sono utilizzabili. L’applicazione di questo metodo trova un grosso limite pratico, ma non concettuale, nella complessità dell’impianto di stazione.

Il metodo di Műller non prende in considerazione il fatto che ogni evento della circolazione è associato a possibili ritardi. Pertanto esso si limita a verificare che sia rispettata la condizione di congruità fra tempo disponibile e durata del della circolazione, supposta perfettamente regolare. Gli effetti dei ritardi, specie in termini di aggravamento all’interno dell’impianto non vengono pertanto posti in risalto e tantomeno quantizzati ed associati a particolari zone dell’impianto. Non è da escludere che ai tempi di Műller questo tipo di problemi si ponessero in forma marginale.

Un’alternativa è rappresentata dalle simulazioni,nei quali tutto il processo operativo viene riprodotto matematicamente con continuità, compresi i caratteri aleatori..

Quando la prospettiva temporale è lunga (l’impianto è per esempio da disegnare), sono possibili tanti gradi di libertà quanti sono i gruppi di soluzioni equivalenti prodotti dall’analisi topologica; a questo aspetto positivo fa però riscontro il massimo di elementi di incertezza sulla circolazione futura. Sarà giocoforza definire quest’ultima in forma aleatoria ed il problema da risolvere consisterà nel cercare le soluzioni compatibili con essa e quindi operare una scelta progettuale. Le soluzioni valide dovranno in altri termini dare una ragionevole sicurezza che tutti gli orari di servizio che potranno emergere nel lungo periodo d’impiego dell’impianto non troveranno in questo un elemento d’ostacolo.

Il primo metodo operativo che ha permesso di risolvere il problema della valutazione delle prestazioni di un impianto, consentendo la determinazione del numero di treni ammissibili e della quantità di ritardi causata dai conflitti, è quello ideo Potthoff, risalente agli inizi degli anni ’60.

quanto congloba e fa sue le ipotetiche strutture di orario con le quali un impianto dovrà funzionare in un lungo periodo di tempo. Se la verifica dà risultati positivi significa che, per qualsiasi ipotesi di circolazione che ne rispetti i limiti, l’orarista riuscirà a trovare una soluzione conveniente se non migliore.

Nei prossimi paragrafi verrà trattata tale metodo nel dettaglio.

Quale che sia il caso da affrontare la condizione risolutiva sarà una condizione di congruità tra il tempo disponibile (tempo di riferimento) e la durata dell’insieme delle circolazioni dei treni; tali circolazioni dovranno ovviamente rispettare le note condizioni di compatibilità o di incompatibilità degli itinerari, nonché essere soggette ad eventuali regole di precedenza.

4.2.1 La condizione generale di verifica di un nodo

Il problema della capacità di circolazione di un impianto può essere formulato come segue: “ dato un impianto di struttura e caratteristiche note e date determinate regole operative, verificare se un assegnato programma di circolazione di treni, che deve svolgersi in un prestabilito arco temporale, è compatibile con l’impianto stesso”. Segue, come ovvia estensione, che se la verifica è positiva devono potersi stabilire i margini di ampliamento del programma di circolazione di treni assegnato.

Come si può notare la soluzione del problema posto deriva dall’incontro di componenti che si condizionano reciprocamente, e precisamente:

a) la struttura dell’impianto; b) le regole operative;

c) il programma di circolazione;

d) il tempo disponibile per lo svolgimento della circolazione.

E’ facilmente intuibile in cosa consistono le componenti a e d, mentre è opportuno precisare le altre due.

Le regole operative sono essenzialmente di due tipi, uno definisce il comportamento degli operatori ed ha lo scopo di assicurare il regolare funzionamento dell’impianto, riguardo ad esempio i criteri con cui risolvere i conflitti di precedenza che possono insorgere tra treni lenti e veloci o comunque di caratteristiche differenti; l’altro invece è inteso a realizzare il funzionamento dell’impianto in condizioni di sicurezza degli operatori e trova attuazione sia in norme di comportamento degli operatori sia in apposite apparecchiature di comando e controllo.

Il programma di esercizio, a sua volta, è rappresentato nella forma più chiara dall’orario di servizio, nel quale sono riconoscibili il numero di treni previsto e, per ogni treno, l’origine, la destinazione e gli istanti di arrivo e partenza dall’impianto. Inoltre, poiché lo svolgimento della circolazione non sarà perfettamente regolare, per ogni treno è necessario conoscere gli istogrammi o le funzioni di probabilità dei suoi eventuali anticipi o ritardi. Questa appena descritta sarebbe la forma ideale di un programma di esercizio, in realtà – specie in relazione a situazioni future per le quali sono

impossibili osservazioni – sarà giocoforza adottare delle formulazioni meno dettagliate, introducendo se mai ipotesi basate sull’esperienza di situazioni analoghe.

4.2.2 La verifica di un nodo semplice

Si consideri ora un’intersezione semplice (Figura 4.2-1) contrassegnata dalla lettera x, in corrispondenza della quale non si potrà avere che la circolazione di un treno per volta. Pertanto il tempo T disponibile per la circolazione andrà opportunamente suddiviso fra le circolazioni delle linee

1 e 2.

Figura 4.2-1 Intersezione semplice

Inoltre, se un treno deve attendere per dare il passo ad un'altra linea, esso toglierà alla quota di

T disponibile per la sua linea un tempo pari all’attesa. In generale quindi il tempo T disponibile sarà

suddiviso in tre parti:

- tempi necessari ai treni per attraversare l’intersezione; da qui in avanti questi tempo saranno denominati tempi di occupazione e la loro sommatoria sarà indicata con la lettera B;

- tempi di attesa, o ritardo, e la loro sommatoria sarà indicata con la lettera R;

- tempi eventualmente disponibili per ulteriori circolazioni non previste nel programma di esercizio. Pertanto la condizione che permette di stabilire la compatibilità fra impianto e programma di esercizio potrà essere espressa analiticamente nella forma:

T ≥ B + R

dove la condizione di uguaglianza esprime la saturazione dell’impianto, ovvero la mancanza di margini di tempo disponibili per altre circolazioni.

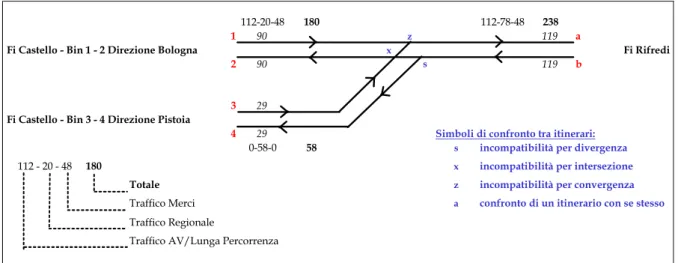
Prendendo un esempio (Figura 4.2-2 Esempio di nodoFigura 4.2-2) leggermente più complesso rispetto all’intersezione semplice precedente, vediamo che i movimenti possibili non sono solo l’occupazione del nodo da parte di un treno alla volta. Anche in questo caso, come per tutti gli altri casi di maggior complessità, vale la condizione di verifica precedente, solo che l’applicazione dei termini B e R dovrà tenere conte della varietà delle situazioni prevedibili.

Prendiamo nuovamente in considerazione il caso dell’intersezione semplice di Figura 4.2-1, la sicurezza sarà realizzata se ogni volta che un treno circola su una linea l’altra viene interdetta. Basti per ora pensare che a ciò provvedono i segnali. Durante l’intervallo di tempo T deve svolgersi la circolazione di n1 treni sulla linea 1 e n2 treni sulla linea 2.

112-20-48 180 112-78-48 238

1 90 z 119 a

Fi Castello - Bin 1 - 2 Direzione Bologna x Fi Rifredi

2 90 s 119 b

3 29

Fi Castello - Bin 3 - 4 Direzione Pistoia

4 29 Simboli di confronto tra itinerari:

0-58-0 58 s incompatibilità per divergenza

112 - 20 - 48 180 x incompatibilità per intersezione

Totale z incompatibilità per convergenza

Traffico Merci a confronto di un itinerario con se stesso

Traffico Regionale

Traffico AV/Lunga Percorrenza

Figura 4.2-2 Esempio di nodo complesso

Quando un treno attraversa il nodo, esso interdice la circolazione sull’altra linea a partire dall’istante in cui il segnale viene messo in via libera e fino all’istante in cui la sua coda non avrà sorpassato un dato punto L, disimpegnando completamente il nodo e rendendolo disponibile per una successiva circolazione. Tale tempo viene definito tempo di occupazione e viene indicato con i simboli

t1 e t2 rispettivamente per le circolazioni sulla linea 1 e sulla linea 2.

Si faccia inoltre l’ipotesi che tali tempi siano costanti per la linea, ovverosia che su ogni linea circolino treni di una solo categoria, nonché si supponga di regolare le precedenze fra treni sulla base della regola First In – First Out.

Quando si produce una situazione di interdizione, il treno che trova il suo segnale a via impedita dovrà attendere per un tempo variabile da zero al tempo di occupazione del treno che attraversa il nodo, e ciò evidentemente a seconda dell’istante d’arrivo del secondo treno. Si potrà quindi supporre, trascurando gli effetti del moto vario in frenatura ed avviamento, che un treno interdetto subirà un ritardo medio pari a t1/2 o t2/2.

Occorre ora stabilire quante di queste situazioni si produrranno durante l’intervallo di riferimento T. Questa valutazione dipende dall’orario di servizio e dalle leggi di tipo probabilistico che sintetizzano matematicamente il processo degli arrivi sul nodo.

Una prima ipotesi caratteristica di situazioni di incertezza in fase progettuale consiste nell’assumere costante lungo tutto l’arco di tempo T la densità di probabilità di arrivo di un treno e quindi che non esista un orario di servizio definito. Tale densità avrà espressione:

Pertanto un generico treno circolante sulla linea 1 avrà probabilità di trovare il segnale di via impedita pari a :

p1= n1 · 1/T · t1

ove il prodotto 1/T · t1 esprime la probabilità di occupazione del nodo da parte di un treno della linea 2

ed n2 il numero di volte che questa si produce durante l’arco di tempo T.

Il treno interdetto subirà un ritardo medio pari a

R’1 = p1 · t2/2 = n2 · t22 / (2T)

ritardo che va anche visto come tempo sottratto alla disponibilità di circolazione della linea 1. Poiché infine sulla linea 1 circolano n1 treni, questi subiranno nel loro complesso un ritardo:

R1 = n1 · n2 · t22 / (2T)

e simmetricamente, quelli della linea 2 subiranno un ritardo complessivo:

R2 = n1 · n2 · t12 / (2T)

Per mettere insieme le grandezze fin qui considerate bisogna osservare che il punto x comune alle due linee è anche il punto nel quale le circolazioni sulle due linee utilizzano in comune l’arco di tempo T che va quindi visto come diviso in due parti – variamente frazionate – a disposizione dell’una o dell’altra linea.

Ricordando ancora che i ritardi sono tempi sottratti alle disponibilità delle rispettive linee, la condizione di possibilità di funzionamento di un nodo sarà espressa dalla:

T ≥ n1 · t1 + n2 · t2 + n1 · n2 ( t12 + t22 )/(2T)

A questo punto è opportuno fare alcuni commenti sull’ipotesi formulata per la densità di probabilità di arrivo durante il tempo T. Certamente l’ipotesi in questione appare irrealistica quando l’arco di tempo T sia molto lungo, ad esempio 24 ore; essa tuttavia tende ad assumere maggior concretezza man mano che T si riduce. I risultati ai quali in tal modo si perviene hanno in ogni caso un valore indicativo da non sottovalutare anche per intervalli abbastanza lunghi nel tempo, perché la verifica di capacità di circolazione permette di stabilire a priori che ogni programma reale di circolazione che la soddisfi sarà realizzabile ed i ritardi che esso genera saranno inferiori a quelli calcolati. Indicazioni di questo genere sono estremamente importanti in sede di progetto. Indicazioni di questo genere sono estremamente importanti in sede di progetto di un impianto destinato a durare decenni.

Si può ora esaminare brevemente cosa accade quando i treni di una corrente di traffico abbiano un margine di precedenza definibile attraverso un margine r di occupazione preventiva da parte del treno privilegiato; sino quelli della linea 1 a godere di questo diritto, essi allora occuperanno il nodo per un tempo t1 + r, imponendo così un ritardo ai treni della linea 2 pari a:

R2 = n1 · n2 · (t1 + r)2 / (2T)

simmetricamente si avrà per i treni della linea 1 un ritardo:

R1 = n1 · n2 · (t2 - r)2 / (2T)

per cui la precedente relazione indicante la possibilità di funzionamento di un nodo diviene:

(

)

[

]

2

2

T

t

t

r

t

t

n

n

t

n

t

n

T

≥

+

+

+

+

−

Al limite la precedenza assoluta dei treni della linea 1 deriva dalla condizione

R1 = 0 => r = t2

per cui abbiamo

(

)

2

T

t

t

n

n

t

n

t

n

T

≥

+

+

+

la quale comporta ritardi maggiori di quelli calcolabili del caso senza precedenze.

4.3 La capacità di circolazione di un nodo complesso

4.3.1 Nodo semplice e nodo complesso

Nel paragrafo precedente è stato trattato il problema della capacità di circolazione di un nodo semplice, illustrandone la risolubilità in relazione alla variabilità delle ipotesi di circolazione. Tuttavia il modello dell’impianto preso in esame rivela subito i suoi limiti, che appaiono veramente angusti; essi riguardano da un lato la sua estrema semplicità e dall’altro il fatto che i metodi analitici sviluppati non sembrano trasferibili ai tipi di impianto utilizzati dalle ferrovie.

Infatti nel nodo semplice la circolazione di un treno avviene secondo due sole modalità, e cioè in presenza o in assenza di un treno interferito, e l’attraversamento del nodo è l’unico movimento ipotizzabile, beninteso sull’una o sull’altra linea.

In un generico impianto di stazione è invece prevedibile una molteplicità di movimenti e le situazioni di compatibilità e di incompatibilità possono riguardare più di due treni contemporaneamente. Inoltre la presenza dei deviatoi fa sì che la configurazione dell’impianto sia variabile, mentre nel nodo semplice si aveva una configurazione invariante.

Per la verifica della capacità di circolazione di un impianto comunque complesso occorrerà pertanto trovare un metodo di analisi che permetta di analizzare in modo ordinato e completo tutte le possibilità di circolazione; sulla base delle conoscenze così acquisite si dovrà quindi verificare se è possibile, con opportuni accorgimenti, utilizzare i metodi sviluppati in relazione al nodo semplice.

Prima di proseguire è opportuno chiarire la differenza tra i due termini di impianto e di nodo

complesso, i quali non sono sinonimi.

Col termine impianto si intende il complesso di binari e di dispositivi (deviatoi, intersezioni e comunicazioni) che li collegano in modo che l’impianto stesso possa svolgere le funzioni che gli sono assegnate, operando sotto un’unica giurisdizione.

Il nodo complesso è invece costituito dalla parte o dalle parti di un impianto, le cui prestazioni sono determinanti per la capacità di circolazione realizzabile dall’impianto stesso. Al limite nodo complesso e impianto possono coincidere. Nel seguito verranno esposte le considerazioni che consentono di riconoscere la struttura dei nodi complessi nell’ambito di un dato impianto. E’ evidente fin d’ora che il potersi riferire ad una parte invece che al complesso di un impianto consentirà di ridurre sensibilmente i calcoli necessari per gli scopi proposti.

Possono inoltre darsi particolari di nodo complesso, uno di questi ad esempio è tipico dei grandi nodi ferroviari attorno alle metropoli, dove in una situazione di rete molto complessa i vari impianto sono molto ravvicinati fra loro: in questi casi si possono riconoscere nodi complessi che ricadono sotto la giurisdizione di una o più stazioni adiacenti.

4.3.2 Gli itinerari e le matrici degli itinerari

I movimenti che i treni eseguono nelle stazioni sono di tre tipi ossia di entrata, di uscita e all’interno dell’impianto. I tratti di binario percorsi nei primi due tipi di movimento vengono definiti

itinerari, quelli percorsi nel terso tipo sono detti istradamenti. La distinzione deriva dal fatto che

mentre i primi due riguardano la circolazione vera e propria, gli istradamenti invece riguardano le manovre. La trattazione che segue non prende in considerazione gli istradamenti in quanto ritenuti non rilevanti al fine delle verifiche da compiere, con l’avvertenza tuttavia che qualora dovessero assumere rilievo per motivi di frequenza o di durata essi possano essere aggiunti e classificati fra gli itinerari.

Ciò posto e ribadito che per itinerario si intende un percorso definito di entrata e/o di uscita da un impianto, è evidente che disponendo opportunamente i deviatoi si potrà realizzare un certo numero di itinerari che consentiranno lo svolgimento delle funzioni di circolazione richieste all’impianto. Gli itinerari vanno quindi in primo luogo riconosciuti ed elencati e quindi posti in confronto tra loro col

duplice scopo di stabilire la loro compatibilità reciproca e di riconoscere quali sono le configurazioni operative che l’impianto può assumere.

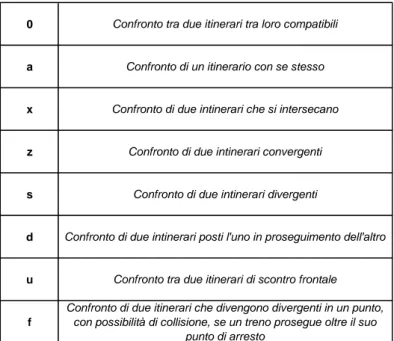
Per il riconoscimento degli itinerari per le entrate si considerano come punti origine i segnali di protezione alle entrate dell’impianto e punti destinazione i segnali di arresto, viceversa per le uscite. Ottenuto così l’elenco degli itinerari si tratta ora di confrontarli fra loro e la struttura logica che consente con completezza ed ordine questa operazione è costituita dalla Matrice degli Itinerari. In questa matrice si fa corrispondere ad ogni riga e ad ogni colonna un itinerario dell’elenco; in tal modo i vari elementi della matrice identificheranno una determinata coppia di itinerari e gli elementi in questione saranno costituiti da simboli convenzionali che specificano la compatibilità o l’incompatibilità della coppia (Figura 4.3-1).

0 Confronto tra due itinerari tra loro compatibili

a Confronto di un itinerario con se stesso

x Confronto di due intinerari che si intersecano

z Confronto di due intinerari convergenti

s Confronto di due intinerari divergenti

d Confronto di due intinerari posti l'uno in proseguimento dell'altro

u Confronto tra due itinerari di scontro frontale

f

Confronto di due itinerari che divengono divergenti in un punto, con possibilità di collisione, se un treno prosegue oltre il suo

punto di arresto

Figura 4.3-1 Situazioni di compatibilità e di incompatibilità tra itinerari

La situazione 0 si verifica quando gli itinerari non hanno punti in comune ed è impossibile che i treni che li percorrono possano entrare in collisione. Il caso a presenta scarso interesse pratico trattandosi di un itinerario con se stesso.

I casi x, z, s, e u rendono incompatibili le coppie di itinerari a confronto, mentre la d ha valutazione diversa a seconda che si considerino uno o due treni. Difatti, nel caso di un solo treno, si tratterebbe di un libero transito, mentre se il confronto riguarda due treni i due itinerari sono evidentemente incompatibili.

I confronti di tipo f, infine, hanno valutazione diversa per le varie amministrazioni. Mentre alcune considerano compatibili coppie di itinerari di questo tipo nel rispetto di determinate norme, alte li considerano incompatibili.

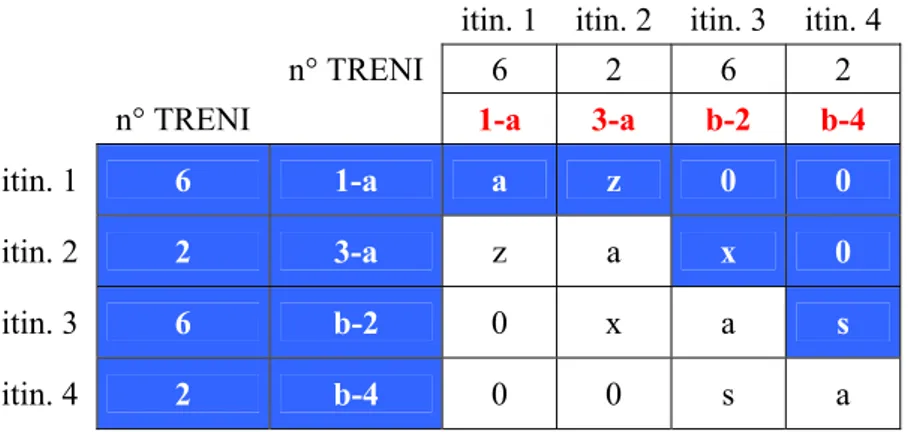
Nel prossimo capitolo vedremo numerose matrice degli itinerari e potremo riconoscerne le caratteristiche principali (in Figura 4.3-2 se ne riporta un esempio). Innanzitutto la matrice, per definizione, è quadrata. Inoltre, avendo adottato la convenzione di elencare gli itinerari nello stesso

ordine sulle righe e sulle colonne, tutti gli elementi situati sulla diagonale principale rappresentano i confronti tra itinerari con se stessi, cioè di tipo a.

itin. 1 itin. 2 itin. 3 itin. 4

n° TRENI 6 2 6 2

n° TRENI 1-a 3-a b-2 b-4

itin. 1 6 1-a a z 0 0

itin. 2 2 3-a z a x 0

itin. 3 6 b-2 0 x a s

itin. 4 2 b-4 0 0 s a

Figura 4.3-2 Esempio di Matrice degli Itinerari

La diagonale principale divide, a sua volta, la matrice in due parti, e tutte le coppie di elementi o caselle simmetriche rispetto alla diagonale principale definiscono, a due a due, la medesima coppia di itinerari. E’ pertanto inutile compilare la metà inferiori della matrice. Da quanto precede risulta infine che gli elementi significativi di una matrice NxN sono n(n-1)/2, cioè tanti quante sono le combinazioni senza ripetizione di n elementi, due a due.

4.3.3 Il grafo degli itinerari e l’albero delle soluzioni di circolazione

Nella matrice degli itinerari vengono confrontati tra di loro a coppie ciò che consente di riconoscere eventuali combinazioni di più di due itinerari possibili contemporaneamente. Questo inconveniente è superabile mediante una particolare rappresentazione costituita dal grafo degli

itinerari (in Figura 4.3-3 si riporta il grafo relativo alla matrice degli itinerari di Figura 4.3-2). Per

disegnare tale grafo i singoli itinerari vengono evidenziati con una linea a tratto continuo che unisce i punti rappresentativi.

1

3

2 4

La figura così ottenuta è una trasformata dello schema d’impianto, ricavata facendo corrispondere agli itinerari dei punti ed alla compatibilità fra itinerari dei segmenti che collegano i loro punti rappresentativi. Ebbene questo risultato, lungi da essere un virtuosismo inutile, viene ottenuto mediante l’integrazione di un impianto con determinate regole d’esercizio – quelle di incompatibilità e di compatibilità – e la sua rappresentazione grafica esprime con completezza tutte le ipotesi di esercizio che possono trovare attuazione dell’impianto stesso. Infatti se tre vertici sono collegati da lati in modo da costituire un triangolo, gli itinerari corrispondenti ai tre vertici costituiscono una terna di itinerari compatibili, e quindi attuabili contemporaneamente; i poligoni di ordine superiori a tre costituiscono ennuple di itinerari compatibili se e solo se i poligono in questione sono completi di diagonali.

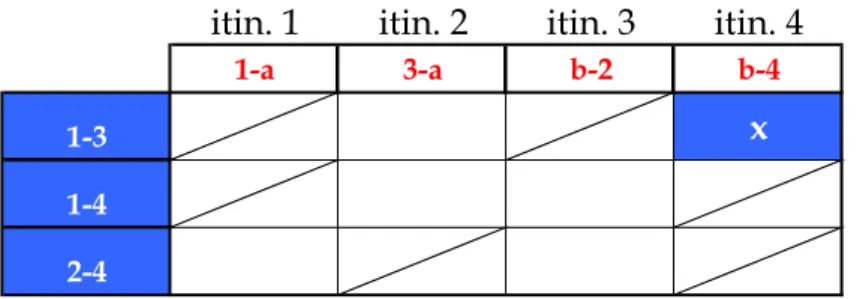
La ricerca delle ennuple nel grafo, basata sulla sua osservazione, è tuttavia difficile e diviene praticamente impossibile non appena il grafo debba rappresentare un elevato numero di itinerari. Questa ricerca può però essere compiuta metodicamente costruendo matrici ausiliarie che progressivamente consentono di ricavare le ennuple compatibili di ordine maggiore a 2 (Figura 4.3-4). Il procedimento è del tutto analogo a quello utilizzato per descrivere la matrice degli itinerari, solo che in corrispondenza delle righe verranno riportate le coppie di itinerari compatibili lette sulla prima matrice e sulle colonne tutti gli itinerari possibili. Si confronteranno in questo modo gli itinerari a tre a tre, individuando le terne degli itinerari compatibili. A questo punto si possono cercare gli itinerari compatibili a quattro a quattro, confrontando le terne appena individuate con tutti gli itinerari, per mezzo di una nuova matrice ausiliaria. Il procedimento si ripete quindi in modo del tutto analogo per le ennuple di ordine superiore e si arresta quando si compila una matrice priva di compatibilità

Nell’esempio riportato vediamo che tre coppie di itinerari compatibili individuate non sono a loro volta compatibili con nessuno de1 quattro itinerari; ci aspettavamo tale risultato visto che il grafo relativo non mostra nessun triangolo ne quadrato con diagonali.

itin. 1 itin. 2 itin. 3 itin. 4

1-a 3-a b-2 b-4

1-3 x

1-4 2-4

Figura 4.3-4 Esempio di matrice ausiliaria

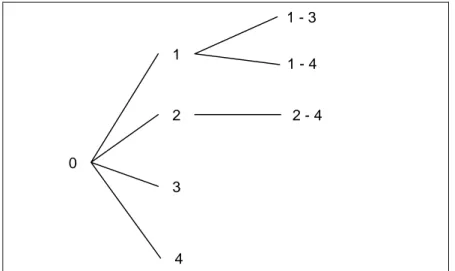
I risultati delle ennuple compatibili possono essere rappresentati in una forma grafica più ordinata dei grafi appena esaminati. Questa è la forma ad albero. La costruzione dell’albero avviene pertanto da un vertice, al quale viene attribuito l’indice zero; questo vertice viene poi collegato mediante rami con tanti punti quanti sono gli itinerari possibili nell’impianto; ad ogni punto d’itinerario dipartono poi tanti rami quante sono le coppie che esso può costituire; da queste partono poi le possibili terne, e così via. l’albero così ottenuto è asimmetrico in conseguenza del metodo

seguito, poiché se dal vertice 1, per esempio, si dirama la coppia 1-4, sarà del tutto inutile riportare la coppia 4-1 al vertice 4 perché sarebbe una ripetizione inutile

1-3, 1-4, 2-4 tre coppie di itinerari che saturano il nodo

4 3 2 1 0 1 - 3 1 - 4 2 - 4

Figura 4.3-5 Esempio di forma ad albero

L’albero così costituito ha un preciso significato fisico, in quanto ai sui vertici corrispondono altrettanti stati dell’impianto. Gli stati definiti dall’albero rappresentano tutte e sole le soluzioni disponibili per i problemi di circolazione che possono porsi all’impianto, dal che deriva la denominazione di albero delle soluzioni di circolazione.

4.3.4 La verifica del nodo complesso

Si è già evidenziato che il nodo complesso si differenzia da quello semplice per la maggior varietà di situazioni operative che in esso possono concretizzarsi.

Attraverso l’analisi delle matrici, dei grafi e degli alberi degli itinerari la varietà di situazioni viene definita ed ordinata in tutte le sue forme e combinazioni.

Pertanto la disponibilità di un assieme ordinato di casi operativi, e cioè itinerari semplici e combinazioni di itinerari compatibili, permette di sintetizzare attraverso operazioni aritmetiche di media ponderale, le varie grandezze numeriche e fisiche associate alla circolazione del nodo. In altri termini è possibile valutare il numero medio di circolazioni possibili in un nodo, il tempo medio d’occupazione del nodo ed infine la quantità di ritardi generati dal processo di circolazione.

E’ possibile quindi definire una condizione di verifica del nodo complesso, del tutto analoga a quella definita per il nodo semplice. Siano:

- n : numero medio di circolazioni;

- t : tempo medio di occupazione del nodo da parte di un gruppo di n treni ciascuno;

-

∑

- N : numero complessivo di treni che circola nel nodo durante il tempo T.

Sia inoltre costante la probabilità di presentazione sul nodo di ogni treno nell’arco di tempo T. Sulla base delle definizioni appena introdotte si può ricondurre il processo di circolazione sul nodo ad una successione di N/n eventi, per ognuno dei quali n treni circolano contemporaneamente occupando il nodo per un tempo paria a t.

Questa schematizzazione permette di sostituire al nodo complesso un nodo semplice fittizio, come quello esaminato all’inizio del capitolo, costituito da due ipotetiche linee intersecantisi, le quali però possono essere ognuno percorsa da n treni contemporaneamente.

Il processo di circolazione così schematizzato permette allora di definire il tempo di occupazione complessivo B nella forma:

t n N B=

Per quanto riguarda i ritardi, questi vanno esaminati e valutati in forma globale, come risultati dell’assieme delle singole situazioni di reale incompatibilità, ma vanno anche visti in relazione all’effetto che essi producono sul nodo fittizio prima definito ed in particolare sulla capacità di circolazione delle due ipotetiche linee che lo costituiscono. Ciò consentirà di adattare al nodo complesso la condizione di verifica vista in precedenza:

T ≥ B + R

La quantità complessiva di ritardi risulterà come sommatoria dei ritardi prodotti per ogni situazione reale di incompatibilità, ed il suo valore consentirà altresì una valutazione della qualità di circolazione del nodo.

Per valutare invece gli effetti dei ritardi sulla capacità di circolazione del nodo fittizio, bisogna innanzitutto tenere presente che i ritardi in questione afferiscono in ogni caso a gruppi di n treni ognuno; pertanto se ad esempio un gruppo di 2 treni subisce un ritardo di 4 minuti per una situazione di incompatibilità, la quantità complessiva di ritardo generato sarà evidentemente 8 minuti, mentre la quantità di tempo che per effetto del ritardo viene sottratta alla disponibilità di circolazione sulla linea fittizia, percorribile e percorsa da 2 treni, resta pari a 4 minuti.

Consegue da ciò che se si procede al calcolo delle quantità di ritardo globalmente generate dal nodo, già indicate con

∑

∑

e quindi la condizione di verifica del nodo complessivo può essere sintetizzata nell’espressione:

n R t n N T ≥ +

∑

Si tratta ora di esplicitare i vari termini che compaiono in essa. La valutazione di n pone dei problemi di complessità combinatoria, per i quali la letteratura tecnica non suggerisce – almeno finora – una formulazione analitica risolutiva che sia contemporaneamente semplice e rapida ad applicarsi.

La complessità deriva dal fatto che si tratta di analizzare non solo l’intero aspetto delle combinazioni degli itinerari compatibili, ma occorre anche tener conto della frequenza di utilizzazione degli itinerari stessi durante il tempo di riferimento T.

La valutazione di n si può conseguire attraverso una doppia ponderazione delle combinazioni che non saturano il nodo durante il tempo di occupazione. Lo stato di saturazione è quello che si verifica quando il nodo è impegnato da una ennupla di itinerari compatibili che escludono tutti gli altri. Ad esempio, sia costituita da una terna di itinerari una delle ennuple che godono di tale proprietà; è evidente che alla terna corrisponderanno tre coppie di itinerari compatibili, ottenibili sopprimendo ciclicamente uno degli itinerari della terna stessa. Ebbene le tre coppie non devono essere prese in considerazione per la valutazione di n perché non saturano il nodo.

La ricerca delle combinazioni valide può essere sviluppata esplorando l’albero delle soluzioni di circolazione, cominciando dalle ennuple di ordine superiore.

La ricerca delle combinazioni di itinerari che saturano il nodo è abbastanza meccanica, perché una ennupla terminale di ramificazione determina, come è facile constatare:

a) la soppressione di tutte le ennuple dei nodi che si incontrano risalendo da esse verso il nodo 0, che è la radice dell’albero;

b) la soppressione delle ennuple parziali che la costituiscono, che non siano già state soppresse con l’operazione del punto precedente. Per ognuna di queste ennuple va ripetuta l’operazione del punto a.

Alcuni studiosi russi che si sono occupati di questo problema suggeriscono una valutazione empirica che scaturisce da una osservazione relativa alla matrice degli itinerari.

Si conservi ancora l’ipotesi secondo la quale durante il tempo T ogni itinerario venga utilizzato da un solo treno, ovvero sia:

Se tutte le caselle della matrice fossero occupate da segni di incompatibilità si potrebbe avere, evidentemente, solo una circolazione per volta, e cioè:

n = 1

Se tutte le coppie di itinerari diversi fra loro fossero invece compatibili si potrebbero avere tante circolazioni contemporanee quanti sono gli itinerari del nodo; se questi sono n' si avrebbe quindi

n = n'

quelli esaminati sono i casi limite entro i quali può variare n, per cui si può scrivere:

n = 1 ÷ n'

Ora, anziché procedere all’analisi delle combinazioni d’itinerari che saturano il nodo si può utilizzare un’espressione empirica, la quale gode della proprietà di avere lo stesso campo di applicabilità definito dalla relazione precedente.

L’espressione in questione permette di determinare il numero di n come rapporto fra il numero di caselle costituenti una matrice ed il numero di caselle che presentano segni di incompatibilità. E’ facile verificare come il campo di variabilità di n, così determinabile, coincida con quello dell’espressione precedente.

Si tratta ora di generalizzare questa espressione per il caso in cui durante il tempo T i vari itinerari siano utilizzati da un numero diverso di treni. Cioè, indicando con i e j due generici itinerari può essere al limite, sempre:

ni ≠ nj => ni ≥ 1 e nj ≥ 1

Si può allora pensare di ampliare la matrice degli itinerari riportando ogni riga ed ogni colonna tante volte quanti sono i treni che devono percorrere un itinerario. Ad esempio se un itinerario viene percorso da 3 treni la riga corrispondente andrà ripetuta tre volte. Dovendo allora compilare una casella della matrice relativa ad una coppia di itinerari utilizzati uno da 3 e l’altro da 4 treni, nella casella si troverà ripetuto 12 volte il segno che definisce la relazione di compatibilità (od incompatibilità) fra essi. Ogni casella della matrice originale in altri termini avrà un peso pari a ni x nj.

Se allora il numero complessivo di treni è N =

∑

∑

j i

n

n

N

n

∑

=

dove la sommatoria è estesa alle sole caselle che presentano segni di incompatibilità.

Poiché anche il campo di variabilità della precedente relazione è n = 1 ÷ n', risulta sempre inferiore a quello determinabile con un calcolo esatto. Infatti il calcolo effettuato mediante l’ultima relazione non tiene di conto della struttura della matrice e del peso che in essa possono avere le ennuple di ordine superiore, mentre nel calcolo esatto queste sono preponderanti.

Ora, il sano empirismo della relazione in questione sta nel fatto che essa fornisce valori che l’esperienza indica come più realistici di quelli derivanti dal calcolo esatto, in quanto la possibilità di organizzare la circolazione in lotti di treni che saturino sempre il nodo è tutt’altro che facile da ottenersi e conduce a risultati finali di potenzialità eccessivi. Va infatti ricordato che questo metodo, che ha la caratteristica della compattezza, deve fornire risultati che assicurino la possibilità di essere tradotti in termini reali mediante orari di servizio. La condizione di saturazione definita in precedenza rappresenta invece un limite fisico superiore di capacità di circolazione, al più raggiungibile episodicamente e per tempi molto brevi.

Per la valutazione del tempo medio di occupazione t da introdurre nel calcolo di B, è necessario introdurre e precisare la differenza tra tempi di occupazione e tempi di interdizione. Il primo fra questi si compone delle fasi di decisione, formazione, percorrenza da parte del treno e

liberazione.

In conseguenza dell’ultimazione di un itinerario, gli itinerari con esso compatibili non possono essere costituiti ed il tempo durante il quale sono soggetti a questa condizione è, appunto, il tempo di interdizione.

I tempi di interdizione sono generalmente diversi dai tempi di occupazione. Tali tempi possono infatti essere inferiori nelle stazioni ove operi un apparato centrale a comandi di itinerario dotato di un sistema di liberazione progressiva dei tratti d’itinerario disimpegnati da un treno che lo percorre.

Tali tempi possono altresì essere maggiori e non di poco; ciò avviene quando l’incompatibilità deriva dalla confluenza di due itinerari che immettono su una linea a semplice binario. L’itinerario che subisce gli effetti della incompatibilità resta condizionato fintanto che il treno partito non ha liberato l’intera tratta fino alla stazione limitrofa.

Calcolati sulla base dei dati d’impianto e di quelli del materiale rotabile i tempi di occupazione e di interdizione si può costruire una matrice detta dei tempi di occupazione, derivandola dalla matrice degli itinerari.

Ogni riga e colonna corrisponde quindi ad un itinerario e quindi gli elementi della matrice presenteranno gli effetti in termini di tempi di occupazione o di interdizione che l’itinerario che definisce la riga esercita su quello che definisce la colonna di ogni elemento.

Pertanto nella nuova matrice le caselle della diagonale principale conterranno i tempi tii di

occupazione dei vari itinerari; le caselle che presentano segni di incompatibilità riporteranno i tempi di interdizione tij dell’itinerario verso quello j. In generale sarà inoltre

tii ≠ tij

ciò vuol dire che la matrice dei tempi di occupazione non è simmetrica rispetto alla diagonale principale. Ricordando quanto esposto in precedenza, ogni elemento della matrice in esame riguarda un numero ipotetico di possibili eventi pari a ni x nj cioè avrà un peso proporzionale a questo numero.

dal che immediato procedere alla valutazione del tempo come media ponderale dei tempi tij:

j i ij j i n n t n n t

∑

∑

ove le sommatorie sono estese a tutte le caselle con segno di incompatibilità, ivi comprese quelle delle diagonali principali per le quali i=j.

Le situazioni di incompatibilità, considerati come ognuna a se stanti, possono essere viste come altrettante analoghe situazioni di nodo semplice per ognuna delle quali si produce in ritardo atteso pari a:

T

t

n

n

R

2

=

Utilizzando le matrici

n

n

t

t

che la caratteristica di incompatibilità di un nodo complesso presenta due tipi di incompatibilità che non possono generare ritardo (quelle di tipo a e s) in quanto caratterizzate dalla presenza di un solo treno. Per esse è quindi:

0

=

ij

R

R

=

0

Possiamo quindi scrivere:

2

N

n

n

R

N

t

n

n

T

≥

∑

+

∑

∑

che consente di verificare se un nodo complesso ha la capacità o meno di sopportare la circolazione di N =

∑