Capitolo 1 Rappresentazione delle traiettorie

(1)

Capitolo 1

Rappresentazione delle traiettorie

In questo capitolo è affrontato il problema della ricerca di una opportuna rappresentazione matematica delle traiettorie che rispetti i vincoli geometrici e fisici imposti dal problema. Nel caso in esame le traiettorie da seguire, come

verrà dimostrato in seguito, saranno di classe C3

. Lo strumento utilizzato a tale scopo, che sarà descritto in dettaglio nei prossimi paragrafi, è quello delle spline del quarto ordine. Si tratta di curve polinomiali di quarto grado del tipo p(s) = (x(s), y(s)) della forma

x(s) = x0+ x1s + x2s 2 + x3s 3 + x4s 4 y(s) = y0+ y1s + y2s 2 + y3s 3 + y4s 4 con s ∈ R.

1.1 Cenni di teoria delle curve

Nel seguito della trattazione la norma euclidea di un vettore p è denotata da k p k ed un punto generico del piano (x y) è rappresentato dal vettore reale

p = [x y]T _{∈ R}2

(2)

1.1 Cenni di teoria delle curve

1.1.1 Curve regolari

Si consideri una particella puntiforme che si muove nello spazio

tridimen-sionale nell’intervallo di tempo [t0 t1]. Fissato un sistema di riferimento, per

ogni t ∈ [t0 t1] si indichi con {x(t) y(t) z(t)} le coordinate della particella

all’istante t. La funzione ϕ : [t0 t1] → R

3

, continua, di componenti scalari x(t), y(t), z(t) è detta curva oraria (o legge oraria) del moto considerato. Con notazione vettoriale si può scrivere

ϕ = x(t)i + y(t)j + z(t)k (1.1)

in cui i, j, k rappresentano i versori coordinati del sistema di riferimento assegnato. I vettori

˙

ϕ = ˙x(t)i + ˙y(t)j + ˙z(t)k (1.2)

¨

ϕ = ¨x(t)i + ¨y(t)j + ¨z(t)k (1.3)

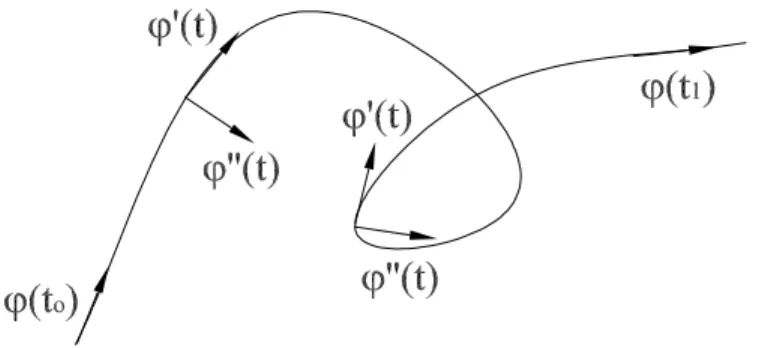
rappresentano rispettivamente il vettore velocità ed il vettore accelerazione. Come si può vedere dalla figura 1.1 in cui è rappresentato il percorso

del-Figura 1.1: Vettore velocità e vettore accelerazione della particella

(3)

mentre il vettore accelerazione, nel caso in cui il modulo del vettore velocità

k ˙ϕ k rimanga costante, è ad essa ortogonale.

In generale è indicata come curva un’applicazione continua ϕ : I → Rn _dove

I è un intervallo della retta reale. Le equazioni

           x1 = ϕ1(t) x2 = ϕ2(t) . . . xn = ϕn(t) (1.4)

che esprimono le componenti di ϕ sono dette equazioni parametriche della curva di parametro t.

Definizione (Curve C1

)

Una curva parametrica p(s) è detta di classe C1

se continua con la sua deriva-ta prima.

Definizione (Curve regolari)

Sia I un intervallo chiuso e limitato [a b]. Una curva ϕ : I → Rn_{è detta}

rego-lare se l’applicazione ϕ è di classe C1

in I = [a b] e se per ogni t ∈ [a b] il vet-tore ˙ϕ(t) è diverso dal vettore nullo, ossia se le derivate ˙ϕ1(t), ˙ϕ2(t), . . . , ˙ϕ_n(t)

non sono mai contemporaneamente nulle.

Assegnati due valori distinti al parametro t, t0, t1 ∈ [a b] è possibile

rap-presentare la retta passante per ϕ(t0) e ϕ(t1), la cui equazione parametrica

risulta essere

xi(t) = ϕ(t0) + (t − t0)

ϕi(t1) − ϕ_i(t0)

t1− t0

∀i ∈ N (1.5)

Poichè il vettore ˙ϕ(t0) di coordinate ( ˙ϕ_i(t0))_i=1,2,...,n è il vettore tangente alla

curva ϕ nel punto ϕ(t0) è possibile esprimere il versore tangente come

τ =

˙ ϕ(t0)

| ˙ϕ(t0) |

(4)

1.1.2 Curve orientate

E’ possibile associare alla curva ϕ : I → Rn _{un verso di percorrenza o}

orientamento, indotto dalla particolare rappresentazione parametrica.

Con riferimento alla figura 1.2 si dice che il punto P0 = ϕ(t0) precede

Figura 1.2: Curva orientata

il punto P1 = ϕ(t1) nel verso introdotto dal parametro t (o verso delle t

crescenti), se t0 < t1.

1.1.3 Lunghezza di una curva

Si consideri una curva continua ϕ : [a b] → Rn _{definita su di un intervallo}

chiuso e limitato [a b]. Ad ogni partizione {a = t0 < t1 < · · · < t_n = b}

di [a b] può essere associata la poligonale P inscritta nella curva, di vertici

ϕ(a), ϕ(t1), . . . , ϕ(b) e viceversa. La lunghezza di tale poligonale è

l(P) =

n

X

i=1

k ϕ(ti) − ϕ(ti−1) k (1.7)

tale numero fornisce, in generale, un’approssimazione per difetto della lunghez-za della curva ϕ. Ovviamente quanto più piccola è la lunghezlunghez-za dei segmenti che compongono la poligonale, tanto migliore sarà l’approssimazione (si veda la figura 1.3).

(5)

Figura 1.3: Polinomiale inscritta nella curva

numero

L(ϕ) = sup (l(P)) (1.8)

dove P varia tra tutte le possibili poligonali inscritte nella curva. Se tale es-tremo superiore è finito, si dice che la curva è rettificabile. Viene introdotto, in seguito, un teorema fondamentale sulla rettificabilità delle curve di classe C1

[a b], di cui per brevità è omessa la dimostrazione.

Teorema di rettificabilità delle curve C1

Se ϕ : [a b] → Rn _{è una curva di classe C}1

, allora essa è rettificabile e la sua lunghezza L(ϕ) è data dall’integrale

L(ϕ) =

Z b

a

(6)

Osservazione - Data una curva ϕ : [a b] → Rn _{se ϕ}

1 e ϕ2 sono le curve

che si ottengono restringendo la ϕ agli intervalli [a c] e [c b], si ha che

L(ϕ) = L(ϕ1) + L(ϕ2) (1.10)

La definizione data di lunghezza di una curva continua a valere per le curve regolari a tratti.

Definizione di curva regolare a tratti - Una curva ϕ : [a b] → Rn _{è regolare}

a tratti se esiste una partizione {a = a0 < a1 < · · · < a_n= b} dell’intervallo

[a b] tale che per ogni i = 1, 2, . . . , n la curva ϕi= ϕ |_|a_i

−1,a1| è regolare.

Se ϕ : [a b] → Rn _{è una curva regolare a tratti la sua lunghezza vale}

L(ϕ) = n X i=1 ϕi= n X i=1 Z ai ai −1 | ˙ϕi(t) | dt (1.11)

1.1.4 Ascissa curvilinea

Fra tutte le rappresentazioni parametriche di una curva regolare ha par-ticolare rilevanza geometrica quella fornita mediante la nozione di ascissa curvilinea.

Assegnata una particolare rappresentazione parametrica ϕ : [a b] → Rn_della

curva regolare γ e fissato t0 ∈ [a b] la funzione

s(t) =

Z t

t0

| ˙ϕ(τ ) | dτ (1.12)

è strettamente crescente, derivabile con ds/dt > 0 ∀t; s = s(t) è quindi

un cambio di parametro ammissibile s : [a b] → [s(a) s(b)]. Il parametro s è detto ascissa curvilinea. Se t = t(s) è il cambiamento inverso di s = s(t) e γ(s) = ϕ(t(s)) allora per ogni valore del parametro s risulta

dγ(s) ds = dϕ dt (t(s)) dt ds(s) = ˙ ϕ(t(s)) | ˙ϕ(t(s)) | (1.13)

(7)

e quindi

| dγ(s)

ds | = 1 ∀s ∈ [s(a) s(b)] (1.14)

˙γ(s) è il versore tangente alla curva nel generico punto di ascissa curvilinea s.

1.1.5 Curvatura di una curva piana

Sia data una curva regolare ϕ : [a b] → Rn_{, parametrizzata con}

l’ascis-sa curvilinea s. Si supponga che γ(s) sia di classe C2

. La curvatura è una quantità scalare che descrive (a meno del segno) le caratteristiche geo-metriche della curva, indipendentemente da cambiamenti di coordinate o di parametro.

Si indichi con τ (s) il versore tangente alla curva γ nel punto s ∈ I.

τ(s) = ˙γ(s)

| ˙γ(s) | (1.15)

¨

γ(s) è un vettore ortogonale al vettore tangente ˙γ(s)∀s ∈ I.

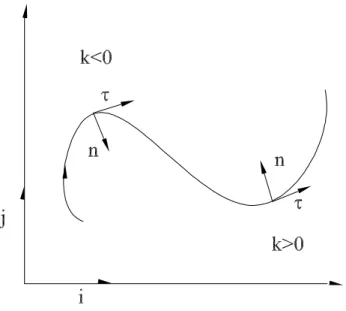
Si indichi inoltre con n(s) il versore normale alla curva che si ottiene ruotan-do il vettore tangente τ (s) di π/2 nel verso che va da j ad i come indicato nella figura 1.4.

Il vettore ˙τ (s), essendo ortogonale al vettore tangente τ (s), è parallelo al versore normale n(s). Pertanto esiste sempre un numero reale k(s) per cui

˙τ (s) = −k(s)n(s) (1.16)

k(s) rappresenta la curvatura della curva piana γ nel punto γ(s). Il reciproco del modulo della curvatura è il raggio di curvatura. Si può dimostrare (in questa trattazione la dimostrazione è omessa per brevità) che per una curva piana di equazioni ϕ(s) = [x(s) y(s)], la curvatura nel punto ϕ(s) è data da

(8)

1.2 Introduzione alle spline del quarto ordine

Figura 1.4: Curvatura di una curva piana

k(s) = x ′_(s)y′′_{(s) − x}′′_(s)y′_(s) (x′_(s)2 + y′_(s)2 )3_/2 (1.17) Definizione (Curve C2 )

Una curva parametrica p(s) è detta di classe C2

, se è di tipo C1

e la sua

derivata seconda p′′_{(s) è una funzione continua lungo la curva.}

Osservazione - Se p(s) è una curva di classe C2

, allora la curvatura k(s) è una funzione continua lungo la curva.

1.2 Introduzione alle spline del quarto ordine

(9)

Definizione 1 (Curve C3

)

Una curva parametrica p(s) è detta di tipo C3

, se è di tipo C2

e la funzione

p′′′(s) è continua lungo la curva.

Osservazione - Se p(s) è una curva di classe C3

, allora la funzione dk/ds è continua lungo la curva.

Definizione 2 (Traiettorie C1

, C2

, C3

)

Una traiettoria sul piano (x y), cioè una serie di punti sul piano (x y), è

di classe Ci_{(i = 1, 2, 3) se esiste una curva parametrica di classe C}i _{la cui}

immagine è la traiettoria considerata.

Proposizione 1 Sia v(t)τ la velocità del baricentro di un veicolo, e sia tale che ∀t 6= 0 v(t) 6= 0, allora la traiettoria sul piano (x y) generata dal

baricentro di tale autoveicolo nel suo moto è di tipo C3

. Dimostrazione

Definiamo massa sospesa ms di un veicolo tutto ciò che “sta sopra le

sospen-sioni”. Ai fini dello studio della dinamica globale del veicolo la massa sospesa o cassa è considerata come un unico corpo rigido.

Il moto del veicolo sia descritto rispetto ad un sistema di riferimento solidale alla strada indicato con (x0, y0, z0; O0) e di versori (i0, j0, k0), con l’asse z0

ver-ticale e diretto verso l’alto. Si tratta del sistema di riferimento comunemente identificato con assi suolo, e che, per la dinamica dei veicoli, può essere con-siderato inerziale. Si definisce inoltre (figura 1.5) un sistema di riferimento solidale al veicolo (x, y, z; Gs), di versori (i, j, k), e quindi detto di assi corpo.

L’origine viene fissata nel baricentro Gs della massa sospesa ms. Posto il

veicolo in condizioni di moto rettilineo uniforme su strada piana, si assume l’asse x parallelo alla strada e diretto in avanti, l’asse z ortogonale alla strada e diretto verso l’alto e l’asse y perpendicolare agli altri due e diretto verso

sinistra. Quindi in queste condizioni, sia x che y sono ortogonali a z0.

Per determinare la posizione e l’orientamento della cassa, ovvero degli assi corpo, rispetto al sistema di riferimento fisso solidale alla strada è necessario

(10)

Figura 1.5: Sistema di riferimento

determinare il valore di sei coordinate.

La posizione di un punto qualsiasi della massa sospesa fornisce la prime tre

coordinate. Se si sceglie il baricentro Gs si hanno quindi quali coordinate i

valori xGs

0 , y Gs

0 , z Gs

0 . Le altre tre coordinate sono gli angoli che servono per

(11)

strada.

Nella dinamica del veicolo si usa lo schema detto roll-pitch-yaw (RPY), ovvero rollio-beccheggio-imbardata illustrato in figura 1.5. Si tratta di una sequenza di tre rotazioni “semplici”, cioè rispetto ad un asse coordinato. Si impiega quindi il seguente schema logico che introduce dei riferimenti inter-medi ed in cui due terne successive hanno sempre una direzione a comune. Tutte le rotazioni sono considerate positive se antiorarie

(i0, j0, k0) ψ → |{z} k1=k0 (i1, j1, k1) θ → |{z} j2=j1 (i2, j2, k2) φ → |{z} i=i2 (i, j, k) (1.18)

Essendo la massa sospesa assimilata ad un unico corpo rigido ha senso il concetto di velocità di rotazione Ω. La velocità di rotazione è determinata solo dagli andamenti delle tre coordinate angolari ψ(t), θ(t), φ(t) secondo la relazione

Ω_{= ˙}_φi2(ψ, θ) + ˙θj1(ψ) + ˙ψk0 (1.19)

Nella nostra analisi considereremo trascurabili i contributi dovuti al moto di rollio e beccheggio del veicolo. In queste condizioni la velocità angolare

risul-ta Ω = ˙ψk0, inoltre poichè risultano θ e φ piccoli considereremo l’asse k0 del

sistema di riferimento solidale al suolo, parallelo all’asse k del sistema di assi corpo. La velocità del baricentro del veicolo sarà, come detto in precedenza, tangente alla traiettoria.

Considerato costante il coefficiente d’aderenza, a causa della deformabilità dei pneumatici, le forze di contatto tra veicolo e strada non possono presentare delle discontinuità. Non essendo realizzabili sotto tale ipotesi, variazioni im-pulsive nelle accelerazioni, laterali o longitudinali, la velocità delle singole ruote risulta continua. Tale condizione si manifesta anche in presenza di angolo di sterzo variabile nel tempo a causa dell’elasticità della tiranteria. La velocità del baricentro del veicolo e la velocità angolare della cassa sono combinazione lineare delle velocità possedute dai singoli pneumatici,

(12)

pertan-1.2 Introduzione alle spline del quarto ordine

to entrambe sono di classe C1

. Risultano quindi essere funzioni continue v(t), ˙v(t), ψ(t), ˙ψ(t), ¨ψ(t).

Si consideri ora il percorso dato da

p(t) = [x(t) y(t)]T con t ∈ [t0 t1] (1.20)

Il vettore tangente unitario può essere espresso nella forma ˙p(t) k ˙p(t) k = [ ˙x(t) ˙y(t)]T p ˙x(t)2 + ˙y(t)2 = v [cos ψ(t) sin ψ(t)]T p v2 cos ψ(t)2 + v2

sin ψ(t)2 = [cos ψ(t) sin ψ(t)]

T

(1.21) la cui continuità è facilmente deducibile data la continuità di ψ(t). Si può osservare che

( ¨

x(t) = ˙v cos ψ − v ˙ψ sin ψ

¨

y(t) = ˙v sin ψ + v ˙ψ cos ψ (1.22)

e che

( _...

x (t) = ¨v cos ψ − ˙v ˙ψ sin ψ − v ¨ψ sin ψ − v ˙ψ2

sin ψ ...

y (t) = ¨v sin ψ + ˙v ˙ψ cos ψ + v ¨ψ cos ψ − v ˙ψ2

sin ψ (1.23)

Entrambe le espressioni risultano continue, poichè combinazioni di funzioni continue.

Si consideri ora l’espressione della curvatura (1.2) k(t) = ˙x(t)¨y(t) − ¨x(t) ˙y(t)

( ˙x(t)2

+ ˙y(t)2

)3_/2

Dalle considerazioni appena svolte risulta chiaramente che essa è una fun-zione continua.

Ancora si consideri la funzione dk ds = ( ˙x...y −...x ˙y)( ˙x2 + ˙y2 ) − 3( ˙x¨y − ¨x ˙y)( ˙x¨x + ˙y ¨y) ( ˙x2 + ˙y2 )3 (1.24)

(13)

1.3 Descrizione delle spline del quarto ordine

Sostituendo in questa le espressioni appena trovate ed effettuando le oppor-tune semplificazioni si ottiene

dk

ds =

˙Ω(t)v(t) − Ω(t) ˙v(t)

v(t)3 (1.25)

si può notare agevolmente che essa risulta continua, in quanto composta da funzioni continue.

Si può quindi concludere che p(t) è una curva C3

¥

1.3 Descrizione delle spline del quarto ordine

Siano assegnati n punti Pi sul piano {x y}. Si voglia tracciare la spline

del quarto ordine che interpoli i punti assegnati. Affinchè il problema abbia soluzione unica è necessario che i punti siano almeno cinque. Nel caso in cui n sia maggiore di cinque saranno generate n-4 tratti di spline del quarto ordine, imponendo, oltre al passaggio per gli n punti assegnati, che la curva

risultante sia continua di classe C3

nei punti di interfaccia tra i tratti generati. In tale modo si ottiene un sistema lineare di 10(n − 4) equazioni in 10(n − 4) incognite. Le equazioni che formano il sistema si ottengono

• 2n equazioni imponendo il passaggio per i punti assegnati.

• 2(n-4) equazioni imponendo la continuità della curva polinomiale a tratti nei punti all’interfaccia tra due tratti di spline.

• 2(n-4) equazioni imponendo la continuità della derivata prima calcolata nei punti d’interfaccia.

• 2(n-4) equazioni imponendo la continuità della derivata seconda calco-lata nei punti d’interfaccia.

• 2(n-4) equazioni imponendo la continuità della derivata terza nei me-desimi punti d’interfaccia.

(14)

1.4 Esempi di traiettorie generate con spline del quarto ordine

Si enuncia una utile proprietà posseduta da questa famiglia di curve, omet-tendone la dimostrazione per brevità.

Proprietà 1 (Generazione di tratti rettilinei)

Siano assegnati n punti (n > 5) Pi appartenenti al piano {x y}. Se tali punti

giacciono su una retta, allora il percorso generato p(s) è rettilineo ∀s ∈ R.

1.4 Esempi di traiettorie generate con spline

del quarto ordine

Si mostrano alcune traiettorie generate attraverso l’interpolazione di punti assegnati con le rispettive curvature. Si tratta di curve che riproducono possibili traiettorie percorse da un veicolo in varie curve. Sono presentati un tornante con raggio di curvatura (calcolato dal centro carreggiata) pari a 40 metri (figure 1.6, 1.7), una chicane destra-sinistra di raggi 80 e 60 metri rispettivamente (figure 1.8, 1.9), una curva con raggio crescente da 40 ad 80 metri (figure 1.10, 1.11), una curva con raggio decrescente da 60 a 20 metri (figure 1.12, 1.13) ed infine un ampia curva a 90 gradi con raggio di curvatura pari a 180 metri (figure 1.14, 1.15). Per la generazione delle spline è imposto il passaggio per 15 punti, ottenendo quindi 11 tratti di spline del quarto ordine. Nel caso della curva con ampio raggio di curvatura i punti di passaggio sono 13, ottenendo in questo caso una curva del quarto ordine per 9 tratti.

(15)

1.4 Esempi di traiettorie generate con spline del quarto ordine −10 0 10 20 30 40 50 60 70 80 90 −50 −40 −30 −20 −10 0 10 20 30 40 Traiettoria metri metri

Figura 1.6: Esempio di traiettoria in un tornante

0 50 100 150 200 250 −0.03 −0.025 −0.02 −0.015 −0.01 −0.005 0 0.005 Curvatura metri 1/R c (1/m)

(16)

1.4 Esempi di traiettorie generate con spline del quarto ordine −50 0 50 100 150 200 −20 0 20 40 60 80 100 120 140 160 Traiettoria metri metri

Figura 1.8: Esempio di traiettoria in una chicane

0 50 100 150 200 250 300 −0.015 −0.01 −0.005 0 0.005 0.01 0.015 0.02 0.025 Curvatura metri 1/R c (1/m)

(17)

1.4 Esempi di traiettorie generate con spline del quarto ordine 0 20 40 60 80 100 120 140 −60 −40 −20 0 20 40 Traiettoria metri metri

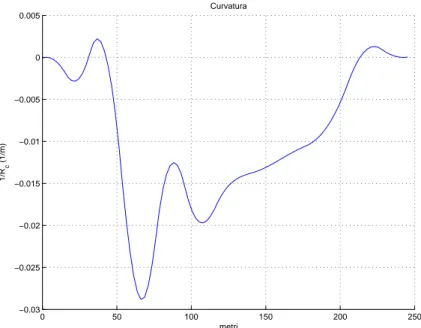
Figura 1.10: Esempio di traiettoria in una curva con raggio di curvatura crescente 0 50 100 150 200 250 −0.03 −0.025 −0.02 −0.015 −0.01 −0.005 0 0.005 Curvatura metri 1/R c (1/m)

Figura 1.11: Esempio di curvatura in una curva con raggio di curvatura crescente

(18)

1.4 Esempi di traiettorie generate con spline del quarto ordine −10 0 10 20 30 40 50 60 70 80 90 −20 −10 0 10 20 30 40 50 Traiettoria metri metri

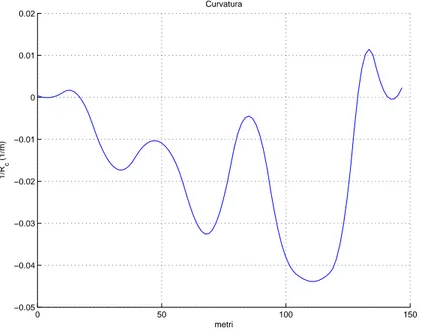
Figura 1.12: Esempio di traiettoria in una curva con raggio di curvatura decrescente 0 50 100 150 −0.05 −0.04 −0.03 −0.02 −0.01 0 0.01 0.02 Curvatura metri 1/R c (1/m)

Figura 1.13: Esempio di curvatura in una curva con raggio di curvatura decrescente

(19)

1.4 Esempi di traiettorie generate con spline del quarto ordine 0 50 100 150 200 250 −50 0 50 100 150 Traiettoria metri metri

Figura 1.14: Esempio di traiettoria in una curva con ampio raggio di

curvatura 0 50 100 150 200 250 300 350 400 −7 −6 −5 −4 −3 −2 −1 0 1x 10 −3 _Curvatura metri 1/R c (1/m)

Figura 1.15: Esempio di curvatura in una curva con ampio raggio di