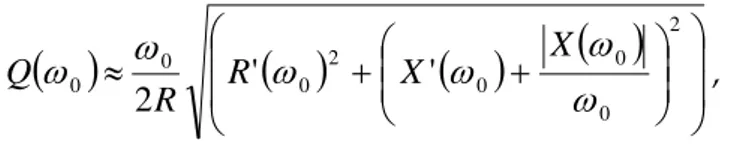Capitolo 1 Antenne meandered

Capitolo 1

Antenne meandered

1.1 Concetti preliminari e generali

In questo capitolo s’intende mettere in luce come le antenne ripiegate, costituite da numerosi elementi, offrano una buona efficienza di irradiazione e una considerevole diminuzione delle dimensioni, se paragonate ad un dipolo a λ/2 operante alla stessa frequenza.

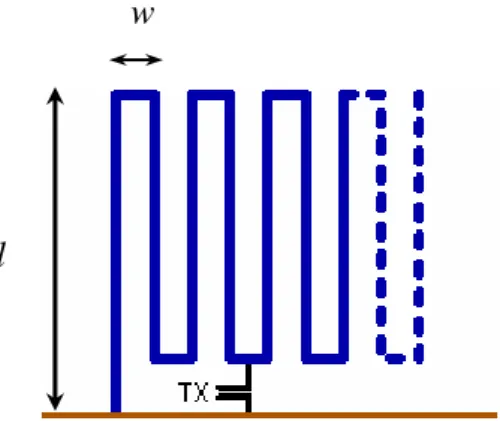
Le antenne meandered sono una classe di strutture filari costituite da sezioni a meandri, creati nell’intento di ridurre le dimensioni dell’antenna, fissata la lunghezza d’onda di risonanza di interesse. Ogni sezione è ottenuta ripiegando l’antenna filare su se stessa e congiungendo le sezioni una dopo l’altra. La frequenza di risonanza e le altre caratteristiche dipendono primariamente dal numero delle sezioni per lunghezza d’onda (N) e dalla separazione fra i bracci ripiegati (w). Generalmente w ha valori piccoli rispetto alla grandezza dell’antenna e in questo modo diventa trascurabile la radiazione indesiderata dovuta ai segmenti più piccoli (in fig. 1.1.1 sono i cavi orizzontali).

Fig. 1.1.1 - Esempio di antenna meandered.

l

Sull’efficienza incidono solo le perdite ohmiche presenti nel filo e la larghezza della banda dell’antenna è generalmente minore di quella di un monopolo standard.

Si definisce fattore di riduzione delle suddette antenne la quantità β (β<1).

Esso è un parametro caratteristico di queste antenne ed è il rapporto fra la lunghezza del monopolo ripiegato l e la lunghezza convenzionale L del monopolo con la stessa frequenza di risonanza:

L

l

=

β

Il fattore di riduzione fornisce una grossolana informazione sulla spaziatura e sul numero di ripiegamenti necessari per ottenere da un dipolo lineare risonante ad un certa frequenza, una struttura ripiegata e compatta risonante alla stessa frequenza. Di solito il valore di β, seppure sempre inferiore all’unità per definizione, è superiore a 0.5 e il numero delle insenature generate non supera il valore di 7.

La forma attorcigliata di alcune geometrie, come quella a meandri, permette la riduzione delle dimensioni di un’antenna poiché all’interno della stessa superficie può essere racchiuso un maggiore perimetro filare. Ciò implica che un’antenna con tale geometria avrà la stessa superficie/volume del suo equivalente euclideo, ma sarà molto più lunga. Tipicamente, queste antenne hanno una dimensione massima fisica che è molto piccola se confrontata con la lunghezza d’onda di lavoro. Da qui, la definizione di strutture elettricamente compatte: la lunghezza d’onda non definisce più vincoli sulla lunghezza dell’antenna, come nel caso standard del dipolo, ma le dimensioni e più precisamente l’ingombro sono in una certa misura svincolati dalla lunghezza d’onda e semmai dipendono dal numero di ripiegamenti e dalle misure dei segmenti che compongono l’antenna.

In prima approssimazione si potrebbe credere vantaggioso aumentare il numero dei ripiegamenti così da ottenere una struttura con maggior perimetro possibile; in pratica ciò comporta maggiori rischi per quanto riguarda l’accoppiamento tra i segmenti. A causa di questo fenomeno infatti la corrente elettrica, invece di fluire seguendo il regolare tracciato

filare, “salta” seguendo il percorso più breve, generando flussi di corrente indesiderati che deteriorano le prestazioni.

Riguardo a queste strutture ripiegate sono stati condotti degli studi per ricavare se e quali limiti possa generare la compattezza e quali relazioni sussistano tra le proprietà caratteristiche radiative dell’antenna compatta e la riduzione delle dimensioni di questa. In particolare, è stato ricavato che antenne geometricamente compatte portano degradazione sull’ampiezza di banda e sulla dissipazione di potenza.

Wheeler [1] ha affrontato lo studio della relazione tra banda ed efficienza di un elemento radiante definendo il fattore di potenza d’irradiazione (F.p.i.) come il rapporto tra la resistenza d’irradiazione dell’antenna (Rirr) e la sua reattanza d’ingresso (Xin); questo

rapporto risulta essere proporzionale al prodotto Banda-Efficienza e al volume occupato dall’antenna stessa. In formula:

pato VolumeOccu Efficienza Banda Xi R i p F n rr i ∝ ⋅ ∝ = . . . (1.1.2)

Come precisato dalla formula, diminuire il volume occupato significa peggiorare le prestazioni o in termini di efficienza o in termini di ampiezza di banda. È quindi necessario trovare il giusto mezzo nella ricerca della riduzione delle dimensioni in modo da non compromettere l’efficienza o l’ampiezza della banda dell’antenna.

In uno studio successivo, Chu [2] ha ricavato una relazione ancora più stretta e precisa: ha dimostrato che il fattore di antenna è proporzionale al raggio di un’ipotetica sfera che contenga al suo interno la struttura in analisi.

È stata definita proprio da lui e da altri colleghi come Fano e Adler [3] una grandezza denominata SAL (Small-Antenn-Limit) che precisa i requisiti per i quali, mantenendo una buona efficienza, una struttura possa essere chiamata elettricamente compatta. Il SAL è definito come il limite superiore di frequenza di un’antenna per la quale valga

dove k, la costante di propagazione dell’onda, vale 2π/λ e a è il raggio della sfera che circoscrive la massima dimensione dell’antenna. In pratica, un’antenna risonante alla frequenza f0=c/λ0, per essere definita elettricamente corta deve avere dimensione massima

non superiore al valore λ0/2π.

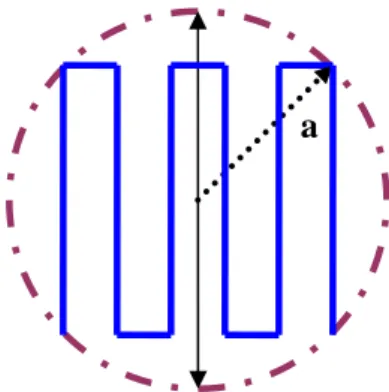
Ponendo un’antenna elettricamente compatta in condizione di risonanza nel rispetto di questo limite, il valore della sua resistenza d’irradiazione converge verso quello di un monopolo lineare avente la stessa altezza totale, indipendentemente dalle differenze riscontrabili con questo per quanto riguarda la lunghezza effettiva del filo e la geometria. In figura 1.1.2 è rappresentata la situazione in cui il vincolo dimensionale, perchè la riduzione dell’ingombro non porti degradazioni, viene rispettato.

Fig. 1.1.2 – Sfera che racchiude idealmente la struttura elettricamente compatta.

Wheeler e Chu hanno equiparato il monopolo elettricamente piccolo ad un capacitore di volume cilindrico di altezza d e area A. Questi hanno dimostrato che la reattanza del monopolo elettricamente piccolo, capacitiva, è una funzione dell’area A e dell’altezza d dell’antenna. Cioè può essere espresso genericamente tramite la formula:

d

A

C

=

ε

dove ε è la permettività elettrica dell’aria e C è il valore capacitivo equivalente dell’antenna. L’equivalente capacitivo dell’antenna C può indicarsi come una funzione del volume

occupato dall’antenna Ve, pari a A·d, e della sua altezza equivalente. La formula si modifica allora così: 2 d V C=

ε

È stato inoltre dimostrato che il volume Ve occupato dall’antenna è in stretta relazione con la

sfera che racchiude per intero il dispositivo e si è concluso che il volume occupato Ve può

essere alternativamente definito definendo il raggio di quella sfera. Il raggio di questa sfera è una funzione del fattore di qualità Q ed è pari a

3 1 2 9 2 ⎟⎟_⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ = Q r

π

λ

Il fattore di qualità Q fornisce un’indicazione sull’ampiezza della banda dell’antenna. Come si vede, all’aumentare di r e quindi del volume occupato, il fattore di qualità diminuisce, mentre, a parità di efficienza, la banda dell’antenna aumenta. Questa è un’ulteriore prova del fatto che aumentare il volume occupato porta a un degrado delle prestazioni. Di seguito (fig. 1.1.3) è riportato il grafico relativo all’andamento del fattore di qualità in una struttura elettricamente corta al variare del volume occupato.

Fig. 1.1.3 – Fattore di qualità Q in funzione del prodotto k·a a tratto continuo; la curva esatta (linea tratteggiata) è stata ricavata da McLean [4].

Nel 1987 uno studio monografico di Fujimoto, Henderson, Hirasawa e James [5] riassumeva tutte le scoperte fatte su queste innovative strutture. Questo gruppo di studiosi ha cercato di caratterizzare queste strutture non più dal punto di vista della struttura geometrica o del volume occupato ma i loro studi si sono soffermati sulla definizione delle meandered a partire dal fattore di qualità Q.

Essi hanno stabilito che per un’antenna elettricamente corta contenuta in un volume fissato il valore minimo del fattore di qualità Q è una grandezza connaturata. Ciò pone dei limiti alla banda ottenibile per queste antenne. Infatti, maggiore è il valore di Q, minore è l’ampiezza di banda.

L’efficienza delle antenne elettricamente corte è determinata dall’entità delle perdite nel conduttore, nel dielettrico e nei materiali con i quali è costruita l’antenna. L’efficienza può essere espressa come

Rm

Rr

R

+

=

η

dove Rr è la resistenza d’irradiazione e Rm è la resistenza che rappresenta la perdita nel

materiale.

L’impedenza d’ingresso di una struttura di questo tipo ha una parte immaginaria di solito capacitiva e nell’ottica di trasferire il massimo contributo di potenza dal generatore alla struttura radiante in modo da ottimizzare l’efficienza, l’antenna e la rete che conferisce l’eccitazione devono essere perfettamente adattate. Il massimo adattamento tra l’antenna e la rete d’alimentazione avviene massimizzando la grandezza ηs, pari a

m a

s

η

η

η

=

⋅

dove ηa è l’efficienza del sistema globale, cioè di antenna e rete di adattamento, mentre ηm è

l’efficienza della rete di adattamento.

m a a m

Q

Q

+

=

1

η

η

dove Qa è il fattore di qualità dell’antenna elettricamente corta, mentre Qm è il fattore di

qualità della rete d’adattamento del sistema.

Per quanto riguarda l’ampiezza di banda, nel 2001 Sten [6] ha determinato la formula per ricavarne un valore approssimato. La formula è riportata di seguito.

S

Q

S

B

=

−

1

dove S è il valore del ROS e Q è il fattore di qualità dell’antenna.

All’inizio di quest’anno sono stati pubblicati due articoli di S.R. Best [7-8] che offrono un’ulteriore conferma a queste teorie e approfondiscono una nuova tematica. Lo studioso, infatti, si propone di ricavare quale sia la dipendenza tra il volume che racchiude l’antenna, la geometria che definisce il dispositivo e le grandezze radiative.

Egli ha condotto un test su strutture elettricamente compatte con diverse geometrie costitutive con il vincolo che occupassero lo stesso spazio (avessero la stessa altezza e volume occupato equivalente) ed ha concluso che la scelta della geometria non influisce sulle grandezze elettromagnetiche ma che solo l’ingombro fisico dell’antenna, definito come il volume cilindrico o sferico che le racchiude, può modificare tali grandezze.

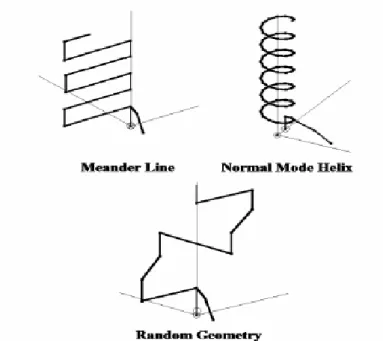
Nel suo studio egli modellizza tre diversi tipi di antenne elettricamente compatte giacenti su un piano di massa infinito, costruite perchè risuonino alla stessa frequenza: una meander line, una ad elica e una con una geometria casuale, riportate in fig. 1.1.4.

Fig. 1.1.4 – Antenne elettricamente compatte con uguale altezza adattate tramite stub in parallelo chiuso in corto circuito sul piano di massa.

Queste diverse strutture hanno la stessa altezza equivalente nella direzione identificata dall’asse z, lo stesso diametro della sezione del filo conduttore e volume occupato equivalente, ma non stessa lunghezza effettiva.

La loro impedenza d’ingresso è stata corretta, per un perfetto adattamento, con l’ausilio di uno stub in parallelo chiuso in corto circuito, debitamente dimensionato, che rende l’impedenza d’ingresso di tali strutture pari a circa 50Ω (valore di adattamento d’impedenza). Tutte le antenne di fig. 1.1.4 risultano risuonare approssimativamente alla stessa frequenza (nel caso specifico 412MHz). Per ogni diversa geometria, infatti, la frequenza di risonanza è determinata dalla lunghezza totale del filo e dal suo diametro. Fissando i limiti d’ingombro secondo le specifiche richieste, la frequenza di risonanza può essere variata soltanto scegliendo una certa configurazione geometrica piuttosto che un’altra, variando così l’unico parametro significativo in questo senso: la lunghezza del filo. Aumentare la lunghezza totale del filo dell’antenna mantenendo costante la sua altezza provoca l’abbassamento del valore della frequenza di risonanza.

La scelta della geometria e quindi della lunghezza del filo impiegato non deforma il diagramma d’irradiazione e quando siano fatte funzionare alla frequenza di risonanza, le antenne mostrano lo stesso comportamento elettromagnetico, sempre consistente con quello di un monopolo posto su un piano di massa.

Quindi, mentre può essere utilizzata una qualsiasi geometria, variando così la lunghezza del filo impiegato per ottenere una certa frequenza di lavoro, le proprietà radiative dell’antenna sono praticamente indipendenti dalla scelta della geometria e dalla lunghezza totale del filo. La geometria inoltre ha influenza solo sulla parte immaginaria dell’impedenza. Ognuna di queste strutture, osservata senza l’utilizzo dello stub correttore che attui l’adattamento d’impedenza, mostra un’impedenza d’ingresso formata da un contributo reale resistivo piccolo e un contributo reattivo di tipo capacitivo piuttosto elevato. La presenza di una reattanza capacitiva è da spiegarsi con la tendenza di queste strutture a creare un’auto-induttanza che cresce al crescere della lunghezza e del raggio della sezione del filo impiegato (pur mantenendo inalterata l’altezza dell’antenna), che non riesce ad equiparare il contributo capacitivo che si viene a creare nel punto d’alimentazione. In altre parole, un’antenna filare generica con induttanza propria Ls, raggiunge l’adattamento se,

aumentando l’auto-induttanza Ls tramite l’incremento della lunghezza totale del filo, si

raggiunge una configurazione per cui ωLs bilancia perfettamente1/(ωCg), dove Cg è la capacità

che si sviluppa tra il filo e il piano di massa nel punto in cui si inserisce l’alimentazione. Per strutture elettricamente corte avviene sempre che 1/(ωCg)»ωLs cosicché la parte capacitiva

determina un contributo dominante nella reattanza complessiva dell’impedenza d’ingresso. La resistenza d’irradiazione di antenne elettricamente compatte è stabilita esclusivamente dall’altezza dell’antenna e dal volume occupato, relativamente alla lunghezza d’onda della risonanza.

Il fattore di qualità (Q), definito come il rapporto tra l’energia reattiva (W) e la potenza fornita all’antenna (Pa) misurate ad una certa pulsazione ω0, nel caso di antenne ripiegate

( )

( )

( )

( )

ω

ω

ω

ω

ω

ω

in cui R e X sono la resistenza e la reattanza d’ingresso dell’antenna e R’ e X’ sono le loro rispettive derivate prime.

Poiché è stato ricavato che per le tre diverse strutture di fig. 1.1.4 il fattore di qualità Q, riscontrato alla frequenza di risonanza, è praticamente lo stesso (si veda la figura 1.1.5), è ragionevole concludere che questa grandezza muti in funzione del volume dei dispositivi e non della geometria con la quale essi sono realizzati.

Fig. 1.1.5 – Diagramma del fattore di qualità (Q) in funzione della frequenza per le tre diverse strutture adattate tramite stub in parallelo chiuso in corto circuito su piano di massa.

In effetti, Q è una funzione della reattanza X e della sua derivata X’ (entrambe calcolate alla frequenza di risonanza), grandezze che dipendono dal volume equivalente della struttura e non dalla specifica geometria con cui è realizzata l’antenna.

Fissata l’altezza, aumentare per esempio il volume del cilindro che idealmente racchiude la struttura e quindi il volume occupato dall’antenna stessa si traduce nell’aumento della X’ e quindi del fattore di qualità.

1.2 Conclusioni

È stato chiarito che per antenne elettricamente compatte la risonanza ad una certa frequenza si ottiene agendo opportunamente sulla geometria e con essa, sulla lunghezza totale del filo. Aumentare la lunghezza del filo porta, in piena aderenza con le strutture lineari standard, alla diminuzione della frequenza di risonanza.

Le proprietà radiative di antenne elettricamente compatte che occupino volumi equivalenti sono in pratica le stesse, indipendentemente dalle anche considerevoli differenze nella geometria.

L’ottimizzazione della resistenza di irradiazione e del fattore di qualità Q non è in maniera significativa funzione della geometria dell’antenna o della lunghezza totale del filo. Per migliorare le prestazioni di queste antenne è necessario occupare efficientemente il volume effettivamente occupato in modo da renderle linearmente più estese possibile, mantenendo limitato l’ingombro effettivo della struttura.

Esistono, però dei limiti alla miniaturizzazione, oltre i quali s’incorre nel degrado delle prestazioni. Per ottenere buone prestazioni non si deve valicare il limite costituito dal valore del SAL (Small-Antenna-Limit) che fissa il volume minimo all’interno del quale deve essere circoscrivibile idealmente la struttura elettricamente compatta perché funzioni efficientemente.