Capitolo 3

Capitolo 3

Decomposizione coerente del target: metodo di Cameron e

SSCM

Sommario

3.1 Introduzione 3.2 Notazioni

3.3 Il metodo di decomposizione di Cameron

3.4 I problemi del metodo di classificazione di Cameron 3.5 Il metodo SSCM

3.1 Introduzione

L’obiettivo della teoria della decomposizione del target è quello di esprimere il meccanismo di scattering come la somma di elementi indipendenti e di associare un meccanismo fisico ad ogni componente[5-6]. Si possono distinguere due teorie di decomposizione del target: Coherent Target Decomposition (CTD) e Partially Coherent

Target Decomposition (PCTD). Il primo metodo di decomposizione è stato sviluppato

per caratterizzare onde completamente polarizzate, per le quali tutta l’informazione polarimetrica è contenuta nella matrice di scattering. L’idea è quella di scomporre la matrice di scattering come combinazione lineare di matrici 2x2 linearmente indipendenti e ortonormali che formano una base di sviluppo. I metodi di decomposizione coerente più conosciuti sono quelli di Huynen, Pauli, Krogager, Cameron e SSCM. Il secondo metodo di decomposizione è invece usato per caratterizzare onde parzialmente polarizzate per le quali l’informazione polarimetrica può essere espressa solo dalla matrice di Mueller, dalla matrice di covarianza o di coerenza. I metodi PCTD vengono usati in applicazioni a scarsa risoluzione (che non richiedono risoluzioni spaziali elevate), dal momento che una accurata stima delle matrici di covarianza e coerenza richiede l’uso di una finestra sufficientemente larga nella quale i segnali di speckle e della scena possono considerarsi localmente stazionari ed ergodici [5-19]. I metodi CTD invece estraggono informazioni polarimetriche direttamente dalla matrice di scattering e sono quindi preferibilmente applicati ad immagini ad elevata risoluzione. Questi metodi sono quindi consigliati per la caratterizzazione e identificazione di point targets come navi o man-made objects [5]. In questo capitolo saranno descritti due metodi di decomposizione coerente del target: il metodo di Cameron e il relativo algoritmo di classificazione e il metodo SSCM

(Symmetric Scattering Characterization Method). I metodi di decomposizione di

Cameron e SSCM sono stati già applicati ad immagini SAR polarimetriche per la caratterizzazione di targets con scattering simmetrico e coerente, in particolare sono stati usati per caratterizzare e identificare lo scattering di oceano e navi. In entrambi la matrice di scattering è decomposta in tre componenti ortogonali: una componente non reciproca, una componente simmetrica massima e una componente simmetrica minima [7]. Nel metodo di Cameron la componente simmetrica massima è rappresentata da un

punto, z , nel piano complesso, tale che z <1, e viene associata, secondo una metrica, ad una delle sette classi di scatteratori elementari: triedri, diedri, dipoli, diedri stretti, cilindri, ¼ wave, eliche o elementi non simmetrici. Il metodo SSCM è invece una rivisitazione del metodo di Cameron. In questo caso la componente simmetrica massima, dopo essere stata diagonalizzata, è espressa come combinazione lineare delle matrici di scattering di un triedro e un diedro, e i coefficienti della combinazione lineare sono usati per mappare tale matrice sulla sfera di Poincarè. Inoltre, poiché CTD può essere applicata solo se è verificata la condizione di scattering coerente, nel metodo SSCM ci si pone il problema di verificare il grado di coerenza dello scattering dovuto a bersagli puntiformi o estesi [5-14].

3.2 Notazioni

Ogni matrice di scattering _S~_∈C2_xC2 _{può essere rappresentata dalla somma}

d c b a S S S S S~=α~ +β~ +γ~ +δ~ (3.1) dove, usando la base di Pauli,

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 1 0 0 1 2 1 ~ a S (3.2) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 1 0 0 1 2 1 ~ b S (3.3) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 0 1 1 0 2 1 ~ c S (3.4) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 0 1 1 0 2 1 ~ d S (3.5) e α,β,γ,δ∈C.

(

)

T s s s s SG = ₁, ₂, ₃, ₄

Il vettore _SG_∈C4 _{è messo in relazione con la matrice S}~_∈C2_xC2 _{attraverso gli}

operatori _{M :C}4 _→C2_xC2_{, V :C}2_xC2 _→C4_{. Usando l’operatore V si può esprimere}

il vettore SG in questo modo:

d c b a S S S S SG =αˆ +βˆ +γˆ +δˆ (36) Si definiscono il prodotto interno, la norma e il vettore unitario nel modo seguente:

)

(

_uG,_vG _=uG_⋅vG∗, _uG_,vG_∈C4 _(3.7)

)

(

u u uG = G,G (3.8) u u u G G = ˆ (3.9)

Si definisce la matrice di rotazione

( )

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ) cos( ) sin( ) sin( ) cos( ~ ψ ψ ψ ψ ψ R (3.10)

e l’operatore di rotazione R

( )

_{ψ = R}~_(ψ)⊗R~_(ψ):C4 _→C4 _{tale che:}

3.3 Il metodo di decomposizione di Cameron

Le due proprietà fisiche fondamentali di un diffusore sono la reciprocità e la simmetria. La reciprocità divide lo spazio della matrici di scattering in due sottospazi, uno contenente le matrici di scattering di diffusori reciproci e l’altro contenente solo le matrici di scattering di diffusori non reciproci [6-7-11]. Le condizioni che permettono di applicare il teorema di reciprocità possono non essere sempre rispettate. Se il principio di reciprocità non è applicabile ciò è probabilmente dovuto alla presenza, nel mezzo trasmissivo, di materiali speciali, come ferriti o plasma gassosi (materiali per i quali l’interazione con il campo elettromagnetico non è lineare o che sono descritti da tensori di permeabilità, dielettricità o conduttività non simmetrici) oppure, nel caso di bassa

RCS, a causa del rumore o di errori di misura [11]. La matrice di scattering di un target

reciproco, sotto forma di vettore occupa il sottospazio _{W C}4

rec ⊂ generato

dall’operatore di proiezione P _rec

⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 0 2 / 1 2 / 1 0 0 2 / 1 2 / 1 0 0 0 0 1 rec P (3.12)

Ogni matrice di scattering può essere decomposta in modo univoco in due componenti ortogonali, SG_rec∈W_rec e S_⊥∈W⊥rec

G S P I S S P S S S S rec rec rec rec G G G G G G G ) ( − = = + = ⊥ ⊥ (3.13)

Il grado con cui una matrice di scattering si attiene al principio di reciprocità è dato dal parametro θ_rec che è l’angolo tra la matrice di scattering e il sottospazio reciproco W : _rec

S P_rec rec =cos−1 ˆ θ , 0<θ_rec< 2 π (3.14)

Le matrici di scattering per le quali θ_rec=0, si attengono strettamente al principio di reciprocità, mentre le matrici di scattering per le quali θ_rec=π /2 violano tale principio.

La matrice di scattering che corrisponde ad un diffusore reciproco, S~_rec =MSG_rec, può poi essere decomposta in componenti che corrispondono a diffusori simmetrici e asimmetrici. Un diffusore simmetrico è un diffusore che ha un’asse di simmetria nel piano ortogonale alla LOS. Sfortunatamente il sottospazio reciproco non può essere suddiviso in due sottospazi ortogonali, quello dei diffusori simmetrici e quello dei diffusori asimmetrici, perché le matrici di scattering che corrispondono a diffusori simmetrici non formano un sottospazio. Una matrice di scattering corrisponde ad un diffusore simmetrico se e solo se è diagonalizzabile tramite una rotazione. Indicando l’insieme delle matrici di scattering che corrispondono a diffusori simmetrici con

2 2 _C

C

X_sim ⊂ ⊗ , se S~∈X_sim allora esisterà un angolo ψ tale che d X R S R~(ψ)~~(− )ψ ∈ (3.15)

dove X è il sottospazio delle matrici diagonali e _d R~(ψ)è la matrice di rotazione (3.10). Se supponiamo che S~∈X_rec, S~ si può decomporre, usando la base di Pauli,come nella (3.1) con δ =0: c b a S S S S~=α~ +β~ +γ~ (3.16)

dove S~_a,S~_b,S~_c sono definite nelle (3.2-3.4).

Per caratterizzare meglio il sottoinsieme X_sim ⊂ X_rec, esaminiamo l’effetto della rotazione sulle matrici della base di Pauli

a

aR S

S

c b bR S S S R~(ψ)~ ~(−ψ)=cos(2ψ)~ +sin(2ψ)~ (3.18) c b cR S S S R~(ψ)~ ~(−ψ)=−sin(2ψ)~ +cos(2ψ)~ (3.19)

Se, allora, S~ è simmetrica, oltre che reciproca, usando le (3.17-3.19) otteniamo il seguente vincolo su β e γ (Appendice A I):

( )

2 cos(2 ) 0 sin ψ +γ ψ =

β (3.20) e utilizzando la (3.20) si può dimostrare che la (3.16) diventa (Appendice I)

) ~ ) sin( ~ ) (cos( ~ ~ c b a S S S S =α +δ ϑ + ϑ (3.21) ) ˆ ) sin( ˆ ) (cos( ˆ c b a S S S SG=α +δ ϑ + ϑ (3.22) dove si definiscono ) sin( ) cos( 2 ϑ γ ϑ β δ ψ ϑ + = − = (3.23)

Passando alla rappresentazione vettoriale, cerchiamo ora una decomposizione per

rec rec W SG ∈ tale che 2 S S SG_rec = G_sim + G (3.24) ' '₎ˆ ˆ , ( ˆ ) ˆ , (S S S S S S

SG_sim = G_{rec a a} + G_rec (3.25) c b S S Sˆ' ₌cos(_ϑ)ˆ ₊sin(_ϑ)ˆ _(3.26)

' '₎ˆ ˆ , ( ˆ ) ˆ , (S S S S S S S DG = G _{a a} + G (3.27)

con ˆS' _{data dalla (3.26), allora}

sim

SG è ottenuta da SG_rec in questo modo

rec sim DS

SG = G (3.28) Nella (3.26) ϑ è scelto in modo da massimizzare (_S ,_Sˆ')

rec G , e risulta essere 2 χ ϑ = (3.29) dove

(

)

₂

(

_{2 2}

)

2 ) sin( γ β β βγ γ β βγ χ γ _{+ −} + + = ∗ ∗ ∗ ∗ (3.30)

(

)

₂

(

_{2 2}

)

2 2 2 ) cos( γ β β βγ γ β χ γ _{+ −} + − = ∗ ∗ (3.31)

Le due precedenti valgono se β 2 ≠ γ 2 e _βγ∗ +_β∗_γ ≠0_{, se invece} 2 2

γ β = allora ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ < + − ≥ + = ∗ ∗ ∗ ∗ 0 , 4 0 , 4 γ β βγ π β βγ π χ γ (3.32)

Se si verifica la condizione che β 2 = γ 2e 0_βγ∗ +_β∗_γ = _allora

rec

SG appartiene alla classe delle matrici di scattering che corrispondono ad eliche e in questo caso si può scegliere arbitrariamente χ, per esempio χ =0.

Il grado con cui SG_recsi discosta dall’appartenere al sottospazio W è misurato _sim dall’angolo

(

)

rec rec rec rec S D S S D S G G G G ⋅ =_cos−1 , τ (3.33)

Se τ =0 allora P_recSG è la matrice di scattering di un diffusore simmetrico, man mano che τ aumenta lo scattering rappresentato da P_recSG diventa sempre più asimmetrico. Quando τ raggiunge il suo massimo, π/4, P_recSG è la matrice di scattering di un’elica sinistra o destra.

La componente simmetrica di una matrice di scattering si può rendere diagonale pre-moltiplicando per la matrice di rotazione e post-moltiplicando per la sua inversa, come in (3.15). L’angolo ψ è calcolato usando (3.15),(3.16),(3.20),(3.25-3.28)

(

)

χ ψ 4 1 ˆ ) ˆ , ( tan 2 1 1 ' ₌₋ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − = − b rec c rec S S D S S D G G χ∈

(

−π,π

]

(3.34)

Anche 2_ψ' _±π/ _{diagonalizzano la matrice, comunque scegliendo ψ}' _{±π/2 per la}

diagonalizzazione gli elementi diagonali sono invertiti; allora si sceglie l’angolo ψ tale che l’elemento diagonale superiore sia quello massimo e ψ ∈

(

−π/2,π/2

]

{

ψ ,'ψ' π/2

} (

π/2,π /2

]

ψ ∈ ± ∩ − (3.35) L’angolo di rotazione calcolato tramite la (3.34) è ambiguo e questa ambiguità è dovuta alla sua dipendenza dalla funzione _tan−1 _{. Per questo motivo occorre restringere il range}

di variazione dell’angolo di rotazione a

(

−π/2,π/2

]

. Per alcuni diffusori ψ può essere ambiguo anche all’interno dell’intervallo

(

−π /2,π/2

]

, in questo caso è necessario restringere ancora l’intervallo di variazione di ψ . Questo si verifica per

triedri e diedri. Nel caso di triedri l’angolo per la diagonalizzazione è completamente ambiguo e in questo caso scegliamo ψ =0. Per i diedri un angolo di rotazione ψ è indistinguibile da un angolo di rotazione ψ ±π/2, e quindi il range di variazione va ristretto a

(

−π/4,π/4

]

⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎨ ⎧ − ≤ + < < − < − = 4 2 4 4 4 2 π ψ π ψ π ψ π ψ ψ π π ψ ψ se se se d (3.36)

La matrice di scattering di un diffusore simmetrico può essere decomposta nel modo seguente ρ i sim ae SG = R(ψ₀)Λˆ(z) (3.37)

dove a= SG , ρ è la fase assoluta e dipende solo dalla distanza tra il trasmettitore e il diffusore, ψ₀ è l’angolo di orientazione del diffusore nel piano perpendicolare alla LOS. Il legame tra gli angoli ψ₀ e ψ è espresso nell’equazione (3.38), mentre nella (3.39) è definito il vettore Λˆ z( ) ψ ψ₀ =− (3.38) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + = Λ z z z 0 0 1 1 1 ) ( ˆ 2 , z∈C, z <1 (3.39)

Invertendo la (3.37) e considerando che R-1 (ψ)=RT (ψ)= R (−ψ), si trova che

a e z iρ = Λ )ˆ( R-1 Ssim G ) (ψ_{0 =} a eiρ R(ψ)SG_sim (3.40)

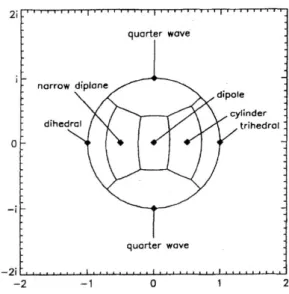
Facendo riferimento alla (3.11), si capisce che Λˆ z( )è la forma vettoriale della matrice di scattering di un diffusore simmetrico normalizzata e diagonalizzata. Il parametro che determina il tipo di scatteratore è z . Quindi uno scatteratore cui è associata una

particolare matrice di scattering è rappresentato da un punto nel disco unitario del piano complesso (vedi figura Fig.3.1).

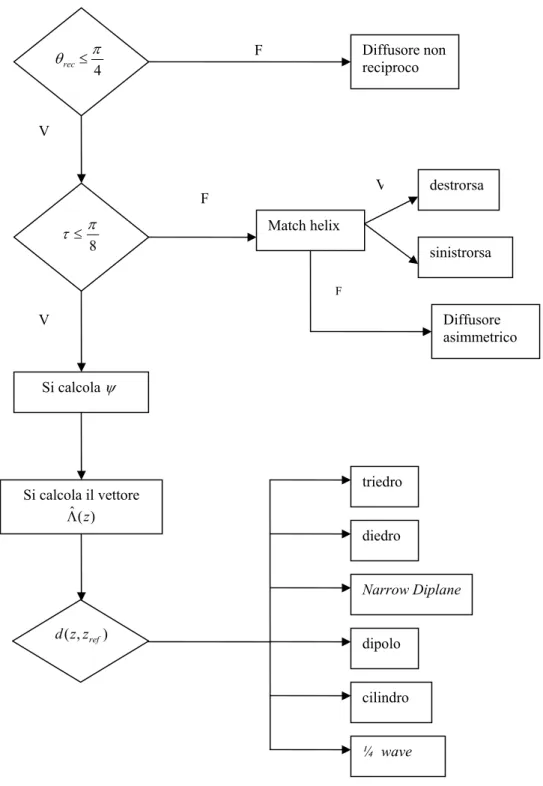
Nello schema di classificazione proposto da Cameron, illustrato in figura Fig. 3.2, la metrica utilizzata per la classificazione, d(z,z_ref), è derivata prima della diagonalizzazione [5-6]

(

)

(

2

)

(

2

)

1 1 1 , 1 max cos ) , ( ref ref ref ref z z z z zz z z d + + + + = ∗ ∗ − _(3.41)

Generalmente, però, la matrice di scattering è diagonalizzata prima della classificazione,

Fig. 3.1:disco unitario, dove sono rappresentati i diffusori elementari (punti scuri) e le zone di decisione, ricavate usando la metrica d(z,zref)

) ( ˆ z

Λ e Λˆ(z_ref). Questo porta alla seguente equazione per d(z,z_ref), che è anche più semplice della (3.41)

(

2

)

(

2

)

1 1 1 ) , ( ref ref ref z z zz z z d + + + = ∗ (3.42)

I vettori Λˆ(z_ref) dei diffusori elementari usati per la classificazione sono

) 1 ( ˆ ) ( ˆ _=Λ Λ_triedro z (3.43) ) 1 ( ˆ ) ( ˆ _{=Λ −} Λ_diedro z (3.44) ) 2 / 1 ( ˆ ) ( ˆ _{=Λ −} Λ_nd z (3.45) ) 0 ( ˆ ) ( ˆ _=Λ Λ_dipolo z (3.46) ) 2 / 1 ( ˆ ) ( ˆ _{=Λ −} Λ_cilindro z (3.47) ) ( ˆ ) ( ˆ 4 / 1 z =Λ i Λ (3.48)

4

π

θ_rec≤ Diffusore non _reciproco

V 8 π τ ≤ F F Match helix destrorsa sinistrorsa V Diffusore asimmetrico F V Si calcola ψ Si calcola il vettore ) ( ˆ z Λ ) , (z zref d triedro diedro Narrow Diplane dipolo cilindro ¼ wave

3.4 I problemi del metodo di classificazione di Cameron

1) Il metodo di decomposizione coerente del target (CTD) può essere applicato solo in condizioni di coerenza, ovvero quando tutta l’informazione polarimetrica è contenuta nella matrice di scattering. Il metodo di classificazione di Cameron non include nessuno strumento per accertarsi della coerenza del diffusore e quindi potrebbe essere erroneamente usato in aree dove lo scattering non è coerente[5-6].

2) Nel metodo di Cameron per ogni pixel dell’immagine e per ogni diffusore elementare è calcolata la metrica tramite la (3.41) o (3.42) in modo da assegnare il pixel alla classe più vicina. Cameron stesso dice, però, che questo metodo porta ad una classificazione grossolana. Questo può essere giustificato calcolando per ogni punto del disco unitario il rapporto tra il modulo del parametro z del diffusore che è stato classificato e il modulo del parametro z _ref

del diffusore elementare più vicino, secondo la (3.41) o la (3.42). In figura Fig.3.3 è rappresentato per ogni punto del disco unitario il valore di tale rapporto e come si può notare il metodo di Cameron tollera una dispersione elevata, fino a ±8db. Questo può essere un problema, per esempio, quando dobbiamo applicare tale metodo ad un sistema SAR con certi requisiti in termini di calibrazione radiometrica. La dispersione di z da z , infatti, può essere messa _ref

in relazione con lo squilibrio tra i canali VV e HH di un sistema SAR. Quindi se i requisiti in termini di calibrazione radiometrica di un sistema SAR richiedono che lo squilibrio tra i due canali debba essere inferiore ad 1 db è necessario mettere una soglia di 1 db da applicare al rapporto

(

)

db ref

z

z / così da limitarne

la dispersione. Adottando però una tale soglia molti pixel rimangono non classificati [5-6].

3.5 Il metodo SSCM

Adottando come metrica per la classificazione quella proposta da Cameron, cioè la (3.41), c’è il problema che per ogni coppia di punti complessi coniugati e appartenenti al bordo del disco unitario, _d(_eiφ,_e−iφ)=0 _{(dato che ( , )}

[

_{0, /2}

)

2

1 z ∈ π

z

d ). Quindi la

rappresentazione tramite il disco unitario è una distorsione dello spazio dei diffusori simmetrici. Cameron suggerisce, allora, di usare una superficie chiusa, che, per esempio, può essere ottenuta congiungendo il disco unitario in corrispondenza delle coppie di punti complessi coniugati che appartengono al bordo del disco. La sfera di Poincarè sembra essere, allora, una rappresentazione più adatta per il vettore max

sim

SG [5].

Tale rappresentazione è adottata nel metodo SSCM dove il vettore max

sim

SG , che dopo la diagonalizzazione può essere decomposto nel modo seguente

ˆ ˆ

max _{=α +δ}

G

è rappresentato da un punto sulla sfera di Poincarè. Per rappresentare il vettore ΛG sulla sfera di Poincarè le sue coordinate sono derivate

dalla (3.49) in funzione dei parametri α e δ

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ − + − −} + = Λ _{α δ α δ αδ}∗ _α∗_{δ αδ}∗ _α∗_δ δ α i 2 2 2 2 2 2 1 G (3.50)

ΛG può essere espresso in funzione degli angoli ψ_c,χ_c che individuano un punto sulla sfera di Poincarè

(

1 cos(2χ_c)cos(2ψ_c) cos(2χ_c)sin(2ψ_c) sin(2χ_c)

)

=

ΛG (3.51)

dove ψ_c,χ_c possono essere espressi in funzione dei parametri α e δ (Appendice II). Un diffusore simmetrico può quindi essere rappresentato come un punto sulla sfera di Poincarè di latitudine 2 e longitudine ψ_c 2 . Le coordinate dei sei diffusori elementari χ_c sono riportate nella tabella seguente (Tab.1):

Scattering triedro diedro dipolo Cilindro Nd ¼

(ψ_c,χ_c) (0°,0°) (90°,0°) (45°,0°) (18,43°,0°) (81,88°,0°) (0°,45°)

Per rimuovere l’ambiguità sull’angolo di rotazione, si considera solo metà sfera con ψ_c che varia nell’intervallo

[

0,π/2

]

. Se ψ_c∈

]

π/2,π

]

, le coordinate del diffusore simmetrico (ψ_c,χ_c) sono sostituite con (π −ψ_c,−χ_c) e l’angolo di rotazione ψ con

2 / π

ψ ± .

Solo un diffusore simmetrico e coerente può essere rappresentato da un punto sulla sfera, mentre un diffusore simmetrico e parzialmente coerente è rappresentato da un

punto interno alla sfera ad una distanza dal centro della sfera determinata dal grado di coerenza P _sym

(

)

2 2 2 2 2 2 4 δ α αδ δ α + + − = ∗ sym P (3.52)

dove il simbolo indica l’operazione di media spaziale.

Ci sono due metodi per accertarsi della coerenza dello scattering. Il primo è il test di coerenza per target distribuiti, per i quali lo scattering coinvolge molte celle di risoluzione. Il secondo è il test di coerenza per target puntiformi, per i quali, cioè, il segnale occupa una sola cella di risoluzione. In questo caso lo scattering si può considerare coerente se nella cella di risoluzione c’è uno scatteratore coerente dominante.

a) Implementazione del test di coerenza per target distribuiti

La distanza tra il centro della sfera di Poincarè e il punto che individua lo scatteratore,P , è utilizzata per stimare la coerenza dello scattering. _sym

Utilizzando un filtro a finestra mobile, opportunamente dimensionato, si crea una mappa di coerenza e i pixel per i quali P è vicino ad 1 rappresentano aree _sym

nelle quali lo scattering è localmente coerente. A causa dell’operazione di media spaziale, può accadere che le aree dove sono presenti targets con piccole variazioni nella struttura siano classificate come non coerenti, in questo caso il test di coerenza fornisce delle informazioni sbagliate. Per risolvere questo problema, una volta eseguito il test di coerenza per targets estesi, nelle aree classificate come non coerenti viene applicato il test di coerenza per target puntiformi.

b) Implementazione del test di coerenza per target puntiformi

Il test si basa sul confronto tra il rapporto segnale-rumore, calcolato sull’immagine ISAR, e una soglia denominata Rician Threshold. Per ogni cella di risoluzione si calcola il rapporto segnale rumore nel modo seguente [17]

BACKGROUND l k IMM l k _P P SNR , . = (3.53) 2 2 , 2 , 2 , , HV l k HH VV l k VV HH l k l k i i i P = + + − + _(3.54)

La coppia ( lk, ) individua la cella di risoluzione in esame, p l k

i _, è il campione dell’immagine ISAR nella cella ( lk, ) e nel canale polarimetrico

HV HH

VV VV HH

p= + , − , 2 ,P_k,l è, quindi, la potenza del segnale contenuto nella cella in esame e P_BACKGROUND è la potenza media del rumore. La (3.53) è derivata dal rapporto segnale rumore definito in funzione delle frequenze spaziali in [17], adattato al caso di immagini ISAR polarimetriche. Il rapporto segnale rumore calcolato come nella (3.53), viene poi confrontato con una soglia,λ_Rician, e se

IMM l k

SNR _. > λ_Rician (3.55)

allora il target contenuto nella cella ( lk, ) è classificato come coerente e quindi sarà possibile rappresentarlo come un punto sulla sfera di Poincarè. Nell’ articolo preso come riferimento [5] λ_Rician =15db.

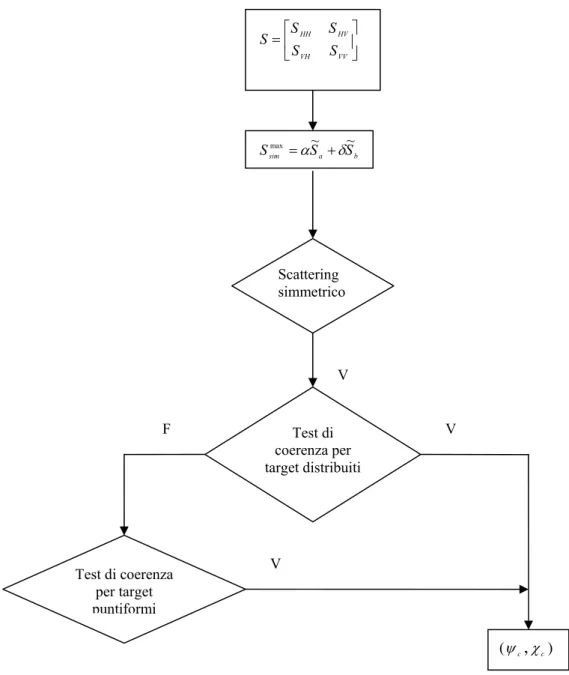
Il metodo SSCM si può, allora, riassumere nei seguenti passi:

1) Si calcolano i parametri α e δ della componente simmetrica massima usando l’algoritmo di Cameron e in particolare usando (3.16), (3.23), (3.29-3.31) . 2) Prima di analizzare la componente di scattering simmetrica massima si misura il

creare una mappa; i pixel per i quali il grado di simmetria è 0≤τ <π /8, sono assegnati alla classe degli scatteratori simmetrici.

3) A questo punto il test di coerenza per target distribuiti è applicato all’interno della classe che corrisponde ad uno scattering simmetrico. Si costruisce la mappa del grado di coerenza, P , usando una finestra mobile opportunamente _sym

dimensionata. Quindi, nelle aree classificate come non coerenti, è applicato il test di coerenza per bersagli puntiformi, che si basa sulla soglia di Rician. Le dimensioni dei filtri a finestra mobile usati per costruire le mappe del grado di simmetria e coerenza sono state scelte in modo da essere comparabili alle dimensioni degli oggetti che si voglio rilevare ed identificare nell’immagine. 4) Per i pixel classificati come coerenti vengono calcolati e analizzati i parametri

(ψ_c,χ_c) che rappresentano la componente simmetrica massima sulla sfera di Poincarè.

Nella figura 3.5 è illustrato lo schema a blocchi del metodo SSCM.

Nel metodo SSCM, a differenza che in quello di Cameron, non è definita nessuna metrica che consenta di classificare i centri di scattering. Uno degli sviluppi futuri sarà allora quello di definire una metrica tridimensionale per classificare i diffusori che possono essere rappresentati come punti sulla sfera di Poincarè.

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = VV VH HV HH S S S S S b a sim S S Smax ₌α~ ₊δ~ Scattering simmetrico (ψc,χ ) c Test di coerenza per target puntiformi Test di coerenza per target distribuiti V V F V