stato 0

CAPITOLO 3 – LA RICERCA DELLA FORMA DELLA MEMBRANA 3.1 Definizione dello “stato 0”

Uno dei problemi più delicati che occorre affrontare nella progettazione delle strutture a membrana pretensionate, consiste nella definizione del loro “stato 0”, ovvero, della configurazione che le membrane assumono nelle normali condizioni di esercizio sotto l’azione del peso proprio e della pretensione imposta.

In assenza di qualunque pretensionamento, una membrana non possiede infatti una forma propria, ma, al contrario, si adatta ai carichi che di volta in volta agiscono su di essa; in particolare, se la membrana è completamente priva di rigidezza flessionale, la forma della sua superficie media varia continuamente, istante per istante, inseguendo la configurazione funicolare dei carichi che su di essa sono applicati.

Di solito il peso proprio delle membrane è trascurabile e, per tale motivo, incapace di influenzare apprezzabilmente la forma della membrana. Il contrario accade per il carico da neve che risulta sempre preponderante rispetto alle altre azioni esterne; tuttavia, se la costruzione è rimovibile ed il suo uso è limitato ai soli mesi caldi, tale condizione risulta statisticamente irrilevante e poco significativa in termini progettuali. Considerazioni analoghe, rinforzate dalla pochezza delle masse in gioco, valgono per le azioni sismiche. Da quanto detto emerge che l’azione esterna a cui fare riferimento nella progettazione è costituita dal vento che per tale tipologia costruttiva è sempre particolarmente severa.

Nel seguito, stante le incertezze del quadro normativo nazionale e tenendo sullo sfondo il dettato della normativa europea (EC1), si assumerà in via cautelativa che l’azione del vento possa essere ben rappresentata da un carico unitario di 1000 kN/m2 agente staticamente su ciascuna superficie esposta nel modo più sfavorevole, ossia, in pressione o in depressione.

3.2 Il metodo della “densità di sforzo” per la ricerca dello stato 0

Il metodo è stato proposto nel 1972 da Linkwitz e Schek [3] per la definizione della forma ed il calcolo della copertura dello Stadio Olimpico di Monaco. Entrambi gli autori sono membri di un grande, prestigioso ed attivissimo gruppo di ricerca sulle strutture leggere (ILEK) fondato presso l’Università di Stoccarda da Frei Otto. Il metodo da essi proposto riconduce il problema fortemente non lineare della ricerca della forma ottimale

delle reti di funi o delle membrane pretensionate a quello delle condizioni di equilibrio statico di una travatura reticolare, governato da un sistema di equazioni lineari di facile soluzione. Il metodo è basato su una semplicissima (e per questo geniale) osservazione consistente nell’assumere costante in ciascun tratto in cui la generica fune può pensarsi idealmente suddivisa dai nodi della maglia, il rapporto fra lo sforzo assiale presente nel tratto, inizialmente incognito, e la lunghezza anch’essa incognita del tratto stesso, da cui il nome di metodo della densità di sforzo.

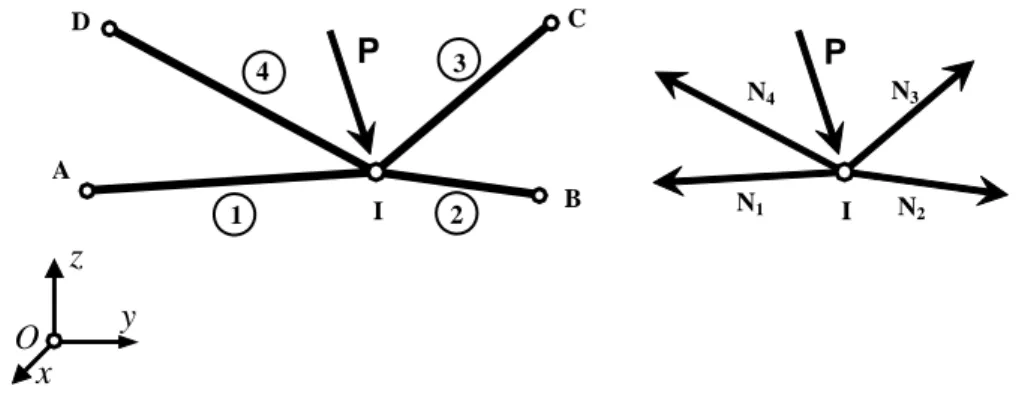
Con riferimento ad una rete spaziale di funi, consideriamo l’equilibrio del generico nodo I rappresentato nella figura 2 seguente,

D C P I B 1 A y x 2 4 3 z O P I N1 N2 N3 N4

Fig. 2: Un nodo di una rete di fune e lo schema statico corrispondente

e supponiamo che tale nodo sia collegato ai nodi adiacenti A, B, C e D mediante i tratti di fune completamente tesi, 1, 2, 3 e 4, rispettivamente. L’equilibrio fra le forze interne ed il carico esterno è espresso in forma vettoriale da:

0 P N N N N1+ 2 + 3+ 4+ I = ,

dove le forze interne incognite si assumono positive se si allontanano dal nodo. Mettendo in evidenza i valori degli sforzi assiali nei diversi tratti, la stessa equazione può essere scritta come 0 P n n n n1+ 2 2+ 3 3 + 4 4 + I = 1 N N N N ,

in cui N1, N2, N3 ed N4 sono gli sforzi assiali incogniti, mentre n1, n2, n3 ed n4 sono i

versori, anch’essi incogniti se la geometria non è completamente nota, dei diversi tratti di fune orientati positivamente se uscenti dal nodo I.

Proiettando l’equazione precedente sugli assi x, y e z del riferimento globale, si

ottengono le tre equazioni scalari:

⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ = + − + − + − + − = + − + − + − + − = + − + − + − + − 0 0 0 4 3 2 1 4 3 2 1 4 3 2 1 z I DI I D CI I C BI I B AI I A y I DI I D CI I C BI I B AI I A x I DI I D CI I C BI I B AI I A P L z z N L z z N L z z N L z z N P L y y N L y y N L y y N L y y N P L x x N L x x N L x x N L x x N ,

valide per ciascun nodo del sistema strutturale. In esse, LAI, LBI, LCI e LDI sono le lunghezze attuali dei tratti che collegano il nodo I ai nodi circostanti, mentre PxI, PyI e PzI sono le componenti del carico PI nel sistema di riferimento globale (O, x, y, z). Se tali equazioni

sono scritte per tutti gli N nodi della rete di funi si ottiene un sistema di 3×N equazioni che traducono le condizioni di equilibrio dell’intero sistema.

Le stesse equazioni descrivono anche le condizioni per l’equilibrio statico dei nodi di una travatura reticolare spaziale soggetta a condizioni di carico e di vincolo generiche.

Vi sono però delle differenze sostanziali fra le due tipologie strutturali considerate. Infatti, nel caso delle travature reticolari la geometria del sistema è nota così come lo sono i carichi, per cui il sistema delle equazioni di equilibrio viene normalmente utilizzato per determinare gli sforzi assiali incogniti nelle aste e le reazioni vincolari, se la travatura è staticamente determinata.

Nel caso delle reti di funi, invece, la geometria del sistema è incognita, per cui sono incognite sia le coordinate dei nodi, e conseguentemente le lunghezze delle aste, sia i valori degli sforzi assiali nei diversi tratti di fune assieme alle eventuali reazioni vincolari.

L’idea di Linkwitz e Schek consiste nell’assumere costanti e noti i valori dei rapporti

k k k N L

q = / fra lo sforzo assiale Nk e la lunghezza Lk del tratto di fune k-esimo cui si riferiscono, per cui, ad esempio, il sistema precedente diviene

⎪ ⎩ ⎪ ⎨ ⎧ = + − + − + − + − = + − + − + − + − = + − + − + − + − 0 ) ( ) ( ) ( ) ( 0 ) ( ) ( ) ( ) ( 0 ) ( ) ( ) ( ) ( 4 3 2 1 4 3 2 1 4 3 2 1 z I I D I C I B I A y I I D I C I B I A x I I D I C I B I A P z z q z z q z z q z z q P y y q y y q y y q y y q P x x q x x q x x q x x q ,

dove q1, q2, q3 ed q4 sono le densità di sforzo nei tratti di fune considerati.

Se tali equazioni vengono scritte per tutti i nodi della rete, si ottiene un sistema di 3×N

equazioni lineari, risolvibile attualmente per via numerica con estrema facilità, nelle 3×N

incognite x_i, y_i,z_i,i=1,_LN costituite dalle coordinate dei nodi del sistema. Ovviamente, per addivenire alla geometria dello stato 0 della membrana non occorre conoscere i valori delle densità di sforzo tratto per tratto ma è sufficiente conoscerne solo i rapporti.

Risolto il sistema di equazioni, la geometria della rete è finalmente nota per cui si conoscono le lunghezze delle funi tratto per tratto. Se si vuole che il tratto k-esimo nello stato 0 sia soggetto allo sforzo di pretensione Nk, nell’ipotesi di comportamento lineare del

materiale ed ipotizzando deformazioni piccolissime se non infinitesime, è sufficiente assegnare al tratto stesso la lunghezza iniziale

k k k k EA q l L + = 1 1 0 ,

in cui EAk è la rigidezza estensionale della fune.

3.3 Il reticolo di base

Per poter applicare il metodo della densità di sforzo occorre disporre di un reticolo di

base i cui nodi siano posti in corrispondenza biunivoca con i punti della membrana nella

configurazione iniziale definita dallo stato 0.

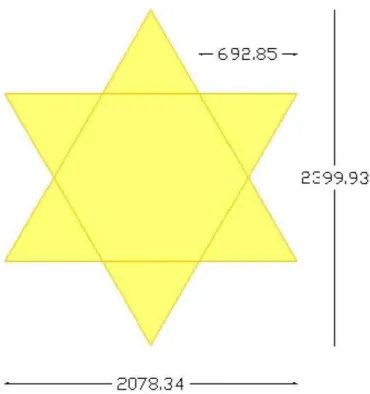
Nel caso progettuale in esame, l’area da ricoprire con la tensostruttura a membrana risulta quella a stella esagonale riportata nella figura 3 seguente. Ciascun triangolo ha il lato l ≅6,93m e l’altezza h= 3 2×l=6,00m, per cui le cui dimensioni complessive in pianta della tensostruttura sono 20,78×24,00m, in essa indicate.

Fig. 3: La pianta a stella esagonale dello spazio polifunzionale

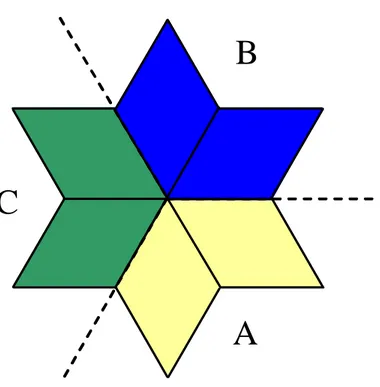
Questa a sua volta può essere vista come costituita da dodici triangoli, di cui sei esterni (le punte) e sei più interni (l’esagono regolare) mostrati nella figura 4a, oppure dai sei parallelogrammi mostrati nella successiva figura 4b.

a)

b)

Ne risulta che un buon reticolo di base è quello riprodotto nella figura 5 seguente, in cui ciascuno dei dodici triangoli equilateri suddetti è suddiviso a sua volta in 64 triangoli equilateri eguali ma più piccoli aventi il lato 1/8 del lato dei triangoli più grandi.

Fig. 5: Il grigliato di base

Tale suddivisione riflette la necessità tecnologica di poter costruire la membrana unendo strisce di materiale di larghezza non superiore a tre metri.

3.4 La presenza di simmetrie di rotazione

Guardando la tensostruttura nel suo insieme, si osserva facilmente come l’intera costruzione possa pensarsi generata mediante due rotazioni successive di una sua piccola parte rispetto ad un asse verticale. Ne risulta che l’insieme che occorre analizzare è costituito da due parallelogrammi consecutivi come mostrato nella successiva figura 6.

A

B

C

Fig. 6: Le simmetrie di rotazione

Ciò è dovuto essenzialmente alla forma scelta per la membrana che traduce la presenza di una simmetria rotazionale tripla per la presenza nella struttura di contrasto di un elemento curvo che si ripete tre volte nelle zone di altezza maggiore e della continuità della membrana in uno dei due parallelogrammi fra i due triangoli che lo compongono. Tenuto conto della presenza di tali simmetrie, lo studio della tensostruttura può essere limitato alla parte mostrata in figura 7 che ne costituisce il modulo.

A

A

1

A

2

3.5 La generazione dei nodi, delle aste e dei pannelli

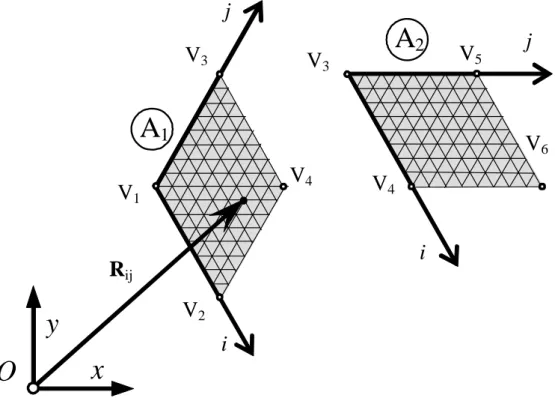
La generazione dei nodi del reticolo per ciascuno dei due parallelogrammi che costituiscono il modulo, si effettua facilmente avvalendosi in ciascuna regione di un proprio sistema di riferimento locale obliquo basato sulle coordinate discrete intere i e j, come mostrato nella successiva figura 8.

A

V

A

x

y

O

V

V

V

j

V

V

V

V

R

i

i

j

Fig. 8: I sistemi di riferimento locali

Note le posizioni di tre vertici dei parallelogrammi, e detto n il numero di suddivisioni scelto lungo ciascun lato, i vettori posizione dei nodi di ciascun reticolo si ricavano mediante le relazioni: per la parte A1 1 , , 1 1 , , 1 ) 1 ( ) 1 ( ) , ( 2 1 3 1 1 × − = + = + − + − × − + = j i n j n n V V i n V V V j i R _{L L} ; per la parte A2 1 , , 1 1 , , 1 ) 1 ( ) 1 ( ) , ( 4 3 5 3 3 × − = + = + − + − × − + = j i n j n n V V i n V V V j i R _{L L} .

A ciascuna coppia di valori i e j viene associato un numero progressivo. Quest’ultimo, oltre ad identificare il nodo, serve per fissare la topologia del reticolo attraverso le usuali matrici delle incidenze standard delle aste e dei pannelli.

In ciascuno dei parallelogrammi sono definite due serie di aste dirette parallelamente ai lati ed una terza serie di aste oblique. Di conseguenza ciascun parallelogramma elementare risulta suddiviso in due pannelli ulteriori di forma triangolare.

La determinazione delle incidenze delle travi e dei pannelli è estremamente semplice. Complessivamente il modulo risulta costituito da 153 nodi, 408 aste e 256 pannelli. 3.6 Le condizioni a contorno

Per la generazione dei nodi, delle aste e dei pannelli, alcuni nodi sono stati vincolati a terra, mentre la maggior parte di essi sono stati lasciati liberi. Ad altri nodi invece sono state date particolari condizioni al contorno per tener conto delle simmetrie strutturali e della presenza delle travi arcuate. Per il terzo di reticolo esaminato, la numerazione dei nodi posti al suo contorno è riportata nella figura 9.

I nodi 9 e 153 sono vincolati a terra e quindi sono bloccati gli spostamenti lungo x, y e z. I nodi 1, 11, 21, 31,41, 51, 61, 71, 81 e 145 sono vincolati a stare sull’asta parabolica e quindi le loro coordinate sono note.

I nodi 10, 19, 28, 37, 46, 55, 64 e 73 sono obbligati a muoversi sul piano verticale di simmetria che contiene gli stessi nodi.

I nodi 82, 91, 100, 109, 118, 127 e 136 hanno bloccata la componente di spostamento lungo y mentre sono liberi di muoversi parallelamente a x e z.

I rimanenti nodi sono liberi di muoversi nello spazio.

Tutte le aste hanno densità di sforzo unitaria, mentre quella delle aste dei bordi liberi vale 10.

3.7 La soluzione ottenuta

Date le prececdenti condizioni al contorno il metodo della “densità di sforzo” fornisce la soluzione riportata nelle seguenti figure 10 ed 11 in cui sono riportate la pianta ed il prospetto della membrana.

Fig. 11: La soluzione ottenuta in prospetto

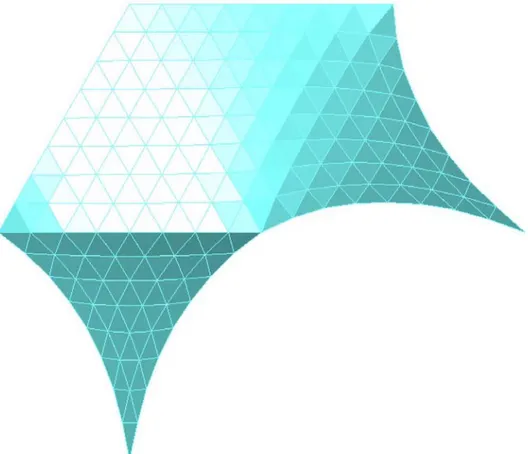
Tenuto conto delle simmetrie di rotazione, l’intera membrana risulta quella riportata nelle successive figure 12 e 13.