4.1 INTRODUZIONE 4. RISCALDAMENTO AD INDUZIONE

UNIVERSITA’ DEGLI STUDI DI PISA 33

4.

RISCALDAMENTO AD INDUZIONE

Questo capitolo descrive la modalità di riscaldamento ad induzione e la sua applicabilità alla geometria del catodo in esame. Nella prima parte sono riportate le equazioni che descrivo l’induzione elettromagnetica, segue poi l’applicazione della modalità di riscaldo al catodo in esame con le relative simulazioni numeriche e le conclusioni.

4.1

INTRODUZIONE

In un corpo sottoposto ad un campo magnetico variabile nel tempo si generano delle forze elettromotrici descritte dalla legge di Faraday. Se il materiale è conduttore, tali forze elettromotrici generano delle correnti, dette correnti di Foucault, che danno luogo a delle perdite per effetto Joule direttamente all’interno del corpo da trattare. Nel riscaldamento ad induzione si genera ancora calore per il passaggio di correnti attraverso il materiale ma sono indotte da sorgenti separate. Il materiale da riscaldare diventa il circuito secondario del trasformatore.

I principali vantaggi del riscaldamento ad induzione sono:

- Alta velocità di riscaldamento del materiale;

- Riscaldamento diretto dell’emettitore;

- Basse temperature degli avvolgimenti;

- Alto rendimento termico;

- Si evita il contatto diretto tra riscaldatore (circuito primario) e tubo principale (circuito secondario).

La figura sotto riportata mostra un trasformatore con un primario costituito da una avvolgimento a singolo strato ed un secondario a singolo avvolgimento cortocircuitato,

UNIVERSITA’ DEGLI STUDI DI PISA 34 separati da un piccolo divario di aria. Quando la corrente alternata attraversa il primario si instaura una forza elettromotrice nel secondario che causa un passaggio di correnti; tali correnti tendono a cancellare il flusso che le produce, in accordo alla legge di Lenz.

Figura 4.1 - Campo magnetico e correnti indotte in un trasformatore

4.2

INDUZIONE ELETTROMAGNETICA

4.2.1 EQUAZIONI DI MAXWELL

Trascurando le correnti di spostamento date dalle frequenze in gioco e supponendo le grandezze sinusoidali, le equazioni di Maxwell possono essere scritte nella forma: ∇ · = 0 ∇ x = − = − ∇ x = = (4.1)

Dalla legge di Ohm inoltre si ha

UNIVERSITA’ DEGLI STUDI DI PISA 35 Tenuto conto che, con riferimento ad un sistema di coordinate cilindriche ( , , ) sono diverse da zero solo le componenti di e di , omettendo i pedici, dalle prime due equazioni di Maxwell

! " + $ "% = & ' & " = % (4.3)

combinando le due equazioni insieme si ottiene:

(_!

"( +$_" ! _" −)*+_' % = 0 (4.4)

dove ponendo: ,- = μ/2

(_!

"( +$_" ! _" − 2 ,-% = 0 (4.5)

L’equazione sopra riportata è una tipica equazione alla Bessel la cui sui soluzione generale è:

% = 1(23 4 + 235 4 ) + 6(ker 4 + :35 4 ) (4.6) con :

4 = √2/<

< = =_*+-' = =_>?+' spessore di penetrazione

23 parte reale della funzione di Bessel

235 parte immaginaria della funzione di Bessel :3 parte reale della funzione di Kelvin

UNIVERSITA’ DEGLI STUDI DI PISA 4.2.2 SPESSORE DI PENETRAZ

Per completezza è necessario interpretare in maniera corretta il termine chiamato spessore di penetrazione.

un conduttore, la distribuzione della corrente all'interno della sezione del conduttore è uniforme. Tuttavia, quando la corrente è alternata, la distribuzione non è uniforme e avremo sempre il valore massimo

conduttore che diminuirà

Questo fenomeno di distribuzione di corrente non uniforme all'interno della sezione di un conduttore è chiamato effetto pelle

pezzo in lavorazione che si trova all'interno di una bobina di induzione. Questo è uno dei fattori principali che causa la concentrazione di correnti indotte nello strato di superficie ("pelle") del pezzo

applicazioni elettriche con corrente alternativa. A causa di questo effetto la densità di corrente e quindi la potenza sarà concentrata in uno strato superficiale del conduttore. Questo strato è chiama

dalle proprietà dei materiali (resistività elettrica e permeabilità magnetica relativa). Si evidenzierà un effetto pelle più pronunciato quando viene applicata alta frequenza o quando il raggio del pezzo in lavorazione è grande.

4.3

RISCALDAMENTO AD IND

TUBOLARI

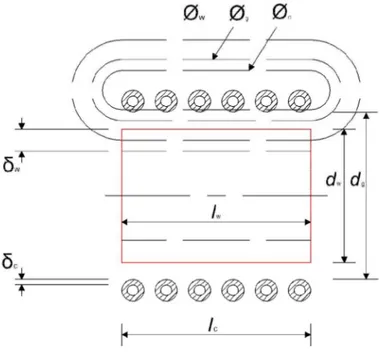
Considerando una geometria tubolare

Figura

UNIVERSITA’ DEGLI STUDI DI PISA SPESSORE DI PENETRAZIONE

Per completezza è necessario interpretare in maniera corretta il termine chiamato spessore di penetrazione. Quando una corrente elettrica continua attraversa un conduttore, la distribuzione della corrente all'interno della sezione del conduttore è uniforme. Tuttavia, quando la corrente è alternata, la distribuzione non è uniforme e avremo sempre il valore massimo della densità di corrente sulla superficie del conduttore che diminuirà passando dalla superficie del conduttore verso il centro. Questo fenomeno di distribuzione di corrente non uniforme all'interno della sezione di uttore è chiamato effetto pelle. Pertanto, l'effetto pelle sarà presente anche nel pezzo in lavorazione che si trova all'interno di una bobina di induzione. Questo è uno dei fattori principali che causa la concentrazione di correnti indotte nello strato di superficie ("pelle") del pezzo. L'effetto pelle è di grande importanza pratica nelle applicazioni elettriche con corrente alternativa. A causa di questo effetto la densità di corrente e quindi la potenza sarà concentrata in uno strato superficiale del conduttore. Questo strato è chiamato lo spessore di penetrazione,δ,e dipende dalla frequenza e dalle proprietà dei materiali (resistività elettrica e permeabilità magnetica relativa). Si evidenzierà un effetto pelle più pronunciato quando viene applicata alta frequenza o quando il raggio del pezzo in lavorazione è grande.

RISCALDAMENTO AD INDUZIONE PER GEOMETRIE

TUBOLARI

Considerando una geometria tubolare

Figura 4.2- Esempio di geometria tubolare

36 Per completezza è necessario interpretare in maniera corretta il termine <

uando una corrente elettrica continua attraversa un conduttore, la distribuzione della corrente all'interno della sezione del conduttore è uniforme. Tuttavia, quando la corrente è alternata, la distribuzione non è uniforme e della densità di corrente sulla superficie del dalla superficie del conduttore verso il centro. Questo fenomeno di distribuzione di corrente non uniforme all'interno della sezione di . Pertanto, l'effetto pelle sarà presente anche nel pezzo in lavorazione che si trova all'interno di una bobina di induzione. Questo è uno dei fattori principali che causa la concentrazione di correnti indotte nello strato di . L'effetto pelle è di grande importanza pratica nelle applicazioni elettriche con corrente alternativa. A causa di questo effetto la densità di corrente e quindi la potenza sarà concentrata in uno strato superficiale del conduttore. e dipende dalla frequenza e dalle proprietà dei materiali (resistività elettrica e permeabilità magnetica relativa). Si evidenzierà un effetto pelle più pronunciato quando viene applicata alta frequenza o

UNIVERSITA’ DEGLI STUDI DI PISA 37 con raggio esterno @ ed interno b, è possibile ricavare la relazione tra A e B che rappresentano le due costanti arbitrarie nella soluzione in forma generale dell’equazione di Bessel (equazione (4.6)), usando il fatto che per r = b la tensione indotta eguaglia la derivata temporale del flusso interno al tubo. Il foro del cilindro cavo è aria, per tale motivo la densità di flusso è uniformemente distribuito e proporzionale a _A%_B: C2D2 = EB2D2 = − (6D2-) = − (μA%B)D2- (4.7) EB = −)*FG!H>B ( ->'B = − )B!H FIJ( (4.8)

μ" è la permeabilità relativa del materiale.

Inoltre è noto che:

EB = − K !_"L_"MB = −4N1(23 O42 + 235O42) + 6(:3 O42 + :35O42)P (4.9)

Eguagliano le due equazioni di E_B è possibile ottenere il valore di 6 1⁄ .

Il termine 6 1⁄ risulta essere di fondamentale importanza nella determinazione la distribuzione di %, E internamente al corpo e quindi della potenza che si sviluppa. In breve è possibile scrivere le distribuzioni del campo magnetico e della corrente di densità come: ! !R = (BS" T"U) BSV T") (BS" TWU) BSV TW)∗ Y(6 1)⁄ (4.10) Z Z[ = (BS" \ _{T"U) BSV}\ _T") (BS"\ _{TWU) BSV}\ _TW)∗ ](6 1)⁄ (4.11)

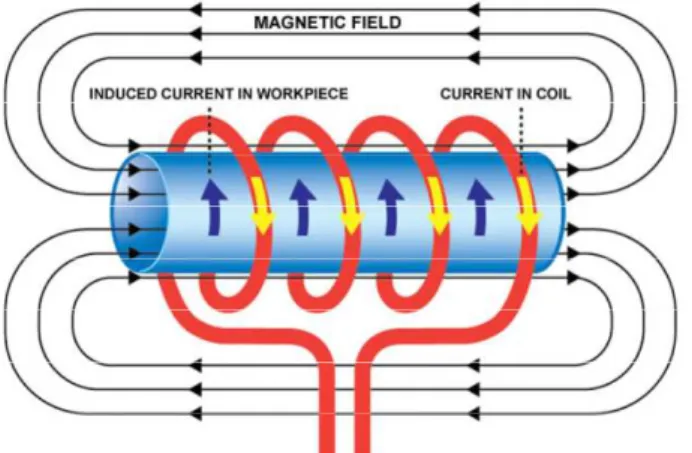
UNIVERSITA’ DEGLI STUDI DI PISA 38 Dove le funzioni Y(6 1)⁄ e ](6 1)⁄ vanno a zero quando i termini :3 e :35 vanno a zero o quando 6 1⁄ è piccolo e %_[ , E^ rappresentano rispettivamente il campo magnetico e la densità di corrente superficiale. In pratica la distribuzione varia con le grandezze 2/@, @/<, /@; di seguito riportiamo l’andamento di |E E⁄ |_[ per la geometria in esame nei casi due casiY = 10a% e Y = 10b% .

Figura 4.3 - Caduta della densità di corrente per geometrie tubolare in funzione del rapporto r/R e R/delta [12]

Figura 4.4 – Caduta della densità di corrente per geometrie cilindriche in funzione del rapportor/R e R/delta [12]

UNIVERSITA’ DEGLI STUDI DI PISA 39 La distribuzione di corrente è sempre meno uniforme rispetto al caso di riscaldamento per conduzione diretta di corrente continua.

E’ possibile calcolare la potenza nelle sue componenti attiva e reattiva usando il teorema di Poynting che esprime la conservazione dell'energia del campo elettromagnetico nel caso in cui i campi elettrico e magnetico siano accoppiati.

c + d = − e x e∗ = −ρge x e∗ =hij_l(k(Npnopq+ jqnopqP t1/4- (4.12)

dove:

p_nopq+ jq_nopq =_ui- (pqv_{(pqv TWU) BSV TW)}\TWU) BSV\TW)∗ w(6 1⁄ ) (4.13)

Moltiplicando l’espressione di Poynting per la superficie 2D@x si ottenere la potenza totale dissipata per effetto Joule nel corpo:

cy = K'W!_JR(L wzBS(2D@x) = (D@-x)%[-μ"μA2DYwzBS (4.14) Di seguito riportiamo gli andamenti della funzione w_zBS nel caso di permeabilità relativa pari ad 1.

UNIVERSITA’ DEGLI STUDI DI PISA 40 Osservando l’equazione di c_y, si può notare che per una geometria data e per una potenza necessaria le uniche variabili risultano essere la frequenza e %_[ . Come visibile dal grafico, anche il termine w_zBS racchiude la dipendenza dalla frequenza nel termine chiamato spessore di penetrazione.

4.4

EMETTITORE RISCALDATO PER INDUZIONE

4.4.1 CALCOLO DEI PARAMETRI NECESSARI AL RISCALDAMENTO

Per una completa comprensione di questa modalità di riscaldamento si è scelto di ricavare il termine %_[ per tre frequenze:

Y$ = 10a%

Y- = 10b%

Ya = 10{%

Date le frequenze in gioco e la geometria del nostro corpo è possibile ricavare:

<?$ = 0,00577 4 w zBS?$= 0,028 c• = 11,73 • %^?$= 631 ̇752,96 1/4 <?- = 0,000577 4 wzBS?- = 0,142 c• = 11,73 • %^?- = 28 ̇053,18 1/4 † † <?a_w= 5,77 · 10_{zBS?a= 0,1}‡b 4 c• = 11,73 • %^?a = 8 ̇631,38 1/4

Dove per semplicità si è utilizzato lo spessore di penetrazione riferito alla resistività del materiale più conduttivo e cioè il tantalio.

In questa prima analisi si utilizza l’ipotesi di riscaldamento ideale delle superfici del corpo, di conseguenza tutta l’energia in ingresso nel materiale verrà immagazzinata come calore. Durante il riscaldamento, la distribuzione di temperatura nel volume non

UNIVERSITA’ DEGLI STUDI DI PISA 41 è uniforme, pertanto esisterà un gradiente di temperatura che causerà un flusso di calore dalla superficie calda verso tutto il resto del materiale.

La temperatura media di incremento _T(K) è definita come la temperatura di equilibrio termico raggiunta nel corpo dopo lo spegnimento della sorgente di energia. Appare in ogni equazione come funzione del tempo e della potenza in ingresso.

Nel riscaldamento ad induzione si assume che il calore venga prodotto uniformemente in un piccolo strato della superficie.

Fortunatamente il corpo in esame è di dimensioni ridotte, pertanto è possibile trascurare il gradiente di temperatura tra superficie e parete interna del tantalio nel calcolo della potenza necessaria al riscaldamento.

4.4.2 DISTRIZBUZIONI DELLA TEMPERATURA MEDIANTE SIMULAZIONE

NUMERICA

A tal punto è possibile verificare, mediante l’aiuto del programma di simulazione COMSOL, il raggiungimento della temperatura per le frequenze in gioco, assegnando direttamente il campo magnetico superficiale %^ sotto le ipotesi di isolamento magnetico e termico delle superfici e caratteristiche del materiale costanti, in un modello assialsimmetrico.

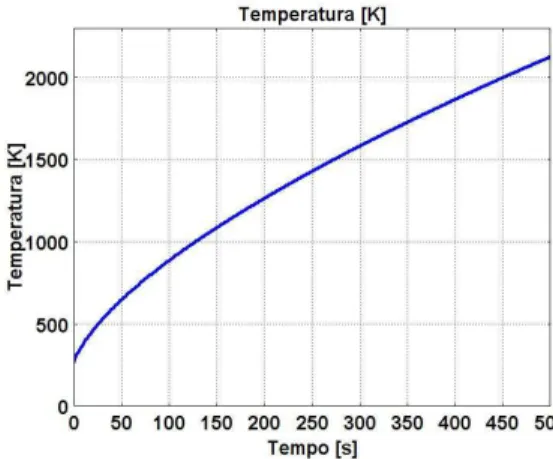
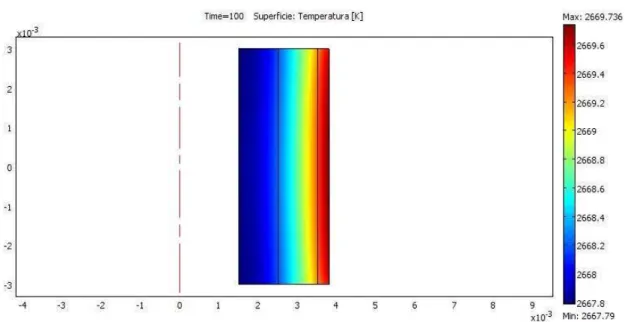
Di seguito sono visualizzate la distribuzioni della temperatura internamente al corpo al tempo t=100 s e l’andamento temporale della temperatura considerando un punto a distanza r = 2 mm rispetto all’asse di simmetria del corpo nelle tre frequenze.

UNIVERSITA’ DEGLI STUDI DI PISA 42 Frequenza Y_$ = 10a%

Figura 4.6 - Distribuzione della temperatura interna al pezzo al tempo di 100s alla frequenza di 1 kHz

Frequenza Y_- = 10b%

Figura 4.7 - Distribuzione della temperatura interna al pezzo al tempo di 100s alla frequenza di 0.1 MHz

UNIVERSITA’ DEGLI STUDI DI PISA 43 Frequenza Y_a = 10{%

Figura 4.8 - Distribuzione della temperatura interna al pezzo al tempo di 100s alla frequenza di 10 MHz

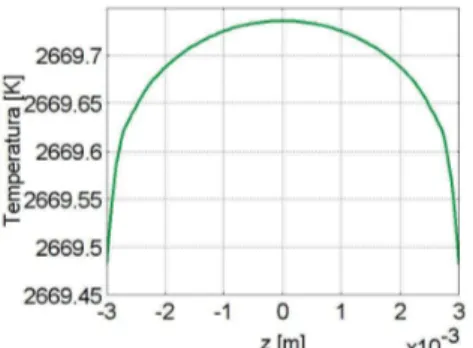
Figura 4.9 - Temperatura al variare del tempo di un punto posizionato a 0,2mm dall’asse di simmetria, per le tre frequenze in esame

UNIVERSITA’ DEGLI STUDI DI PISA 44 Come visibile per ogni frequenza in gioco è possibile raggiungere la temperatura di 1.900 K in meno di 100 secondi anche se è da notare che maggiore è la frequenza in gioco, maggiore è l’uniformità assiale della temperatura. Di seguito sono riportati i grafici dove sono messe in evidenza le temperature della superficie esterna del catodo (distanza dall’asse di simmetria pari a 3.8mm e altezza del cilindro variabile da -3mm a 3mm, coordinata z) nelle tre differenti frequenze analizzate.

Figura 4.10 - Distribuzione della temperatura sulla superficie esterna del catodo alla frequenza di 1kHz

Figura 4.11 - Distribuzione della temperatura sulla superficie esterna del catodo alla frequenza di 100kHz

Figura 4.12 - Distribuzione della temperatura sulla superficie esterna del catodo alla frequenza di 10MHz

UNIVERSITA’ DEGLI STUDI DI PISA 45 E’ possibile notare come la differenza tra temperatura massima e temperatura minima della superficie alle differenti frequenze, passi da 1,5 K della Figura 4.10, a 0,75 K della Figura 4.11 fino a 0.28 K della Figura 4.12.

4.4.3 CARATTERISTICHE DEL MATERIALE VARIABILI CON LA

TEMPERATURA

L’analisi precedente è stata condotta nell’ipotesi di caratteristiche dei materiali costanti. Nella realtà al variare della temperatura le caratteristiche che costituiscono il materiale variano notevolmente, ad esempio il calore specifico, la resistività, la permeabilità magnetica. Soffermandoci sulle ultime due citate è evidente che se si prendono in considerazione due materiali (1,2) aventi la stessa resistività ma differente permeabilità µ, allora Jˆ

J( = =

F(

+ˆ . Se µ aumenta di un valore ‰, δ diminuisce di √‰ e

t/< aumenta di √‰. A causa di ciò la distribuzione della densità di corrente si restringerà verso la superficie. La potenza dissipata nel pezzo c_y aumenta linearmente a causa di µ, ma l’effetto di Š/< potrebbe incidere negativamente a seconda del posizionamento nella curva di p. Se p era alla sinistra del massimo, aumenterà all’avvicinarsi al punto di massimo e poi decrescerà. Fortunatamente i materiali che costituiscono il corpo in esame sono paramagnetici, per tanto la caratteristica della variazione di µ è trascurabile, inoltre è possibile trascurare anche il comportamento critico prima del punto di Curie. Di notevole importanza è invece l’influenza della resistività sul comportamento fisico delle correnti interni al materiale. Se aumenta di una quantità ‰, < aumenta di √‰ e Š/< diminuisce di √‰. La corrente penetrerà più profondamente nel metallo. La potenza c_y dipenderà da p con le stesse modalità descritte precedentemente per µ.

Come visto nel caso di riscaldamento mediante conduzione diretta di corrente, le resistività del tantalio e della grafite si comportano diversamente al variare della

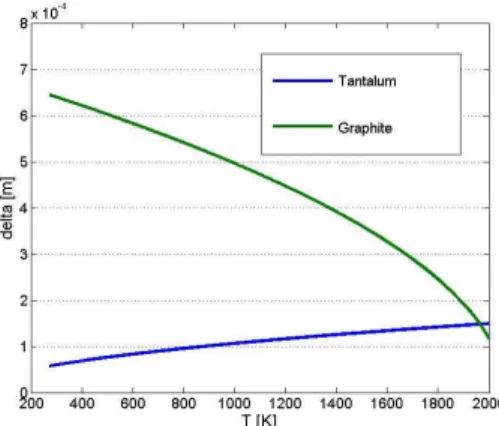
UNIVERSITA’ DEGLI STUDI DI PISA 46 temperatura. Di seguito sono riportati gli andamenti dello spessore di penetrazione per le tre frequenze considerate.

Figura 4.13 - Andamento dello spessore di penetrazione al variare della temperatura per il tantalio e la graffite, alla frequenza di 1 kHz

Figura 4.14 - Andamento dello spessore di penetrazione al variare della temperatura per il tantalio e la graffite, alla frequenza di 0.1 MHz

Figura 4.15 - Andamento dello spessore di penetrazione al variare della temperatura per il tantalio e la graffite, alla frequenza di 10 MHz

UNIVERSITA’ DEGLI STUDI DI PISA 47 Oltre ai parametri considerati è necessario riportare anche l’andamento della quantità di calore teorica in :•ℎ/ŠŒ• necessaria per riscaldare da 0°C fino alla temperatura T voluta una tonnellata di un definito materiale. Come evidenziato dal grafico sottostante l’andamento non è lineare, ciò implica che l’andamento dei calori specifici è crescente all’aumentare della temperatura, cioè più la temperatura aumenta maggiore è l’apporto energetico che bisogna fornire per riscaldare ulteriormente il pezzo.

Figura 4.16 - Quantità di calore teorica necessaria per riscaldare da 0°C fino a 1’400°C alcuni materiali [12]

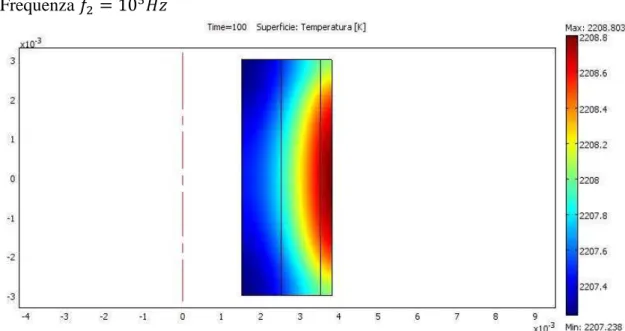
Risulta meno pronunciato invece l’andamento della conducibilità termica Ž [• 4⁄ •] in funzione della temperatura.

UNIVERSITA’ DEGLI STUDI DI PISA 48

4.4.4 SIMULAZIONE NUMERICA DELLA DISTRIBUZIONE DI TEMPERATURA

PER CARATTERISTICHE VARIABILI

Per capire l’effetto complessivo dei parametri sopra descritti di seguito riportiamo la distribuzione della temperatura nel pezzo al tempo t=100s e l’andamento al centro dell’emettitore al variare del tempo in condizioni di caratteristiche variabili, per la sola frequenza f=1kHz.

Y$ = 10a%

Figura 4.18 - Distribuzione della temperatura interna al pezzo al tempo di 100s alla frequenza di 10 MHz con caratteristiche dei materiali variabili

Figura 4.19 - Andamento della temperatura nel tempo nel punto a distanza 0.2 mm dall’asse di simmetria alla frequenza di 1 KHz con caratteristiche dei materiali

UNIVERSITA’ DEGLI STUDI DI PISA 49 E’ evidente come la variazione delle caratteristiche del materiale abbia un effetto globalmente peggiorativo nel riscaldamento del pezzo. Infatti come visibile è sempre possibile raggiungere la temperatura voluta, ma con un maggior tempo di riscaldamento.

4.5

DIMENSIONAMENTO DEGLI AVVOLGIMENTI

4.5.1 MODELLO FISICO

Risulta necessario procedere con il dimensionamento preliminare dell’avvolgimento che costituisce il circuito primario. Partendo dall’intensità del campo magnetico %_[ necessario a produrre calore in ingresso sulla superficie del corpo da riscaldare, esistono tre componenti di flusso,Ø_y il flusso che collega il pezzo, Ø_‘ il flusso nel traferro , Ø_’ flusso che attraversa la superficie dell’avvolgimento.

UNIVERSITA’ DEGLI STUDI DI PISA 50 Il flusso interno al pezzo Ø_y e la potenza c_y sono legate al valore di H_e dalla relazione:

cy = K'W!_JR(L wzBS 2D@x = D@-x %[-μ"μA2DYwzBS (4.15)

Øy = %” μ"μA1y •zBS− w zBS (4.16)

Il flusso nel traferro Ø_‘:

Ø‘ = %” μA1‘ (4.17)

Anche nell’avvolgimento è presente l’effetto pelle, così la corrente è forzata a fluire sulla superficie esterna. Il flusso attraverso gli avvolgimenti vale:

Ø’ = :" FGJ–_-> – %[ 1 − (4.18)

Con :_" fattore di correzione che tiene di conto della spaziatura tra gli avvolgimenti (:_" è compreso tra 1 ed 1.5).

Il flusso totale è la somma delle tre componenti:

ØA = Øy + Ø‘+ Ø’ (4.19)

In genere è rappresentabile quanto detto mediante una serie di circuiti elettrici equivalenti. Baker [13] rappresenta la teoria del riscaldamento ad induzione mediante un circuito equivalente molto simile a quello normalmente utilizzato per i trasformatori dove la resistenza e la reattanza del pezzo, dell’aria e dell’avvolgimento

(@_y, —_y, —_‘, 3 —_’ sono tutte in serie e connesse in parallelo con una indefinita X che rappresenta l’impedenza dell’effetto terminale del pezzo. Questa teoria è semplificata nel caso in esame con un circuito in serie. L’ipotesi tacita in tale semplificazione è che tutti i percorsi condividono una comune intensità del campo magnetico %_” . L’ipotesi fatta implica l’esistenza di accoppiamento molto vicino tra il pezzo e l’avvolgimento, e

UNIVERSITA’ DEGLI STUDI DI PISA 51 che tutto il flusso definito come Ø_’ colleghi l’avvolgimento. Il flusso definito Ø_A può quindi essere rappresentato come:

Figura 4.21 – Circuiti equivalenti

L’impedenza corrisponde a: ˜ = @_y + @_™ + š —_y+ —_‘+ —_’›

Resistenza del pezzo: @_y = œ μ_"w1_y [Œℎ4^]

Resistenza dell’avvolgimento: @_’ = œ •I> –J–

- [Œℎ4^] Reattanza del gap: —_‘ = œ 1_‘ [Œℎ4^]

Reattanza del pezzo: —_y = œ μ_"•1_y [Œℎ4^]

Reattanza dell’avvolgimento: —_’ = œ •I> –J–

- [Œℎ4^]

con: œ =->?+Gž–(

Ÿ– [Œℎ4^/4

-_]

Queste equazioni possono essere utilizzate per il calcolo delle maggiori caratteristiche dell’avvolgimento come: rendimento, il fattore di potenza dell’avvolgimento e il kVA, la tensione per avvolgimento e la corrente per avvolgimento.

Rendimento dell’avvolgimento : =_WW¡

–UW¡

UNIVERSITA’ DEGLI STUDI DI PISA 52

dove: ˜- = @_’+ @_y -+ —_‘+ —_y+ —_’

-Potenza dell’avvolgimento : c = c_y/

t1 = c/¢Œ^Ø

Tensione per avvolgimento: _ž&–

–=

¤¥

’¦""S§ S ¨S" ©ªª¦Ÿ‘VTS§ ¦ ¦ ©ŸS = ¤¥ !GŸ–

Corrente per avvolgimento «_’¬_’ = %_Ax_’

La relazione che determina il collegamento tra il problema della determinazione dello spessore dell’isolamento termico, nella trattazione semplificata, ed il dimensionamento dell’avvolgimento è esplicita e chiara nella relazione sopra scritta e riguardante il rendimento dell’avvolgimento:

c = cy/ = cy_W¡UWW¡_{– –} (4.20)

cy = •- tŒx. ¯+ cŸ¦[[ (4.21)

4.5.2 IPOTESI DI ISOLAMENTO TERMICO DELLE SUPERFICI

La potenza c è funzione di della resistenza @_’, la quale dipende dal diametro interno dell’avvolgimento °_’ e dal tipo di materiale di cui è costituito . Maggiore è il diametro dell’avvolgimento, e quindi la distanza tra primario e secondario, maggiore è la potenza c necessaria ad ottenere l’intensità del campo magnetico %_[ voluto. La distanza °_’ è legata alla temperatura di fusione del materiale che costituisce l’avvolgimento e che viene investito dalle perdite di calore superficiali del pezzo in riscaldamento. @_’ inoltre dipende dalla resistività del materiale, minore è la resistività dell’avvolgimento, minori saranno le perdite per effetto Joule prodotte e quindi minore

UNIVERSITA’ DEGLI STUDI DI PISA 53 sarà la c . Da tale considerazioni è evidente che il materiale ideale per la realizzazione del secondario è caratterizzato da un’alta temperatura di fusione ed una bassa resistività.

Ipotizzando la superficie del pezzo da riscaldare isolata termicamente, nell’equazione sopra riportata si annulla il termine c_Ÿ¦[[, ed è possibile scegliere il materiale dell’avvolgimento esclusivamente in base alla resistività. Di seguito sono riportati i valori della potenza c ottenuta in condizione di isolamento termico delle superfici del pezzo e avvolgimento in rame per le tre frequenze in esame:

† † Y = 10 a_% ™z = 1,62 ∗ 10‡±²4 °¢ = 0.0076 4 c = 921,43 • = 0,01 † † Y = 10 b_% ™z = 1,62 ∗ 10‡±²4 °¢ = 0.0076 4 c = 29,93 • = 0,40 † † Y = 10 {_% ™z = 1,62 ∗ 10‡±²4 °¢ = 0.0076 4 c = 28,98 • = 0,41

E’ possibile notare che alla frequenza di 1000 Hz si renda necessaria una potenza di gran lunga superiore ai 100 W disponibili.

4.5.3 ANALISI TERMICA DELLE DISPERSIONI

Fino ad adesso l’analisi è stata condotta in condizioni di isolamento termico delle superfici e cioè uguaglianza tra energia in ingresso nel corpo ed energia immagazzinata. Se, al contrario, le superfici sono prive di isolamento termico si hanno perdite superficiali per irraggiamento e per conduzione, pertanto il bilancio energetico risulta essere:

cy = •- tŒx. ¯+ cŸ¦[[ (4.22)

con:

cxŒ^^ = Ž ∆¯ ”_´ + µ ¶ 1^ ·¸_{− ·}

UNIVERSITA’ DEGLI STUDI DI PISA 54

µ emissività della superficie

¶ costante di Stefan Boltzmann [E 4⁄ -^œ¸ ]

1^ superficie radiante [4-] Ž conducibilità termica ¹_T»º¼ ∆¯ ´ gradiente di temperatura¹ » T¼

Figura 4.22 – Perdite di calore del corpo

Le perdite per conduzione riguardano la parte in tantalio che nel catodo si estende per tutta la lunghezza del tubo. Si ipotizza un gradiente di temperatura pari a 50 K/mm . La potenza immagazzinata un dato del problema, come già detto corrisponde alla potenza necessaria a riscaldare il corpo in esame dalla temperatura ambiente T=273 K alla temperatura di emissione dell’emettitore ovvero T=1.900 K nel tempo voluto e corrisponde a circa 12W. Nel caso di superfici libere da qualunque tipo di isolamento termico risulterebbe

cV"" = cV""¯©+ cV""´©½¾= 63 •

c_’¦§ = c_{’¦§ ¯©} = 20•

con una c_Ÿ¦[[ = 83 • e quindi una c_y = 12 + 83=95 W. Considerando un rendimento dell’avvolgimento pari a 0,41, valore associato ad una frequenza pari a

UNIVERSITA’ DEGLI STUDI DI PISA 55 disponibili. Inoltre il calore disperso per irraggiamento surriscalderebbe l’avvolgimento a temperature molto elevate, ben sopra alla temperatura di fusione del rame. Per tali motivi si rende necessario l’utilizzo di uno scudo termico che diminuisca la dispersione di calore per irraggiamento e che protegga di conseguenza l’avvolgimento.

4.5.4 ANALISI TERMICA DELLE DISPERSIONI CON INSTALLAZIONE DI UNO

SCUDO TERMICO

Si consideri lo scudo termico di superficie ¿_[ concava contenente il corpo di superficie ¿_B convesso. Il fattore di vista À_[B vale 1 poiché tutte le radiazioni emesse dal corpo cadono sullo scudo, mentre À_[B non è unitario perché una frazione dell’energia emessa dal corpo si chiude sul corpo stesso.

Con riferimento alla figura sottostante (dove sono stati omessi i punti delle derivate) si indica con Á_Bƒ e Á_[ƒ le potenze emesse da ciascuna superficie, mentre Á_BOƒ e Á_[Oƒ quelle incidenti.

UNIVERSITA’ DEGLI STUDI DI PISA 56 Indicando con Á_[B Oƒ eÁ_[[ Oƒ le potenze scambiate rispettivamente dal corpo e dallo scudo. Dal bilancio energetico si ha:

Á[Oƒ = À[BÂÁBƒ + 1 − µB ÁBOƒ Ã + À[[ÂÁ[ƒ + 1 − µB Á[Oƒ Ã

Á_BO _{= ÀB[¹Á©+ 1 − µ}ƒ ƒ _{[ Á}ƒ_[O¼ (4.25)

Otteniamo così un sistema di due equazioni in due incognite che, risolto, ci permette di ricavareÁ_[ƒ . Risolvendo il sistema per sostituzione si ottiene:

Áƒ =[O _$‡ÄÄHR _RRÅ_$‡ÆHƒ U[Ä_HRR_‡ÄUÄ_RHRH_$‡Æ$‡Æ_RH_$‡Æ]ŃR_R (4.26) Ricordando che è À_B[ = 1 eÀ_[[ = 1 − À_[B e utilizzando la relazione di Prevost (per la potenza scambiata complessiva) si ha:

Á[[ Oƒ = ÇÁ[ƒ − µ[Á[ƒ Ç =ÇÄRHˆ ÆRÅRƒ ‡ÆRÅHƒ Ç ÈHUÄRHˆÉÈRÈR (4.27) dato che: Á[ƒ = Seµ[σ Te¸ ÁƒB= SpµBσ Tp¸ Á_[[ Oƒ = ÇÁ_[ƒ − µ_[Á[ƒ Ç =ÇÄRHÆRÅRƒ ‡ÆRÅHƒ Ç ˆ ÈHUÄRHˆÉÈRÈR = ¶ Ç”RH”R¯R͇”H¯HÍÇ ˆ ÈHUÄRHˆÉÈRÈR (4.28)

Sotto le ipotesi di superfici isoterme ed essendo lo scudo un corpo convesso è possibile scrivere À_[B = ”H

”R .

Trascurando la resistenza termica conduttiva dello schermo termico, la potenza scambiata dallo scudo con l’esterno sarà:

Áƒ_Ÿ¦[[ = S_eµ_[σ |T_e¸_{− T}

qÎn¸ | (4.29)

UNIVERSITA’ DEGLI STUDI DI PISA 57 Nell’analogia elettrica è possibile rappresentare lo scambio termico come due resistenze in serie dove la prima rappresenta lo scambio tra corpo e scudo termico, mentre la seconda lo scambio tra scudo ed ambiente.

Figura 4.24 – Circuito equivalente

Uguagliando le equazioni relative a Á_[[ Oƒ e Áƒ_Ÿ¦[[ si ottiene una equazione ad una incognita·_[ . ÁƒŸ¦[[ = ¶Ç”RH”R¯R͇”H¯H Í_Ç ˆ ÈHUÏHÏR ˆÉÈRÈR = Seµ[σ |Te ¸_{− T} qÎn¸ | (4.30) Te¸ = ÐHÍÑH ˆ ÈHÒÑHÑRˆÉÈRÈR UÓÔÕÖÍ ÆR×Ï ÑH ˆ ÈHÒÑHÑRˆÉÈRÈR UÆR×R (4.31)

Di seguito è riportato l’andamento della ·_[ e della Áƒ_Ÿ¦[[ al variare dell’emissività per un dato diametroØ_[.

Figura 4.25 - Temperatura dello scudo termico e potenza irradiata verso l’esterno al variare dell’emissività

UNIVERSITA’ DEGLI STUDI DI PISA 58 Come intuibile minore è l’emissività minore risultano essere le perdite di calore verso l’esterno.

Non è possibile utilizzare uno scudo termico costituito da materiale metallico, altrimenti, essendo interposti tra pezzo da riscaldare ed avvolgimento, subirebbe un riscaldamento esattamente per lo stesso meccanismo di induzione utilizzato per il riscaldamento del corpo. Per tanto la scelta ricade su materiali ceramici a bassa emissività ed alta temperatura di fusione come ad esempio 6¬o1x_-Ù_a .

Dalle equazioni sopra riportate è possibile notare come la ·_[ e quindi la Áƒ_Ÿ¦[[ dipendano dal diametro Ø_” dello scudo. Di seguito è riportato l’andamento della temperatura dello scudo ·_[ e delle perdite superficiali dello scudo per irraggiamento verso l’esterno Áƒ_Ÿ¦[[ al variare del diametroØ_” per una emissività pari a 0.3.

Figura 4.26 - Temperatura e perdite per irraggiamento dello scudo verso l’esterno al variare del diametro dello scudo

All’aumentare di Ø_[ diminuisce la temperatura dello scudo ma aumentano le dispersioni a causa del fatto che aumenta la superficie di scambio con l’esterno¿_[ .

Di seguito riportiamo l’andamento delle c_Ÿ¦[[ ovvero di tutte le perdite di calore (irraggiamento e conduzione) in funzione del diametro Ø_[.

UNIVERSITA’ DEGLI STUDI DI PISA 59

Figura 4.27 - Perdite termiche totali in funzione del diametro esterno dello scudo termico

E’ evidente come le perdite per irraggiamento nel caso di utilizzo dello scudo termico diminuiscano notevolmente in confronto con le perdite per irraggiamento nel caso di superficie del pezzo non schermata (83 W).

Il minimo della curva c_Ÿ¦[[ si ha in corrispondenza di Ds uguale al diametro esterno del pezzo in riscaldamento e cioè 7,6 mm. Ipotizzando un avvolgimento direttamente a contatto con lo scudo termico ed avente anch’esso diametro interno Ds (condizione puramente teorica ma impossibile nella pratica in quanto avremmo trasmissione di calore per conduzione dal pezzo attraverso lo scudo termico fino all’avvolgimento), il relativo rendimento assumerebbe un valore come precedentemente riportato di 0,41 che con una c_y = 12 + 65,9 = 77,9 • porterebbe ad una c = 190•, valore ben al di sopra dei 100W disponibili. Da questo esempio puramente teorico è chiaro come l’induzione elettromagnetica non possa essere utilizzata come modalità di riscaldamento per l’emettitore in esame.

UNIVERSITA’ DEGLI STUDI DI PISA 60

4.5.5 DISTRIBUZIONI DELLA TEMPERATURA DI CATODO E SCUDO

TERMICO MEDIANTE SIMULAZIONE NUMERICA

A verifica dei risultati ottenuti analiticamente, è possibile mediante l’ausilio di COMSOL, ricavare la temperatura dello scudo termico in 1x_-Ù_a posizionato alla distanza di 0,05mm dalla superficie di tantalio e l’andamento della temperatura di un punto a distanza 3.855mm dall’asse di simmetria (punto contenuto all’interno dello scudo termico) nel tempo.

Figura 4.28 - Temperatura dello scudo termico al tempo 100s

Figura 4.29 - Andamento della temperatura nel tempo di un punto interno allo scudo termico

UNIVERSITA’ DEGLI STUDI DI PISA 61 Come visibile, le temperature dello scudo ricavate mediante l’ausilio del programma di simulazioni risultano compatibili con quelle ricavate analiticamente.