Capitolo 4

Capitolo 4

Analisi dell'evoluzione della popolazione biologica

4.1 Approssimazione di funzioni

4.1.1 Cenni teorici

Il problema dell'approssimazione di funzioni, d'importanza fondamentale nella matematica applicata, consiste nella sostituzione di una funzione complessa, di grado anche elevato, con una più semplice, scelta nell'ambito di una fissata classe di funzioni a dimensione finita.

Una tipica situazione in cui si presenta un'operazione di questo tipo è la seguente: la funzione da approssimare non è nota, ma di essa si conoscono alcuni valori su un insieme di punti e si vogliono avere indicazioni sul comportamento della funzione in altri punti. E' il caso di funzioni date in forma tabellare, corrispondenti, ad esempio, proprio a dati sperimentali. In queste situazioni, approssimare una funzione, significa darne un modello rappresentativo.

In base al tipo e alla quantità dei dati, e alle caratteristiche del problema, si può scegliere tra due differenti approcci. Il primo, assumendo esatti i dati, cerca di costruire la curva che passi per certi punti assegnati (interpolazione), il secondo, invece, suppone i dati affetti da errore e cerca di costruire una curva che si discosti poco dai dati, in modo da non perdere le informazioni in essi contenute (tecnica di ‘smoothing’).

In generale un problema di interpolazione è posto nei seguenti termini: dati n punti distinti xi si vuole determinare una funzione f(x) che in essi soddisfi m condizioni di interpolazione (vincoli che la funzione e/o le sue derivate devono soddisfare nei punti xi). Nel caso in cui le condizioni sono f(xi)=yi, con yi valori assegnati, per i=1,...,n, si parla di interpolazione di Lagrange. Se poi la funzione f è supposta appartenente ad uno spazio vettoriale a dimensione finita il problema è detto di interpolazione lineare , e si riconduce alla determinazione delle componenti nella base prescelta (es. polinomi, funzioni trigonometriche, esponenziali, ecc.).

Storicamente le funzioni interpolanti più note e utilizzate sono state i polinomi, perché di facile valutazione, facilmente sommabili, integrabili e derivabili. Si ricorre, allora, frequentemente alla interpolazione polinomiale, tenendo conto però del fatto che i polinomi hanno dei problemi d'efficienza ed accuratezza, in quanto presentano delle forti oscillazioni tra i dati. Questo problema pone dei limiti nella scelta dei polinomi, che in generale non superano l'ottavo - nono grado, cioè si usano polinomi che al massimo interpolano nove - dieci punti. Infatti, avendo a disposizione n+1 dati, il polinomio di Lagrange che se ne ricava è di grado n.

Nel caso in cui ci si trovi di fronte a problemi d'interpolazione con un numero elevato di punti, a causa della scarsa efficienza del modello polinomiale, la funzione interpolante è cercata in una classe più ampia, che include quella dei polinomi. Si tratta delle funzioni interpolanti a tratti, definite su di un numero finito e contiguo d'intervalli, in ognuno dei quali coincidono con un polinomio. In particolare, le funzioni polinomiali a tratti di

grado m sono polinomi di grado m in ogni sottointervallo. Queste funzioni

non essere regolari in tutto l'intervallo di definizione, potrebbero ad es. avere derivate discontinue nei punti d'interpolazione.

Il compromesso si può raggiungere tramite particolari funzioni polinomiali a tratti di grado m, che comprendono i polinomi, si tratta delle funzioni spline

di grado m. Le funzioni appartenenti a questa classe sono continue con le

loro derivate fino a quella d'ordine m-1. Le più impiegate nelle applicazioni, sono le spline cubiche (o di terzo grado), che hanno la caratteristica di essere continue insieme alle loro derivate prima e seconda.

Le tecniche d'approssimazione di funzioni non si esauriscono con l'interpolazione. Quando i dati (xi , yi) sono in numero m elevato o affetti da errore (es. misurazioni sperimentali o indagini statistiche) non è ragionevole forzare la funzione a passare esattamente per gli m punti, ma è più conveniente effettuare uno smoothing, cioè una ‘levigatura’, al fine di minimizzare l'errore contenuto nei dati.

La risoluzione di tale problema richiede la scelta del tipo di funzione approssimante (modello) f(x), e di una misura del suo scostamento dai dati. Anche se la scelta del modello dipende generalmente dalle informazioni che si hanno sul problema, solitamente si adoperano modelli lineari, per la loro efficienza di calcolo , e in particolare i polinomi del tipo

1 2 1 1

...

=

+

+

+

c

c

x

c

x

P

Per quanto riguarda la misura dello scostamento dai dati, si usa, generalmente, il residuo, cioè il vettore di componenti r

i = y i - f(x i ), i=1,...,m.

Quando si cerca una funzione tale da minimizzare la norma di ordine 2 del residuo, definita come:

ciò equivale a minimizzare il quadrato di tale norma, e si parla, allora, di

problema di minimi quadrati.

La funzione approssimante viene scelta in modo che la somma dei quadrati degli errori di approssimazione nell’insieme di punti pre-determinato, sia minima. Tale funzione approssimante risente dunque dell’andamento globale dei valori da approssimare.

Nel caso in cui la funzione f(x) è il polinomio P n-1

(x) (polinomio di minimi

quadrati di grado n-1), l' imposizione delle condizioni di minimo (grad E = 0) alla

funzione

che fornisce i coefficienti (c 1 ,c 2 …,c n

) del polinomio che realizza la migliore approssimazione del modello prescelto.

Ciò equivale ad ipotizzare che la funzione scelta per effettuare l'interpolazione sia la seguente:

ossia una funzione che lega la variabile indipendente x con la variabile y utilizzando i k parametri non noti

che dovranno quindi essere determinati. Se consideriamo il valore di xi ottenuto attraverso l'indagine statistica notiamo che a tale valore corrispondono

• il valore ottenuto attraverso l'indagine statistica

• il valore

ottenuto dalla funzione teorica di interpolazione. In base a questo fatto :

• al valore può essere assegnato il nome di valore ‘effettivo’

il criterio dei minimi quadrati permette di determinare i valori dei parametri ignoti

della funzione

mediante un criterio di accostamento , che consiste nel trovare il punto di minimo rispetto ai parametri

a

Il punto di minimo di tale funzione viene trovato utilizzando, se applicabili, i teoremi visti per la ricerca dei punti di massimo e di minimo relativo per le

punti di massimo e di minimo relativo prevede prima di tutto la soluzione, rispetto ai coefficienti

a

e successivamente nella verifica, per mezzo della matrice Hessiana, della natura del punto critico così trovato. In generale infatti, per studiare i massimi ed i minimi relativi ad una funzione di 3 o più variabili, non è sufficiente guardare il segno del determinante della matrice Hessiana e quello della derivata seconda rispetto alla prima variabile, ma occorre determinare il segno degli autovalori della matrice stessa.

Oltre a verificare l’annullamento del relativo gradiente, se la matrice Hessiana ha autovalori tutti positivi in un punto critico, esso è di minimo Matrice Hessiana per una

funzione f di n variabili derivabile 2 volte con continuità (La matrice è simmetrica n x n )

La funzione interpolante trovata con il procedimento dei minimi quadrati prende anche il nome di funzione di regressione. Quando la serie di funzioni considerata è costituita da polinomi di grado non superiore al primo si afferma che la curva di regressione è lineare.

4.1.2 Esempio di calcolo: retta di regressione

Si consideri il metodo di costruzione della curva di regressione avente come base dello spazio di funzioni l’insieme {1, x} , tuttavia il metodo dei minimi quadrati consente di costruire una curva di regressione per combinazione lineare di uno spazio di funzioni qualsiasi. E’ noto che per due punti passa una ed una sola retta; considerando una serie di n punti con n>2, non è possibile costruire una retta di interpolazione a meno che volutamente o fortuitamente la serie di n punti abbia andamento lineare, quello che potremo però fare è costruire la retta che meglio approssima la serie di n punti.

In termini più formali, avendo a disposizione la serie di n punti (n coppie di dati):

Si vuole determinare la retta y=mx+q tale che la somma degli scarti quadratici dai punti della serie sia minima.

Come visto, lo scarto quadratico è definito pari a

(y

-y(x

))

differenza tra il valore reale della serie e quello stimato dalla retta di regressione.

Il residuo è definito come la somma degli scarti quadratici medi, ed in questo caso può essere espresso come:

in cui y(xi) = mxi + q è il valore stimato dalla retta di regressione lineare

nel punto xi.

Dall’analisi matematica, si ricava che la retta per cui il residuo è minimo è fornita dal minimo locale della equazione di residuo rispetto alle due variabili m e q.

La tecnica di ricerca di un minimo locale implica la risoluzione del sistema

di equazioni ottenuto uguagliando a zero le derivate parziali dell’ equazione precedente:

Si ottiene così un sistema lineare di due equazioni e due incognite, nelle variabili m e q:

si osservi che le uniche variabili sono m e q, mentre tutti gli altri termini sono numeri calcolabili dai dati in ingresso, ovvero:

n : numero dei dati in ingresso

: somma delle ascisse dei punti noti

: somma dei quadrati delle ascisse dei punti noti

: somma delle ordinate dei punti noti

: somma dei prodotti delle ascisse per le ordinate dei punti noti La soluzione del sistema di equazioni è, quindi:

Sostituendo sopra i dati a disposizione si ottengono i coefficienti della retta di regressione cercata

4.1.3 Calcolo dei coefficienti del polinomio interpolante n punti assegnati, rappresentato nella forma di Newton.

Dati n punti xi e n valori corrispondenti yi, esiste un unico polinomio interpolante tali punti. La sua rappresentazione però non è unica, ma dipende dalla base scelta nello spazio vettoriale dei polinomi di grado n-1. Una rappresentazione particolarmente conveniente da un punto di vista della complessità di calcolo è la seguente:

pn-1(x) = an + an-1(x-xn) + an-2(x-xn)(x-xn-1) + ... + a1 (x-xn)...(x-x2),

detta formula di Newton. Indicati, infatti, i coefficienti ai con y[xi,..., xi+k], essi si possono ottenere mediante la seguente formula ricorsiva:

dove y[xi,...,xi+k] è detta differenza divisa di ordine k relativa ai nodi xi, ... ,xi+k.

Inoltre, dati n punti distinti xi e n valori corrispondenti yi esiste un unico polinomio di grado n-1 tale che: Pn-1(xi)=yi, i=1,..., n. La rappresentazione di Newton di tale polinomio è esprimibile anche come:

4.1.4 Calcolo dei coefficienti della spline cubica naturale interpolante n punti assegnati.

Dati n punti distinti xi e n valori corrispondenti yi, una spline cubica interpolante tali punti è una funzione continua insieme alle sue derivate prima e seconda, e coincide con un polinomio di 3° grado in ogni intervallo [xi, xi+1], i = 1,..., n-1. Il numero di coefficienti da determinare è 4(n-1) = 4n-4, mentre le condizioni di interpolazione e quelle di continuità sono n+3(n-2) = 4n- 6, quindi mancano 2 equazioni affinché il problema sia ben posto. La spline cubica naturale è quella che sfrutta i 2 restanti gradi di libertà imponendo l'annullamento delle derivate seconde negli estremi. Si può verificare con semplici calcoli, che la spline è univocamente determinata dalle sue derivate seconde nei nodi xi, e che queste si ottengono risolvendo un sistema lineare.

Inoltre, dati n punti distinti xi e n valori corrispondenti yi esiste un'unica spline cubica s(x) interpolante tali punti, che soddisfi le condizioni s''(x1) = s''(x2) = 0. Tale funzione è un polinomio di terzo grado, in ogni intervallo [xi, xi+1] i=1,...,n-1, quindi, per la sua valutazione in un punto x dell’intervallo [xi, xn] occorre determinare l'intervallo i-esimo contenente x e quindi, noti i coefficienti, calcolare il valore del polinomio relativo ad esso.

4.1.5 Calcolo dei coefficienti del polinomio dei minimi quadrati di 2° grado.

Come visto, la determinazione del polinomio di minimi quadrati di 1° grado si concretizza nella risoluzione del seguente sistema:

la cui soluzione fornisce i coefficienti (c1,c2) del polinomio c1+c2x che realizza l'approssimazione ottimale .

Analogamente, la determinazione del polinomio di minimi quadrati di 2° grado si effettua con la risoluzione del seguente sistema:

la cui soluzione fornisce i coefficienti (c1,c2, c3) del polinomio c1+c2x+c3 x 2 che realizza l'approssimazione ottimale.

4.2 Interpolazione dei dati

Di seguito vengono indicati i metodi di analisi dei dati utilizzati . L’obiettivo che ci si propone è quello di definire un modello per i dati sperimentali a disposizione attraverso funzioni note.

4.2.1 Elaborazione preliminare : normalizzazione

Un processo che spesso si rende necessario di fronte ad una grande quantità di dati, è la loro normalizzazione. Essa consiste nel centrare i valori attorno al valore medio nullo e scalandoli di un fattore pari alla deviazione standard: ) ( _ )) ( ( _ dato std deviazione dato valormedio dato to normalizza dato = −

Dati n campioni si definiscono: Valore medio:

Deviazione standard:

Una definizione alternativa di deviazione standard che è possibile trovare in letteratura è la seguente:

La normalizzazione dei dati sperimentali consente, in alcuni casi, di elevare l’accuratezza delle successive elaborazioni. Infatti consente di gestire e rappresentare correttamente dati che, per loro natura, hanno una base dei tempi o valori molto disomogenei tra loro.

4.2.2 Interpolazione mediante regressione

E’ spesso utile, se non necessario, determinare funzioni che descrivano le relazioni intercorrenti tra una serie di variabili osservate sperimentalmente. L’identificazione dei coefficienti di tali funzioni spesso porta alla formulazione di sistemi lineari di equazioni sovra-determinate, in cui le equazioni a disposizione sono in numero maggiore delle incognite. Un metodo per determinare i coefficienti passa attraverso l’ operatore Matlab ‘\’ (‘backslash’).

Supponiamo di aver operato una serie temporale di osservazioni, e di aver ricavato la seguente successione di dati:

t = [ 1 2 3 4 5 6 7 8 9 10];

y = [14 15 19 27 44 75 165 413 1195 1379];

Questi potrebbero essere ad esempio i dati ricavati secondo una delle tecniche messe a disposizione nella parte del programma relativa al conteggio degli individui biologici.

La loro rappresentazione è la seguente

Esistono vari tipi di approccio al problema. Tra questi si focalizzerà l’attenzione sui seguenti:

- regressione di tipo polinomiale

- regressione mediante funzione di tipo esponenziale - regressione con funzione di tipo iperbolico

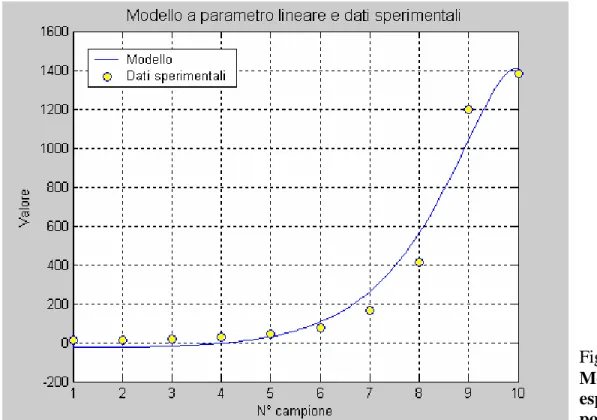
- regressione con funzione di tipo ‘Error function’ Fig. 4.1

Visualizzazione dei dati sperimentali

4.2.3 Regressione di tipo polinomiale con polinomio di ordine 2

Un approccio possibile per fornire un modello ai dati raccolti sperimentalmente è realizzare il fitting mediante una funzione polinomiale del tipo:

I coefficienti

a

quadrati: come indicato in precedenza, questo approccio consiste nella minimizzazione della somma dei quadrati delle deviazioni dei dati dal modello stesso.

Si ottiene così un sistema di n ( n è il numero di campioni a disposizione, in questo caso si ipotizza n=6 ) equazioni in tre incognite:

rappresentabile da una matrice di dimensioni n x 3, ottenuta riportando nella prima colonna n termini ad uno, nella seconda il vettore dei termini

La soluzione del sistema precedente si ottiene attraverso la relazione a = X \ y

che fornisce direttamente i coefficienti del modello del secondo ordine :

Il polinomio del secondo ordine cercato può essere così espresso: y =343.7667 −248.0985*t+35.2045 *t2

Esprimendo il problema in forma generale, si ha che i modelli lineari sono descritti dalla relazione matriciale:

Dove:

y è il vettore n x 1 dei risultati X è la matrice n x m del modello ß è il vettore m x 1 dei coefficienti

La soluzione del problema secondo i minimi quadrati è esprimibile con un vettore b , i cui coefficienti stimano quelli del vettore incognito ß. Le equazioni in notazione matriciale sono espresse dalla relazione seguente, in cui

X

X

Risolvendo rispetto a b si ottiene la relazione:

L’operatore ‘\’ (‘backslash’) di fatto risolve un sistema di equazioni lineare a coefficienti non noti secondo l’approccio indicato. E’ chiaramente possibile inserire il vettore b così ottenuto nella formula che esprime il modello per ottenere i valori predetti .

Infatti :

Il simbolo sopra la lettera indica che è un valore stimato di un parametro. Il residui sono dati dalla relazione matriciale:

E’ evidente che il modello del secondo ordine non è sufficientemente ad interpolare in modo corretto i dati a disposizione. Al fine di ridurre l’errore, una tecnica può essere quella di incrementare l’ordine del modello, oppure di realizzarne uno sfruttando tipi differenti di funzioni.

4.2.4 Regressione di tipo polinomiale con polinomio di ordine 3

Si riportano i risultati che si ottengono da una analisi con modello polinomiale di ordine 3.

In questo caso la funzione ha la forma:

3 3 2 2 1 0

a

t

a

t

a

t

a

y

=

+

+

+

ed il sistema corrispondente sarà di n di equazioni in 4 incognite ( matrice n x 4 ).

In questo caso si ottengono i seguenti risultati: t = [ 1 2 3 4 5 6 7 8 9 10];

y = [14 15 19 27 44 75 165 413 1195 1379];

a = X \ y

Il polinomio del terzo ordine cercato è quindi:

E’ evidente il miglioramento in termini di approssimazione dei dati sperimentali. Ciò incoraggia nel proseguire l’analisi e considerare il polinomio del quarto ordine.

4.2.5 Regressione di tipo polinomiale con polinomio di ordine 4

Il polinomio che stiamo cercando ha la forma

4 4 3 3 2 2 1 0

a

t

a

t

a

t

a

t

a

y

=

+

+

+

+

ed il sistema corrispondente sarà di n di equazioni in 5 incognite ( matrice n x 5 ).

t = [ 1 2 3 4 5 6 7 8 9 10];

y = [14 15 19 27 44 75 165 413 1195 1379];

Fig. 4.3

Visualizzazione dei dati sperimentali e del modello di ordine 3

a = X \ y

Il polinomio del quarto ordine è quindi:

4 3 2 8992 . 0 1274 . 24 2628 . 181 2257 . 478 6667 . 337 t t t t y = − + − + − Fig. 4.4 Visualizzazione dei

Nella figura seguente si riportano per confronto gli andamenti dei modelli polinomiali finora esaminati, insieme alla rappresentazione del modello con polinomio di ordine 5 (colore rosso).

Tipicamente, nella pratica non si prosegue oltre l’ordine pari a metà del numero complessivo di dati sperimentali (in questo caso 10), ed è per questo che non vengono presi in considerazione polinomi di ordine superiore. Si ricorda infatti che, per il teorema di Lagrange, esiste sicuramente un polinomio di grado n (9 in questo caso) che passa per gli

Fig. 4.5

4.2.6 Regressione mediante funzione di tipo esponenziale

Anziché una funzione polinomiale, è possibile utilizzare una funzione di tipo esponenziale a dipendenza lineare dalla variabile. Può essere interessante considerare una funzione esponenziale del tipo

Analogamente al caso precedente, al fine di determinare i coefficienti incogniti

a

termini unitari, nella seconda n termini del tipo

e

te

t = [ 1 2 3 4 5 6 7 8 9 10];

y = [14 15 19 27 44 75 165 413 1195 1379];

Il polinomio ha quindi espressione:

y

=

568

+

3292

e

−

4620

te

Il modello scelto non è corretto, ma è interessante verificare il caso in cui si utilizzi il termine esponenziale positivo

e

t t

te

a

e

a

a

y

=

+

+

Al fine di determinare i coefficienti incogniti

a

riportando nella prima colonna n termini unitari, nella seconda n termini del tipo

e

t

te

t = [ 1 2 3 4 5 6 7 8 9 10]; y = [14 15 19 27 44 75 165 413 1195 1379]; Fig. 4.6 Modello esponenziale negativo

Si ottengono i seguenti coefficienti:

Il polinomio relativo a questo modello è quindi:

y

=

−

27

.

9409

+

0

.

7320

e

−

0

.

0667

te

Segue la rappresentazione grafica:

Fig. 4.7 Modello esponenziale positivo

4.2.7 Regressione mediante funzione di tipo iperbolico

Come ulteriore passo di analisi si prende in considerazione la funzione tangente iperbolica e la si confronta con i dati sperimentali raccolti.

Definendo un argomento a e le seguenti due funzioni:

2

)

(

α

=

e

−

e

senh

2

)

cosh(

α

=

e

+

e

+

−

e

e

e

e

La funzione su cui si va ad indagare ha quindi la forma generale

)

tanh(

a

a

a

a

y

=

+

α

−

Poiché non si aveva a disposizione un tool Matlab per la soluzione del sistema non lineare associato, si è dovuti ricorrere ad una equivalente routine IDL (Research Systems). Di seguito si riportano le istruzioni della funzione costruita:

Fig. 4.8

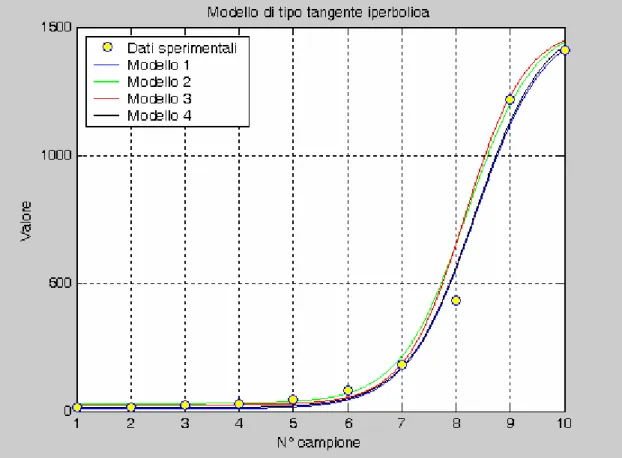
Tale routine prevede sia l’indicazione delle derivate parziali della funzione in esame rispetto ai coefficienti incogniti, sia l’immissione di una stima iniziale dei coefficienti stessi. Ne segue che i valori finali ottenuti sono condizionati in modo significativo dalle indicazioni immesse via utente. Per ridurre al massimo questa dipendenza, si è ripetuta l’analisi un numero significativo di volte con valori iniziali diversi. Di seguito si riportano alcuni risultati ottenuti.

I parametri imposti sono: X=[1,2,3,4,5,6,7 ,8,9,10,11] Y=[14,17,23,29,48,75,81,183,434,1219,1411] weights = 1.0/Y A = [1000.0,1000,0.8,7.1] Si ottengono i coefficienti: 761.34 751.57 0.799 6.67

La funzione ha quindi l‘espressione:

)

67

.

6

799

.

0

tanh(

*

57

.

751

34

.

761

+

−

=

α

y

Coefficienti A[0] A[1] A[2] A[3] Imposto 1000.0 1000.0 0.800 7.1 Calcolato (1) 761.34 751.57 0.799 6.67 Imposto 761.0 751.0 0.799 6.67 Calcolato (2) 772,75 742.64 0.815 6.68 Imposto 758.0 741.0 0.900 7.37 Calcolato (3) 761.80 736.33 0.903 7.37 Imposto 770.0 750.0 0.799 6.67 Calcolato (4) 771.34 756.57 0.799 6.67

Fig. 4.9 Modelli di tipo tangente iperbolica

4.2.8 Regressione mediante funzione di tipo ‘Error function’

La funzione sotto indagine ha in questo caso la forma generale

)

(

a

errorf

a

x

a

a

y

=

+

−

Per definizione, la funzione errore (‘Error function’) è definita come l’integrale della funzione Gaussiana a valore medio nullo e varianza pari ad

½

Anche in questo caso si è ricorsi ad una funzione in linguaggio IDL, il cui listato è di seguito riportato:

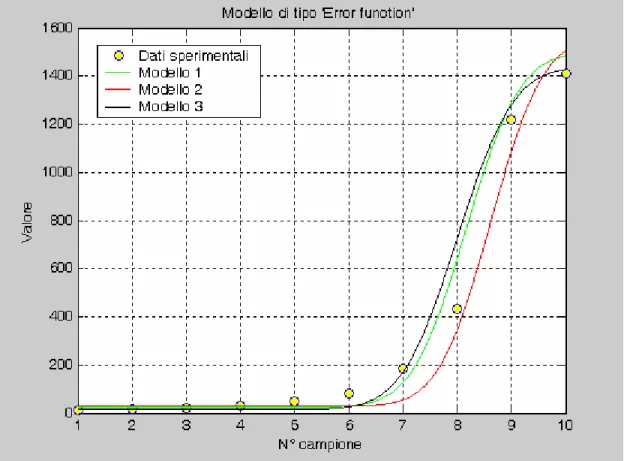
I parametri imposti sono: X=[1,2,3,4,5,6,7,8,9,10,11]

Y=[14,17,23,29,48,75,81,183,434,1219,1411] weights = 1.0/Y

Analogamente al caso precedente si riportano i condizionamenti ed i risultati ottenuti sia in forma tabellare che grafica.

Coefficienti A[0] A[1] A[2] A[3] Imposto 758.0 741.0 0.90 7.4 Calcolato (1) 761.80 736.33 0.903 7.37 Imposto 758.0 741.0 0.93 8.0 Calcolato (2) 794.12 765.56 0.927 7.37 Imposto 758.0 741.0 0.91 7.0 Calcolato (3) 756.42 730.43 0.869 6.96

Fig. 4.10 Modelli di tipo ‘Error function’

4.3 Caricamento, visualizzazione, interpolazione dei dati

La relativa sezione di programma prende avvio dalla pressione

del tasto ‘Elaborazione campioni’ dell’interfaccia principale (vedi

figura 4.11).

Viene così visualizzata una nota informativa di presentazione (fig. 4.12)

Fig. 4.11 Tasto ‘Elaborazione campioni’

L’utente ha la possibilità di immettere i dati sia sottoforma di campioni progressivi, che specificando l’istante di tempo a cui sono stati accolti. Per confermare il dato si preme ‘Ok’; per confermare la fine di un gruppo di dati si preme ‘Fine’. Automaticamente si passa all’inserimento del gruppo successivo, fino a raggiungere il numero di gruppi inizialmente indicato. La fine dell’inserimento dei dati è indicato come in figura:

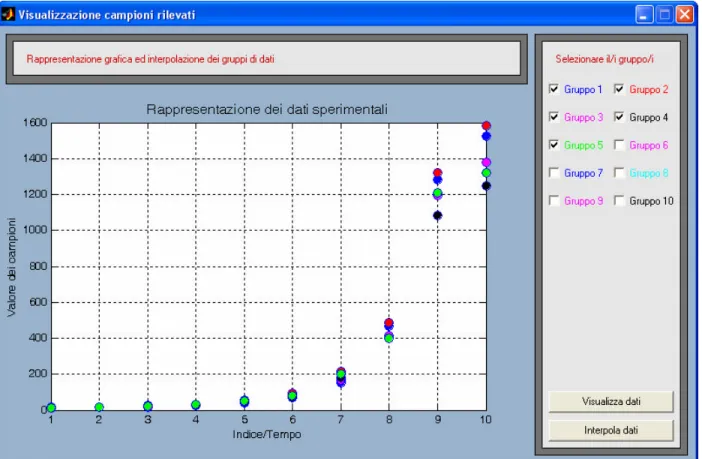
A questo punto viene attivata l’interfaccia di visualizzazione ed elaborazione dei dati. L’utente seleziona i gruppi che intende visualizzare spuntandoli in alto a destra. E’ possibile sia la selezione singola che

Fig. 4.13 Interfaccia di immissione numero gruppi Fig. 4.14 Interfaccia di immissione dati sperimentali Fig. 4.15 Ultimazione inserimento

Premendo il tasto ‘Visualizza dati’ si ha la presentazione a video dei campioni, come indicato in figura 4.16.

Per dare maggiore leggibilità alla visualizzazione, ciascun gruppo è rappresentato con il colore indicato nel campo di selezione.

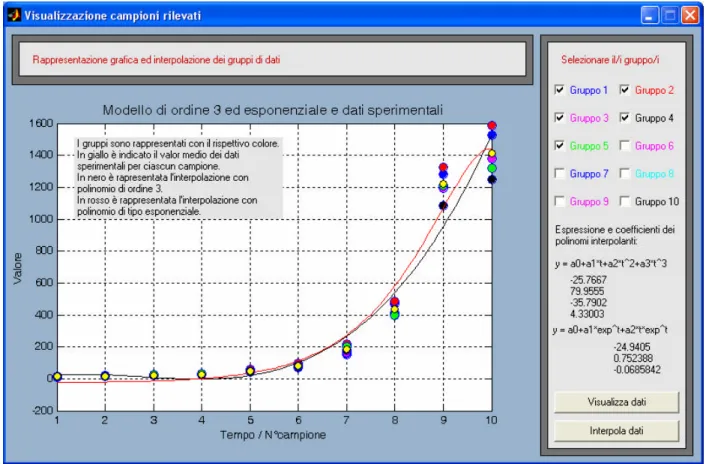
La pressione del tasto ‘Interpola dati’ avvia la procedura di interpolazione.

Vengono analizzati i gruppi selezionati, viene eseguita e visualizzata una media dei valori campione per campione, vengono infine mostrate le curve interpolanti che minimizzano la norma due del residuo (tecnica dei minimi quadrati descritta in precedenza).

A titolo esemplificativo nella figura successiva sono riportati i risultati ottenuti con polinomio di ordine 3 e funzione esponenziale. A lato vengono anche mostrati i coefficienti delle due funzioni.