CAPITOLO 3
Calcolo della matrice di scattering generalizzata
3.1 GSM aria-apertura
Utilizzando la formulazione della matrice di scattering generalizzata, ottenuta nel capitolo precedente per quanto riguarda il Mode Matching in termini di onde dirette e riflesse, si ha:
(
) (
)
(
)
(
)
(
)
⋅
−
=
⋅
+
⋅
⋅
=
−
⋅
=
−
⋅
⋅
⋅
+
=
− − 12 2 22 1 1 2 1 12 11 2 21 2 1 1 2 1 112
S
M
I
S
M
I
M
M
S
S
I
M
S
I
M
M
M
M
I
S
(3.1.1) con( )
( )
1 1 1 * 2 A H SM
P
C
M
P
C
− −=
⋅
=
⋅
(3.1.2) dove = 22 21 12 11 S S S S S (3.1.3)Si noti che la matrice di scattering generalizzata può essere ricavata dalla conoscenza delle matrici di potenza in aria PA e nella apertura PS e dalla matrice di accoppiamento C .
Calcolo della potenza in aria
Ricordando che il generico elemento della matrice della potenza in aria è
(
*)
ˆ ij C i j A z S P =∫∫
Eur × uurH ⋅i dS (3.1.4)la matrice della potenza associata ai modi di Floquet, separando i contributi dovuti alle due possibili polarizzazioni, può essere definita come:
0 0 TE TE A A TM TM A P P P − − = (3.1.5)
Si noti che nella (3.1.5) le matrici TE TM A
P − e TM TE
A
P − sono state omesse perché, data l’ortonormalità tra i modi con polarizzazione TE e quelli con polarizzazione TM, tutti i loro elementi sono nulli. Nella (3.1.4), in accordo con la (2.3.4), il coefficiente moltiplicativo complesso relativo al modo i-esimo dello sviluppo modale di Floquet del campo magnetico, può essere espresso in funzione di quello del campo elettrico, secondo la relazione:
ˆ
(
)
i i z i
H
=
Y
i
×
E
uur
uur
Applicando la (2.3.4) alla (3.1.4) si ottiene:
(
)
(
)
(
)
(
)
* * * *ˆ
ˆ
ˆ
ˆ
ij C ij C TE TE TE TE TE i j A j z z S TM TM TM TM TM i j A j z z SP
Y
E
i E
i dS
P
Y
E
i E
i dS
− −=
× ×
⋅
=
× ×
⋅
∫∫
∫∫
ur
ur
ur
ur
(3.1.6)Si noti che la potenza assume valori diversi a seconda che si tratti di modi TE o TM. Applicando alla (3.1.6) l’uguaglianza vettoriale A×B×C =
(
A⋅C) (
B− A⋅B)
C e notando che, per entrambe le relazioni, il secondo termine dell’uguaglianza vettoriale è nullo (inquanto il prodotto scalare tra i vettori di campo, definiti lungo la direzione trasversa, ed il versore delle direzione di propagazione, è nullo), si ottiene:
(
)
(
)
* * * * ij C ij C TE TE TE TE TE i j A j S TM TM TM TM TM i j A j SP
Y
E
E
dS
P
Y
E
E
dS
− −=
⋅
=
⋅
∫∫
∫∫
ur
ur
ur
ur
(3.1.7)Data l’ortonormalità delle funzioni di base dello sviluppo di Floquet , le (3.1.7) possono essere scritta come:
* * 0 0 ij ij TE TE TE i A TM TM TM i A Y se i j P altrimenti Y se i j P altrimenti − − = = = = (3.1.8)
Ricordando che la matrice P è definita dalla (3.1.5) si evince che tale matrice è diagonale A con il generico valore di posto ij dato da:
* * 1 1 0 ij A TE i TE A TM A i TE TE TM Y per i j n P Y per n i j n n altrimenti ≤ = ≤ = + ≤ = ≤ + (3.1.9)
Calcolo della potenza complessa nella sezione disomogenea
Per una guida riempita in modo non omogeneo di dielettrico non è possibile definire le ammettenze o le impedenze modali, come è possibile fare per i modi di Floquet. Continuano comunque a valere alcune proprietà utili per il calcolo della potenza.
Partendo dalla definizione della potenza come flusso del vettore di Poynting attraverso la superficie data dalla sezione della guida stessa, si determina l’espressione del generico elemento ij della matrice di potenza.
ˆ
ij j i z S
P =
∫∫
Euuur uur×H∗⋅i dS (3.1.10)Scomponendo il campo elettrico e magnetico nelle sue due componenti tangenziale e longitudinale, si ottiene che la potenza su ciascuna sezione dipende dalle sole componenti trasverse . Si ha infatti che
(
) (
)
(
)
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ . ij j zj z i zi z z S j i zj z i j zi z zj z zi z z S P E E i H H i i dS E H E i H E H i E i H i i dS τ τ τ τ τ τ ∗ ∗ ∗ ∗ ∗ = + × + ⋅ = = × + × + × + × ⋅∫∫
∫∫
uuur uuuruuur uuur uuur uuur (3.1.11)
Svolgendo i prodotti vettoriali e scalari e con opportune considerazioni geometriche, la (3.1.11) può essere scritta come:
ˆ .
ij j i z S
P =
∫∫
Euuur uuurτ ×Hτ ∗⋅i dS (3.1.12)La potenza è quindi completamente indipendente dalle componenti dei campi lungo la direzione di propagazione. Il passo successivo è quello di esprimere la potenza in funzione del solo valore del campo elettrico, valore ricavato dalla soluzione del problema agli autovalori generalizzato. Utilizzando la prima equazione di Maxwell, formulata in assenza di sorgenti, è possibile esprimere il valore del campo magnetico in funzione di quello del campo elettrico, secondo la relazione 1 . i i H E jωµ = − ∇× uur ur uur (3.1.13)
Esprimendo sia il campo elettrico E che l’operatore i ∇r secondo le loro componenti tangenziali e longitudinali, si ottiene che:
(
)
ˆi i zi i i z
E τ Eτ τE j Eβ τ i
∇ ×ur uur uur uur= ∇ × + ∇ uur + uur × (3.1.14)
La (3.1.13) diventa
(
)
{
}
1 ˆ . i i zi i i z H E E j E i jωµ τ τ τ β τ = − ∇ × + ∇ + × uur uur uur uur uur
(3.1.15)
Per il calcolo della potenza occorre la sola componente trasversa del campo magnetico:.
(
)
(
)
(
)
1 ˆ 1 ˆ ˆ . i zi i i z i zi z i z H E j E i j E i E i j τ τ τ τ τ β ωµ β ωµ ωµ = − ∇ + × = = − ∇ × − ×uuur uur uur
uur uur (3.1.16)
Sostituendo i valori ottenuti nella (3.1.12) si ottiene:
(
*)
(
*)
1 ˆ i ˆ ˆ ij j zi z i z z S P E E i E i i dS j τ τ τ β ωµ ωµ = × ∇ × − × ⋅ ∫∫
uuur uur uur (3.1.17)ed esplicitando i passaggi si ricava:
(
*)
*(
*)
1 ˆ ˆ j ˆ ˆ . ij j zi z z j i z z S S P E E i i dS E E i i dS j τ τ τ τ β ωµ ωµ=
∫∫
uuur× ∇uur × ⋅ −∫∫
uuur× uur × ⋅ (3.1.18)Si noti che il secondo addendo dipende dalle sole componenti tangenziali mentre il primo presenta una dipendenza anche dal valore della componente longitudinale del campo elettrico. Applicando alla (3.1.18) l’identità vettoriale A×B×C=
(
A⋅C) (
B− A⋅B)
C e notando che(
A⋅ C)
=0 per entrambi i membri della stessa, si ricava che:* * * 1 j ij j zi j i S S P E E dS E E dS j τ τ τ τ β ωµ ωµ
= −
∫∫
uuur uur⋅ ∇ +∫∫
uuur uur⋅ (3.1.19)In questo caso non vale il principio di ortonormalità delle basi utilizzato per ricavare la matrice delle potenze in aria e quindi il calcolo va ripetuto per tutti gli elementi della matrice
e non solo per quelli sulla diagonale. In particolare per i modi complessi, ovvero quelle coppie di modi che, in caso di guide prive di perdite, sono caratterizzati da costante di propagazione complessa coniugata, il campo elettrico non si accoppia con il campo magnetico del medesimo modo, ma con quello del modo complesso a lui associato.
A questo punto si noti che la formulazione FEM utilizzata non ricava il valore dei campi che effettivamente si propagano nel tratto guidato, valori che compaiono nella (3.1.19), ma dei valori normalizzati. A tale proposito si ricordi che, per rendere il problema agli autovalori reale e di primo grado, si è operato il cambio di variabili:
x x y y z z
e =βE e =βE e = −jE (3.1.20)
dove le lettere minuscole sono riferite ai valori dei campi ottenuti dalla risoluzione del problema agli autovalori mentre le lettere maiuscole sono riferite ai valori dei campi che effettivamente si propagano nel tratto guidato della apertura.
Applicando il cambio di variabili inverso alla formula della potenza (3.1.19), si ricava l’espressione da utilizzare nel software:
* * 1 1 ij j zi j i i S i S P eτ τe dS eτ eτ dS ωµβ ωµβ
=
∫∫
uur uur⋅ ∇ −∫∫
uur uur⋅ (3.1.21)Calcolo della matrice di accoppiamento
Si ricordi che, dalla (2.2.8), il generico elemento della matrice di accoppiamento viene definita come:
(
*)
ˆ C ij i j z S C =∫∫
E huur uur× ⋅i dS (3.1.22)Nella (3.1.22) S è la superficie della apertura, il vettore c Euuri indica la componente del campo elettrico in apertura relativa al modo i-esimo, il vettore huurj la componente trasversa del
campo magnetico in aria ed i$ è il versore che identifica la direzione di propagazione. Come z
avveniva per il calcolo della matrice della potenza nella apertura, il vettore campo elettrico
i
E uur
è il valore del campo che effettivamente si osserva nella sezione in z= del tratto 0 guidato dello schermo, e non quello ricavato dalla risoluzione del problema agli autovalori. Riscrivendo la (3.1.22) in funzione di tale considerazione ed espandendo i vettori nelle loro componenti lungo gli assi cartesiani si ottiene:
(
)
(
* *)
1 ˆ
.
C
FEM FEM FEM
x y z x y ij xi yi z i x j y j z i S C e i e i j e i h i h i i dS β = + + × + ⋅
∫∫
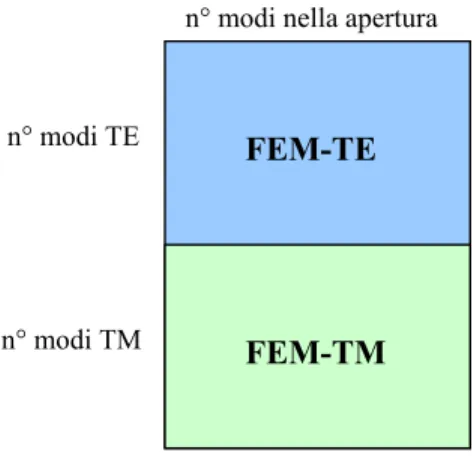
$ $ $ $ $ (3.1.23)Si noti che nella formulazione precedente è stato aggiunto l’apice FEM alle componenti di campo elettrico nella apertura. Si ricordi che, come si evidenzia nella (2.3.7), il campo magnetico in aria assume valori differenti a seconda che si tratti di modi con polarizzazione TE ovvero TM. A seguito di questa considerazione, si evince che la matrice C , le cui dimensioni sono [n0 modi in aria × n0 modi in apertura], può essere considerata suddivisa in due parti, a seconda delle famiglie modali a cui appartengono i modi dello sviluppo in aria. La separazione è illustrata in maniera intuitiva nella Fig 3.1.
Fig 3.1 Struttura della matrice di accoppiamento con la divisione in famiglie modali TE e TM
Nella figura viene inoltre evidenziato come nella analisi FEM della apertura non si faccia distinzione tra famiglie modali TE e TM. Dalle considerazioni fatte ne risulta che l’espressione nella (3.1.23) è equivalente alla
FEM-TE
FEM-TM
n° modi nella apertura n° modi TE
(
)
(
)
(
)
(
)
* * * * 1 ˆ 1 ˆ C CFEM TE FEM FEM FEM TE TE
x y z x y
ij x i y i z i x j y j z
i S
FEM TM FEM FEM FEM TM TM
x y z x y ij x i y i z i x j y j z i S C e i e i j e i h i h i i dS C e i e i j e i h i h i i dS β β − − = + + × + ⋅ = + + × + ⋅
∫∫
∫∫
$ $ $ $ $ $ $ $ $ $ (3.1.24)Si noti che il prodotto vettoriale tra le componenti di campo magnetico in aria e la componente longitudinale del campo elettrico nell’apertura non dà contributi lungo la direzione di propagazione. Le (3.1.24) diventano:
(
) (
)
{
}
(
) (
)
{
}
* * * * 1 ˆ 1 ˆ C CFEM TE FEM FEM TE TE
x y x y
ij x i y i x j y j z
i S
FEM TM FEM FEM TM TM
x y x y ij x i y i x j y j z i S C e i e i h i h i i dS C e i e i h i h i i dS β β − − = + × + ⋅ = + × + ⋅
∫∫
∫∫
$ $ $ $ $ $ $ $ (3.1.25)Svolgendo i prodotti vettoriali e scalari si ottiene:
(
)
(
)
* * * * 1 1 C CFEM TE FEM TE FEM TE ij x i y j y i x j
i S
FEM TM FEM TM FEM TM ij x i y j y i x j i S C e h e h dS C e h e h dS β β − − = − = −
∫∫
∫∫
(3.1.26) Gli integrali che compaiono nelle (3.1.26) vanno risolti numericamente in quanto il campoelettrico calcolato dal FEM non è noto in forma analitica. I segni di integrali devono quindi essere sostituiti dalle sommatorie su un numero prescelto di punti per ogni sottodominio in cui è stata suddivisa l’apertura. Si ottiene quindi:
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
* * 1 1 * * 1 1 1 , , , , 1 , , , , p elem p elem N NFEM TE FEM TE FEM TE
ij x i nk nk y j nk nk y i nk nk x j nk nk n k
i N N
FEM TM FEM TM FEM TM
ij x i nk nk y j nk nk y i nk nk x j nk nk n k i C e x y h x y e x y h x y C e x y h x y e x y h x y β β − = = − = = = − = −
∑ ∑
∑ ∑
(3.1.27)dove con Nelem si è indicato il numero di triangoli in cui è stato discretizzato il dominio
l’integrazione e con N il numero di punti all’interno di ogni triangolo su cui effettuare p l’integrazione.
3.2 Calcolo della GSM totale
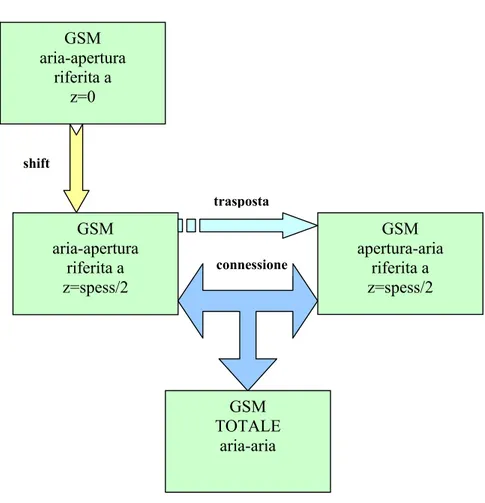
La GSM dello schermo può essere ottenuta dalla cascata delle matrici di scattering relative alla discontinuità aria-schermo e alla discontinuità schermo-aria (data dalla trasposta della precedente) aventi entrambe piano di riferimento a z d= 2 con d spessore dello schermo. Le operazioni elencate corrispondono allo schema a blocchi di Fig 3.2.
Fig 3.2 Nella figura è rappresentato lo schema a blocchi della procedura utilizzata per il calcolo della GSM totale
Si noti che lo schema a blocchi è riferito alla Fig 2.3 dove l’asse z è disposto sulla perpendicolare allo schermo ed è rivolto nella direzione di propagazione. Nello schema, con spess lo spessore dello schermo .
GSM aria-apertura riferita a z=0 shift GSM aria-apertura riferita a z=spess/2 GSM apertura-aria riferita a z=spess/2 connessione trasposta GSM TOTALE aria-aria
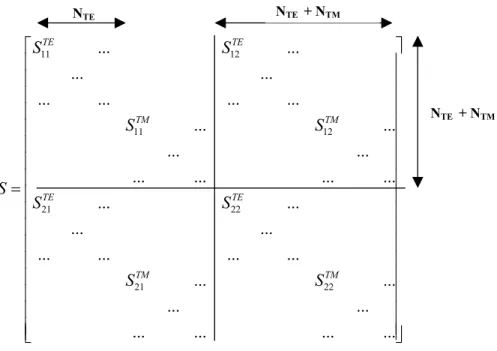
Nel range frequenziale in cui vengono tipicamente utilizzate le FSS, il solo modo fondamentale dello sviluppo modale di Floquet è in conduzione, mentre tutti gli altri modi di ordine superiore sono evanescenti. Sotto tale ipotesi, il comportamento della FSS può essere descritto in termini di coefficienti di riflessione e di trasmissione considerando solo i primi termini delle sottomatrici di S, come mostrato in Fig 3.3.
11 12 11 12 21 22 21 22 ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... TE TE TM TM TE TE TM TM S S S S S S S S S =
Fig 3.3 Schema della matrice di scattering generalizzata
Si noti in particolare che i coefficienti S11TE e S sono i coefficienti di riflessione e di 21TE
trasmissione per la polarizzazione TE mentre S11TM e S21TM sono i coefficienti di riflessione e di
trasmissione per la polarizzazione TM.
NTE + NTM
NTE + NTM
Shift del piano di riferimento
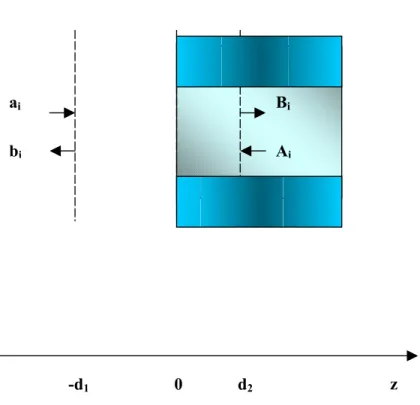
Dalla matrice di scattering generalizzata riferita ad una sezione, è possibile calcolare la matrice di scattering generalizzata riferita ad altri piani, ottenuti traslando in direzioni opposte il piano di riferimento della sezione associato all’ascissa z=0.
Fig 3.4 Traslazione dei piani di riferimento delle distanze d2 e –d1
La matrice
SHIFT
S del tratto compreso tra z = d2 e z = –d1, comprendente la discontinuità in
z=0 descritta dalla S , è data da
SHIFT
S = ⋅ ⋅ (3.2.1) T S T
dove la matrice T ha la seguente espressione:
Bi Ai ai bi z d2 -d1 0
1 1 (1) ( ) (1) 2 ( ) 2 ... 0 0 ... A z A z G z G z jk d jk nA d jk d jk nG d e e T e e − − = (3.2.2) Nel caso considerato della discontinuità aria dielettrico le due traslazioni diventano d1= per 0 lo shift in aria ed d2 =spess 2 per il tratto guidato nello schermo.
Calcolo della trasposta
Consideriamo ora una generica matrice di scattering, il sistema può essere scritto come
11 12 21 22 r r r r B S A S a b S A S a = + = + (3.2.3)
Pertanto scrivendo la definizione della matrice GSM in funzione della sua trasposta ottengo:
22 22 12 11 r r r r b S a S A B S a S A = + = + (3.2.4)
dal confronto tra la (3.2.4) e al (2.2.9) e ricordando che Ai,Bi sono i coefficienti complessi
dello sviluppo modale di Floquet in aria mentre ai,bi sono i coefficienti dello sviluppo modale
dell’onda nel tratto guidato. Si ottiene:
22 11, 21 12, 12 21, 11 22
r r r r
Di fatto il calcolo della trasposta determina la matrice di scattering generalizzata in cui i modi nell’apertura sono quelli incidenti e quelli in aria sono trasmessi. La procedura illustrata equivale a scambiare le porte di ingresso con quelle di uscita.
Calcolo della cascata
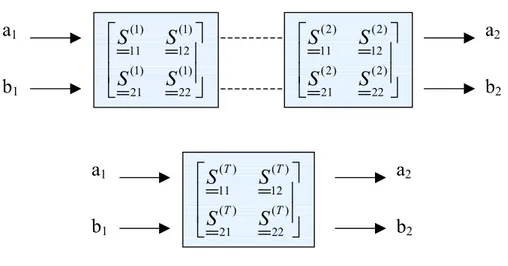
Si considerino due discontinuità descritte ciascuna dalla propria matrice di scattering generalizzata. Lo schema a blocchi è rappresentato in Fig 3.5.
Fig 3.5 Nella figura è rappresentato lo schema a blocchi della cascata di due discontinuità
La connessione viene effettuata attraverso il metodo della matrice di scattering generalizzata in modo che le sottomatrici costituenti la matrice complessiva abbiano le seguenti espressioni.
(1) (1) 11 12 (1) (1) 21 22