CAPITOLO 3

CAPITOLO 3

METODI DI VERIFICA

La grande diffusione di elementi strutturali in vetro che ha avuto luogo negli ultimi venticinque anni sotto la spinta di ingegneri ed architetti alla ricerca della massima traspa-renza e leggerezza strutturale ha portato con sé la necessità di sviluppare metodi di verifica sempre più precisi e più adatti ad essere applicati ad un materiale così diverso da quelli tra-dizionalmente usati nelle costruzioni.

Questa necessità si scontra con le notevoli difficoltà legate alla natura stessa del vetro, materiale fragile per eccellenza ed alla molteplicità di fattori che influenzano la resistenza.

A tutt’oggi risulta difficile trovare un accordo sul metodo di verifica più affidabile: molti ne sono stati proposti dai ricercatori che hanno accettato questa sfida, ma sembra an-cora lontana la formulazione definitiva di una norma europea per le strutture in vetro.

In questo capitolo si vuole esporre una panoramica dei metodi di verifica esistenti per illustrare i diversi fattori di cui si deve tener conto per una corretta progettazione di ele-menti in vetro.

È bene precisare subito che molte teorie sono state sviluppate per precisi elementi strutturali sottoposti a precise condizioni di carico (per la maggior parte lastre inflesse) e valgono quindi sotto determinate condizioni. Quando si affronta una struttura non standard, come la trave studiata in questa tesi, è bene procedere con molta prudenza e svolgere paral-lelamente alla progettazione, una campagna di indagini sperimentali su campioni in vera grandezza.

3.1 Tensioni ammissibili

Il metodo delle tensioni ammissibili, che nel passato ha guidato generazioni di inggneri nelle verifiche di sicurezza strutturale si presta molto male ad essere adottato per e-lementi in vetro.

Il semplice confronto tra la massima tensione principale di trazione e la tensione am-missibile, espresso dalla disuguaglianza

𝜎𝑚𝑎𝑥 ≤ 𝜎𝑎𝑑𝑚 (3.1)

non sembra adatto a cogliere la complessità di un fenomeno aleatorio come la rottura del vetro.

Non vengono infatti considerate variabili importanti come le dimensioni delle lastre, la probabilità che siano presenti difetti, la storia di carico, il tempo di applicazione del cari-co, le condizioni ambientali.

Il metodo delle tensioni ammissibili conserva comunque il pregio della grande sem-plicità e può trovare qualche applicazione soprattutto in fase di predimensionamento e per elementi secondari soggetti a condizioni di carico standard.

Tra le tante tabelle disponibili in letteratura, quelle ritenute più affidabili sono ricavate dalla normativa tedesca Tabella 3.1.

Tensioni Ammissibili [MPa]

Tipo di Vetro: Verticale Di Copertura Carichi da Impatto

annealed 18 12 80 stratificato di sicurezza 22,5 15 (25*) 120 temperato 50 50 170 fuso temperato 37 37 smaltato temperato 30 30 fuso 10 8 retinato 8 8

*ipotesi di lastra superiore frantumata

3.2 Metodi di verifica europei

I metodi di verifica delle strutture in vetro possono essere divisi in due famiglie: i metodi europei, che derivano dal metodo sviluppato in Germania e denominato

Da-mage Equivalent Load and Resistance (DELR) ed i metodi nordamericani che invece si

ba-sano sul Glass Failure Prediction Model (GFPM).

Tutti i metodi presentati si basano su una determinazione accurata delle tensioni prin-cipali di trazione, che in presenza di grandi deformazioni flessionali coinvolgono effetti del secondo ordine e richiedono una analisi non lineare per geometria.

3.2.1 Prove di norma per la determinazione della resistenza

Alla base dei diversi metodi per la verifica di sicurezza di un elemento strutturale di vetro c’è sempre una procedura standardizzata per la determinazione della resistenza carat-teristica.

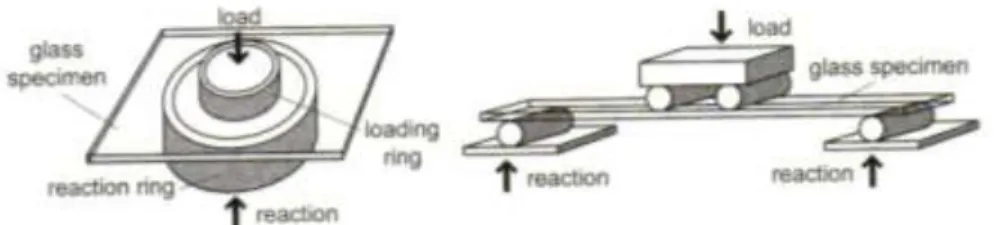
Le procedure di prova seguite in Europa seguono essenzialmente due schemi: la prova a flessione su quattro punti (four-point bending - 4PB) per indurre stati di tensione mono-assiali (𝜎1 ≠ 0; 𝜎2 = 0) e la prova su doppio anello (coaxial double ring - CDR) per indur-re stati di tensione biassiali (𝜎₁= 𝜎₂).

Figura 3.1: rappresentazione schematica della prova CDR (a sinistra) e della prova 4PB (a destra). La prova di flessione su quattro punti si adatta a descrivere il comportamento di ele-menti di forma allungata sottoposti a flessione (per esempio i gradini di una scala) mentre la prova su doppio anello riproduce l’effetto di un carico trasversale su una lastra di vetro. La prova su doppio anello ha il vantaggio di non essere influenzata dalla direzione dei di-fetti superficiali, inoltre rispetto alla prova di flessione su quattro punti (nella quale i bordi sono le zone più sollecitate) è più adatta a riprodurre lo stato di flessione uniforme (gli ef-fetti di bordo vengono in gran parte eliminati). Per questi motivi la prova CDR viene prefe-rita per la determinazione della resistenza a flessione.

La norma europea EN 1288-1 [43] indica le procedure fondamentali per eseguire la prova.

Prima di tutto viene rilevata l’importanza delle condizioni superficiali del provino, che vengono definite attraverso due caratteristiche principali: la condizione ottenuta con un

particolare metodo di trattamento che produce uno specifico spettro di danneggiamento (a-brasione, acidatura) e le sollecitazioni residue (precompressione termica o chimica).

Viene poi normalizzata la velocità di carico (la prova CDR viene eseguita con una ve-locità di carico costante pari a 𝑑𝜎_𝑑𝑡 = 2,0 ± 0,4 𝑀𝑃𝑎/𝑠𝑒𝑐 ).

Altro parametro che influenza la prova è l’area della superficie caricata, legata alla probabilità che siano presenti difetti superficiali di grandi dimensioni (l’influenza dell’area della superficie è maggiore per elementi non danneggiati). Vengono definiti tre tipi di pro-va in funzione delle dimensioni degli anelli: la propro-va R400 (definita in EN 1288-2) nella quale l’area maggiormente sollecitata è pari a 0,24 m2

, le prove R45 ed R30 (EN 1288-5) nelle quali l’area maggiormente sollecitata è pari rispettivamente a 254 mm2

e 113 mm2. Infine vengono definite le condizioni dell’ambiente circostante che possono influenza-re la prova (umidità influenza-relativa compinfluenza-resa fra 40% e 70%, temperatura di 23 ± 5 °𝐶).

Prove su doppio anello R400 su campioni intensamente danneggiati hanno evidenziato che per il calcolo della probabilità di rottura 𝐺 𝜎𝑏𝐵,𝐴0 può essere adottata la distribuzione

di Weibull: 𝐺 𝜎𝑏𝐵,𝐴0 = 1 − 𝑒𝑥𝑝 − 𝜎_{𝑏𝐵 ,𝐴0} 𝜃_𝐴0 𝛽 (3.2) dove:

𝜎𝑏𝐵,𝐴0 è la tensione di rottura di una lastra con distribuzione uniforme di tensioni

sulla superficie 𝐴0;

𝜃𝐴0 è il fattore di scala della distribuzione delle resistenze a flessione di prova;

𝛽 è il parametro di forma della distribuzione delle resistenze a flessione di prova.

Quindi la probabilità di rottura di una lastra di superficie 𝐴 = 𝑛 ∙ 𝐴0 e data da: 𝐺 𝜎_{𝑏𝐵,𝐴} = 1 − 1 − 𝐺 𝜎_{𝑏𝐵,𝐴0} 𝑛 = 1 − 𝑒𝑥𝑝 − 𝜎𝑏𝐵 ,𝐴0 𝜃_𝐴0 −𝛽 𝑛 = = 1 − 𝑒𝑥𝑝 −_𝐴𝐴 0∙ 𝜎_{𝑏𝐵 ,𝐴0} 𝜃_𝐴0 −𝛽 (3.3)

Se si ipotizza che la distribuzione sia la stessa per tutte le lastre si ha anche: 𝐺 𝜎𝑏𝐵,𝐴 = 1 − 𝑒𝑥𝑝 − 𝜎𝑏𝐵 ,𝐴_𝜃

𝐴

−𝛽

Confrontando la (3.3) e la (3.4) si ottiene: 𝜎𝑏𝐵,𝐴𝛽 = 𝜎𝑏𝐵,𝐴0𝛽 ∙ 𝐴 𝐴0 (3.5) da cui: 𝜎𝑏𝐵 ,𝐴 𝜎_{𝑏𝐵 ,𝐴0} = 𝐴0 𝐴 1 𝛽 (3.6)

La (3.6) rappresenta il rapporto fra le tensioni di rottura di lastre con area diversa a pa-rità di probabilità di crisi (size effect).

La (3.6) può essere generalizzata scrivendo:

𝜎𝑏𝐵,𝐴𝛽 ∙ 𝐴 = 𝑐𝑜𝑠𝑡. (3.7)

Questa equazione è formalmente analoga alla relazione che definisce la resistenza dell’acciaio a sollecitazioni di fatica (curva di Wöhler):

∆𝜎𝑚 _{∙ 𝑁 = 𝑐𝑜𝑠𝑡. (3.8)}

dove:

∆𝜎 è l’ampiezza dell’oscillazione di tensione che porta a rottura in N cicli 𝑚 è la pendenza della curva di Wöhler;

Si può quindi pensare [31] di estendere al vetro la formula di accumulazione lineare del danneggiamento di Miner:

∆𝜎𝑖 𝑖𝑚∙ 𝑛𝑖 = ∆𝜎𝑒𝑞𝑚 ∙ 𝑁 = ∆𝜎𝑚𝑎𝑥𝑚 ∙ 𝑁𝑒𝑞 (3.9)

Analogammente dalla (3.7) si ricava:

𝜎𝑖 𝑏𝐵,𝐴𝛽 ∙ 𝐴𝑖 = 𝜎𝑏𝐵,𝐴,𝑒𝑞𝛽 ∙ 𝐴𝑖 𝑖 = 𝜎𝑏𝐵,𝐴,𝑚𝑎𝑥𝑚 ∙ 𝐴𝑒𝑞 (3.10)

si può, cioè determinare una tensione uniformemente distribuita di danneggiamento equivalente:

𝜎_{𝑏𝐵,𝐴,𝑒𝑞} = ∆𝜎𝑖 𝑏𝐵 ,𝐴𝛽 ∙𝐴𝑖

I metodi che verranno di seguito descritti si basano sulla possibilità di confrontare una tensione non uniforme (espressa generalmente in termini di tensione massima sulla super-ficie dell’elemento) con la tensione uniforme ottenuta nei test di laboratorio attraverso la tensione di danneggiamento equivalente.

3.2.2 Metodo DELR

Il metodo DELR (Damage Equivalent Load and Resistance) è frutto di ricerche svolte presso il Rheinische-Westfälische Technische Hochschule di Aachen a partire dalla secon-de metà secon-degli anni ’70 ed è secon-descritto compiutamente in [31].

Il metodo, sviluppato per la piastre ed esteso successivamente alle travi in vetro, ha il pregio di essere in accordo con le recenti generazioni di normative basate sui coefficienti parziali di sicurezza.

La verifica consiste in un confronto tra la massima tensione principale di calcolo 𝜎𝑚𝑎𝑥 ,𝑑 ed una resistenza equivalente che tiene conto della distribuzione di tensioni nel ve-tro, delle dimensioni del dettaglio, della durata del carico, delle condizioni ambientali.

La disuguaglianza di verifica può essere scritta:

𝜎

≤

𝛼𝜎 𝑞,𝜎𝑉 ∙𝛼 𝐴𝑟𝑒𝑑 ∙𝛼 𝑡 ∙𝛼 𝑆𝑣 ∙𝛾𝑀 ,𝐸

+

𝜎𝑉,𝑘

𝛾𝑀 ,𝑉 (3.12) dove:

𝛼𝜎 𝑞, 𝜎𝑉 è un coefficiente che tiene conto della distribuzione di tensioni sulla superficie del vetro (q è il carico uniformemente distribuito, 𝜎𝑉 è la tensione residua dovuta alla tempera); per semplicità si può assume-re cautelativamente 𝛼𝜎 = 1;

𝛼 𝐴_𝑟𝑒𝑑 è un coefficiente che tiene conto della dimensione dell’area della su-perficie decompressa 𝐴𝑟𝑒𝑑 (per vetri annealed, 𝐴𝑟𝑒𝑑 è pari all’intera superficie); per calcolare il coefficiente si può usare la relazione

𝛼 𝐴𝑟𝑒𝑑 = 𝐴𝑟𝑒𝑑 _𝐴0 1

𝛽

dove  è il parametro di forma della distribu-zione di Weibull e può essere assunto pari a 25;

𝛼 𝑡 è un coefficiente che tiene conto della durata di applicazione del ca-rico; Sedlacek et al. [31] propone 𝛼 𝑡 = 3,9;

𝛼 𝑆𝑣 è un coefficiente che tiene conto della combinazione di carico e delle condizioni ambientali (è legato al fenomeno dell’accrescimento su-bcritico delle cricche); in [31] sono forniti dei grafici che legano qualitativamente il valore di 𝛼 𝑆𝑣 ai rapporti fra le diverse

nenti di carico (peso proprio, vento, neve); l’intervallo di variazione è compreso fra 0,4 ed 1,0;

𝜎𝑚𝑎𝑥 ,𝑑 è il valore di calcolo della massima tensione principale di trazione nell’elemento, calcolata secondo le norme correnti per le azioni (in particolare secondo EN 1990 ed EN 1991);

𝜎𝑏𝐵,𝐴0,𝑘 è il valore caratteristico della resistenza a flessione determinata

me-diante prova a flessione coassiale su doppio anello R400 secondo EN 1288-2:2000 [43] (frattile 5%, livello di affidabilità 0,95, area della superficie di prova2 𝐴_𝑜 = 0,24 𝑚2);

𝜎𝑉,𝑘 è il valore caratteristico (frattile 5%) della compressione(valore as-soluto della tensione, quindi valore positivo per la compressione) della tensione superficiale residua (normalmente indotta dalla tem-pera termica o chimica);

𝛾𝑀,𝐸 è il coefficiente parziale di sicurezza per la resistenza a flessione, pa-ri al rapporto fra la resistenza carattepa-ristica valutata con prove su doppio anello con campioni di vetro nuovi e la resistenza caratteri-stica valutata con provini artificialmente danneggiati (si assume 𝛾𝑀,𝐸 = 1,8);

𝛾𝑀,𝑉 è il coefficiente di sicurezza per le tensioni superficiali residue.

La verifica può essere estesa alle travi adattando i coefficienti:

𝜎

≤

𝜎 𝑞,𝜎𝑉 𝐵𝑍∙𝛼 𝐿𝑟𝑒𝑑 ∙𝛼𝐵𝑍 𝑡 ∙𝛼 𝑆𝑣 ∙𝛾𝑀 ,𝐸

+

𝜎𝑉,𝑘

𝛾𝑀 ,𝑉 (3.13) in questo caso:

𝜎𝑏𝐵,𝐿0,𝑘 è la resistenza caratteristica (frattile 5%) con lunghezza di

decom-pressione 𝐿_𝑜 = 0,46 𝑚; la lunghezza di decompressione è la lun-ghezza del bordo in cui la tensione indotta dai carichi supera la compressione residua dovuta alla tempera;

𝛼 𝐿𝑟𝑒𝑑 = 𝐿𝑟𝑒𝑑 _𝐿0 1

𝛽

con 𝛽 = 5 o 𝛽 = 12,5 a seconda della lavorazione dei bordi; 𝛼𝜎 𝑞, 𝜎𝑉 si assume pari ad 1,0 per distribuzioni di tensione uniformi, a 0,94

per distribuzioni paraboliche e a 0,86 per distribuzioni triangolari;

2

Superficie interna dell’anello di carico, che nella prova a doppio anello può essere considerata a ten-sione costante.

𝛾_𝑀,𝐸 si propone il valore 1,4 per 𝛽 = 12,5;

3.2.3 Metodo di Shen

Una variante semplificativa del metodo DELR è stata proposta da Xiaofeng Shen [32]. Nella disuguaglianza di verifica, dal lato della resistenza vengono usati solo due coef-ficienti che possono essere determinati con semplici tabelle. L’effetto delle tensioni residue dovute alla tempera è compreso indirettamente in questi due coefficienti.

Questo metodo è valido solo per piastre di vetro (annealed o temperato) caricate tra-sversalmente e con appoggi continui sui quattro lati.

Il formato della verifica è il seguente:

𝜎

≤ 𝜎

∙

𝛾𝑅

dove:

σmax ,d è il valore di calcolo della tensione principale massima;

σ_k è il valore caratteristico della resistenza a flessione determinato con la prova su doppio anello;

𝜂_𝐹 è un coefficiente che tiene conto dell’area della superficie e della di-stribuzione di tensione;

𝜂_𝐷 è un coefficiente che tiene conto della durata di applicazione del ca-rico;

𝛾𝑅 è il coefficiente parziale di sicurezza per la resistenza (il valore indi-cato dall’autore è pari a 1,25 per edifici di media importanza).

La verifica deve essere fatta separatamente per le diverse durate di applicazione del carico.

I coefficienti 𝜂_𝐹 ed 𝜂_𝐷 possono essere ricavati dalle seguenti tabelle.

A = 0,5 – 4,0 m2 A = 4 – 10 m2

ANG 1,0 0,9

FTG 1,0 1,0

tabella 3.2: coefficiente 𝜂𝐹 per vetri annealed (Annealed Glass - ANG) e

Carichi Permanenti (50 anni) Neve (30 giorni) Vento (10 min) ANG 0,27 0,45 0,69 FTG 0,74 0,83 1,00

tabella 3.3: coefficiente 𝜂𝐷 per vetri annealed (Annealed Glass - ANG) e temperati

(Fully Tempered Glass – FTG)

3.2.4 Metodo di Siebert

Anche Geralt Siebert [33] ha proposto una variante dei metodi precedentemente di-scussi, che consiste nella seguente disuguaglianza:

𝜎

∙ 𝑓

∙ 𝑓

∙ 𝑓

≤

𝑓𝑃

dove:

σges ,d,max è il valore di calcolo della tensione principale massima, comprensivo della tensione residua superficiale (σ_{ges ,d,max} = σ_d,max + σ_E); σd,max è la tensione principale dovuta alle azioni;

σ_E è la tensione residua superficiale (valore con segno: la compressione è negativa);

𝑓_𝐴 è un coefficiente che tiene conto della diversa area della superficie del campione e dell’effettivo elemento strutturale;

𝑓_𝜎 è un coefficiente che tiene conto della diversa distribuzione di ten-sione fra campione ed elemento strutturale;

𝑓_𝑡𝑆 è un coefficiente che tiene conto della durata di applicazione del ca-rico delle condizioni ambientali e della grandezza relativa dei diversi carichi;

𝜃 è il parametro di scala della distribuzione di Weibull della resistenza a flessione del provino (ha le dimensioni fisiche di una tensione) 𝑓𝑃 è un fattore che tiene conto del grado di sicurezza che si vuole

La tensione principale dovuta alle azioni esterne viene calcolata come nel metodo DELR, ma in questo caso la tensione residua σ_E è considerata come un’azione (si racco-manda di moltiplicare le tensioni residue per un fattore parziale di sicurezza 𝛾𝑣 = 1,25; il fattore viene posto al numeratore per analogia con i fattori di sicurezza delle azioni, anche se concettualmente dovrebbe essere posto al denominatore o essere ≤ 1 perché la tensione residua aumenta la resistenza).

Per ottenere i dati sulla resistenza si raccomanda la prova standard su doppio anello R400 secondo EN 1288-2:2000 [43] eseguita su campioni di vetro annealed danneggiati artificialmente.

Per tener conto di distribuzioni non omogenee di tensione nell’elemento, viene intro-dotta l’area efficace:

𝐴_{𝑁,𝑒𝑓} = 𝜒∙𝜎𝑔𝑒𝑠 ,𝑑 𝑥,𝑦 𝜎𝑔𝑒𝑠 ,𝑑,𝑚𝑎𝑥 𝛽 𝑑𝐴 𝐴 (3.16) dove:

σges ,d x, y è la tensione principale nel punto (x,y) (riferita alla tensione di aper-tura della cricca quindi σges ,d x, y ≥ 0 );

σ_{ges ,d,max} è la tensione principale massima sulla superficie; 𝐴 è l’area della superficie della lastra di vetro;

𝜒 è un fattore di correzione per il rapporto tra tensione principale mas-sima e minima (a favore di sicurezza si può assumere 𝜒 = 1,0; per campi di tensione monoassiali si consiglia 𝜒 = 0,83

Detta 𝐴_{𝐿,𝑒𝑓} l’area efficace del campione si possono calcolare i coefficienti: 𝑓_𝐴 = _𝐴𝐴 𝐿,𝑒𝑓 1 𝛽 (3.17) 𝑓𝜎 = 𝐴𝑁 ,𝑒𝑓_𝐴 1 𝛽 = 𝜎𝑔𝑒𝑠 ,𝑑,𝑒𝑓 𝜎𝑔𝑒𝑠 ,𝑑,𝑚𝑎𝑥 (3.18)

𝑓𝐴 è identico al coefficiente 𝛼 𝐴 del metodo DELR, mentre 𝑓𝜎 dipende dal livello di tensione residua (essendo questa considerata come un’azione).

Il coefficiente 𝑓𝑡𝑆 è pari al prodotto dei fattori 𝛼 𝑡 ed 𝛼 𝑆𝑉 usati nel metodo DELR. Il fattore aggiuntivo 𝑓_𝑃 consente di scegliere una probabilità di crisi 𝐺_𝑎 ed è definito da: 𝑓𝑃 = 𝑙𝑛 _1−𝐺1 𝑎 −1 𝛽 (3.19)

Per 𝛽 = 25 e 𝐺_𝑎 = 1,5 ∙ 10−3 _{si ottiene 𝑓}

𝑃 = 1,3.

Un confronto fra il metodo DELR ed il metodo di Siebert, evidenzia che il coefficien-te parziale di sicurezza di Siebert per le coefficien-tensioni residue è meno caucoefficien-telativo, tuttavia per vetri annealed i due metodi danno risultati molto simili [14]:

𝜎_𝑅𝑑 =𝜎𝑏𝐵 ,𝐴0,𝑘 𝛾𝑀 = 45 𝑀𝑃𝑎 1,8 ≈ 𝜃 𝑓𝑃 = 32 𝑀𝑃𝑎 1,3 ≈ 25 𝑀𝑃𝑎

Il motivo per cui i coefficienti sono diversi è che nel metodo di Siebert la resistenza è basata sul parametro di scala di Weibull 𝜃, mentre nel metodo DELR è basata sul valore caratteristico 𝜎𝑏𝐵,𝐴0,𝑘.

3.2.5 Normativa europea prEN13474

Uno standard europeo per le verifiche di elementi in vetro è ancora in fase di revisione presso i comitati CEN/TC 250 (Structural Eurocodes) e CEN/TC 129 (Glass in buildings).

In questo paragrafo si farà riferimento alla parte terza (Metodo generale di calcolo e determinazione della resistenza attraverso prove di laboratorio) nella versione del gennaio 2007 [41].

Le verifiche consistono nel confronto fra gli effetti delle azioni di calcolo ed i rispetti-vi limiti di calcolo.

Per gli stati limite ultimi (ULS) si ha:

𝐸_{𝑈𝐿𝑆,𝑑} ≤ 𝑅_𝑑 (3.20)

mentre per gli stati limite di esercizio (SLS) si ha:

𝐸𝑆𝐿𝑆,𝑑 ≤ 𝐶𝑑 (3.21)

dove:

𝐸𝑈𝐿𝑆,𝑑 = 𝐸 𝐹𝑈𝐿𝑆,𝑑 è l’effetto (espresso come tensione) di una combinazione di carico agli stati limite ultimi;

𝐸_{𝑆𝐿𝑆,𝑑} = 𝐸 𝐹_{𝑆𝐿𝑆,𝑑} è l’effetto (espresso come tensione o come deformazione) di una combinazione di carico agli stati limite di esercizio;

𝑅𝑑 è il valore di calcolo della resistenza, espressa in termini di massima tensione consentita per lo stato limite ultimo 𝑓_𝑔,𝑑, considerando il coefficiente parziale di sicurezza per il mate-riale per lo stato limite ultimo 𝛾_𝑀;

𝐶𝑑 è il valore di calcolo relativo al criterio di verifica agli stati li-mite di esercizio rilevante, espresso in termini di massima ten-sione consentita allo stato limite di esercizio 𝑓_𝑔,𝑑, o di limite di deformabilità 𝑤_𝑑, considerando il coefficiente parziale di sicu-rezza per il materiale per lo stato limite di esercizio 𝛾𝑀;

ULS SLS

Annealed (ANG) 𝛾𝑀,𝐴= 1,8 𝛾𝑀,𝐴= 1,5

Temperato (FTG) 𝛾𝑀,𝑣 = 1,2 𝛾𝑀,𝑣 = 1,0

tabella 3.4: valori raccomandati per i coefficienti parziali di sicurezza per il materiale.

Per quanto riguarda le azioni e le combinazioni di carico, per gli stati limite di eserci-zio si adottano le combinaeserci-zioni frequenti (EN 1990), mentre per gli stati limite ultimi si applicano le combinazioni fondamentali.

Adottando i simboli usuali per gli Eurocodici, per lo stato limite ultimo si ha: 𝐹_𝑑 = 𝛾_𝐺∙ 𝐺 + 𝛾_𝑄𝑄_𝑘,1+ 𝛾_𝑄 𝜓𝑖 0,𝑖𝑄𝑘,𝑖

per lo stato limite di esercizio si ha: 𝐹_𝑑 = 𝐺 + 𝜓₁𝑄_𝑘,1+ 𝜓_{𝑖 2,𝑖}𝑄_𝑘,𝑖

Per vetri stratificati, nel caso in cui l’interlayer sia in grado di trasferire degli sforzi di taglio, la norma prEN 13474-3 suggerisce di procedere al calcolo di deformazioni e tensio-ni attraverso gli spessori equivalenti:

𝑕_{𝑒𝑓 ,𝑤} = 1 − 𝜔 𝑕3 _{𝑖 𝑖}3+ 𝜔 𝑕_{𝑖 𝑖} 3 (per il calcolo delle deformazioni)

e

𝑕𝑒𝑓 ,𝜎,𝑗 = 𝑕𝑒𝑓,𝑤

3

𝑕𝑗+2𝜔𝑕𝑚 ,𝑗 (per il calcolo delle tensioni)

dove:

𝜔 è un coefficiente compreso tra 0 e 1 (0 rappresenta un trasferimento nullo del ta-glio e 1 un trasferimento completo);

𝑕_𝑖, 𝑕_𝑗 sono spessori degli strati di vetro;

𝑕𝑚,𝑗 è la distanza fra il piano medio dello strato j-esimo dal piano medio del vetro stra-tificato, ignorando lo spessore dell’interlayer.

Dal lato della resistenza, si distinguono due casi a seconda del tipo di vetro(annealed o temperato).

Per vetri annealed si usa la relazione:

𝑓

=

𝛾𝑀 ,𝐴

dove:

𝑓𝑔,𝑘 è il valore caratteristico della resistenza a flessione (𝑓𝑔,𝑘 = 45 𝑁/𝑚𝑚2); 𝛾_𝑀,𝐴 è il coefficiente parziale riportato nella tabella 3.4;

𝑘𝑠𝑝 è un fattore che tiene conto del profilo della superficie (Tabella 3.5) 𝑘𝑚𝑜𝑑 è un fattore che tiene conto della durata di applicazione del carico.

Vetro

(qualsiasi composizione)

Fattori per il profilo di superficie ksp

vetro float

1,0 vetro tirato

(drawn shet glass) 1,0

vetro smaltato float o tirato*

(enamelled float or drawn sheet glass) (1,0)

vetro stampato

(patterned glass) 0,75

vetro smaltato stampato*

(enamelled patterned glass) (0,75)

vetro lustro armato

(polished wired glass) 0,75

vetro stampato armato

(patterned wired glass) 0,6

*tipi generalmente non disponibili come vetro annealed (valori ugualmente richiesti per cal-colare la resistenza dei vetri temperati e induriti).

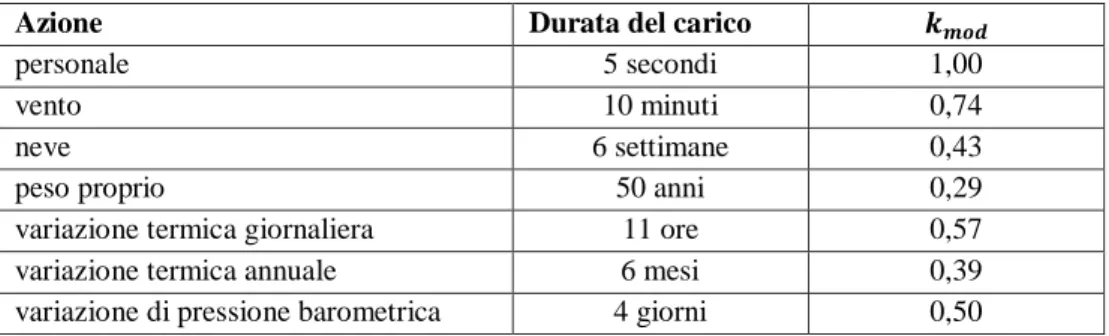
Il valore di 𝑘𝑚𝑜𝑑 può essere calcolato con la relazione:

𝑘_𝑚𝑜𝑑 = 0,663 ∙ 𝑡−161 _{(con un valore massimo di 1 ed un minimo di 0,25)}

oppure con la Tabella 3.6:

Azione Durata del carico 𝒌𝒎𝒐𝒅

personale 5 secondi 1,00

vento 10 minuti 0,74

neve 6 settimane 0,43

peso proprio 50 anni 0,29

variazione termica giornaliera 11 ore 0,57

variazione termica annuale 6 mesi 0,39

variazione di pressione barometrica 4 giorni 0,50

Tabella 3.6: valori del coefficiente di durata del carico kmod.

Per vetri temperati e induriti, invece bisogna aggiungere un termine che tiene conto delle tensioni di compressione indotte dal procedimento di tempera (tensioni residue).

La resistenza può essere scritta:

𝑓

=

𝛾𝑀 ,𝐴

+

𝑘𝑣 𝑓𝑏,𝑘−𝑓𝑔,𝑘

𝛾𝑀 ,𝑣

dove:

𝛾_𝑀,𝑣 è il coefficiente parziale riportato nella tabella 3.4;

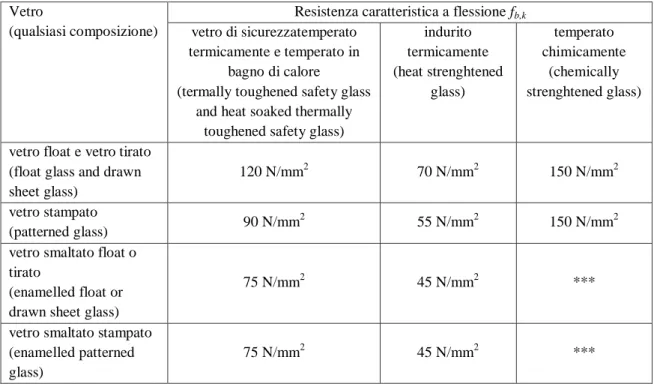
𝑓_𝑏,𝑘 è il valore caratteristico della resistenza a flessione del vetro temperato; 𝑘𝑣 è il fattore di incremento della resistenza (strenghtening factor) del vetro

Vetro

(qualsiasi composizione)

Resistenza caratteristica a flessione fb,k vetro di sicurezzatemperato

termicamente e temperato in bagno di calore (termally toughened safety glass

and heat soaked thermally toughened safety glass)

indurito termicamente (heat strenghtened glass) temperato chimicamente (chemically strenghtened glass)

vetro float e vetro tirato (float glass and drawn sheet glass) 120 N/mm2 70 N/mm2 150 N/mm2 vetro stampato (patterned glass) 90 N/mm 2 55 N/mm2 150 N/mm2

vetro smaltato float o tirato

(enamelled float or drawn sheet glass)

75 N/mm2 45 N/mm2 ***

vetro smaltato stampato (enamelled patterned glass)

75 N/mm2 45 N/mm2 ***

Tabella 3.7:resistenza caratteristica del vetro temperato e indurito.

Alcuni processi produttivi possono ridurre localmente l’efficacia della tempera (dispositivi di afferraggio delle lastre per vetri temperati verticalmente): I valori dei coefficienti che tengono conto di questo effetto sono riportati nella Tabella 3.8.

Processo di produzione Strenghtening factor kv

tempera orizzontale 1,0

tempera verticale 0,6

Tabella 3.8: fattore di riduzione della resistenza legato al processo produttivo.

Si osserva che le relazioni riportate per il calcolo della resistenza non contengono al-cun coefficiente che tenga in conto l’area della superficie del dettaglio. Versioni precedenti della norma prevedevano un fattore 𝑘𝐴 = 𝐴125 al denominatore che suscitava alcune con-traddizioni [14]. Non era invece presente il coefficiente 𝑘𝑠𝑝, funzione della finitura super-ficiale.

Altra differenza rispetto ai metodi precedentemente descritti è costituita dal coeffi-ciente 𝑘𝑚𝑜𝑑 che rimpiazza 𝛼 𝑡 ed 𝛼 𝑆𝑉 ,con una procedura simile a quella seguita da Shen. Tuttavia 𝑘_𝑚𝑜𝑑 e 𝜂_𝐷 non sono identici: 𝑘_𝑚𝑜𝑑 non tiene conto delle grandezze relative dei diversi carichi della combinazione, i pochi valori presenti nella Tabella 3.6 includono evidentemente assunzioni semplificative implicite.

3.2.6 Esempio di calcolo della resistenza secondo prEN 13474-3:2007

A titolo di esempio si procede al calcolo della resistenza per una lastra di vetro annea-led e per una lastra temperata chimicamente, considerando tre diversi valori di 𝑘𝑚𝑜𝑑.

Per carichi di lunga durata (peso proprio) si ha: 𝑘𝑚𝑜𝑑 = 0,29 (50 anni);

per carichi di media durata (neve) si ha: 𝑘𝑚𝑜𝑑 = 0,43 (6 settimane); per carichi di breve durata (vento) si ha:

𝑘𝑚𝑜𝑑 = 0,74 (10 minuti);

si assumono valori di 𝑘𝑠𝑝 e 𝑘𝑣 pari a: 𝑘_𝑠𝑝 = 1,0 (vetro float)

𝑘_𝑣 = 1,0 (tempera orizzontale)

Si esegue il calcolo per gli Stati Limite Ultimi, quindi si assume: 𝛾𝑀,𝐴 = 1,8 (vetro annealed)

Le resistenze caratteristiche sono pari a: 𝑓𝑔,𝑘 = 45 𝑁/𝑚𝑚2 (vetro annealed);

𝑓𝑏,𝑘 = 150 𝑁/𝑚𝑚2 (vetro temperato chimicamente).

Per il caso di vetro annealed si applica la (3.22): 𝑓_𝑔,𝑑 =𝑘𝑚𝑜𝑑𝑘𝑠𝑝𝑓𝑔,𝑘

𝛾𝑀 ,𝐴

e quindi

𝑓𝑔,𝑑 =0,29∙1∙45_1,8 = 7,25 𝑁/𝑚𝑚2 (per il peso proprio);

𝑓_𝑔,𝑑 =0,43∙1∙45_1,8 = 10,75 𝑁/𝑚𝑚2 _{(considerando come azione variabile} dominante il carico neve);

𝑓𝑔,𝑑 =0,74∙1∙45_1,8 = 18,5 𝑁/𝑚𝑚2 (considerando come azione variabile dominante il vento).

Per vetro temperato chimicamente si applica la (3.23): 𝑓𝑔,𝑑 = 𝑘𝑚𝑜𝑑𝑘𝑠𝑝𝑓𝑔,𝑘 𝛾𝑀 ,𝐴 + 𝑘𝑣 𝑓𝑏,𝑘−𝑓𝑔,𝑘 𝛾𝑀 ,𝑣 e quindi

𝑓_𝑔,𝑑 = 7,25 +1∙ 150−45 _1,2 = 95 𝑁/𝑚𝑚2 _{(per il peso proprio);} 𝑓𝑔,𝑑 = 10,75 +1∙ 150−45 _1,2 = 98 𝑁/𝑚𝑚2 (per la neve);

𝑓𝑔,𝑑 = 18,5 +1∙ 150−45 _1,2 = 106 𝑁/𝑚𝑚2 (per il vento).

3.3 Metodi di verifica nordamericani

3.3.1 Glass failure prediction model (GFPM)

Questo metodo di verifica si basa direttamente sulla teoria statistica sulla rottura dei materiali fragili sviluppata da Weibull nel 1939.

Secondo questa teoria la probabilità di crisi può essere rappresentata dalla relazione:

𝑃𝑓 = 1 − 𝑒−𝐵 (3.24)

Dove B è una funzione di rischio che dipende da tutti i fattori rilevanti ed in particola-re dalle condizioni della superficie e dalla distribuzione delle tensioni. Il modell GFPM propone la funzione di rischio:

𝐵 = 𝑘 𝑐 𝑥, 𝑦 𝜎𝑒𝑞,𝑚𝑎𝑥 𝑞, 𝑥, 𝑦 𝑚

𝐴 𝑑𝐴 (3.25)

nella quale:

𝑐 𝑥, 𝑦 è il fattore di correzione per sforzo biassiale (funzione del rappor-to fra tensione principale massima e minima);

𝐴 è l’area della superficie;

𝜎𝑒𝑞 ,𝑚𝑎𝑥 𝑞, 𝑥, 𝑦 è la tensione principale massima equivalente nel punto (x,y) do-vuto al carico q;

𝑚 𝑒 𝑘 sono i parametri dei difetti superficiali (surface flaw parameters);

Per lastre di vetro rettangolari sottoposte a carico trasversale uniforme di durata 𝑡_𝑝 (e-spressa in secondi) viene introdotta la seguente espressione:

𝐵 = 𝑘 𝑎 𝑏 1−𝑚 _{𝐸 𝑕}2 𝑚 𝑡𝑑 60 𝑚 16 𝑅 𝑚 , 𝑞 ,𝑎_𝑏 (3.26) dove:

a e b sono le dimensioni della lastra;

h è lo spessore della lastra;

E è il modulo di Young;

La funzione adimensionale 𝑅 𝑚, 𝑞,𝑎_𝑏 dipende dal parametro di imperfezione 𝑚 e dalla distribuzione delle tensioni adimensionalizzae sulla superficie

𝑅 𝑚, 𝑞,𝑎_𝑏 =_{𝑎 𝑏}1 𝑐 𝑥, 𝑦 𝜎 𝑚𝑎𝑥 𝑞 , 𝑥, 𝑦 𝑚_𝑑𝐴 𝐴 (3.27) il carico adimensionalizzato è: 𝑞 = 𝑞 𝑎 𝑏 _{𝐸 𝑕4}2 (3.28) La tensione adimensionalizzata è: 𝜎 = 𝜎 𝑞, 𝑥, 𝑦 _{𝐸 𝑕}𝑎 𝑏₂ (3.29)

I parametri 𝑚 𝑒 k vengono determinati sperimentalmente con una procedura piuttosto complessa [14].

La verifica è condotta sul piano delle probabilità di crisi: stabilita una probabilità am-missibile, la si confronta con quella calcolata con la (3.24).

3.3.2 Normativa statunitense (ASTM E 1300)

La normativa statunitense si basa sul GFPM. La resistenza è definita fissando una probabilità limite di crisi pari a 0,008.

La norma si applica solo a lastre rettangolari di vetro monolitico, stratificato o vetro camera isolante, sottoposte a carico laterale uniforme e vincolate con appoggi lineari su

uno, due, tre o quattro bordi (quindi non si applica a parapetti, pavimenti in vetro, ed altre applicazioni strutturali, né a vetri armati, stampati, smaltati, satinati o sottoposti ad altri trattamenti superficiali).

Il formato della verifica è il seguente:

𝑞 ≤ 𝐿𝑅 = 𝑁𝐹𝐿 ∙ 𝐺𝑇𝐹 (3.30)

dove:

q è il carico uniformemente distribuito; LR è la resitenza (Load Resistance);

NFL è il carico non fattorato (Non-Factored Load);

GTF è un fattore relativo al tipo di vetro (Glass Type Factor);

La differenza principale rispetto ai metodi europei è che la verifica viene quindi effet-tuata sul piano dei carichi e non delle tensioni. Inoltre non si fa uso di alcun coefficiente parziale di sicurezza.

Il fattore GTF può essere determinato con la Tabella 3.9.

Anche il carico NFL viene fornito in tabelle in funzione della geometria della lastra e delle condizioni di vincolo.

GTF

Per tipo di vetro

Durata dei carichi

Breve lunga

annealed (ANG) 1 0,5

indurito (HSG) 2 1,3

temperato (FTG) 4 3

Tabella 3.9:fattori per il tipo di vetro (lastra monolitica o laminata)

Tutti i valori sono calcolati con il GFPM assumendo 𝑘 = 2,86 ∙ 10−53 𝑁−7𝑚12, 𝑚 = 7 e per il modulo elastico 𝐸 = 71,7 𝐺𝑃𝑎.

Per i casi non coperti dalla normativa si suggeriscono delle tensioni ammissibili per carichi di durata 3 secondi e una probabilità di crisi 𝑃𝑓 < 0,05.

3.3.3 Normativa canadese (CAN/CGSB 12.20)

Anche la normativa canadese applica il GFPM, la verifica però consiste in un confron-to fra la combinazione di tutte le azioni di progetconfron-to 𝐸𝑑 e la resistenza di progetto 𝑅𝑑che in-cludono dei coefficienti parziali:

𝐸𝑑 ≤ 𝑅𝑑 (3.31)

Il termine relativo alle azioni è:

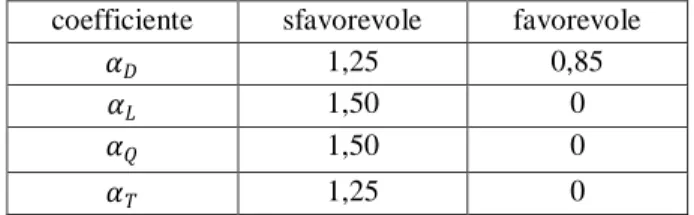
𝐸_𝑑 = 𝛼_𝐷𝐷 + 𝛾 ∙ 𝜓 ∙ 𝛼_𝐿𝐿 + 𝛼_𝑄𝑄 + 𝛼_𝑇𝑇 (3.32) dove:

𝐷 è il carico permanente (Dead Load); 𝐿 𝑒 𝑄 sono carichi variabili (live Loads); 𝑇 sono gli effetti delle variazioni termiche.

𝛼_𝑖 sono i coefficienti parziali di sicurezza (Tabella 3.10);

𝛾 è il fattore di importanza (generalmente 𝛾 = 1, per edifici a basso rischio 𝛾 ≥ 0,8);

𝜓 è il fattore di combinazione(pari ad 1,0 se tra L,Q e T agisce una sola azione, pari a 0,7 se agiscono contemporaneamente due azioni e pari a 0,6 se agisco-no tutte insieme);

coefficiente sfavorevole favorevole

𝛼𝐷 1,25 0,85

𝛼𝐿 1,50 0

𝛼𝑄 1,50 0

𝛼𝑇 1,25 0

Tabella 3.10:coefficienti parziali (lato azioni).

Il termine relativo alle resistenze è:

𝑅 = 𝑐1∙ 𝑐2∙ 𝑐3∙ 𝑐4∙ 𝑅𝑟𝑒𝑓 (3.33)

dove:

𝑐1 è il fattore che tiene conto del tipo di vetro;

𝑐2 è il fattore che tiene conto del trattamento termico; 𝑐₃ è il fattore che tiene conto della durata del carico;

𝑐4 è il fattore che tiene conto della ripartizione del carico (pari ad 1,0 per vetri monolitici, a 1,7 e 2,0 per vetri-camera doppi e tripli);

𝑅_𝑟𝑒𝑓 è la resistenza di riferimento (data da tabelle in normativa).

Per le applicazioni non standard ed i casi non coperti dalla norma vengono fornite del-le relazioni per stimare l’effetto dell’area della superficie e l’effetto della durata dei cari-chi:

𝑅_𝐴 = 𝑅_𝑟𝑒𝑓 ∙ 𝐴 −1 𝑚 (3.34)

dove l’area A è espressa in m2 _{ed il coefficiente 𝑚 varia tra 5 e 7;} 𝑅𝑡 = 𝑅𝑟𝑒𝑓 ∙ 𝑡 −1 𝑛 (3.35)

dove la durata t è espressa in minuti ed il coefficiente 𝑚 è pari a 15 per vetri annealed,

30 per vetri induriti e 70 per vetri temperati;

Per casi generali la norma raccomanda tensioni limite di 25 MPa lontano dai bordi e

20 MPa sui bordi.

3.4 Confronto tra i diversi metodi

Un paragone tra i metodi europei e quelli nordamericani risulta particolarmente com-plicato a causa delle incompatibilità concettuali nei due approcci.

Innanzi tutto i valori della resistenza vengono ricavati da prove di laboratorio diverse: prova con doppio anello R400 per i metodi europei e lastra rettangolare sottoposta a carico uniforme per i metodi americani. Inoltre le procedure usate per riprodurre il danneggia-mento della superficie sono diverse.

Nei metodi nordamericani la resistenza di calcolo è determinata attraverso due para-metri, 𝑘 ed 𝑚 , dipendenti dalle condizioni della superficie, la cui determinazione è legata alla storia tensionale che conduce alla crisi, mentre i metodi europei usano la resistenza ca-ratteristica definita come il frattile 5% della tensione di rottura misurata negli esperimenti (in realtà, in contrasto con il concetto generale di grandezza caratteristica, questo parame-tro non è una reale proprietà del materiale, ma dipende dalla geometria, dalle condizioni della superficie, dal carico e dalle condizioni ambientali dei campioni, che vengono consi-derate attraverso una serie di coefficienti).

Le effettive condizioni di esercizio vengono messe in conto nei metodi europei attra-verso coefficienti correttivi (leggermente differenti fra i vari metodi), mentre le norme nor-damericane forniscono grafici e tabelle per i casi più comuni dalle quali si può ottenere il carico trasversale uniforme (funzione della geometria e delle condizioni di vincolo) che il pannello può sopportare per un determinato periodo temporale di riferimento.

Il tipo di vetro viene considerato attraverso l’aggiunta delle tensioni residue di tempe-ra nei metodi europei e atttempe-raverso dei coefficienti dipendenti dal ttempe-rattamento termico (e dal-la durata del carico) nei metodi nordamericani.