Capitolo 2
Teoria geometrica della diffrazione
La predizione della propagazione radio deterministica in scenari urbani e indoor è un problema elettromagnetico molto complicato. La complessità dello scenario fa divenire impossibile predire la propagazione radio con un alto grado di accuratezza. Tuttavia, al variare delle caratteristiche dell’ambiente in studio possono essere seguite certe tecniche oppure altre. Diversi metodi sono stati usati in modelli deterministici e semi-deterministici:
- Teoria geometrica della diffrazione (geometrical theory of diffraction, GTD); - Ottica fisica (phisical optics, PO);
- Equazioni integrali (integral equation, IE);
- Differenze finite nel dominio del tempo (finite-difference time-domain, FDTD ). La seconda tecnica che si basa sul metodo di Kirchhoff-Huygen viene applicata soprattutto per predire la propagazione in ambienti urbani e rurali con particolare attenzione al fenomeno delle diffrazioni multiple. Le ultime due tecniche essendo rigorose sono di difficile utilizzo perché richiedono una discretizzazione degli ostacoli in elementi con dimensioni più piccole di una frazione della lunghezza d’onda
(tipicamente λ/8). A 2.4 GHz, frequenza di lavoro dello standard 802.11b la lunghezza d’onda è 12.5 cm, di conseguenza il numero di elementi risultanti per un tipico scenario urbano o indoor diventa enorme. Conseguentemente i requisiti di spazio di memoria e tempo di CPU, generalmente, non fanno adottare queste tecniche in modelli ambientali 3D convenzionali.
La maggioranza dei modelli di propagazione deterministica e semi-deterministica in scenari indoor utilizza il metodo GTD nella sua versione uniforme (uniform theory of diffraction, UTD). Lo scopo del capitolo è presentare una descrizione della tecnica GTD [14-15]; essa è stata utilizzata per implementare il tool di predizione della propagazione del campo elettromagnetico analizzato nel capitolo 3. Come mostrato successivamente, gli ambienti sono descritti geometricamente usando modelli sfaccettati cosicché molte espressioni GTD sono particolarizzate per ostacoli con facce piane.
L’approccio GTD è una tecnica basata su raggi. Il campo elettromagnetico è calcolato come una somma di contributi individuali associati con i rispettivi raggi. Nella loro propagazione i raggi interagendo con ostacoli subiscono riflessioni, diffrazioni, rifrazioni. Le sezioni 2.1 e 2.2 presentano le leggi che governano la propagazione del campo considerando le antenne come sorgenti di campo e mettendo in relazione i loro diagrammi di irradiazione con il campo propagato. La sezione 2.3 affronta l’applicazione del teorema delle immagini alle riflessioni dei raggi. Espressioni pratiche del campo riflesso sono derivate partendo dal diagramma d’irradiazione dell’antenna trasmittente e delle proprietà del materiale di cui è costituita la faccia riflettente. Il fenomeno della diffrazione da parte di spigoli è analizzato nella sezione 2.4 dove le espressioni GTD/UTD sono riferite a spigoli rettilinei che sono il principale tipo di spigoli che si trovano in scenari urbani e indoor. La sezione 2.5 presenta una soluzione applicando l’ottica geometrica al calcolo del campo trasmesso. La sezione 2.6 affronta gli effetti multipli, cioè una combinazione di più di due riflessioni, diffrazioni e/o trasmissioni.
2.1 – Approccio GTD/UTD
Il campo elettrico creato nel punto di osservazione PO da una sorgente posizionata in S sarà approssimato dalla somma:
T E 1 N T i E = =
∑
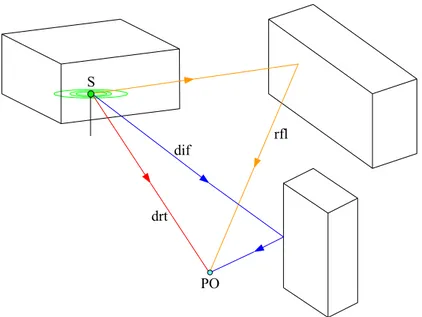
Ei (2.1)dove rappresenta il campo elettrico dovuto a ciascuno degli N raggi che collegano il punto S con PO: raggio diretto, raggi riflessi, raggi diffratti, raggi trasmessi, raggi riflessi-diffratti, raggi doppiamente riflessi, etc. La figura 2.1 mostra alcuni dei percorsi appartenenti ai raggi che esistono nel collegamento sorgente-punto di osservazione in un semplice modello di uno scenario urbano: raggio diretto (drt), raggio riflesso (rfl), raggio diffratto (dif).
i E S rfl dif drt PO
Fig. 2.1 – Esempio di tre raggi che raggiungono il punto di osservazione PO.
Ciascuno dei termini nella somma (2.1) può essere calcolato usando la formulazione “ray tube” della GTD/UTD. Il campo elettrico associato con un raggio che si propaga è dato da
0 β 1 2 1 2 ( ) (0) ( )( ) j p E P E p p
e
ρ ρ ρ ρ − = + + (2.2)dove E P è il campo elettrico in un punto a distanza p dal punto di riferimento (p=0), ( ) (0)
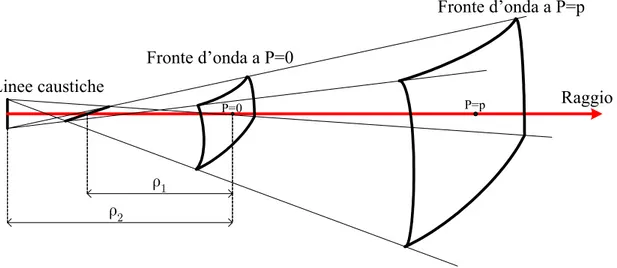
E è il campo elettrico nel punto di riferimento , e ρ ρ1, 2 sono i raggi di curvatura principali del fronte d’onda associato con il raggio misurati rispetto al punto di riferimento; ρ ρ1, 2 dipendono dalle linee caustiche.
Nella (2.2), β0 è il numero d’onda nello spazio libero, che è dato da β0 2
λ
π
= (2.3) dove è la lunghezza d’onda. λ
Raggio Linee caustiche Fronte d’onda a P=0 Fronte d’onda a P=p P=0 P=p ρ1 ρ2
Fig. 2.2 – Propagazione Ray tube.
Due casi particolarmente interessanti sono quelli di raggi aventi un campo elettrico associato con fronte d’onda sferico e cilindrico:
• Onda sferica. Questo caso si verifica quando entrambe le linee caustiche degenerano nello stesso punto cosicché i fronti d’onda sono sferici.
0 β ( ) (0) j p E P E p
e
ρ ρ − = + (2.4)Quando il punto caustico è preso come punto di riferimento la (2.4) può essere scritta come segue [15]:
0 β 0 ( ) j p E P E p
e
− = (2.5)dove E0 è un vettore che può essere visto come un fattore di eccitazione per l’onda sferica.
• Onda cilindrica. Questo caso nasce quando una delle linee caustiche è all’infinito così ρ1= ∞ , i fronti d’onda sono cilindrici ed il campo elettrico in P diventa 0 β 2 2 ( ) (0) j p E P E p
e
ρ ρ − = + (2.6)Quando il punto di riferimento si trova sulla linea caustica, la (2.6) può essere scritta come segue [15]:
0 β 0 ( ) j p E P E p
e
− = (2.7)In questa equazione E0 può essere di nuovo visto come un fattore di eccitazione per l’onda cilindrica.
Quando un raggio raggiunge un ostacolo, si origina un raggio riflesso (vedi fig. 2.1). Le leggi dell’ottica geometrica (geometric optics, GO) applicate alla riflessione danno le caratteristiche del raggio riflesso: la direzione di propagazione, i raggi principali di curvatura del fronte d’onda riflesso, e il campo nel nuovo punto di riferimento, che è il punto riflettente. Quindi il raggio riflesso si propaga secondo la (2.2). Quando un raggio raggiunge uno spigolo (vedi figura 2.1), si forma un’infinito numero di raggi diffratti. Come prima, in maniera simile, le leggi GTD/UTD forniscono le caratteristiche dei raggi diffratti emergenti [16].
I principi GTD/UTD sono applicabili quando il campo incidente è un campo “raggio-ottico”, (ray-optical field) [15], cioè quando questo può essere espresso attraverso la (2.2). Nel contesto della comunicazione mobile la precedente condizione è soddisfatta, eccetto in casi speciali come sarà puntualizzato più tardi nelle sezioni 2.4 e 2.6. Assumendo nel modello geometrico facce piatte, gli spigoli sono rettilinei e i fronti d’onda sono più semplici di quelli in figura 2.2: fronti d’onda sferici per i raggi diretti e riflessi, e fronti d’onda quasi cilindrici nel caso di raggi diffratti quando il punto di osservazione è lontano dallo spigolo che li ha generati.
2.2 – Campo Diretto
Il contributo al campo nel punto di osservazione PO dovuto al raggio diretto è dato da
0 β ( ) ( , ) j r t E PO E r
e
− = θ φ (2.8) con 0 0 ζ ( , ) ( , ) 2 t t t PG E π = θ φ E θ φ (2.9) e dove 0 0 0 µ ζ 376.73 ε= ≅ Ω è l’impedenza intrinseca dello spazio libero, è la potenza fornita dal trasmettitore ai morsetti di ingresso dell’antenna trasmittente, è il guadagno dell’antenna trasmittente e
t P t G 0( , ) E θ φ è il diagramma d’irradiazione normalizzato dell’antenna trasmittente. Il prodotto è chiamato EIRP (effective isotropic radiated power) e tiene conto della potenza realmente irradiata = , dove
è l’efficienza d’irradiazione dell’antenna
t t PG r P Ptη η η r r d P G P P D = = + , è la potenza dissipata sull’antenna per effetto Joule o a causa di perdite nelle parti dielettriche dell’antenna, G e D sono rispettivamente il guadagno e la direttività dall’antenna.
d P
Considerando un punto generico di osservazione P ( , , )r θ φ , nella regione di campo lontano, si definisce direttività nella direzione ( , )θ φ il rapporto tra la densità di potenza irradiata nel punto P dall’antenna in esame e la densità di potenza media
nello stesso punto:
2 0 2 ( , , ) 1 2 ζ ( , ) lim 4 r r E r D P r θ φ θ φ π →∞ = .
Nel tool sviluppato, come sarà spiegato in dettaglio nel capitolo 3, abbiamo la possibilità di impiegare nella predizione della propagazione del campo due tipi di antenne trasmittenti: dipolo elettrico corto e/o dipolo a mezz’onda le quali hanno un diagramma d’irradiazione normalizzato descritto dalle seguenti espressioni:
• Dipolo elettrico corto (l<<λ) E0( , )θ φ = jsin( )θ iθ
• Dipolo a mezz’onda (l =λ/2) 0 cos( cos ) 2 ( , ) sin E j i π θ = θ θ φ θ
Le coordinate sferiche ( , del punto di osservazione PO si riferiscono ad un sistema di coordinate solidale con l’antenna e l è la lunghezza del dipolo, mentre, di solito i parametri geometrici delle facce si riferiscono ad un sistema differente, un sistema di coordinate cartesiane o rettangolari. Per il calcolo del campo elettrico è necessaria una trasformazione di coordinate tra questi due sistemi di identificazione delle coordinate. Per far questo si può utilizzare il metodo dei coseni direttori descritto in Appendice 2A.
, ) rθ φ
Le espressioni (2.8) e (2.9) possono essere usate quando il punto di osservazione è nella regione di campo lontano dell’antenna (far-field region) ovvero se sono soddisfatte le due seguenti condizioni [25]:
¾ r >> λ ¾ r > 2 max 2d λ
con λ e indicanti rispettivamente la lunghezza d’onda di lavoro e la dimensione massima dell’antenna. Tipicamente, nelle comunicazioni mobili queste due condizioni sono verificate; con riferimento allo standard Wi-Fi a 2.4 e 5 GHz la lunghezza d’onda vale rispettivamente 12.5 cm e 6 cm, poiché le antenne utilizzate hanno la dimensione massima di un paio di decine di cm al più, nell’ipotesi peggiore
max d 2 2 max 2 2(0.2) 1.3 0.06 d = =
λ quindi già ad 1.5 m possiamo ritenere soddisfatte le due ipotesi. Questo ci fa ritenere ragionevole l’espressione (2.8) la quale contiene un termine di tipo 1/r ma non contiene termini di tipo 1/ 1/ che fanno parte del campo elettrico esistente nelle vicinanze di un’antenna trasmittente.
2
r e r3
Tuttavia, le due condizioni sopra menzionate possono non essere vere nel caso si utilizzi un array di antenne o un’antenna elettricamente larga. In questi due casi devono essere considerati diversi centri di fase. Il campo elettrico generato da un’antenna con N centri di fase è dato da
0 β 0 0 1 ζ ( ) ( , ) 2 i j r N ti ti i i i i P G E PO E r
e
π − = =∑
θ φ (2.10)2.3 – Campo Riflesso
Per ottenere il campo riflesso quando un raggio raggiunge una superficie, si possono usare le espressioni generali dell’ottica geometrica che sono applicabili nei casi in cui tutte le facce sono larghe in termini di lunghezza d’onda, la superficie si trova nella regione di campo lontano dell’antenna trasmittente e il raggio di curvatura della superficie nel punto di riflessione è elettricamente largo. Queste espressioni sono valide sia per superfici curve sia per superfici piatte appartenenti ad una microcella. Assumendo che gli ostacoli ambientali non abbiano superfici curve e che la GO sia
applicabile, una maniera più efficiente per calcolare i contributi al campo totale dei raggi riflessi consiste nell’applicare il teorema delle immagini e i coefficienti di riflessione di Fresnel invece delle espressioni generali GO [15-17]. Il teorema delle immagini può essere derivato dalle leggi GO quando le superfici sono piane, così in tali casi, entrambi i metodi forniscono lo stesso risultato.
2.3.1
– Metodo delle immagini
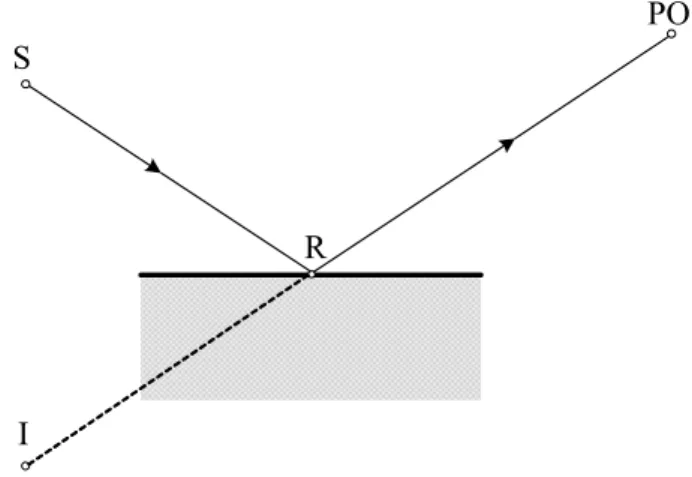
Dato un punto sorgente (S) ed una faccia, i raggi riflessi dalla faccia possono essere considerati come raggi irradiati direttamente da un punto sorgente virtuale chiamato sorgente immagine (I). La sorgente immagine è posizionata simmetricamente a S rispetto al piano che contiene la faccia (vedi fig. 2.3). Si nota che la posizione di I dipende esclusivamente dalla locazione di S e dalla posizione e orientazione della faccia. Quindi, I è indipendente dal punto di osservazione. Il campo irradiato dalla sorgente immagine è ottenuto dalle caratteristiche d’irradiazione della sorgente reale (S) e dalle proprietà elettriche della faccia (vedi cap.3).
S
I
R
PO
Fig. 2.3 – Applicazione del metodo delle immagini alla riflessione di un raggio.
Per un dato punto di osservazione (PO), il punto di riflessione (R) è facilmente calcolato come intersezione tra il segmento I-PO e la faccia. La sezione 3.2 descrive un algoritmo efficiente di intersezione raggio-faccia.
In uno scenario modellato con N facce piane il numero di immagini è N. Di conseguenza, il massimo numero di raggi riflessi che raggiunge un punto di osservazione è N. Ovviamente, in un ambiente reale il numero di raggi riflessi che raggiungono un osservatore è più piccolo. Questo per due ragioni:
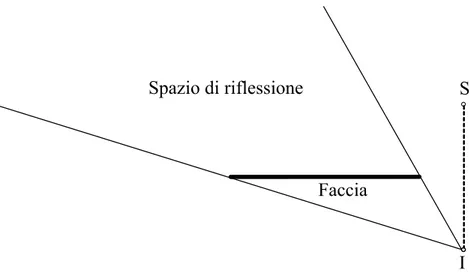
1. A causa delle dimensioni finite delle facce, solo osservatori posizionati nello spazio di riflessione (reflection space, RS) (vedi fig.2.4) della faccia possono ricevere raggi riflessi. In pratica, un osservatore è nell’RS di una faccia quando R è dentro essa.
S
I Spazio di riflessione
Faccia
Fig. 2.4 – Lo spazio di riflessione (RS) di una faccia riflettente.
2. La seconda ragione è che il raggio riflesso (da R a PO) o il raggio incidente (da S a R) possono essere ostacolati da altre facce presenti nell’ambiente. Questo può essere scoperto attraverso un test di visibilità. I raggi che subiscono una doppia riflessione possono essere analizzati in maniera simile. Le sorgenti dei raggi doppiamente riflessi sono le immagini delle immagini del primo ordine (immagini di singole riflessioni). Queste sono chiamate immagini del secondo ordine. Il numero di immagini del secondo ordine sarà Tre condizioni devono essere soddisfatte per una doppia riflessione:
( 1
¾ Il punto di osservazione deve essere nell’RS della seconda faccia. In altre parole, il secondo punto di riflessione deve giacere sulla seconda faccia.
¾ Il secondo punto di riflessione deve essere contenuto nell’RS della prima faccia. In altre parole il primo punto di riflessione deve giacere sulla prima faccia.
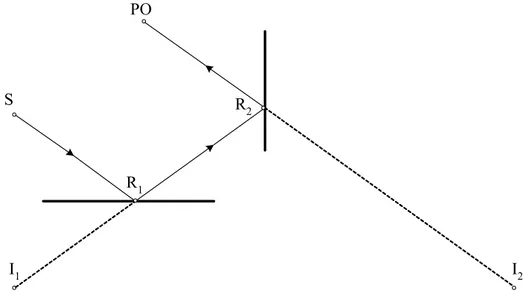
¾ Nessuno dei tre percorsi mostrati in figura 2.5 (S-R1, R1-R2, R2-PO) deve essere ostacolato da altre facce dell’ambiente (tests di visibilità).
S
I1 I2
PO
R1
R2
Fig. 2.5 – Applicazione del metodo delle immagini ad una doppia riflessione.
Le riflessioni multiple possono essere analizzate con lo stesso criterio. Il numero di immagini per le riflessioni del k-esimo ordine sarà ( 1)k 1
N N− − .
Dunque, la determinazione di un raggio che tra S e PO subisce K riflessioni passando da altrettanti punti di riflessione R R1, 2,..,R avviene con la seguente K procedura:
1) Calcolo delle posizioni di I I1, ,..,2 I . Si determina la posizione di K I come 1 punto simmetrico di S rispetto alla faccia 1, poi la posizione di I come 2
punto simmetrico di I rispetto alla faccia 2, fino a calcolare la posizione di 1 K
I come simmetrica di IK−1 rispetto alla faccia K.
2) Calcolo delle posizioni di RK,RK−1,..,R . L’intersezione tra 1 IK −PO e la faccia K è R , tra K IK−1−RK e la faccia K-1 è RK−1, e così via, in generale, si calcola R come intersezione tra il segmento k Ik−Rk+1 e la faccia k. Alla fine si arriva a calcolare la posizione di R come intersezione tra 1 I1−R2e la faccia 1.
3) Test di visibilità. A questo punto occorre controllare che il raggio riflesso esistente tra S e PO che appare come una “spezzata” sia effettivamente presente, ovvero che non ci sia oscuramento da parte di nessun ostacolo sui K+1 “sottocammini” risultanti: S− , R1 R1−R2, …, RK −PO.
E’ importante notare che usando il metodo delle immagini si gestisce solo un numero limitato di raggi eliminando il trattamento di molti raggi irrilevanti che partono dalla sorgente ma non raggiungono l’osservatore in meno di un certo numero di riflessioni.
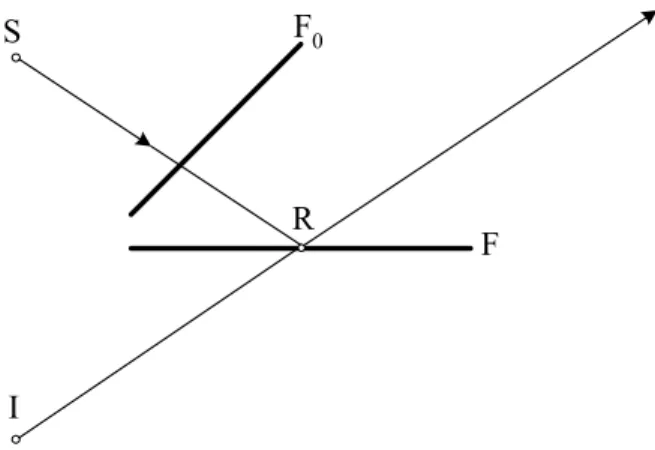
Data una sorgente (S) (che può essere una sorgente reale o una sorgente immagine) quando una faccia F è totalmente oscurata da un’altra , essa non potrà mai originare una riflessione singola né far parte delle facce che compongono una riflessione multipla (vedi fig. 2.6).
0 F S I R F F0
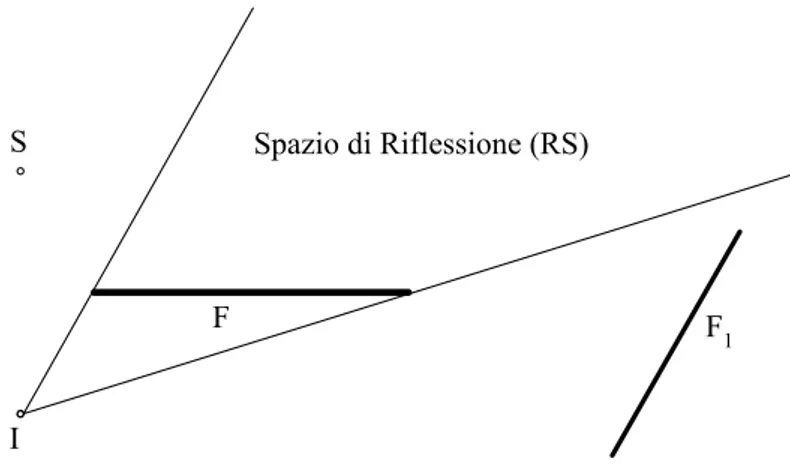
Inoltre possiamo semplificare questo studio considerando la posizione delle facce rispetto agli RSs. Se una faccia è totalmente esterna al RS della faccia non può esistere una doppia riflessione S- - (vedi fig. 2.7).
1 F F F F1 S I Spazio di Riflessione (RS) F F 1
Fig. 2.7 – La faccia F1 è all’esterno dell’RS della faccia F, non può esistere la doppia riflessione S-F-F 1.
In conclusione il metodo delle immagini permette di ottenere l’esatto percorso seguito dal raggio riflesso, così è possibile ottenere oltre al modulo anche la fase dei campi associati con i raggi riflessi. Allora, i contributi multipath al punto di osservazione possono essere sommati coerentemente per ottenere il campo ricevuto.
2.3.2
– I Coefficienti di riflessione di Fresnel
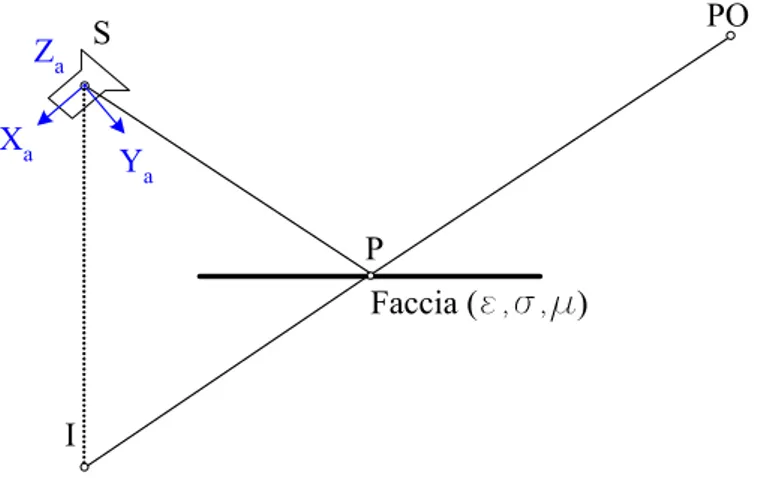
Concentriamoci adesso sull’applicazione del teorema delle immagini al problema della riflessione. La figura 2.8 mostra un caso di riflessione. La faccia in figura appartiene ad una parete le cui permittività, conduttanza, permeabilità, sono definite dai parametri ε, , e µ rispettivamente. Il diagramma d’irradiazione dell’antenna
è definito rispetto agli assi mostrati in figura. Si posiziona il centro di fase dell’antenna (S) nell’origine del suo sistema di coordinate.
σ
( , ) E θ φ
S I P PO Faccia (e,s,m) Xa Ya Za
Fig. 2.8 – L’antenna trasmittente davanti ad una faccia piana, punto immagine I e punto di riflessione P.
Secondo il principio di Fermat, il percorso del raggio riflesso S-P-PO indicato in figura 2.8 può essere ottenuto minimizzando il tempo di percorrenza di questo cammino. In altre parole il raggio incidente è riflesso in direzione speculare. Questo concetto è anche conosciuto come legge di Snell: l’angolo che il raggio incidente forma con la normale alla superficie interessata alla riflessione α è uguale all’angolo i
che il raggio riflesso forma con la medesima normale. r
α
Come però abbiamo descritto nella precedente sezione il punto P può essere ottenuto come punto di intersezione tra la linea retta passante per I-PO e la faccia, essendo I l’immagine del punto sorgente S. I punti S, P, PO, e I appartengono allo stesso piano che è conosciuto come piano incidente. Il piano incidente è sempre perpendicolare alla faccia piana.
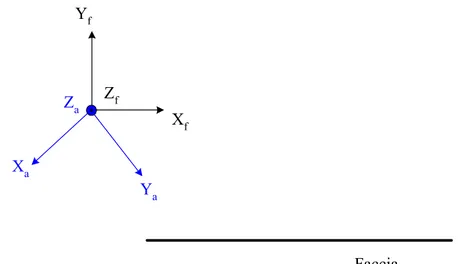
Per calcolare efficientemente i campi riflessi in un elevato numero di punti useremo il sistema di assi chiamato a faccia-fissa di figura 2.9. Da questi assi possiamo ottenere gli assi a immagine-fissa disegnati in figura 2.10. Gli assi a faccia fissa condividono l’origine con gli assi a antenna fissa ma l’asse è perpendicolare alla faccia. Gli assi a faccia-fissa possono essere definiti in uno step di preprocessing creando parallelo al vettore normale alla
f f f (X ,Y , Z ) i i i (X ,Y , Z ) f f f (X ,Y , Z ) f Y f Y
faccia, parallelo a uno dei due lati della faccia e perpendicolare agli altri due assi con il verso tale che formino una terna destrorsa. Gli assi a immagine fissa sono definiti da una traslazione degli assi a faccia fissa. Il centro degli assi a immagine fissa si trova nell’immagine I dell’antenna con centro di fase in S.
f X Zf f f f X ,Y ,Z Faccia Xa Ya Za Xf Yf Zf
Fig. 2.9 – Sistema di assi ad antenna fissa (Xa,Ya,Za) e sistema di assi a faccia fissa (Xf,Yf,Zf).
Faccia Xf Yf Zf Xi Yi Zi Antenna Antenna Immagine
Fig. 2.10 – Sistema di assi ad immagine fissa (Xi,Yi,Zi).
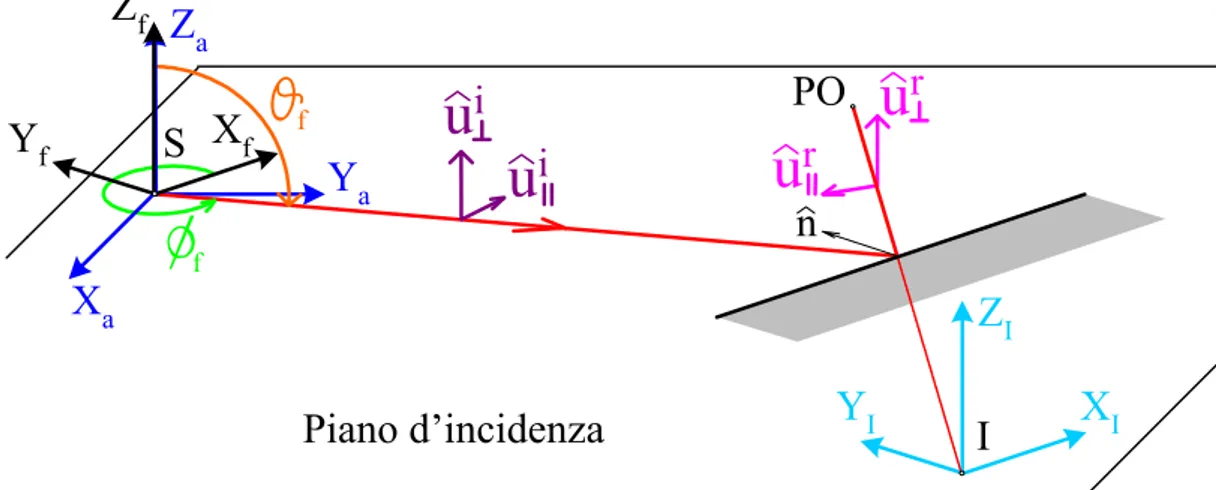
Usando gli assi a faccia fissa possiamo espandere direttamente il campo incidente nei cosiddetti vettori di polarizzazione parallela e perpendicolare (al piano di
incidenza) perché adesso i versori sferici ,rf θ φf, f sono paralleli agli assi a raggio-fisso [15]. Le componenti del campo parallela e perpendicolare sono anche chiamate hard e soft, rispettivamente. Possiamo notare che è parallelo alla direzione dell’onda incidente,
f r f
θ è parallelo al vettore di polarizzazione parallela u , e i φf è parallelo al vettore di polarizzazione perpendicolare ui⊥. Scegliamo i versi dei vettori di polarizzazione in modo tale che i versori di componente parallela, componente perpendicolare e direzione di propagazione formino in questo ordine una terna destrorsa.
Per convenzione utilizziamo gli apici “i” e “r” per indicare grandezze relative al raggio incidente e riflesso rispettivamente. In maniera del tutto simile si può espandere il campo riflesso nelle componenti parallela e perpendicolare. In figura 2.11 questi vettori sono identificati come e ur ur⊥, rispettivamente. Essi sono in relazione diretta con i versori sferici rI, ,θ φI I del sistema a immagine fissa:
r
u e ur⊥ sono paralleli a φ e I θI rispettivamente e è parallela alla direzione del raggio riflesso (vedi fig. 2.11a e 2.11b). Le componenti perpendicolari dei campi incidente e riflesso hanno direzione e verso coincidenti
I r
i r u⊥ =u⊥.
Usando i sistemi di coordinate a faccia-fissa e immagine-fissa, il campo incidente in PO è dato da
(
)
(
)
0 f f 0 f f β f f f f β f f f f ˆ ˆ ( ) ( , ) ( , ) ˆ ˆ ( , ) ( , ) f f j r i f f f j r i i f e E P E E r e E u E u r θ φ − − ⊥ = + = − + θ φ θ φ θ φ θ φ θ φ θ φ (2.11)dove ( , , )rf θ φf f sono le coordinate sferiche di P nel sistema di coordinate a faccia fissa e
f
Eθ , sono le componenti di campo del diagramma d’irradiazione dell’antenna trasmittente rispetto agli assi a faccia fissa.
f
X
aY
aZ
an
PO
S
I
Y
IX
IZ
IY
fX
fZ
fPiano d’incidenza
f fu
r
u
r
u
i
u
i
Fig. 2.11a – Per il raggio incidente come per il raggio riflesso i vettori: polarizzazione parallela,
polarizzazione perpendicolare, direzione del raggio formano una terna destrorsa.
XI YI ZI Xa Ya Za a a n PO I Xf Yf Zf a I Faccia rf f f rI I I S f
Il campo riflesso in P può essere ottenuto dal campo incidente e dalla matrice di riflessione di Fresnel
R
: (2.12) ( ) ( ) r E P =R
E PiQuando Ei ed Er sono scomposti nelle loro componenti ⊥ e si possono scrivere nella seguente maniera:
(2.13) 0 0 r i r R E E R E E ⊥ ⊥ ⎡ ⎤ ⎡ ⎤⎡ ⎤ = ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦i ⊥
dove R⊥ e R sono i coefficienti di Fresnel per la polarizzazione perpendicolare e parallela, rispettivamente. Allora si può ottenere la seguente approssimazione GO per il campo riflesso nel punto di osservazione PO:
(
)
(
)
(
)
( )
(
)
(
)
0 f f 0 f f 0 f f β f f f f β f f f f β I I I I ˆ ˆ ( ) ( , ) ( , ) ˆ ˆ ( , ) ( , ) ˆ ˆ ( , 2 ) ( , 2 ) I I I j r r r r I j r I I I j r I I I e E PO R E u R E u r e R E R E r e R E R E r θ φ π θ π φ − ⊥ ⊥ − ⊥ − ⊥ = − + = − − + = − + − θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ (2.14)dove ( , , )rI θ φI I sono le coordinate sferiche di PO nel sistema di assi a immagine fissa. Per non appesantire l’espressione è stata omessa la dipendenza dei coefficienti di Fresnel da α , angolo di incidenza, cioè angolo formato dal raggio incidente e dal vettore normale alla faccia. Allora R⊥ =R⊥( )α , R =R( )α ed α 0,
2 π ⎡ ⎤ ∈ ⎢⎣ ⎥⎦ vale: 3 3 2 2 2 3 3 2 per 2 2 2 0 2 2 I I I I I I I I π π φ φ π π φ π φ π α π π φ φ π π φ φ π − − = − − < < < < dove φI ∈[0, 2 )π
I coefficienti di Fresnel sono dati da:
(
)
(
) (
)
2 0 r 2 0 r 2 β ε sin r 2 2 2 β ε sin 2 2 r r (1 ε ) 1ε sin cos ε sin cos
j d j d R
e
e
α α α α α − ⊥ − − − = − + − − − + α (2.15)(
)
(
) (
)
2 0 r 2 0 r 2 β ε sin 2 2 2 r r 2 2 2 β ε sin 2 2 r r r r (ε sin ε cos ) 1ε sin ε cos ε sin ε cos
j d j d R
e
e
α α α α α α α − − − − − = − + − − − α (2.16)dove è lo spessore della parete cui appartiene la faccia che causa la riflessione, ε è la permittività relativa del materiale costituente la faccia ovvero la parte reale della costante dielettrica complessa che vale:
d r
cplx
ε εr jσ
ω
= − (2.17)
Le varie proprietà elettromagnetiche di materiali da costruzione possono essere ottenute da [18]. Notiamo che il campo riflesso in PO può essere calcolato considerando un’antenna equivalente nel punto immagine I, con il seguente diagramma d’irradiazione riferito al sistema a immagine fissa:
0 I β I I I I tI I I I ( , , ) ( , ) j r e E r E r − = θ φ θ φ (2.18) dove
(
f f)
tI( , )I I ( , 2I I)ˆI ( , 2I I) E θ φ = R E⊥ θ θ π−φ θ +R Eφ θ π −φ φˆI (2.19) Quindi possiamo considerare il campo riflesso, equivalente ad un campodiretto di un’antenna che ha come sistema di coordinate associato il sistema a immagine fissa con il diagramma (2.18). Questo significa che per un problema di seconda riflessione, può essere applicata la stessa procedura utilizzata nel caso della prima riflessione, ma iniziando l’analisi dall’antenna immagine equivalente.
2.4 – Campo diffratto
Il campo diffratto da uno spigolo è dato da [16]:
0 β ( ) ( ) ( ) i d i j s d i E s E Q s s
D
ρρe
− = + (2.20)dove E Qi( d)è il campo incidente nel punto di diffrazione , D è la matrice dei coefficienti di diffrazione e s è la distanza tra punto di osservazione (PO) e punto di diffrazione. Per applicare la (2.20) il campo incidente deve essere riferito a un sistema di coordinate a spigolo-fisso associato con il piano incidente. Questo è il piano che contiene lo spigolo e il raggio incidente (vedi fig. 2.12 ).
d Q s g g g e g s
Fig. 2.12 – Diffrazione operata da uno spigolo rettilineo: definizione degli assi a spigolo-fisso.
I versori del sistema di coordinate a spigolo fisso sono: il versore nella direzione del raggio incidente , il vettore perpendicolare al piano incidente ˆs′ φˆ′ , e il vettore parallelo al piano incidente γˆ′ (vedi fig. 2.12 e 2.13). Questi ultimi due vettori possono essere ottenuti con la seguente espressione:
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ e s e s s φ γ φ ′ × ′ = − ′ × ′= ×′ ′ (2.21)
dove è il vettore lungo lo spigolo. ˆe
I raggi diffratti si propagano dal punto di diffrazione nelle direzioni , definite nel seguente modo
ˆs ˆ ˆ ˆ ˆ
s e′⋅ = ⋅s e (2.22)
Gli infiniti raggi che soddisfano questa equazione formano un cono il cui vertice è il punto di diffrazione (vedi fig. 2.13). Questo è il cosiddetto “cono di Keller”.
PO S a e s s g g Qd
Fig. 2.13 – Definizione dei parametri geometrici coinvolti nella diffrazione generata da uno spigolo
rettilineo.
Il termine ρi nella (2.20) è il raggio di curvatura dell’onda incidente nel piano di incidenza. Quando il fronte d’onda incidente è sferico esso coincide con la distanza tra l’antenna trasmittente S e Qd, che chiamiamo s′.
L’equazione (2.20) fornisce il campo diffratto riferito al sistema di coordinate associato con il piano di diffrazione (vedi fig. 2.12). Questo è il piano che contiene lo spigolo e il raggio diffratto. I versori del sistema di coordinate associato sono: , il ˆs
vettore ˆφ perpendicolare al piano di diffrazione, e il vettore γˆ parallelo a tale piano (vedi fig. 2.12 e 2.13). Questi ultimi due vettori possono essere calcolati come segue:
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ e s e s s φ γ φ × = × = × (2.23)
Le componenti di campo lungo le direzioni ˆφ′ e ˆφ sono perpendicolari allo spigolo. Esse sono le cosiddette componenti perpendicolari. Le componenti di campo nella direzione γˆ′e γˆ sono le cosiddette componenti parallele.
Quando il campo è scomposto nelle suddette polarizzazioni e la forma convenzionale dei coefficienti di diffrazione diventa
⊥ 0 0 D D
D
⊥ − ⎡ ⎤ = ⎢ − ⎥ ⎣ ⎦ (2.24)dove e sono i coefficienti di diffrazione che verranno descritti in dettaglio nel prossimo paragrafo. Adesso esaminiamo più in dettaglio la (2.20) evidenziando le componenti di campo e .
D D⊥
⊥
Il campo incidente nel punto di diffrazione Qd è dato da:
(
)
(
)
0 a a 0 a a β a a a a β a a a a ˆ ˆ ( ) ( , ) ( , ) ˆ ˆ ( , ) ( , ) j s i d a a j s E Q E E s E E se
e
θ φ γ φ ′ − ′ − = + ′ ′ ′ = − + ′ θ φ θ φ θ φ θ φ θ φ θ φ (2.25)dove sono le coordinate sferiche di nel sistema di assi a antenna-fissa e sono le componenti di campo del diagramma d’irradiazione dell’antenna trasmittente rispetto allo stesso sistema.
a a
( , , )s′θ φ Qd
a, a
Eθ Eφ
Il campo diffratto che giunge in PO il quale si trova a distanza s da , nel caso di fronte d’onda incidente sferico, vale:
d Q
(
)
(
)
(
)
(
)
0 0 a a 0 a a β β ( ) a a a a β ( ) a a a a ( ) ( ) ( ) ˆ ˆ ( , ) ( , ) 1 ˆ ˆ ( , ) ( , ) d i j s d j s s j s s d s E s E Q s s s s s D E D E ss s s D E D E s s LD
e
e
e
γ φ γ φ − ′ − + ⊥ ′ − + ⊥ ′ = ′ + ′ + = − − − − ′ + ′ = + ′ + θ φ θ φ θ φ θ φ θ φ θ φ (2.26)dove Ld è un parametro distanza dato da
d ss L s s ′ = ′ + (2.27)
sul quale torneremo nel prossimo paragrafo, ( , , )s γ φ sono le coordinate sferiche di PO nel sistema di coordinate a spigolo-fisso e α è l’angolo interno allo spigolo (vedi fig. 2.14a e 2.14b).1 Xa Ya Za PO S g g Piano di diffrazione Piano d’incidenza a a a d Q
Fig. 2.14a – Per il raggio incidente i vettori: polarizzazione parallela, polarizzazione perpendicolare
(al piano di incidenza), direzione del raggio formano una terna destrorsa.
Per il raggio diffratto i vettori: polarizzazione parallela, polarizzazione perpendicolare (al
piano di diffrazione), direzione del raggio formano una terna destrorsa.
1 Notare che il piano d’incidenza nel caso di raggio diffratto è definito in maniera diversa dal piano
s
g
s
g
X
aY
aZ
aS
PO
X
eY
eZ
e a n-face 0-facea
Fig. 2.14b – Diffrazione vista sul piano orizzontale: sˆ , ,′ ′ ′γ φˆ ˆ e sˆ, ,γ φˆ ˆ formano terne destrorse.
2.4.1
– I Coefficienti di diffrazione
Prima di scrivere le espressioni dei coefficienti di diffrazione per la polarizzazione parallela e perpendicolare è bene dire che essi dipendono da due matrici di coefficienti di riflessione. Le due matrici sono associate alle due facce la cui intersezione costituisce lo spigolo rettilineo che provoca la diffrazione. Chiameremo l’oggetto formato dalle due facce più lo spigolo “wedge”.
E’ consuetudine etichettare le due facce del wedge come 0-face e n-face ma la designazione di quale faccia è chiamata in un modo o nell’altro è un fatto arbitrario. Per convenzione consideriamo gli angoli φ′ e φ (definiti nel precedente paragrafo) come misurati partendo dalla 0-face.
Allora i coefficienti di diffrazione possono essere espressi come [14, 19]: 4 0 0 1 2 3 4 0 ( , , , , , , ) 2 2 β sin j n n D L n R R d d d R d R n
e
π φ φ γ π γ − ⊥ ⊥ ⊥ ⊥ − ′ ⎡ ⎤ = = ⎣ + + + ⎦ (2.28) 4 0 0 1 2 3 4 0 ( , , , , , , ) 2 2 β sin j n n D L n R R d d d R d R ne
π φ φ γ π γ − ⊥ − ′ ⎡ ⎤ = = ⎣ + + + ⎦ (2.29)dove 1 0 ( ) cot β ( ) 2 d F La n π + −φ φ′ + φ φ ⎡ ⎤ ⎡ ′ ⎤ = ⎢ ⎥ ⎣ − ⎦ ⎣ ⎦ (2.30) 2 0 ( ) cot β ( ) 2 d F La n π − −φ φ′ − φ φ ⎡ ⎤ ⎡ ′ ⎤ = ⎢ ⎥ ⎣ − ⎦ ⎣ ⎦ (2.31) 3 0 ( ) cot β ( ) 2 d F La n π+ +φ φ′ + φ φ ⎡ ⎤ ⎡ ′ ⎤ = ⎢ ⎥ ⎣ + ⎦ ⎣ ⎦ (2.32) 4 0 ( ) cot β ( ) 2 d F La n π φ φ− + ′ − φ φ ⎡ ⎤ ⎡ ′ ⎤ = ⎢ ⎥ ⎣ + ⎦ ⎣ ⎦ (2.33)
Gli angoli γ γ φ′, , ,′ e φ sono mostrati in figura 2.12; è il numero d’onda e nè un parametro relativo all’angolo
0 β
α interno al wedge (vedi fig. 2.13) che vale: 2
n π α
π
−
= (2.34)
dove α è misurato in radianti.
Esplicitiamo adesso le matrici di riflessione di Fresnel relative rispettivamente alla 0-face e n-face:
0 0 0 ( ) 0 0 ( R R
R
θ ) θ ⊥ ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ (2.35) ( ) 0 0 ( n n n R RR
θ ) θ ⊥ ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ (2.36)dove θ0 è l’angolo definito da n sˆ ˆ0i ′ = −cosθ0, con cosθ0 ≥ , cioè 0 0 0 2
π θ
≤ ≤
θn è l’angolo definito da ˆ ˆn sni ′ = −cosθn, con cosθn ≥ , cioè 00
2 n
π θ
≤ ≤
e nˆ0,n è il versore normale alla 0-face e n-face rispettivamente, nel punto di diffrazione. Nelle (2.30)-(2.33) L è il parametro distanza dato da:
2 1 2 1 2 ( ) sin ( )( ) i i i i i i s s L s s ρ ρ ρ γ ρ ρ ρ + = + + (2.37)
dove ρ1,2i sono i raggi di curvatura del fronte d’onda incidente in . Per un fronte d’onda incidente sferico
d Q 1 2
i i i s
ρ =ρ =ρ = , il parametro distanza può essere scritto ′ come: 2 sin ss L s s γ ′ = ′ + (2.38)
inoltre, ricordando che nel tool analizzato nel capitolo 3 i punti in cui si cerca di predire il campo elettrico appartengono tutti al piano orizzontale (si tratta infatti di uno studio in 2D), ogni punto descritto in coordinate sferiche si trova ad avere la seconda coordinata sferica (rispetto a qualsiasi sistema di assi definito fino ad ora) pari a 2 π . Allora sostituendo 2 π γ = nella (2.38) otteniamo L ss s s ′ = ′ + che coincide con la (2.27). La funzione a±( )δ± è data da 2 2 ( ) 2 cos 2 n N a δ π δ ± ± ± ± = ⎛ − ⎜ ⎝ ⎠ ⎞ ⎟ (2.39)
dove δ± = ± e Nφ φ′ ± sono gli interi più vicini che soddisfano le seguenti equazioni: 2n Nπ +−( )δ± = π (2.40)
2n Nπ −−( )δ± = − (2.41) π
[ ]
F x è la funzione di transizione di Fresnel argomento del prossimo paragrafo [15].
2.4.2 – La funzione di transizione di Fresnel
La funzione di transizione di Fresnel è definita come: 2 [ ] 2 jx j F x j x d x
e
∞ −e
τ τ =∫
(2.42)Per valori positivi di x, la funzione può essere valutata approssimativamente come segue: -Per x>5.5 2 3 3 15 75 [ ] 1 2 4 8 16 j j F x 4 x x x x = + − − + (2.43)
-Per si può usare uno schema di interpolazione basato sui valori della seguente tabella 0.3≤ ≤x 5.5
x
F x
[ ]
0.3 0.5729 + j0.2677 0.5 0.6768 + j0.2682 0.7 0.7439 + j0.2549 1.0 0.8095 + j0.2322 1.5 0.8730 + j0.1982 2.3 0.9240 + j0.1577 4.0 0.9658 + j0.1073 5.5 0.9797 + j0.0828 -Per 0≤ < .3x 0 2 4 4 4 2 [ ] 2 3 j j x j x F x x xe
e
πe
π π π − ⎛ ⎞ + ⎜ ⎝ ⎛ ⎞ ⎜ = − − ⎜⎜ ⎟ ⎝ ⎠ ⎟ ⎠ ⎟ ⎟ (2.44) - Per x<0 * [ ] [ ] F x =F x (2.45)dove l’asterisco indica il complesso coniugato.
La figura 2.14c mostra l’andamento del modulo e della fase della funzione di transizione di Fresnel in funzione dell’argomento, su scala semilogaritmica.
Figura 2.14c – Funzione di transizione di Fresnel
2.4.3
–
Confini d’ombra e regioni di transizione
I coefficienti di diffrazione assumono valori rilevanti quando si annulla l’argomento di una delle quattro cotangenti di cui sono composti. L’argomento si annulla proprio sui confini d’ombra, in questo modo i campi diffratti compensano le discontinuità del “campo somma” di campo diretto e campi riflessi valutato utilizzando esclusivamente l’ottica geometrica. Ma analizziamo più dettagliatamente il fenomeno dei confini d’ombra. Osservando la figura 2.14 e ricordando le convenzioni enunciate nel paragrafo 2.4.1 si capisce che la 0-face è posizionata a φ = , mentre la n-face è 0 posizionata a φ =nπ. I casi in cui si verifica effettivamente la diffrazione sono quelli in cui i wedges hanno un angolo interno più piccolo di 180° (α <180°) , ovvero un angolo esterno maggiore dell’angolo piatto, cioè: π <nπ <2π ⇒ 1< <n 2. I casi n=1 e sono casi limite: il primo consiste in un wedge con un
angolo esterno (o interno) di
2
n=
πradianti, quindi in una faccia piana che non provoca diffrazione bensì solo riflessione, il secondo consiste in un wedge “virtuale”, cioè con un angolo esterno di 2π radianti.
Riguardo φ e φ′ , in generale: 0< <φ′ nπ e 0< <φ nπ . I casi nei quali 0, n
φ′ = π e φ =0, nπ sono conosciuti rispettivamente come incidenza radente e diffrazione radente, essi non vengono considerati nell’algoritmo di ray-tracing (di cui
parleremo nella sezione 3.1) alla base del tool da noi sviluppato perché apportano un contributo trascurabile al campo elettrico totale.
Un’osservazione attenta del wedge in figura 2.14 rivela che sia la 0-face che la n-face possono creare un confine d’ombra d’incidenza ISB (incidence shadow boundaries), nonché un confine d’ombra di riflessione RSB (reflection shadow boundaries). Occorre dunque, esaminare quattro casi:
1) n-face oscurata (incidenza sulla 0-face):
si trova (vedi fig. 2.15a) la seguente relazione 0< <φ′ (n−1)π Poiché φISB = +φ π′ ⇒ π φ< ISB <nπ
S 0-face n-face ISB ISB (2-n)
π
Fig. 2.15a – n-face oscurata.
2) 0-face oscurata (incidenza sulla n-face):
si trova (vedi fig. 2.15b) la seguente relazione π φ< <′ nπ Poiché φISB = −φ π′ ⇒ 0<φISB <(n−1)π
0-face n-face ISB ISB S (2-n)
π
Quindi, per i casi 1) e 2) vale: ISB
φ −φ′ =π e tutte le possibili situazioni loro relative sono visualizzate in figura 2.16
RSB Incidenza su 0-face Incidenza su n-face NO ISB π π π (n-1) π (n-1) π n π n
Fig. 2.16 – Posizionamento del confine d’ombra d’incidenza ISB.
3) Riflessione dalla 0-face:
si trova (vedi fig. 2.17a) la seguente relazione 0< < φ π′ Poiché φRSB = −π φ′ ⇒ 0<φRSB <π S 0-face n-face RSB RSB n0 (2-n)
π
4) Riflessione dalla n-face:
si trova (vedi fig. 2.17b) la seguente relazione (n−1)π φ< <′ nπ Poiché ψ φ= −′ (nπ π− ) e ( ) (2 1) RSB n n n n φ = π ψ− = π− φ′− π π+ = − π φ− ⇒ (′ n−1)π φ< RSB <nπ 0-face n-face RSB S nn RSB y (2-n)
π
Fig. 2.17b – Riflessione dalla n-face.
Tutte le possibili situazioni relative ai casi 3) e 4) sono visualizzate in figura 2.18.
RSB π π π (n-1) π (n-1) π n π n Riflessione dalla n-face
Riflessione dalla 0-face
Una particolarità esiste quando (n−1)π φ π≤ ≤′ perché non c’è un ISB, tuttavia in questa regione i campi sono riflessi sia dalla 0-face che dalla n-face, cosicché sono creati due RSB simultanei (vedi fig. 2.19).
0-face RSBn S nn n-face n0 RSB0 RSBn RSB0 (2-n)
π
Fig. 2.19 – Presenza simultanea di due RSB.
Attorno ai confini d’ombra si trovano le cosiddette regioni “di transizione”. I punti appartenenti a queste regioni soddisfano la relazione β0La±<2π. Fuori dalle suddette zone, le funzioni di transizione di Fresnel di (2.30)-(2.33) possono essere approssimate [3] da così, lontano dal punto di diffrazione, il campo diffratto (2.20) può essere considerato un campo valutato attraverso un raggio ottico. Invece, per i punti di osservazione all’interno delle regioni di transizione, il campo diffratto risultante non mostra un comportamento di tipo ray-optical.
0
[ ]
F β La± ≈1
2.5 – Campo Trasmesso
Quando un raggio raggiunge l’interfaccia tra due mezzi, una porzione dell’energia è riflessa dal primo mezzo (raggio riflesso) e una parte dell’energia è rifratta (trasmessa) attraverso il secondo mezzo (raggio rifratto o trasmesso). Nella sezione 2.3 abbiamo affrontato l’approccio GO per il campo riflesso. I campi incidente e riflesso erano in relazione attraverso i coefficienti di riflessione, particolarizzati per il caso in cui il
primo mezzo fosse lo spazio libero. In maniera simile i coefficienti di trasmissione possono essere usati per mettere in relazione i campi associati con i raggi incidente e rifratto [20].
2.5.1
–
Legge di Snell per la rifrazione
La direzione del raggio rifratto è data dalla legge di Snell della rifrazione:
0sinθi = sinθr
β β (2.46)
dove θi è l’angolo incidente formato dalla direzione d’incidenza e il vettore normale all’interfaccia (puntante verso il primo mezzo) nel punto di rifrazione, θr è l’angolo di rifrazione formato dal raggio rifratto e il vettore normale all’interfaccia (puntante verso il secondo mezzo), e e β sono i numeri d’onda nel primo e nel secondo mezzo (vedi fig. 2.20).
0 β
Inoltre, la legge di Snell enuncia che il raggio incidente, il vettore normale all’interfaccia nel punto di rifrazione e il raggio rifratto giacciono sullo stesso piano (piano di incidenza). Questo fatto insieme alla (2.46) determina la direzione del raggio trasmesso. Mezzo 1 Mezzo 2
β
0
β
iθ
θ
r2.5.2 – Trasmissione in scenari indoor e outdoor
Nel contesto della propagazione outdoor l’influenza dei raggi trasmessi è molto bassa. Quando un raggio è trasmesso attraverso una parete esterna di un edificio è rapidamente attenuato dagli ostacoli che gli si pongono innanzi dopo la trasmissione. Quindi il campo dei raggi che una volta entrati in un edificio riemergono all’esterno del medesimo è trascurabile. Invece, nel fenomeno della propagazione indoor, i raggi trasmessi attraverso le pareti giocano un importante ruolo cosicché essi devono essere presi in considerazione. Molti autori propongono coefficienti di trasmissione ottenuti da misure dirette con pareti da costruzione tipiche [21]. Questi coefficienti empirici sono facili da includere in modelli di propagazione e in molti casi forniscono buoni risultati. Ma essi ignorano parametri come l’angolo d’incidenza e la larghezza della parete. Le pareti da costruzione hanno una larghezza finita tale che quando un raggio è trasmesso attraverso di loro esso subisce due rifrazioni: la prima dal mezzo esterno (ad es.:aria) al mezzo parete (ad es.:calcestruzzo), la seconda dal mezzo parete al mezzo esterno. Similmente il fenomeno della riflessione su una parete di larghezza finita è diverso da quello su un’interfaccia tra due mezzi di estensione infinita.
Nella maggioranza dei modelli outdoor le riflessioni su pareti di edifici sono trattate assumendo la larghezza dei muri infinita e i coefficienti di riflessione hanno espressioni diverse da (2.15)-(2.16). Ma nei modelli indoor quando per simulare la trasmissione si considera finita la larghezza delle pareti, anche le riflessioni devono tener conto di questa caratteristica più reale.
2.5.3 – Coefficienti di trasmissione
Coefficienti di trasmissione approssimati dati in termini di coefficienti di riflessione possono essere ottenuti da [22].
In questa sezione, sono presentati coefficienti di trasmissione “deterministici” per pareti di spessore finito, come funzione delle proprietà elettriche dei materiali di
cui sono composte e del raggio incidente. Essi sono stati ricavati da [23, 24] sotto le seguenti assunzioni:
¾ Il mezzo parete è omogeneo e isotropico.
¾ Le due interfacce sono localmente piane nei punti di trasmissione. Questa è un’ ipotesi comune nel contesto GO.
Queste ipotesi non sono sempre realistiche in un ambiente indoor ma i risultati ottenuti (vedi sezione 4.7) rivelano una notevole accuratezza di questo modello di trasmissione.
Il campo trasmesso attraverso una parete di larghezza finita (per parete s’intende un qualunque elemento con uno spessore, ad esempio, un muro, una porta, una finestra, una vetrata, un separé in legno, ed altro) vale:
t i
E =
T
E (2.47)dove è il campo incidente sulla prima interfaccia della parete (vedi fig. 2.21) e è la matrice di trasmissione. i E
T
β
0
β
iθ
θ
r0
β
rθ
θ
iε
r
,
d
Fig. 2.21 – Trasmissione attraverso una parete.
Quando i campi incidente e trasmesso sono scomposti nelle loro componenti parallela e perpendicolare, la matrice di trasmissione è data da:
0 0 T T T ⊥ ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ (2.48)
con
(
)
(
) (
)
2 0 r 2 0 r β ε sin cos 2 r 2 2 2 β ε sin 2 2 r r 4 ε sin cos( )ε sin cos ε sin cos
i i i jd i i j d i i i i T
e
e
θ θ θ θ θ θ θ θ − + ⊥ − − = − + − − − + θ (2.49)(
)
(
) (
)
2 0 r 2 0 r β ε sin cos 2 r r 2 2 2 β ε sin 2 2 r r r r 4ε ε sin cos( )ε sin ε cos ε sin ε cos
i i i jd i i j d i i i T
e
e
θ θ θ θ θ i θ θ θ − + − − = − + − − − θ (2.50)dove θi è l’angolo di incidenza sulla prima interfaccia della parete (vedi fig. 2.21), θr è l’angolo di rifrazione al primo mezzo, che può essere ottenuto con (2.46), dè la larghezza della parete, è il numero d’onda nello spazio libero, ε è la permittività relativa del mezzo di cui è costituita la parete e β è il numero d’onda nel mezzo parete
0 β r 2 β εr π λ = (2.51) dove λ è la lunghezza d’onda nello spazio libero.
Indicando ora con e rispettivamente i punti dati dall’intersezione del raggio incidente con la prima interfaccia della parete e dal primo raggio rifratto con la seconda interfaccia della parete, possiamo scrivere che il campo incidente in vale:
1 P P2 1 P
(
)
0 1 a a β 1 a a a a 1 ˆ ˆ ( ) ( , ) ( , ) j t i a a E P E E te
θ φ − = θ θ φ + φ θ φ (2.52)dove è la distanza tra il centro di fase dell’antenna trasmittente (S) e il punto . Possiamo affermare che S, ,PO appartengono allo stesso piano: il piano di incidenza (vedi fig. 2.22a e 2.22b).
1
t P1
1, 2 P P
Analogamente al caso di raggio riflesso, il campo trasmesso e il campo nel punto di osservazione PO dopo aver subito una trasmissione attraverso una parete, (esplicitando le componenti parallela e perpendicolare) valgono [26]:
(
)
(
)
(
)
(
)
(
)
(
)
0 1 a a 0 1 a a 0 1 a a 0 1 a a β 1 a a a a 1 β a a a a 1 β a a a a 1 β a a a a 1 ˆ ˆ ( ) ( , ) ( , ) ˆ ˆ ( , ) ( , ) ˆ ˆ ( , ) ( ) ( , ) ˆ ˆ ( , ) ( , ) j t t i i i j t t t j t a a j t a a E E P E u E u t T E u T E u t T E T E t T E T E te
T
T
e
e
e
θ φ θ φ − ⊥ − ⊥ ⊥ − ⊥ − ⊥ = = − + = − + = − − + = + θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ (2.53)(
)
0 0 a a β β a a ˆ a a ˆ ( ) ( , ) ( , ) j r j r t t a a E PO E T E T E r re
− θ φe
− ⊥ = = θ θ φ + φ θ φ (2.54)dove è la distanza tra S e PO, e r β0 1
1 t t j t E =E t
e
.X
aY
aZ
aS
Piano d’incidenza
a aPO
u
i
u
i
u
t
u
t
Fig. 2.22a – Per il raggio incidente come per il raggio trasmesso i vettori: polarizzazione parallela,
polarizzazione perpendicolare, direzione del raggio formano una terna destrorsa.
X
aY
aZ
aS
a ar
a aP
1P
2PO
t
1 θi θr2.6 – Effetti multipli
In ambienti complessi come scenari urbani e indoor per dare un’accurata stima del campo nel punto di osservazione devono essere inclusi gli effetti multipli. La figura 2.23 mostra esempi di effetti doppi coinvolgenti riflessioni e/o diffrazioni.
TX
RX
TX
RX
Fig. 2.23 – Esempi di raggi che subiscono doppia riflessione (rosso), doppia diffrazione (blu),
riflessione-diffrazione (verde), diffrazione-riflessione (viola).
Nelle microcelle e picocelle, i campi rappresentanti due o tre interazioni sono sufficientemente precisi da fornire un buon risultato (eccetto in certi casi come lunghi corridoi indoor). Ma in grandi celle, a volte è necessario considerare contributi al campo di ordine più elevato.
Conoscendo la riflessione, la diffrazione, o i punti di trasmissione, un contributo di effetto multiplo può essere sviluppato steb-by-step in maniera simile a come abbiamo analizzato gli effetti di singola riflessione, singola diffrazione, e singola trasmissione discussi nei precedenti paragrafi. Il capitolo 3 presenta un’efficiente tecnica di ray-tracing per determinare i punti di riflessione, diffrazione e trasmissione in effetti multipli.
Appendice 2A: Trasformazione di vettori
2A.1 Trasformazione vettoriale tra sistemi di
coordinate rettangolari e sferiche
La descrizione di un vettore in un sistema di coordinate rettangolari (o cartesiane) è dove i valori
ˆx ˆy
v=xa +ya + ˆzaz ( , , )x y z costituiscono il vettore di coordinate cartesiane o rettangolari (vedi figura 2A.1).
x y z ax ay az v
Fig. 2A.1 – Sistema di coordinate cartesiane.
La descrizione di un vettore in un sistema di coordinate sferiche è v=raˆr +θaˆθ +φaˆφ dove i valori ( , , )r θ φ costituiscono il vettore di coordinate sferiche (vedi figura 2A.2). Le relazioni tra i versori dei sistemi di coordinate rettangolari e sferiche sono:
v
r
θ
φ
ar aθ aφFig. 2A.2 – Sistema di coordinate sferiche.
ˆx sin cos ˆr cos cos ˆ sin a = θ φa + θ φaθ − φˆaφ
ˆa
(2A.1) ˆy sin sin ˆr cos sin ˆ cos
a = θ φa + θ φaθ + φ φ ˆa
(2A.2) ˆaz =cosθaˆr −sinθ θ (2A.3)
ˆr sin cos ˆx sin sin ˆy cos a = θ φa + θ φa + θaˆz
ˆz a
(2A.4) ˆ cos cos ˆx cos sin ˆy sin
aθ = θ φa + θ φa − θ ˆa
(2A.5) ˆaφ = −sinφaˆx+cosφ y (2A.6)
Quindi la matrice di trasformazione da sistema di coordinate cartesiane a sistema di coordinate sferiche è data da
(2A.7)
sin cos sin sin cos
cos cos cos sin sin sin cos 0 r x y z θ φ θ φ θ θ θ φ θ φ θ φ φ φ ⎛ ⎞ ⎛ ⎞⎛ ⎞ ⎜ ⎟ ⎜= − ⎟⎜ ⎟ ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎜ − ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠⎝ ⎠
e la matrice di trasformazione da sistema di coordinate sferiche a sistema di coordinate cartesiane è data da
sin cos cos cos sin sin sin cos sin cos cos sin 0 x r y z θ φ θ φ φ θ φ θ φ φ θ θ θ φ − ⎛ ⎞ ⎛ ⎞⎛ ⎞ ⎜ ⎟ ⎜= ⎟⎜ ⎟ ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎜ − ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠⎝ ⎠ (2A.8)
2A.2 Trasformazione vettoriale tra sistemi di
coordinate rettangolari
Adesso consideriamo due diversi sistemi di coordinate cartesiane con versori a a aˆ ˆ ˆx, ,y z e a a aˆ ˆ ˆx′ ′ ′, ,y z come mostra la figura 2A.3. Esprimiamo un vettore v con coordinate
( , , )x y z e ( ,x y z′ ′ ′ in questi sistemi di coordinate: , )
ˆx ˆy ˆz, ˆx ˆy v =xa +ya +za v =x a′ ′ +y a′ ′ +z aˆ′ z′ (2A.9) ax az ay ax az ay
Fig. 2A.3 – Sistemi di coordinate cartesiane.
Le relazioni tra i versori tra i sistemi di coordinate sono:
(2A.10) ˆx (ˆ ˆ ˆx x) x (ˆ ˆ ˆx y) y (ˆ ˆ ˆx z) a′ = a a a′⋅ + a a a′⋅ + a a a′⋅ z ˆz z z (2A.11) ˆy (ˆ ˆ ˆy x) x (ˆ ˆ ˆy y) y (ˆ ˆy z) a′ = a′ ⋅a a + a′ ⋅a a + a′⋅a a (2A.12) ˆz (ˆ ˆ ˆz x) x (ˆ ˆ ˆz y) y (ˆ ˆ ˆz z) a′ = a a a′⋅ + a a a′⋅ + a a a′⋅ ˆx (ˆ ˆ ˆx x) x (ˆ ˆ ˆy x) y (ˆ ˆ ˆz x) a = a a a′⋅ ′ + a′ ⋅a a′ + a a a′⋅ ′ (2A.13) ˆy (ˆ ˆ ˆx y) x (ˆ ˆ ˆy y) y (ˆ ˆ ˆz y) z a = a a a′⋅ ′ + a′ ⋅a a′ + a a a′⋅ ′ (2A.14) ˆz (ˆ ˆ ˆx z) x (ˆ ˆ ˆy z) y (ˆ ˆ ˆz z) z a = a a a′⋅ ′ + a′ ⋅a a′ + a a a′⋅ ′ (2A.15)
I prodotti scalari sono i coseni degli angoli formati dai versori dei due sistemi di coordinate. Considerando le equazioni 2A.9-15, la matrice di trasformazione dal sistema di coordinate al sistema di coordinate
è data da ˆ ˆ (a ai′⋅ )j ˆ ˆ ˆ ( , , )a a ax y z ˆ ˆ ˆ ( , , )a a ax′ ′ ′y z ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ x x x y x z y x y y y z z x z y z z x a a a a a a x y a a a a a a y z a a a a a a z ′ ⎛ ′⋅ ′⋅ ′⋅ ⎞ ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟′ = ′ ⋅ ′⋅ ′ ⋅ ⎜ ⎟ ⎜ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟′ ⎜ ′⋅ ′⋅ ′⋅ ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠⎝ ⎠ ⎟ (2A.16)
e la matrice di trasformazione dal sistema di coordinate ˆ ˆ ˆ( , , )a a ax′ ′ ′ al sistema di y z coordinate ( , , )a a aˆ ˆ ˆx y z è data da ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ x x y x z x x y y y z y x z y z z z x a a a a a a x y a a a a a a y z a a a a a a z ′ ′ ′ ⎛ ⋅ ⋅ ⋅ ⎞ ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟= ′⋅ ′ ⋅ ′⋅ ⎜ ⎟ ⎜ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ′⋅ ′ ⋅ ′⋅ ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠⎝ ⎠ ′ ′ ⎟ ′ (2A.17)
2A.3 Trasformazione vettoriale tra sistemi di
coordinate sferiche
La trasformazione vettoriale da un sistema di coordinate sferiche ˆ ˆ ˆ( , , )a a ar θ φ ad un altro sistema di coordinate sferiche ˆ ˆ ˆ( , , )a a ar′ ′ ′ può essere ottenuto indirettamente θ φ nella maniera seguente. Prima, il vettore è trasformato dal sistema di coordinate sferiche ˆ ˆ ˆ( , , )a a ar θ φ nel corrispondente sistema di coordinate cartesiane
usando la (2A.8). Dopo il vettore è trasformato dal sistema di coordinate cartesiane associato con il sistema di coordinate sferiche finale
ˆ ˆ ˆ ( , , )a a ax y z
ˆ ˆ ˆ
( , , )a a ax′ ′ ′y z ( , , )a a aˆ ˆ ˆr′ ′ ′ usando la θ φ (2A.16). Finalmente il vettore è trasformato nel sistema di coordinate sferiche finale applicando la (2A.7). Questa procedura è riassunta nella riga sottostante:
eq. 2A.8 eq. 2A.16 eq. 2A.7