CAPITOLO III
Evoluzione dei procedimenti di calcolo
Si passano in rassegna le problematiche relative al calcolo delle antenne strallate illustrando i criteri che negli anni hanno permesso di modellare sia la struttura che le azioni agenti. Particolare rilievo è dato al comportamento non lineare di queste strutture e all’azione del vento, che gioca, nella pratica, un ruolo fondamentale.
3.1 Problematiche fondamentali
Un’antenna strallata è soggetta alle seguenti azioni: a. peso proprio degli elementi strutturali; b. peso proprio delle antenne vere e proprie; c. variazioni termiche;
d. carico di ghiaccio e neve; e. azione del vento;
f. azione sismica;
g. pre-tensione negli stralli.
Sui pianerottoli e sulle eventuali stazioni di osservazione è bene considerare anche un certo carico accidentale, distribuito o concentrato, al fine di condurre verifiche a carattere locale.
Le azioni statiche o a carattere debolmente variabile, da potervi essere ricondotte, a, b, c, d, g non presentano particolari difficoltà sia dal punto di vista della modellazione sia dell’analisi.
Purtroppo, per la notevole snellezza raggiunta da queste costruzioni, non si può prescindere dalle loro caratteristiche dinamiche se vogliamo simulare il comportamento sotto l’azione del vento o l’azione sismica. Per l’azione del vento molte normative forniscono l’equivalente azione statica ma precisano un’altezza limite oltre la quale questo modello non è più valido. E’ proprio il comportamento sotto l’azione del vento che ha portato, in passato, allo sviluppo di tecniche di modellazione e calcolo quanto più verosimili.
Un altro tema sul quale si è discusso molto, più per i ponti strallati (in passato) che non per le antenne, è stato il comportamento non lineare delle funi tese, prive di rigidezza flessionale.
Nel seguito si affrontano i problemi relativi al calcolo nei vari metodi, proposti da Autori italiani, usati in passato fino ad arrivare ai procedimenti più moderni, facilitati, almeno dal punto di vista analitico, dai personal computers.
3.1.1 La non linearità geometrica
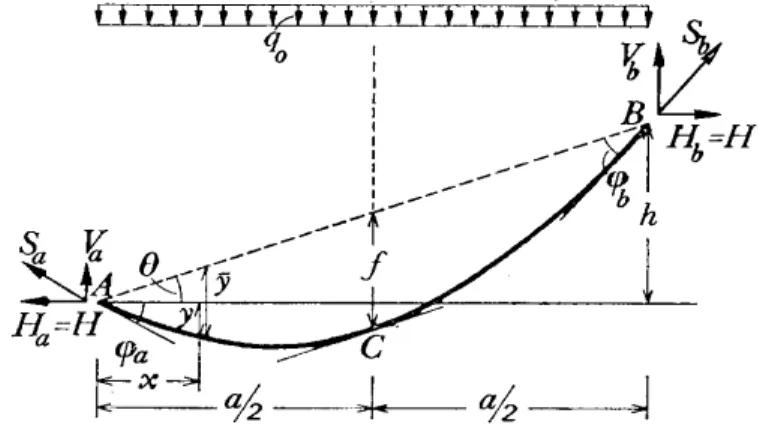
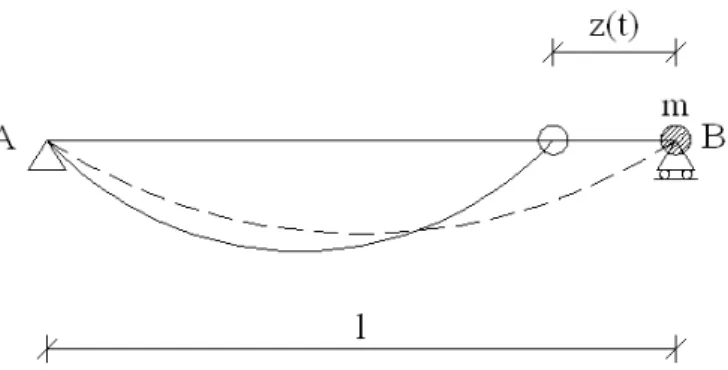
Consideriamo una fune vincolata con cerniere agli estremi, posti a quote diverse, proprio come uno strallo (fig. 1). La fune sia soggetta al peso proprio o ad un’azione uniforme sulla proiezione orizzontale qo.
Figura 1- Schema della fune.
Per l’equilibrio alla traslazione orizzontale risulta che le reazioni orizzontali agli appoggi sono uguali ed opposte di valore H.
Per l’equilibrio alla rotazione attorno a B si ottiene:
V a:= q o a2⋅ − H ha⋅
Poiché la fune è priva di rigidezza flessionale, il momento deve essere nullo in qualsiasi sezione x; scrivendo l’equilibrio alla rotazione si ottiene:
H y 1⋅ q o a⋅ 2 ⋅x q o x⋅ 2 2 − (1)
che , per la sezione di mezzeria (x = a/2; y1 = f), è:
H q o a 2 ⋅ 8f := (2’) f q o a⋅ 2 8H := (2’’)
relazione che lega il tiro della fune con la freccia in mezzeria e viceversa. La deformata della fune si ottiene sostituendo la 2’ nella 1:
y 1 4 f⋅ x⋅ a2 a−x ( ) ⋅ :=
che si riconosce essere l’equazione di una parabola. Se si riferisce l’ordinata all’asse orizzontale passante per l’appoggio A, si ottiene:
y h x⋅ a 4 f⋅ x⋅ a2 a−x ( ) ⋅ − :=
Per l’equilibrio alla traslazione orizzontale di ogni sezione deve risultare che la componente orizzontale dello sforzo nella fune è sempre pari ad H (tiro della fune). Allo sforzo S nella sezione di mezzeria si dà il nome di sforzo medio; esso vale:
S H
cos
( )
θ :=(3)
essendo θ l’angolo fra la corda AB e l’orizzontale per A.
La lunghezza complessiva della fune si calcola arrestando lo sviluppo in serie della curvatura al secondo termine, ipotesi tanto più valida quanto più la fune è tesa: l a 1 cos
( )
θ 8 3 f2⋅(
cos( )
θ)
3 a2 ⋅ + ⋅ := (4’)oppure, in funzione del tiro H e del carico Q:
l a 1 cos
( )
θ Q2⋅(
cos( )
θ)
3 24 H⋅ 2 + ⋅ := (4’’) con Q:=q o a⋅Se alla fune si modifica la lunghezza, cambierà la freccia in mezzeria; l’espressione che lega le due variazioni si ottiene differenziando l’equazione 4’: ∆l 16 3 f cos⋅
(
( )
θ)
3 a ⋅ ⋅∆f := (5)La relazione 5 permette di calcolare la variazione della freccia dovuta, per esempio, ad una variazione di temperatura o all’allungamento elastico della fune.
f l
1 10 ≤
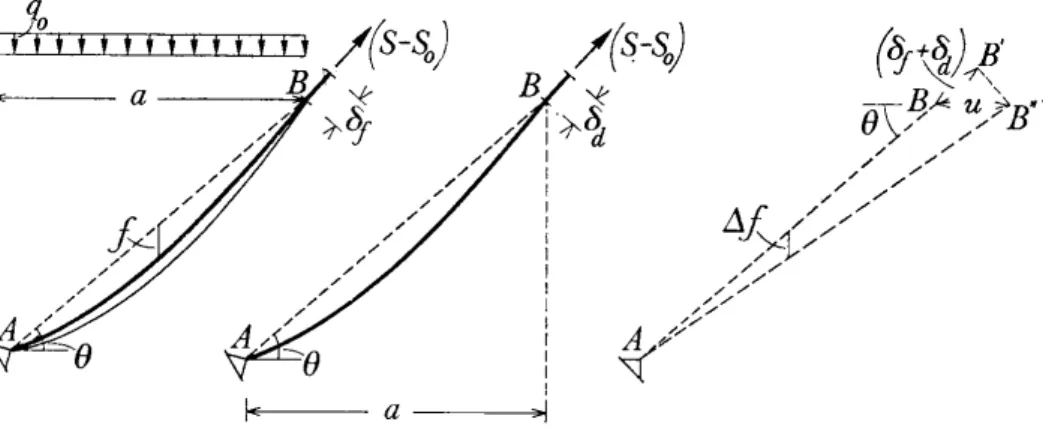
e che lo sforzo medio sotto il peso proprio valga So. Se questo sforzo aumenta e passa al valore S, la fune è più tesa e si stende diminuendo la sua lunghezza e la freccia fra gli estremi A-B (fig. 2).
Figura 2 – Spostamenti dell’estremo mobile dello strallo.
L’allungamento che ne risulta, senza considerare la deformazione del cavo, è dato dalla formula 4’’:
δ f Q 2 a ⋅ cos θ⋅
( )
24 1 S o2 1 S2 − ⋅ := (6)Inoltre si ha allungamento elastico della fune per effetto dell’incremento di sforzo (S-So):
δ d
(
S−S o)
⋅l E st A⋅ :=(7)
dove con Est si è indicato il modulo elastico apparente della fune.
Nelle antenne strallate l’ancoraggio dello strallo all’asta subisce solitamente spostamenti orizzontali u. Questo risulta dalla composizione degli spostamenti forniti dalle 6, 7 in direzione della corda A-B riportato all’orizzontale:
u
(
δ f δ d+)
cos( )
θ :=u Q 2 a ⋅ 24 1 S o2 1 S2 − ⋅ l E st A⋅ cos θ⋅
( )
⋅(
S−S o)
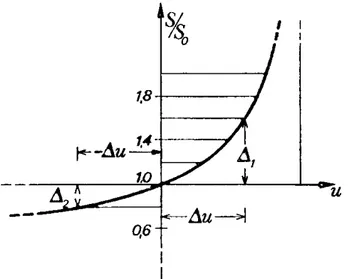
+ := (8)Questa relazione mostra la non linearità che c’è fra lo spostamento u dell’ancoraggio della fune con lo sforzo S in essa. Inoltre se supponiamo che siano collegati nello stesso punto più stralli, per alcuni di essi lo spostamento u avrà un certo verso (diciamo positivo, come nell’esempio), per altri avrà il verso opposto. Ebbene, ad uno stesso spostamento in valore assoluto, corrispondono variazioni di sforzo molto diverse a seconda del verso considerato (fig. 3).
Figura 3 - Diagramma sforzo medio S - spostamento orizzontale u dell'ancoraggio.
Infine, se si vuole conoscere la freccia che si ha per lo spostamento δf basta sostituire ∆l = δf nell’equazione 4’: f o2−f2 3 8 1 cos
( )
θ 2 ⋅ ⋅ u fa⋅ (9) in cui:fo è la freccia prima che avvenga δf;
3.1.2 L’interazione vento-struttura
Consideriamo un cilindro che abbia altezza predominante rispetto al diametro della sua circonferenza di base; immergiamo questo cilindro nella corrente di un fluido. Il flusso che si genera intorno alla zona perturbata dipende dalla velocità, dalle caratteristiche del fluido e dal diametro del cilindro.
A basse velocità di flusso, i filetti fluidi si dividono e scorrono aderendo al profilo dell’ostacolo per poi riassumere caratteristiche di continuità al di là di esso: si ha il flusso laminare. In queste condizioni, supponendo il fluido ideale, il corpo non oppone nessuna resistenza alla corrente (paradosso di D’Alembert). Il diagramma delle pressioni nella zona sopravento ed in quella sottovento ha risultante nulla.
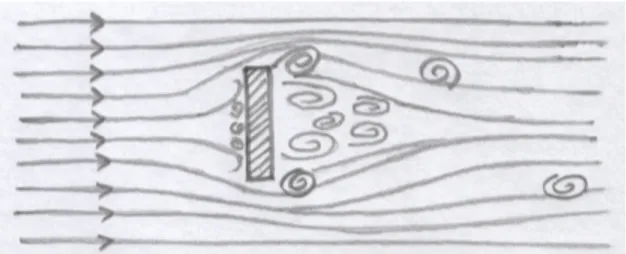
Se la velocità della corrente cresce, il flusso cambia gradualmente le sue caratteristiche finché, ad una certa velocità, non riesce più ad aderire alla parte sottovento del profilo. In questa condizione il diagramma delle pressioni ammette risultante non nulla: fluido e ostacolo si scambiano una certa azione. La pressione nella parte sottovento diventa negativa ed il fluido si muove, qui, in direzione opposta a quella della corrente. Nel punto di incontro di queste due correnti antagoniste, che di solito coincide con due spigoli opposti dell’ostacolo, si forma un vortice che va ingrandendosi fintanto che le sue dimensioni non gli permettono di restare in posizione. Il vortice dunque si stacca e viene trasportato dal resto della corrente (fig. 4).
Figura 4 - Rappresentazione schematica del distacco dei vortici.
Questo fenomeno avviene alternativamente da una parte e dall’altra, ed ogni volta si genera una variazione di pressione nella zona sottovento che agisce con un certo impulso sull’ostacolo. I vortici si staccano ad intervalli di tempo
regolari e si trovano sempre alla stessa distanza nella scia della corrente fluida. Ciò dà origine a forze impulsive periodiche sul cilindro, che viene messo in vibrazione.
Lo studioso che condusse prove sperimentali su questo fenomeno fu Strouhal il quale trovò la relazione fra velocità del fluido V, diametro del cilindro D e frequenza n del distacco dei vortici:
n D⋅ V 0.2
Quando ad un sistema libero di vibrare sono applicati impulsi periodici, esso tende a porsi in vibrazione. Se il periodo di vibrazione proprio del sistema ed il periodo degli impulsi sono diversi, si può avere opposizione di fase per cui, ad un certo punto, gli impulsi stessi si oppongono alla vibrazione del sistema arrestandola. Lo stesso fenomeno poi si ripete, cioè la vibrazione del sistema inizierà con un certo valore, raggiungerà un massimo e scenderà fino ad annullarsi e così via.
Quando periodo del sistema e periodo degli impulsi sono uguali non si può avere opposizione di fase. L’ampiezza della vibrazione tende ad aumentare indefinitamente, eccitata ogni volta dagli impulsi: si verifica la risonanza del sistema che porta inevitabilmente a rottura.
Riportandosi al caso reale, un’antenna strallata può essere vista come un ostacolo nel flusso del vento: difficilmente questo flusso avrà caratteristiche ideali.
Innanzitutto la velocità del vento varia in riferimento alla quota rispetto al suolo ed è tanto maggiore quanto più si va in alto; è sempre turbolenta nel campo di altezza di interesse per le costruzioni civili; la pressione che esercita varia in funzione della densità dell’aria.
L’azione del vento è fortemente di carattere aleatorio. La forza esercitata dal vento varia nel tempo principalmente per i seguenti motivi:
- a causa delle raffiche;
- a causa del distacco alternato dei vortici; - a causa delle turbolenze di scia.
Il flusso del vento alle varie altezze non è quasi mai costante ma si verificano sempre delle raffiche più o meno intense (fluttuazioni di velocità). Sono proprio le raffiche che generano gli impulsi più pericolosi per la struttura. Inoltre un’antenna strallata non ha sezione cilindrica ma a spigoli vivi (sezione triangolare o quadrata) tanto che il distacco dei vortici è maggiormente favorito; essa avrà più modi di vibrare e quindi più frequenze fondamentali di vibrazione. Nel seguito si tenterà di modellare proprio l’azione delle raffiche. Anche gli stralli possono venire eccitati sia nel loro piano che fuori da esso e la loro vibrazione andrà ad interagire con quella dell’asta (fenomeni di “galloping”).
Fortunatamente però, la struttura sarà dotata di una capacità, seppur minima, di smorzamento delle vibrazioni: parte dell’energia verrà persa per attrito fra fluido ed ostacolo e parte per attrito interno (deformazioni plastiche del materiale, smorzatori opportunamente inseriti).
3.2 L’analisi statica non lineare
Questo metodo di analisi, implementato o meno su codice di calcolo, ci permette di determinare le sollecitazioni globali nelle parti che compongono l’antenna strallata: l’asta verticale e gli stralli. E’ valido per strutture non molto alte, considerato che l’azione del vento è modellata come uniforme (a tratti o su tutta l’altezza).
3.2.1 L’antenna con più ordini di stralli soggetta al vento
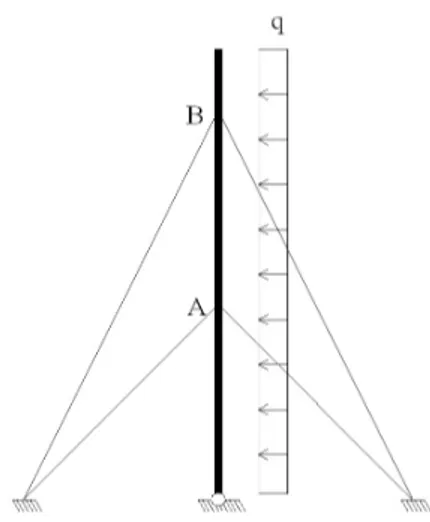
Consideriamo un’antenna strallata di altezza e caratteristiche di resistenza note, vincolata a due ordini di stralli tripli con disposizione in pianta a 120°. Si considera l’azione del vento uniformemente ripartita sull’altezza (fig. 5).
Figura 5 – Schema tipico di un’antenna strallata.
In primo luogo si determina in quale direzione deve spirare il vento per sollecitare al massimo uno degli stralli. Supponiamo che la risultante del vento R abbia una certa retta d’azione inclinata dell’angolo α rispetto ad una fune (fig. 6).
Figura 6 – Disposizione degli stralli in pianta.
Per l’equilibrio alla traslazione lungo l’asse della fune 1 si ha:
R cos⋅
( )
α +H 2 cos 60°⋅ ( )−H 1 0mentre in direzione ortogonale, sempre rispetto alla fune 1:
R sin⋅
( )
α −H 2 sin 60°⋅ ( ) 0Da queste si ricava H1 in funzione di R e dell’angolo α. Per massimizzare il tiro H1 basta derivare la sua espressione rispetto ad α e porla uguale a 0; si ottiene:
α = 30°
per cui la direzione della fune 2 e la retta di azione di R sono fra loro perpendicolari.
Gli stralli devono essere presollecitati per garantire la stabilità dell’antenna; di solito si prende come valore di tentativo il 20% circa della reazione del carico vento sull’altezza di competenza dello strallo. L’azione del vento tenderà ad aumentare lo sforzo nello strallo sopravento mentre andrà a diminuire la presollecitazione negli stralli sottovento: affinché lo strallo lavori “a compressione” deve essere opportunamente preteso in modo da non scaricarsi. Il punto di ancoraggio dei tre stralli all’antenna, per congruenza, subirà il medesimo spostamento orizzontale u. Come visto in precedenza (diagramma di fig. 3), l’incremento si sforzo ∆S nello strallo sopravento è molto maggiore rispetto a quello dello strallo sottovento: si può dire che lo strallo teso è più rigido di quello “compresso” e quindi fornisce un contributo preponderante nell’incassare l’azione esterna.
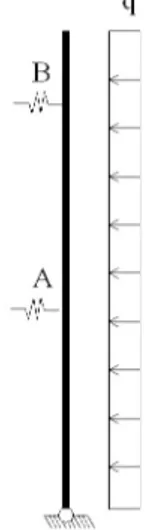
L’antenna strallata viene schematizzata come una trave continua su appoggi elasticamente cedevoli in corrispondenza dell’ancoraggio degli stralli (fig. 7).
Figura 7 – Schema adottato per l’analisi statica non lineare.
La cedevolezza di questi appoggi non è nota a priori, poiché dipende dalla tensione nella fune.
Per risolvere questo problema si esegue un procedimento iterativo nel calcolare le reazioni di appoggio, che si arresta quando, per due passi successivi, si ottengono valori delle reazioni pressoché coincidenti.
a) Ricerca della rigidezza delle molle.
In primo luogo si valutano i coefficienti elastici tangenti per i nodi A e B (fig. 7); a tal fine basta derivare le espressioni 6 e 7 rispetto ad un incremento di sforzo dS: c Q 2 a ⋅ cos θ⋅
( )
12 1 S2 ⋅ l E st A⋅ − := (10)Come detto, si assegna una pretensione agli stralli pari a circa il 20% della reazione orizzontale del vento R che compete a ciascun ordine, diciamo So. Al primo passo si introduce So nella 10.
Si applica ora, al nodo in esame, una forza unitaria orizzontale in direzione dello strallo teso (supponiamo il 2, fig. 8); questa genera incrementi di sforzo ∆Si nelle funi.
Figura 8
Si scrivono le equazioni di equilibrio alla traslazione orizzontale del nodo (x ed y) e alla traslazione verticale (che è nulla se si trascura la deformabilità assiale dell’asta):
∆S1 ∆S3
∆S2 cos θ⋅
( )
2⋅∆S1⋅cos( )
θ cos π 6 ⋅ − 1 c1 ∆S1⋅ + c2 ∆S2⋅ +c3 ∆S3⋅ 0Si risolve il sistema determinando ∆S1, ∆S2, ∆S3. Nel caso dell’esempio è intuitivo che sarà ∆S2 = -2 ∆S1.
A questo punto si calcola il coefficiente elastico tangente in direzione orizzontale per i due (o più) ordini di stralli:
co:= cos∆S2
( )
θ ⋅c2(11)
ricordando che θ è l’angolo che la corda dello strallo fa con l’orizzontale. L’unità di misura di co sarà lunghezza/forza.
Si risolve la trave su appoggi elastici ricavando le reazioni d’appoggio RA ed RB.
b) Ricerca degli spostamenti dei nodi e delle variazioni ∆Si negli stralli.
Nel nodo A o B si ha che ogni strallo sopravento è sottoposto allo sforzo medio: S 1i:= cosR A
( )
θ S2i RB cos( )
θ :=uguali fra loro (il pedice i sta per “iniziale”).
Se lo strallo sottovento è sottoposto alla pretensione So, la sua geometria è definita dalle relazioni:
H o S o cos θ:= ⋅
( )
f o q a 2 ⋅ 8 H o⋅ := l o a cos1( )
θ 83 f o 2 cos( )
θ(
)
3 ⋅ a2 ⋅ + ⋅ :=Si ipotizza una certa perdita di tensione nello strallo sottovento, ∆S3, e si calcolano i nuovi sforzi negli altri due. Risulterà:
S 3 S o ∆S 3:= −
S 1 S 1i ∆S 3:= + S 2 S 2i ∆S 3:= +
Quindi, utilizzando l’espressione 8, si calcolano gli spostamenti orizzontali u1 ed u2 ed u3.
La condizione di congruenza del nodo A o B si ottiene applicando ad esso il principio dei lavori virtuali: come sistema di forze fittizio si applica H3 = 1 alla fune sottovento e, come sistema di spostamenti, quelli effettivi; si ottiene:
u 3 u 1 u 2:= +
(13)
La 13 non risulterà in generale soddisfatta se vi si sostituiscono i valori ricavati con la 8 perciò bisogna modificare la perdita di tensione ipotizzata,∆S3. Se u3 ricavato con la 8 risulta essere minore rispetto a quello ottenuto con la 13 bisogna diminuire lo sforzo S3 o, che è lo stesso, aumentare ∆S3. Si va avanti fintanto che i valori di u3 calcolati con la 8 e con la 13 risultano uguali.
c) Iterazione del procedimento.
Una volta ottenuta la convergenza su u3, si prendono i valori di S1, S2 ed S3 calcolati con le 12. Quindi si sostituiscono nella 10, ottenendo dei nuovi valori dei coefficienti elastici tangenti da inserire nel sistema delle equazioni di equilibrio di ogni nodo.
Come risultato avremo valori aggiornati dei ∆Si e, applicando la 11, nuovi valori del coefficiente elastico in direzione orizzontale. Con questo sarà possibile risolvere la trave su appoggi elastici e calcolare le reazioni RA ed RB di secondo tentativo. Il processo è velocemente convergente e già alla terza iterazione si ottengono valori delle reazioni molto simili fra loro.
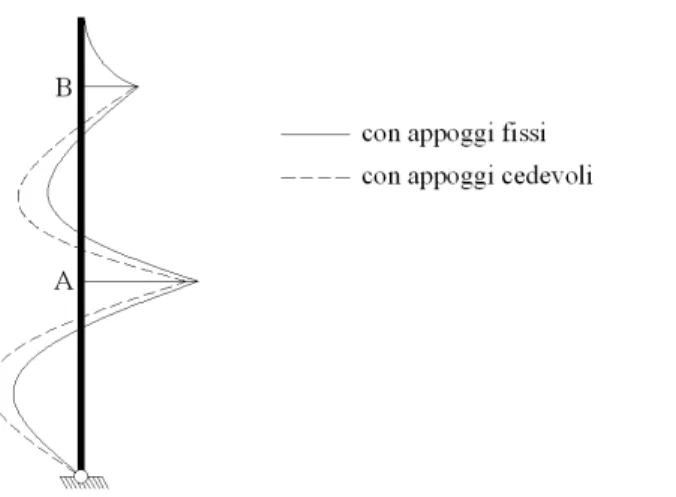
C’è da notare che le reazioni di trave continua su appoggi fissi sono, alla fine, poco diverse da quelle ottenute considerando gli appoggi cedevoli. Ciò che conta è che risultano sensibili le differenze fra i diagrammi del momento flettente (fig. 9).
3.3 Il comportamento dinamico
Si passano in rassegna alcuni metodi di indagine dinamica utilizzati in passato che, nonostante siano obsoleti per la capacità di calcolo odierna, permettono di capire le principali problematiche di comportamento e modellazione delle strutture strallate.
In primo luogo si considera la semplice fune sospesa ed i risultati ottenuti ci permetteranno di introdurre un procedimento di calcolo dinamico iterativo per ciminiere e antenne strallate.
Poi si farà riferimento alla simulazione numerica dell’interazione dinamica vento-struttura ed infine verrà considerata l’influenza, sul comportamento globale, della pressione del vento sugli stralli.
3.3.1 Comportamento dinamico della fune sospesa
Questo procedimento fa ricorso ad un modello della fune che si riduce a quello di un oscillatore semplice: la massa dello strallo viene concentrata in un punto (in mezzeria o ad un estremità) così come la forza perturbatrice. Nonostante questa semplificazione si riesce a calcolare una stima degli effetti dinamici che risultano comunque superiori a quelli statici di prima analisi. Si studiano prima le oscillazioni trasversali e poi quelle longitudinali.
3.3.1.a) Fune soggetta ad oscillazioni trasversali
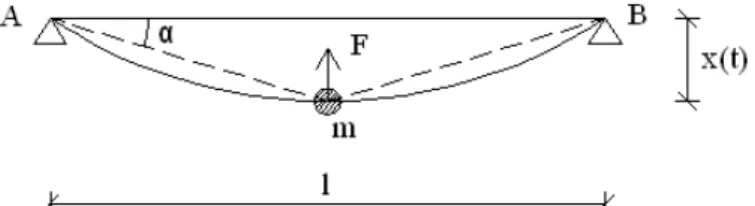
Si considera la fune perfettamente elastica e vincolata con cerniere agli estremi; la massa e la forza di richiamo siano concentrate in mezzeria. Si ipotizzano piccole deformazioni in modo da poter confondere la deformata con
due spezzate. Si studia l’oscillatore semplice il cui spostamento è la freccia in mezzeria della fune (fig. 10).
Figura 10 - Modello dello strallo soggetto ad oscillazioni trasversali.
Per le ipotesi semplificative adottate le forza di richiamo risulta:
F:=2 H⋅
(
+ F el)
⋅sin( )
α(14)
in cui:
H è il tiro della fune;
Fel è la forza elastica dovuta all’allungamento della fune:
F el E st A⋅ l2 4 x t( ) 2 + l 2 1 − ⋅ 2 E st⋅ ⋅A x t( ) 2 l2 ⋅ := (15)
Est il modulo di elasticità apparente della fune; A l’area della fune.
Sostituendo l’espressione approssimata della 15 nella 14 e facendo le seguenti posizioni: k o:= 4 H⋅l ε 2 E st⋅ ⋅A H l⋅2 := si ottiene: F:=k o x t()⋅ + k o ε⋅ x t⋅ ( )3
ε è detto parametro perturbativo. Dunque, l’equazione del moto libero di questo oscillatore “non lineare” è:
m 2 t x t( ) d d 2 ⋅ + ko x t()⋅ +ko ε⋅ x t()⋅ 3 0 (16)
2 t x t( ) d d 2 ω o2⋅x t( ) + +ω o2⋅ x tε⋅ ( )3 0 (17) con ω o2 k om .
Risolvendo direttamente l’equazione differenziale 17, la soluzione conterrebbe termini secolari del tipo t⋅cos(ωt) che la renderebbero debolmente convergente e quindi mal approssimabile. Per ovviare a ciò si adotta una nuova variabile così definita:
t:=s 1⋅ + ε ω 1⋅ +ε2⋅ω 2+εn⋅ω n
(18)
Sostituendo la nuova variabile nella 17 ed arrestando lo sviluppo in serie di potenze della ε al termine quadrato, si ottiene la seguente equazione:
2 s x s( ) d d 2 1+ ε ω1⋅ + ε2⋅ω2 ⋅ωo2⋅
(
x s( )+ ε x s⋅ ( )3)
+ 0 (19)La soluzione di questa sarà del tipo:
x s( ):=x o s( )+ ε x1 s()⋅ + ε2⋅x 2 s( )
(20)
A questo punto si sostituisce la 20 nella 19 e si raggruppano tutti i termini facenti capo ad ε e a ε2. Uguagliando a zero i coefficienti del parametro deformativo così trovati si ottengono queste tre equazioni:
2 s x o s ( ) d d 2 ω o2⋅x o s( ) + 0 (21) 2 s x 1 s( ) d d 2 ω o2⋅x 1 s( ) + −ω o2⋅2⋅ω 1⋅x o s( ) +x o3 2 s x2 s ( ) d d 2 ωo2⋅x2 s( ) + −ωo2⋅3 xo s⋅ ( )2⋅x1 s( )+2⋅ω1⋅x1 s( )+ xo s( )3+ω12+ 2⋅ω2⋅xo s( )
Il sistema 21 si risolve a cascata; la prima equazione è quella dell’oscillatore semplice la cui soluzione è:
x o s( ):=a cos⋅
(
ω o s⋅ φ+)
con ampiezza a e fase φ dipendenti dalle condizioni al contorno.
La sostituzione della 22 nella seconda equazione del sistema, genera un termine secolare che può essere eliminato se si annulla il suo coefficiente:
2⋅ω1 3 a 2 ⋅ 4 + 0
Così si ottiene la prima costante:
ω 1 − a38⋅ 2
(23)
Allo stesso modo, sostituendo xo(s) e x1(s) nella terza equazione del sistema, si genera un altro termine secolare la cui eliminazione ci fornisce:
ω 2:= 25651⋅a4
(24)
Una volta risolto il sistema e trovata la soluzione in funzione di s con l’espressione 20, si procede al cambio di variabile ottenendo la soluzione definitiva della 17: x t( ) a cos⋅
(
ω t⋅+ θ)
ε a 3 32 ⋅ ⋅cos 3(
⋅ t⋅ω + θ)
+ := (25) con: ω 1 ω o 1− 38⋅a2⋅ε 51 256a 4 ⋅ ⋅ε2 + ⋅ :=ω rappresenta la pulsazione propria dell’oscillatore non lineare in funzione dalla potenza del parametro perturbativo ε. Come era prevedibile è fortemente non lineare con l’ampiezza della oscillazione.
L’espressione 25 mostra come l’oscillazione sia composta dall’armonica fondamentale di periodo T = 2π/ω e dalle armoniche secondarie perturbative: il secondo termine a secondo membro ci dice che T2 = T/3 e l’ampiezza della seconda armonica è inferiore a quella fondamentale (fig. 11).
Figura 11 – Oscillazione trasversale della fune: sovrapposizione delle armoniche. 3.3.1.b) Fune soggetta ad oscillazioni longitudinali
Il caso dello strallo soggetto ad oscillazioni assiali è modellato con una fune che ha un estremo fisso (l’ancoraggio al suolo) e l’altro mobile (l’ancoraggio sull’asta). Come massa equivalente si considera, in prima approssimazione, la metà di quella della fune; essa viene concentrata sull’appoggio mobile (fig. 12).
Figura 12 – Schema della fune soggetta ad oscillazioni lungo il proprio asse.
Se poniamo:
q: peso per unità di lunghezza del cavo; σo: tensione iniziale della fune;
σ: tensione all’istante t;
lo spostamento z(t) risulta legato alla variazione di tensione mediante la formula (confronta formule 6,7):
z t( ) Q 2 l ⋅ 24 A⋅ 2 − 1 σ2 1 σ o2 − ⋅ l E st⋅
(
σ σ o−)
+ := (26)Indicando con Fo lo sforzo medio iniziale del cavo, con F lo sforzo medio all’istante t e con ∆F = F-Fo, si ha:
z t( ) Q 2 l ⋅ 24 F o2−F2 F2⋅F o2 ⋅ − l E st A⋅ ⋅∆F + := (27)
Sostituendo al posto di F l’espressione ∆F-Fo, sviluppando e trascurando il termine quadrato di ∆F, si ottiene:
z t( ) Q 2 l ⋅ E st⋅ ⋅A+12 F o⋅ 3⋅l 12 F o⋅ 2⋅
(
F o 2 ∆F+ ⋅)
⋅E st⋅A ∆F ⋅ := (28)Si ricava ∆F facendo le seguenti posizioni:
β 1 Q 2 E st ⋅ ⋅A 12 F o⋅ 3 + := k E st A⋅ β l⋅ := ε 2 k⋅ F o := quindi: ∆F k 1−ε z t⋅ ( )⋅z t( ) := (29)
Pertanto l’equazione del moto dell’oscillatore equivalente alla fune è:
2 t z t( ) d d 2 ωo2⋅1−ε z t1⋅ ( )⋅z t( ) + 0 (30) con ω o2 mk
Sviluppando in serie il termine
(
1−ε z t⋅ ( ))
−1 ed arrestandosi alla secondapotenza si ha: 2 t z t( ) d d 2 ωo2⋅z t( ) + + ωo2⋅
(
ε z t⋅ ( )2+ε2⋅z t( )3)
0 (31)Come per l’equazione differenziale 17, anche qui si opera il cambio di variabile della 18 secondo le potenze del parametro perturbativo ε.
Allo stesso modo si ottiene un sistema di equazioni differenziali risolvibile a cascata; si deve fare in modo di annullare i coefficienti dei termini secolari nelle soluzioni che questa volta danno le seguenti frequenze incognite:
ω1 0:= ω 2 a
2
24 :=
Riportando nuovamente la soluzione in funzione del tempo t si ha infine:
z t( ) a cos⋅
(
ω t⋅+ θ)
a 2 6 cos 2⋅(
ω t⋅+ θ)
a2 2 − ⋅ ⋅ε + 5 96a 3 ⋅ ⋅cos 3 ⋅(
ω t⋅+ θ)
⋅ε2 + := (32) con ω ω o 1 a 2 24 ε 2 ⋅ + :=Il procedimento è stato esposto arrestando gli sviluppi in serie di potenze alla seconda potenza poiché, per i termini successivi, i coefficienti erano infinitesimi di ordine superiore rispetto alla potenza di ε.
Come ricordato in precedenza, la schematizzazione del modello è ben lontana dalla realtà ma grazie alle notevoli semplificazioni di calcolo che ne derivano offre una valida stima degli effetti non lineari, di ordine superiore rispetto alla risposta principale del sistema.
Il metodo permette di studiare le oscillazioni libere della fune, una volta fissata l’ampiezza a delle oscillazioni. Se il problema da studiare fornisce eccitazioni forzate, come l’azione del vento nelle antenne strallate o l’azione sismica, il procedimento dà ancora la soluzione ma va applicato in maniera iterativa.
3.4 Metodo iterativo per l’analisi dinamica di strutture strallate in regime di non linearità degli stralli
Intorno alla metà degli anni ’80, lo studio dei problemi dinamici in strutture a comportamento non lineare veniva affrontato numericamente con la tecnica degli elementi finiti. Nel caso delle antenne strallate, lo strallo, non lineare per geometria, veniva discretizzato in una serie di elementi ma questo comportava, anche con l’uso di un elaboratore elettronico, operazioni di calcolo onerose.
Il metodo che verrà esposto fu concepito proprio per disporre di uno strumento speditivo al fine di poter fare scelte preliminari orientative; inoltre si conciliava bene con la pratica progettuale ordinaria che non faceva uso dei calcolatori. Se si considera che l’effetto non lineare dell’oscillazione rappresenta un contributo di ordine superiore rispetto a quello lineare e che di solito uno strallo è inserito come componente di una struttura soggetta a forze variabili, si capisce come una soluzione approssimata del problema trovò ampia giustificazione.
Nel campo delle ciminiere strallate, questa procedura fu applicata soprattutto per l’analisi sismica; l’azione del vento veniva al solito considerata come statica dalle varie normative dei paesi europei.
Il metodo si basa essenzialmente sull’equivalenza dell’energia di deformazione del modello reale con quella di un oscillatore fittizio.
Il modello adottato per lo studio degli effetti non lineari del moto di una fune è quello introdotto nel paragrafo 3.3.1 nel quale la “massa equivalente” dello strallo si concentra in mezzeria, per le oscillazioni trasversali, o sull’estremo libero di muoversi, per le oscillazioni longitudinali (figg. 10, 12). Sotto queste ipotesi si sono formulate le equazioni di moto oscillatorio libero della fune:
2 t x t( ) d d 2 ωo2⋅x t( ) + + ωo2⋅ x tε⋅ ( )3 0 (17) con ω o2 4 Hl m⋅⋅ ε ω o⋅ 8 E st⋅ ⋅A l3⋅m
nel caso di oscillazioni trasversali. Per le oscillazioni longitudinali si è ottenuto: 2 t z t( ) d d 2 ωo2⋅1−ε z t1⋅ ( )⋅z t( ) + 0 (30) con: β 1 Q 2 E st ⋅ ⋅A 12 F o⋅ 3 + := k E st A⋅ β l⋅ := ε 2 k⋅ F o := ω o 2 k m (33)
dove:
ωo pulsazione del sistema lineare; ε parametro perturbativo; H tiro della fune;
Fo sforzo medio della fune; m massa equivalente del cavo; Est modulo di elasticità della fune; l luce della campata;
Q peso totale del cavo.
Le equazioni 17 e 30, esprimendo una legge di moto oscillatorio libero, si prestano, come visto nel paragrafo 3.3, ad essere risolte col “metodo perturbativo” e forniscono una soluzione ben approssimata. Nel caso di oscillazioni forzate, siano queste originate da sisma o vento, il secondo membro delle suddette equazioni è diverso da zero. L’applicazione dello stesso processo risolutivo diventa difficoltosa per la nascita di termini secolari che non possono essere eliminati.
Quando però si vuole conoscere solamente la risposta massima dell’oscillatore non lineare, rinunciando alla descrizione completa del moto, si può applicare un metodo risolutivo basato sul criterio energetico che, anche se dotato di minor grado di approssimazione rispetto al metodo perturbativo, risulta di immediata applicazione. Ecco perché veniva utilizzato insieme agli spettri di risposta per l’azione sismica.
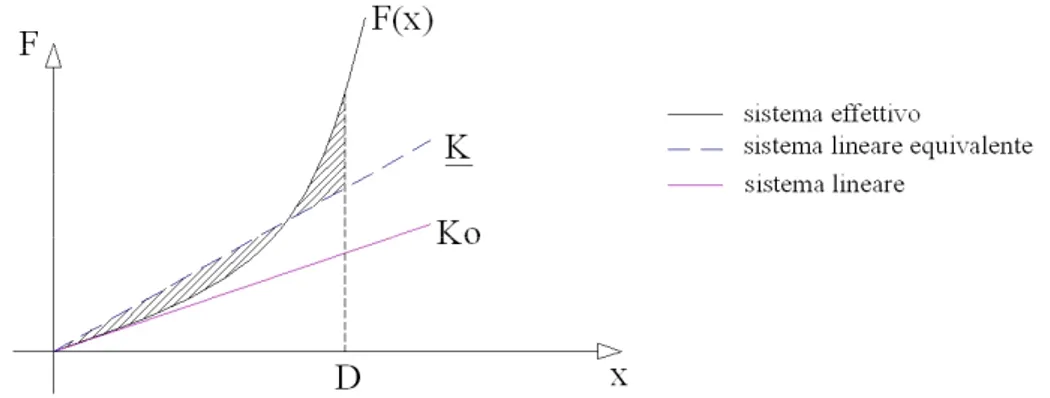
Il comportamento dell’oscillatore non lineare viene simulato da un oscillatore lineare equivalente, ponendo la condizione che il lavoro di deformazione compiuto fra la posizione iniziale, xo = 0, e quella massima finale, xmax = D, sia lo stesso per il sistema reale e per quello equivalente (figg. 13, 14).
La costante elastica k dell’oscillatore equivalente si ottiene, in funzione di xmax = D, dall’uguaglianza: k D⋅ 2 2 0 D x F x( ) ⌠ ⌡ d (34)
Nel caso delle oscillazioni trasversali si ha (confronta col paragrafo 3.3.1.a):
Figura 13 - Ricerca di k per l'oscillatore equivalente: caso delle oscillazioni trasversali.
F x( ):=k o x⋅ + k o ε⋅ x⋅ 2 (35) con k o:= 4 H⋅l ε 2 E st⋅ ⋅A H l⋅2 :=
Sostituendo la 35 nella 34 si ottiene:
k D⋅ 2 2 k o D⋅ 2 2 k o ε⋅ 4 D 4 ⋅ + da cui k k o 1 ε D 2 ⋅ 2 + ⋅ := (36)
La frequenza angolare ω del sistema effettivo non lineare può essere quindi valutata come la frequenza del sistema lineare equivalente di rigidezza k:
ω k m ω o 1 ε D⋅ 2 2 + ⋅ := (37)
Se prendiamo lo spettro di risposta del terremoto di progetto, lo spostamento massimo D del sistema è legato alla velocità spettrale in funzione del periodo T e del fattore di smorzamento ξ:
D S v T ξ
( )
, ω :=D 1 ε D 2 ⋅ 2 + ⋅ S v T ξ
( )
, ω oSe la struttura si trova, come di solito accade, nel campo dei periodi intermedi si può considerare costante la velocità Sv.
Si indichi con Do il massimo spostamento dell’oscillatore lineare determinabile dallo spettro con i parametri
T o 2⋅π ω o := e ξ; allora D 1 ε D 2 ⋅ 2 + ⋅ S v T o ξ
(
,)
ω o D o da cui si ricava: D 1 2⋅ D oε 2 ⋅ + −1 ε := (38)Il valore di D così ricavato rappresenta il massimo spostamento dell’oscillatore non lineare effettivo, cioè della struttura data. La sua pulsazione effettiva ω si ricava dalla espressione 37 in cui, questa volta, D è noto.
Il caso dell’oscillazione lungo l’asse della fune (trattato col metodo perturbativo nel paragrafo 3.3.1.b) rappresenta la classica situazione che si verifica in un’antenna strallata sottoposta ad oscillazioni forzate: il moto del traliccio determina lo spostamento dell’ancoraggio dello strallo che viene così eccitato e a sua volta trasferisce la sua risposta al traliccio stesso.
Come visto in precedenza (confronta con la formula 29), la forza di richiamo non lineare è: F z( ) k z⋅ 1−ε z⋅ := (39’) F z( ) k z⋅ 1+ ε z⋅ := (39’’)
a seconda che lo spostamento z dell’estremo della fune determini, rispettivamente, una diminuzione o un aumento della freccia (fig. 14).
Figura 14 - Ricerca di k per l'oscillatore equivalente, oscillazioni longitudinali. A causa del diverso comportamento dello strallo per spostamenti opposti del suo estremo, si hanno due valori per k.
Procedendo in maniera analoga al caso di oscillazione trasversale, applicando la 34, si ottiene: k 1 D⋅ 2 2 0 D z k z⋅ 1−ε z⋅ ⌠ ⌡ d k 2 D⋅ 2 2 0 D z k z⋅ 1+ε z⋅ ⌠ ⌡ d e sviluppando k 1 2 k⋅ D2⋅ε2 ln 1 1−ε D⋅ −ε D⋅ ⋅ := k 2 2 k⋅ D2⋅ε2 ln 1 1+ε D⋅ + ε D⋅ ⋅ :=
Come valore medio di rigidezza del sistema lineare equivalente, che oscilla intorno alla posizione di equilibrio, si può assumere la media di k1 e k2:
k k D2⋅ε2 ln 1 1−ε2⋅D2 ⋅ := (40)
e quindi il rapporto fra la pulsazione del sistema equivalente e del sistema effettivo è: ω2 ω o2 1 D2⋅ε2 ln 1 1−D2⋅ε2 ⋅ (41)
Se assumiamo ancora costante la velocità spettrale Sv(T,ξ), che si verifica nel campo dei periodi intermedi, oppure si trascura la variazione dovuta alla differenza fra ω e ωo, si ha:
S v D o ω o⋅ D⋅ω da cui D o2 D2 ω2 ω o2 (42) Introducendo la 41 nella 42: D o2 D2 1 D2⋅ε2 ln 1 1−D2⋅ε2 ⋅
che fornisce lo spostamento massimo effettivo dell’estremo dello strallo:
D e D o2⋅ε2 1 − ε2eD o 2⋅ε2 ⋅ := (43)
Infine, il valore della pulsazione effettiva sarà:
ω D o D ⋅ω o :=
(44)
L’applicazione del metodo, in modo iterativo, era agevole per le antenne strallate ed i camini degli impianti industriali con un solo ordine di stralli, soggetti all’azione sismica. Nondimeno, si poteva studiare il comportamento di strutture alte a più ordini di stralli impostando semplici routine sui calcolatori. Considerando, ad esempio, la ciminiera strallata di figura 15, si adottava un modello a due gradi di libertà costituito dai due oscillatori singoli: il fusto dell’antenna e il complesso dei cavi (fig. 16).
Il primo passo era dunque quello di risolvere il problema dinamico lineare del modello di figura 16.
Figura 15 – Struttura tipica per la quale veniva largamente impiegato il metodo iterativo per il calcolo dinamico esposto.
La risoluzione del sistema delle due equazioni di moto agli autovalori, necessita la conoscenza delle pulsazioni dei sistemi isolati (asta e stralli) per il primo modo di vibrare, rispettivamente ω1 e ω2.
Figura 16 - Modello dell'oscillatore riferito allo schema di figura 15. m1= massa dell’antenna; k1= rigidezza dell’antenna; m2=massa complesso stralli; k2=rigidezza stralli.
L’asta si schematizza come una trave appoggiata alla base e all’ancoraggio degli stralli: si determina ω1.
Per quanto riguarda ω2, che rappresenta la pulsazione del complesso degli stralli in regime lineare, occorre prima determinare la rigidezza k del singolo strallo con la prima e la seconda delle 33. La rigidezza k2 del complesso di stralli, per sollecitazione nel piano orizzontale al livello dell’ancoraggio, dipenderà dalla disposizione in pianta e dall’inclinazione sull’orizzontale. A questo punto si calcola:
ω 2 k 2 m 2 := ω 12 ω 1 m 1 m 2 ⋅ :=
Con questi coefficienti è possibile risolvere l’equazione caratteristica del sistema: si ricavano gli autovalori, si calcolano i corrispondenti autovettori e quindi i coefficienti di partecipazione. Si ottengono così le equazioni disaccoppiate di moto in coordinate principali, le cui soluzioni sono fornite direttamente dallo spettro di risposta del terremoto di progetto. Si usa poi la composizione dei modi per determinare lo spostamento massimo della sommità e dell’ancoraggio degli stralli.
Questi valori devono essere corretti per tener conto degli effetti non lineari. A tal fine si calcola con la 43 lo spostamento effettivo D, funzione di ε e dello spostamento lineare Do. Quindi, con la 44, la pulsazione ω2’ del sistema di stralli.
Con questa si ripercorre il procedimento risolutivo per una seconda volta ottenendo, alla fine, ω2’’ e così via. L’iter si arresta quando si ottengono due valori consecutivi dello spostamento D simili fra loro.
Il metodo mette in luce la notevole influenza del comportamento non lineare degli stralli: si ottengono spostamenti in sommità ridotti del 35% circa rispetto al caso lineare; lo sforzo assiale massimo che sollecita lo strallo si riduce del 50% e anche di più, durante le varie iterazioni, rispetto al valore iniziale. L’applicazione del metodo a vari casi sperimentali portò alla consapevolezza che gli effetti di non linearità dovuti alla presenza degli stralli erano tanto più accentuati quanto minore era la pretensione delle funi; inoltre, se venivano trascurati nell’analisi dinamica, portavano ad una sopravvalutazione delle deformazioni e delle sollecitazioni a favore di sicurezza. Tale sicurezza, però, era eccessiva e portava ad errori rilevanti nel calcolo dei carichi di collasso di una struttura strallata.
3.5 L’interazione dinamica vento-struttura: un metodo di simulazione numerica applicato alle antenne strallate
Nella maggior parte dei casi, basta guardare le disposizioni normative dei vari paesi, le azioni indotte dal vento sulle strutture si calcolano facendo riferimento alla pressione cinetica prodotta dal massimo valore della velocità media del vento, prevedibile nella vita utile della struttura. Questo modo di procedere è adatto alla maggior parte delle strutture civili di forma regolare aventi certi limiti di sviluppo sia in altezza che in luce: la loro deformabilità è limitata e non interagisce con l’azione del vento di carattere aleatorio e impulsivo.
Esistono però alcune classi di strutture per le quali un tale modo di procedere risulta inadeguato per coglierne il comportamento: stiamo parlando dei ponti sospesi, delle antenne strallate, strutture in genere molto flessibili. Prova ne sono i numerosi insuccessi, alcuni dei quali hanno fatto “storia” come il crollo delle antenne strallate cilindriche in Inghilterra (vedi cap. II) o il crollo del Tracoma Narrows Bridge.
Questi fatti hanno portato l’attenzione degli ingegneri su questo settore sviluppando, dagli anni ’70, numerose ricerche per mettere a punto dei criteri progettuali in grado di cogliere gli effetti dinamici del vento. Di seguito si espone un metodo di simulazione numerica adottato in Italia dalla seconda metà degli anni ’80, grazie anche all’uso corrente dei calcolatori programmabili (alcune formulazioni si trovano riprese negli odierni Eurocodici).
3.5.1 Il vento di progetto e le forze aerodinamiche
Nonostante la sua natura fortemente aleatoria, ai fini dell’analisi strutturale si può rappresentare il vento come un flusso omogeneo ed unidirezionale di aria avente velocità:
V tot t() V v t():= +
(45)
in cui:
v(t) fluttuazione della velocità.
La fluttuazione della velocità è considerata come un evento stocastico a valore medio nullo. Nel seguito si trascurano gli effetti prodotti dalle forze aerodinamiche agenti perpendicolarmente alla direzione del flusso principale (quello che investe la struttura) ed eventuali fenomeni di instabilità aerodinamica sugli stralli.
Si indagherà invece sugli effetti prodotti dalle forze aerodinamiche agenti nella direzione del flusso medio, dette “drag forces”, che possono essere valutate con la seguente relazione: F t( ) 0.5⋅ C Dρ⋅ ⋅ U tot t()A⋅ 2 π 4⋅ C Mρ⋅ ⋅ bA⋅ tU tot t() d d ⋅ + := (46) nella quale:
A area della superficie investita;
b profondità della struttura in direzione del flusso medio; ρ densità dell’aria;
CD coefficiente di resistenza aerodinamica; CM coefficiente di “massa virtuale”;
U tot t() Vtot t() Vst t():= −
velocità relativa vento-struttura; con Vst = velocità del punto della struttura investito dal vento.
Il dato di partenza che dobbiamo conoscere per poter svolgere la simulazione deve essere la storia delle velocità del vento; dall’equazione 45 si vede che l’effetto di Vtot(t) può essere scomposto nelle componenti V e v(t), studiandole separatamente.
Per quanto riguarda la V si considera un valore mediato su un dato intervallo di tempo ed avente periodo di ritorno compatibile con la vita utile dell’opera; in genere si sceglie un tempo di ritorno di 50 anni. Tale valore può essere determinato con elaborazioni statistiche partendo dai dati di ventosità della zona di interesse. Così si determina la velocità media di riferimento ad una certa quota; per conoscerne il valore ad una quota qualsiasi, si assegna una
legge di variazione con l’altezza: le numerose esperienze in letteratura dimostrano che è accettabile una legge logaritmica o esponenziale.
La storia delle fluttuazioni della velocità del vento v(t) viene studiata considerandola come processo stocastico stazionario a media nulla; le funzioni che definiscono un processo del genere sono riportate di seguito.
a) Spettro Sv(n)
Rappresenta il contenuto energetico della generica frequenza n del processo. Per descrivere lo spettro delle fluttuazioni della velocità del vento vari autori hanno proposto diversi modelli fra cui si ricorda:
“Modello di Davenport” n S v n⋅ ( ) k V 10⋅ 2 4 x 2 1+ x2
(
)
4 3 ⋅ (47) x 1200 n⋅ V 10 := dove:k coefficiente di rugosità del sito; V10 velocità media a 10 m dal suolo; “Modello di Kaimal” n S v n⋅ ( ) V k2 200 x⋅ 1+ 50 x⋅ ( ) 5 3 (48) x n z⋅ V z( ) := V k2 k V 10⋅ 2 dove:
V(z) velocità media alla quota z. b) Autocorrelazione Rv(τ)
Fornisce informazioni sul legame che c’è fra i valori della funzione v(t) (fluttuazione di velocità) calcolata all’istante t e a (t + τ). Per avere un’idea del suo significato, basti pensare che per τ = 0 l’autocorrelazione coincide con la
varianza del processo. La funzione di autocorrelazione per v(t) può essere ricondotta alla seguente espressione:
R v τ
( )
e τ θ − ⋅σ v2 := (49) θ A V 10 := dove:A costante che assume il valore 151,29 m; σv2 varianza del processo v(t).
c) Cross-Spettro Sv1v2(r,n)
Siano P1(y1;z1) e P2(y2;z2) due punti appartenenti ad un piano (y;z) ortogonale al flusso medio del vento e distanti r l’uno dall’altro; siano v1(t) e v2(t) le fluttuazioni di velocità nei due punti. Si definisce cross-spettro di v1(t) e v2(t) la seguente funzione: S v1v2 r n( , ):= S v1 n( ) S v2 n⋅ ( )⋅e−f (50) dove: f n Cz z1 z2
(
−)
2 ⋅ +Cy y1 y2⋅(
−)
2 Vz12+ Vz22 ⋅ := r:=(
y 2 y 1−)
2+(
z 2 z 1−)
2 e di solito si assume Cy = 16 e Cz = 10.Questa funzione non ha un significato fisico concreto. d) Cross-Correlazione Rv1v2(τ)
Fornisce una quantificazione del rapporto esistente fra v1(t) e v2(t + τ) nei punti P1e P2. In particolare è di interesse la cross-correlazione per τ = 0 perché ci dà informazione sulla contemporaneità della fluttuazione nei due punti. Fra le varie espressioni proposte si sceglie:
R v1v2 0( ) e r β − (51) β V M c f 1⋅ := in cui:
VM è la media delle velocità medie nei punti P1 e P2; r come detto, la distanza fra i due punti;
c il coefficiente di decadimento esponenziale (compreso fra 7 e 8); f1 frequenza del primo modo di vibrare;
oppure R v1v2 0( ) e r λ − (52) λ V M θ⋅ 2 := θ A V 10 := e) Distribuzione di probabilità W(v)
Con buona approssimazione si ritiene valida, per i dati di vento, la distribuzione di densità di probabilità di Gauss:
W v( ) 1 2⋅ σ vπ⋅ e v t( ) V− ( )2 2⋅σ v2 − ⋅ := (53)
3.5.2 Metodi di analisi della risposta strutturale: analisi nel dominio delle frequenze e nel dominio del tempo
Qualsiasi metodo che si propone di studiare gli effetti dinamici del vento su una struttura, ha come obbiettivo quello di trovare una forza di progetto da applicare ad essa, espressa nel seguente modo:
F prog K F stat:= ⋅
In questa:
K è il fattore di raffica della risposta (gust response factor, G.R.F.);
Fstat è la forza che produce, in condizioni statiche, gli stessi effetti del flusso d’aria avente velocità costante pari a V, media del processo V(t).
L’incognita di questo problema è il parametro K (o G.R.F.). Si possono condurre due tipi di analisi:
1) analisi nel dominio delle frequenze (frequency domain, F.D.); 2) analisi nel dominio del tempo (time domain, T.D.)
Quando si opera in F.D., utilizzando certe informazioni di natura probabilistica sulla v(t), si determina dapprima lo spettro della forza aerodinamica, poi lo spettro di risposta della struttura ed infine il G.R.F. In generale i metodi che fanno uso di questo procedimento comportano la necessità di linearizzare i vari passaggi, talvolta introducendo semplificazioni non accettabili; evitare la semplificazione conduce a complicare notevolmente il procedimento dal punto di vista del calcolo.
Operando invece in T.D. si deve costruire una time history del vento che abbia le stesse proprietà del vento di progetto (spettro, velocità media, correlazione, densità di probabilità). Da questa si determina la corrispondente time history delle forze aerodinamiche e della risposta della struttura; tramite un’analisi statistica di quest’ ultima si calcola infine il G.R.F. Il procedimento non subisce complicazioni di calcolo se in alcune fasi si introducono relazioni non lineari; è per questo che è più utilizzato rispetto all’analisi nel dominio delle frequenze.
3.5.3 Analisi nel dominio delle frequenze
Per semplicità di esposizione vediamo come si studiano gli effetti dinamici del vento schematizzando una struttura come un oscillatore semplice:
Figura 17 - Oscillatore semplice.
Fissiamo le seguenti ipotesi:
- la forza media prodotta dal flusso di aria sia uguale alla forza prodotta in condizioni statiche dalla sola V;
- le fluttuazioni della forza siano legate alle fluttuazioni della velocità con legame lineare, cioè: la componente fluttuante v(t) è piccola rispetto a V; sia trascurabile il secondo addendo a destra della formula 46; sia trascurabile la velocità della struttura.
Conoscendo al velocità media e le fluttuazioni di velocità del vento nel punto in cui si è concentrata la massa, lo spettro delle forze aerodinamiche è ricavabile da: n S f n⋅ ( ) F2 4 n⋅ S v n⋅ ( ) V2 (55) in cui:
Sf(n) è lo spettro delle forze aerodinamiche; F è la forza media.
Quindi, nelle ipotesi di struttura a comportamento elastico lineare e di equazione di moto lineare a coefficienti costanti, si dimostra che lo spettro di risposta è dato da:
n S y n⋅ ( ) Y2 4⋅χ m n( )2 n S f n⋅ ( ) F2 ⋅ ⋅χ a n( )2 (56) dove:
Sy(n) è lo spettro della risposta della struttura; Y è la risposta media;
χm(n) è la funzione di ammettenza meccanica;
χa(n) è la funzione di ammettenza aerodinamica, che di solito si considera pari ad 1 per le antenne strallate.
Ottenuto lo spettro di risposta della struttura si determina il fattore di raffica nel seguente modo: GRF 1 k σ y Y ⋅ + := (57) con: k 2 ln n o T⋅
(
⋅)
0.57 2 ln n o T⋅(
⋅)
+ σ y2 Y2 π n o⋅ ⋅S v n o( )
β V⋅ 2 in cui:no è la frequenza fondamentale della struttura; β è lo smorzamento.
Questo metodo di analisi risulta preferibile per quelle strutture che meglio si assimilano ad oscillatori semplici come ad esempio i serbatoi pensili o le torri porta fari in cui la massa in gioco è schematizzabile come concentrata in un solo punto (fig. 18).
(a) (b)
Per i sistemi a più gradi di libertà le fasi da sviluppare sono le stesse e le relazioni che si ottengono sono simili alle precedenti; in figura 19 si ricapitolano i passi dell’analisi nel dominio delle frequenze.
Figura 19
3.5.4 Analisi nel dominio del tempo
Questo modo di procedere risulta particolarmente adatto allo studio delle alte antenne strallate in quanto prevede la discretizzazione della struttura in un certo numero di punti caratteristici dove vengono concentrate le masse (fig. 20). La prima fase è quella di generare le time histories delle velocità del vento agenti sulle N masse; al solito vanno assegnate le caratteristiche dello spettro, della correlazione, della distribuzione di probabilità del vento di progetto.
Figura 20 – Antenna strallata: schema e modello relativo per l’analisi nel dominio del tempo. 3.5.4.a) Generazione delle time histories della fluttuazione di velocità v(t)
Il metodo si basa sull’assunto che due funzioni fra loro correlate, hanno per somma una funzione il cui spettro è dato dalla somma degli spettri delle
funzioni addende. Tramite l’algoritmo seguente si generano N time histories del tipo: u i t() 1 L j 2 S i n j⋅
( )
⋅∆n j⋅cos 2(
⋅ n jπ⋅ ⋅t+ ψ ji)
∑
= := (58) dove:L è il numero di parti in cui è stato suddiviso lo spettro nell’intervallo si frequenza considerato: (nult - nin)/∆n;
nj sono i valori della frequenza nei punti centrali degli intervalli sopra definiti;
ψij sono valori casuali, distribuiti uniformemente fra 0 e 2π.
Le T.H. così generate risultano scorrelate fra loro poiché non abbiamo imposto nessuna condizione che le leghi.
Per stabilire un legame, si determinano altrettante N time histories aventi una matrice di correlazione Rij = Rwiwj(0) prefissata in modo che risulti:
w i t() 1 L j C ij n j t()⋅
∑
= := (59)Se D è la matrice di correlazione delle ui(t), che sarà diagonale, essendo le storie fra loro scorrelate, si dimostra che i coefficienti Cij della 59 sono dati da:
C ii R ii σ u2 1 i 1− k C ik
∑
= − := C ij R ij σ u2⋅C jj 1 j 1− k C ik C jk⋅ C jj∑
= − :=Se gli N punti in cui si considerano concentrate le masse sono alla stessa quota, la i-esima storia della velocità totale è data da:
V i t() Vi w i t():= +
(60)
in cui wi(t) è la componente fluttuante definita nella 45 con vi(t).
Quando gli N punti sono a quote diverse (caso delle antenne strallate) oppure lo spettro che vogliamo imporre varia in funzione della quota, il procedimento esposto sopra subisce le modifiche seguenti.
Tramite la 58 si generano le N time histories ui(t) ma, anziché considerare lo spettro effettivo Si(n), si introduce lo spettro S(n) così ottenuto:
S(n) = min { Si(n) } ; i = 1,2,..,N
Allo stesso modo si correlano le ui(t) applicando la 59.
A questo punto, sempre con la 58, si generano altre N time histories εi(t) il cui spettro sia dato dalla differenza fra lo spettro di progetto in ogni punto e lo spettro minimo:
S εi n( ):=S i n( ) −S n( )
Essendo le εi(t) scorrelate fra loro, si possono sommare alle wi(t) ottenute con la 59 senza che venga alterata la matrice di correlazione imposta. In questo caso la 60 diventa:
V i t() Vi w i t():= + +ε i t()
(61)
in cui la fluttuazione di velocità indicata con vi(t) nella 45 è data da:
v i t() w i t() ε i t():= +
Questo metodo, benché sia di facile applicazione e risponda bene ai problemi derivanti dal vento nell’ingegneria civile, non è del tutto esente da difficoltà applicative. Se ne riportano alcune, senza addentrarci troppo nei dettagli.
In primo luogo, se si considera lo spettro a partire da nin = 0 Hz si ottiene un valore della varianza delle time histories generate diverso dall’integrale dello spettro stesso. Si è visto che per diminuire questa differenza è bene considerare nin = (1,5 ÷ 2)⋅T , essendo T il periodo di campionamento.
Nel caso delle masse poste a quote diverse i due insiemi di time histories ui(t) ed εi(t) non sono effettivamente scorrelati al loro interno, come invece si suppone all’inizio del metodo. Ciò non può essere evitato a meno di ricorrere a modifiche delle matrici di correlazione che comunque portano ad approssimazioni; inoltre le εi(t) portano un contributo più piccolo rispetto alle ui(t) quindi si possono accettare i valori così come sono.
Quando si fa la somma delle wi(t) con le εi(t) i termini diagonali della matrice Rw+ε sono diversi da quelli della matrice R risultando così alterata nuovamente
la varianza. Per diminuire questa incongruenza si può determinare le fluttuazioni εi(t), anziché con la 58, con:
ε i t() 1 L j 2 S i n j⋅
( )
⋅∆n j− 2 S n j⋅( )
⋅∆n j(
)
⋅cos 2(
⋅ n jπ⋅ ⋅t+ψ ij)
∑
= := (58’)Nelle varie calibrazioni del metodo si è comunque registrato che un aumento del grado di correlazione, benché in contrasto con le ipotesi iniziali, porta, nelle applicazioni pratiche, ad operare a favore di sicurezza.
3.5.4.b) Calcolo delle time histories della forza aerodinamica F(t)
Una volta che sono state costruite le storie della velocità totale del vento secondo la formula 45, si possono determinare le storie della forza aerodinamica applicando la:
F t( ) 0.5⋅ C Dρ⋅ ⋅ U tot t()A⋅ 2 π 4⋅ C Mρ⋅ ⋅ bA⋅ tU tot t() d d ⋅ + := (46)
per ogni punto in cui è stata concentrata la massa della struttura o porzione di essa. Si ricorda che Utot(t) = Vtot(t) – Vst(t) con Vst velocità della struttura. A seconda dei casi è possibile scegliere se:
- applicare la 46 nella sua forma completa;
- trascurare il secondo addendo a secondo membro (termine di massa virtuale);
- considerare la velocità assoluta anziché quella relativa, ipotesi accettabile per le costruzioni poco deformabili (per conformazione o con limiti imposti);
- trascurare i termini di fluttuazione v(t)2 .
3.5.4.c) Determinazione delle time histories della risposta strutturale y(t)
Note le storie F(t) della forza aerodinamica applicata nelle varie masse, si indichi con y la direzione di applicazione di tali forze. Le storie y(t) della risposta strutturale si calcolano integrando il sistema di equazioni differenziali del moto:
m i 2 t y i t() d d 2 ⋅ c ty i t() d d ⋅ + + k i y i t()⋅ F i t() (62) ; i = 1,2,..,N in cui:
mi massa applicata nel nodo i-esimo;
c coefficiente di smorzamento della struttura;
ki rigidezza alla traslazione lungo y nel nodo i-esimo; yi spostamento del nodo i-esimo.
Il prossimo passo sarà quello di analizzare statisticamente le storie della risposta per poter calcolare il fattore di raffica G.R.F.
Nella figura seguente è riportato lo schema riassuntivo delle operazioni da compiere quando si vuole procedere all’analisi nel dominio del tempo.
Figura 21
3.5.5 Metodi per determinare il picco di risposta della struttura
Quando si deve determinare il valore di picco di un processo casuale, il problema deve essere così impostato: innanzi tutto si considera un insieme di eventi che descrivono il processo in esame, poi si formano dei campioni contenenti un numero prefissato di eventi, quindi si determina la funzione distribuzione di probabilità dei valori massimi. All’interno di queste distribuzioni si fissa un criterio per scegliere il valore di picco più appropriato. Se trasferiamo il problema alla ricerca del picco di risposta di una struttura sollecitata dall’azione del vento si devono definire i seguenti parametri:
- intervallo su cui devono essere calcolati i massimi; - distribuzione dei valori massimi;
- criterio di scelta del valore di picco.
a) si prendono i valori massimi calcolati su time histories della risposta strutturale generate da storie di velocità del vento con V = V50 e intervallo di campionamento pari a 10 minuti;
b) si assume che la distribuzione di probabilità cumulativa della risposta sia del tipo:
P x( ):=1−e−z x( )
con z(x) monotona quindi, supponendo i valori massimi fra loro staticamente indipendenti, la loro distribuzione di probabilità tende a quella di Gumbel: F x( ) e e α − −U ( ) − :=
dove α ed U sono parametri da determinare;
c) poiché questa distribuzione dei massimi ha forma abbastanza appuntita, si sceglie come valore di picco la moda della distribuzione.
In base a quanto visto si può decidere di applicare un procedimento rigoroso oppure uno dei metodi semplificati proposti al tempo.
Il calcolo esatto prevede i seguenti passi.
- conoscere un numero sufficientemente grande di time histories della risposta della durata di 10 minuti;
- per ogni time history calcolare il massimo;
- determinare la distribuzione di probabilità dei massimi modellando i dati secondo Gumbel;
- calcolare la moda della distribuzione di Gumbel.
Questo modo di procedere aveva il grande inconveniente di richiedere una grande mole di dati (le T.H.) che, simulate numericamente, richiedevano grande impegno di calcolo. Furono proposti allora alcuni procedimenti semplificati che permettevano di definire il picco di risposta a partire dalla conoscenza di una sola time history della durata di 10 minuti.
Il primo modo di procedere prevede la definizione di un periodo di campionamento T inferiore a 10 minuti; in ogni campione dell’unica time history nota, si considera il massimo della risposta (supponendo che questi
valori siano statisticamente indipendenti). Quindi si modellano questi massimi ottenendo la distribuzione secondo Gumbel; come valore di picco si assume quello che ha periodo di ritorno pari a 10 minuti. Fu dimostrato che i periodi di campionamento ideali erano:
T1 = 1 minuto; T2 = 10 secondi.
Il secondo metodo prevedeva di assumere come valore di picco della risposta direttamente il valore massimo che compariva nella time history considerata. Determinato con uno dei modi visti il picco della risposta ypicco si calcola il fattore di raffica così:
GRF y picco Y :=
(63)
dove Y è il valore medio della risposta strutturale.
Abbiamo visto che i metodi di indagine del comportamento delle strutture sensibili ai carichi da vento, nella fattispecie antenne strallate e serbatoi pensili, possono essere affrontati nel dominio delle frequenze o in quello del tempo. Dalle esperienze fatte in passato, risultò che entrambi i metodi davano risultati equivalenti in termini di risposta e quindi di G.R.F. Il carico computazionale aumenta in modo considerevole quando si operi nel dominio del tempo, data la necessità di sviluppare due fasi nelle quali sono necessarie delle integrazioni numeriche:
a) generazione di time histories aventi un certo grado di correlazione, tramite l’integrazione dello spettro in un campo di frequenze assegnato; b) calcolo delle time histories della risposta strutturale attraverso
l’integrazione delle equazioni di moto.
Tale modo di procedere fu applicato con successo alle antenne strallate perché permetteva una discretizzazione della struttura concentrando le masse in punti caratteristici. Questi punti erano i nodi di ancoraggio degli stralli e le mezzerie delle varie campate (fig. 20). Il calcolo della risposta veniva effettuato in modo iterativo a causa della non linearità geometrica del comportamento degli stralli
(vedi par. 3.4). L’azione di ritegno degli stralli veniva modellata inserendo delle molle ad asse orizzontale aventi una costante elastica determinata come visto nel paragrafo 3.2 e aggiornata ad ogni iterazione.
Il metodo esposto fu verificato e convalidato anche sperimentalmente su un modello di antenna strallata di 40 m con doppio ordine di stralli; tale struttura era usata come modello in scala per studi su antenne di altezza molto maggiore.
3.6 L’azione del vento sugli stralli: influenza sul comportamento non lineare delle antenne strallate
Fino ad ora abbiamo trattato il comportamento sotto l’azione del vento di un’antenna strallata senza mai considerare l’effetto del vento sugli stralli. Nella letteratura del tempo questo effetto veniva sempre trascurato ma, grazie all’avvento del calcolo automatico, furono messe a punto procedure che non trascuravano questa influenza sul comportamento globale della struttura. Ci si rese conto che, da un lato, il comportamento dello strallo forniva maggiore rigidezza all’insieme stralli e antenna diminuendo gli spostamenti e, dall’altro, che lo strallo sottovento poteva diminuire la sua tensione e lavorare in zone pericolose dal punto di vista dinamico.
Ricordiamo che i contributi fondamentali al comportamento non lineare di un’antenna strallata sono di due tipi:
a) non linearità dovuta ai grandi spostamenti che interessano gli stralli e che si ritrova nel comportamento non lineare degli appoggi elastici (ai quali viene assimilata l’azione di ritegno degli stralli);
b) non linearità dovuta ai grandi spostamenti dell’antenna con conseguente eccentricità dei carichi assiali concentrati e distribuiti.
Come visto nel paragrafo 3.2 l’analisi statica di un’antenna strallata viene fatta considerando che, sotto il carico vento massimo, la deformata della struttura mantenga allineati in punti di attacco degli stralli. In questa situazione il comportamento è quello di trave continua su appoggi elasticamente cedevoli ed è quindi agevole trovare le reazioni Ri che il sistema degli stralli fornisce all’antenna. Si impone poi la congruenza degli spostamenti del sistema
antenna-stralli oppure si impongono limitazioni di esercizio agli spostamenti dettate dalla funzionalità delle antenne installate in sommità o lungo lo sviluppo della struttura. A titolo di esempio l’inclinazione massima ammissibile per le antenne trasmittenti è:
θ 20λ l ⋅ :=
dove λ è la lunghezza d’onda del segnale trasmesso ed l è l’altezza a cui è posta l’antenna (il risultato è in gradi sessagesimali).
Consideriamo, per semplicità di esposizione, che l’azione del vento solleciti il piano di giacenza di due stralli opposti, l’uno sopravento l’altro sottovento (fig. 22).
Una volta fissate l’inclinazione massima dell’antenna e le reazioni Ri dei punti di attacco degli stralli si deve risolvere il seguente problema: trovare la pretensione e l’area Aci degli stralli concorrenti nell’attacco i-esimo in modo che il punto di attacco stesso si sposti di δi sotto l’azione di Ri.
Figura 22 - Schematizzazione del sistema degli stralli e dell’antenna.
Per effettuare un dimensionamento di massima, così da avere i dati di partenza per affinare il calcolo, si usavano le formule seguenti. Per trovare Aci e To,i negli stralli di un certo ordine si impone l’equilibrio di ogni singolo ancoraggio alla traslazione orizzontale:
R i Ac i cos ε i:= ⋅
( )
⋅(
σ i1 σ i2−)
nella quale Aci è l’area della fune (supponendo tutte uguali le funi dello stesso ordine), σi1 e σi2 sono rispettivamente le tensioni nello strallo sopravento ed in quello sottovento, εi è l’inclinazione della corda rispetto all’orizzontale. Si ricorda che la presente è stata ricavata sotto l’ipotesi di piccoli spostamenti in modo che l’angolo della fune con l’orizzontale sia pressoché lo stesso prima e dopo la deformazione e si possa confondere tale inclinazione con quella della corda corrispondente.
Dalla 64 si ricava Aci ipotizzando un valore per la differenza di tensione tra i due stralli di:
σ i1 σ i2−
(
)
0.7⋅σ admcon σadm la tensione ammissibile per la fune. Si pone poi:
To,i = (0,4÷0,5) Aci σadm
in modo da avere questi due valori: σi1 = (0,75÷0,85) σadm < σadm σi2 = (0,05÷0,15) σadm > 0
e ciò permette di scongiurare, in prima approssimazione, che lo strallo sottovento perda tutta la sua pretensione iniziale ovvero che quello sopravento superi la tensione ammissibile.
3.6.1 Metodo tradizionale di risoluzione dello strallo
Si richiamano brevemente alcuni aspetti del modo di procedere nella risoluzione classica del sistema di stralli, ampiamente descritta nel paragrafo 3.2, mettendo in evidenza i limiti del procedimento.
Nell’ipotesi di avere un solo strallo di peso totale Q (fig. 23), ancorato ad estremi posti a diversi livelli, l’equazione che lega lo spostamento orizzontale dell’ancoraggio di sommità e la tensione nello strallo è:
δ Q 2 a ⋅ 24 Ac⋅ 1 σ o2 1 σ2 − ⋅ l E st cos ε⋅
( )
⋅(
σ σ o−)
+ := (65)nella quale:
δ spostamento orizzontale in sommità; σo pre-tensione dello strallo;
ε inclinazione della corda con l’orizzontale; Est modulo di elasticità equivalente della fune.
L’equazione 65 evidenzia la non linearità del legame fra gli spostamenti e le tensioni, cosicché a spostamenti uguali, ma di senso opposto, si hanno variazioni di tensione diverse (rispetto alla pre-tensione iniziale).
Figura 23 - Schema dello strallo senza considerare l'azione del vento su esso.
Il procedimento iterativo che porta alla soluzione di un sistema di stralli per un’antenna strallata, consiste nel variare la pre-tensione e l’area Ac in modo che in corrispondenza della differenza (σ1-σ2) voluta, si abbia lo spostamento δ* imposto (o congruente per l’ordine di stralli considerato) (fig. 24).
Le critiche che venivano poste al procedimento sopra descritto erano:
1) scarsa possibilità di automatizzazione, infatti si faceva strada l’uso dei calcolatori programmabili quindi servivano istruzioni da poter convertire in linguaggio informatico (Fortrand, Mathlab, C++);
2) non si tiene conto in alcun modo della presenza del vento sul sistema di stralli (ovviamente, se ne tiene consto sul sistema antenna);
3) l’equazione 65 non converge sul limite inferiore della tensione nello strallo sottovento quindi non fornisce un valore concreto.
3.6.2 La soluzione in ambito non lineare tenendo conto dell’influenza del vento sullo strallo
Si illustra adesso il metodo di calcolo proposto alla fine degli anni ’80 da alcuni Autori che permette di modellare il comportamento dello strallo sotto l’azione del peso proprio, di un’eventuale guaina di ghiaccio e dell’azione del vento, nonché di determinare la configurazione deformata. Si cerca anche di individuare un valore minimo delle tensioni, tenendo conto del comportamento dinamico dello strallo, per cui si ha la disattivazione dello stesso che può portare la struttura in una zona di comportamento pericolosa.
Lo strallo, nella configurazione deformata, viene schematizzato come nella figura seguente: