4. Il piano delle prove

4. Il piano delle prove

4.1 Premessa

In questo capitolo verrà impostato il piano delle prove di asportazione laser su PMMA per il conseguimento dell’obiettivo preposto, ovvero la realizzazione di cavità di forma complessa. Il concetto fondamentale legato a questo studio di fattibilità consiste nella scomposizione di strutture tridimensionali complesse in parallelepipedi di sezione variabile ed altezza corrispondente ad una profondità di asportazione nota.

Tutti i modelli proposti di seguito, necessari per prevedere, in base alle conoscenze in possesso, i valori delle grandezze in analisi, verranno successivamente verificati attraverso la misura e l’interpolazione dei dati sperimentali ottenuti attraverso il processo di asportazione laser.

In questo modo, partendo dall’analisi di tre parametri (potenza della radiazione incidente, velocità di scansione e distanza focale) si perfeziona progressivamente la tecnica di asportazione ampliando il modello attraverso l’analisi di nuovi parametri influenti nel processo come il passo di scansione e l’orientamento della direzione di scansione.

4.2 Impostazione del piano delle prove

L’obiettivo dell’asportazione mediante vaporizzazione laser, su PMMA, è quello di ricavare, all’interno di questo particolare polimero, impronte tridimensionali la cui complessa morfologia rende inapplicabili tecniche convenzionali di sottrazione di materiale, come ad esempio la lavorazione alle macchine utensili.

La realizzazione di strutture tridimensionali complesse (schematizzata in fig.4.1) avviene per asportazione progressiva, strato dopo strato, all’interno del blocco di PMMA; la profondità di asportazione (D) corrispondente ad una determinata combinazione dei parametri influenti nel processo, corrisponde allo spostamento verso l’alto, da imporre alla piattaforma, in modo da riportare la superficie ottenuta attraverso la precedente vaporizzazione, alla corretta distanza focale. Attraverso la scansione di una superficie si ottiene quindi l’asportazione di uno strato avente come spessore la profondità di penetrazione della radiazione luminosa. Dato che i movimenti del fascio sono controllati dalle rotazioni degli specchi galvanometrici, il metodo

più veloce per ottenere la scansione di una superficie, con la conseguente asportazione di uno strato di materiale, si realizza attraverso l’accostamento di tracce rettilinee.

D

+D

Fig.4.1 Schema di asportazione strato per strato

La traccia rettilinea rappresenta, dunque, l’unità di base ripetendo la quale si riesce a provocare un’asportazione selettiva di uno strato. La conoscenza del tasso di asportazione monodirezionale è, quindi, una nozione fondamentale senza la quale non si può accedere a procedimenti più complessi con il dovuto rigore scientifico.

La prima fase del piano delle prove consisterà dunque, nello sviluppare un modello affidabile che consenta di prevedere il tasso di asportazione caratteristico di una traccia rettilinea ricavata su di una delle quattro facce disponibili del blocchetto di PMMA. La geometria dell’impronta lasciata dal laser, è caratterizzata da un profilo complesso su cui influiscono diversi parametri di processo, tra cui:

• potenza associata alla radiazione incidente (Pin);

• velocità di scansione (v); • distanza focale (f);

• TEM caratteristico del fascio;

• caratteristiche termofisiche del materiale.

Quando la radiazione colpisce il materiale, causa una vaporizzazione del PMMA proporzionale alla densità di potenza locale, generando un’impronta il cui profilo segue quello della

distribuzione dell’energia del fascio all’interno di una sezione perpendicolare all’asse di propagazione (ovvero il TEM del fascio).

Come sarà chiarito in seguito, il profilo della traccia è caratterizzato da due grandezze fondamentali, la profondità D (Depth) e la larghezza W (Width), che consentono di approssimare la forma complessa dell’impronta come un triangolo.

W

D

Fig.4.2 Profilo di una traccia singola (f=200mm, Pin=20W e v=25mm/s)

Una volta elaborato il modello, i dati teorici verranno confrontati con quelli ottenuti mediante il processo di asportazione laser. Per misurare le dimensioni caratteristiche della traccia ottenuta verrà utilizzato un proiettore di profili con un ingrandimento pari a 20 volte il valore effettivo. Le nozioni acquisite nel caso dell’asportazione monodirezionale saranno, in seguito, impiegate con l’obiettivo di realizzare l’asportazione di superfici mediante l’accostamento di più tracce rettilinee. Si analizzerà l’influenza del passo di scansione, ovvero della distanza tra due tracce singole consecutive, cercando di ottimizzare il grado di finitura superficiale mantenendo, contemporaneamente un sufficiente tasso di asportazione.

Seguendo questo proposito si dovrà verificare se esiste una corrispondenza tra il modello teorico, che si fonda sulla sovrapposizione geometrica dei profili delle singole tracce (come si evince dalla fig.4.3), e l’effetto reale dovuto a più scansioni rettilinee consecutive; non si può infatti, trascurare il fatto che le asportazioni successive non costituiscono una pura ripetizione della medesima asportazione lineare in quanto le condizioni al contorno in termini di temperatura del materiale ed uniformità della superficie colpita, cambiano in modo significativo con l’aumentare delle passate.

D

R

T

Fig.4.3 Realizzazione di una superficie passante

L’influenza del passo di scansione sulle due necessità contrastanti rappresentate da finitura superficiale e tasso di asportazione, verrà dunque, analizzato prendendo in esame i dati sperimentali ottenuti con una seconda campagna di prove; la profondità di asportazione generata dalla scansione di una superficie ottenuta con il metodo di sovrapposizione di tracce lineari, saranno misurate con il medesimo proiettore di profili mentre la morfologia della zona lavorata sarà analizzata dapprima tramite un sistema di visione, basato sull’utilizzo di una telecamera con ingrandimento di 50x, e successivamente con un rugosimetro, al fine di misurare in modo preciso il grado di finitura della superficie ottenuta.

1° strato,scansione 0°

2° strato,scansione 90°

4° strato,scansione 90° 3° strato,scansione 0°

Una volta determinata la combinazione dei parametri di processo che fornisce un soddisfacente tasso di asportazione garantendo, parimenti, valori accettabili della rugosità superficiale, si procederà alla vaporizzazione di più strati successivi analizzando l’effetto della sovrapposizione di scansioni ottenute cambiando l’orientamento delle tracce che costituiscono ogni singolo strato, come mostrato in fig.4.4 . Gli eventuali miglioramenti attesi, in termini di grado di finitura della superficie, dovranno essere verificati misurando con il rugosimetro le superfici ottenute con la nuova serie di test effettuata. Dovrà essere dimostrata, inoltre, la corrispondenza lineare tra la profondità di asportazione raggiunta ed il numero di passate con il quale è stata ottenuta.

4.3 Traccia singola

Quando il raggio laser focalizzato colpisce la superficie del materiale la temperatura della area colpita aumenta così rapidamente da portare il PMMA prima a fusione ed in seguito alla decomposizione, lasciando una caratteristica impronta sul pezzo; il meccanismo di decomposizione dipende strettamente dall’energia dei legami chimici dei monomeri di MMA che costituiscono la catena polimerica e dalla struttura stessa del polimero (termoplastico ed amorfo). Il fatto che il PMMA vaporizzi in forma di monomero quando viene raggiunta la sua temperatura di ebollizione, consente di ottenere delle impronte che non sono contaminate dai prodotti di degradazione chimica; a questo effetto positivo è però associato lo svantaggio di una ottima solubilità tra il vapore di monomero e le zone del polimero in cui si è oltrepassata la temperatura di transizione vetrosa (rammollimento). A tale inconveniente si supplisce con il sistema di aspirazione, descritto nel par. 3.2.3 .

Quando il fascio laser si muove lungo una traiettoria rettilinea, l’azione dinamica dovuta allo spostamento consente di espellere con maggior facilità la minima frazione di materiale fuso che tenderebbe a risolidificarsi sui bordi dell’impronta; la maggior parte del liquido, invece, vaporizza istantaneamente trasformandosi nel monomero volatile, la cui propagazione avverrebbe in modo random in tutte le direzioni se non fosse forzata dall’azione della bocca di aspirazione.

Il profilo della traccia dipende dalla diffusività termica del pezzo, ovvero dalla velocità con la quale il calore si disperde all’interno del materiale, e dalla distribuzione spaziale dell’energia associata alla radiazione. Poiché la diffusività termica dei materiali polimerici è molto bassa, il parametro che più influenza il profilo della traccia è il TEM del laser. Nel par.3.2.1.1 è stato

osservato che il Tranverse Electromagnetic Mode caratteristico del laser SYNRAD, è assimilabile ad un profilo gaussiano (TEM00) dato che le irregolarità riscontrate nella geometria

dell’impronta, ottenuta esponendo al fascio defocalizzato una barretta di materiale acrilico, si sono rivelate di ordine inferiore rispetto al picco centrale di assorbimento.

Il profilo della traccia sarà quindi descrivibile come una curva di Gauss la cui larghezza e profondità dipenderanno dai parametri di potenza della radiazione incidente e velocità di scansione. Un aumento della potenza incidente causerà una maggiore asportazione, mentre un aumento della velocità di scansione ne provocherà la diminuzione.

Maggiore è la potenza a cui viene impostato il laser, maggiore sarà l’energia associata alla radiazione, disponibile per il processo di asportazione. Per quanto riguarda la velocità di scansione, nel modello teorico elaborato nel par.2.1.2.1 si era dimostrato che se vale:

(

)

D 2 36

0 =

<< π λ allora D è proporzionale a v-1,

dove D è la profondità della traccia in millimetri, w0=0,35mm è il raggio dello spot e

λ=10,64µm la lunghezza d’onda della radiazione. Dato che D<<36mm per ogni combinazione

di parametri esaminata, la profondità della traccia viene quindi ritenuta proporzionale all’inverso della velocità; questo assunto è facilmente comprensibile se si considera che maggiore è la velocità di scansione, minore sarà il tempo in cui la radiazione inciderà su di un determinato punto della traiettoria rettilinea causando conseguentemente una profondità di asportazione minore.

Per determinare come la potenza e la velocità di scansione influenzino la larghezza e la profondità del profilo della traccia singola, è stata predisposta una prima serie di prove di asportazione rettilinea (monodirezionale) sui blocchetti di PMMA aventi le dimensioni di un cubo di lato pari a 40mm. Nel determinare il layout delle prove si è tenuto conto delle necessità di avere una superficie piana e regolare, perpendicolare alle tracce realizzate con il laser; questo consente, oltre ad un preciso riferimento sull’attrezzatura di interfaccia con la piattaforma mobile (descritta nel par.3.4), una corretta misurazione sul proiettore di profili dove si vuole visualizzare un ingrandimento della sezione trasversale delle tracce. Le superfici lucide e trasparenti, ottenute per estrusione a caldo, non sono, infatti, rigorosamente perpendicolari tra loro e presentano un raggio di raccordo, approssimativamente di 0,5mm, che se ingrandito sul proiettore di profili, non consente di ottenere un’immagine nitida del profilo della traccia. Numerose combinazioni di potenza e velocità di scansione, generano, infatti,

tracce le cui dimensioni caratteristiche sono confrontabili, se non addirittura minori dell’ordine di grandezza del raggio di raccordo suddetto.

Le due superfici fresate, opposte e parallele tra loro, sono perpendicolari alle quattro superfici lucide ottenute per estrusione come mostrato in fig.4.5 .

Sup. fresata

Sup. fresata

40

60

Fig.4.5 Impostazione del layout delle prove

La realizzazione di una traccia rettilinea passante viene effettuata, come sarà spiegato in seguito, tramite la scansione di un segmento di 60mm centrato nell’origine degli assi del programma CADMARK e quindi, nel centro della piattaforma mobile; il blocchetto di PMMA, viene invece, centrato attraverso l’attrezzatura, come mostrato in fig. 4.6 .

∆Y=8mm

X Y

La prima traccia viene realizzata ad una distanza dal bordo pari ad 8mm e tale da garantire che il processo di asportazione non risenta della dispersione del calore verso l’esterno; per far questo, utilizzando la vite di manovra con passo pari ad 1mm, si posiziona il pezzo in modo tale che il raggio puntatore (laser a semiconduttore della potenza di 2mW ed emittente nel rosso) risulti a filo del bordo del blocchetto. A questo punto si ruota otto volte la vite di manovra in senso orario generando lo spostamento di 8mm. Gli spostamenti successivi garantiscono la spaziatura tra le scansioni e sono pari a 6mm; date le dimensioni assai ridotte dei profili delle tracce, ottenute attraverso una serie di prove preliminari, con questa spaziatura non esiste la possibilità che un’impronta sia influenzata, per effetto termico, dalle scansioni successive. I profili delle tracce sono tutti simmetrici in quanto ottenuti dalla scansione del medesimo segmento di 60mm posizionato centrato rispetto all’origine degli assi; di conseguenza, il raggio in uscita risulta centrato rispetto all’asse Y. Ogni canale è stato dunque generato, spostando il pezzo mediante la traslazione della slitta (manovrata dalla vite di passo unitario), mediante una deflessione del fascio operata da un solo specchio galvanometrico, come rappresentato in fig.4.7 .

α Lente a campo piano

X Y

Fig.4.7 Scansione di una traccia rettilinea

Per misurare la profondità D e la larghezza W caratteristiche di una sezione trasversale della traccia rettilinea, non è stato possibile sezionare il blocco di PMMA, in quanto i danneggiamenti superficiali indotti dal taglio e dalla successiva operazione di spianatura alle

macchine utensili, seppur microscopici, avrebbero irrimediabilmente deformato il profilo delle tracce falsando la rilevazione. Per ovviare a questo inconveniente è stato necessario realizzare delle tracce che attraversano l’intero spessore (40mm) del blocco in lavorazione utilizzando, poi, le superfici fresate come piani di riferimento per la misura sul proiettore di profili; onde evitare che la geometria del profilo generato sulla faccia fresata, risentisse del transitorio di avvio o di arresto della scansione (governato dal programma CADMARK con i parametri di ON-OFF DELAY), il laser viene attivato 10mm prima del bordo del blocco, e spento 10mm dopo la fuoriuscita dalla superficie, come mostrato nella fig.4.5 .

4.3.1 Parametri variabili

La prima fase dello studio sperimentale consiste nella realizzazione di un numero adeguato di tracce singole per analizzare la variabilità delle grandezze caratteristiche del profilo e conseguentemente il tasso di asportazione. Il layout precedentemente descritto consente la vaporizzazione di cinque tracce su ognuna delle quattro facce laterali, per un totale di 20 tracce. Durante la prima fase di asportazione monodirezionale, i seguenti parametri rimarranno

costanti:

• tipo di materiale lavorato→ PMMA (con proprietà chimico-fisiche illustrate in tab. 3.2) • TEM del fascio laser→ gaussiano,

• portata della bocca di aspirazione→ Q=0,35m3_/s,

• inclinazione della cappa rispetto al piano di lavoro→ α=60°,

• la diffusività termica→ β=6.₁₀-4 _cm2_{/s (talmente bassa da non influire sulla geometria}

della traccia),

• Temperatura iniziale del materiale→ Tambiente oscillante tra 20°C-23°C

I parametri variabili influenti nel processo risultano essere:

• potenza della radiazione incidente (regolata tramite il programma CADMARK che varia la percentuale del duty cycle dell’alimentatore) compresa tra un minimo di 2,5W (5% del ciclo di lavoro) ed un massimo di 12,5W( 25% del ciclo di lavoro);

• velocità di scansione (regolata tramite il programma CADMARK che varia la velocità di rotazione degli specchi galvanometrici) compresa tra un minimo di 25mm/s ed un masimo di 125 mm/s.

• distanza focale (regolata tramite il programma BACH installato sul terminale che gestisce lo spostamento della piattaforma mobile). In una prima serie di prove si

utilizzerà la distanza focale che fornisce il minor diametro dello spot (DSPOT=0,7mm)

sulla superficie da lavorare (ovvero f=200mm); successivamente si utilizzerà una distanza focale f=210mm per determinare quali siano gli effetti della defocalizzazione sulla profondità e la larghezza del profilo.

Su ogni faccia vengono ricavate tracce con potenza costante, e velocità che aumentano ogni volta di 25mm/s; le potenze utilizzate variano, invece, ogni 2,5W. La scelta del campo di potenza per questo primo test, è stata motivata dalla maggior affidabilità dell’alimentatore riscontrata per basse percentuali del duty-cycle, durante la fase di set-up della macchina, descritta nel par.3.2.1.2; il campo di velocità è stato scelto conseguentemente considerando che, per quanto affermato nel par. 4.3, la profondità della traccia D è direttamente proporzionale alla potenza ed inversamente proporzionale alla velocità di scansione.

Il rapporto tra potenza (espressa in W) e velocità di scansione (espressa in m/s) è uguale ad una energia per unità di lunghezza (espresso in J/m):

[ ]

P_in

=

ε (4.1).

Durante una prima serie di processi di vaporizzazione, effettuata per testare la funzionalità della macchina e delle attrezzature, si è notato che valori di ε superiori a 400-500J/m hanno generato tracce con profondità elevate e larghezze basse (come quella in fig.4.2 ottenuta con

f=200mm, Pin=20W e v=25mm/s) tali da rendere il profilo scarsamente utile per gli scopi

preposti. L’intervallo di velocità di scansione, per questa fase dello studio sperimentale, è stato scelto in modo da ottenere, una volta fissato il campo di variazione della potenza, valori di ε compresi tra 50J/m e 500J/m.

Una volta scelto un campo ottimale di variazione dell’energia per unità di lunghezza ε, verranno realizzate tracce con un ciclo di carico prossimo al 100% (per il quale è stata riscontrata una buona corrispondenza tra il valore effettivo ed i 50W attesi) e velocità di scansione corrispondenti. Questo consentirà di estendere i campi di partenza abbastanza ristretti, rispetto alle potenzialità della macchina (Potmax=50W, vmax=2500mm/s).

4.3.2 Profondità della traccia

La profondità della traccia è la grandezza fondamentale che caratterizza il profilo della sezione trasversale, ottenuto mediante la vaporizzazione. Di seguito verrà riportato, in primo luogo, il modello fisico che fornisce una stima della profondità di asportazione utilizzando le

conoscenze riportate nel cap.2; successivamente i risultati ottenuti saranno confrontati con i valori sperimentali ottenuti, misurando le profondità delle tracce sul proiettore di profili.

4.3.2.1 Modello previsionale

Questo studio sperimentale è finalizzato all’ottenimento di strutture tridimensionali complesse, mediante vaporizzazione laser, da utilizzare come stampi per ricavare prototipi; il processo di realizzazione deve essere quindi veloce ed affidabile per poter essere competitivo con le tecniche già collaudate di prototipazione rapida.

Per queste ragioni di tipo pratico, è necessario stimare i parametri caratteristici del processo ed il conseguente tasso di asportazione, tramite un modello che abbia attinenza fisica ma che utilizzi equazioni semplici senza richiedere laboriose integrazioni numeriche come avviene, invece, nel modello proposto da Berrie e Birkett [6] (par.2.1.2.1).

Si assumerà, in accordo con la legge di Beer-Lambert, che la potenza del laser sia assorbita da un sottile strato al di sotto della superficie del PMMA e che il riscaldamento del polimero consumi un determinato calore specifico costante in corrispondenza della temperatura di vaporizzazione; come ulteriore ipotesi, si assumerà che i prodotti gassosi del processo di vaporizzazione assorbano una percentuale trascurabile della radiazione incidente sulla superficie del pezzo.

Come punto di partenza per l’elaborazione del modello viene utilizzato l’assunto che la massa (m) del materiale asportato risulta proporzionale alla quantità di calore (Q) disponibile per il processo di vaporizzazione [29, 11, 1]. Quest’ultimo è dato dalla differenza tra il calore proveniente dal laser (Qin) e un certo valore di soglia (Qsoglia), al di sotto della quale non si

manifesta alcuna asportazione. Risulta per cui:

) (Q_in Q_soglia k

kQ

m= = − (4.2)

dove k (espresso in kg/J) è una costante di proporzionalità correlata all’energia del legame chimico che congiunge i monomeri di MMA nella catena polimerica; essa è uguale all’inverso del calore latente di pirolisi del materiale (L) che viene espresso in kJ/kg. I valori del coefficiente L sono noti in letteratura sia per il processo di pirolisi convenzionale, che prevede la decomposizione del materiale mediante un progressivo trattamento termico, sia per il processo di vaporizzazione laser che viene, invece, considerato come una pirolisi istantanea

(Flash pyrolysis). In questo secondo caso i valori di L oscillano nell’intervallo 1800-2200 kJ/mole [1], fornendo valori di k pari a 0,45-0,55.10-6 kg/J.

Il calore di soglia (Qsoglia) rappresenta, invece, le due principali perdite di energia nel processo

di vaporizzazione:

• l’energia necessaria al riscaldamento dell’area irradiata e delle zone limitrofe prima che inizi la vaporizzazione;

• l’energia persa a causa della conduzione del calore fuori dalla zona irradiata (questo termine verrà ritenuto trascurabile vista la bassa diffusività termica del PMMA).

I valori del calore di soglia (Qsoglia) ottenuti nel processo di pirolisi flash, vanno da un minimo

di 0,5mJ ad un massimo di 0,9mJ e sono estremamente sensibili al tipo di struttura molecolare del solido amorfo.

L’energia assorbita è data dal prodotto tra la potenza incidente ed il tempo di irradiazione (∆t):

t P

Q_in =α _in∆ (4.3)

dove α è la percentuale di radiazione assorbita (riportata in tab.3.2) dal PMMA. Se il fascio laser si muove con velocità costante (v) e potenza stabile (Pin), l’area A della zona colpita non

varia durante la scansione; supponendo, per semplicità, A quadrata e di lato a (A=a2), e considerando che l’energia su di essa incidente abbia profilo uniforme, il volume di materiale asportato vale Vol=AD, dove D è la profondità della traccia in una sezione ortogonale alla direzione di taglio (D). Il tempo di irradiazione è rapportato alla velocità di scansione dalla

v a t =

∆ (4.4)

La profondità (D) del profilo della traccia è correlata alla superficie della zona irradiata (A) attraverso la densità (ρ) del materiale:

DA m Volm =

=

ρ (4.5)

Sostituendo le (4.2), (4.3), (4.4) nella (4.5) si ottiene la

2 a kQ v P a k D in soglia ρ ρ α − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = (4.6) ;

considerando che 2 2 1 c a kQ c a k v P soglia in = = = ρ ρ α ε (4.7)

ed essendo c1 e c2 indipendenti da ε, la (4.6) diventa:

2 1 c c

D= ε− (4.8) .

Dalla (4.8) si evince che la profondità della traccia è linearmente dipendente dall’energia per unità di lunghezza (ε), almeno all’interno dei campi di variazione della potenza e della velocità impostati per questo semplice modello. Si nota, inoltre, come debba essere vinto un certo valore minimo (c2) al di sotto del quale non si manifesta asportazione; il termine noto della

retta espressa dalla (4.8) è funzione, infatti, del calore di soglia (Qsoglia). Dato che il profilo

della distribuzione spaziale dell’energia laser (TEM) non è uniforme, la dimensione tipica dello spot (a), può essere pensata come l’effettiva larghezza per la quale si ottiene il medesimo tasso di asportazione utilizzando un profilo uniforme. Se il profilo della traccia viene supposto triangolare (come in fig.4.2) allora l’effettiva lunghezza di a vale metà della larghezza della traccia ( a=W/2 ), in quanto affinché venga asportata la medesima quantità di materiale deve valere: Vol a D DW a

2 2 ₌

= .

Esistono due fondamentali limitazioni in questo semplice modello; la prima consiste nell’aver trascurato il cambiamento di temperatura del volume di materiale interessato, mentre la seconda è dovuta alla dipendenza delle perdite di calore dalla velocità di scansione e dalla potenza della radiazione. L’equazione (4.6) non prende infatti, in considerazione la variazione della temperatura del volume irradiato istante per istante; in realtà sia la percentuale di radiazione assorbita (α), che entrambi i termini che determinano la perdita di calore (il valore di soglia (Qsoglia) e la diffusività termica (β) ) ed infine anche il processo stesso di

vaporizzazione variano in funzione della temperatura. Questo porta alla conclusione che anche la costante k risulta essere funzione della temperatura; se si volessero prendere in considerazione tutte le dipendenze dei parametri in esame dalla temperatura si tornerebbe alla soluzione non lineare impostata da Berrie e Birkett.

Un altro limite di questa teoria semplificata è la dipendenza della dispersione di calore dalla velocità di scansione e dalla potenza del fascio. Nella maggior parte dei casi il calore speso per la vaporizzazione del materiale risulta maggiore delle perdite dovute al riscaldamento del materiale o alla conduzione e la temperatura di vaporizzazione viene raggiunta istantaneamente prima che vi possa essere un riscaldamento apprezzabile delle zone circostanti; questa peculiarità del processo di vaporizzazione del PMMA, come già detto, consente di ottenere un’ottima qualità dei bordi di taglio ed un bassissimo danneggiamento termico. Solamente nel caso di basse potenze del laser e basse velocità di scansione il bilancio termico si sposta a favore del termine conduttivo; in questo caso il volume di materiale riscaldato e la percentuale di calore perso risultano superiori rispetto al caso di un raggio più potente e veloce. Per questo motivo si prevede che il modello sovrastimi i valori delle profondità ottenute con basse potenze (2,5-5W) e basse velocità di scansione (25-50mm/s).

Sostituendo i valori della costante k, del calore di soglia Qth e della lunghezza caratteristica

dello spot a (pari alla metà del diametro dello spot a quella determinata distanza focale) nelle (4.7) si ricavano il coefficiente angolare ed il termine noto della retta (4.8):

c1=1,225.10-6m2/J

c2=3,4.10-6m .

L’equazione della retta ottenuta con questo semplice modello risulta dunque essere: 6 6 _{3,4 10} 10 225 , 1 − ⎟− × − ⎠ ⎞ ⎜ ⎝ ⎛ × = v P D in _(4.9)

dove D è espresso in metri, Pin è espressa in watt e v in m/s.

Una teoria analoga può essere sviluppata per il processo di asportazione lineare con distanze focali maggiori di 200mm. Se la superficie del pezzo viene posizionata ad una distanza tale da cadere, all’interno della profondità di campo della lente di focalizzazione, le caratteristiche del raggio non variano molto e l’energia rimane ancora sufficientemente concentrata. L’unico parametro che varia è la lunghezza caratteristica dello spot a, che può essere facilmente calcolata conoscendo la geometria del raggio laser; l’angolo di semiapertura del tronco di cono che costituisce il fascio vale:

028 , 0 tan = − = f r R γ (4.10)

dove R=6mm è il raggio del fascio prima della lente a campo piano ed r=0,35mm è il raggio dello spot alla distanza di focalizzazione f=200mm. Per distanze focali maggiori di 200mm il fascio laser diverge con un angolo all’incirca uguale a quello di focalizzazione ed assume la classica forma “a clessidra”. Ad una distanza focale f’=210mm, il diametro dello spot vale:

mm f f f SPOT f SPOT, ' =φ , +( '− )tanγ =1,36 φ (4.11)

ed a vale dunque 0,68mm. Il coefficiente angolare della retta ottenuta con la nuova distanza focale vale c3=1,12.10-6m2/J , mentre il termine noto vale c4=0,91.10-6m .

0 0,02 0,04 0,06 0,08 0,1 0,12 0 20 40 60 80 100 Pot/vel (J/m) Profondità D (mm) D f=200mm D f=210mm

Fig.4.8 Confronto tra le rette ottenute a diverse focalizzazioni

Come è evidente dalla fig.4.8, la retta ottenuta per distanza focale f=210mm presenta una pendenza minore rispetto a quella ricavata con f=200mm che fornisce, a parità di potenza e velocità di scansione, una profondità della traccia minore come è suggerito dal fatto che l’energia disponibile per la vaporizzazione è concentrata in un’area più ampia rispetto a quella ottenuta con la corretta distanza focale.

4.3.2.2 Misura dei dati sperimentali

I profili delle tracce ottenute sul PMMA, vengono misurati su di un proiettore di profili che consente di ingrandire di un fattore 20 la superficie fresata del blocchetto; quest’ultima viene appoggiata sul piano di vetro di una tavola portapezzo (1), munita di due slitte a regolazione micrometrica che ne consentono lo spostamento lungo due assi perpendicolari; l’immagine del

profilo, ottenuta illuminando il blocchetto dall’alto (2), viene ingrandita da una lente (3) posta al di sotto della tavola portapezzo e proiettata tramite un sistema di specchi su un piano di misura in vetro smerigliato (4). Su questo un piano di misura vengono posizionate lastre di vetro sulle quali sono incise griglie di riferimento che consentono di stimare la distanza relativa tra due punti dell’immagine ingrandita.

Fig.4.9 Proiettore di profili

Tramite i micrometri della slitta (1) vengono rilevate le quote della superficie del blocchetto e del punto di massima penetrazione del fascio all’interno del materiale; la differenza tra queste due quote fornisce la profondità della traccia con precisione dell’ordine di 1/100 di mm, ovvero la precisione caratteristica delle viti micrometriche. Se, invece, si misurasse la profondità direttamente sul piano di vetro smerigliato, tramite un comune righello, la precisione dello strumento risulterebbe pari, soltanto, ad 1/20 di mm.

I profili delle tracce ottenute mediante vaporizzazione laser, vengono schematizzati come triangoli isosceli in cui l’altezza coincide con la profondità del profilo e la base con la larghezza, come illustrato in fig.4.10.

Dato che il valore dell’ascissa nell’equazione della retta (4.6) è data dal rapporto tra potenza associata alla radiazione e velocità di scansione, gli stessi valori dell’energia per unità di

lunghezza ε possono essere ottenuti con più combinazioni dei due parametri variabili; ad esempio 100J/m possono essere ottenuti con:

• P=2,5W, v=25mm/s • P=5W, v=50mm/s • P=10W, v=100mm/s.

Fig. 4.10 Ingrandimento (50x) di un profilo ottenuto con f=200mm, Pin=12,5W, v=50mm/s

Per ogni combinazione dei parametri di potenza e velocità, è stata rilevata la profondità D sul proiettore di profili e riportata nel grafico di fig.4.11; le combinazioni che generano la stessa ε hanno fornito, come previsto, valori simili della profondità. Si è utilizzato un programma di calcolo statistico, che determina tramite un metodo iterativo la retta dei minimi quadrati caratteristica di questa distribuzione dei dati, notando che vi è soltanto una minima differenza nel considerare tutti i valori della profondità rilevati per una medesima ε oppure unicamente il loro valor medio.

Il valore del coefficiente di correlazione che fornisce un’indicazione di come i dati possano essere ben rappresentati da una linea retta, vale nel caso in esame, rc=0,998.

Il coefficiente angolare ed il termine noto della retta dei minimi quadrati valgono rispettivamente:

c1=1,22.10-6 m2/J

c2=9,08.10-6 m ;

0 0,2 0,4 0,6 0,8 1 1,2 0 100 200 300 400 500 600 700 800 900 1000 Energia/lunghezza (J/m) Profondità D (mm) Dsperimentale

Fig.4.11 Profondità D rilevata sperimentalmente a f=200mm

Confrontando le due rette si nota una la precisa corrispondenza dell’andamento tra i valori ricavati con il modello teorico ed i valori sperimentali ottenuti dalla misurazione delle tracce ricavate mediante vaporizzazione laser (fig. 4.11). Lo scostamento maggiore tra dai teorici e sperimentali si osserva per bassi ε in quanto, per basse potenze e velocità di scansione, si fanno più considerevoli le perdite di calore dovute alla conduzione verso l’interno del materiale; questa differenza si fa, percentualmente, meno sensibile con l’aumentare della profondità della traccia. 0 0,2 0,4 0,6 0,8 1 1,2 1,4 0 200 400 600 800 1000 Energia/Lunghezza (J/m) Profondità D (mm) D teorica D sperimentale

Fig,4.12 Confronto tra la retta dei minimi quadrati ottenuta sperimentalmente e la retta derivata dal modello teorico

Per avere un’ulteriore conferma della validità del modello proposto, si è proceduto ad un confronto con uno dei modelli più noti in letteratura, ovvero la curva di Powell [20]. Il modello elaborato da Powell fornisce una curva del tipo

1 0 b in v P b D ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = (4.12)

dove D è la profondità della traccia in mm, Pin è la potenza associata alla radiazione incidente

in watt, v è la velocità di scansione in m/min, mentre b0 e b1 sono due costanti. Il coefficiente

b0 è una costante sperimentale che dipende dalla combinazione tra parametri del laser e

distanza focale (nel caso in esame è stato ricavato a ritroso utilizzando alcuni valori misurati della profondità D) pari a 8.10-2 ; la costante b1 dipende, invece, dal tipo di materiale. Nel caso

dei polimeri, indipendentemente dalle caratteristiche chimiche del pezzo in lavorazione,

b1=0,74 . Come si può osservare l’equazione 4.12 dedotta dal modello di Powell, sviluppato

per il taglio laser di fogli di polimero, è di tipo sperimentale e non rispetta l’uguaglianza tra le grandezze fisiche.

Il modello di Powell si adatta meglio, ai dati sperimentali rilevati, per ε>600J/m (ovvero per elevate potenze di taglio e basse velocità di scansione) rispetto al modello qui discusso, mentre accade il viceversa per valori di ε compresi tra 50-500J/m. Questo fatto non deve sorprendere, in quanto il modello di Powell è stato elaborato per stimare la profondità di taglio dell’intero spessore dei laminati di acrilico, mentre il modello lineare ha lo scopo di descrivere il processo di vaporizzazione di tracce monodirezionali. L’esistenza di una diretta correlazione tra i due modelli in un ragionevole intervallo della variabile ε conferisce un’ulteriore conferma all’affidabilità del modello lineare.

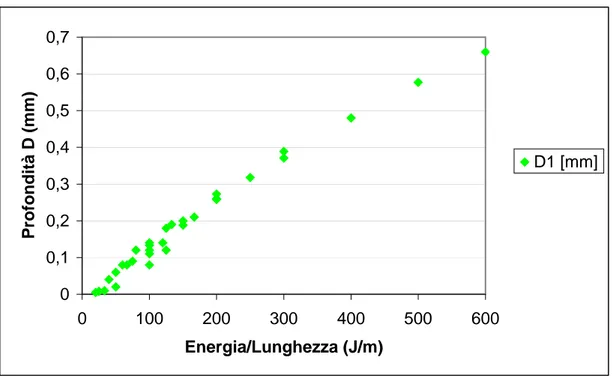
Si può quindi concludere che il modello presentato fornisce una buona rappresentazione della realtà fisica, peraltro assai complessa e non lineare, ed è di notevole utilità per stimare con ottima precisione la profondità di asportazione nel caso di vaporizzazione monodirezionale. Nel caso di vaporizzazione monodirezionale a distanza focale f=210mm, i risultati ottenuti sono riportati in fig. 4.13 ; utilizzando il solito programma di calcolo statistico si determina la retta dei minimi quadrati con un coefficiente di correlazione pari a 0,972. I valori sperimentali risultano leggermente più dispersi rispetto al caso di focalizzazione sulla superficie del pezzo (f=200mm), ma il modello risulta ancora ben corrispondente con il processo di asportazione. I valori ottenuti per i coefficienti sono:

c3=1,09.10-6m2/J

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0 100 200 300 400 500 600 Energia/Lunghezza (J/m) Profondità D (mm) D1 [mm]

Fig. 4.13 Profondità D rilevata sperimentalmente a f=210mm

Il medesimo processo è stato ripetuto anche per f=220mm; con questa distanza focale, però, non si ottengono valori sufficienti della profondità, mentre l’ampiezza del danneggiamento termico dovuto alla minore densità di energia, non consente di utilizzare questa focalizzazione per gli scopi prefissati.

4.3.3 Larghezza della traccia

La larghezza della traccia è la seconda grandezza fondamentale che ne caratterizza il profilo della sezione trasversale, ottenuto mediante la vaporizzazione. Di seguito verrà riportato, in primo luogo, un modello intuitivo che prevede la dimensione di questa grandezza al variare dei parametri di processo (potenza e velocità di scansione). Le nozioni utilizzate per la sua elaborazione derivano essenzialmente dalla legge di Beer-Lambert che regola la penetrazione di una radiazione luminosa all’interno di un solido non riflettente. Successivamente i risultati ottenuti saranno confrontati con i valori sperimentali ottenuti, misurando le larghezze delle tracce sul proiettore di profili.

4.3.3.1 Modello previsionale

La larghezza di una traccia, esattamente come la profondità, dipende strettamente dal TEM del fascio laser, dai parametri di processo e dalla distanza focale. Se si considera un’impronta generata da un singolo impulso, in caso di TEM gaussiano, la profondità di asportazione è massima al centro dello spot e decresce verso la sua circonferenza esterna seguendo una legge del tipo _e−x2_{; il diametro per il quale la profondità di asportazione è nulla, determina la} larghezza caratteristica dell’impronta. L’aumento della potenza o la diminuzione della velocità di scansione determinano un aumento della profondità di asportazione ma non della larghezza, il cui valore massimo è sempre legato al diametro dello spot che dipende unicamente dalla distanza focale e non dagli altri parametri di processo (come mostrato in fig.4.14).

La distanza focale che determina il diametro dello spot, è, quindi, il parametro fondamentale che determina le caratteristiche della curva che descrive la larghezza in funzione dell’energia per unità di lunghezza ε.

W

=D

D

D

D

Fig.4.14 Aumentando l’energia specifica la profondità aumenta mentre la larghezza si assesta su di un valore costante

In linea teorica, l’aumento della densità di energia (derivante da un aumento di potenza o da una riduzione di velocità di scansione) provoca un aumento della larghezza della traccia fino a quando questa non raggiunge il suo valore massimo corrispondente al diametro dello spot.

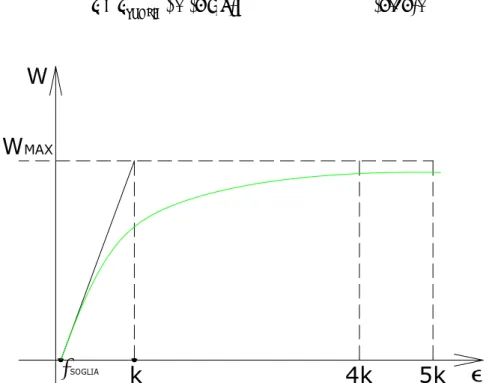
La relazione che descrive la larghezza in funzione dell’energia per unità di lunghezza ε può, dunque, essere descritta da una curva che aumenta, quasi linearmente fino ad un certo valore, e successivamente si assesta su di un valore costante di dimensioni paragonabili a quelle del diametro dello spot. La relazione ipotizzata è la seguente

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − = k W W SOGLIA MAX ε ε exp 1 (4.13)

dove WMAX rappresenta il valore teorico al quale tende la larghezza (espresso in mm), εSOGLIA è

il valore dell’energia specifica al di sotto del quale non si manifesta asportazione (espresso in J/m) e k è la costante di aumento esponenziale della larghezza (espressa in J/m); il valore

WMAX di larghezza massima viene raggiunto per valori di

(

)

5k

4k

k

W

Fig. 4.15 Definizione grafica dei parametri che caratterizzano la curva della larghezza

La εSOGLIA qui introdotta è il medesimo valore di soglia che era stato determinato

dall’intersezione della retta delle profondità con l’asse delle ascisse; a livello teorico, infatti, valori di ε insufficienti per ottenere asportazione non consentono di rilevare né profondità né larghezza.

4.3.3.2 Misura dei dati sperimentali

La misura della larghezza delle tracce viene effettuata sul proiettore di profili con i medesimi accorgimenti descritti in precedenza. I valori sperimentali ottenuti con le due diverse distanze focali (f=200mm ed f=210mm) sono riportate in fig.4.14.

I coefficienti, ricavati tramite il programma di calcolo statistico, relativi alle due regressioni non lineari, sono riportati in tab. 4.1.

f=200mm f=210mm

WMAX 0,7mm 1,36mm

εSOGLIA 15J/m 18J/m

k 45J/m 60J/m

Tab.4.1 Coefficienti delle regressioni non lineari

Gli indici di correlazione non lineari (R2) valgono R2=0,919 nel caso di f=200mm e R2=0,928 per f=210mm.

Confrontando i valori della εSOGLIA ricavati nel caso della profondità e della larghezza, a

distanza focale f=200mm, si nota che nel primo caso il valore (pari a 7,5J/m) è esattamente la metà del secondo, riportato in tab.4.1.

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0 100 200 300 400 500 600 700 800 900 1000 Energia/Lunghezza (J/m) Larghezza W (mm) W f=200mm W f=210mm

Una possibile spiegazione di questa incongruenza sta nell’errore commesso nella misurazione; quando, infatti, l’energia specifica è molto bassa e prossima ai valori di soglia la superficie del PMMA colpita fonde ma non vaporizza, per cui, pur non riuscendo a rilevare alcuna profondità di asportazione si arriva a misurare la larghezza della zona danneggiata termicamente.

La tendenza dei dati sperimentali ricalca con notevole precisione la curva supposta; risulta ben evidente l’andamento asintotico della larghezza all’aumentare dell’energia per unità di lunghezza per entrambi gruppi di valori rilevati. L’asintoto orizzontale della curva ottenuta con f=210mm ha un valore maggiore in quanto lo spot del fascio laser assume dimensioni maggiori a causa della defocalizzazione; aumentando la distanza focale si assiste, dunque, ad un comportamento opposto tra profondità di asportazione (diminuisce) e larghezza della traccia (aumenta).

Il danneggiamento termico, spesso riscontrato durante la misurazione della larghezza delle tracce sul proiettore di profili, consiste in rigonfiamenti del bordo di taglio, indotti dal calore, che corrono paralleli alla traccia. Questi difetti possono causare un peggioramento della qualità del processo ed a volte addirittura occludere le tracce ricavate con basse energie specifiche o a distanze focali maggiori di 210mm. L’alterazione dei bordi di taglio è dovuta ad un abbassamento della densità del PMMA (ρ=1,18 kg/dm3) generata dalla radiazione che provoca un aumento di volume e conseguentemente un rigonfiamento del polimero. La riduzione della densità avviene, presumibilmente durante il processo di riscaldamento dove molte catene polimeriche sono già state spezzettate in blocchi più piccoli senza essere asportate. Questo processo di “degradazione” del peso molecolare è più pronunciato nelle tracce ottenute con più passate sovrapposte (come sarà illustrato di seguito) in quanto ogni riscaldamento dovuto alla fase precedente all’asportazione amplia la zona interessata dal processo.

4.3.4 Rettilineità della traccia

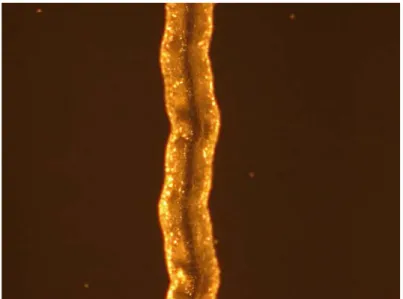
Un difetto riscontrabile, anche ad occhio nudo, sulle tracce realizzate è rappresentato da una ondulazione periodica e con ampiezza costante; il periodo di tale oscillazione aumenta all’aumentare della velocità di scansione e viceversa mentre risulta indipendente dalla potenza e dalla distanza focale. Si è notato che per velocità di scansione pari a 50mm/s il periodo dell’oscillazione vale all’incirca metà del periodo dell’oscillazione riscontrata a velocità di 100mm/s.

Fig. 4.17 Oscillazione rilevata in una traccia (f=200mm, Pin=5W,v=50mm/s, WF=300)

La causa di queste oscillazioni è da ricercare nel sistema di movimentazione del fascio ed in special modo nei parametri di impostazione degli specchi deflettori e degli attuatori galvanometrici. Affinché la radiazione incidente non danneggi gli specchi, attraverso una sovraesposizione costante in un unico punto, gli attuatori vengono dotati dal costruttore, di una oscillazione permanente e non eliminabile la cui frequenza può essere regolata variando il parametro di WOBBLE FREQUENCE (WF o frequenza di tremolio) nel set-up della testa di movimentazione presente all’interno del programma CAD-MARK. Questo parametro adimensionale ha un valore di default pari a 300 e può variare in un intervallo compreso tra 100 e 1000.

Fig.4.18 Traccia discontinua (f=200mm, Pin=5W,v=50mm/s, WF=1000)

Ripetendo il processo di vaporizzazione lineare, e mantenendo tutti gli altri parametri costanti, non si è notato alcun effetto apprezzabile per valori inferiori a WF=300, mentre per valori prossimi al massimo impostabile è stata riscontrata una lieve diminuzione dell’ampiezza

dell’oscillazione concomitante ad una interruzione della continuità della traccia che assume l’aspetto di una linea trattegiata.

Le variazioni effettuate sul parametro di WOBBLE FREQUENCE non hanno, quindi, eliminato il problema delle oscillazioni indotte nel processo di asportazione lineare.

Questo difetto deve essere opportunamente ridotto per garantire un andamento rettilineo della traccia che consenta di sviluppare il secondo passo di questo studio sperimentale, ovvero l’asportazione di uno strato di materiale mediante l’accostamento di più tracce rettilinee.

Accertata l’inutilità di una variazione delle impostazioni dei galvanospecchi, si è intervenuti aumentando sensibilmente la velocità di scansione in modo da rendere il periodo dell’oscillazione maggiore della lunghezza della traccia. Per garantire la confrontabilità delle nuove tracce con quelle già ottenute sono stati scelti 5 valori campione della variabile ε (energia per unità di lunghezza): (50,100,150,200,250) J/m. Ognuno di questi valori di ε è stato ottenuto con 5 possibili combinazioni ottenute con potenze di (15,20,30,40,50)W e velocità corrispondenti, derivate dalla eq. 4.1.

Fig.4.19 Rettilineità di una traccia (f=200mm,Pin=50W,v=500mm/s,WF=300)

Analizzando le nuove tracce ottenute si è verificato che per velocità di scansione maggiori di 300-400mm/s l’oscillazione si riduce sensibilmente e l’unico effetto apprezzabile è una modesta curvatura della traccia testimone del fatto che il periodo dell’onda è superiore alla lunghezza della scansione. Per tutte le prove successive si adotteranno velocità superiori a 30mm/s e con potenza prossima a 50W per evitare la zona delle potenze medie dove era stato

registrato uno scostamento marcato dalla proporzionalità diretta con i cicli di carico dell’alimentatore (par.3.2.1.2); in questo modo, oltre ad evitare l’insorgere di oscillazioni lungo la direzione della traccia, si diminuiscono sensibilmente i tempi di scansione e complessivamente i tempi di processo.

4.3.5 Variazione del profilo di una traccia

Una volta nota la dipendenza tra le caratteristiche geometriche di una singola traccia ed i parametri di processo che l’hanno generata, è utile analizzare quali possono essere le modalità operative che consentono di variarne profilo. Il fine di questa ulteriore analisi sulla vaporizzazione monodimensionale, è strettamente legato all’ottenimento di un profilo ottimale da utilizzare in modo ripetitivo per l’asportazione di uno strato di materiale.

Si è già osservato come un aumento della distanza focale causa un incremento della larghezza (W) ed una diminuzione della profondità di asportazione (D), rispetto ad una traccia ottenuta, a parità di parametri, con la distanza focale f=200mm che assicura il minimo diametro dello spot. Aumentando la distanza focale è quindi possibile, ottenere un aumento dell’angolo di apertura α (fig.4.20) tra i due bordi obliqui, a scapito della profondità di asportazione.

α

α

Fig.4.20 Aumento dell’angolo di apertura del profilo

Contrariamente, la diminuzione dell’angolo α che causa un aumento dell’inclinazione dei bordi obliqui rispetto alla superficie del blocchetto, non può essere effettuata variando la quota della piattaforma mobile, ovvero cambiando la distanza focale. Per diminuire l’angolo di apertura è stato elaborato un metodo che prevede l’utilizzo di ulteriori scansioni sopra la traccia già realizzata.

4.3.5.1 Modello previsionale

Utilizzando la sovrapposizione delle passate si riesce ad ottenere una riduzione dell’angolo di apertura a scapito di un aumento della profondità di asportazione; durante la seconda passata, realizzata senza variare i parametri di potenza e velocità di scansione, il raggio laser, non trovando materiale da vaporizzare all’interno della traccia ottenuta con la scansione precedente, genera un aumento della penetrazione in un punto generico del profilo che, in prima approssimazione, risulta pari alla profondità di asportazione dovuto alla prima passata in quella determinata posizione rispetto all’asse del fascio.

a

a b

b

α

α

2D

D

Fig.4.21 Schema di asportazione per passate sovrapposte

Dalla schematizzazione visualizzata in fig.4.21, si deduce che la larghezza della traccia deve mantenersi costante, mentre la profondità è direttamente proporzionale al numero di passate necessario per portare i bordi della traccia ad una determinata inclinazione. In questo modello teorico sono stati trascurati gli effetti di:

• defocalizzazione causata dal fatto che il fascio focalizzato sulla superficie del blocco (f=200mm) non lavora, all’interno della traccia pre-esistente, nelle condizioni che garantiscono la maggiore concentrazione dell’energia. Questo effetto si fa tanto più pronunciato all’aumentare della profondità totale della traccia e quindi del numero di passate.

• riflessione della radiazione sui bordi inclinati della traccia pre-esistente.

L’effetto della defocalizzazione nel processo si manifesterà in una minor profondità della traccia rispetto a quella teorica che prevede un tasso di asportazione costante per ogni passata; se, ad esempio, si prende in considerazione un canale ottenuto mediante 6 vaporizzazioni successive la profondità ottenuta risulterà, probabilmente, minore di quella teorica calcolata moltiplicando per sei la profondità di penetrazione di una singola passata.

Per quanto riguarda, invece, la riflessione operata dai bordi inclinati si deve ricordare che il problema dell’assorbimento disuniforme è legato alla polarizzazione della luce incidente; se questa è polarizzata linearmente ed il piano in cui oscilla il vettore del campo elettrico E, associato alla radiazione, coincide con il piano di incidenza (onde di tipo p) allora esiste un angolo (chiamato angolo di Brewster) per il quale tutta la luce viene trasmessa.

onde p

n

<n

ϑ

ϑ

ϑ

ϑ

ϑ

n

=n

1,5

n

=n

1

Fig.4.22 Definizione dell’angolo di Brewster

In fig.4.22 viene mostrata la dipendenza della riflettività di una superficie trasparente (come ad esempio il PMMA) con indice di rifrazione n2 maggiore di quello dell’aria (n1), da cui la

radiazione proviene; si vede chiaramente che per θi=56° le onde p associate alla radiazione, vengono completamente assorbite dal materiale.

Nel caso di luce polarizzata linearmente, dunque, la lavorazione di superfici inclinate crea una variazione dell’angolo di incidenza (θi) e conseguentemente induce disuniformità nell’assorbimento.

Il laser SYNRAD utilizzato sull’apparato sperimentale ha, invece, una polarizzazione random che consente di avere effetti costanti, indipendentemente dall’inclinazione della superficie da lavorare, per cui si può ragionevolmente supporre che, qualora si manifestino fenomeni di riflessione della radiazione incidente, questi non siano dipendenti dalla polarizzazione del raggio.

4.3.5.2 Misura dei dati sperimentali

Al fine di accertare l’esattezza del modello proposto per la variazione del profilo delle tracce, sono state realizzate delle prove di asportazione a passate multiple sovrapposte utilizzando due diversi valori di energia per unità di lunghezza ε=50J/m (Pin=50W,v=1000mm/s)ed ε=100J/m (Pin=50W,v=500m/s) e due distanze focali f=200mm, f=210mm. Sulla superficie del blocchetto di PMMA sono state ricavate sei tracce equidistanti, realizzate partendo da un minimo di 2 scansioni sovrapposte fino ad arrivare 12, ed aumentando ogni volta di due il numero delle passate.

Dalle fig.4.23 e 4.24 si nota facilmente come con il metodo pratico sopra esposto si riesca ad aumentare progressivamente la profondità della traccia mantenendone invariata la larghezza.

P=50W,v=1000mm/s,f=200m 0 0,1 0,2 0,3 0,4 0,5 0,6 0 2 4 6 8 10 12 N° di passate Profondità, Larghezza (mm) Profondità Larghezza

Fig.4.23 Profondità e larghezza in funzione del numero di passate (50J/m)

La profondità delle tracce ottenute varia linearmente con il numero di passate ma il tasso di asportazione per passata risulta inferiore alla profondità di asportazione ottenuto con una sola

passata sul materiale intonso. Il coefficiente angolare della retta delineata in fig.4.23, vale infatti: passata mm n D 04 , 0 11 07 , 0 52 , 0 − ₌ = ∆ ∆ (4.15)

che risulta inferiore agli 0,07mm/passata prospettati con il modello teorico di fig.4.21. Come già anticipato nel paragrafo precedente la defocalizzazione locale ed interna alla traccia è con elevata probabilità la responsabile maggiore di questa riduzione del tasso di asportazione. L’aumento del diametro dello spot all’interno del profilo triangolare, derivante dal fatto che il fascio laser rimane focalizzato sulla superficie del blocchetto, causa un abbassamento della densità di energia che rende le passate successive alla prima, meno incisive.

La larghezza della traccia si mantiene grosso modo uniforme all’aumentare del numero di passate; si osservano, infatti, soltanto modeste oscillazioni attorno al valore di W=0,37mm che possono derivare sia dalla instabilità della distribuzione di energia all’interno dello spot del fascio laser, sia dagli errori di misura dato che la precisione ottenibile sul proiettore di profili si spinge al massimo fino ad 1/100 di millimetro.

P=50W,v=500mm/s,f=200m 0 0,2 0,4 0,6 0,8 1 1,2 0 2 4 6 8 10 12 N° di passate Profondità, Larghezza (mm) Profondità Larghezza

Fig.4.23 Profondità e larghezza in funzione del numero di passate (100J/m)

Le medesime considerazioni possono essere fatte per il secondo layout di prove in cui è stata variata unicamente la velocità di scansione, in modo da generare un’energia su unità di lunghezza ε pari a 100J/m. Il tasso di asportazione per passata è ancora una volta inferiore alla profondità di penetrazione di una singola scansione su materiale non lavorato (0,09mm/passata

effettivo contro 0,13mm/passata teorico), mentre la larghezza rimane costante ed oscilla intorno al valore W=0,4mm.

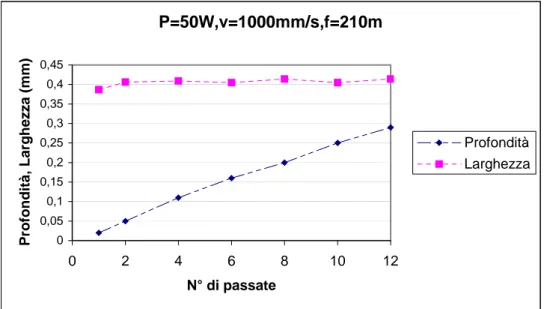
Ripetendo questa duplice serie di prove per una distanza focale f=210mm, il modello non solo rimane valido (come mostrato in fig. 4.24 e 4.25), ma fornisce una attinenza migliore ai dati sperimentali rilevati. P=50W,v=1000mm/s,f=210m 0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0 2 4 6 8 10 12 N° di passate P rofondità, Larghezza (mm) Profondità Larghezza

Fig.4.24 Profondità e larghezza in funzione del numero di passate (50J/m)

P=50W,v=500mm/s,f=210m 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0 2 4 6 8 10 12 N° di passate P rofondità, Larghezza (mm) Profondità Larghezza

Fig. 4.25 Profondità e larghezza in funzione del numero di passate (100J/m)

Per velocità pari a 1000mm/s si ottiene un tasso di asportazione per passata di 0,02mm/passata che è equivalente alla profondità di penetrazione di una singola scansione nel materiale non lavorato; per velocità di 500mm/s il tasso di asportazione vale, invece, 0,06mm/passata contro

lo 0,08 teorico. Questa miglior corrispondenza tra modello teorico e dati sperimentali deriva dal fatto che le minori profondità di asportazione raggiunte con f=210mm mediante una singola scansione, presentano alla passata successiva condizioni di taglio meno complicate (in termini di inclinazione dei bordi obliqui e diminuzione della concentrazione dell’energia all’interno dell’impronta) di quelle che si riscontravano con f=200mm.

Qualora si rendesse necessario ottenere un aumento dell’inclinazione dei bordi inclinati senza aumentare la profondità del profilo della traccia, il modello esposto non risulterebbe valido; in questo caso, per diminuire l’angolo di apertura della traccia (α), si dovrebbe diminuire la larghezza del solco lasciandone inalterata la profondità. Per ottenere questo effetto sono state realizzate delle tracce con differente numero di passate (N), variando il duty cycle (e quindi la potenza della radiazione (Pin) ) con velocità di scansione costante e pari a 500mm/s. I risultati

sono riportati in fig.4.26 .

D W N=1,Pot=50W -> W=400µm N=4,Pot=12,5W -> W=328µm N=10,Pot=5W -> W=292µm N=20,Pot=2,5W -> W=264µm D MA X =1 35 µ m

Fig.4.26 Variazione della larghezza (W) della traccia; tutte le tracce hanno più o meno la stessa profondità (D=(130+5)µm)

Utilizzando l’ipotesi che il tasso di asportazione di una passata rimanga costante all’aumentare del numero di scansioni, si nota che la profondità di una traccia ottenuta con Pin=50W e v=500mm/s può essere ricavata anche tramite due passate sovrapposte con parametri di processo Pin=25W e v=500mm/s. Seguendo questa considerazione vengono realizzate 4 tracce caratterizzate da potenze decrescenti: 50W, 12,5W, 5W e 2,5W.

Lo scopo di questa serie di prove è stato quello di dimostrare che utilizzando più passate con minor potenza, è possibile ricavare profili delle tracce più stretti. La spiegazione di questo fenomeno sta nel fatto che utilizzando valori della potenza (2,5W) poco al di sopra del livello di soglia necessario per provocare la asportazione di materiale, le zone circostanti all’area colpita dallo spot, non raggiungono la temperatura di vaporizzazione e quindi non vengono asportate.

Gli effetti prodotti da queste sovrapposizioni sono tuttavia insufficienti a modificare significativamente l’inclinazione dei bordi inclinati; quando, nei passi successivi, si procederà alla vaporizzazione di più strati di materiale si utilizzerà sempre il primo modello in quanto l’utilizzo del secondo comporterebbe un eccessivo aumento del numero di passate.

4.3.5.3 Interdipendenza tra lunghezza e profondità

Analizzando la superficie lavorata del blocchetto di PMMA, tramite un sistema di visone costituito da una telecamera con un ingrandimento pari a 50, si nota che la profondità della traccia D risulta uniforme su tutta la lunghezza della traccia. L’effetto del susseguirsi degli impulsi laser (con frequenza di 5kHz) durante il movimento di scansione non genera difetti rimarcabili sull’uniformità del profilo in quanto nel periodo caratteristico, pari a 200µs, lo spot avanza solamente di 0,2mm, per velocità di 1000mm/s.

Le perdite di calore dovute al riscaldamento del volume asportato ed alla conduzione, fanno sì che nel processo di asportazione ci sia sempre una certa quantità di energia che si disperde all’interno del materiale e che, quindi, non è disponibile per la vaporizzazione del polimero. A seconda della quantità di calore perduta e del tempo disponibile per la sua dispersione, si è notato che la zona colpita dal laser può variare di dimensione.

In particolare, se la traccia è realizzata con più passate, la profondità della traccia risulta influenzata dal tempo di raffreddamento che intercorre tra due scansioni consecutive; se, come è stato assunto, il processo di vaporizzazione avviene a velocità costante, questo tempo dipende unicamente dalla lunghezza della traccia. Se questo tempo è breve, l’energia necessaria per la seconda vaporizzazione è più bassa e la profondità attesa risulterà maggiore; conseguentemente, per solchi di breve lunghezza, realizzati a parità di set-up della macchina, si otterranno profondità superiori rispetto a quelli caratterizzati da lunghezze maggiori.

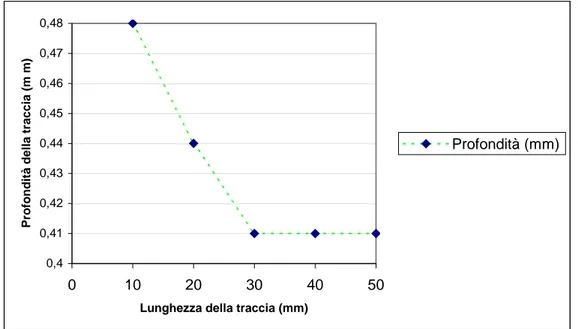
L’influenza del tempo di raffreddamento sulla profondità delle tracce è stata analizzata facendo variare la lunghezza di ogni traccia di 10mm in un intervallo compreso tra 10mm e 50mm.

Ogni traccia è stato ottenuta sovrapponendo 4 scansioni con Pin=50W e v=500m/s; i risultati

hanno mostrato che la profondità del profilo aumenta del 9% per lunghezze di 20mm e del 17% per lunghezze di 10mm mentre nessuna variazione apprezzabile è stata riscontrata nei profili delle tracce con lunghezza superiore. Anche se le variazioni indotte dalla lunghezza, sono dell’ordine della decina di µm e possono essere interpretate come une errore dovuto allo strumento di misura, nella seconda fase delle prove dove si analizzerà l’asportazione di uno strato mediante accostamento di tracce lineari si farà in modo da rispettare i tempi di raffreddamento del materiale (stimato intorno a 10-1s per il caso dell’asportazione monodirezionale). 0,4 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0 10 20 30 40 50

Lunghezza della traccia (mm)

Profondità della traccia (m m)

Profondità (mm)

Fig. 4.27 Profondità della traccia in funzione della lunghezza; Pin=50W,v=500mm/s, n° passate=4, f=200mm

4.4 Sovrapposizione delle tracce

Il processo di vaporizzazione laser fin qui analizzato ha avuto come obiettivo la realizzazione di tracce singole di lunghezza pari allo spessore del blocchetto di PMMA e profilo variabile a seconda dei parametri impostati. Come già accennato in precedenza (par. 4.2) la traccia verrà utilizzata come unità di base ripetendo la quale sarà possibile ottenere l’asportazione selettiva di uno strato di materiale.

Affiancando un certo numero di tracce, fino quasi a sovrapporle, è possibile ottenere una superficie costituita da una successione di creste e valli che costituiscono i residui delle

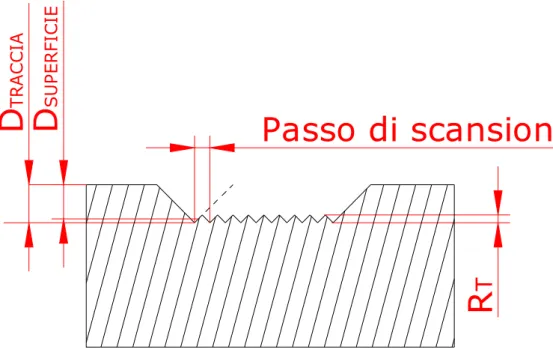
scansioni monomonodirezionali. Se si esamina una sezione trasversale di fig.4.3 si ottiene un profilo come quello schematizzato in fig.4.28.

R

T

D

D

Passo di scansione

Fig. 4.28 Profilo di una superficie (strato) ottenuta attraverso la sovrapposizione di più tracce rettilinee

Dalla fig.4.28 si vede che la sovrapposizione delle tracce non è completa ed i vertici dei triangoli (con cui si schematizzano i profili) sono distanziati tra loro di una quantità fissa che rappresenta il passo di scansione. Da questo nuovo parametro di processo dipendono le dimensioni dei testimoni delle singole asportazioni rettilinee che rimangono sul fondo dello strato sotto forma di un alternarsi regolare di picchi e valli della stessa ampiezza; questa ampiezza indicata con RT, rappresenta la rugosità totale intesa come la massima distanza

picco-valle. Si nota inoltre che, una volta fissata la geometria della traccia, la RT è linearmente

dipendente dal passo di scansione, per cui una riduzione di quest’ultimo genera un miglioramento del grado di finitura superficiale del fondo dello strato. Il passo di scansione non può, però essere diminuito indiscriminatamente, in quanto oltre un certo valore il raggio che realizza la seconda passata va ad influire sulla profondità della prima traccia già realizzata aumentandone il valore secondo le leggi delineate nel par.4.3.5.2. Questo effetto di ricalcamento delle tracce genera un profilo dello strato disuniforme e caratterizzato da una profondità superiore a quella stimata teoricamente.

L’obiettivo dello studio di questo nuovo parametro di processo sarà dunque quello di trovare un giusto compromesso tra queste due necessità contrastanti.

Il primo passo da compiere per procedere alla vaporizzazione di uno strato, è dunque, quello di scegliere i parametri di processo (potenza e velocità di scansione) che consentono di ottenere una traccia con caratteristiche ottimali.

• Profondità: dato che lo spessore di uno strato è funzione della profondità di penetrazione (D) delle singole tracce che lo costituiscono, questa non deve avere valori troppo elevati; se, infatti, si vuole ricavare un’impronta tridimensionale complessa approssimandola attraverso la sovrapposizione di più strati, la risoluzione con la quale si riesce a riprodurre tale cavità è funzione dello spessore dello strato stesso. Maggiore sarà lo spessore dello strato, minore sarà la risoluzione del processo di vaporizzazione strato per strato. Per questo motivo si escludono tutte le combinazioni dei parametri caratteristici dell’asportazione monodimensionale che generano tracce con profondità del profilo superiore a 0,25mm.

• Larghezza: il profilo non deve essere eccessivamente stretto e profondo (angoli di apertura α bassi), in quanto, a parità di passo di scansione e penetrazione D, si ottiene una rugosità RT superiore, rispetto ad una forma caratterizzata da α maggiori. Per

questo motivo la larghezza della traccia W non dovrà essere inferiore a 2D, garantendo, in questo modo, un αminimo pari a 90°.

• Uniformità: per avere una corretta sovrapposizione delle tracce occorre che il profilo caratteristico della sezione trasversale sia uniforme lungo tutta la scansione. L’asportazione deve essere continua ed ininterrotta per poter generare uno strato il più regolare possibile.

• Rettilineità: le tracce devono essere rettilinee in modo da evitare la reciproca intersezione ed indurre, in questo modo, irregolarità sul fondo dello strato. Questo difetto dipende, oltre che dalle oscillazioni delle singole tracce, anche dal passo di scansione; minore è il passo, infatti, e maggiori saranno le probabilità che le ondulazioni delle tracce vadano a collidere.

• Ripetibilità: la traccia, in quanto unità di base del l’asportazione per strati, deve essere caratterizzata sempre dalla stessa profondità e dalla stessa larghezza; il profilo deve quindi poter essere ripetuto più volte con la certezza della stabilità dimensionale. Questa particolare caratteristica dipende strettamente dall’affidabilità dell’alimentatore che genera il duty cycle del laser e dalla velocità di rotazione degli attuatori galvanometrici che muovono gli specchi. Per generare radiazioni, caratterizzate sempre dalla medesima energia per unità di lunghezza (ε), conviene impostare il ciclo di carico sul valore massimo e regolare la velocità di scansione in modo da ottenere il valore

voluto. L’alimentatore, infatti, presenta una buona stabilità per cicli di carico prossimi al 100%, mentre per valori inferiori il campo di oscillazione della potenza è assai più ampio.

I parametri di processo scelti in modo da fornire un ragionevole compromesso per tutte le esigenze sopra esposte sono:

o Pin=50W (duty cycle del 100%), o v=500mm/s,

o f=200mm.

L’energia per unità di lunghezza vale ε=100J/m mentre la profondità vale D=0,13mm e la larghezza W=0,40mm. In questo modo si utilizzano valori stabili della potenza e velocità di scansione che riducono sensibilmente il problema delle ondulazioni della traccia. Inoltre il valore ε=100J/m, già ampiamente usato nelle prove precedenti, ha fornito tracce con caratteristiche geometriche oscillanti in un campo ristretto (∆D=∆W= +2.₁₀-2_mm).

Il secondo passo da compiere nell’analisi teorica del processo di vaporizzazione di uno strato, è lo studio degli effetti indotti dalle variazioni del passo di scansione.

4.4.1 Passo di scansione

Questo parametro che interviene nel processo di vaporizzazione degli strati di PMMA influisce sensibilmente sulla rugosità totale RT e conseguentemente sulla regolarità e sull’uniformità del

fondo dello strato.

Il passo di scansione può essere impostato manualmente tramite disegno CAD, o scelto tra una serie di valori presenti nel programma CAD-MARK che governa il processo di scansione. Nel primo caso, per ottenere una determinata distanza tra le scansioni, si disegnano, all’interno della superficie da asportare, una serie di segmenti paralleli tra loro e separati da una opportuna spaziatura; successivamente il file contenente la superficie, opportunamente “campita” con i segmenti paralleli che rappresentano le scansioni da effettuare, viene passato sul programma CAD-MARK che avvia la scansione. In questo modo si può scegliere il passo di scansione che meglio si adatta alle esigenze dell’asportazione, ma il processo risulta lungo e laborioso.

Nel secondo caso si fa effettuare la campitura della superficie direttamente dal programma CAD-MARK scegliendo un multiplo intero del passo di scansione minimo, realizzabile dalla macchina, pari a 25µm. Un passo impostato pari a 10 unità di base vale 250µm, e così via.

Un altro parametro gestito dal programma CAD-MARK è l’orientamento della campitura interna; questo ulteriore parametro verrà esaminato in seguito.

Uno schema del processo di riempimento è presentato in fig.4.29.

Disegno della figura in ambiente CAD

Parametri di processo:Pin,v,f

Campitura della figura nel programma CAD-MARK con il passo di scansione impostato

-Posizione della scansione -Impostazione dei tempi di ON/OFF

Fig.4.29 Schema del procedimento logico per la scansione di superfici

Questo secondo metodo è sicuramente migliore del primo in quanto l’unità di base è sufficientemente piccola da consentire un notevole campo di variazione del passo di scansione e, inoltre, i tempi di processo vengono abbattuti notevolmente dal riempimento automatico della figura.

I valori del passo di scansione presi in esame sono: (250-200-150-100-50-25)µm.

Nei paragrafi successivi si analizzerà come le caratteristiche geometriche dello strato asportato, dipendano dal passo di scansione. Più precisamente si studieranno gli effetti di questo parametro sulla profondità dello strato e sulla rugosità superficiale del fondo dell’impronta ottenuta per vaporizzazione.

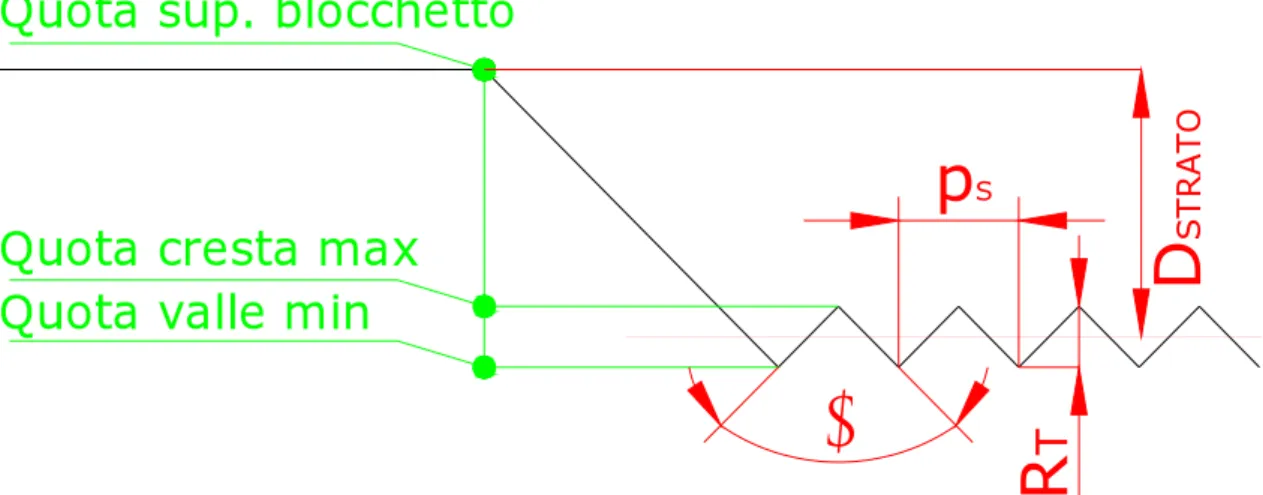
4.4.1.1 Modello previsionale

Se si considera una sezione trasversale del blocchetto di PMMA rappresentato in fig.4.3, si ottiene un profilo come quello in fig. 4.28. Ammettendo che questo sia stato realizzato da N