Capitolo 3 Identificazione con modello energetico e momento motore sul drum nullo

(1)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo

Capitolo 3

Identificazione con modello energetico

e momento motore sul drum nullo

3.1 Introduzione

In tutti i settori scientifici è forte l’esigenza di poter prevedere il comportamento dei sistemi dinamici sia per pervenire ad una corretta interpretazione dei fenomeni sia per svolgere previsioni, diagnosi e simulazioni. L’industria aeronautica, meccanica, edile ma anche il settore economico e biologico, da cui si è preso spunto per la realizzazione degli algoritmi genetici, possono essere citati come esempi di realtà che necessitano di previsioni del comportamento di sistemi dinamici.

Il grande interesse del settore industriale, verso la generazione di modelli capaci di simulare il comportamento reale dei sistemi, è dovuto al fatto che avere a disposizione tali modelli, durante la progettazione, può ridurre considerevolmente le indagini sperimentali su prototipi o componenti singoli, che oltre a richiedere elevati investimenti possono necessitare di lunghi periodi di realizzazione.

Con il termine di modello si vuole indicare, in generale, la rappresentazione di un oggetto, di un sistema fisico o di un fenomeno, che ne riproduce alcune caratteristiche e comportamenti al fine di poterli conoscere e studiare anche qualora l’oggetto modellizzato non sia disponibile. La disciplina che permette l’elaborazione di modelli matematici, che descrivono in maniera affidabile sistemi dinamici anche molto complessi, prende il nome di identificazione dei sistemi ed è largamente utilizzata in tutti i settori scientifici.

(2)

reali. Le metodologie disponibili si basano sull’analisi delle risposte del sistema soggetto ad ingressi affetti da disturbi per cui appare chiaro come in questo contesto, le tecniche di filtraggio abbiano un ruolo fondamentale al fine di poter separare il segnale vero dai disturbi.

Il principio fondamentale delle tecniche di identificazione è quello di minimizzare la differenza tra la risposta analitica del modello e la risposta misurata nel sistema reale sottoposto allo stesso ingresso.

L’identificazione dei sistemi si può schematizzare in due fasi fondamentali:

1. realizzazione di campagne sperimentali sull’oggetto o sul sistema che si vuole identificare, in numero sufficiente da essere utilizzate in parte per la generazione del modello ed in parte per la sua validazione;

2. individuazione del modello matematico in grado di descrivere il sistema dinamico, White Box, Black Box, Gray Box, e delle metodologie numeriche per effettuare l’ identificazione.

3.2 Identificazione di sistemi

Le tecniche per la costruzione di un modello matematico che descriva un sistema dinamico possono essere suddivise in tre categorie:

• "White Box"o "Scatola trasparente";

• "Black Box" o "Scatola nera";

• "Grey Box" o "Scatola grigia".

Nell’approccio White Box il modello viene ricavato a partire dalle equazioni del moto che descrivono la dinamica del sistema. Questi modelli a scatola trasparente sono modelli a sfondo fisico, in cui cioè il comportamento delle parti che costituiscono il sistema è descrivibile da equazioni dinamiche. I vantaggi di una descrizione del genere derivano dal non avere la necessità di grandi campagne di prova e dalla possibilità di poter aggiungere al sistema nuovi componenti. Per contro gli svantaggi sono dovuti alla necessità di adottare ipotesi semplificative che molte volte non riescono a ridurre la dimensione di modelli relativi a sistemi molto complessi.

(3)

L’approccio Black Box è tipico in quelle applicazioni in cui non è possibile o non interessa ottenere per il sistema un modello a sfondo fisico. Questi modelli approssimano la dinamica del sistema con sufficiente accuratezza garantendo una descrizione sintetica ma priva di alcun fondamento fisico. I modelli ARMAX, ARX, ARMA, BOX-JENKINS vengono utilizzati all’interno di questo approccio per stimare, direttamente dai dati sperimentali, i parametri che compaiono nel modello. I vantaggi offerti da questo metodo sono relativi alla semplicità con cui i sistemi, anche molto complessi, vengono descritti. Gli svantaggi derivano dalla necessità di una vasta campagna di prove e dall’impossibilità di controllare il sistema non conoscendone le leggi costitutive elementari che lo governano.

La tecnica Grey Box è un approccio intermedio ai due appena decritti. Infatti viene usato qualora, pur conoscendo (almeno in parte) la struttura del modello matematico che descrive la dinamica del sistema non si conoscano i valori dei parametri che lo costituiscono. Necessariamente i pro e i contro di un metodo simile si pongono a metà strada tra quelli dei modelli a scatola trasparente e nera.

Evidentemente, qualsiasi sia l’approccio utilizzato per la descrizione del modello matematico, è chiaro che questo si prefigga come obbiettivo quello di descrivere il legame tra i segnali misurati, distinti in segnali di ingresso, anche detti input, e in segnali di uscita, output. I segnali di uscita, y(t), sono determinati nel loro complesso dagli input di comando u(t) e da quelli di disturbo e(t), come illustrato in figura 3.1.

y(t)

e(t)

u(t)

_Sistema

dinamico

figura 3.1 Rappresentazione schematica della relazione tra gli input di comando e di

disturbo e l’uscita.

In molti casi di identificazione di sistemi, l’effetto del rumore sull’uscita non è significativa se comparata con l’effetto generato dall’ingresso di comando. Con un basso rapporto tra l’ingresso di comando e quello di disturbo è dunque meno importante avere un

(4)

capire il ruolo del disturbo all’interno del modello. Nel caso di un aeroplano gli ingressi di disturbo sono rappresentati da raffiche o turbolenze mentre nel caso di test dinamometrici i disturbi possono essere individuati nelle vibrazioni della strumentazione utilizzata. In ogni caso il rumore non ha necessariamente un significato fisico per cui viene considerato disturbo semplicemente tutto ciò che non è dovuto all’input u(t). Questo spiega come ripetendo il test con lo stesso input si abbiano segnali di uscita tipicamente differenti.

Il problema relativo alla scelta dell’approccio con cui modellizzare il sistema è relativo alla determinazione di un metodo che riproduca al meglio l’interazione tra u(t), e(t) e y(t), schematizzata in figura 3.1 attraverso il blocco sistema dinamico. L’identificazione del sistema descrive l’interazione tra questi segnali considerando il tempo come una variabile discreta, dal momento che le strumentazioni utilizzate durante le prove registrano esclusivamente segnali ad istanti di tempo discreti, normalmente equidistanziati secondo un intervallo temporale chiamato sampling interval.

Il processo che porta, attraverso stadi iterativi, alla determinazione della migliore struttura del modello che riproduce con la più alta affidabilità i dati relativi al sistema in oggetto può essere sintetizzato come segue:

fase sperimentale: 1. realizzazione di un esperimento (definizione delle condizioni di prova, della strumentazione utilizzata, la modalità di eccitazione del sistema e le tecniche di misurazione) idoneo alla raccolta dei dati di ingresso e uscita, necessari per l’identificazione del sistema;

2. i dati raccolti devono essere ripuliti dai segnali di disturbo;

fase analitica: 3. scegliere e definire una struttura del modello:

4. calcolare i parametri della struttura in modo che questa risponda al meglio ai dati sperimentali;

5. analizzare le proprietà del modello ottenuto;

6. se il modello ottenuto si ritiene soddisfacente si conclude l’ operazione di identificazione altrimenti è necessario ritornare al passo 3 al fine di definire una nuova struttura o al passo 4 per provare con un diverso metodo di stima dei parametri.

(5)

3.3 Varianti di modelli per la descrizione di sistemi dinamici

Un sistema dinamico può essere descritto, come già introdotto nel paragrafo 3.2, attraverso tre diversi approcci, scatola trasparente, scatola nera e scatola grigia, che possono essere realizzati attraverso modelli differenti.

Nel caso dell’approccio scatola trasparente un sistema dinamico lineare può essere descritto:

• nel dominio del tempo attraverso una equazione differenziale di ordine n:

( )

_{( )}

( )

_{( )}

t u b ... dt t u d b dt t u d b t y a ... dt t y d a dt t y d a _m ₁ 0 1 m 1 m m m m 0 1 n 1 n 1 n n n n ₊ ₊ ₊ ₌ ₊ ₊ ₊ − − − − − − _(3.1)

in cui i coefficienti ai e bj sono i parametri da stimare;

• nel dominio del tempo tramite n equazioni differenziali di ordine uno, detta rappresentazione in variabili di stato:

( )

( ) ( )

   + + = + + = t t D t C t t K t B t A t e u x y e u x x& (3.2)

in cui x

( )

t ∈ℜn è il vettore delle variabili di stato mentre A, B, C, D, K sono delle opportune matrici. Da notare che se K=0 la sorgente dell’errore va ad influenzare solo l’uscita e non viene costruito nessun modello che rappresenti le proprietà del disturbo. Se invece si ha D=0 gli ingressi di comando non influenzano direttamente l’uscita bensì indirettamente attraverso le variabili di stato;

• nel dominio della frequenza:

( )

s GU

( )

s HE

( )

s

Y = + (3.3)

in cui, per un sistema lineare tempo invariante, G è la funzione di trasferimento che indica, nel dominio della variabile complessa, il rapporto tra il generico ingresso di comando e la generica uscita, mentre H è il modello del disturbo che descrive come il disturbo in uscita

(6)

Nel caso di approccio scatola nera il modello più utilizzato è quello ARX [8] in cui la relazione base tra i segnali di ingresso e di uscita, nel caso in cui il segnale di disturbo possa essere ignorato, è data dall’equazione lineare alle differenze:

( )

t a y(t T) a y(t 2T) ... a y

(

t nT

)

bu(t T) b u

(

t 2T

)

... b y

(

t mT

)

y = ₁ − + ₂ − + + _n − + ₁ − + ₂ − + + _m − (3.4)

in cui i coefficienti a_i e b sono i parametri da identificare. In questo caso l’uscita al tempo _j t è data da una combinazione lineare dell’ingresso e dell’uscita stessa ad istanti di tempo diversi da quello attuale. Disponendo di misure sperimentali, le tecniche di identificazione di sistema, devono ricavare:

• i coefficienti a_i e b ; _j

• quanti ritardi temporali sono necessari ai fini della descrizione della dinamica del sistema;

• il valore del tempo di ritardo T.

Esistono diverse varianti del modello ARX note come modelli errore di uscita (output-error OE), modelli ARMAX, modelli FIR e modelli BOX-JENKINS (BJ), i quali presentano strutture simili a quella esposta sopra ma contenenti anche la caratterizzazione delle proprietà del disturbo e.

3.4 Identificazione del sistema ruota-tamburo

3.4.1 Considerazioni preliminari

Nei capitoli precedenti è stato più volte evidenziato come il presente lavoro di tesi si inserisca all’interno di un più ampio progetto di ricerca svolto al DIA che si prefigge come obbiettivo finale la realizzazione di un modello, rappresentativo della dinamica di velivoli al suolo, che consenta di interpretare adeguatamente la dinamica del pneumatico e dunque le forze scambiate tra il suolo e la ruota sul quale il pneumatico è montato. Il numero esiguo dei test in possesso, l’assenza di registrazioni relative alla forza longitudinale, i dati affetti da disturbi e il fatto che le modalità con cui le prove sono state condotte non siano

(7)

completamente definite hanno tuttavia complicato l’identificazione del modello. Per questo, l’approccio adottato per la realizzazione del modello è quello definito a scatola grigia, in quanto pur essendo possibile definirne la struttura, nota attraverso le equazioni della dinamica del sistema, non si conoscono i valori dei parametri che vi compaiono. I parametri presenti nel modello, caratterizzanti sia le proprietà del pneumatico che le forze di interazione suolo-pneumatico, sono stati dunque identificati, come ampiamente descritto nel capitolo 2, i primi attraverso strutture utilizzate in [3] e in [4] in ambiti simili, i secondi mediante una procedura di identificazione manuale che ha permesso di poter risalire alle strutture e ai valori numerici delle costanti presenti.

Avendo un modello basato sulla descrizione fisica del problema che fornisce buoni risultati si vogliono ottimizzare i parametri che compaiono nelle F e _b F_roll, mantenendo invariate le dipendenze dei parametri funzionali δ, R, h, R dalla velocità e dal carico _e verticale, in modo da migliorare ulteriormente l’andamento delle risposte ottenibili.

3.4.2 Programma per l’identificazione

Il miglioramento richiesto viene ottenuto sfruttando la funzione "lsqnonlin" dell’Optimization Toolbox di Matlab in grado di identificare i valori numerici da assegnare alle costanti presenti nelle strutture che definiscono µ_b e µ_roll. La struttura del programma è tale da permettere di confrontare iterativamente i dati sperimentali delle velocità angolari della ruota e del tamburo, con quelli ottenuti dalla simulazione del modello in funzione del valore attuale dei parametri. In base al risultato di tale confronto il programma adatta ad ogni passo successivo il valore di tutti i parametri, procedendo iterativamente fino ad ottenere il minor scostamento tra i dati suddetti. La funzione lsqnonlin consente di determinare la migliore approssimazione di funzioni non lineari con la tecnica dei minimi quadrati (cfr. Appendice D). In sintesi, data una funzione F(x,t):

( )

( ) ( )

          φ − φ − φ − =           = 2 1 1 1 2 1 ... t ,t y t ,t y ... f f ,t F x x x x x (3.7)

(8)

in cui y(x,t) è l’output che deve inseguire con errore trascurabile il segnale Φ(t) per un vettore x e uno scalare t, i parametri x per i quali f_i

( )

x →0 sono quelli che minimizzano la funzione f

( )

x ottenuta come somma dei quadrati delle componenti di F(x,t), ossia:

[ ]

[

f ( ) f ( ) f ( ) ... f ( )

]

2 1 min ) ( f min 2 m 2 3 2 2 2 1 n n x _x x x x x x + + + + = ℜ ∈ ℜ ∈ (3.8)

La funzione lsqnonlin determina i parametri del modello attraverso l’equazione (3.8) che può essere riscritta in forma compatta come segue:

∑

= ℜ ∈ ℜ ∈ = m 1 i 2 i n 2 2 n ₂ f ( ) 1 min ) ( F 2 1 min x x x x (3.9)

All’utente, attraverso la lsqnonlin, non spetta il compito di impostare la somma dei quadrati bensì quella di definire la funzione di costo F detta anche funzione dei residui. Nel caso in esame si vogliono determinare i parametri capaci di minimizzare la differenza tra la velocità angolare simulata e sperimentale sia per la ruota che per il tamburo per cui la funzione di costo F è data dalla media pesata di due contributi F_ω_w e

D F_ω : D w (1 )F F F=α _ω + −α _ω (3.10)

in cui le componenti delle funzioni

w

F_ω e

D

F_ω sono costituite dai residui, ad ogni istante di campionamento, espressi come percentuali dei rispettivi valori sperimentali:

( )

(

)

( )

                   ω ω − ω ω ω − ω = ω m samp w m samp w m sim w 1 samp w 1 samp w 1 sim w w t t t , ... t t t , t , F x x x ,

( )

(

)

( )

                 ω ω − ω ω ω − ω = ω m samp D m samp D m sim D 1 samp D 1 samp D 1 sim D D t t t , ... t , t t , t , F x x x x (3.11)

(9)

funzione costo F delle funzioni F_ω_w e

D

F_ω ; ovviamente il suo valore individua quale tra i valori sperimentali delle velocità angolari della ruota e del tamburo verrà meglio approssimato.

3.4.3 Modello in ambiente Simulink adattato al programma di

identificazione

Il programma per l’identificazione dei parametri attraverso il modello non lineare adotta il modello Simulink QSTM_08, sviluppato a partire dal modello QSTM_07 da cui differisce unicamente per alcune strutture e non per le equazioni relative al modello energetico in esso implementate.

Lo schema di primo livello illustrato nella figura 3.2 mostra come, anche in questo caso, il sistema venga forzato da tre ingressi, uno rappresentato dal momento frenante applicato

4 mi_b 3 Omega_W 2 Omega_D 1 sx T orque_sim Omega_D N_0 N V Om ega_W T_D F x h sx m i_b TYRE MECHANICS Memory1 RD T_D F x N Om ega_D DYNAMOMETRIC MACHINE 0 Constant Omega_W N Tw F x h Om ega_W WHEEL DYNAMICS T ORQUE DRUM Memory 1 1 1 Braking T orque T _W

(10)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 1 [samp_t,samp_T ] measured data T _D Torque Drum Step Sindelay Multiport Switch1 Finite step T _D_0 Constant 1

figura 3.3 Modello QSTM_08 Simulink: ingresso Torque Drum (II livello).

alla ruota, l’altro dal momento applicato al tamburo e un terzo costituito dal carico verticale N_0 costante per ogni test. Come si vede nella figura 3.3, l’ingresso rappresentato dal Torque Drum può essere impostato, analogamente al modello QSTM_07, su diverse tipologie di segnale in cui T_D_0 rappresenta un valore costante specifico della condizione di moto in esame (cfr. Appendice E). L’ingresso Braking Torque, costituito da un vettore il cui valore viene settato anche in questo caso su diverse tipologie di segnale in funzione della condizione di moto in esame, viene assegnato al sistema ruota-tamburo dall’esterno attraverso il comando sim presente nel codice di identificazione (cfr. Appendice E). Inoltre, il programma per l’identificazione prevede che nel caso l’ingresso Braking Torque venga settato sul momento frenante sperimentale, il primo valore registrato, la cui entità, diversa da zero, è funzione del test considerato, venga sostituito da un valore nullo. Questa sostituzione si rende necessaria al fine di evitare che nei primissimi istanti dall’applicazione del momento frenante il sistema risponda in modo anomalo, a causa di

(11)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n fi g u ra 3 .4 (a ) M o d el lo Q S T M _ 0 8 S im u lin k : b lo cc o W h ee l D y n am ic s (I I l iv el lo ). WHEEL DYNAM ICS Wheel angular acceleration

Gestione del bloccaggio del pneumatico

Se t > 0 Xo = 0

NAND = 0 se entrambi sono veri ovvero se omega = 0 e la coppia

frenante è maggiore delle altre

1 Omega_W 0 0 ang. acceleration TT Tyre Torque ST OP Stop Simulation == Relational Operator 0 Omega Mux NAND 1 s xo Integratore con saturazione a 0 e reset se va a 0 1 s xo Integrator brake energy Omega_W_0 Initial angular velocity 0 Initial condition [1] 1/IW u[1]==0.0 u[1] >u[2] 1 0 NAND_out Omega_Wd Energy_B Brake energy (dissipated) |u| |u| 5 h 4 x 3 F 2 Tw 1 N

(12)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n u llo 7 7 fi g u ra 3 .4 (b ) M o d el lo Q S T M _ 0 8 S im u lin k : b lo cc o D y n am o m et ri c M ac h in e (I I l iv el lo ).

DYNAMOMETRIC MACHINE MODEL

Drum T orque 1 Omega_D Vhx_d Sum1 Sum ST OP Stop Simulation1 == Relational Operator1 u2 Math Function 1 s xo Integrator RD Omega_D_0 Initi al Angular Velocity of the Drum

RD ID/2 1/ID Energy_D Drum energy DT Drum T orque 1 0 Omega_Dd Accel eration 4 N 3 x 2 F 1 T _D

(13)

una forzante costituita al tempo zero da un gradino che evolve in rampa, negli istanti immediatamente successivi. Inoltre un momento frenante positivo al tempo zero comporta che la ruota parta bloccata, resettando la velocità angolare alla condizione iniziale, come è evidente dall’analisi dell’operatore logico NAND presente nello schema di secondo livello della ruota, figura 3.4(a). Sempre dall’osservazione delle figure 3.4(a) e (b) si può notare come un’ulteriore differenza tra i modelli QSTM_07 e QSTM_08, necessaria al fine di garantire una corretta identificazione dei parametri, sia rappresentata dalla sconnessione degli "stop simulation" nei blocchi Wheel Dynamics e Dynamometric Machine attivi con velocità angolari nulle. Infatti la funzione lsqnonlin, durante l’identificazione, può assegnare ai parametri valori per i quali lo scorrimento pratico s_x superi il massimo valore per cui il modello è stato realizzato determinando il bloccaggio della ruota e in alcuni casi anche il repentino rallentamento del tamburo fino al suo completo arresto. All’annullamento delle velocità angolari, se gli stop simulation sono attivi si assiste ad un’immediata interruzione della simulazione e dell’identificazione senza che il ciclo sia arrivato a convergenza, in caso contrario l’identificazione prosegue assegnando ai parametri dei valori capaci di ridurre il massimo errore percentuale.

Un’altra differenza tra i modelli QSTM_07 e QSTM_08 è costituita dalla function Tyre_08 contenuta nel blocco Tyre Mechanics, differente dalla Tyre_07 unicamente per la presenza di nuovi parametri tra le uscite e di controlli sul raggio di rotolamento frenato

b e

R e sullo scorrimento s_x, necessari per la gestione del bloccaggio della ruota e del tamburo.

3.4.4 Risultati dell’identificazione

L’analisi dei parametri identificati attraverso l’uso della funzione lsqnonlin, evidenzia come i risultati ottenuti siano funzione delle scelte fatte circa l’intervallo temporale nel quale valutare le funzioni F_ω_w e

D

F_ω , del peso α e della modalità di uscita dal processo iterativo di identificazione ma non dei valori iniziali assunti dai parametri.

Con riferimento all’identificazione dei parametri che compaiono nel coefficiente di attrito

b

(14)

relativa agli istanti immediatamente successivi all’applicazione del momento frenante, e nell’intervallo 2÷8 secondi, analisi di lungo periodo nel quale gli effetti del transitorio sono ormai estinti. Inoltre l’identificazione relativa al corto periodo è stata attuata in alcuni test attraverso il modello lineare in s_x, descritto nel paragrafo 2.8, in altri utilizzando il modello non lineare completo (QSTM_08).

Nel caso dell’identificazione del parametro K_roll, presente nel coefficiente di attrito di rotolamento µ_roll, l’analisi è stata svolta unicamente nell’intervallo temporale 2÷8 secondi attraverso il modello non lineare. Bisogna evidenziare come le identificazioni dei parametri che compaiono nei coefficienti d’attrito µ_be µ_roll siano state svolte considerando come forzanti al sistema un momento frenante pari a quello sperimentale e un momento nullo sul tamburo.

I valori dei parametri sono stati inoltre ottenuti per tre diversi valori di α pari a 0.5, 0.95, 1 al fine di poter valutare il valore di α in grado di fornire le curve simulate più rappresentative degli andamenti delle velocità angolari per la ruota e il tamburo e per poter valutare l’effettiva influenza del tamburo nel processo identificativo.

Attraverso l’ottimizzatore di opzioni optimset si è imposto che, la funzione lsqnonlin termini l’identificazione quando la tolleranza tra due valori consecutivi della f

( )

x è di

7

10− , che nel caso in cui la convergenza non fosse stata ancora raggiunta permette di identificare i parametri senza allungare eccessivamente i tempi di simulazione, ragguardevoli nei casi di più parametri in contemporanea. L’analisi dei valori assunti dalla

( )

x

f durante i cicli iterativi evidenzia che durante la prima iterazione f

( )

x diminuisce sensibilmente rispetto al valore corrispondente ai parametri originali del modello mantenendosi successivamente in un regione approssimabile con un plateau come illustrato nel caso di figura 3.5. Tale regione è caratterizzata da set di parametri i cui valori sono diversi ad ogni iterazione ma comunque tali da aumentare la precisione del segnale simulato su quello inseguito rispetto a quelli iniziali. Ovviamente di tali set, che sono tutti validi, vengono infine assunti nel modello quelli corrispondenti al raggiungimento della tolleranza richiesta. In ogni caso si è ritenuto necessario variare la tolleranza sulla funzione

( )

x

f o sullo step x, la cui tolleranza è di 10−6, ogni qual volta il valore assegnato ai parametri non corrisponde al plateau dellaf

( )

x bensì ad una regione dellaf

( )

x

(15)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 5 10 15 20 25 30 0 0.01 0.02 f( x ) Test3 Test3 Test3 Test3 _αααα=0.95=0.95=0.95=0.95 0 5 10 15 20 25 30 2 4 6 Kµ s x 0 5 10 15 20 25 30 -60 -40 -20 C 0 0 5 10 15 20 25 30 0 1 2 Iteration C 1

figura 3.5 Valori assunti da f

( )

x ,

x s

K_µ , C , ₀ C₁ durante l’identificazione dei tre parametri per il test 3 con α = 0.95.

Un’ estesa campagna di identificazione dei parametri, realizzata mediante valori iniziali diversi da quelli originali del modello, ha permesso di poter affermare che l’ottimizzatore adottato possiede una scarsa sensibilità alla condizione iniziale. Infatti, nel caso di identificazione di un solo parametro, sia con il modello lineare in s_x che con il modello non lineare completo, si assiste alla convergenza del ciclo iterativo alla medesima soluzione, indipendentemente dal valore iniziale. Effettivamente con il modello lineare in

x

s la soluzione viene raggiunta per effettiva convergenza alla soluzione mentre nel caso di modello non lineare per raggiungimento della tolleranza imposta sulla f

( )

x . Nel caso dell’identificazione dei tre parametri K_µ_s_x , C e ₀ C₁, al variare dei valore iniziale, si ottengono invece dei valori diversi ma comunque molto vicini tra loro.

(16)

Le tabelle 3.1 e 3.2 riassumono le identificazioni svolte per il sistema ruota-tamburo di cui successivamente si riportano i risultati nel dettaglio.

CORTO PERIODO

x s K_µ MODELLO LINEARE IN s_x : x s K_µ ,R _e x s K_µ con K_roll =0

MODELLO NON LINEARE COMPLETO QSTM_08 :

x s

K_µ con K_roll =0,K₂ =0

tabella 3.1 Test per la determinazione, nel corto periodo, dei parametri evidenziati.

LUNGO PERIODO

x s K_µ x s K_µ , C , ₀ C₁ x s K_µ , C con ₀ C₁=0 x s K_µ ,C , ₀ C₁ con K_roll =0

MODELLO NON LINEARE COMPLETO QSTM_08:

roll

K

tabella 3.2 Test per la determinazione, nel lungo periodo, dei parametri evidenziati.

Corto periodo

• parametroK_µ_s_xattraverso modello lineare in s_x.

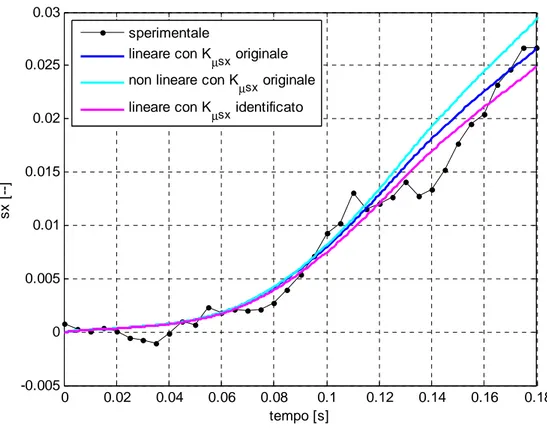
Il valore di K_µ_s_x identificato col modello lineare in s_x, illustrato ampiamente nel paragrafo 2.8, determina, per i tre test, un’uscita s_x simulata con parametri identificati che si avvicina maggiormente ai dati sperimentali, rispetto all’uscita simulata coi parametri originali, all’aumentare del carico. Infatti attraverso le figure 3.6, 3.7, 3.8, in cui si

(17)

confrontano le curve s_x

( )

t ottenute per i tre test attraverso il modello non lineare completo, il modello lineare con parametri originali e identificati e i dati sperimentali, si denota che il miglioramento ottenuto attraverso l’identificazione diminuisce andando dal test1 al test 3 per il quale risulta trascurabile. Per i test1 e test2 si vede come la curva magenta, relativa al sistema lineare con

x s

K_µ identificato, approssimi la curva dei dati sperimentali molto meglio rispetto alla curva blu, relativa allo stesso modello ma con

x s

K_µ originale. Entrambe risultano poi discoste dalla curva relativa al modello non lineare completo a causa dell’aver considerato V& =0 e R_e_b =R_e.

I poli del sistema lineare con parametro identificato valgono -351.3, -213.7, -74.6 rispettivamente per il test1, test2, test3.

Ad ultimo si sottolinea come le identificazioni dei parametri attraverso modello lineare in

x

s vengono realizzate mediante ottimizzazione della funzione di costo costituita in questo caso dal residuo, ad ogni istante di campionamento, dello scorrimento s_x.

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 -0.005 0 0.005 0.01 0.015 0.02 0.025 0.03 tempo [s] s x [ --]

sx - Confronto curve - Test1 sx - Confronto curve - Test1 sx - Confronto curve - Test1 sx - Confronto curve - Test1

sperimentale lineare con K

µsx originale

non lineare con K

µsx originale

lineare con K

µsx identificato

figura 3.6 Confronto tra curve nel periodo di tempo 0÷0.18 secondi, identificazione di

x s

(18)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 -0.01 0 0.01 0.02 0.03 0.04 0.05 0.06 tempo [s] s x [ --] sperimentale lineare con K µsx originale

non lineare con K

µsx originale

lineare con K

µsx identificato

x s

K_µ con modello lineare in s_x per il test2.

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 -0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 tempo [s] s x [ --] sperimentale lineare con K µsx originale

non lineare con K

µsx originale

lineare con K

µsx identificato

x s

(19)

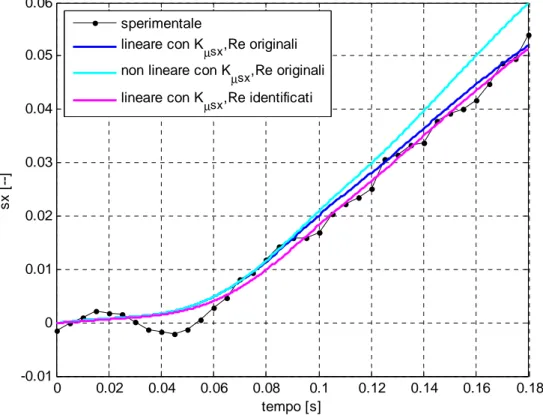
• parametri K_µs_x, R attraverso modello lineare in _e s_x.

Il secondo test di identificazione nel breve periodo, con modello lineare in s_x, è relativo alla valutazione dei parametri

x s

K_µ ,R ; infatti negli istanti immediatamente successivi _e all’applicazione del momento frenante, a causa della forte inerzia del tamburo, si ha V& =0 per cui R può essere considerato costante con ottima approssimazione. _e

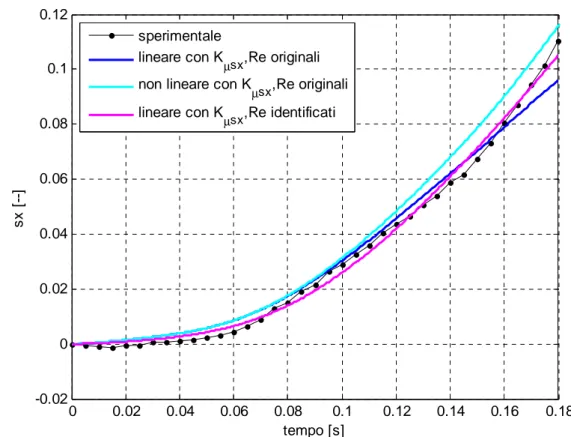
L’identificazione di K_µ_s_xe R , eseguita con tolleranza sulla funzione pari a _e 10−7, permette di ottenere curve simulate molto vicine alle curve sperimentali, come mostrato attraverso le curve magenta nelle figure 3.9, 3.10, 3.11. Nonostante questo i valori ottenuti per R non sono fisicamente accettabili in quanto, come già visto nel paragrafo 2.7.2, il _e valore del raggio di puro rotolamento deve essere compreso tra i valori dell’altezza h tra mozzo e suolo e il raggio indeformato R , ossia: ₀

[0.5028 0.5272 0.5707] < R < 0.59625 _e

Diminuendo la tolleranza, al fine di ottenere valori fisicamente accettabili per R , si _e è ottenuto che nessuno dei valori identificati soddisfa l’intervallo sopraccitato. Evidentemente gli unici valori in grado di soddisfarlo sono rappresentati unicamente dai valori originali.

Ne consegue che, nelle figure 3.9, 3.10, 3.11 la curva che deve essere effettivamente presa in considerazione corrisponde a quella blu, ottenuta attraverso il modello lineare in

x

s con i parametri originali. Nonostante questo è evidente come, pur coi parametri originali, il modello lineare in s_x approssimi meglio i dati sperimentali rispetto al modello non lineare, costituendo dunque una conferma della validità delle ipotesi alla base del modello lineare.

(20)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 -0.005 0 0.005 0.01 0.015 0.02 0.025 0.03 tempo [s] s x [ --] sperimentale lineare con K µsx,Re originali

non lineare con K

µsx,Re originali

lineare con K

µsx,Re identificati

x s

K_µ e R con modello lineare in _e s_x per il test1.

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 -0.01 0 0.01 0.02 0.03 0.04 0.05 0.06 tempo [s] s x [ --] sperimentale lineare con K µsx,Re originali

non lineare con K

µsx,Re originali

lineare con K

µsx,Re identificati

x s

(21)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 -0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 tempo [s] s x [ --] sperimentale lineare con K µsx,Re originali

non lineare con K

µsx,Re originali

lineare con K_µ_sx,Re identificati

x s

K_µ e R con modello lineare in _e s_x per il test3.

• parametro K_µs_x attraverso modello non lineare con l’ipotesi K_roll =0.

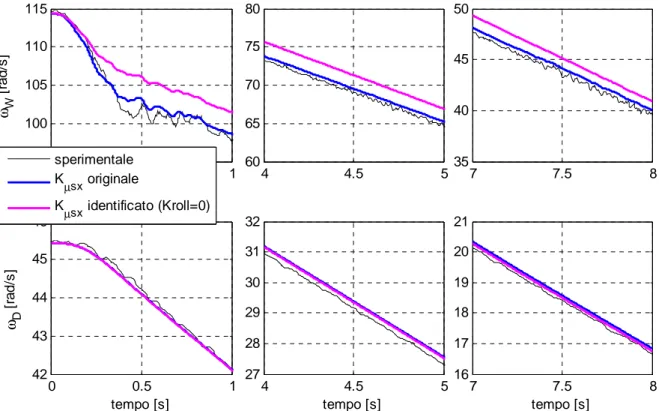
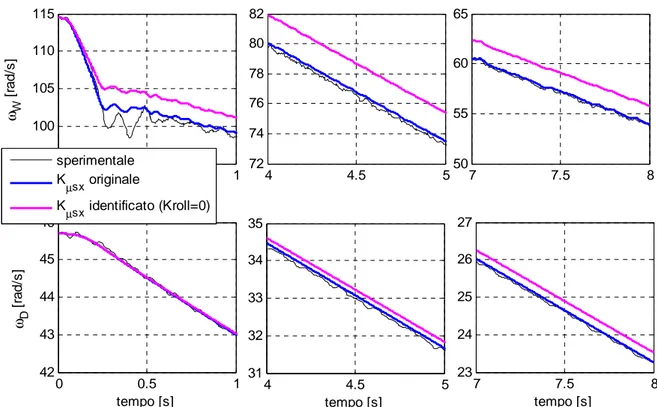
L’identificazione del parametro K_µ_s_xnegli istanti 0÷0.18 secondi, attraverso il modello non lineare completo, con l’ipotesi K_roll =0 ha generato valori diversi da quelli originali per i tre valori del peso α. Le figure successive illustrano, sia per la ruota che per il tamburo, alcuni ingrandimenti relativi al confronto tra le velocità angolari sperimentali e simulate, con i parametri originali e identificati, e gli errori percentuali riferiti all’intero periodo di simulazione.

L’aver ipotizzato K_roll =0, comporta una buona approssimazione dei dati sperimentali solo nei primissimi istanti dal momento che, subito dopo l’applicazione del momento frenante, il valore dello scorrimento pratico è piccolo. Nel momento in cui s_x inizia ad aumentare il termine 2

x

s non è più trascurabile, per cui aver assunto nel modello K_roll =0 determina col trascorrere del tempo, una divergenza sempre maggiore tra le curve sperimentali e simulate.

(22)

La figura 3.15 mette a confronto gli errori percentuali delle velocità angolari della ruota e del tamburo, calcolate con i parametri originali del modello e con i parametri identificati con l’ipotesi K_roll =0 per i tre test nel caso α = 0.5. L’osservazione dei tre grafici illustra quanto spiegato in precedenza, evidenziando come attraverso i parametri originali si ottengano curve che approssimano meglio i dati sperimentali rispetto a quelle prodotte con

x s

K_µ identificato. Inoltre la figura mette in risalto come nel corto periodo il modello non sia in grado di produrre per la ruota un output capace di inseguire con buona approssimazione il segnale sperimentale. Tale scostamento, evidente nel test 1 e nel test2, in cui l’errore massimo è rispettivamente del 6.2% e 6.5% nel caso di parametri identificati e del 2.3% e 3.8% nel caso di parametri originali, diventa sproporzionato nel test 3 in cui il valore massimo è del 35% con parametro identificato e del 29% con parametro originale.

La figura 3.16 mette a confronto gli errori percentuali per il test 1 in cui i parametri sono stati identificati con i tre diversi valori di α.

0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 60 65 70 75 80 7 7.5 8 35 40 45 50 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K_µ sx originale K_µ_sx identificato (Kroll=0) 4 4.5 5 27 28 29 30 31 32 tempo [s] 7 7.5 8 16 17 18 19 20 21 tempo [s]

figura 3.12 Ingrandimenti delle velocità angolari della ruota e del tamburo, identificazione

di

x s

(23)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 72 74 76 78 80 82 7 7.5 8 50 55 60 65 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx originale K_µ_sx identificato (Kroll=0) 4 4.5 5 31 32 33 34 35 tempo [s] 7 7.5 8 23 24 25 26 27 tempo [s]

di K_µ_s_x con l’ipotesi K_roll =0 per il test2 e α = 1.

0 0.5 1 70 80 90 100 110 120 ωW [ ra d /s ] 4 4.5 5 90 92 94 96 7 7.5 8 80 82 84 86 88 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx originale K_µ_sx identificato (Kroll=0) 4 4.5 5 40 40.5 41 41.5 42 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 tempo [s]

(24)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n u llo 8 9 fi g u ra 3 .1 5 R af fr o n to t ra g li er ro ri p er ce n tu al i d el le v el o ci tà a n g o la ri d el la r u o ta e d el ta m b u ro n ei tr e te st p e r α = 0 .5 , i d en tif ic az io n e d i x s K µ c o n l’ ip o te si 0 K ro ll₌ . 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 αααα =0.5 Test1 =0.5 Test1 =0.5 Test1=0.5 Test1 e % tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 αααα =0.5 Test2 =0.5 Test2 =0.5 Test2 =0.5 Test2 tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 35 40 tempo [s] α

ααα=0.5 Test3=0.5 Test3=0.5 Test3=0.5 Test3

e% della ω

W con parametri originali

e% della ω

D con parametri originali

e% della ω

W con parametri identificati

e% della ω

(25)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n fi g u ra 3 .1 6 R af fr o n to t ra g li er ro ri p er ce n tu al i d el le v el o ci tà a n g o la ri d el la r u o ta e ta m b u ro p er il te st 1 a i d iv er si v al o ri d i α , id en tif ic az io n e d i x s K µ co n l’ ip o te si K ro ll₌ 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 α

ααα=1 Test1=1 Test1=1 Test1=1 Test1

e % tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 αααα =0.95 Test1 =0.95 Test1 =0.95 Test1 =0.95 Test1 tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 αααα =0.5 Test1 =0.5 Test1 =0.5 Test1=0.5 Test1 tempo [a]

e% ω_W con parametri originali e% ω_D con parametri originali e% ω_W con parametri identificati e% ω_D con parametri identificati

(26)

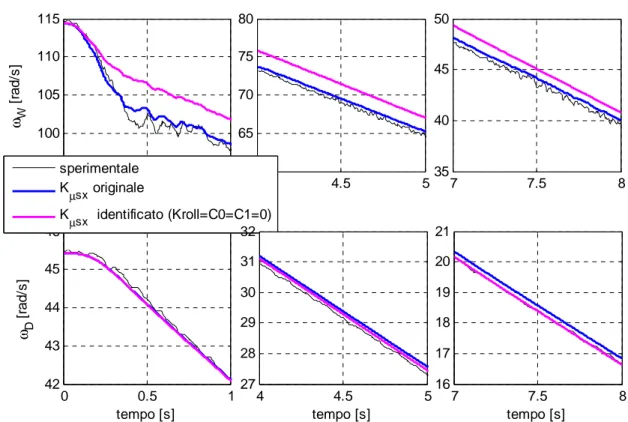
• parametroK_µs_xcon l’ipotesi K_roll =0, K₂ =0 attraverso modello non lineare.

L’ultimo caso analizzato nel corto periodo, con modello non lineare, è quello relativo all’identificazione del parametro K_µ_s_xcon l’ipotesi K_roll =0,K₂ =0. Con tali ipotesi le forze longitudinali di contatto suolo-pneumatico vengono riscritte come segue:

    µ = ⋅ = _µ N F N ) s ( sign s K F 0 roll roll x x x s b (3.12)

in cui cioè si è eliminata, in entrambe le componenti, la dipendenza quadratica dallo scorrimento pratico. Anche in questo caso le simulazioni ottenute approssimano bene i dati sperimentali nei primi 0÷0.18 secondi in cui lo scorrimento è piccolo e tale che s2_x ≅0. Negli istanti successivi, con l’aumentare di s_x, si assiste ad una graduale divergenza tra le curve simulate e quelle sperimentali.

Anche in questo caso, come nel precedente, vengono riportanti degli ingrandimenti di alcuni grafici relativi al confronto tra le velocità angolari sperimentali e simulate, con i parametri originali e identificati, figure 3.17, 3.18, 3.19. Inoltre le figure 3.20 e 3.21 illustrano gli errori percentuali riferiti all’intero periodo di simulazione, per i tre test con parametri originali e identificati ottenuti attraverso un peso α pari a 0.5 e per il test1 al variare di α. Da notare che i casi analizzati attraverso i suddetti grafici sono gli stessi delle figure 3.12, 3.13, 3.14, 3.15 e 3.16 relative al caso K_roll =0; in questo modo si possono evidenziare meglio le differenze apportate dalle diverse identificazioni .

(27)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 60 65 70 75 80 7 7.5 8 35 40 45 50 0 0.5 1 42 43 44 45 46 tempo [s] ω D [ ra d /s ] sperimentale K_µ_sx originale K_µ_sx identificato (Kroll=C0=C1=0) 4 4.5 5 27 28 29 30 31 32 tempo [s] 7 7.5 8 16 17 18 19 20 21 tempo [s]

di K_µ_s_xcon l’ipotesi K₂ =K_roll =0 per il test1 e α = 0.95.

0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 70 75 80 85 7 7.5 8 50 55 60 65 0 0.5 1 42 43 44 45 46 tempo [s] ω D [ ra d /s ] sperimentale K_µ_sx originale K_µ_sx identificato (Kroll=C0=C1=0) 4 4.5 5 31 32 33 34 35 tempo [s] 7 7.5 8 23 24 25 26 27 tempo [s]

figura 3.18 Ingrandimenti delle velocità angolari della ruota e del tamburo, identificazione =

(28)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.5 1 70 80 90 100 110 120 ωW [ ra d /s ] 4 4.5 5 90 92 94 96 7 7.5 8 80 82 84 86 88 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx originale K_µ_sx identificato (Kroll=C0=C1=0) 4 4.5 5 40 40.5 41 41.5 42 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 tempo [s]

di

x s

(29)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n fi g u ra 3 .2 0 R af fr o n to t ra g li er ro ri p er ce n tu al i d el le v el o ci tà a n g o la ri d el la r u o ta e ta m b u ro n ei tr e te st p e r α = 0 .5 , i d en tif ic az io n e d i x s K µ co n l’ ip o te si 0 K K ro ll 2 = = . 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 αααα =0.5 Test1 =0.5 Test1 =0.5 Test1 =0.5 Test1 e % tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 8 αααα =0.5 Test2 =0.5 Test2 =0.5 Test2 =0.5 Test2 tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 35 40 tempo [s] α

e% della ω_W con parametri originali e% della ω

e% della ω

(30)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n u llo 9 5 fi g u ra 3 .2 1 R af fr o n to t ra g li er ro ri p er ce n tu al i d el le v el o ci tà a n g o la ri d el la r u o ta e d el ta m b u ro p er il te st 1 ai d iv er si v al o ri d i α , id en tif ic az io n e d i x s K µ co n l’ ip o te si 0 K K ro ll 2 = = . 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 α

ααα=1 Test1=1 Test1=1 Test1=1 Test1

e % 0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 α

ααα= 0.95 Test1= 0.95 Test1= 0.95 Test1= 0.95 Test1

0 2 4 6 8 -2 -1 0 1 2 3 4 5 6 7 α

e% ω

(31)

Lungo periodo

• parametro

x µs

K attraverso modello non lineare.

L’ identificazione del parametro K_µ_s_x nel periodo di tempo 2÷8 secondi comporta un netto miglioramento dell’inseguimento della curva sperimentale, sia per la ruota che per il tamburo, rispetto ai casi di identificazione nel breve periodo con le ipotesi K_roll =0 e

0

K_roll = ,K₂ =0.

Le figure 3.22, 3.23, 3.24 riportano gli ingrandimenti delle velocità angolari per la ruota e il tamburo per i casi di identificazione di

x s

K_µ per il test 1 con α pari a 0.95, il test 2 con α pari ad 1 e per il test 3 con α = 0.5, al fine di poter continuare il raffronto dei risultati già iniziato nell’identificazione di corto periodo attraverso modello non lineare. La migliore approssimazione ottenuta attraverso questa identificazione, rispetto a quelle svolte in precedenza, induce a rappresentare gli errori percentuali per i tre test per tutte le configurazioni di α, figure 3.25, 3.26, 3.27. La figura 3.28 mostra in particolare un ingrandimento del test3 che esclude la zona di picco presente nei primi istanti del test.

0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 64 66 68 70 72 74 7 7.5 8 35 40 45 50 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx originale K_µ_sx identificato 4 4.5 5 27 28 29 30 31 32 tempo [s] 7 7.5 8 16 17 18 19 20 21 tempo [s]

(32)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 72 74 76 78 80 82 7 7.5 8 52 54 56 58 60 62 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx originale K_µ_sx identificato 4 4.5 5 31 32 33 34 35 tempo [s] 7 7.5 8 23 24 25 26 27 tempo [s]

figura 3.23 Ingrandimenti delle velocità angolari della ruota e del tamburo,

identificazione di x s K_µ per il test2 e α = 1. 0 0.5 1 70 80 90 100 110 120 ωW [ ra d /s ] 4 4.5 5 90 91 92 93 94 7 7.5 8 81 82 83 84 85 86 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx originale K_µ_sx identificato 4 4.5 5 40 40.5 41 41.5 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 tempo [s]

figura 3.24 Ingrandimenti delle velocità angolari della ruota e del tamburo,

identificazione di

x s

(33)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n F ig u ra 3 .2 5 E rr o ri p er ce n tu al i p er le v el o c ità an g o la ri d el la ru o ta e d el ta m id en tif ic az io n e d i x s K µ p er il t es t1 a l v ar ia re d el p es o α . 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 αααα =1 Test1 =1 Test1 =1 Test1 =1 Test1 e % tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 αααα =0.95 Test1 =0.95 Test1 =0.95 Test1 =0.95 Test1 tempo [s] 0 2 4 6 8 -3 -2 -1 0 1 2 3 tempo [s] α

e% ω_W con parametri originali e% ω

e% ω

(34)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n u llo 9 9 fi g u ra 3 .2 6 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d i x s K µ p er il t es t2 a l v ar ia re d el p es o α . 0 2 4 6 8 -2 -1 0 1 2 3 4 αααα =1 Test2 =1 Test2 =1 Test2 =1 Test2 e % tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 αααα =0.95 Test2 =0.95 Test2 =0.95 Test2=0.95 Test2 tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 tempo [s] α

e% ω_W con parametri originali e% ω_D con parametri originali e% ω

e% ω

(35)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n fi g u ra 3 .2 7 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m id en tif ic az io n e d i x s K µ p er il t es t3 a l v ar ia re d el p es o α . 0 2 4 6 8 -5 0 5 10 15 20 25 30 αααα =1 Test3 =1 Test3 =1 Test3 =1 Test3 e % tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 αααα =0.95 Test3 =0.95 Test3 =0.95 Test3 =0.95 Test3 tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 tempo [s] α

e% ω

(36)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n u llo 1 0 1 fi g u ra 3 .2 8 In g ra n d im e n ti d eg li er ro ri p er ce n tu a li d el le v el o ci tà a n g o la ri d el la r u o ta e d el ta m b u ro p er il te st 3 . 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 αααα =1 Test3 =1 Test3 =1 Test3 =1 Test3 e % tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 αααα =0.95 Test3 =0.95 Test3 =0.95 Test3 =0.95 Test3 tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 tempo [s] α

e% ω

(37)

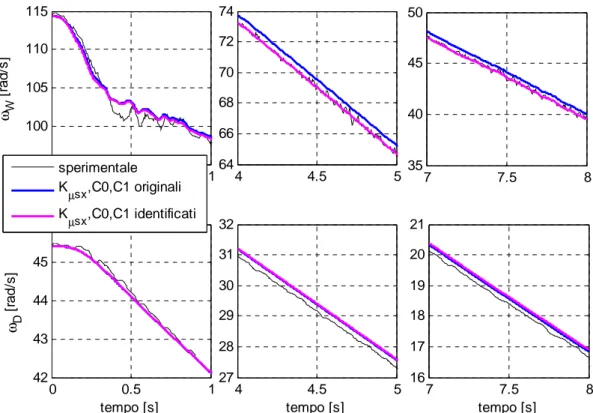
• parametri K_µs_x, C e ₀ C₁ attraverso modello non lineare.

Attraverso l’identificazione simultanea di

x s

K_µ , C e ₀ C₁ si ottengono dei valori per i tre parametri per i quali le curve simulate delle velocità angolari della ruota e del tamburo si accostano ai dati simulati con ottima approssimazione.

Anche in questo caso vengono riportati alcuni ingrandimenti delle velocità angolari della ruota e del tamburo e gli errori percentuali per i tre test per ogni valore di α, figure 3.29 – 3.35 al fine di poter continuare il raffronto con gli altri casi presi in esame.

Nell’appendice F vengono inoltre riportati alcuni grafici in cui sono descritte le dipendenze tra i parametri fondamentali del modello e il tempo di simulazione.

0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 64 66 68 70 72 74 7 7.5 8 35 40 45 50 0 0.5 1 42 43 44 45 46 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx,C0,C1 originali K_µ_sx,C0,C1 identificati 4 4.5 5 27 28 29 30 31 32 tempo [s] 7 7.5 8 16 17 18 19 20 21 tempo [s]

di

x s

(38)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.5 1 95 100 105 110 115 ωW [ ra d /s ] 4 4.5 5 72 74 76 78 80 82 7 7.5 8 52 54 56 58 60 62 0 0.5 1 42 43 44 45 46 tempo [s] ω D [ ra d /s ] sperimentale K_µ_sx,C0,C1 originali K_µ_sx,C0,C1 identificati 4 4.5 5 31 32 33 34 35 tempo [s] 7 7.5 8 23 24 25 26 27 tempo [s]

di

x s

K_µ , C e ₀ C₁ per il test 2 con α = 1.

0 0.5 1 70 80 90 100 110 120 ω W [ ra d /s ] 4 4.5 5 90 91 92 93 94 7 7.5 8 81 82 83 84 85 86 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] sperimentale K_µ sx,C0,C1 originali K_µ_sx,C0,C1 identificati 4 4.5 5 40 40.5 41 41.5 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 tempo [s]

(39)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n fi g u ra 3 .3 2 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m id en tif ic az io n e d i x s K µ , 0C e 1C p er il t es t1 a l v ar ia re d el p e so α . 0 2 4 6 8 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 αααα=1 Test1 =1 Test1 =1 Test1=1 Test1 e % tempo [s] 0 2 4 6 8 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 αααα=0.95 Test1 =0.95 Test1 =0.95 Test1 =0.95 Test1 tempo [s] 0 2 4 6 8 -6 -5 -4 -3 -2 -1 0 1 2 3 tempo [s] α

e% ω

(40)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n u llo 1 0 5 fi g u ra 3 .3 3 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m b u ro , id en tif ic az io n e d i x s K µ , 0C e 1C p er il t es t2 a l v ar ia re d el p e so α . 0 2 4 6 8 -2 -1 0 1 2 3 4 αααα =1 Test2 =1 Test2 =1 Test2=1 Test2 e % tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 αααα =0.95 Test2 =0.95 Test2 =0.95 Test2 =0.95 Test2 tempo [s] 0 2 4 6 8 -2 -1 0 1 2 3 4 tempo [s] α

e% ω

(41)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n fi g u ra 3 .3 4 E rr o ri p er ce n tu al i p er le v el o ci tà an g o la ri d el la ru o ta e d el ta m id en tif ic az io n e d i x s K µ , 0C e 1C p er il t es t3 a l v ar ia re d el p e so α . 0 2 4 6 8 -5 0 5 10 15 20 25 30 35 αααα =1 Test3 =1 Test3 =1 Test3 =1 Test3 e % tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 35 αααα =0.95 Test3 =0.95 Test3 =0.95 Test3 =0.95 Test3 tempo [s] 0 2 4 6 8 -5 0 5 10 15 20 25 30 35 tempo [s] α

e% ω

e% ω_D con parametri originali e% ω

(42)

C a p ito lo 3 - I d en tif ic a zi o n e co n m o d el lo e n e rg et ic o e m o m en to m o to re s u l d ru m n u llo 1 0 7 fi g u ra 3 .3 5 In g ra n d im e n ti d eg li er ro ri p er c en tu a li d el le v el o ci tà a n g o la ri d el la r u o ta e d el ta m b u ro p er il te st 3 . 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 αααα =1 Test3 =1 Test3 =1 Test3 =1 Test3 e % tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 αααα =0.95 Test3 =0.95 Test3 =0.95 Test3 =0.95 Test3 tempo [s] 0 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 tempo [s] α

e% ω_W con parametri identificati e% ω

(43)

• parametri K_µs_x,C attraverso modello non lineare e con l’ipotesi ₀ C₁ = 0 .

Con questa identificazione si vuole valutare l’effettiva dipendenza diretta del coefficiente

µb dalla velocità di avanzamento la cui equazione, sotto l’ipotesi C1= 0, si riduce in:

(

K s_x C₀s2_x

)

sign(s_x)

x s

b = +

µ µ (3.12)

L’identificazione con C₁= 0 comporta che, per il test1 e il test2, per valori del peso α pari ad 0.95 e 0.5, la funzione lsqnonlin converga dopo numerose iterazioni ai valori originali mentre con α=1 non riesca ad identificare alcun parametro. In ogni caso, sempre per i test1 e 2, simulando il sistema mediante i valori originali di

x s

K_µ e C , con l’ipotesi ₀ C₁= 0, si ha in pochi decimi di secondo il bloccaggio della ruota e l’arresto del tamburo in circa tre secondi, come illustrato in figura 3.36. Questo comportamento però non si rileva nel test3 per il quale l’identificatore assegna ai parametri

x s

K_µ e C valori diversi da quelli originali ₀ per i quali durante la simulazione non si ha l’arresto del sistema, figura 3.37. Risulta dunque chiaro che la dipendenza diretta del coefficiente µb dalla velocità è comunque

funzione del carico verticale applicato.

0 0.5 1 1.5 2 2.5 3 3.5 4 0 10 20 30 40 50 O m e g a D ru m [ ra d /s ] 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0 50 100 150 tempo [s] O m e g a W h e e l [r a d /s ] sperimentale non lineare con K

µsx,C0,C1 originali non lineare con K

µsx,C0 identificati (C1=0)

(44)

Capitolo 3- Identificazione con modello energetico e momento motore sul drum nullo 0 0.5 1 70 80 90 100 110 120 ωW [ ra d /s ] 4 4.5 5 90 91 92 93 94 95 7 7.5 8 80 82 84 86 88 0 0.5 1 45 45.5 46 46.5 47 tempo [s] ωD [ ra d /s ] sperimentale K_µ_sx,C0,C1 originali K_µ_sx,C0 identificati (C1=0) 4 4.5 5 40 40.5 41 41.5 tempo [s] 7 7.5 8 36 36.5 37 37.5 38 tempo [s]

di

x s

K_µ e C con l’ipotesi ₀ C₁= 0 per il test 3 con α = 0.5.

E’ inoltre utile evidenziare come in questo caso la funzione f(x) oscilli tra un valore

minimo e uno massimo a causa di una fluttuazione di

x s

K_µ e C attorno ad una linea di ₀ confine quasi orizzontale, come indicato in figura 3.38 in cui la f(x) viene rappresentata in

scala logaritmica per apprezzarne meglio le variazioni. Le figure 3.39 e 3.40 riportano inoltre lo spostamento nel piano (

x s

K_µ ,C , 0) del punto identificato ad ogni iterazione e il ₀ tragitto compiuto per andare dal punto iniziale X0, relativo ai valori originali diK_µ_s_x ,C , ₀

a quello finale Xf, corrispondente ai valori identificati.

• K_µs_x,C e ₀ C₁ attraverso modello non lineare con l’ipotesi K_roll =0.

L’identificazione nel lungo periodo dei tre parametri K_µ_s_x, C e ₀ C₁ con l’ipotesi 0

K_roll= comporta un pessimo inseguimento della curva dei dati sperimentali, come è chiaramente visibile sia dagli ingrandimenti delle figure 3.41, 3.42, 3.43 ma soprattutto dagli errori percentuali illustrati nelle figure 3.44-3.47. Dalle figure è evidente come il termine quadratico in sx del coefficiente di attrito di rotolamento abbia un forte peso