Capitolo 4

Capitolo 4

Modelli Frattali delle immagini SAR

4.1 Introduzione ai Frattali

La geometria frattale può essere vista come la naturale estensione della geometria classica e nasce dall'esigenza di descrivere insiemi e funzioni fortemente irregolari. Tale esigenza si è manifestata soprattutto negli ultimi anni, vale a dire quando si è osservato che molti fenomeni naturali potevano essere meglio rappresentati con insiemi irregolari piuttosto che con le figure della geometria classica.

Le superfici frattali, sin dai primi studi di Mandelbrot [9], sono state largamente usate al fine di modellare le forme naturali. La definizione di insieme frattale nasce con la definizione, data da Hausdorff, relativa alla misura dell’estensione di un insieme nello spazio ¡ . Secondo Mandelbrot, n un insieme in ¡ è un frattale se la sua dimensione di Hausdorff è un valore n frazionario strettamente maggiore della sua dimensione topologica n. Dai numerosi studi fatti successivamente si è giunti alla conclusione che non esiste una definizione unica di frattale. Questo implica che non è possibile stabilire quando un insieme è frattale, si può soltanto affermare che un insieme A possiede una natura frattale se rispetta i seguenti assunti [10]:

I. Possiede una struttura fine, vale a dire un livello di dettaglio estremo fino a scale arbitrariamente piccole;

II. E’ troppo irregolare perché sia descritto dal tradizionale linguaggio geometrico, sia localmente sia globalmente;

III. A possiede un’autosimilarità, magari in maniera approssimata o statistica;

IV. Normalmente, la sua “dimensione frattale” è più grande della sua dimensione topologica;

V. Nella maggior parte dei casi di interesse A è definito in maniera molto semplice, spesso ricorsivamente.

Le superfici naturali soddisfano all’incirca tutte le proprietà sopra elencate, di conseguenza possono ragionevolmente essere modellate tramite funzioni frattali.

Negli ultimi 20 anni, i frattali sono stati applicati con successo nella modellizazione del traffico informatico, del clutter marino, della voce, del traffico stradale, delle immagini radiografiche ed in altre applicazioni.

I primi studi [11] relativi agli scenari naturali furono condotti da Pentlad il quale mostrò che un’immagine fotografica di una superficie frattale conservava le stesse caratteristiche frattali del soggetto ripreso (intese come dimensione frattale). Direttamente da queste osservazioni nasce l’idea di modellare le immagini SAR di scenari naturali tramite i frattali [12], ed in particolare negli ultimi anni alcuni studiosi hanno dimostrato che il comportamento frattale della superficie marina viene in qualche modo conservato nell’eco elettromagnetico del segnale radar. [13] [14]

4.2 Modelli Frattali

4.2.1 Fractional Brownian Motion (fBm)

Questo modello fu introdotto da Kolmogorov nel 1968 ed è uno dei modelli frattali tra i più usati in letteratura nelle applicazioni di Image Processing. Il modello fBm è stato usato nella modellizzazione delle immagini SAR relative a superfici marine, campi coltivati, foreste, ed altro.

L’estensione bidimensionale delle funzioni fBm ci conduce alla superficie

h(x,y) che risulta essere un processo bidimensionale non stazionario,

Gaussiano a media nulla, con funzione di autocorrelazione:

(

)

2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 1 2 2 ( , , , ) ( )H ( )H ( ) ( ) H 0 1 h R x x y y ∝_ x +x + y +y − x −y + x −y _ <H<   (4.1)

La varianza risulta spazio variante e si assume essere della seguente forma:

2 2 2

( , ) ( )H H

h x y x y

σ ∝ + =ρ (4.2)

con ρ = x2+ y2

Il parametro di Hurst (H) assume valori appartenenti a (0,1) ed è legato con la dimensione frattale D dalla relazione D=3-H. L’interpretazione del parametro H è legata alla “rugosità” (irregolarità) della superficie generata; questa aumenta con H →0, mentre per H →1 la funzione generata tende ad una classica forma Euclidea (Fig. 4.1a, 4.1b).

Dato che il modello fBm è non stazionario, ma ha incrementi stazionari, risulta conveniente studiare le caratteristiche di questo processo usando l’autocorrelazione e lo spettro del processo relativo ai sui incrementi, definito come:

( , ; , ) ( , ) ( , )

h x y x y h x x y y h x y

∆ ∆ ∆ @ + ∆ + ∆ − (4.3)

il quale risulta essere un processo stazionario, Gaussiano, a media nulla, la cui densità spettrale di potenza (psd) è:

(

)

2 2 2 1 ( , ) I x y H x y S f f f f ∝ + (4.4)

Fig. 4.1 – Superfici fBm generate per valori diversi del parametro di Hurst: (a)relativa ad H=0.2, (b) relativa ad H=0.9

La varianza σ_∆h relativa al processo degli incrementi, spesso chiamata

“structure function of the fBm” , è una funzione delle direzioni spaziali

(∆ ∆x, y): 2 2 ( , ) ( , ; , ) H h x y h x y x y σ_∆ ∆ ∆ = Ε ∆_ ∆ ∆ _∝ ∆ρ (4.5) dove: ∆ = ∆ + ∆ρ x2 y2

Si osserva che la densità di probabilità del primo ordine del processo degli incrementi è invariante alle traslazioni, alle rotazioni ed alla combinazione delle due trasformazioni. In questo senso l’fBm è un campo Gaussiano autosimilare.

A causa della non stazionarietà del modello fBm, la densità spettrale di potenza non può essere definita; seguendo un approccio direttamente derivato dalla teoria 1-D delle funzioni fBm, è possibile definire una densità di probabilità generalizzata per il modello fBm 2-D tramite una media spaziale della distribuzione di Wigner-Ville, dalla quale risulta:

(

)

2 2 2 2 1 ( _x, _y) _H x y S f f f f + ∝ + (4.6)

Dalla relazione precedente possiamo dedurre che la funzione di

50 100 150 200 250 50 100 150 200 250 50 100 150 200 250 50 100 150 200 250 (a) (b)

autocorrelazione generalizzata Rh(∆ ∆x, y) ha una simmetria circolare e che il valore di questa per una data distanza ∆ = ∆ + ∆ρ x2 y2 , rappresenta la correlazione media tra due punti aventi distanza Euclidea pari a ∆ρ.

Per quanto detto si osserva che il processo fBm 2-D è un campo isotropico, nel senso che sia la sua varianza insieme a quella relativa al processo dei sui incrementi ed alla correlazione media (R ) sono indipendenti dalla direzione h

angolare (hanno, infatti, simmetria circolare).

Esiste in ogni caso la possibilità [15] di modificare questo modello al fine di modellare campi anisotropici, cosa che di fatto lo renderebbe molto più adatto nel rappresentare situazioni reali. Una tecnica usata per accentuare l’anisotropia del modello è quella di intervenire sul metodo di determinazione degli incrementi; scegliendo ad esempio diversi ordini di incremento lungo le due direzioni ortogonali nello spazio si può giungere al suddetto scopo. In particolare, la funzione strutturante σ_∆h può essere riscritta come: 2 ( ) aniso H h f σ_∆ ∝ ∆ρ θ (4.7) dove: 0<H <1, , ∆ = ∆ + ∆ρ x2 y2 θ = ∠ ∆ + ∆( x j y)

Introducendo la funzione f, periodica di periodo π , si riesce a modellare la dipendenza dalla direzione angolare; nel caso di modello fBm isotropico risulterà f=cost.

4.2.2 Fractional Gaussian Noise (fGn)

Nel momento in cui la superficie naturale da modellare è ipotizzata stazionaria, vengono considerati modelli più semplici del precedente come ad esempio i processi Gaussiani frazionari bidimensionali (2D-fGn).

Tale modello si verifica essere stazionario, isotropico, con una densità spettrale di potenza:

(

)

2 2 2 1 ( x, y) d x y S f f f f ∝ + (4.8)

dove d è un parametro con valore compreso nell’intervallo (0.3, 2) relativo al grado di irregolarità della superficie modellata. Per bassi valori del parametro la “rugosità” aumenta. Si può dimostrare che per 0.5< <d 1 la funzione di autocorrelazione del modello fGn può essere espressa in forma chiusa e risulta: 2 2 ( , ) d h R ∆ ∆ ∝ ∆x y ρ − (4.9) dove: ∆ = ∆ + ∆ρ x2 y2

Si osserva che anche in questo caso che la correlazione spaziale ha una simmetria circolare. Inoltre per valori del parametro 1

2

d > si osserva che il

processo ha un comportamento LRD (Long Range Dependance), in altre parole la correlazione tra due punti decade in relazione alla loro distanza in maniera crescente per d →1.

Concludendo possiamo affermare che questo modello stazionario, isotropico non tiene conto della direzionalità del campo modellato. Si precisa inoltre che dal momento che in letteratura non viene definito un diretto legame tra d e la dimensione frattale, le superfici generate tramite questo modello non possono essere considerate frattali.

4.2.3 Fraction Differencing (FD)

Al fine di modellare funzioni bidimensionali che rappresentino immagini digitali, si può far uso di processi noti come Fraction Differencing nella loro versione bidimensionale. La densità spettrale di questo processo è del tipo:

(

)

2 2 2 1 ( , ) 2sin x y d x y S f f f f π ∝ + (4.10) con 0< <d 3.

Ancora una volta sia lo spettro di potenza che la funzione di autocorrelazione dipendono dalla sola coordinata radiale. Si osserva inoltre che lo spettro segue la seguente espressione:

2 0

lim d ( )

f→ f S f =K (4.11)

dove f = f_x2+ f_y2 e K∈¡ . Dall’equazione (4.11) si evince che lo ₊

superficie FD è un processo LRD, la sua funzione di autocorrelazione decresce lentamente all’aumentare della distanza radiale.

Il modello FD può essere visto come una estensione nel discreto del modello fGn, infatti per piccoli valori di f la densità spettrale di potenza può essere approssimata con la (4.8).

In conclusione, i processi FD sono stazionari, isotropici, non rappresentano la direzionalità del campo e non sono dichiaratamente frattali.

4.2.4 Modello FARIMA

I modelli fin qui proposti non si adattano in modo soddisfacente alla modellizzazione di superfici con correlazione spaziale a breve distanza ed a lunga distanza. A tale scopo esiste un’estensione del modello Fraction

Differencing noto come Fractionally Integrated Autoregressive Moving Average (FARIMA). La densità spettrale di potenza di questo processo viene

espressa come:

(

)

(

)

2 2 2 2 2 ( , ) 2sin ARMA x y FARIMA x y d x y S f f S f f f f π + ∝ + (4.12) dove la parte 2 1 1 ( ) ( ) ( ) j f ARMA z e A z S f B z π − − =

= rappresenta lo spettro di un processo

monodimensionale ARMA con A z( −1) e B z( −1) polinomi MA e AR di ordine n e m rispettivamente.

La parte ARMA permette di controllare la dipendenza a breve raggio della superficie tramite un decadimento esponenziale per brevi ritardi, mentre la

parte FD dello spettro terrà conto della correlazione iperbolica per il decadimento a lungo raggio. A proposito della caratteristica LRD, si osserva che nelle vicinanze dell’origine, la densità spettrale viene approssimata con:

( )

2

( )

2 _{2 2}

( 0) 2sin d d con:

FARIMA x y

S f → = π f − ≈ π f − f = f + f (4.13) In letteratura [16] questo modello è stato applicato con buoni risultati per la sintesi di strutture di superficie presenti in natura (natural texture). Relativamente a questo campo di applicazione, viene presentata [17] una efficace modellizzazione della superficie marina, la quale, in condizioni meteorologiche buone, può essere considerata un processo stazionario con comportamento omogeneo.

4.3 Modello Frattale per la superficie marina

(Modello di Weierstrass)

Viene presentata nella letteratura scientifica [18] una soluzione alternativa ai modelli precedentemente esposti direttamente ricavata dalla struttura geometrica della superficie del mare. Al fine di esporre al meglio la genesi di questo nuovo modello è necessaria una breve introduzione sulle caratteristiche geometriche e su alcuni principi fondamentali che regolano il comportamento della superficie del mare.

4.3.1 Introduzione

Il moto delle onde del mare è causato dal vento. Quando il vento soffia su una superficie d'acqua liscia essa si increspa; se il vento è persistente l'increspatura aumenta, fino alla nascita del moto ondoso. Quando il vento cessa, le onde si propagano lontano (anche centinaia di Km) e diventano onde swell (onde lunghe).

I fenomeni di generazione e propagazione delle onde del mare sono analiticamente descritti dall'equazione dell'impulso (legge di Newton applicata all'unità di massa) e dall'equazione di continuità (conservazione della massa per unità di volume).

Nell'equazione dell'impulso sono presenti diverse forze che agiscono sul mare e possono essere suddivise in due classi: le forze esterne (vale a dire la forza gravitazionale, la forza di Coriolis, la forza centrifuga e la forza della marea) e le forze interne come la pressione e la viscosità.

L'equazione dell'impulso, espressa in coordinate cartesiane, porta ad un sistema di equazioni differenziali non lineari, la cui soluzione rappresenta l'evoluzione dinamica delle onde di superficie.

A causa della complessità del fenomeno, non esiste una soluzione in forma chiusa. Per ottenere alcuni utili risultati, queste equazioni possono essere linearizzate nel caso di mare sottoposto alla pressione di piccole

perturbazioni d'onda. La soluzione risultante può essere espressa nella

forma:

( )

(

α

)

ξ r,t =asin K⋅r−Ωt+

(4.14)

in cui ξ

( )

r,t rappresenta l’altezza del mare nel punto individuato dal vettore

r all’istante t (Fig. 4.2); il termine K⋅r è il prodotto scalare tra il vettore d’onda K ed r ed α è un termine di fase appartenente all’intervallo [- π,+

π].

La relazione (4.14) è valida quando il suolo è piatto, l’acqua ha una profondità costante, la forza di Coriolis è trascurabile, la densità dell’acqua è costante, si trascurano le viscosità e quando si considera un corpo d’acqua di estensione infinita completamente ricoperto da onde.

Il numero d’onda Κ=2π⁄Λ (Λ è la lunghezza d’onda del mare) e la frequenza angolare Ω sono tra loro legate dalla relazione di dispersione (Fig. 4.3a, Fig. 4.3b), che per acqua profonda vale:

3 K K g s ρ τ + = Ω (4.15)

in cui τ_s è la tensione superficiale, ρ è la densità dell’acqua e g è l’accelerazione di gravità.

Per grandi Λ tali che Ω= gK , le onde del mare sono chiamate onde

gravitazionali (gravity waves); nella condizione opposta, cioè per piccoli Λ

tali che

(

)

3

K s ρ τ =

Ω , le onde del mare sono chiamate onde capillari (capillary waves).

La transizione dal regime gravitazionale al regime capillare si ha in corrispondenza del minimo della velocità di fase (Fig. 4.4):

K K g K V s phase _ρ τ + = Ω =

(4.16)

Derivando rispetto a K ed uguagliando a zero si ottiene:

ρ τ π ρ τ s T s T g g K = ⇒ Λ = 2 (4.17)

Nella regione intermedia coesistono i due regimi per cui occorre usare la relazione di dispersione completa.

Una rappresentazione realistica della superficie del mare deve essere caratterizzata dalla presenza di un gran numero di onde che vanno dal regime gravitazionale a quello capillare.

Fig. 4.3a – Relazione di dispersione per acque profonde

Fig. 4.3b – Relazione di dispersione per acque profonde (ingrandimento della zona di non linearità)

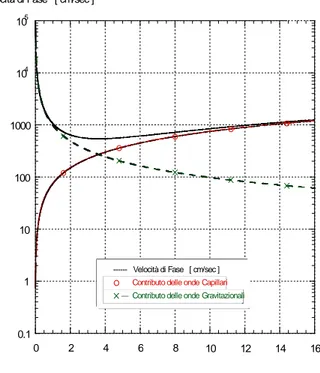
La figura seguente (4.4) riporta l’andamento della velocità di fase in funzione del numero d’onda K distinguendo tra i contributi relativi alle onde capillari e gravitazionali: 0 20 40 60 80 0 2 4 6 8 10 12 14 16 [ rad/sec ] K [ rad/cm] 0 2 4 6 8 10 12 14 0 0.5 1 1.5 2 2.5 3 3.5 4 [ rad/sec ] K [ rad/cm]

Fig. 4.4 – Velocità di fase in funzione del numero d’onda in base alle diverse tipologie di onde

4.3.2 Modello stazionario

Come primo passo viene determinato un modello stazionario della superficie marina che rappresenta la forma del mare ad un fissato istante di tempo. Senza perdere in generalità si assume t = 0 per cui dalla equazione (4.14) si ottiene:

( )

=

_∑

(

⋅ +

)

n n n n K r a r α ξ sin (4.18)

Indicando con Nf il numero di componenti significative si ha:

( )

_∑

−

(

)

= + ⋅ = 1 0 sin f N n n n n K r a r α ξ (4.19)

Il vettore d’onda K_n può essere riscritto come:

      = n n n n n K K K β β sin cos (4.20)

La fase β_n è misurata in senso antiorario rispetto all’asse K_x e rappresenta la direzione di propagazione della n-esima componente rispetto all’asse x (Fig.

0.1 1 10 100 1000 104 105 0 2 4 6 8 10 12 14 16

--- Velocità di Fase [ cm/sec ]

Contributo delle ondeCapillari Contributo delle ondeGravitazionali

Velocità di Fase [ cm/sec ]

Fig. 4.5 – Vettore numero d’onda

Il vettore r può essere riscritto in coordinate cartesiane:

      = y x r (4.21)

Esplicitando il prodotto scalare Kn⋅r nella eq. (4.19) si ottiene:

( )

_∑

−

[

(

)

]

= + + = 1 0 sin cos sin , f N n n n n n n K x y a y x β β α ξ (4.22) Prendendo K_n ed a_n come: n f n K b K = ₀ con b_f > 1 (4.23) n n a a = con 0 < a < 1 (4.24) l’espressione della superficie del mare assume la forma:

( )

_∑

−

[

(

)

]

= + + = 1 0 0 cos sin sin , f N n n n n n f n y x b K a y x β β α ξ (4.25)

Dalle equazioni (4.23) e (4.24) si vede che se l’indice n aumenta le ampiezze

an decrescono e lo stesso comportamento vale anche per le lunghezze d’onda:

n f n b K₀ 2π = Λ Prendendo ( −2) = s a b a con 1 ≤ s < 2 e ba> 1 (4.26) si ottiene:

( )

_∑

− ( )

[

(

)

]

= − _{+ +} = 1 0 0 2 sin cos sin , f N n n n n n f n s a K b x y b y x β β α ξ (4.27)

L’equazione (4.27) rappresenta il modello frattale di una superficie marina stazionaria ed è una funzione frattale bidimensionale.

Riscrivendo tale espressione in coordinate polari

( )

r,θ si ottiene:

( )

_∑

− ( )

[

₍

₎

]

= − _{− +} = 1 0 0 2 cos sin , f N n n n n f n s a K b r b rθ β θ α ξ (4.28)

È interessante osservare che:

fissato θ =ϑ la superficie ξ ,

( )

rϑ è una curva frattale con dimensione: ln( ) 3 (2 ) ln( ) a f b s s b ζ = − − (4.29) fissati θ =ϑ e βn =β si ottiene una curva frattale di Weierstrass, di

dimensione frattale s, che rappresenta il modello frattale monodimensionale del mare in cui tutte le componenti spaziali si propagano nella medesima direzione angolare.

4.3.3 Modello dinamico

Dal momento che la superficie del mare è tempo-variante, è necessario estendere il modello precedente come segue:

(

)

_∑

− ( )

{

[

_{( )}

_{( )}

]

_{( )}

}

= − _{+ −Ω +} = 1 0 0 2 sin cos sin , , f N n n n n n n f n s a K b x t y t t t b C t y x σ β β α ξ (4.30) in cui: bf > 1, ba> 1, 1 ≤ s < 2.

Il modello di equazione (4.30) rispecchia la soluzione (4.27) salvo le direzioni angolari βn

( )

t che sono considerate tempo-varianti.

Quest’ultima condizione significa che il moto delle onde può deviare dalla direzione rettilinea durante il tempo di osservazione (questo effetto è più evidente per le onde capillari piuttosto che per le gravitazionali).

Anche le fasi α_n

( )

t sono dipendenti dal tempo; l’introduzione di una modulazione di fase significa che fissato un punto di coordinate (x,y) e quando la direzione di propagazione delle onde è costante, la dipendenza dal

tempo del moto delle onde marine può differire dalla legge puramente sinusoidale. Ciò produce correlazione temporale tra le onde del mare.

Si analizzano nel seguito i parametri del modello:

• Nf numero di componenti sinusoidali;

• σ deviazione standard dell’ampiezza delle onde del mare; è legata all’altezza significativa dell’onda hs dalla relazione hs = 4σ;

• C fattore di controllo in ampiezza; è impostato per avere una deviazione standard del mare uguale a σ. È possibile dimostrare che:

( ) ( ) 2 2 2 2 2 1 1 f s a N s a b C b − −  ₋    = − (4.31) • b_f fattore di scala in frequenza; influisce sulla distribuzione spettrale

delle componenti sinusoidali;

• ba fattore di scala in ampiezza; controlla l’ampiezza delle onde del mare;

• Ωn frequenza angolare;

• s coefficiente di rugosità (1 ≤ s < 2); fornisce una misura dell’irregolarità della superficie ed è legato alla vera dimensione frattale s_ξ della superficie del mare dalla relazione:

(

) ( )

_{( )}

( )

_{( )}

s b b se b b s s f a f a − ≤ ≤ − − = 2 1 ln ln 0 ln ln 2 3 ξ

• K0 numero d’onda spaziale fondamentale; è dato da 2π Λ0con Λ0

lunghezza d’onda fondamentale.

Processo stocastico βn(t) :

Rappresenta la direzione angolare di propagazione della n-esima componente.

Si assume che tale processo sia stazionario e così caratterizzato:

Valore medio

( )

{

n t

}

n

Una tipica scelta, valida per mare pienamente sviluppato, è β_n =ϕ_w in cui

ϕw rappresenta la direzione angolare del vento.

Funzione di Autocovarianza

( ) ( )

( )n n e C n β τ τ β τ _{τ β} − = 1 (4.33)

in cui τ

( )

β_n è il tempo di correlazione angolare che gode della proprietà

( ) ( )

βn τ βn

τ ₊1 < in quanto onde con lunghezza d’onda più piccola hanno una

più grande correlazione angolare.

Il valore di τ

( )

βn può essere calcolato una volta nota la distribuzione del

primo ordine del processo. Notare che la varianza σβ_n 1τ

( )

βn

2 =

della coordinata angolare incrementa all’aumentare di n. In altre parole ciò significa che le onde capillari sono più sparpagliate rispetto alle onde gravitazionali.

Per descrivere completamente la correlazione tra τ

( )

β_n e τ

( )

β_m con n≠m, occorre fornire la funzione di cross-covarianza _{β β}

( )

τ

m n

C .

Per evitare ulteriori complicazioni nel modello, assumiamo in prima approssimazione che i processi β_n

( )

t siano indipendenti. Questa assunzione è in buon accordo con la soluzione dell’equazione (4.14), che è valida se le onde componenti il mare sono indipendenti.

Funzione densità di probabilità del primo ordine

Una descrizione statistica di β_n

( )

t è fornita definendo la funzione densità di probabilità (pdf) del primo ordine del processo ψ_n

( )

t =β_n

( )

t −β_n:

( )

 _ _      = π ψ ψ ψ 2 2 cos 2 rect g P n e n n (4.34)

La costante g_n è una costante di normalizzazione ed è data da:

(

)

(

n

)

n e n e e g n 2 1 1 22 1 2 + Γ + Γ = − π (4.35)

in cui Γ

( )

• è la funzione gamma ed e_n è un parametro che controlla la dispersione della distribuzione di β_n

( )

t attorno al suo valore medio β_n. Considerando che le onde capillari sono disperse in tutte le direzioni angolari e che le onde lunghe sono più concentrate attorno alla direzione angolare media, i parametri e_n sono presi in accordo alla seguente espressione:

2 1 1 1       + + = n n e T n (4.36)

dove n_T è l’ordine dell’onda sinusoidale il cui numero d’onda

T

n

K è il più vicino al numero d’onda di transizione K_T. La precedente espressione rappresenta il passaggio tra il regime capillare ed il regime gravitazionale e corrisponde a quel valore di K che minimizza la velocità di fase Ω

( )

Kn Kn . Il

risultato è: s T n K g K T τ ρ = ≅ (4.37)

Applicando questa condizione al nostro modello si ha:

                        = f s T b g K n ln 1 ln int 0 τ ρ (4.38)

in cui int

( )

• è l’operatore che prende il più grande intero minore dell’argomento.

Notare che per n=nT la pdf Pn

( )

ψ diventa una funzione a coseno rialzato

con roll-off uguale ad 1.

La figura (4.6) mostra l’andamento di Pn

( )

ψ , per alcuni valori di n, ottenuto

dalla (4.34). Come era logico attendersi, le onde lunghe (piccoli n) hanno una distribuzione più appuntita rispetto alle onde capillari (grandi n), la quale tende ad essere uniforme nell’intervallo

[

−π,+π

]

.

-0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 -3 -2 -1 0 1 2 3 n=20 n=60 n=1000 n=0 n=200 P n ( ψ ) ψ (rad)

Fig. 4.6 – Andamento della funzione di densità di probabilità P_n

( )

ψ

Processo α_n(t) :

Si assume che tale processo sia stazionario e così caratterizzato:

Valore medio:

( )

{

t

}

=0 Eαn (4.39) Funzione di Autocorrelazione:

( )

( )n n e R τα τ α τ π − = 3 2 (4.40) Le fasi αn(t) sono ragionevolmente assunte indipendenti con funzione densità di probabilità del primo ordine uniforme nell’intervallo

[

−π,+π

]

.

In più si assume che α_m(t) è indipendente da β_n(t) per ogni valore di m ed n.

E’ possibile dimostrare che la funzione di autocorrelazione della superficie

(

x y t, ,

)

ξ espressa in (4.30), può essere calcolata in una forma chiusa come:

( )

( )

( )

(

) ( )

[

(

~ ~ ₂

)

]

cos ~ ~ , ~ 1 0 2 ~ 2 2 2 2 2 2 π β ϑ σ π ϑ ξ =

∑

∑

− + ∞ + ∞ − = − = − n n m n m N n R r n s a s m m S r K J e b C r R f n

(4.41)

coefficienti della trasformata serie di Fourier di P_n

( )

ψ , considerata una funzione periodica di periodo 2π (si veda eq. 4.34) e J_m

(

K r_n%

)

sono le funzioni di Bessel del primo tipo di ordine m. Si nota che la funzione di autocorrelazione dipende dalla direzione angolare ϑ , questo significa che il modello è anisotropico.

Calcolando la Trasformata di Fourier della (4.41) ed esprimendo il risultato in coordinate polari si ottiene la densità spettrale di potenza del modello di Weierstrass:

(

)

( ) ( )

(

)

( ) ( )

_{( )}

[

(

)

]

(

)

       − Φ + = Φ

∑

∑

∑

− = ∞ =     + − − − =     + − − 1 0 1 2 2 2 2 2 2 1 0 2 0 2 2 2 2 2 2 2 cos 2 4 2 , 2 2 2 2 2 2 f n n f n n N n m n n m n n K K R n n s a N n n n K K R n n s a K K R I m m S e R b K K R I e R b C K W β π σ

_(4.42)

in cui R_n =εΛ_n è ancora la lunghezza di autocorrelazione spaziale ed

( )

0,....2

n

I ⋅ =n m sono le fuzioni di Bessel modificate.

Integrando rispetto a Φsi ottiene la densità spettrale di potenza radiale:

( )

(

)

2 2 2 1 2 2 ₂ 2( 2) 2 2 0 0 0 ( ) 2 n n f R K K N s n n n n n C S K σ K b R e I R b K K  ₊    − − _{ }   −   = =

∑

(4.43)

L’uso di un elevato numero di parametri garantisce una grande flessibilità del modello. Ogni parametro prende in considerazione un aspetto fisico del mare: distribuzione delle ampiezze e delle lunghezze d’onda, rugosità, correlazione spaziale e temporale delle onde, direzione del vento e propagazione dell’onda swell. Queste caratteristiche permettono al modello di generare molte delle possibili condizioni marine.

4.4 Applicazione dei modelli alle immagini SAR

Gli studi svolti sino ad oggi nell’ambito della tecnica radar ci permettono di ipotizzare che con grande probabilità la struttura delle immagini SAR marine sia direttamente riconducibile alla struttura della superficie del mare nel momento dell’acquisizione. Questa affermazione è motivabile [19] in sintesi, osservando che l’operazione di ricostruzione dell’immagine, operata dal SAR tramite la somma di echi coerenti, è un’elaborazione lineare del segnale reirradiato, di conseguenza le proprietà della superficie potranno subire delle trasformazioni lineari, ma saranno comunque conservate.

La struttura direzionale di una superficie marina, come ampiamente dimostrato nella letteratura scientifica, risulta contraddistinta da un’evidente anisotropia, dovuta alla direzionalità introdotta dall’azione del vento nel meccanismo di generazione del moto ondoso. Le immagini SAR acquisite in presenza di vento persistente mostrano una marcata direzionalità ed una dipendenza angolare della correlazione spaziale (anisotropia). Gli stessi effetti si riscontrano in presenza di onde lunghe (swell) provenienti da zone lontane.

Queste osservazioni, unite alla considerazione che all’interno di una regione di analisi ridotta le immagini SAR possono essere considerate stazionarie, ci permettono di escludere a priori l’impiego del modello fBm, il quale è per sua natura non stazionario. Per quanto riguarda il modello fGn , anch’esso mostra le sue grosse carenze nel momento in cui si vogliano riprodurre l’anisotropia e la direzionalità peculiari dello spettro direzionale del mare. I modelli che più sembrano convenienti al fine di riprodurre le caratteristiche essenziali delle immagini SAR del mare sopra esposte, si rivelano essere il modello FARIMA (Par. 4.2.4) ed il modello di Weierstrass (Par. 4.3.3). Durante tutta l’analisi si suppone di modellare lo spettro direzionale S K( , )θ delle immagini SAR del mare come prodotto di due termini:

( , ) _noise( ) _mare( , )

Stima dello spettro direzionale S f( _x, f_y)

tramite algoritmo di Welch Immagine

SAR

( _x, _y)

S f f

Selezione della regione ad alto contributo informativo e della regione relativa al

rumore

dove S_noise( )K è un contributo di rumore dovuto al sistema di acquisizione

SAR ed alle successive elaborazioni, mentre Smare( , )K θ è contributo informativo legato alle condizioni della superficie marina.

Si osserva che la componente della densità spettrale di potenza dell’immagine SAR indicata con S_mare( , )K θ , relativa all’espressione (4.44),

sarà rappresentata mediante un modello di Weierstrass con parametri frattali diversi da quelli caratteristici della superficie del mare. Il legame tra i parametri frattali della superficie marina e quelli della corrispondente immagine SAR, una volta individuato, ci consentirà l’inversione spettrale a partire dai dati misurati dal sensore.

Con lo schema a blocchi riportato di seguito, si illustrano le operazioni che conducono all’estrazione delle due densità spettrali a partire dai dati reali.

Fig. 4.7 – Schema a blocchi riassuntivo delle analisi spettrali condotte

Calcolo dello spettro medio

del rumore S_noise( )K

( )

noise

S K

Attenuazione del rumore e stima dello spettro omnidirezionaleS_mare( )K

Spettro direzionale (forma polare) filtrato

e

“ripulito” dal rumore

( )

mare

S

K

Algoritmo di conversione della rappresentazione da cartesiana a polare

Tramite una stima spettrale basata sul metodo di Welch, si calcola lo spettro direzionale dell’immagine SAR della superficie del mare; da questo si seleziona una regione in cui supponiamo essere contenuta la gran parte dell’informazione relativa alla superficie marina. Tale zona viene delimitata da due rette parallele alla direzione del massimo dello spettro direzionale (relativo al numero d’onda dominante K_picco), che intersecano la circonferenza con centro l’origine e raggio pari a K_picco, nel valore a -3dB rispetto al valore massimo S K( _picco,θ_picco). Allo stesso tempo si seleziona una regione dello spettro direzionale in cui si suppone essere presente solo rumore. Si passa poi alla forma polare dello spettro direzionale, sul quale nel settore riguardante il rumore sarà calcolato, tramite la media per i valori di θ interni a tale regione, un vettore medio rappresentativo del rumore sull’immagine S_noise( )K .

Una volta nota la densità spettrale media relativa al rumore, appare evidente la possibilità di ridurre la presenza dei disturbi nello spettro direzionale in forma polare semplicemente dividendo ogni colonna relativa ad un valore di

θ fissato, per il vettore rappresentativo del rumore S_noise( )K , supposto

valido per ogni θ . A questo punto, come già esposto nel paragrafo 3.2.4, il calcolo dello spettro omnidirezionale Smare( , )K θ corrisponde ad una somma sulle righe della matrice contente lo spettro direzionale in forma polare. Si osserva che le caratteristiche del rumore medio stimato sull’immagine SAR si prestano bene ad una modellizzazione con il modello FARIMA, mentre lo spettro omnidirezionale della componente S_mare( )K sarà

modellizzato tramite il modello frattale della superficie marina (Par. 4.3.3), il quale, come vedremo nel seguito, sarà completamente caratterizzato mediante l’esplicitazione dei valori assunti da 5 parametri (featrures frattali).

4.4.1 Stima dei parametri del modello FARIMA

Riprendiamo l’espressione della densità spettrale di potenza relativa a questo modello (4.12):

(

)

(

)

(

)

(

)

2 2 2 2 2 ( , ) , * , 2sin ARMA x y FARIMA x y ARMA x y FD x y d x y S f f S f f S f f S f f f f π + ∝ = + (4.45)

La particolarità di questo modello riguarda la capacità di modellare con successo sia le proprietà di correlazione a lungo raggio (LRD), tramite la parte Fraction Differencing, sia le dipendenze a breve raggio, tramite la parte ARMA, come descritto in maniera esaustiva in letteratura [17].

Si osserva che la parte FD è dominante alle basse frequenze, mentre può essere trascurata alle alte dove prevale la parte ARMA.

La stima dei parametri di questo modello è organizzata in maniera ciclica, in altre parole si parte stimando il valore del parametro d e per ogni valore trovato si esegue un secondo processo di stima rivolto alla determinazione dei polinomi che andranno a formare la risposta in frequenza ottima, nel senso del minimo errore quadratico medio, per quel particolare valore del parametro d. Una volta terminato il ciclo, ossia quando verrà soddisfatta la condizione esposta nel seguito, si disporrà della soluzione che meglio approssima lo spettro di partenza.

Stima di parametri Fraction Differencing:

Supponiamo di avere a disposizione lo spettro medio SMEDIO( fx2+ fy2) del processo da modellare, nel nostro caso il rumore, indicando con

2 2

r x y

f = f + f la frequenza radiale, questo può essere espresso come:

( )

( )

2 ( ) 2sin ARMA r MEDIO r d r S f S f f π = (4.46)

Passando ai logaritmi:

[

]

2

( )

( )

log S_MEDIO(f_r) = −dlog 4sin_ π f_{r }+log_S_ARMA f_r _ (4.47) Supponendo di conoscere una stima ˆSMEDIO(f dello spettro medio su un r) numero N di punti, determinato dalla frequenza di campionamento, _R

aggiungendo a destra ed a sinistra della (4.47) i termini ˆSMEDIO(f e r)

( )

log_S_ARMA 0 _, dopo alcuni passaggi aritmetici, risulta:

( )

( )

( )

( )

2 ˆ

log ( ) log 0 log 4sin

ˆ _{( )} log log ( ) 0 MEDIO r ARMA r ARMA r MEDIO r MEDIO r ARMA S f S d f S f S f S f S π  = _  −_ _ _+       + _{ }+ _{ }     (4.48)

Considerando la ˆSMEDIO(f su un range di frequenze che da zero r) progressivamente si estende, si raggiungerà una situazione in cui:

( )

( )

log 0 0 ARMA r ARMA S f S   →       (4.49)

La condizione (4.49) esprime la volontà di avere nella zona delle basse frequenze (cioè nell’intorno dell’origine dell’asse delle frequenze radiali), un contributo dovuto alla parte ARMA trascurabile rispetto a quello dovuto alla parte FD.

Nel momento in cui tale condizione si verifica, la stima di d viene eseguita tramite una regressione lineare della densità spettrale ˆSMEDIO(f su scala r) log-log.

Stima parametri ARMA:

Per isolare la parte ARMA dallo spettro complessivo ˆS_MEDIO(f , si fa _r) riferimento all’espressione (4.46) che, nel caso in cui si abbia a disposizione un valore di riferimento per il parametro d, si riduce a:

( )

( )

2

( ) 2sin d

ARMA r MEDIO r r

S f =S f π f (4.50) In questa fase dell’analisi si ricerca la risposta in frequenza H f relativa ad ( )r un filtro bidimensionale che, comandato da rumore bianco con varianza γ ,

restituisca in uscita una densità spettrale di potenza che sia una buona stima di S_ARMA

( )

f_r , in particolare risulterà:

( )

2

( )

ARMA r r

S f =γ H f (4.51) Dalla precedente relazione, tramite la (4.50), si comprende che:

( )

( )

2

1

( r) ARMA r MEDIO( r) 2sin r d

H f S f S f π f

γ

= ∝ (4.52)

Si parte quindi dalla conoscenza della risposta in frequenza H f( _r) , a meno

di una costante moltiplicativa 1

γ , e si ricerca il filtro digitale, con risposta

impulsiva H z , tale da approssimarla al meglio. ( )

L’operazione di stima del filtro digitale H z avviene tramite una potente ( ) funzionalità, presente tra gli strumenti di Signal Processing presenti in Matlab, denominata invfreqz. Più precisamente, supponendo che sia:

1 1 ( ) (1) (2) ... ( 1) ( ) ( ) (1) (2) ... ( 1) n m B z b b z b n z H z A z a a z a m z − − − − + + + − = = + + + − (4.53)

tale funzione ci permette di calcolare il polinomio di grado n del numeratore e quello di grado m del denominatore, tali da approssimare, con il minimo errore quadratico medio, la risposta in frequenza data in ingresso.

Nell’applicazione seguita nel presente lavoro, la procedura di stima viene fatta ciclare per valori di m e n variabili sull’intervallo

(

1,30 , alla ricerca

)

della migliore approssimazione che dia luogo ad un sistema stabile (tutti poli all’interno del cerchio unitario).

Una volta terminata questa fase del procedimento, tramite la funzione freqz si determina la risposta in frequenza relativa al filtro digitale H z , che ( ) corrisponderà alla migliore approssimazione (nel senso dei minimi quadrati) per H f( _r) che, tramite un’elevazione al quadrato, per la (4.52) ci permette di approssimare la S_ARMA

( )

f_r .

medio ˆSMEDIO(f , che nel presente lavoro corrisponde a r) Snoise( )K , sarà

facilmente calcolabile dalla (4.46), come:

( )

( )

2 ˆ _{( )} 2sin ARMA r MEDIO r d r S f S f f π = (4.54)

4.4.2 Stima dei parametri del Modello Frattale per la superficie

marina

Si fa uso del modello frattale costruito sulle funzioni di Weierstrass, esposto nel Par. 4.3, per modellizzare lo spettro omnidirezionale Smare( )K dell’immagine SAR della superficie marina.

Ricordiamo che questo modello è caratterizzato da una funzione densità spettrale di potenza radiale del tipo:

( )

(

)

2 2 2 1 2 2 ₂ 2( 2) 2 2 0 0 0 ( ) 2 n n f R K K N s n n W n n n C S K σ K b R e I R b K K  +    − − _{ }   −   = =

∑

(4.55) che è perfettamente caratterizzata una volta definiti 6 parametri:

• N_f numero di componenti sinusoidali;

• σ deviazione standard dell’ampiezza delle onde del mare

• b fattore di scala in ampiezza

• s coefficiente di rugosità

• K0 numero d’onda spaziale fondamentale; è dato da 2π Λ0con Λ0

lunghezza d’onda fondamentale

E’ importante osservare che il numero d’onda massimo misurabile K_max in un sistema SAR è fissato implicitamente dalla condizione di Nyquist ed è pari a: max K r π = ∆ (4.56)

dove r∆ è la risoluzione in distanza del sistema di acquisizione considerato. Si osserva inoltre che vale la seguente relazione:

( 1) max f N o K = b − K _ (4.57) Ne deriva che una volta fissato il numero di componenti sinusoidali N da _f

usare, il valore del fattore d’ampiezza b risulta determinato come:

1 1 max f N o K b K −   =     (4.58)

Di conseguenza i parametri caratteristici del modello si riducono a 5.

Il processo di stima inizia fissando il parametro N_f =50 e per quanto detto sopra, anche il parametro b risulterà determinato. I parametri K , _o ε ed s

saranno determinati tramite un processo ciclico. In particolare il valore di K _o

viene fatto decrescere a partire dal valore del numero d’onda dominante stimato nello spettro omnidirezionale dei dati reali. Per quanto riguarda i valori di s e ε , questi si suppongono appartenenti ad un range, dedotto sperimentalmente, tipico per la superficie del mare; numericamente sarà

(0.5,5)

ε∈ e s∈(1.01,1.50). Il valore della deviazione standard dell’ampiezza delle onde del mare σ è stimato per ultimo, dal momento che, una volta determinati gli altri parametri, può essere visto come una costante di amplificazione per la funzione modellata.

L’insieme delle procedure congiunte di stima dei parametri del modello considerato avviene con l’obiettivo di minimizzare l’errore quadratico medio tra l’andamento della densità spettrale S_mare( )K relativa ai dati reali e