Capitolo 4
Cilindro circolare libero di
ruotare
Il capitolo affronta lo studio di un cilindro circolare libero di ruotare immerso in una corrente fluida uniforme. Dopo una prima parte, dedicata alla definizione dei parametri di discretizzazione numerica che specializzano il modello al caso studiato, si affronta il problema della validazione del modello numerico. Infine, sono presentati i risultati ottenuti dalle simulazioni per le varie condizioni studiate.
4.1. Parametri della discretizzazione numerica
4.1.1. Dominio di calcolo
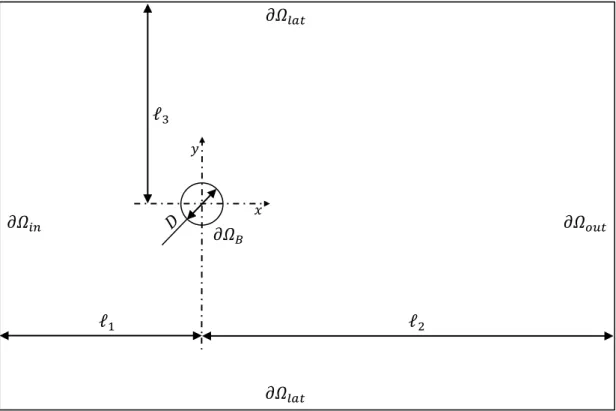
In Figura 4.1 è riportato il dominio di calcolo. I valori delle relative caratteristiche dimensionali sono riportati in Tabella 4.1.
D 1
ℓ𝓁! 25 D
ℓ𝓁! 50 D
ℓ𝓁! 25 D
La triangolazione del dominio è ottenuta grazie al generatore di mesh
BAMG, integrato nel software FreeFem++. La griglia utilizzata è di tipo
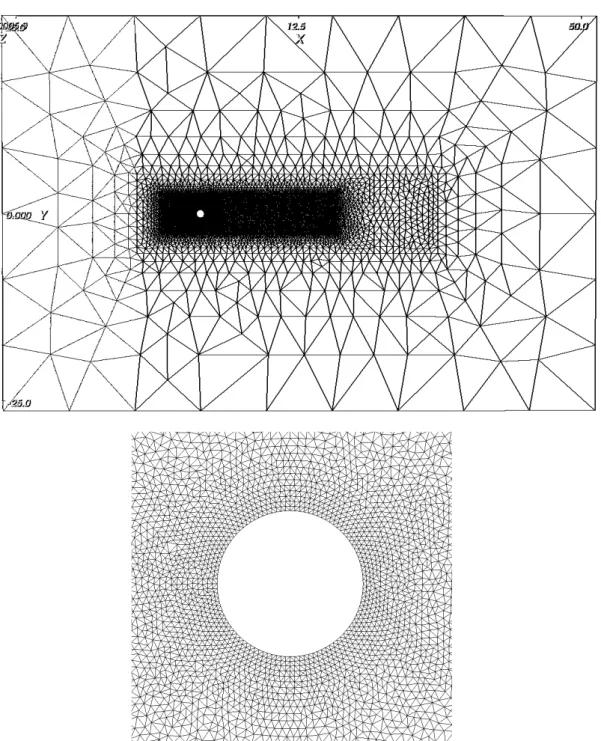
non-strutturato, quindi la corrispondenza tra ciascun elemento e i suoi nodi è esplicitamente memorizzata in una matrice di connettività1. L’uso di griglie non-strutturate offre una maggiore flessibilità sia per quanto riguarda la geometria da trattare che per la possibilità di raffinare localmente la griglia. Di contro, però, si ottiene un algoritmo meno efficiente in termini di memoria e di tempo di calcolo rispetto a uno schema analogo su griglie strutturate. Nel presente studio sul dominio di calcolo si realizzano due raffittimenti intermedi della mesh nelle zone vicine al bordo 𝜕𝛺!, dato che la presenza di forti gradienti di velocità necessita una maggiore accuratezza di calcolo. Il risultato della triangolazione è riportato in Figura 4.2.
ℓ𝓁! ℓ𝓁! ℓ𝓁! 𝜕𝛺!"# 𝜕𝛺!" 𝜕𝛺!"# 𝜕𝛺!"# 𝜕𝛺! 𝑥 𝑦 𝐷
Figura 4.2 – Risultato della triangolazione sul dominio di calcolo
4.1.2. Scelta del metodo di risoluzione del problema
fluido-struttura
Nel paragrafo 3.3 del capitolo precedente sono stati presentati alcuni tra gli schemi che possono essere utilizzati per la risoluzione del problema fluido-struttura studiato: un metodo di Eulero Esplicito (EE), uno di Eulero Implicito (EI) e un modello di Crank-Nicholson (CN). Per questa tipologia di problemi è necessario utilizzare metodi iterativi più
onerosi dal punto di vista computazionale, come i modelli EI e CN, essenzialmente per dare un’esatta valutazione dell’accelerazione del corpo nei primi istanti del moto. Infatti, il problema principale nasce dalla determinazione di forze istantanee di reazione all’accelerazione del corpo, dette forze di massa aggiunta. Tuttavia, date le simmetrie del cilindro, tali forze sono nulle per moti di rotazione attorno all’asse di simmetria, per cui è sufficiente utilizzare un metodo di EE.
4.1.3. Condizioni inziali e condizioni al contorno
Il caso prevede che il corpo libero di ruotare sia investito da una corrente uniforme, quindi per la condizione inziale s’impone che:
𝒖 = 1 ∙ 𝒊 𝑖𝑛 0 × Ω
mentre per le condizioni al contorno si possono scrivere le seguenti relazioni (si ricorda che 𝒖 𝑥, 𝑦, 𝑡 = 𝑢! 𝑥, 𝑦, 𝑡 , 𝑢!(𝑥, 𝑦, 𝑡) !):
𝒖 = 1 ∙ 𝒊 𝑖𝑛 0, 𝑇 × ∂Ω!" 𝑢! = 0 𝑖𝑛 0, 𝑇 × ∂Ω!"# 𝒖 = −𝑦 ∙ 𝜗!∙ 𝒊 + 𝑥 ∙ 𝜗!∙ 𝒋 𝑖𝑛 0, 𝑇 × ∂Ω!
La prima condizione assicura che in inflow ci sia lo stesso profilo di velocità uniforme per tutto l’intervallo temporale, mentre la seconda equivale a imporre che la velocità lateralmente ritorni alle caratteristiche del flusso indisturbato con componente verticale nulla. Infine, la terza equazione accoppia il problema del flusso con quello del corpo: il rispetto della condizione di non scorrimento, impone che la velocità del campo 𝒖 in corrispondenza del bordo ∂Ω! uguagli la velocità periferica del cilindro dovuta alla rotazione 𝜗!.
4.2. Validazione del modello
4.2.1. Validazione per confronto con una soluzione
numerica
impulsiva all’istante iniziale e poi di lasciare il corpo libero di ruotare all’interno di un fluido in quiete. La vorticità, per mezzo della viscosità del fluido, diffonde radialmente nel campo e contemporaneamente le azioni viscose sul bordo del cilindro inducono una coppia frenante che porta il corpo a rallentare fino a fermarsi. La soluzione prevede che le particelle fluide descrivano delle traiettorie circolari concentriche con una velocità esprimibile in coordinate cilindriche come:
𝒗(𝑟) = 𝑣!(𝑟) 𝒆𝝑
dove r è la coordinata radiale e 𝒆𝝑 è il versore tangenziale. La soluzione di questo problema può essere ottenuta sia dal modello presentato nel capitolo precedente, impostando le opportune condizioni al contorno, ma anche attraverso la risoluzione di una PDE ordinaria del 2° ordine, ricavabile direttamente dell'equazione di bilancio di quantità di moto. Il confronto tra queste due soluzioni fornisce un buon metodo per la validazione del modello numerico sviluppato nel presente lavoro.
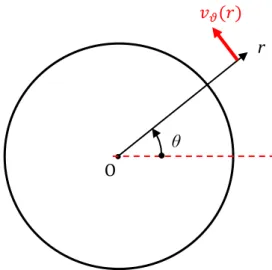
4.2.1.1. Scrittura delle equazioni del modello validante Si consideri un cilindro che ruota con una velocità angolare 𝜗 e si fissi un sistema di riferimento polare avente origine O nel centro del cilindro, come mostrato in Figura 4.3. La viscosità del fluido permette una diffusione della quantità di moto che porta all'instaurarsi di un campo di velocità bidimensionale assialsimmetrico attorno al cilindro.
r
θ
𝑣!(𝑟)
Figura 4.3 – Sistema di riferimento polare relativo al cilindro O
L'equazione dì bilancio di quantità di moto per il caso di un fluido incomprimibile può essere scritta come:
𝜕𝒗 𝜕𝑡 + 𝝎 Λ 𝒗 = −𝑔𝑟𝑎𝑑 𝑝 𝜌+ 𝑣! 2 − 𝜈 𝑟𝑜𝑡 𝝎 dove: 𝒗 è il vettore velocità 𝝎 è il vettore vorticità 𝑝 è la pressione 𝜈 è la viscosità cinematica
Esplicitando i termini dell'equazione in funzione delle componenti di velocità e utilizzando le espressioni relative ai termini differenziali in coordinate cilindriche, si ottengono le seguenti espressioni:
𝝎 = 𝜔 𝑟 𝒌 = 𝜕𝑣! 𝜕𝑟 + 𝑣! 𝑟 𝒌 𝝎 Λ 𝒗 = −𝑣! 𝜕𝑣! 𝜕𝑟 + 𝑣! 𝑟 𝒆𝒓 𝑟𝑜𝑡 𝝎 = − 𝜕 !𝑣 ! 𝜕𝑟! + 1 𝑟 𝜕𝑣! 𝜕𝑟 − 𝑣! 𝑟! 𝒆𝝑 𝑔𝑟𝑎𝑑 𝑝𝜌+𝑣2! = 𝜕𝑟𝜕 𝑝𝜌+𝑣2!! 𝒆𝒓
Proiettando, infine, le equazioni lungo i versori 𝒆𝝑 e 𝒆𝒓, relativi alla coordinata tangenziale e radiale del sistema di riferimento, si giunge alla seguente scrittura: 𝜕𝑣! 𝜕𝑡 = 𝜈 𝜕!𝑣 ! 𝜕𝑟! + 1 𝑟 𝜕𝑣! 𝜕𝑟 − 𝑣! 𝑟! (𝒆𝝑) 𝜕 𝜕𝑟 𝑝 𝜌+ 𝑣!! 2 = 𝑣! 𝜕𝑣! 𝜕𝑟 + 𝑣! 𝑟 (𝒆𝒓)
La risoluzione della prima equazione consente di ricavare il valore della velocità tangenziale, mentre dalla seconda, una volta nota la 𝑣!, è possibile ottenere il valore della pressione.
4.2.1.2. Discretizzazione delle equazioni del modello validante
Al fine di validare il modello sviluppato in FreeFem++ è sufficiente risolvere, delle due equazioni precedenti, quella relativa alla componente tangenziale, dato che la pressione non rientra nella valutazione della coppia frenante sul corpo. Quindi, dopo aver adimensionalizzando l’equazione rispetto al dimetro D del cilindro e alla velocità periferica iniziale 𝑣! , è necessario passare alla sua forma discreta. In particolare l’equazione è discretizzata mediante un metodo alle differenze finite con uno schema centrato del 2° ordine nello spazio e uno schema di Eulero esplicito per la derivata temporale. Quindi, l’equazione che risolve il campo al nodo j-esimo e al tempo n+1-esimo è la seguente (per chiarezza di scrittura si omette il simbolo 𝜗 nell’indicazione della velocità): 𝑣!!!!= 𝑣 !!+ ∆𝑡 𝑅𝑒 𝑣!!!! − 2 ∙ 𝑣 !!+ 𝑣!!!! ∆𝑥! + 𝑣!!!! − 𝑣 !!!! 2 ∙ 𝑟!∙ ∆𝑥 − 𝑣!! 𝑟!! + 𝑜(∆𝑡, ∆𝑥!) dove il termine 1/Re è legato al coefficiente di viscosità scritto in forma adimensionale. Per risolvere questa equazione è necessario esplicitare il valore della velocità periferica del cilindro a ogni passo temporale. Questa velocità è tuttavia ricavabile dell’equazione di dinamica del cilindro, in modo del tutto simile a quanto fatto nel Capitolo 3. Infatti, per ogni istante, la velocità di rotazione del cilindro è fornita dall’equazione:
𝐼! 𝑑𝜗(𝑡)
𝑑𝑡 𝒌 = 𝒓 𝑠 ∧ 𝒏 ⋅ 𝑻 (𝑠, 𝑡)𝑑𝑠 !
dove:
• 𝑻(s, t) è il tensore degli sforzi definito alla coordinata s e al tempo t, che in questo caso deve essere espresso in coordinate cilindriche; • 𝒓 𝑠 è il vettore posizione radiale OP(s);
• 𝐼! il momento polare d’inerzia del cilindro, pari a !"! 𝜌!𝜋𝐷!; • 𝜗 la componente di velocità angolare del corpo;
L’equazione è adimensionalizzata come la precedente e infine discretizzata mediante un metodo alle differenze finite, con uno schema decentrato in avanti del 2° ordine nello spazio e uno schema di Eulero esplicito per la derivata temporale. L’equazione discretizzata diventa:
𝑣!!!! = 𝑣 !!+ 8 ∙ ∆𝑡 𝛼 ∙ 𝑅𝑒 −1.5 ∙ 𝑣!!+ 2 ∙ 𝑣 !!+ 0.5 ∙ 𝑣!! ∆𝑥 − 2 ∙ 𝑣!! + 𝑜(∆𝑡, ∆𝑥!) Il programma di risoluzione è scritto in ambiente MatLab nel quale, dopo aver stabilito i vari parametri della simulazione, viene assemblata la matrice del sistema, con i coefficienti ricavati dalle espressioni precedenti, e infine la soluzione è ottenuta con un ciclo iterativo nel tempo.
4.2.1.3. Confronto dei risultati
Sono qui riportati i risultati della validazione del modello. Entrambe le simulazioni sono eseguite impostando i seguenti parametri:
• Velocità periferica iniziale 𝑣!(𝑥 = 0,5, 𝑡 = 0) = 2 • Rapporto tra le densità 𝛼 = 1
• Numero di Reynolds 𝑅𝑒 = 100
• Passo temporale ∆𝑡 = 0,005
• Lunghezza del tratto considerato ℓ𝓁 = 2𝐷 (𝐷 = 𝑑𝑖𝑎𝑚𝑒𝑡𝑟𝑜)
Per quanto riguarda il passo spaziale, i due modelli hanno incrementi diversi: nel modello “MatLab” il passo è fissato a 0,1D, mentre nel modello risolto in FreeFem++ il passo dipende dalla mesh bidimensionale utilizzata all’interno del solutore.
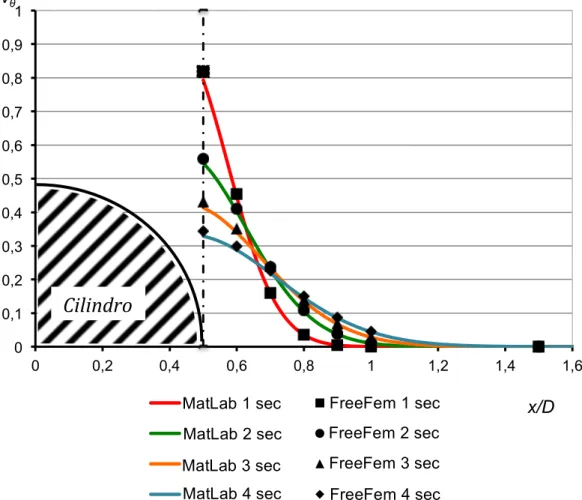
I due programmi, con le prescritte condizioni, forniscono i risultati di Figura 4.4, dove è mostrato l’andamento delle due soluzioni per i primi 4 s di simulazione. Confrontando il risultato ottenuto con il modello alle differenze finite di MatLab (riportato con tratto continuo) con quello del modello agli elementi finiti di FreeFem (riportato nel grafico con degli indicatori discreti), si nota come i due andamenti sostanzialmente coincidano, confermando la validità del modello numerico di FreeFem.
4.2.2. Validazione per confronto con una soluzione
analitica
Si consideri nuovamente un cilindro circolare libero di ruotare posto in un fluido in quiete. Volendo impostare una velocità costante di
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 vθ x/D
Matlab 1 sec Freefem 1 sec
Matlab 2 freefem 2
matlab 3 Freefem 3
Matlab 4 sec "Freefem 4"
Figura 4.4 – Andamento della soluzione per il modello scritto in FreeFem e per il modello scritto in Matlab
Cilindro
MatLab 1 sec MatLab 2 sec MatLab 3 sec MatLab 4 sec FreeFem 1 sec FreeFem 2 sec FreeFem 3 sec FreeFem 4 sec
rotazione
𝛺
sul corpo è necessario che sia applicata una coppia continuativa tale da vincere l’azione viscosa del fluido. Tale coppia è valutabile sia dal modello agli elementi finiti qui sviluppato, sia sfruttando una soluzione classica che prevede l’utilizzo dell’equazione di Bobyleff-Forsyth. Il confronto tra i due risultati consente di ottenere un’ulteriore validazione del modello.4.2.2.1. Valutazione della coppia con il modello analitico
L’equazione di Bobyleff-Forsyth può essere scritta come:Φ ! 𝑑𝑉 = 𝜇 𝜔! 𝑑𝑉 ! − 2𝜇 𝒂 ∙ 𝒏 𝑑𝑆 !"
dove Φ è la funzione di dissipazione, mentre il primo termine a destra dell’uguale è l’integrale dell’enstrofia e il secondo è il flusso dell’accelerazione sul bordo di dominio considerato.
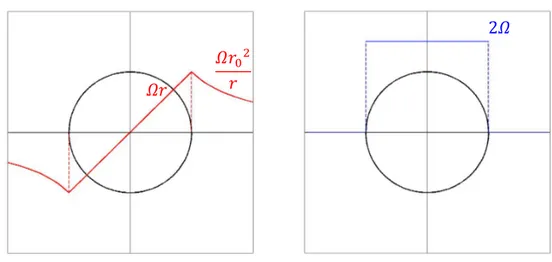
La soluzione asintotica del campo di moto che si ottiene facendo ruotare un cilindro con velocità costante
𝛺
in un fluido in quiete è di tipo stazionario e risulta del tutto equivalente al campo associato a un vortice di Rankine. Quindi possiede le seguenti caratteristiche, schematizzate anche in Figura 4.5: Velocità tangenziale𝑣
!𝛺𝑟
𝑟 < 𝑅
𝛺𝑅
!𝑟 𝑟 ≥ 𝑅
Vorticità𝜔
2𝛺
𝑟 < 𝑅
0 𝑟 ≥ 𝑅
Sostituendo tali espressioni all’interno dell’equazione di Bobyleff-Forsyth, si ottiene il seguente valore della dissipazione:
Φ !
La dissipazione è esattamente pari al valore della potenza necessaria per mantenere la velocità di rotazione costante, legata alla coppia che deve essere applicata in modo da compensare l’azione della viscosità sul corpo. Dunque, attraverso l’equazione di Bobyleff-Forsyth, il valore di tale coppia può essere valutato come:
𝑇 = 4𝜋𝜇Ω𝑅!
4.2.2.2. Valutazione della coppia con il modello ad
elementi finiti
Impostando le opportune condizioni al contorno, anche il modello agli elementi finiti consente di valutare la coppia necessaria a mantenere la velocità di rotazione del cilindro costante. In particolare il modello risolve a ogni passo tutto il campo e valuta la coppia dovuta alle azioni viscose direttamente integrando sul bordo il tensore degli sforzi moltiplicato per il raggio. Al contrario della soluzione analitica, che si riferisce alla sola soluzione stazionaria a regime, nel modello agli elementi finiti è studiata la soluzione evolutiva. Ciò comporta che, solo dopo un certo transitorio necessario per la diffusione della vorticità nel
𝑣!
𝑅 𝑅
Ω Ω
𝜔
Figura 4.5 - Andamento della velocità tangenziale e della vorticità per un vortice di Rankine
2𝛺 𝛺𝑟
𝛺𝑟!!
𝑟
campo, la soluzione numerica porterà a un valore della coppia confrontabile con quello espresso dalla soluzione analitica.
4.2.2.3. Confronto dei risultati
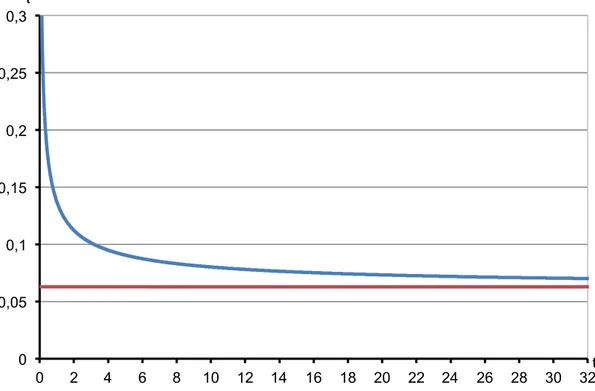
Per la validazione si consideri un cilindro circolare di diametro unitario che ruota con velocità angolare costante pari a 4 (espressa in termini adimensionali). Applicando i metodi appena descritti, si ottengono gli andamenti della coppia necessaria a mantenere tale velocità di rotazione costante. Tali andamenti sono riportati in Figura 4.6. Come previsto il modello numerico fornisce un valore della coppia che tende a convergere verso il valore ottenuto con la soluzione analitica.
Figura 4.5 – Confronto tra il risultato ottenuto con il modello agli elementi finiti, indicato in blu, e
la soluzione analitica, indicata in rosso. È possibile notare come la soluzione numerica tenda, al passare del tempo, a convergere verso il valore della soluzione analitica ottenuta con l’equazione di
Bobyleff-Forsyth. 0 0,05 0,1 0,15 0,2 0,25 0,3 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 Mt t
4.3. Risultati
In questa sezione sono presentati i risultati delle simulazioni per il caso del cilindro circolare libero di ruotare. Lo scopo di queste prove è studiare l’effetto che ha la presenza di un grado di libertà di rotazione del cilindro sull’evoluzione della scia, in riferimento alle caratteristiche del
vortex-shedding. I parametri fondamentali che caratterizzano la soluzione
sono il numero di Re e il valore del rapporto di massa 𝛼 = 𝜌! 𝜌!2. In questa logica si sono sviluppate due tipologie distinte di prove:
• Caso A: 𝛼 fissato e numero Re variabile; • Caso B: Re fissato e valore di 𝛼 variabile.
4.3.1. Caso A: 𝜶 fissato e numero di Re variabile
Si consideri un valore di 𝛼 = 1 e i seguenti numeri di Re:𝑅𝑒 = 55 75 100 150
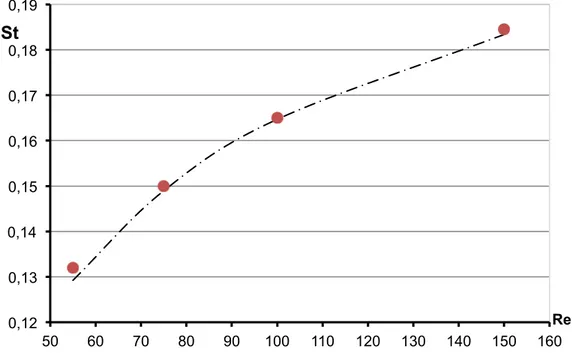
Dal punto di vista qualitativo il cilindro circolare, una volta che il flusso ha raggiunto una condizione stabile, presenta un moto rotatorio periodico con una frequenza perfettamente in linea con i valori di frequenza di distacco dei vortici, che rimangono in sostanza inalterati rispetto ai valori del cilindro fisso. Tale risultato è evidenziato in Figura 4.7, dove è riportato l’andamento dello St in funzione del Re, sia per il caso del cilindro stazionario (Williamson e Brown, 1998) che per il cilindro libero di ruotare.
Per evidenziare meglio il comportamento del cilindro rispetto al fenomeno del distacco dei vortici, in Figura 4.8 è fornita una rappresentazione del campo di vorticità attorno al corpo in relazione alla velocità di rotazione raggiunta dal cilindro all’istante considerato, di cui si dà un’indicazione qualitativa in un grafico (𝜔 − 𝑡) posto al fianco dei vari screenshot. Si può osservare che, nel momento in cui si inizia a formare il vortice orario (Figura 4.8a), il cilindro ruota in senso antiorario e presenta la velocità 𝜔 massima. Mano a mano che il punto singolare degenere di riattacco percorre tutta la base del corpo (Figura 4.8b-4.8c), la velocità si riduce fino a che non si inverte il senso di rotazione, raggiungendo poi il minimo di velocità nel momento in cui il vortice si stacca dalla base (Figura 4.8d). L’entità della fluttuazione della velocità di rotazione del cilindro nel tempo è riportata in Figura 4.9 per i 4 valori del numero di Re studiati. Per tutti i casi si ha un comportamento qualitativamente simile, sennonché la frequenza di rotazione varia in ragione della frequenza di distacco dei vortici, come già sottolineato, e la massima velocità tende ad aumentare con il Re.
Figura 4.7 – Confronto tra il numero di Strouhal ricavato nel caso del cilindro circolare libero di ruotare ( ) e quello ottenuto dalla relazione St= 𝟎, 𝟐𝟔𝟔𝟓 −
𝟏, 𝟎𝟏𝟖 √𝑹𝒆⁄ (−. −) (Williamson e Brown, 1998). 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 50 60 70 80 90 100 110 120 130 140 150 160 St Re
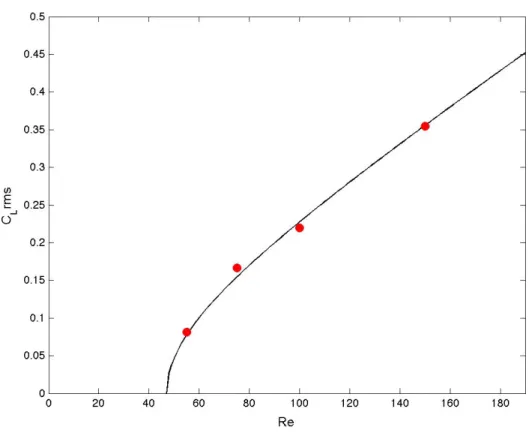
Per quanto riguarda i coefficienti di forza, si ritrovano andamenti, sia qualitativi che quantitativi, del tutto simili a quelli del cilindro circolare fisso: al crescere del numero di Re, si ha una diminuzione del coefficiente di resistenza medio CD dovuta a un progressivo aumento della pressione di base Cpb, mentre il valore r.m.s.3 del coefficiente di portanza CL, pur rimanendo a valor medio nullo, presenta ampiezze di oscillazione via via crescenti. Queste grandezze sono riportate nelle Figure 4.11 e 4.12. Nella prima è mostrato l’andamento del CD medio corrispondente ai 4 numeri di Re analizzati in Figura 4.10, dove si nota un andamento che tende essenzialmente a coincidere con quello del caso del cilindro fisso. In Figura 4.12 sono confrontati i valori r.m.s. dei CL ottenuti nel presente studio per i numeri di Re considerati con i rispettivi valori relativi al caso del cilindro circolare fisso, riportati in (Norberg 2003).
𝝎
𝒕
𝝎
𝒕
𝝎
𝒕
𝝎
𝒕
𝜔! 𝑡̃ 𝜔! 𝑡̃ 𝜔! 𝑡̃ 𝑡̃ 𝜔! 𝜔 𝑡 𝑡 Re=55 Re=75 Re=100 Re=150
Figura 4.11 – Andamento del valore del CD per il caso del cilindro circolare fisso,
presentato in (Cheng et al., 2001) (
−
) e per il caso del cilindro circolare libero di ruotare per 𝛼=1 ( )Figura 4.12 – L’andamento del valore r.m.s. del CL per il caso del cilindro circolare
fisso presentato in (Norberg 2003) (−) è mostrato a confronto con il valore r.m.s del C per il caso del cilindro circolare libero di ruotare per 𝛼=1 ( )
4.3.2. Caso B: numero di Re fissato e 𝜶 variabile
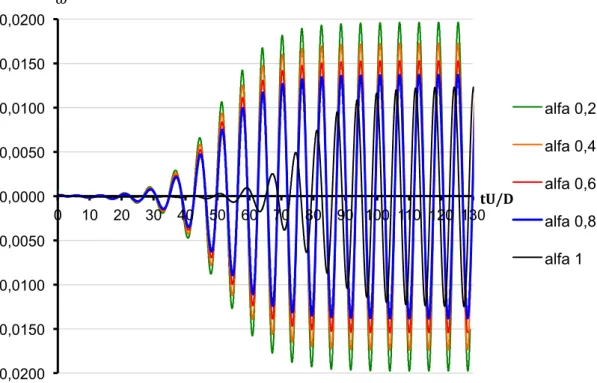
Si consideri un numero di Re fissato e si faccia variare la densità del corpo, in particolare selezionando Re=100 e valori di 𝛼 da 1 a 0,2. La scelta di utilizzare valori bassi del rapporto di massa permette di ottenere velocità di rotazione relativamente alte, in modo da mettere maggiormente in evidenza eventuali dipendenze del fenomeno del distacco dei vortici dalla velocità di rotazione del corpo. Gli andamenti della velocità di rotazione nel tempo, riportati in Figura 4.13, mostrano che la periodicità della rotazione rimane la stessa per ogni valore della massa, confermando quindi una sostanziale indipendenza della frequenza di distacco dei vortici dalle caratteristiche di rotazione del cilindro.
Figura 4.13 – Andamento della velocità di rotazione per vari valori del rapporto tra le densità 𝜶 per Re=100
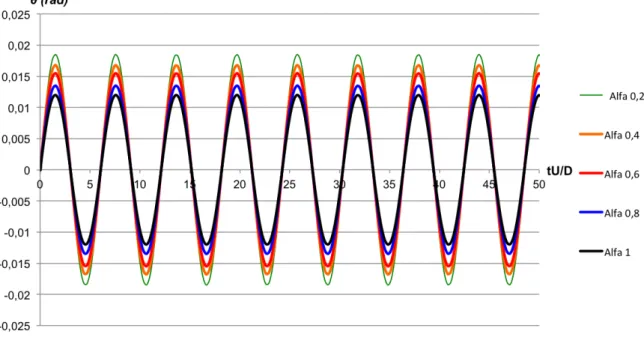
Dalle velocità di rotazione è possibile estrapolare i valori delle escursioni della rotazione del cilindro al variare del rapporto di massa 𝛼, che sono riportati in Figura 4.14 per alcuni periodi di vortex shedding per la condizione del flusso a regime. Tali andamenti, anch’essi periodici alla frequenza di distacco dei vortici, mostrano che minore è il peso del
-0,0200 -0,0150 -0,0100 -0,0050 0,0000 0,0050 0,0100 0,0150 0,0200 0 10 20 30 40 50 60 70 80 90 100 110 120 130 tU/D alfa 0,2 alfa 0,4 alfa 0,6 alfa 0,8 alfa 1 ω
corpo e maggiori sono le ampiezze di rotazione raggiunte, che rimangono tuttavia di entità modesta per ogni valore di 𝛼.
Figura 4.14 – Andamento dell’angolo di rotazione nel tempo per i vari valori di 𝜶 a Re=100 nelle
condizioni di flusso a regime.
Infine i coefficienti di forza, riportati in Figura 4.15, mostrano dei risultati coincidenti per tutti i valori di α, confermando la sostanziale ininfluenza della rotazione sulla dinamica di vortex-shedding, almeno per i numeri di Re considerati in queste simulazioni.
-0,4 -0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 5 15 25 35 45 55 65 75 85 95 105 115 125 t U/D CD CL