Capitolo 3 Torri di Snelson

(1)

Capitolo 3

Torri di Snelson

3.1 Descrizione

La costruzione a scopo decorativo di strutture tensintegre a forma di torre è stata compiuta in più occasioni dall’artista Kenneth Snelson (Fig. 3.1). Le torri di Snelson sono modulari. Ogni modulo è costituito da un assemblaggio reticolare di “puntoni” e “tiranti”1_{. I moduli, ciascuno dei quali ha n ≥}

2 puntoni, si susseguono in numero m ≥ 3 lungo un asse principale, che conviene prendere verticale.

Ogni torre ha simmetria ciclica: una rotazione di 2π

n intorno all’asse

prin-cipale porta il sistema in s`e. Le torri che descriveremo qui sono a base

trian-golare; la descrizione si generalizza facilmente a moduli con base poligonale qualsiasi (il numero di lati del poligono di base `e uguale al numero di puntoni

n del modulo).

3.1.1 Il modulo elementare

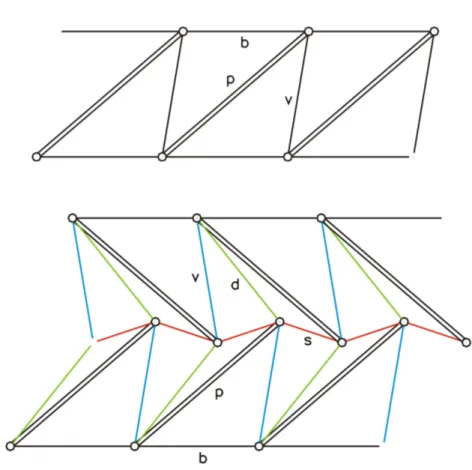
La Fig. 3.2 mostra il modulo a base triangolare, composto da nove tiranti e tre puntoni. Tre tiranti formano il triangolo orizzontale inferiore (superiore)

A B C (A B C); questi saranno indicati con la lettera b. Entrambi i triangoli

sono inscritti in cerchi centrati su un asse verticale. Le tre coppie di nodi

AA, BB, e CC sono connesse da puntoni, indicati con p. Infine, tre

cosid-detti tiranti verticali, indicati con v, collegano le coppie di nodi BA, CB, e

AC. Com’`e tipico di una struttura tensintegra, tutti i nodi sono collegati da

un’unica spezzata di tiranti.

La geometria del modulo ha simmetria ciclica, in quanto l’effetto di una

1_{L’uso di questi termini `e giustificato a posteriori una volta risolto il problema di ricerca}

di forma.

(2)

(3)

rotazione di 2π/3 intorno all’asse verticale, lascia il sistema inalterato. Ogni configurazione di un modulo ciclicamente simmetrico `e definita da quattro

parametri di modulo (Fig. 3.2): r e r, i raggi dei cerchi circoscritti ai triangoli

inferiore e superiore2_{; h, la distanza tra questi triangoli, o altezza del modulo;}

ϕ, l’angolo di rotazione del triangolo superiore relativamente al triangolo

inferiore, positivo se antiorario intorno all’asse verticale, o twist (quando il twist nullo i puntoni sono verticali).

Figura 3.2: Modulo elementare a base triangolare.

Una topologia diversa ma equivalente pu`o essere ottenuta attraverso un’al-tra scelta dei collegamenti nodali: connettendo i tiranti verticali ai nodi CA,

AB, and BC si ottiene un modulo che si dice con orientamento opposto

(Fig. 3.3). Nel seguito ci riferiremo a moduli orientati in senso opposto man-tenendo la stessa nomenclatura per entrambi. Ad esempio, i tiranti verticali connettono sempre le coppie BA, CB, and AC; quando le rotazioni relative di due moduli con orientamento opposto sono positive (da A a B in entram-bi) esse hanno direzione opposta rispetto ad un riferimento globale. La soluzione del problema di ricerca di forma per il modulo `e stata data da vari autori [24, 37]. Questa soluzione che verr`a ricavata nel seguito, impone una condizione solamente sul twist:

ϕ = π

n +

π

2 . (3.1)

Le Figure 3.4 e 3.5 mostrano esempi di moduli con lo stesso orientamento nella configurazione tensintegra.

2_{Nel prosieguo, per brevit`a, ci riferiremo a r e r come ai raggi dei corrispondenti}

(4)

Figura 3.3: Assonometrie di moduli orientati in senso opposto, n = 3.

(5)

(6)

`

E possibile definire una geometria con pi`u simmetrie prendendo uguali i raggi dei triangoli, r = r. Questo `e equivalente ad introdurre altri tre assi di simmetria (rotazioni di π): infatti una rotazione di π intorno all’asse che passa per il punto medio del puntone AA ed il punto medio del tirante verticale CB lascia il sistema inalterato (Fig. 3.6); gli altri assi sono ottenuti attraverso le operazioni di simmetria ciclica. In generale un modulo possiede

n assi di simmetria di questo tipo3_{. Chiameremo questa propriet`a simmetria}

centrale dispari.

Figura 3.6: Modulo a base triangolare con la propriet`a di simmetria centrale dispari.

3.1.2 Assemblaggio di due moduli

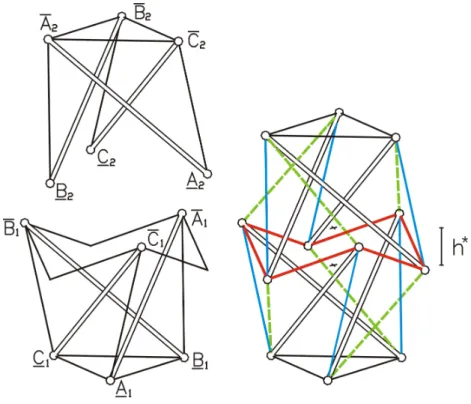
Questo assemblaggio `e ottenuto dalla ‘sovrapposizione’ di due moduli ele-mentari con orientamento opposto (Fig. 3.7). Utilizzeremo i pedici 1 e 2 per le quantit`a relative rispettivamente al primo ed al secondo modulo. Le operazioni da eseguire per assemblare i moduli possono essere ordinate nel modo seguente. I tre tiranti del triangolo inferiore del secondo modulo sono rimossi. I nodi inferiori del secondo modulo A₂, B₂, C₂ sono connessi ai punti medi dei tiranti superiori del primo modulo, in modo tale che ognuno di questi tiranti viene diviso in due elementi distinti; i sei tiranti risultanti

3_{Nel caso di un numero pari di puntoni, gli assi di simmetria passano per i punti medi}

dei due tiranti verticali, o dei due puntoni, che sono scambiati tra di loro da una rotazione di π intorno all’asse verticale (vedi il modulo a quattro barre nelle Figure 3.4, 3.5).

(7)

sono chiamati tiranti di sella, e saranno indicati con la lettera s. la pro-iezione su un piano orizzontale dei tiranti di sella forma l’esagono di sella. Posizioniamo i nodi A1 e A2 in due vertici contigui dell’esagono, in questo

modo la sequenza delle connessioni dell’esagono di sella risulta: A1A2, A2C1,

C1B2, B2B1, B1C2, C2A1. Infine aggiungiamo sei ulteriori tiranti, tre in

ogni modulo, che collegano i nodi: A₁A₂, C₁B₂, B₁C₂, A1C2, C1A2, B1B2;

questi sono chiamati tiranti diagonali, e saranno indicati con d.

Comple-Figura 3.7: Assemblaggio di due moduli. In blu sono indicati i tiranti verticali, in verde i tiranti diagonali, in rosso i tiranti di sella.

tato l’assemblaggio, possiamo osservare che ogni tirante diagonale connette un puntone del primo modulo con un puntone del secondo modulo; inoltre l’esagono di sella `e l’unica parte in comune tra i due moduli.

Configurazioni che hanno la propriet`a di simmetria ciclica sono descritte dai seguenti parametri: i raggi dei moduli, r₁, r1, r2, r2; le loro altezze,

h1, h2; le loro rotazioni relative o twist , ϕ1, ϕ2; un nuovo parametro, la

sovrapposizione tra i moduli o overlap h∗

12, cio`e, la distanza tra i centri dei

triangoli A₂B₂C₂ e A1B1C1.

Una configurazione con pi`u simmetrie si ottiene se le altezze ed i twist di ogni modulo sono uguali, ed i raggi inferiore e superiore del primo

(8)

mo-Figura 3.8: Esempi di assemblaggio di moduli con la propriet`a di simmetria centrale pari (le superfici di alcuni triangoli sono evidenziate per facilitare la comprensione dell’illustrazione).

(9)

dulo sono uguali rispettivamente ai raggi superiore ed inferiore del secondo. Questo `e equivalente a considerare una simmetria centrale rispetto al punto medio del segmento che congiunge i centri dei triangoli appena menzionati. Chiameremo questa propriet`a simmetria centrale pari4_.

3.1.3 Assemblaggio della torre

Per ottenere una torre a tre moduli è sufficiente sovrapporre un nuovo mo-dulo all’assemblaggio di due moduli ripetendo le operazioni appena descritte utilizzando i pedici 2 e 3 (il terzo modulo è orientato in senso opposto ri-spetto al secondo). Il risultato di questa operazione è illustrato in Fig. 3.9. Questo assemblaggio contiene ora i due tipi di modulo presenti in una torre5_,

Figura 3.9: Torre di tre moduli.

differenti nella topologia, chiamati modulo intermedio e modulo di estremit`a.

4_{Il caso generale di n puntoni per modulo con n dispari `e analogo, mentre, per n pari}

l’operazione di simmetria `e composta dalla simmetria centrale rispetto allo stesso punto e da una rotazione di π

nintorno all’asse principale verticale.

(10)

I parametri che descrivono la geometria della torre, sono quelli propri di ogni modulo ed i due overlap h∗

12, h∗23.

Un modulo di estremità è ‘limitato’ da un triangolo e da un esagono di sella; un modulo intermedio è limitato da due esagoni di sella. I tiranti diagonali sono sei nel modulo intermedio, tre nel modulo di estremità. In ogni torre con più moduli ottenuta per iterazione riconosciamo sempre due tipi di sottostrutture: (una sequenza di) moduli intermedi e due moduli di estremità.

Un tipo di torre con una più speciale simmetria si può ottenere ponendo uguali le altezze ed i twist di tutti i moduli intermedi, con uguali raggi dei loro triangoli ed overlap uguali; le altezze ed i twist dei moduli di estremità, ed i raggi dei triangoli di estremità, sono uguali tra di loro ma possono es-sere diversi dalle rispettive quantità intermedie. Chiameremo questa torre

cilindrica, poich`e tutti i suoi nodi appartengono alla superficie laterale di

un cilindro, eccetto i nodi di estremit`a. Le propriet`a di simmetria delle tor-ri cilindtor-riche dipendono dal numero m di moduli e dal numero di puntoni per modulo. Oltre alla simmetria ciclica, esse posseggono la simmetria cen-trale dispari (pari) nel caso di m dispari (pari): le operazioni di simmetria sono analoghe a quelle che abbiamo descritto nel caso del modulo semplice (dell’assemblaggio di due moduli).

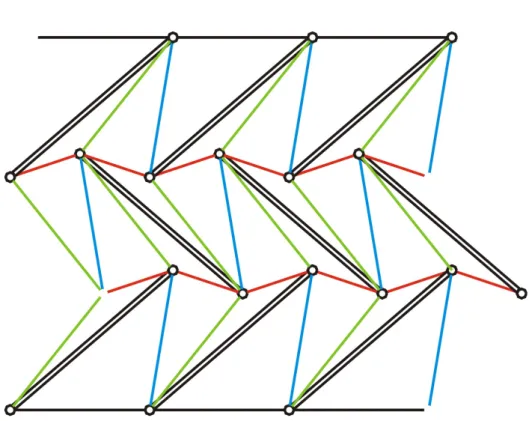
Un aiuto per visualizzare le torri `e fornito dai grafi che ne rappresentano la topologia (Figure 3.11 e 3.12). Questi grafi sono ottenuti nel modo seguente. Prima si proiettano i nodi della torre sulla superficie di un cilindro coassiale all’asse principale, poi si sviluppa questa superficie su un piano e si tracciano dei segmenti tra le coppie di nodi collegati.

3.2 La regola di Maxwell per la torre

Per una torre non vincolata a terra, scriviamo la regola di Maxwell tenendo conto dei 6 moti rigidi:

3nn− ne− 6 = nm− nss , (3.2)

nella (3.2), nn `e il numero totale di nodi, ne `e il numero totale di elementi,

nss `e il numero di stati di sollecitazione autoequilibrati indipendenti e nm `e

il numero di meccanismi indipendenti.

Per una torre di m moduli, con 3 puntoni in ogni modulo, `e facile contare 6m nodi, pari al doppio del numero di puntoni. Per contare il numero di elementi, consideriamo un modulo con un solo poligono di sella. Tenuto conto della simmetria ciclica, questo possiede 6 elementi che si ripetono (un puntone, un tirante verticale, due diagonali e due di sella). Considerare un

(11)

Figura 3.10: Torri a pi`u livelli (le superfici di alcuni triangoli sono evidenziate per facilitare la comprensione dell’illustrazione): n = 2, m = 5 (a sinistra);

(12)

Figura 3.11: Grafi. Modulo elementare n = 3 (in alto); assemblaggio di due moduli n = 3 (in basso).

(13)

(14)

poligono di sella per ogni modulo non cambia il totale poichè le due basi hanno un numero di elementi uguale a quello di un poligono di sella. Inoltre, poichè i due moduli di estremità hanno un solo tipo di tirante diagonale, si ottengono per l’intera torre (6m − 2) tipi di elemento. Questo numero va moltiplicato per l’ordine della simmetria ciclica, quindi nel caso di tre puntoni per modulo otteniamo 3(6m − 2) elementi. La relazione (3.2) si scrive:

3 · 6m − 3(6m − 2) − 6 = nm− nss = 0 . (3.3)

Questo mostra che, per una torre con tre puntoni in ogni modulo, la matrice strutturale `e quadrata. Per una torre con n puntoni in ogni modulo, la (3.2) si riscrive:

3 · 2nm − n(6m − 2) − 6 = nm− nss= 2n − 6 . (3.4)

Quindi la differenza (nm − nss) `e indipendente dal numero di moduli e una

torre siffatta ha almeno (2n − 6) meccanismi indipendenti in ogni configu-razione. Vincolando i poligoni di base a rimanere piani, questi meccanismi sono rimossi e la matrice strutturale `e ancora quadrata6_{. Questa condizione}

permette di estendere i risultati ottenuti per torri con tre puntoni a torri con

n puntoni. Notiamo che se n = 2, allora la regola implica sempre una matrice

quadrata (nel conto degli elementi occorre considerare che ogni poligono di base si riduce ad un singolo elemento).

3.3 Equazioni in simmetria ciclica

Per utilizzare la propriet`a di simmetria ciclica della torre nella scrittura delle equazioni di equilibrio: X i (P − Qj)t_{P Qj} = fP , (3.5) e di congruenza: (P − Q) · (vP − vQ) = eP Q , (3.6)

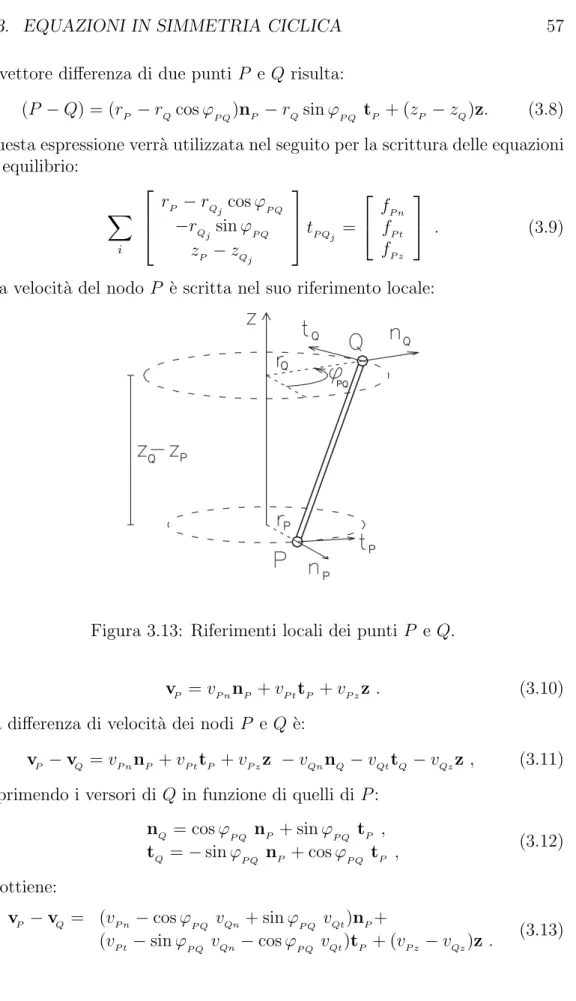
introduciamo un sistema di coordinate cilindriche, {r, ϕ, z}, il cui asse coin-cide con l’asse principale verticale della torre (figura 3.13). Per ogni nodo

P prendiamo un sistema di riferimento locale i cui versori puntano nelle

direzioni normale, tangente e verticale:

{P ; nP, tP, z} . (3.7)

6_{Infatti, senza considerare i moti rigidi, un poligono articolato di n lati con n cerniere}

ha (2n − 6) gradi di libertà nello spazio e (n − 3) gradi di libertà nel piano: vincolando i due poligoni di estremità a rimanere nel piano si eliminano (2n − 6) gradi di libertà.

(15)

Il vettore differenza di due punti P e Q risulta:

(P − Q) = (r_P − r_Qcos ϕ_{P Q})n_P − r_Qsin ϕ_{P Q} t_P + (z_P − z_Q)z. (3.8) Questa espressione verr`a utilizzata nel seguito per la scrittura delle equazioni di equilibrio: X i    rP − r_Qj cos ϕP Q −r_Qj sin ϕ_{P Q} zP − z_Qj    t_{P Qj} =   f_fP n P t fP z   . (3.9)

La velocit`a del nodo P `e scritta nel suo riferimento locale:

Figura 3.13: Riferimenti locali dei punti P e Q.

vP = vP nnP + vP ttP + vP zz . (3.10)

La differenza di velocit`a dei nodi P e Q `e:

vP − vQ = vP nnP + vP ttP + vP zz − vQnnQ− vQttQ− vQzz , (3.11)

esprimendo i versori di Q in funzione di quelli di P : nQ = cos ϕP Q nP + sin ϕP Q tP , tQ = − sin ϕP Q nP + cos ϕP Q tP , (3.12) si ottiene: vP − vQ = (vP n− cos ϕP Q vQn+ sin ϕP Q vQt)nP+ (vP t− sin ϕP Q vQn− cos ϕP Q vQt)tP + (vP z− vQz)z . (3.13)

(16)

Sostituendo la (3.13) e la (3.8) nella (3.6) e semplificando si ottiene: (rP − rQcos ϕP Q)vP n + (rQ− rP cos ϕP Q)vQn+

−rQsin ϕP Q vP t+ rP sin ϕP Q vQt+ (zP − zQ)(vP z − vQz) = eP Q ,

(3.14) questa espressione verr`a utilizzata nel seguito per la scrittura delle equazioni di congruenza degli elementi. La generica equazione di congruenza assume quindi la forma:            rP − rQcos ϕP Q −r_Qsin ϕ_{P Q} zP − zQ rQ − rP cos ϕP Q rPsin ϕP Q z_Q− z_P,            T           vP n vP t vP z vQn v_Qt v_Qz           = eP Q (3.15)

3.4 Analisi del modulo elementare

In questo paragrafo svolgeremo l’analisi del modulo elementare e ne risolve-remo il problema di ricerca di forma.

Consideriamo i nodi di base del modulo incernierati a terra. I tiranti del poligono inferiore possono essere trascurati, poichè le loro estremità restano bloccate. Il sistema risultante è costituito da n nodi collegati da ne = 3n

elementi: n puntoni, n tiranti verticali e n tiranti del poligono superiore. La regola di Maxwell in forma estesa fornisce quindi:

3nn− ne= 0 = nm− nss , (3.16)

la matrice di equilibrio `e quadrata indipendentemente da n.

3.4.1 Equazioni di equilibrio e congruenza

Facendo riferimento ad un modulo a base triangolare (Fig. 3.2) le equazioni di equilibrio relative ai tre nodi superiori A, B e C sono:

(A − A)tp1+ (A − B)tv1+ (A − C)tb1+ (A − B)tb2 = fA , (3.17)

(B − B)tp2+ (B − C)tv2+ (B − A)tb2+ (B − C)tb3= fB , (3.18)

(C − C)tp3+ (C − A)tv3+ (C − B)tb3+ (C − A)tb1= fC . (3.19)

Per l’ipotesi di simmetria ciclica una rotazione di 2π

(17)

Figura 3.14: Modulo elementare a base triangolare.

centrale lascia il sistema inalterato. Di conseguenza, stessa forza e sposta-mento per ciascuno dei nodi superiori rispetto ad un sistema di riferisposta-mento adattato alla simmetria ciclica; stesse tensioni e deformazioni rispettivamen-te nei puntoni, nei tiranti verticali e nei tiranti superiori. Considerando solo le equazioni che non si ripetono, si ottengono i seguenti sistemi ridotti:

AR_{t = f,} _{t =}   _ttp_v tb   , f =   f_fn_b fz   ; (3.20) BR_{v = e,} _{v =}   v_vn_t vz   , e =   e_ep_v eb   . (3.21)

Scriviamo l’equilibrio di un nodo, ad esempio A, utilizzando l’espressione (3.8) del paragrafo 3.3 per ciascuno degli elementi in esso confluenti. Per il puntone, l’angolo ϕ_pda considerare nella (3.8) `e uguale alla rotazione relativa del modulo, ϕ; si ha:

(A − A) = (r − r cos ϕ)n_A + r sin ϕ t_A + h z. (3.22) L’angolo relativo al tirante verticale `e pari a ϕ_v = ϕ − 2π

n , si ha:

(A − B) = [r − r cos(ϕ − 2π

n)]nA+ r sin(ϕ − 2π

n) tA + h z. (3.23)

L’angolo relativo ai tiranti superiori `e ϕ_b = 2π

n in valore assoluto;

consideran-do il giusto verso per ciascun tirante si ha: (A − C) = r[1 − cos(2π

n)]nA + r sin( 2π

(18)

(A − B) = r[1 − cos(2π

n)]nA − r sin( 2π

n) tA. (3.25)

Notiamo che nella scrittura della (3.20) questi due ultimi contributi andranno sommati tra di loro, essendo le tensioni nei rispettivi elementi uguali per l’ipotesi di simmetria ciclica. Quindi le equazioni di equilibrio del generico nodo superiore si scrivono:

   r − r cos ϕ r − r cos(ϕ − 2π n) 2r[1 − cos( 2π n)] r sin ϕ r sin(ϕ − 2π n) 0 h h 0      t_tp_v tb   =   f_fn_b fz   . (3.26) Consideriamo ora le equazioni di congruenza per gli elementi tipici del modulo e utilizziamo l’espressione (3.14).

(A − A) · v_A = (r − r cos ϕ)v_An + r sin ϕ v_At+ h z. (3.27) (A − B) · v_A = [r − r cos(ϕ −2π n)]vAn + r sin(ϕ − 2π n) vAt+ h z. (3.28) (A − C) · (v_A − v_C) = 2r[1 − cos(2π n)]vAn. (3.29)

Come si vede la matrice di congruenza ridotta cos`ı ottenuta `e la trasposta della matrice di equilibrio ridotta che compare nella (3.26):

   r − r cos ϕ r sin ϕ h r − r cos(ϕ − 2π n) r sin(ϕ − 2πn) h 2r[1 − cos(2π n)] 0 0      v_vn_t vz   =   e_ep_v eb   . (3.30)

3.4.2 Ricerca di forma

Per trovare la configurazione tensintegra del modulo imponiamo la condizione di indeterminazione che, per una matrice quadrata, si scrive nella forma (2.40):

det AR_{(r, r, h, ϕ) = 0 .} _(3.31)

Sviluppando il determinante della matrice nella (3.26), si ottiene facilmente: 2 r r h · 1 − cos µ 2π n ¶¸ · sin ϕ − sin µ ϕ − 2π n ¶¸ = 0 . (3.32)

Applicando la formula di prostaferesi per la differenza di seni: sin α − sin β = 2 sin

µ α − β 2 ¶ cos µ α + β 2 ¶ , (3.33)

(19)

la (3.32) diventa: 4 r r h · 1 − cos µ 2π n ¶¸ sin³π n ´ cos ³ ϕ − π n ´ = 0 . (3.34)

Le quantit`a r, r, h sono strettamente positive; osserviamo inoltre che le quantit`a sin¡π n ¢ e cos¡2π n ¢ soddisfano le disuguaglianze: 0 < sin³π n ´ ≤ 1 per n ≥ 2 ; (3.35) −1 ≤ cos µ 2π n ¶ < 1 per n ≥ 2 . (3.36)

Affinch`e la condizione (3.34) sia soddisfatta, dalle (3.35), (3.35) segue che: cos ³ ϕ − π n ´ = 0 . (3.37)

Per evitare l’interferenza tra gli elementi, sul twist si impone la condizione:

−π

n ≤ ϕ ≤ π , (3.38)

la prima (seconda) disuguaglianza `e relativa al contatto tra i tiranti verticali (puntoni)7_{. Dalla (3.38), le soluzioni fisicamente significative della (3.37)}

sono: ϕ₁ = π n + π 2 oppure ϕ2 = π n − π 2 . (3.39)

Osserviamo che la soluzione impone il valore solamente del twist, gli altri parametri possono essere variati a piacimento.

Consideriamo ora la prima soluzione per studiarne la stabilit`a. Indichere-mo con il pedice 1 le quantit`a calcolate per ϕ = ϕ₁. Con questa sostituzione, riscriviamo la matrice di equilibrio:

AR 1= AR(r, r, h, ϕ1)=    r − r cos(π n+ π2) r − r cos(−πn+ π2) 2r[1 − cos(2πn)] r sin(π n +π2) r sin(−πn +π2) 0 h h 0    ; (3.40) ovvero: AR 1 =    r + r sin(π n) r − r sin(πn) 2r[1 − cos(2πn)] r cos(π n) r cos(πn) 0 h h 0    . (3.41)

(20)

Dalla seconda o dalla terza riga di questa matrice si deduce che per un vettore appartenente al nucleo si ha:

tp = − tv . (3.42)

Sostituendo questa relazione nell’equazione corrispondente alla prima riga si ottiene: −2r sin³π n ´ tv + 2r · 1 − cos µ 2π n ¶¸ tb = 0 , (3.43) quindi: tb = r r sin¡π n ¢ 1 − cos¡2π n ¢ tv . (3.44)

Un vettore appartenente al nucleo di AR

1 si scrive: t1 =    −1 1 r r sin(π_n) 1−cos(2π_n)    tv , (3.45)

Ricordando le disuguaglianze (3.35) e (3.36), si deduce che il coefficiente di

tv nella (3.44) `e sempre positivo e che la sollecitazione nei tiranti superiori `e

opposta a quella nei puntoni.

Data la matrice di congruenza ridotta

BR₁ =    r + r sin(π n) r cos( π n) h r − r sin(π n) r cos( π n) h 2r[1 − cos(2π n)] 0 0    , (3.46)

dalla terza riga si vede come un vettore nel nucleo, o meccanismo, abbia la prima componente, o velocit`a tangenziale, nulla; l’equazione corrispondente ad una delle prime due righe diventa:

r cos³π n ´ vt+ hvz = 0 ; (3.47) quindi si ha vz = − r h cos ³π n ´ vt , (3.48)

ed un vettore appartenente al nucleo di BR

1 si scrive: m1 =   0₁ − r_h cos¡π n ¢   vt , (3.49)

(21)

Osserviamo che per la quantit`a cos¡π n ¢ sussiste la disuguaglianza 0 < cos³π n ´ ≤ 1 per n ≥ 2 , (3.50)

quindi, il segno della velocità verticale è opposto a quello della velocità tangenziale.

Avendo determinato il meccanismo e il self-stress possiamo utilizzare la condizione di stabilit`a (2.54):

X

i

ti(vh− vk)

2 _{> 0 ,} _(3.51)

dove h e k sono gli indici dei nodi connessi dall’elemento i-esimo. Nel caso in esame la precedente diventa:

3[(tp+ tv)(vA) 2_{+ t}

b(vA − vB)

2_{] > 0 ;} _(3.52)

il primo addendo tra le parentesi quadre `e nullo, per la (3.42). Quindi, la condizione di stabilit`a richiede soltanto che tb sia positivo:

tb > 0 , (3.53)

Questa condizione, dalle (3.42) e (3.44), implica:

tp < 0 , tv > 0 . (3.54)

Quindi affinch`e alla soluzione ϕ₁ = π n +

π

2 corrisponda una posizione

stabi-le occorre che gli estabi-lementi che abbiamo chiamato ‘puntoni’ (‘tiranti’) siano effettivamente compressi (tesi).

Consideriamo ora la seconda soluzione della (3.37) e denotiamo con il pedice 2 le quantit`a ad essa relative. La matrice di equilibrio ridotta diventa:

AR₂= AR(r, r, h, ϕ₂)=    r − r cos(π n− π2) r − r cos(−πn− π2) 2r[1 − cos(2πn)] r sin(π n − π2) r sin(−πn− π2) 0 h h 0    ; (3.55) semplificando: AR₂ =    r − r sin(π n) r + r sin(πn) 2r[1 − cos(2πn)] −r cos(π n) −r cos( π n) 0 h h 0    . (3.56)

(22)

Come nel caso precedente, otteniamo per le densit`a di forza di puntoni e tiranti verticali la relazione:

tp = − tv , (3.57)

mentre l’equivalente della (3.44) diventa:

tb = − r r sin¡π n ¢ 1 − cos¡2π n ¢ tv . (3.58)

Quindi, un vettore appartenente al nucleo di AR

2 si scrive: t2 =    1 −1 r r sin(π_n) 1−cos(2π n)    tv . (3.59)

La condizione di stabilit`a `e identica alla (3.52) e coinvolge, allo stesso modo, solamente il segno di tb:

tb > 0 , (3.60)

questa condizione, dalle (3.57) e (3.58), implica:

tp > 0 , tv < 0 . (3.61)

Contrariamente al caso precedente, affinch`e alla soluzione ϕ₂ = π n−

π

2

corri-sponda una posizione stabile occorre che gli elementi che abbiamo chiamato ‘puntone’ e ‘tirante verticale’ siano rispettivamente tesi e compressi, ci`o `e ovviamente incompatibile con l’ipotesi iniziale sulla natura degli elementi. Si prende quindi come soluzione del problema di ricerca di forma il valore

ϕ = ϕ₁, con r, r, h qualsiasi. Si pu`o vedere come la seconda soluzione inverta il ruolo degli elementi rispetto al caso precedente. In effetti, le due soluzio-ni, a meno di un operazione di simmetria8_{, coincidono (l’angolo associato ai}

puntoni vale sempre π

n + π2 in valore assoluto) e portano alla definizione di

moduli orientati in senso opposto data in precedenza

3.4.3 Carico geometrico

Calcoliamo il carico geometrico associato al meccanismo e al self-stress uti-lizzando la formula (2.50) scritta per un intervallo di tempo unitario:

gP =

X

j

t_{P Qj}(vP − v_Qj) . (3.62)

8_{L’operazione di simmetria consiste in una riflessione rispetto ad un piano verticale}

(23)

Considerando il nodo A si ottiene:

g_A = v_A(tp + tv) + [(v_A − v_B) + (v_A − v_C)]tb , (3.63)

il primo addendo a secondo membro `e nullo mentre il secondo addendo, utilizzando la (3.11), diventa: g_A =©− sin(2π n)vBtnA +[vAt− cos ( 2π n)vBt ¤ t_A + + sin (2π n)vCtnA + £ v_At− cos (2π n)vCt]tA ª tb , (3.64) per la simmetria ciclica v_Bt = v_Ct = v_At, la componente secondo n_A si annulla, e la precedente diventa: g_A = 2 · 1 − cos µ 2π n ¶¸ v_Attb tA . (3.65)

Si vede come il carico geometrico, a differenza del meccanismo, sia diretto orizzontalmente.

3.4.4 Risposta statica

Diamo uno sguardo d’insieme ai sottospazi associati alla matrice di equilibrio (3.41): AR₁ =    r + r sin(π n) r − r sin( π n) 2r[1 − cos( 2π n)] r cos(π n) r cos( π n) 0 h h 0    , (3.66)

questi sottospazi, con il loro significato fisico sono elencati nella tabella 3.1. Il comportamento elastico della struttura è decomposto nei modi estensionale (1) e geometrico (2) (sezione 2.4.2). Il carico geometrico, dato dalla (3.65), ha la stessa direzione e verso di t ; questo carico è associato ad uno spostamento lungo il meccanismo m1 dato dalla (3.49). Dall’ortogonalità in energia tra i

modi 1 e 2, possiamo dedurre che un carico appartenente all’immagine di AR

1

(24)

KerAR 1 = span{    −1 1 r r sin(π_n) 1−cos(2π n)   } sollecitazioni_{autoequilibrate} velocit´a di deformazione incompatibili Im(AR 1)T = span{  1₁ 0  ,    −1/2 1/2 − r r 1−cos(2π_n) sin(π n)   } sollecitazioni in equilibrio con le forze esterne velocit´a di deformazione congruenti Ker(AR 1)T = span{   0₁ − _hr cos¡π n ¢ 

} forze esterne_{incompatibili} velocit´anodali del meccanismo ImAR 1 = span{  1₀ 0   ,   r 0 h cos ¡_π n ¢ 1  } forze esterne in equilibrio velocit´a nodali congruenti con le vel. di deformaz. Tabella 3.1: Sottospazi associati alla matrice di equilibrio ridotta del modulo elementare

(25)

3.5 Ricerca di forma per la torre

Il problema di ricerca di forma per la torre di Snelson cilindrica è stato già affrontato da Murakami e Nishimura in [20, 22], risolvendo le equazioni di equilibrio per uno stato di self-stress (forze esterne nulle). La soluzione da essi trovata costituisce una soluzione particolare di questo problema. Il pro-blema della ricerca di forma per la torre si complica notevolmente quando il un numero dei moduli è maggiore di due; soluzioni in forma chiusa si possono trovare solo ricorrendo a semplificazioni conseguenti alla particolare simme-tria scelta e ad ulteriori ipotesi. In generale, una torre cilindrica possiede un self-stress e un meccanismo le cui componenti non sono necessariamente le stesse in tutti i moduli non di estremità. Una soluzione particolare si può trovare cercando soluzioni per cui le componenti del self-stress e del mecca-nismo siano le stesse in ogni modulo intermedio. Questa è l’ipotesi utilizzata da Murakami e Nishimura.

Per una torre con le basi vincolate a rimanere piane la matrice di equili-brio è quadrata (paragrafo 3.2), quindi, la soluzione delle equazioni di equi-librio per uno stato di self-stress equivale alla soluzione delle equazioni di congruenza per un meccanismo (velocità di deformazione nulle). Vedremo che questo tipo di torre, come nel caso del modulo elementare, possiede un solo meccanismo ed un self-stress. Di conseguenza, stabilita la condizione di indeterminazione, è sempre possibile scegliere il segno del self-stress, secondo la (2.51), in modo che la struttura sia stabile. In questa tesi la soluzione viene ricavata risolvendo le equazioni di congruenza, sfruttando il fatto che l’unica parte in comune tra due moduli adiacenti è il poligono di sella. I moduli vengono analizzati separatamente, caratterizzandone i meccanismi, per poi imporre la compatibilità dei meccanismi di moduli adiacenti. Questo semplifica la strada sia nel ricavare la soluzione particolare citata, sia nella costruzione di soluzioni generali, anche di torri non cilindriche.

Nel seguito, nella ricerca del meccanismo, scriveremo sempre le equazioni di congruenza imponendo una velocit`a di deformazione nulla, per cui la (3.15) verr`a utilizzata nella forma:

           rP − rQcos ϕP Q −rQsin ϕP Q z_P − z_Q r_Q− r_P cos ϕ_{P Q} rP sin ϕP Q zQ− zP,            T           vP n vP t v_{P z} v_Qn vQt vQz           = 0 . (3.67)

(26)

3.5.1 Le equazioni del poligono di sella

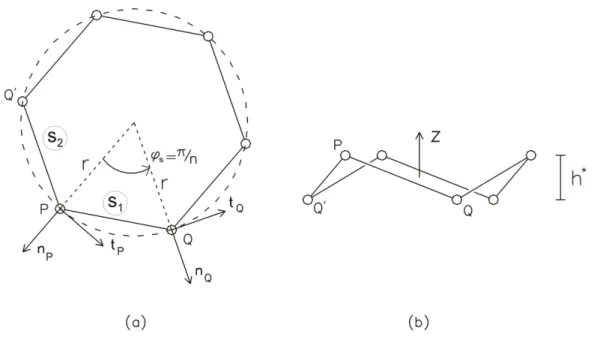
Il poligono di sella, costituito da 2n tiranti, in simmetria ciclica `e caratteriz-zato da due tipi di nodo, P , Q, e due tipi di tirante, che chiameremo s1 ed

s2 (Fig. 3.15).

Figura 3.15: Poligono di sella (n = 3). Vista dall’alto (a); vista laterale (b). I due tipi di nodo giacciono su due piani orizzontali posti ad una distanza pari all’overlap tra due moduli, h∗_{; le distanze dei nodi dall’asse verticale}

della torre sono uguali, cos`ı come gli angoli sottesi dai due tipi di elemento:

rP = rQ = r , ϕs1 = ϕs2 = ϕs=

π

n , (3.68)

Le equazioni di congruenza, utilizzando la (3.67), prendono la forma seguente. Per l’elemento s1: r(1 − cos ϕ_s)(vP n + vQn) + r sin ϕs(vQt− vP t) + h ∗_(v P z − vQz) = 0 ; (3.69) per l’elemento s2: r(1 − cos ϕ_s)(v_{P n} + v_Qn) + r sin ϕ_s(v_{P t}− v_Qt) + h∗_(v P z − vQz) = 0 . (3.70)

Sommando e sottraendo le equazioni precedenti si ottiene, rispettivamente,

r(1 − cos ϕ_s)(vP n + vQn) + h

∗_(v

(27)

e

vP t − vQt = 0 . (3.72)

Quindi le velocità radiali dei nodi P e Q sono legate alla differenza di velocità verticale, mentre le velocità tangenziali sono uguali tra di loro.

Definiamo la velocit`a di espansione verticale di sella come

vh∗ := v_{P z} − v_Qz , (3.73)

e il rapporto tra le velocit`a radiali come

α := vQn vP n

. (3.74)

Sostituendo queste quantit`a nella (3.71) si ottiene:

r(1 − cos ϕ_s)(1 + α)vP n+ h

∗_v

h∗ = 0 ; (3.75)

Questa relazione, insieme alla (3.72), caratterizza il meccanismo di ciascun poligono di sella appartenente alla torre; il ruolo del rapporto α sar`a chiarito nel seguito.

3.5.2 Analisi del modulo di estremit`

a

Il tipico modulo di estremit`a `e rappresentato nella Fig. 3.16. Si possono individuare tre tipi di nodo: i nodi del poligono di base (T ); i nodi del poligono di sella, ulteriormente distinti in nodi di tipo P e Q. Gli elementi sono di sei tipi: i tiranti di base (b); i puntoni, (p); i tiranti verticali (v); i tiranti diagonali (d); i tiranti di sella (s1 e s2). I puntoni connettono i nodi

T e P .

Prima di scrivere le equazioni di congruenza, consideriamo i possibili moti rigidi che rispettano la simmetria ciclica: traslazioni lungo l’asse verticale e rotazioni intorno allo stesso asse. Per eliminare questi moti poniamo le velocit`a tangenziale e verticale del nodo di tipo T pari a zero:

v_{T t} = 0 , v_{T z} = 0 . (3.76)

L’equazione di congruenza relativa ai tiranti di base b impone semplicemente che la velocit`a radiale dei nodi T sia nulla,

v_{T n} = 0 . (3.77)

(28)

Utilizzando la (3.67), scriviamo l’equazione di congruenza per il puntone

p :

(r − r cos ϕ) v_{P n} + r sin ϕ v_{P t}+ h v_{P z} = 0 . (3.78) Per il tirante verticale v l’angolo da considerare `e

ϕ_v = ϕ −2π

n ; (3.79)

quindi la sua equazione di congruenza risulta:

(r − r cos ϕ_v) v_{P n} + r sin ϕ_vv_{P t}+ h v_{P z} = 0 . (3.80) Per il tirante diagonale d l’angolo da considerare `e

ϕ_d= ϕ − π

n; (3.81)

la sua equazione di congruenza risulta:

(r − r cos ϕ_d) vQn + r sin ϕdvQt + (h − h

∗_{) v}

Qz = 0 . (3.82)

Aggiungendo alle precedenti le equazioni (3.71), (3.72), relative ai tiranti di sella, si ottiene il sistema di equazioni per il modulo di estremit`a

BEvE = 0 , (3.83)

che in forma estesa diventa:          r − r cos ϕ r sin ϕ h 0 0 0 r − r cos ϕ_v r sin ϕ_v h 0 0 0 0 0 0 r − r cos ϕ_d r sin ϕ_d h − h∗ r(1 − cos ϕ_s) 0 h∗ _{r(1 − cos ϕ} s) 0 −h∗ 0 1 0 0 −1 0                  vP n v_{P t} vP z vQn v_Qt vQz         = 0 . (3.84) Come gi`a osservato, l’ultima riga mostra che le velocit`a tangenziali dei nodi di sella sono uguali,

v_Qt = v_{P t}. (3.85)

per cui nella (3.84) possiamo sommare la seconda e la quinta colonna ed eliminare l’ultima riga. Ricordando la definizione (3.74), possiamo esprimere

vQn in funzione di vP n:

α := vQn vP n

(29)

Figura 3.16: Modulo di estremit`a. Assonometria (in alto); vista dall’alto della sottostruttura che si ripete (in basso).

(30)

quindi nella (3.84) possiamo sommare la prima colonna alla quarta moltipli-cata per α. Eseguendo queste operazioni otteniamo il sistema ridotto

BR_EvR_E = 0 , (3.87) in forma estesa:       r − r cos ϕ r sin ϕ h 0 r − r cos ϕ_v r sin ϕ_v h 0 α(r − r cos ϕ_d) r sin ϕ_d 0 h − h∗ (1 + α)r(1 − cos ϕ_s) 0 h∗ _−h∗           v_{P n} vP t vP z v_Qz     = 0 . (3.88)

Definiamo delle quantit`a cinematiche intrinseche al modulo: la velocit`a

di espansione radiale,

vr := vP n; (3.89)

la velocit`a di avvitamento,

vt:= vP t− vT t = vP t; (3.90)

la velocit`a di espansione verticale del modulo,

vh := vP z − vT z = vP z; (3.91)

la velocit`a di espansione verticale di sella:

vh∗ := v_{P z} − v_Qz. (3.92)

Dalle ultime due si ottiene per vQz:

v_Qz = vh− vh∗. (3.93)

A questo punto possiamo riscrivere il sistema (3.87) in funzione delle quantit`a intrinseche nel modo seguente:

˜ BR E˜vRE = 0 ; (3.94) in forma estesa:       r − r cos ϕ r sin ϕ h 0 r − r cos ϕ_v r sin ϕ_v h 0 α(r − r cos ϕ_d) r sin ϕ_d h − h∗ _{−h + h}∗ (1 + α)r(1 − cos ϕ_s) 0 0 h∗           vr vt vh vh∗     = 0 . (3.95)

(31)

Affinch`e questo sistema abbia soluzioni non nulle, il suo determinante deve essere nullo.

Introduciamo i seguenti parametri geometrici: il rapporto tra i raggi

inferiore e superiore,

γ = r

r ; (3.96)

il rapporto tra overlap e altezza del modulo,

δ = h∗

h . (3.97)

Nel calcolo del determinante, dividiamo la prima colonna per r, la seconda per r, la terza e la quarta per h; otteniamo la condizione seguente:

det       1 − γ cos ϕ sin ϕ 1 0 1 − γ cos ϕ_v sin ϕ_v 1 0 α(1 − γ cos ϕ_d) sin ϕ_d 1 − δ −1 + δ (1 + α)(1 − cos ϕ_s) 0 0 δ      = cE(ϕ, γ, δ; α) = 0 . (3.98) La precedente rappresenta una condizione di consistenza per il modulo di

estremit`a che lega i parametri geometrici ϕ, γ, δ ed il rapporto delle velocit`a

radiali α. Come si vede, questa condizione `e invariante per riscalamenti delle dimensioni verticali e radiali.

3.5.3 Assemblaggio consistente di due soli moduli

Per un assemblaggio di due moduli (necessariamente di estremit`a) possiamo utilizzare il risultato del paragrafo precedente.

Nel caso più semplice vale la proprietà di simmetria centrale pari: i moduli possono scambiarsi tra loro per simmetria. In particolare, si può scambiare il ruolo dei nodi P e Q, che avranno quindi la stessa velocità radiale. Di conseguenza, il rapporto α deve essere uguale all’unità:

α = 1 . (3.99)

Possiamo quindi imporre la condizione (3.98),

cE(ϕ, γ, δ; 1) = 0 , (3.100)

in cui compaiono solamente i parametri geometrici ϕ, γ, δ. Per esplicitare questa condizione, introduciamo le quantit`a angolari seguenti: il twist, θ0,

soluzione del modulo semplice (3.1) come ricavata in 3.4.2,

θ0 :=

π

n +

π

(32)

l’angolo di rotazione θ, contato a partire dal twist del modulo semplice,

θ := ϕ − θ0. (3.102)

Sviluppando la (3.100) ed applicando le formule trigonometriche di addizione, sottrazione e prostaferesi, si ottiene la condizione:

δ2(γ sinθ0+sinθ)+δ(γ−γ sinθ0+2 sinθ0sinθ−2 sinθ)−2 sinθ0sinθ+2 sinθ = 0 .

(3.103) La precedente costituisce una espressione in forma chiusa per la condizione di indeterminazione per la torre a due moduli con la proprietà di simmetria centrale pari. La (3.103) è una condizione sulla geometria del modulo si estre-mità affinchè esista un meccanismo con α = 1; come vedremo in 3.5.7, questa condizione prende parte alla soluzione particolare di una torre cilindrica.

Nelle Figure 3.17, 3.18 sono mostrati i grafici della funzione δ(ϕ) definita implicitamente dalla (3.103) per vari valori di γ, nei casi di 2, 3 e 4 puntoni per modulo. I grafici sono simmetrici rispetto all’asse ϕ = θ0 − π₂ = π_n. Si

pu`o verificare che per tale valore i tiranti verticali e i puntoni si scambiano di ruolo. L’overlap si annulla in corrispondenza della soluzione ϕ₁ (ϕ₂) per il modulo elementare, ottenuta in 3.4.2: in questa configurazione i due moduli conservano le caratteristiche del modulo elementare.

3.5.4 Analisi del modulo intermedio

Il tipico modulo intermedio `e rappresentato nella Fig. 3.19. Si possono in-dividuare quattro tipi di nodo: i nodi del poligono di sella inferiore (P e

Q); i nodi del poligono di sella superiore (P e Q). Gli elementi sono di otto

tipi: i puntoni (p); i tiranti verticali (v); i due tipi di tirante diagonale (d1

e d2); i tiranti di sella inferiori (s1 e s2); i tiranti di sella superiori (s1 e s2).

I puntoni connettono i nodi P e P . Per eliminare i moti rigidi poniamo le velocit`a tangenziale e verticale del nodo di tipo P pari a zero:

vP t = 0 , vP z = 0 . (3.104)

Dalle equazioni di congruenza dei tiranti di sella si ha che le velocit`a tan-genziali dei nodi inferiori e quelle dei nodi superiori sono rispettivamente uguali:

v_Qt = v_{P t} = 0 , v_Qt = v_{P t}. (3.105) Utilizzando la (3.67), scriviamo l’equazione di congruenza per il puntone p : (r − r cos ϕ) vP n + (r − r cos ϕ) vP n + r sin ϕ vP t + h vP z = 0 . (3.106)

(33)

Figura 3.17: Modulo di estremit`a, α = 1. Grafico di δ in funzione di ϕ per

γ = 0.6, 0.8, 1.0, 1.2, 1.4; n = 2 (in alto), n = 3 (in basso); le frecce indicano

(34)

Figura 3.18: Modulo di estremit`a, α = 1. Grafico di δ in funzione di ϕ per

γ = 0.6, 0.8, 1.0, 1.2, 1.4; n = 4; la freccia indica valori di γ crescenti.

Per il tirante verticale v, l’equazione di congruenza `e

(r − r cos ϕ_v) v_{P n} + (r − r cos ϕ_v) v_{P n} + r sin ϕ_vv_{P t} + h v_{P z} = 0 , (3.107) dove ϕ_v `e dato sempre dalla (3.79). I tiranti diagonali sono di due tipi, per il primo, d1, si ha:

(r − r cos ϕ_d) v_{P n}+ (r − r cos ϕ_d) v_Qn+ r sin ϕ_dv_Qt+ (h − h∗)v_Qz = 0 ; (3.108) per il secondo, d2, si ha:

(r − r cos ϕ_d)vQn+ (h ∗_{− h)v} Qz+ (r − r cos ϕd)vP n+ r sin ϕdvP t+ (h − h ∗_)v P z= 0 ; (3.109) nelle due equazioni precedenti l’angolo ϕ_d `e quello dato dalla (3.81). L’e-quazione dei tiranti di sella (3.71) fornisce, per i tiranti inferiori s₁ e s₂, la condizione seguente:

r(1 − cos ϕ_s)(vP n + vQn) + h

∗_v

(35)

Figura 3.19: Modulo intermedio. Assonometria (in alto); vista dall’alto della sottostruttura che si ripete (in basso).

(36)

per i tiranti superiori s1 e s2, si ha:

r(1 − cos ϕ_s)(v_{P n} + v_Qn) + h∗(v_{P z} − v_Qz) = 0 . (3.111) Come in precedenza, possiamo introdurre i rapporti delle velocit`a radiali, rispettivamente dei nodi inferiori, P , Q, e superiori, P , Q:

α := vQn

v_{P n} , α := v_Qn

v_{P n} . (3.112)

Con queste definizioni le equazioni (3.108), (3.109), (3.110), (3.111) diventa-no:

(r−r cos ϕ_d) vP n+α(r−r cos ϕd) vP n+r sin ϕdvQt+(h−h

∗ ) v_Qz = 0 ; (3.113) α(r −r cos ϕ_d)vP n+(h ∗_−h)v Qz+(r −r cos ϕd)v_{P n}+r sin ϕdv_{P t}+(h−h ∗_)v P z= 0 ; (3.114) r(1 − cos ϕ_s)(1 + α)vP n+ h ∗_v Qz = 0 ; (3.115) r(1 − cos ϕ_s)(1 + α)v_{P n} + h∗(v_{P z}− v_Qz) = 0 ; (3.116) L’insieme delle equazioni cos`ı ottenute costituisce il sistema ridotto delle equazioni di congruenza per il modulo intermedio,

BR

I vRI = 0 , (3.117)

in cui il vettore delle velocit`a ridotto `e

vR I =         vP n vQz v_{P n} v_{P t} v_{P z} v_Qz         , (3.118)

e la matrice di congruenza ridotta `e            

r − r cos ϕ 0 r − r cos ϕ r sin ϕ h 0

r − r cos ϕ_v 0 r − r cos ϕ_v r sin ϕ_v h 0

r − r cos ϕ_d 0 α(r − r cos ϕ_d) r sin ϕ_d 0 h − h∗

α(r − r cos ϕ_d) −h + h∗ r − r cos ϕ_d r sin ϕ_d h − h∗ 0

(1 + α)r(1 − cos ϕ_s) h∗ 0 0 0 0 0 0 (1 + α)r(1 − cos ϕ_s) 0 h∗ −h∗             . (3.119)

(37)

Introduciamo le quantit`a cinematiche intrinseche al modulo: la velocit`a di espansione radiale inferiore,

vr := vP n; (3.120)

la velocit`a di espansione radiale superiore,

vr := vP n; (3.121)

la velocit`a di avvitamento,

vt:= v_{P t}− vP t = vP t; (3.122)

la velocit`a di espansione verticale del modulo,

vh := v_{P z} − vP z = vP z; (3.123)

la velocit`a di espansione verticale della sella inferiore,

vh∗ := v

Qz − vP z = vQz; (3.124)

la velocit`a di espansione verticale della sella superiore,

v_h∗ := v

P z − vQz. (3.125)

La velocit`a verticale del nodo Q, dalle (3.123), (3.125), si esprime come:

v_Qz = vh− v_h∗. (3.126)

Possiamo quindi riscrivere il sistema (3.117) nella forma ˜

BR

I ˜vRI = 0 , (3.127)

in cui il vettore delle velocit`a `e

˜vR I =         vr vr vt vh vh∗ v_h∗         , (3.128)

(38)

e la matrice di congruenza ˜BR I `e            

r − r cos ϕ r − r cos ϕ r sin ϕ h 0 0

r − r cos ϕ_v r − r cos ϕ_v r sin ϕ_v h 0 0

α(r − r cos ϕ_d) r − r cos ϕ_d r sin ϕ_d h − h∗ −h + h∗ 0

r − r cos ϕ_d α(r − r cos ϕ_d) r sin ϕ_d h − h∗ 0 −h + h∗

(1 + α)r(1 − cos ϕ_s) 0 0 0 h∗ 0 0 (1 + α)r(1 − cos ϕ_s) 0 0 0 h∗             . (3.129) Rispetto alla (3.119), nella precedente sono state scambiate la terza e la quar-ta riga. Affinch`e il sistema (3.127) abbia soluzioni non nulle, il determinante della matrice (3.129) deve essere nullo.

Analogamente al caso del modulo di estremit`a, introduciamo i seguenti parametri geometrici: il rapporto tra i raggi inferiore e superiore,

γ = r

r ; (3.130)

il rapporto tra l’overlap inferiore e l’altezza del modulo,

δ = h

∗

h ; (3.131)

il rapporto tra l’overlap superiore e l’altezza del modulo,

δ = h

∗

h . (3.132)

Nel calcolo del determinante, dividiamo la prima e la terza colonna per r, la seconda per r, la quarta, quinta e sesta colonna per h. Otteniamo la condizione: det            

1 − γ−1_{cos ϕ} _{1 − γ cos ϕ} _{sin ϕ} ₁ ₀ ₀

1 − γ−1_{cos ϕ} v 1 − γ cos ϕv sin ϕv 1 0 0 α(1 − γ−1_{cos ϕ} d) 1 − γ cos ϕd sin ϕd 1 − δ −1 + δ 0 1 − γ−1_{cos ϕ} d α(1 − γ cos ϕd) sin ϕd 1 − δ 0 −1 + δ (1 + α)(1 − cos ϕ_s) 0 0 0 δ 0 0 (1 + α)(1 − cos ϕ_s) 0 0 0 δ             = 0, (3.133)

(39)

che scriveremo nella forma abbreviata

cI(ϕ, γ, δ, δ; α, α) = 0 . (3.134)

Questa relazione rappresenta una condizione di consistenza per il modulo

intermedio, condizione che lega i parametri geometrici ϕ, γ, δ, δ e i rapporti

delle velocit`a radiali α, α. Anche in questo caso si vede che questa condizione `e invariante per riscalamenti delle dimensioni verticali e radiali.

3.5.5 Compatibilit`

a tra moduli adiacenti

Le condizioni (3.98) e (3.133) caratterizzano i moduli della torre conside-rati separatamente gli uni dagli altri. Nel momento in cui si considerano due moduli adiacenti, che condividono lo stesso poligono di sella, occorre trovare le condizioni di compatibilit`a per i loro meccanismi. Garantendo la compatibilt`a dei meccanismi di tutti i moduli di una torre, resta soddisfat-ta la condizione di indeterminazione, per la quale deve esistere almeno un meccanismo.

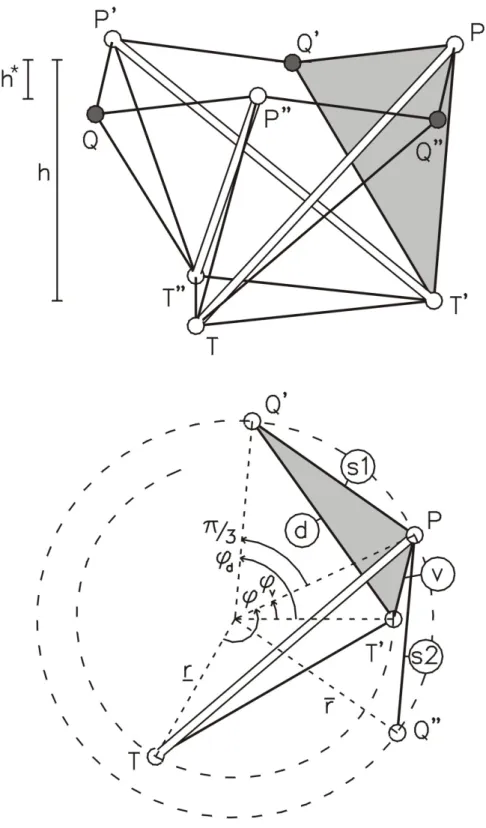
Indichiamo con i pedici i ed (i + 1) le quantit`a relative a due moduli consecutivi, che si susseguono dal basso verso l’alto. Innanzi tutto bisogna richiedere la compatibilit`a della geometria. Il raggio e l’overlap della sella superiore del modulo i sono uguali rispettivamente al raggio e all’overlap della sella inferiore del modulo (i + 1):

ri = ri+1 = r , h ∗

i = h∗i+1= h∗. (3.135)

I nodi Pi e Qi vanno a coincidere rispettivamente con i nodi Q_i+1 e Pi+1 (Fig.

3.20).

Figura 3.20: L’esagono in comune tra i moduli i e (i + 1).

Affinchè i due meccanismi, quello della sella superiore del modulo i e quello della sella inferiore del modulo (i + 1), siano compatibili, le quantità cinematiche di ciascuno devono essere proporzionali tra di loro. Queste quan-tità sono le velocità radiali dei due tipi di nodo e la velocità di espansione

(40)

verticale della sella; la velocit`a tangenziale, uguale per i due nodi, pu`o essere posta nulla. Possiamo scrivere quindi:

(v

P in, vQin, vhi) ∝ (v_Qi+1n, vPi+1n, vhi+1) . (3.136)

Le quantit`a a primo membro e quelle a secondo membro sono legate nello stesso modo dalle equazioni di congruenza; infatti,

r(1 − cos ϕ_s)(v

P in + vQin) + h

∗_v

hi = 0 , (3.137)

oppure

r(1 − cos ϕ_s)(v_Pi+1n + v_Qi+1n) + h∗_v

hi+1 = 0 , (3.138)

per cui è sufficiente che due delle tre componenti nella (3.136) siano propor-zionali affinchè lo siano tutte. Imponendo la proporpropor-zionalità tra le velocità

radiali si ha: _v P in v Qin = vQi+1n v_Pi+1n ⇒ αi = ¡ α_i+1¢−1 ; (3.139)

per cui i rapporti αi e αi+1 devono essere l’uno l’inverso dell’altro.

La precedente rappresenta la condizione di compatibilit`a tra moduli

adia-centi. L’introduzione del rapporto tra le velocit`a radiali del poligono di

sel-la permette sia di ottenere per ciascun modulo una matrice di congruenza quadrata, sia di esplicitare la condizione di compatibilit`a (3.139).

3.5.6 Soluzione della torre

Le (3.98) e (3.134), imposte su ciascun modulo di estremit`a e intermedio, insieme con la (3.139), imposta su ciascun poligono di sella, costituiscono le condizioni necessarie e sufficienti affinch`e la condizione di indeterminazione per la torre di Snelson sia soddisfatta.

Utilizzando i parametri cinematici intrinseci, si pu`o vedere che la matrice di congruenza B dell’intera torre ha l’aspetto rappresentato nella Fig. 3.21.

Si tratta di una matrice in cui gli elementi non nulli sono contenuti nei blocchi mostrati in Fig. 3.21. Il blocco Bi corrisponde al modulo i-esimo ed

ha una parte in comune con il blocco adiacente; questa parte è costituita dall’equazione del poligono di sella condiviso tra i moduli. tipicamente, ogni blocco Bi ha rango massimo. Se cos`ı è, si può dimostrare che il meccanismo

(self-stress) `e unico e coinvolge tutti i moduli della torre, e che le (3.98), (3.134), (3.139) sono soddisfatte se e solo se det B = 0.

Le possibilit`a di utilizzo delle (3.98), (3.134), (3.139) sono molteplici: esse permettono di costruire le configurazioni ciclicamente simmetriche modulo per modulo. Nelle sezioni seguenti illustreremo alcuni modi di procedere, nei casi pi`u semplici.

(41)

Figura 3.21: Aspetto della matrice di congruenza globale della torre.

3.5.7 Soluzione particolare per torri cilindriche

Una torre cilindrica di m moduli ha un modulo intermedio che si ripete con la stessa geometria; per i = 2 . . . m−1 si ha:

       ϕ_i = ϕ , r_i = ri = r , hi = h , h∗_i = h∗_i = h∗ _. (3.140)

Quindi, i rapporti γ_i, δ_i, δi sono costanti da modulo a modulo:

γ_i = 1 , δ_i = δi = δ . (3.141)

I moduli di estremit`a sono uguali tra loro:            ϕ₁ = ϕ_m = ϕ_E , r₁ = rm = rE , r1 = rm = r , h1 = hm = hE , h∗ 1 = h∗m = h∗ . (3.142)

Per una torre cilindrica le quantit`a cinematiche e statiche variano da mo-dulo a momo-dulo. Nella nostra analisi, le condizioni di consistenza dei moduli

(42)

intermedi possono essere soddisfatte con gli stessi valori dei parametri geome-trici e diversi valori dei rapporti α_ie αi, in modo tale da soddisfare comunque

le condizioni di compatibilità tra moduli adiacenti. In questa sezione esplici-teremo una soluzione particolare ottenuta imponendo uguali velocità radiali per tutti i nodi di sella. Ciò equivale ad imporre che i rapporti delle velocità radiali siano pari ad uno:

α_i = αi = 1 . (3.143)

In questo modo la condizione di compatibilit`a tra moduli adiacenti (3.139) ri-mane automaticamente soddisfatta e le condizione di consistenza dei moduli intermedi sono tutte equivalenti. Dalle equazioni di congruenza dei tiran-ti diagonali (terza e quarta riga della (3.129)) si ottiran-tiene che le velocit`a di espansione verticale delle selle sono uguali:

vh∗ = v

h∗; (3.144)

di conseguenza, dalle equazioni dei tiranti di sella (quinta e sesta riga della (3.129)) si ottiene che le velocit`a di espansione radiale inferiore e superiore sono uguali:

vr= vr. (3.145)

Il sistema di equazioni (3.127) si riduce alla forma seguente:       2r(1 − cos ϕ) r sin ϕ h 0 2r(1 − cos ϕ_v) r sin ϕ_v h 0 2r(1 − cos ϕ_d) r sin ϕ_d h − h∗ _{−h + h}∗ 2r(1 − cos ϕ_s) 0 0 h∗           vr vt vh vh∗     = 0 . (3.146)

Per cui, si pu`o scrivere la condizione di consistenza particolare:

det       1 − cos ϕ sin ϕ 1 0 1 − cos ϕ_v sin ϕ_v 1 0 1 − cos ϕ_d sin ϕ_d 1 − δ −1 + δ 1 − cos ϕ_s 0 0 δ      = c p I(ϕ, δ) = 0 (3.147) (qui δ = h∗

h ). Da questa condizione, utilizzando le formule trigonometriche

di addizione, sottrazione e prostaferesi e ricordando le definizioni (3.101) e (3.102): θ0 := π n + π 2 e θ := ϕ − θ0, si ottiene l’espressione seguente:

δ2(sin θ0+ sin θ) + δ(1 − sin θ0+ sin θ0sin θ − sin θ) − sin θ0sin θ + sin θ = 0 .

(43)

La relazione precedente deve sussistere tra i parametri geometrici adimen-sionali del modulo intermedio. La condizione da imporre sulla geometria del modulo di estremità è identica alla soluzione della torre di due moduli (3.103). Ciò perchè i nodi di sella della torre di due moduli hanno tutti la stessa velocità radiale; questa è anche la condizione sui moduli di estremità di una torre cilindrica particolare. Riassumendo, la (3.148), valida per i moduli intermedi, e la (3.103), valida per i moduli di estremità, costituiscono la solu-zione di una torre cilindrica particolare. A questo punto, rispettando queste due condizioni e mantenendo uguali raggi e overlap, possiamo assemblare insieme: moduli intermedi con altezza e twist diversi; moduli di estremità con altezza, twist e raggi di base diversi.

Nelle Figure 3.22, 3.23 sono mostrati i grafici della funzione δ(ϕ) definita implicitamente dalla (3.148), nei casi di 2, 3, 4 puntoni per modulo rispet-tivamente. Ripetiamo alcune osservazioni del tutto analoghe a quelle gi`a svolte per il caso dell’assemblaggio di due moduli. I grafici sono simmetrici rispetto all’asse ϕ = θ0−π₂ = π_n; per tale valore i tiranti verticali e i puntoni

si scambiano di ruolo. L’overlap si annulla in corrispondenza della soluzione

ϕ₁ (ϕ₂) per il modulo elementare, ottenuta in 3.4.2; in questa configurazione i due moduli conservano le caratteristiche del modulo elementare.

3.5.8 Costruzione di soluzioni generali per torri

cilin-driche

Considerando la geometria del caso precedente, le (3.140) e (3.142) denotano i parametri, rispettivamente, dei moduli intermedi e di estremit`a; i rapporti

γ_i, δ_i, δi sono costanti da modulo a modulo:

γ_i = 1 , δ_i = δi = δ , i = 2, . . . , (m − 1) . (3.149)

Come anticipato, le condizioni di consistenza (3.133) di ciascun modulo inter-medio possono essere soddisfatte per identici valori dei parametri geometrici ma diversi valori dei rapporti α_i, αi; la (3.133) per l’i-esimo modulo assume

la forma det           

1 − cos ϕ 1 − cos ϕ sin ϕ 1 0 0

1 − cos ϕ_v 1 − cos ϕ_v sin ϕ_v 1 0 0

α_i(1 − cos ϕ_d) 1 − cos ϕ_d sin ϕ_d 1− δ −1+ δ 0 1 − cos ϕ_d αi(1 − cos ϕd) sin ϕd 1− δ 0 −1+ δ

(1 + α_i)(1 − cos ϕ_s) 0 0 0 δ 0 0 (1 + αi)(1 − cos ϕs) 0 0 0 δ            = 0 , (3.150)

(44)

Figura 3.22: Modulo intermedio, α = α = 1. Grafico di δ in funzione di ϕ;

(45)

Figura 3.23: Modulo intermedio, α = α = 1. Grafico di δ in funzione di ϕ,

n = 4.

che abbreviamo come segue:

cIi(ϕ, δ; αi, αi) = 0 , i = 2, . . . , (m − 1) ; (3.151)

Alla (3.151) va aggiunta la condizione di consistenza (3.103) sui moduli di estremit`a:

cE(ϕE, γE, δE; αE) = 0 . (3.152)

Fissati i parametri ϕ, δ del modulo intermedio, la (3.151) definisce impli-citamente una funzione nel piano di α, α. La funzione `e una iperbole, infatti, la (3.150) si pu`o esprimere nella forma seguente:

αα + a1(ϕ, δ)α + a2(ϕ, δ)α + b(ϕ, δ) = 0 . (3.153)

Ogni modulo intermedio, preso singolarmente, possiede la propriet`a di sim-metria centrale dispari; di conseguenza, la (3.153) deve rimanere soddisfatta scambiando α e α. Ci`o implica che

(46)

ovvero che l’iperbole sia simmetrica rispetto alla retta α = α. Esplicitando la (3.153) rispetto a α con queste sostituzioni si ottiene:

α = −a α + b

α + a . (3.155)

da cui si vede che l’iperbole possiede gli asintoti di equazioni α = −a e

α = −a. Poich`e per la soluzione particolare della torre si ha α = α = 1,

per configurazioni poco differenti da questa l’iperbole `e contenuta nel primo e terzo quadrante del sistema di riferimento, i cui assi sono costituiti dai suoi asintoti. La condizione di compatibilit`a tra i moduli (3.139) definisce anch’essa un’iperbole nel piano di α, α; i suoi asintoti sono le rette α = 0 e α = 0. Fissata la geometria del modulo intermedio, possiamo tracciare le due curve (rami di iperbole possono intersecarsi o meno9_{), che sono molto}

utili per rappresentare le soluzioni generali, come illustrato di seguito. Per le proriet`a di simmetria della struttura, possiamo limitare l’attenzione ad una sola met`a della torre, distinguendo il caso di m dispari da quello di

m pari.

- Numero dispari di moduli. In questo caso, in virt`u della simmetria centrale dispari, abbiamo, per il modulo al centro della torre,

α(m+1

2 ) = α(m+12 ) = 1 + ε , (3.156)

dove ε `e lo scostamento dal valore unitario che caratterizza la soluzione par-ticolare. Con questa condizione possiamo scegliere la geometria del modulo intermedio dalla sua condizione di consistenza, fissando uno dei parametri ϕ,

δ e trovando l’altro in base alla relazione c_I₍m+1

2 )(ϕ, δ; 1 + ε, 1 + ε) = 0 . (3.157)

Una volta trovata la geometria del modulo intermedio possiamo tracciare nel piano di α e α le due iperboli (3.139) e (3.155). Passiamo al modulo adiacente inferiormente tramite la condizione di compatibilit`a tra i moduli (3.139), trovando che α(m+1 2 −1) = α −1 (m+1 2 ) = 1 1 + ε . (3.158)

Dalla condizione di consistenza del modulo ¡m+1

2 − 1

¢

, possiamo ricavare l’altro rapporto delle velocita radiali:

c_I₍m+1 2 −1) µ ϕ, δ; α(m+1 2 −1), 1 1 + ε ¶ = 0 . (3.159)

9_{Per la soluzione particolare i rami nel primo quadrante sono tangenti nel punto di}

(47)

Figura 3.24: Torre cilindrica. Costruzione grafica di una soluzione generale,

m dispari, ε < 0.

La Fig. 3.24, in cui sono riportate le due iperboli, presenta la costruzione grafica dei valori α_i, αi nel passare da un modulo al successivo (nel caso di

ε < 0). Proseguendo in questo modo fino al modulo di estremit`a inferiore,

troviamo per αE il valore:

αE = α−12 . (3.160)

Finalmente, troviamo la geometria del modulo di estremit`a: fissiamo due tra le quantit`a ϕ_E, γ_E, δE per trovare la terza dall’ultima condizione di

consi-stenza (3.152).

- Numero pari di moduli. Il procedimento è analogo, con la differenza che si utilizza la proprietà di simmetria pari. Questa implica uguali velocità radiali per i nodi della sella centrale della torre:

α(m

2+1) = α(

m

2) = 1 . (3.161)

Lo scostamento ε dal valore unitario si assegna a α(m

2):

α(m

(48)

Figura 3.25: Torre cilindrica. Costruzione grafica di una soluzione generale,

m pari, ε > 0.

Possiamo cos`ı scegliere la geometria del modulo intermedio utilizzando la condizione

c_I₍m

2)(ϕ, δ; 1 + ε, 1) = 0 , (3.163)

e tracciare le due iperboli (3.139) e (3.155). Il resto del procedimento `e identico al caso precedente. La Fig. 3.25 mostra come si trovano i valori α_i,

αi passando da un modulo al successivo (nel caso di ε > 0).

Notiamo che sono possibili ‘salti’ sui rami delle iperboli che si trovano nel terzo quadrante dei sistemi di riferimento individuati dai loro asintoti.

3.5.9 Torri rastremate

Nel caso delle torri rastremate, occorre utilizzare la forma pi`u generale del-l’equazione di consistenza (3.134), in cui compare il rapporto tra i raggi superiore ed inferiore, γ, ed il rapporto tra l’overlap inferiore (superiore) e