2 Sistemi dinamici ed Identificazione Strutturale Si intendono richiamare nel presente capitolo i principi della

2 Sistemi dinamici ed Identificazione Strutturale

Si intendono richiamare nel presente capitolo i principi della Dinamica delle Strutture e fare un cenno al problema della Identificazione Strutturale.

In riferimento alle indagini numerico - sperimentali proposte per il campanile in studio, si sintetizzano nel seguito i principi base dei sistemi dinamici sottoposti a vibrazioni libere ed a vibrazioni forzate.

Al fine poi di calibrare un modello numerico della struttura, in relazione ai dati ricavati dall’indagine sperimentale effettuata, si richiamano i risultati classici inerenti la valutazione della forzante armonica sul campanile prodotta dall’oscillazione di una delle campane presenti.

2.1 Introduzione

I problemi legati alla manutenzione ed all’adeguamento del patrimonio edilizio d’interesse storico ed artistico sono da alcuni anni oggetto di crescente interesse e studio.

Tali interventi necessitano di una accurata diagnosi preventiva del manufatto, mirata all’identificazione delle caratteristiche meccaniche dei materiali e dei più significativi parametri strutturali globali.

Questa operazione si avvale sia della sperimentazione, per la quale sono ormai disponibili sofisticate apparecchiature e metodologie di indagine, sia dell’analisi numerica.

Con l’uso combinato di tali strumenti si mira ad identificare un modello numerico del manufatto capace di fornire previsioni sul suo comportamento in situazioni gravose, quali ad esempio quelle sismiche, ed indicazioni progettuali per il restauro e l’adeguamento.

In tale contesto le prove di tipo dinamico, associate a tecniche di Identificazione Strutturale, possono svolgere un ruolo di fondamentale importanza, permettendo di ottenere un numero di informazioni notevolmente più grande rispetto alle classiche prove di tipo statico e quindi di rilevare quei comportamenti che indicano l’insorgere di possibili fenomeni di danneggiamento o di risposte strutturali diverse da quelle teoriche attese. Questa tipologia di prove, qualora venga ripetuta nel tempo, permette anche la realizzazione di un vero e proprio controllo dello “stato di salute” delle strutture e consente quindi di programmare gli interventi di manutenzione eventuali.

I risultati di una corretta sperimentazione ed identificazione dinamica rappresentano la base di riferimento per costruire modelli numerici in grado di riprodurre le risposte sperimentali misurate.

In generale i risultati ottenuti dal modello teorico di una struttura non rispecchiano il comportamento reale della stessa, sia per la difficoltà di simulare le reali leggi di comportamento dei materiali e le condizioni al contorno, sia per le modificazioni che intervengono in fase di realizzazione e durante la vita della struttura.

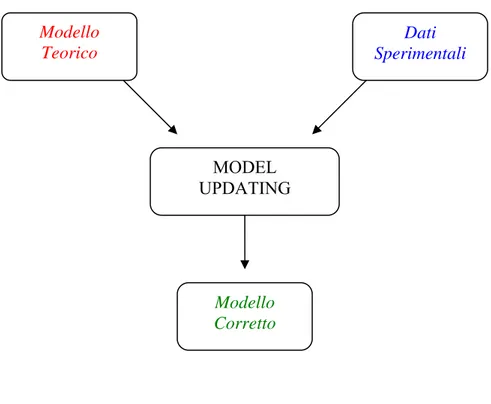
Se si è in possesso di informazioni sul comportamento reale della struttura, allora il modello teorico può essere corretto in modo da ridurre le differenze tra la struttura stessa ed il modello. Queste correzioni vengono eseguite con tecniche dette di “Model Updating” (vedi fig. 2.1).

Modello Teorico Dati Sperimentali MODEL UPDATING Modello Corretto

fig. 2.1 “Model Updating”

Un modello teorico corretto sulla base dei risultati sperimentali può essere utilizzato anche per l’individuazione di fenomeni di danneggiamento strutturale o di deterioramento delle caratteristiche meccaniche dei materiali, attraverso l’analisi delle correzioni stesse introdotte sul modello originario.

Tale modello può inoltre diventare un valido strumento di progettazione, qualora si voglia analizzare l’effetto di modifiche strutturali o di variazioni delle azioni sollecitanti.

Le informazioni necessarie possono essere ricavate in generale come detto da prove sperimentali di tipo statico o dinamico.

Quelle statiche permettono di ottenere informazioni sulla struttura in modo diretto, ma spesso risultano insufficienti per correggere il modello numerico.

Per contro le prove dinamiche sono in grado di fornire un numero di informazioni molto più elevato, ma richiedono un lavoro di analisi a posteriori impegnativo e l’impiego di tecniche avanzate di Identificazione Strutturale.

L’identificazione delle caratteristiche fisico - meccaniche dei sistemi strutturali consiste nella risoluzione di un problema inverso rispetto a quello che si affronta nella progettazione: Nota la risposta strutturale e le azioni a cui è soggetta la struttura, si determinano le caratteristiche meccaniche della struttura stessa.

Le azioni agenti sulla struttura possono essere completamente note, oppure definite statisticamente.

Le modalità di esecuzione delle prove sperimentali e le metodologie di analisi delle misure devono essere inoltre definite in funzione del tipo di struttura in esame e delle caratteristiche da determinare.

Il meccanismo di eccitazione è generalmente mirato a mettere la struttura in movimento applicando una forza o un sistema di forze F

( )

t in punti prestabiliti.

Esistono diversi modi per applicare queste forze; l’eccitazione attraverso sistemi di tipo meccanico (es. vibrodina) comporta il vantaggio di poter imporre, misurare e controllare il moto della struttura, ma anche il grande svantaggio di necessitare di un collegamento rigido con la struttura stessa.

Un altro modo per eccitare la struttura è quello di sfruttare l’eccitazione ambientale, quali rispettivamente il vento per le strutture snelle ed il passaggio di automezzi per le infrastrutture stradali.

Nel caso specifico poi dell’identificazione della risposta dinamica di torri campanarie ci si può spesso avvalere convenientemente dell’utilizzo delle campane stesse al fine di eccitare la struttura; tale metodo risulta infatti generalmente di particolare efficacia ed è anche economico.

La strumentazione di misura è essenzialmente costituita da trasduttori sia per misurare la forza di eccitazione sia per misurare le accelerazioni, le velocità o gli spostamenti della struttura e da un sistema di acquisizione dati.

Le caratteristiche dinamiche della struttura (frequenze proprie, smorzamenti e deformate modali) possono essere determinate analizzando la risposta strutturale (accelerazioni rilevate sulla struttura) mediante tecniche di analisi e trattamento numerico dei segnali digitalizzati. Le misure dinamiche in condizioni di esercizio, consentono di ottenere un numero rilevante di informazioni.

I parametri meccanici stimati con questa metodologia permettono di: - determinare le proprietà elastiche della struttura (nota la geometria del sistema e quindi la massa).

- identificare la struttura con un modello teorico, convalidato mediante confronto con i risultati sperimentali.

- valutare l’effettivo comportamento dei vincoli ed il loro grado di efficienza.

- individuare eventuali dissimmetrie di comportamento, sintomo di possibili danneggiamenti locali.

2.2 Sistemi dinamici

Prevedere e quantificare la risposta di un sistema strutturale sollecitato da una azione dinamica, come è ad esempio l’azione sismica, in termini di spostamenti, sollecitazioni e deformazioni, richiede l’aiuto di modelli matematici e tecniche di analisi proprie della dinamica strutturale.

Si ritiene pertanto utile richiamare alcuni concetti base che permetteranno di comprendere più facilmente quanto verrà esposto nei capitoli successivi.

Un carico dinamico è un qualsiasi carico la cui intensità, direzione o posizione varia nel tempo.

Analogamente la risposta strutturale ad un carico dinamico, cioè le deformazioni e le tensioni risultanti, varia anch’essa nel tempo ed perciò è dinamica.

La caratteristica essenziale di un sistema definito “dinamico” è quella di generare forze d’inerzia non più trascurabili rispetto ad un sistema definito “statico”, cosicché le sollecitazioni interne nella struttura devono equilibrare non solo il carico esterno direttamente applicato, ma anche le forze di inerzia risultanti dall’accelerazione della struttura.

In generale, se le forze d’inerzia rappresentano una parte significativa del carico totale equilibrato dalle forze interne, occorre tener conto del carattere dinamico del problema.

Se invece il moto è così lento che le forze d’inerzia possono ritenersi trascurabili, l’analisi della risposta ad ogni istante può essere effettuata mediante i classici metodi della Statica, anche se il carico e la risposta strutturale che ne consegue sono in realtà variabili nel tempo. Per i sistemi dinamici si definiscono tre categorie di problematiche fondamentali:

1) Problema di progetto: nota l’azione e tendo conto delle limitazioni cui deve sottostare la risposta, si progetta il sistema.

2) Problema di controllo: nota la descrizione del sistema e nota una risposta desiderata, si determina l’azione necessaria a produrla.

3) Problema d’identificazione: nota l’azione e nota sperimentalmente la risposta, si determina un modello della struttura.

Si osserva che la definizione classica inerente al problema d’identificazione si estende anche a quei casi in cui non si conosce l’azione, pur essendo nota sperimentalmente la risposta.

2.3 Richiami di dinamica strutturale

La dinamica dei sistemi strutturali può essere studiata partendo dal Principio di D’Alambert, secondo il quale ogni sistema risulta sempre in equilibrio sotto l’azione delle forze attive

, delle forze reattive e delle forze d’inerzia

( )

{

F t

}

{

Φ

( )

t

}

−m

{ }

a

( )

t .

Tale principio si riassume nella ben nota equazione del moto che segue (posta in notazione matriciale):

( )

{ }

F t +

{ }

Φ

( )

t −m

{ }

a

( )

t =0

Nel caso di un modello continuo la relazione scritta sopra, introdotta la funzione di densità di massa ρ

(

x,y,z,t

)

, detto lo spostamento di un qualunque punto del corpo, definite rispettivamente

(

{

s x,y,z,t

)}

(

)

{

f_v x,y,z,t

}

e

{

f_s

(

x,y,z,t

)

}

come le forze per unità di volume e di superficie agenti sul corpo (avendo indicato con V il volume del continuo e con S la rispettiva superficie esterna), si ha:

(

) (

{

)

}

[

]

{

(

)

}

{

(

}

∫

=

∫

+

∫

∂ ∂ V S s V v x y z t dV f x y z t dS f dV t z y x s t z y x t2 , , , , , , , , , , , , 2 ρ

)

In un sistema dinamico l’analisi è complicata dal fatto che le forze d’inerzia risultano dagli spostamenti strutturali, che a loro volta sono influenzati dalla grandezza delle forze d’inerzia. Pertanto il problema deve essere formulato in termini di equazioni differenziali parziali. Inoltre, poiché la massa è distribuita con continuità, gli spostamenti e le accelerazioni devono essere definiti per ciascun punto del corpo per poter definire in modo completo le forze d’inerzia.

Affrontare il problema nella sua generalità appare da subito notevolmente complicato, se non addirittura proibitivo, se si vuol considerare un modello continuo rappresentativo di una struttura oggetto di un analisi dinamica.

E’ pertanto necessario nella pratica rappresentare la struttura da analizzare mediante un modello quanto più possibile semplice, ma che rifletta tuttavia in modo adeguato le proprietà dinamiche che le competono.

Se ad esempio la massa di una struttura potesse venire concentrata in una serie finita di punti, il problema analitico conseguente ne risulterebbe estremamente semplificato, poiché le forze d’inerzia potrebbero svilupparsi solo in tali punti prestabiliti.

La modellazione di una struttura come un sistema a masse concentrate è solo uno dei possibili metodi di discretizzazione di una struttura reale.

Esistono poi altri metodi, quali ad esempio il metodo degli elementi finiti, che permettono di ridurre le equazioni differenziali che descrivono il moto di un modello continuo a sistemi di equazioni algebriche, la cui soluzione approssima la soluzione esatta tanto meglio quanto migliore è la discretizzazione fatta sul continuo.

Una volta discretizzato un sistema strutturale in modo da ridurre ad un numero finito i gradi di libertà dinamica che gli competono, è possibile esprimere convenientemente l’equazione del moto in forma matriciale secondo quanto segue:

[ ]

m

{ }

q&&

( )

t +

[ ]

c

{ }

q&

( )

t +

[ ]

k

{ }

q

( )

t =

{ }

Q

( )

t

Tale espressione rappresenta un sistema di n equazioni in n incognite, nelle quali in generale le equazioni non risultano disaccoppiate; n è il numero dei gradi di libertà del sistema considerato, una volta che questo sia stato opportunamente discretizzato.

Si sono così introdotte le matrici

[ ]

m ,

[ ]

c e

[ ]

k , rispettivamente definite come matrice delle masse o d’inerzia, matrice di smorzamento e matrice di rigidezza del sistema strutturale discreto.

Tutte e tre le matrici sopra riportate risultano simmetriche.

In generale tali matrici non sono diagonali; conviene pertanto fare una trasformazione in modo che queste lo diventino.

Con ciò si intende andare a disaccoppiare le equazioni del sistema di modo che possano venir risolte ciascuna per proprio conto, estendendo così al caso dello studio dei sistemi a molti gradi di libertà (MDOF) le soluzioni ricavate studiando i sistemi ad un solo grado di libertà (SDOF).

Ritornando ad esaminare l’equazione del moto in forma matriciale scritta precedentemente, rappresenta il vettore degli spostamenti del sistema, mentre è il vettore delle forze applicate.

( )

{

qt

}

{

Q

( )

t

}

Qualora si voglia studiare il caso di oscillazioni libere di un sistema dinamico discretizzato, si ha che

{ }

Q

( )

t =0.

Se invece si vuole studiare un sistema dinamico per il quale le oscillazioni vengono “forzate” da un sistema di forze esterne applicate sulla struttura, risulterà noto il vettore

{ }

Q

( )

t rappresentativo appunto della forzante agente sul sistema.

I sistemi dinamici in teoria possono venire considerati sia “smorzati” che “non smorzati”; si intuisce che ovviamente il secondo caso è prettamente teorico, essendo sempre presenti forze di attrito o di smorzamento nelle strutture reali, a causa delle quali parte dell’energia meccanica viene trasformata e persa attraverso altre forme di energia, come ad esempio sotto forma di calore.

Nel primo caso gli effetti dissipativi sul moto vengono messi in conto mediante la matrice

[ ]

c di smorzamento del sistema.

Si ammette che le forze responsabili dello smorzamento e della conseguente dissipazione del moto siano proporzionali all’ampiezza della velocità ed opposte alla direzione del moto, pertanto nella notazione matriciale la matrice di smorzamento

[ ]

c risulterà moltiplicata per il vettore

{

q&

( )

t

}

delle velocità del sistema.

Non sempre questa schematizzazione interpreta efficacemente le caratteristiche del sistema, ma consente d’altra parte un analisi matematica relativamente semplice e conveniente (modello a smorzamento di tipo viscoso).

In una modellazione a masse concentrate la matrice

[ ]

m delle masse è una matrice diagonale, i cui elementi non nulli sono proprio le masse concentrate associate ai rispettivi gradi di libertà discretizzati ed il rispettivo valore di tali masse dipende dal criterio di influenza adottato nella disretizzazione dell’intera massa della struttura.

Questo modo di procedere nel semplificare il sistema oggetto di studio non è però sempre accettabile nella generalità dei casi, né si può sempre trascurare il fatto che la massa distribuita possa essere associata talvolta a più di un grado di libertà.

Nell’ambito del metodo degli elementi finiti, ad esempio, il campo degli spostamenti in un mezzo continuo è espresso mediante l’introduzione di una matrice di funzioni interpolanti

secondo quanto segue:

(

[

N x,y,z

)

]

(

)

{

s x,y,z,t

}

=

[

N

(

x,y,z

)

]

{

s₀

( )

t

}

dove s₀

( )

t è il vettore degli spostamenti nodali.

In accordo allora a quanto detto sopra, si ricava la matrice “coerente” delle masse del sistema discretizzato:

[ ]

=

_∫

(

) (

[

)

]

[

(

)

]

V T dV z y x N z y x N z y x m ρ , , , , , ,

Di più difficile determinazione è la matrice di smorzamento di un sistema dinamico.

Le capacità dissipative di una struttura dipendono da diversi fenomeni non ancora chiaramente compresi; pertanto non è generalmente possibile costruire la matrice

[

partendo dalla sola conoscenza della geometria della struttura e delle caratteristiche meccaniche dei materiali che la compongono, in modo analogo a quanto è possibile fare per costruire le matrici di rigidezza e di massa della struttura.

]

c

Di solito pertanto i valori degli smorzamenti delle strutture si assegnano globalmente sulla base di risultati sperimentali noti.

Dai metodi grazie ai quali risulta possibile misurare lo smorzamento di una struttura, ciò che è noto è di solito il valore dei rapporti di smorzamento definiti come segue:

m k c i i i 2 = ξ

relativi all’i-mo modo di vibrazione della struttura.

Quindi anziché esser noti gli elementi della matrice

[ ]

c , sono noti gli ξ_i.

Se si assume che la matrice di smorzamento possa essere espressa come combinazione lineare delle matrici di massa e di rigidezza della struttura, si può scrivere:

[ ] [ ] [ ]

c =α m +β k con α e β coefficienti opportuni.

In tal caso la matrice di smorzamento

[ ]

c diventa diagonale ed è definita matrice di smorzamento proporzionale.

Qualora risulti

[

c

]

proporzionale semplicemente a

[ ]

k , caso in cui α =0, il rapporto di smorzamento ξ_i risulta direttamente proporzionale alla pulsazione ω_i della vibrazione del modo che gli corrisponde.

In tal caso i modi superiori al primo (modo di maggior periodo, ovvero di minor frequenza o pulsazione ω , con ₁ ) risultano tanto più smorzati quanto sono più distanti dal modo fondamentale (o primo modo).

1 =

i

Le osservazioni sperimentali avvallano come più realistica questa ipotesi, rispetto al caso inverso secondo cui la matrice di smorzamento

[ ]

c possa risultare proporzionale semplicemente ad

[ ]

m , caso in cui β =0.

Nella pratica si è osservato come, coerentemente al primo dei due casi, eccitando una struttura con una forza pulsante ed incrementando via via la frequenza, le amplificazioni della risonanza risultino sempre meno accentuate in corrispondenza dei modi successivi al primo, fino talvolta a perderle del tutto.

Da ciò si deduce come i modi superiori al primo siano talmente smorzati che, anche in condizione di risonanza, non apportano un contributo rilevante alla risposta complessiva. Per questo motivo di solito l’analisi modale si arresta ai primi modi, fino al terzo o al quarto, tralasciando quelli successivi.

Altri casi particolari rendono la matrice di smorzamento

[ ]

c diagonale. Un caso frequente è quello in cui lo smorzamento risulta molto contenuto.

Per tale situazione l’accoppiamento delle equazioni del sistema algebrico dovuto ai termini fuori della diagonale principale della matrice

[ ]

c può essere considerato alla stregua di un effetto del secondo ordine.

Talvolta trascurando tale effetto si perviene a soluzioni semplificate accettabili.

Si dimostra allora che se la matrice di smorzamento è di tale tipo, i rapporti di smorzamento possono venir espressi come segue:

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = i i i _ω βω α ξ 2 1

Poiché, per quanto detto fino ad adesso, la matrice

[ ]

c viene allora a dipendere dalle matrici e

[

solo attraverso due coefficienti

[ ]

m k

]

α e β, fissati gli smorzamenti di solo due modi, gli altri risultano così implicitamente determinati.

Nel seguito si riportano le soluzioni per il problema dinamico di un sistema discreto ideale a smorzamento nullo, limitatamente ai casi di vibrazioni libere e di vibrazioni forzate.

2.3.1 Sistemi con vibrazioni libere

Si considera per semplicità un sistema dinamico non smorzato, quindi , nel caso di vibrazioni libere.

[ ]

c =0

L’equazione del moto, in forma matriciale, diventa:

[ ]

m

{ }

q_&&

( )

t +

[ ]

k

{ }

q

( )

t =0

Il sistema algebrico che ne consegue è un sistema omogeneo; la soluzione può essere determinata a meno di una costante moltiplicativa.

La risposta del sistema è data dalla descrizione del relativo moto dovuto ad uno spostamento, detto anche perturbazione, dalla posizione di equilibrio statico.

Si ricerca allora una particolare soluzione per la quale le coordinate eseguano lo stesso moto nel tempo.

( )

t q_i

Questa condizione che andiamo ad imporre è definita come condizione di moto sincrono. Ne segue che i rapporti

( )

_{( )}

t q t q

j

i risultano indipendenti dalla variabile tempo.

Dunque la configurazione del sistema non cambia nel tempo; ne cambia solo l’ampiezza. In base all’ipotesi di moto sincrono si può allora scrivere:

( )

( )

n j t f u t q_{j j} , , 1 K = =

con uj costanti nel tempo.

Sostituendo tale relazione nell’equazione del moto si ottiene:

( )

( )

n i u k t f u m t f n j n j j ij j ij , , 1 0 1 1 K && = = +

∑

∑

= = quindi:

( )

( )

i u m u k t f t f j j ij j j ij ∀ = −

∑

∑

&& Posto allora −

( )

_{( )}

=λ t f t f& &

, con λ costante, si ha:

( )

( )

(

)

⎪ ⎩ ⎪ ⎨ ⎧ = − = +

∑

= n j j ij ij m u k t f t f 1 0 0 λ λ &&

Per la risoluzione del sistema si ricerca una soluzione del tipo f

( )

t = Asinωt, o se si preferisce si può anche fissare una soluzione del tipo

( )

i t

e t

f = ω introducendo così la relazione di Eulero, che sostituita sopra porta alle espressioni seguenti:

(

)

⎪ ⎩ ⎪ ⎨ ⎧ = − =

∑

= n j j ij ij m u k 1 2 2 0 ω ω λ

Ovvero si arriva ad ottenere un sistema omogeneo di n equazioni in n incognite, in cui è il parametro.

2 ω Ricercando soluzioni diverse da quella banale si riconosce il problema della ricerca degli autovalori della matrice

[ ]

m −1

[ ]

k , come si evince da quanto segue:

( )

2 _{= −} 2 ₌0 Δω kij ω mij

Tale equazione rappresenta l’equazione secolare della matrice

[ ] [ ]

m −1 k , ed è un equazione di ordine n, con n radici, in generale distinte: 2 2.

1 , ωn

ω _K

Le radici così trovate (gli autovalori) rappresentano le frequenze naturali del sistema dinamico considerato, dove la minore frequenza è detta prima frequenza naturale o anche frequenza fondamentale, e con ciò viene fatta convenzione di ordinare tali autovalori in maniera crescente.

Si conclude così che esistono n frequenze per le quali è possibile un moto armonico del sistema.

Associato a ciascun autovalore ω , esiste un autovettore r ( )

{ }

r

u , detto anche vettore modale, soluzione del problema seguente:

[ ]

{ }

( )

[ ]

{ }

( )r r r u m u k =ω 2 ovviamente con r =1 K, ,n.

I vettori modali possono essere raccolti nella matrice modale come segue:

[ ]

[

{ }

( )

{ }

( )n

]

u u

u = 1 ,_K,

così le n soluzioni del problema degli autovalori possono essere scritte nella forma più compatta:

[ ][ ] [ ][ ]

[ ]

_ω2 u m u k =

con

[ ]

_ω2 _{matrice diagonale dei quadrati delle frequenze naturali del sistema.}

Gli autovettori così ricavati rappresentano fisicamente le forme modali, o anche i modi naturali, del sistema; questi descrivono in sostanza la “forma” dei possibili moti di vibrazione del sistema dinamico.

Fin qui si è riassunto quanto va sotto al nome di analisi modale di un sistema dinamico. Poiché si dimostra che gli autovettori

{ }

( )r

u formano un sistema linearmente indipendente, ogni possibile configurazione del sistema può essere allora costruita come combinazione lineare degli autovettori:

{ }

{ }

( )

{ }

( )n n u c u c u = ₁ 1 +K+

Fisicamente ciò significa che qualsiasi movimento possibile del sistema, conseguenza di un arbitraria eccitazione, può essere considerato come la sovrapposizione dei modi naturali moltiplicati per opportune costanti, in cui proprio tali costanti “misurano” il grado di partecipazione di ogni singolo modo al moto.

Scritto allora che:

( )

{ }

u

[ ]

m

{ }

u c_r = r T

I coefficienti “misurano” il contributo del modo associato cr ( )

{ }

r

u al moto

{

u

}

. Quanto concluso costituisce il noto Teorema di espansione.

Le frequenze naturali ω , assieme ai modi naturali associati _r

{ }

( )r

u , rappresentano una unica caratteristica del sistema dinamico.

Si dimostra poi che ciascun insieme ω ,r ( )

{ }

r

u può venir eccitato indipendentemente dagli altri.

Se ad esempio si impiega una forzante armonica di frequenza ω , allora la configurazione r

assunta dal sistema sarà simile al modo

{ }

( )r

u .

2.3.2 Sistemi con vibrazioni forzate

Si considera per semplicità un sistema dinamico non smorzato, quindi , nel caso di vibrazioni forzate.

[ ]

c =0

L’equazione del moto, in forma matriciale, è la seguente:

[ ]

m

{ }

q&&

( )

t +

[ ]

k

{ }

q

( )

t =

{ }

Q

( )

t

( )

{

Q t

}

è la forzante che agisce sul sistema dinamico studiato. Tale forzante può in generale appartenere ad uno dei casi seguenti:

1) Forzante armonica

2) Forzante periodica, scomponibile in serie di Fourier 3) Forzante impulsiva

4) Forzante random

Si riportano le soluzioni limitatamente ai primi due casi di forzanti. Nel caso di forzante armonica si ha:

( )

{ } { }

Q t = F ₀sinωˆt dove ωˆ è la pulsazione della forzante.

Si ricerca allora una soluzione particolare del tipo seguente:

( )

{ }

q_p t =

{ }

Y ₀sinωˆt

che sostituita nell’equazione del moto, imposto che risulti ωˆ diversa da qualsiasi altra frequenza naturale del sistema (si escludono i casi possibili di risonanza tra sistema e forzante, altrimenti non risulterebbe invertibile la matrice dell’espressione seguente), si ha:

{ }

(

[ ]

[ ]

)

{ }

0 1 2

0 k ˆ m F

Y = −ω −

La soluzione generale del problema è pertanto data dalla somma della soluzione del sistema omogeneo associato e della soluzione particolare trovata sopra:

( )

{ }

_∑

{ }

( )

[ ]

{ }

{ }

( )

[ ]

{ }

{ }

( )

(

[ ]

[ ]

)

{ }

= − − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + = n j j j j T j j T j t F m k u t q m u t q m u t q 1 0 1 2 0

0 cosω _ω & sinω ωˆ sinωˆ



Nel caso invece di forzante periodica, eseguita la scomposizione in serie di Fourier, si ha:

( )

{ }

{ }

(

{ }

{ }

)

∞ = = + + =

∑

∞ = , , 3 , 2 , 1 2 sin cos 2 1 0 1 0 0 0 K j T t j b t j a a t Q j j j π ω ω ω

con T periodo della funzione

{ }

Q

( )

t .

La soluzione del problema è allora del tipo seguente:

( )

{ }

{ }

( )

_∑

∞

(

{ }

( )

{ }

( )

)

= + + = 1 0 j bj aj y t t y t y t y

Distinguendo i sottoproblemi che compongono la soluzione finale (la risposta alle componenti armoniche può essere ottenuta come somma delle risposte a ciascuna componente), si ha:

[ ]

{ }

( )

[ ]

{ }

( )

{ }

[ ]

{ }

( )

[ ]

{ } { }

( )

[ ]

{ }

( )

[ ]

{ } { }

( )

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = + = + = + t j b t y k t y m t j a t y k t y m a t y k t y m j bj bj j aj aj 0 0 0 0 0 sin cos 2 1 ω ω && && &&

Una volta definita la risposta h

( )

t , tale che

{ }

y

( )

t =

[ ]

h

( )

t

{ }

Q

( )

t , e passando al dominio delle frequenze attraverso la trasformata di Fourier, si ha:

( )

{

Y ω

}

=

[

H

( )

ω

]

{

Q

( )

ω

}

Dove

{

Q

( )

ω

}

è appunto la trasformata di Fourier della forzante ed

[

H

( )

ω

]

è la matrice definita come funzione di risposta in frequenza, le cui componenti sono:

( )

( )

_{( )}

ω ω ω j j ij Q Y H =

2.4 Modelli di identificazione

L’obiettivo dell’Identificazione Strutturale Dinamica (IDS) è quello di definire, a partire da misurazioni sperimentali, i valori dei parametri modali fondamentali di una generica struttura al fine di caratterizzarne, attraverso un modello matematico, il comportamento dinamico. La conoscenza di questi parametri consente di definire, con procedure definite di Model Updating, modelli teorici corretti sulla base delle risultanze sperimentali.

L'obiettivo principale del Model Updating è quello di minimizzare le differenze tra le previsioni del modello teorico e le misure sperimentali dei parametri dinamici della struttura in esame.

Il modello così corretto costituisce uno strumento molto efficace per progettare eventuali interventi o modifiche strutturali.

Al fine di calibrare il modello matematico costruito per il campanile in studio si è riprodotta l’azione dinamica esercitata dall’oscillazione di una delle campane presenti.

Con ciò si intendono simulare le condizioni della prova eseguita in condizioni di moto forzato del campanile.

2.5 Eccitazione dinamica prodotta dalle campane

Allo scopo di valutare la forzante sul campanile in studio, generata dall’oscillazione di una delle campane presenti, si richiamano brevemente alcuni risultati classici.

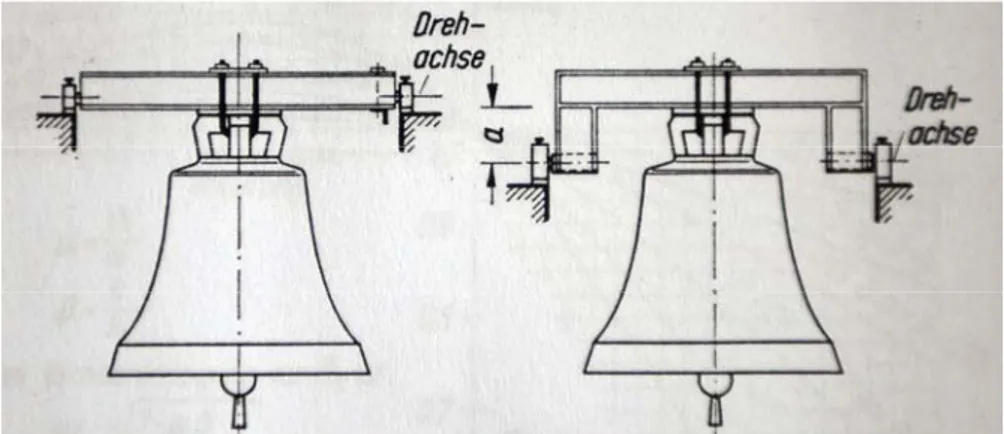
La campana in oggetto è del tipo rappresentato in fig. 2.2 (a destra):

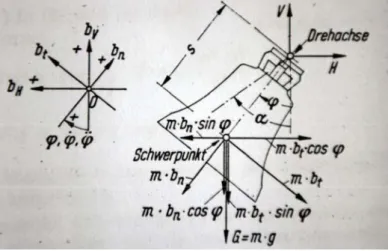
Riferendosi alla rappresentazione di fig. 2.3 è possibile descrivere il moto della campana, una volta definita la massa m della campana stessa, la distanza s tra baricentro e fulcro di rotazione ed il momento d’inerzia I della massa rispetto al fulcro.

fig. 2.3 Schema di riferimento per la descrizione del moto della campana

In assenza di dissipazioni, per il principio della conservazione dell’energia meccanica del sistema durante l’oscillazione, si ha:

E mgs I + (1−cos )= 2 1 _ϕ2 _ϕ &

Imponendo che l’oscillazione abbia inizio con una velocità ω₀ in corrispondenza di una posizione ϕ₀ nota, si può riscrivere l’equazione del moto come segue:

r l g(cos cos )/ 2 ₀ 2 0 2 _{ω ϕ ϕ} ϕ& = + −

dove si è introdotta la cosiddetta “lunghezza ridotta del pendolo equivalente”, pari a .

ms I l_r = /

La velocità angolare massima si ricava imponendo la condizione ϕ =0 e vale:

(

0

)

2 0 1 cos 2 ˆ ω ϕ ω = + − r l g

mentre l’inclinazione massima risulta, ponendo ϕ&

( )

t =0: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = g l_r 2 0 0 cos arccos ˆ ϕ ω α

Derivando la prima equazione scritta sopra rispetto al tempo, si ottiene l’equazione non lineare del secondo ordine che segue:

0 ) ( sin ) (t +mgs t = Iϕ&& ϕ

La soluzione dell’equazione differenziale precedente è perseguibile ricorrendo alla teoria delle funzioni ellittiche.



Formulando in altra maniera il problema, ovvero considerando quale variabile indipendente l’angolo ϕ anziché il tempo , si può scrivere quanto segue (esprimendo la velocità in funzione della posizione angolare della campana):

t

∫

− + =ϕ ϕ ϑ ω ϑ ϕ 0 0 2 0 (cos cos ) 2 ) ( r l g d t

questa ultima relazione può essere modificata , ricorrendo ad un cambiamento di variabile, in una espressione per la quale t(ϕ)è espresso in termini di integrale ellittico di prima specie:

∫

₋ = ) ( 0 1 2sin2 ) ( ϕ ξ ξ χ ξ ϕ d g l t r

nella quale si è assunto quanto segue:

g l_r 4 ˆ2 2 ω χ =

( )

ϑ 2 χsinξ sin =

Nel caso limite _χ2 ₌1, corrispondente ad oscillazioni dalla posizione a bicchiere, ovvero π

ϕ

αˆ = ₀ = , 0ω₀ = e , la relazione precedente può essere integrata in forma chiusa e fornisce la soluzione seguente:

r l g / 4 ˆ2 ₌ ω

( )

π ϕ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ = ⎟⎟⎠ ⎞ ⎜ ⎜ ⎝ ⎛ t l g r e t 4arctan

Nella generalità degli altri casi, ponendo τ =sinξ, si ottiene l’integrale nella forma di Legendre

∫

_{− −} = ) ( 0 (1 2 2)(1 2) ) ( ϕ τ τ τ χ τ ϕ d g l t r

A questo punto occorre introdurre la funzione ellittica Sn di Jacobi, definita come l’inversa dell’integrale ellittico di prima specie, per arrivare ad ottenere la soluzione dell’integrale sopra riportato: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = t g l Sn t₎ r ( τ

Attraverso poi le assunzioni fatte in precedenza si può infine ricavare:

( )

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = t g l Sn t χ r ϕ 2arcsin

Noti dunque i dati relativi alla campana quali massa m, momento d’inerzia I e distanza fulcro baricentro s, è possibile ottenere la soluzione cercata attraverso l’equazione precedente; occorre determinare ovviamente anche l’angolo di inclinazione massima αˆ che la campana esegue durante il proprio moto ed si devono valutare le condizioni iniziali del moto (condizioni al contorno del problema).

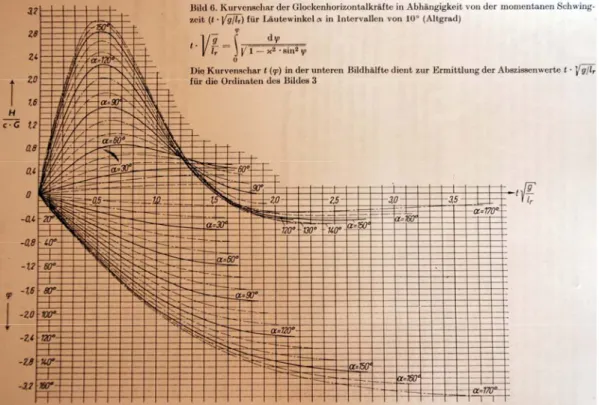
Nella determinazione della funzione ϕ

( )

t può risultare utile un diagramma presente in letteratura e proposto in fig. 2.4.

fig. 2.4 Diagramma per la determinazione della ϕ

( )

t

In fig. 2.4 risulta diagrammata la soluzione dell’integrale nella forma di Legendre per diversi valori di αˆ (si ricorda che solo nel caso limite di αˆ = 180° è possibile ottenere la soluzione in forma chiusa).

In alternativa all’utilizzo del diagramma sopra riportato è ovviamente anche possibile impiegare direttamente la ϕ

( )

t ricavata sperimentalmente, qualora questa venga opportunamente registrata durante la prova dinamica effettuata in regime di oscillazioni forzate.



Presentato fin qui il modello analitico del moto libero della campana, è possibile adesso andare a ricavare l’espressione della legge della forzante che eccita il campanile in studio. Tale forza viene convenientemente ricavata nelle due componenti ortogonali, rispettivamente quella orizzontale H

( )

t e quella verticale V

( )

t , semplicemente andando a considerare l’equilibrio dinamico della campana sotto le azioni della forza peso e delle reazioni prodotte dal vincolo attorno al quale la campana stessa oscilla.

Le condizioni di equilibrio dinamico per la campana sono le seguenti:

( )

( )

( )

( )

⎩ ⎨ ⎧ + = = mg t mb t V t mb t H V H

dove ovviamente valgono:

( )

t b

( )

t

( )

t b

( )

t

( )

t bH =− t cosϕ + n sinϕ

( )

t b

( )

t

( )

t b

( )

t

( )

t b_V = _t sinϕ + _n cosϕ

L’accelerazione centripeta e quella tangenziale valgono rispettivamente:

( )

t s

( )

t b_n = ϕ&2

( )

t s

( )

t b_t = ϕ&&

Si ottiene allora, sostituendo le espressioni delle accelerazioni sopra riportate, quanto segue:

( )

[

( )

( )

( )

( )

]

( )

[

( )

( )

( )

( )

]

⎪⎩ ⎪ ⎨ ⎧ + + = − − = t t t t ms mg t V t t t t ms t H ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ cos sin sin cos 2 2 & && & &&

Se volessimo impiegare direttamente le espressioni sopra riportate per valutare le componenti della forzante impiegando la ϕ

( )

t ricavata sperimentalmente, saremmo costretti a fare operazioni di derivazione su dati sperimentali.

Tale manipolazione dei dati non è mai auspicabile se il fine è quello di compiere analisi sufficientemente accurate, pertanto si cercano in quanto segue delle espressioni alternative da impiegare per la rappresentazione delle componenti della forzante.

Ricordando le espressioni seguenti, ricavate in precedenza, si ha:

( )

t 2g

[

cos

( )

t cos 0

]

/lr 2 0 2 _{ω ϕ ϕ} ϕ& = + − I t mgs t) sin ( )/ ( ϕ ϕ_&& =−

che sostituite, permettono di ricavare:

( )

( )

( )

( )

( )

( )

( )

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − − + = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − = t g l t t c mg t V t g l t t mgc t H r r ϕ ω ϕ ϕ ϕ ϕ ω ϕ ϕ ϕ cos 1 cos cos 2 cos 3 1 sin ) ( sin cos 2 2 sin 2 3 2 0 0 2 2 0 0

Dove c=s/lr è detto coefficiente di forma della campana. Si osserva come non compaiano adesso le derivate della ϕ

( )

t .

Per determinare allora le leggi temporali delle componenti della forzante occorre introdurre nelle equazioni precedenti la funzione ϕ

( )

t , ricordando che il periodo è quello corrispondente ad oscillazioni di ampiezza 4 . αˆ

Si ricorda ancora che ovviamente le componenti delle reazioni vincolari così trovate, considerando l’equilibrio dinamico della campana, rappresentano proprio le componenti della forzante che mette in vibrazione il campanile.

Nell’impiego pratico delle equazioni sopra riportate restano da precisare le condizioni al contorno al tempo iniziale t=t₀ che determinano i valori di ϕ₀ e ω₀.

Si osserva che risulta conveniente assumere ϕ₀ = (angolo di massima oscillazione della αˆ campana) e di conseguenza ω₀ =0.

Risulta così alla fine:

( )

( )

( )

{

[

( )

( )

]

}

⎪ ⎩ ⎪ ⎨ ⎧ − − + = ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ = 1 cos ˆ cos 2 cos 3 1 ) ( sin ˆ cos 2 2 sin 2 3 2 t t c mg t V t t mgc t H ϕ α ϕ ϕ α ϕ

Queste sono le espressioni impiegate per ricostruire l’azione della forzante sul modello teorico, elaborato per il campanile oggetto di studio, al fine di compiere una calibrazione opportuna del modello matematico della struttura.

Resta da osservare che nelle equazioni entrano in gioco i dati riguardanti la campana stessa attraverso il coefficiente c; ovvero occorre determinare il valore della massa della campana, della distanza tra fulcro di rotazione e baricentro ed il valore del momento d’inerzia alla rotazione della campana stessa rispetto all’asse passante per il fulcro.

Tutti questi dati sono stati oggetto di stima attraverso un rilievo diretto sulla campana stessa al fine di ricostruirne la geometria quanto più accuratamente possibile.

In particolare, per convalidare tale rilievo, si è anche fatto ricorso ad una operazione di misura del peso della campana.