CALCOLO DELLE SOLUZIONI MENSILI IN COEFFICIENTI DELLE ARMONICHE SFERICHE DA DATI GOCE

UNIVERSITA’ DI PISA

D

IPARTIMENTO DI

I

NGEGNERIA

I

NDUSTRIALE

T

ESI DI

L

AUREA

S

PECIALISTICA

CALCOLO DELLE SOLUZIONI

MENSILI IN ARMONICHE SFERICHE

DA DATI GOCE

R

ELATORE

A

LLIEVO

Prof. Ing. Giovanni Mengali Rocco Luigi Bosco

C

ORRELATORE

Prof. Ing. Mirko Reguzzoni

Sommario

I movimenti nel mantello e nella litosfera come anche la ridistribuzione dei ghiacciai e delle superfici oceaniche, dovuta alle variazioni climatiche, sono parte di processi dinamici che avvengono all’interno e sulla superficie della Terra. Essi sono responsabili del continuo cambiamento del campo di gravità. Di conseguenza, lo studio del campo gravitazionale e delle sue modificazioni nel tempo può dare utili informazioni sui processi della terra solida e sulle variazioni climatiche. Questi due tipi di fenomeni formano una coppia biunivoca: le variazioni ambientali, ad esempio, sono indotte dal rebound post-glaciazione, dai terremoti, dagli tsunami, dall’erosione del terreno e dalla deriva dei continenti; viceversa l’instabilità della glaciazione odierna, dovuta alle variazioni climatiche, è responsabile dei cambiamenti nella topografia superficiale e nel campo gravitazionale, e delle instabilità nella rotazione della Terra [48].

Allo stato attuale l’importanza della correlazione tra questi due tipi di fenomeni ha assunto una certa priorità in campo scientifico, infatti è in atto un programma dell’Agenzia Spaziale Europea (ESA) di missioni dedicate allo studio della Terra tra cui quella del GOCE [26] che rappresenta la prima di una serie di sei missioni.

Lo scopo di questa tesi è lo studio della variazione temporale del campo gravitazionale attraverso la determinazione delle soluzioni mensili dei coefficienti armonici dai dati della missione europea GOCE.

Si tratta di un obiettivo ambizioso in quanto la missione è disegnata per studiare la parte stazionaria del campo gravitazionale e non quella variabile nel tempo. Tuttavia si vuole verificare se l’informazione di GOCE può contribuire ad aumentare la risoluzione spaziale e l’accuratezza delle soluzioni mensili della missione GRACE.

La parte principale della tesi riguardante l’impostazione dell’analisi dei dati è stata svolta presso il “Laboratorio di Geomatica” del Polo Territoriale di Como del “Politecnico di Milano”, sotto la guida del Prof. Fernando Sansò e del Prof. Reguzzoni Mirko.

Dopo la ricostruzione dei dati mancanti del gradiometro elettrostatico gravitazionale (strumento principale a bordo del GOCE), utilizzando le informazioni della missione GRACE, e la ricostruzione dei dati orbitali mancanti del GPS tramite il propagatore SGP4, si procede alla determinazione dei coefficienti armonici dal segnale, attraverso l’implementazione del cosiddetto metodo space-wise sviluppato dal team di ricercatori del Politecnico di Milano.

Trovate le soluzioni mensili GOCE si sono valutati i risultati in termini di variazione temporale del geoide e delle anomalie di gravità.

Il passo finale è il confronto tra i coefficienti di basso grado ottenuti da GOCE, da GRACE e dai dati dell’SLR analizzati dal centro di Geodesia Spaziale di Matera, per evidenziare la differente capacità risolutiva delle diverse tecniche di osservazione.

I file di Matlab presenti in Appendice, sviluppati durante la soluzione di questa tesi, sono stati formulati in prima persona.

Indice

1 Introduzione

1.1 Il Campo Gravitazionale della Terra . . . .1

1.2 Il potenziale anomalo T e il geoide. . . .11

1.3 Determinazione del campo di gravità dallo spazio. . . .15

1.3.1 Il Satellite Laser Ranging (SLR) .. . . 16

1.3.2 Le missioni CHAMP e GRACE. . . .17

1.3.3 Il GOCE. . . . . . .20

1.3.3.1 Il Gradiometro Elettrostatico di Gravità (EGG). . 23

2 Dati iniziali

2.1 Principio dinamico e dati del Gradiometro. . . .26

2.2 I dati del GPS. . . 31

2.3 Soluzioni mensili di GRACE . . . .32

2.4 Il modello GOCO03S di campo gravitazionale globale. . . .32

2.5 Soluzioni mensili del SLR . . . .33

3 L’analisi dei dati GOCE

3.1 L’HPF e differenti approcci all’analisi dei dati GOCE. . . 34

3.2 L’approccio space-wise. . . .35

3.2.1 La grigliatura dei dati. . . .37

3.2.2 Il calcolo dei coefficienti delle amoniche. . . .38

4 Realizzazione e test del grigliatore

4.1 Introduzione. . . . . . .41

4.2 Interpolazione con spline bilineare. . . .41

4.3 Approssimazione del segnale alla quota media del satellite. .43 4.4 Il problema dei poli. . . .47

4.5 Test del grigliatore . . . .47

5 Propagazione dell’orbita

5.1 Introduzione . . . . .53

5.2 Il formato TLE e l’SGP4. . . .. . . .53

5.3 Il sistema di riferimento TEME. . . .56

5.4 Le misurazioni del SLR. . . .57

5.4.1 Correzione della distanza del satellite per l’effetto della rifrazione atmosferica. . . . . . .58

5.5 Trasformazione delle coordinate del satellite dal sistema di riferimento SEZ al sistema di riferimento ECEF. . . 59

5.6 Stima della velocità del satellite.. . . .60

5.7 Trasformazione delle coordinate del satellite dal sistema di riferimento ECEF al sistema di riferimento TEME. . . .61

5.8 Inizializzazione dell’SGP4 e propagazione dell’orbita. . . .62

5.9 Valutazione dell’algoritmo di propagazione con i dati GPS reali del GOCE. . . . . . .63

5.10 Dati mancanti del GPS. . . .68

5.10.1 Propagazione orbita negli intervalli 2010. . . .69

5.10.1 Propagazione orbita negli intervalli 2011. . . .71

6 Sistemazione del segnale dell’EGG

6.1 Introduzione. . . 75

6.2 Ricostruzione segnale mancante. . . 75

6.3 Eliminazione degli OVER-TREND. . . 78

7 Filtraggio dei dati e calcolo dei coefficienti armonici

7.1 Introduzione. . . 81

7.2 Prima impostazione alla soluzione.. . .. . . 81

7.2.1 Il filtro passa banda. . . .. . 83

7.2.2 Risultati. . . .87

7.3 Seconda impostazione alla soluzione. . . 89

7.3.1 filtro di Wiener. . . 89

7.3.2 Combinazione ai minimi quadrati. . . .93

7.3.3 Conclusioni. . . ... . . . .95

8 Risultati numerici

8.1 Miglioramento nella stima globale della variazione dell’anomalia gravitazionale e dell’altezza del geoide. . . 98

8.2 Soluzioni mensili della variazione dell’altezza del geoide. . .104

8.3 Confronto tra le soluzioni dei coefficienti di basso grado di SLR, GRACE e GOCE. . . 110

9 Conclusioni

9.1 Sviluppi futuri. . . .112

Appendice

. . . .116

Capitolo 1

Introduzione

1.1 Il Campo Gravitazionale della Terra

E’ passato molto tempo da quando Isaac Newton formulò la sua Legge

della gravitazione universale riguardante la mutua attrazione tra due

masse: più di trecento anni fa, guardando la famosa mela cadere dall’albero, diede inizio allo studio del campo di gravità della Terra. Oggi la conoscenza della sua distribuzione è notevolmente aumentata grazie alla Geodesia Spaziale che fa del suo scopo principale la ricerca della direzione radiale definita come la linea lungo la quale agisce la gravità vista come la direzione del pendolo o come la normale alla superficie di un fluido fermo. Questi, però, sono solo modi locali ed empirici per ottenere la sua conoscenza. Per attribuire le misurazioni ad un sistema di riferimento globale unico è necessario un modello matematico che descriva il campo di gravità [8]; di conseguenza lo studio avanzato del campo di gravità è uno degli obiettivi fondamentali della Geodesia.

Poiché i termini gravità e gravitazione sono spesso usati come sinonimi è importante definire la loro differenza prima di entrare nell’argomento. La gravitazione è la forza di attrazione reciproca tra due corpi che hanno massa; la gravità, invece, è la forza agente tra la Terra in rotazione e gli altri corpi, pertanto viene presa in considerazione anche la forza centrifuga.

La gravitazione è una forza di attrazione diretta lungo la linea che connette due oggetti P e Q, considerati come punti, e proporzionale ad entrambe le masse mP e mQ oltre che all’inverso del quadrato della

distanza rPQ tra i due oggetti; è definita dalla seguente relazione, dove

G è la costante gravitazionale:

𝐹 𝑃, 𝑄 =  𝐺!!!!

!_!"! (1.1)

Questa formula è rigorosamente valida per masse puntiformi; la Terra, però, non è una massa puntiforme. Estendendo tale formula ad un corpo generico con densità di massa _ρ e volume _ν, e muovendo una massa di prova unitaria nello spazio circostante, il campo

gravitazionale 𝑓 (ovvero la forza risultante sulla massa di prova nel generico punto P) viene definito in forma vettoriale come segue:

𝑓 𝑃 = 𝐺 !!"

!_!"!

!  𝜌 𝑄 𝑑𝑣! (1.2)

Questa relazione può essere espressa in modo più conveniente attraverso una funzione scalare del punto P definita potenziale

gravitazionale V, ovvero:

𝑓 𝑃 =   ∇𝑉(𝑃) (1.3) Una delle proprietà principali del potenziale gravitazionale è quella di essere una funzione armonica fuori dalla massa che quindi soddisfa l’equazione di Laplace:

∆𝑉 𝑃 = 0 (1.4) Ipotizzando la Terra con una forma perfettamente sferica con massa M omogeneamente distribuita al suo interno, la forza gravitazionale esercitata dal pianeta sulla massa di prova sarà la stessa di quella di una massa puntiforme, di dimensioni infinitamente piccole, con la stessa massa della Terra posta nel centro del pianeta.

Con date ipotesi, il campo gravitazionale di questo corpo immaginario avrà una simmetria sferica con potenziale:

𝑉 𝑃 =  !"_! (1.5) dove r è la distanza del punto P dal centro del pianeta.

La Terra, però, non ha una forma perfettamente sferica e le deviazioni da quest’approssimazione sono significanti. La forma della Terra è molto vicina a quella di un ellissoide oblato, ovvero una sfera con uno schiacciamento ai poli dovuto alla rotazione attorno al suo asse. Il diametro misurato attraverso il piano equatoriale (12756 km) è all’incirca 43 km più grande di quello misurato tra i poli. Per definire la forma dell’ellissoide sono utilizzati due parametri: a che indica il valore del semiasse maggiore, ed e che indica l’eccentricità, cioè il livello di schiacciamento. Il campo gravitazionale generato da questo ellissoide oblato è chiamato campo gravitazionale normale con il suo

associato potenziale normale V0.

Avvicinandoci al nostro pianeta possiamo notare che la sua superficie non è affatto regolare: sulla Terra possiamo distinguere alte montagne, fosse oceaniche e ampie pianure, e se guardassimo al suo interno vedremmo che la distribuzione di massa interna non è omogenea. Tutte queste irregolarità si riflettono sul campo gravitazionale terrestre; per considerarne gli effetti, il potenziale del campo gravitazionale viene rappresentato da una serie di armoniche sferiche:

𝑉 𝑟, 𝜃, 𝜆 = !"_! ! !_! !!!

!!!! !

!!! 𝑃 𝜗 𝐶!"cos 𝑚𝜆 + 𝑆!"sin 𝑚𝜆 (1.6)

o in forma più compatta:

𝑉 𝑟, 𝜃, 𝜆 = !"_! !_!!! !_!!!! !_! !!!𝑉_!"𝑌_!"(𝜗, 𝜆) (1.7) dove:𝑃_!" e 𝑌_!" sono rispettivamente le funzioni normalizzate di

prodotto tra la costante gravitazionale e la massa della Terra; R è il raggio medio di riferimento della Terra; (r, λ, 𝜗) sono le coordinate

sferiche. I coefficienti normalizzati della serie 𝐶_!" e 𝑆_!" (o equivalentemente 𝑉_!") devono essere determinati e rappresentano il cosiddetto modello globale del geopotenziale. Secondo le convenzioni

di normalizzazione, se ϕ rappresenta la latitudine geografica di un

punto del campo, e se u=sinϕ , allora il Polinomio di Legendre non

normalizzato di grado l è definito come:

𝑃_! 𝑢 =_!!!  _!!∙_!!!!_!(𝑢!_{− 1)}! _(1.8)

la definizione del Polinomio di Legendre Associato non normalizzato è allora:

𝑃_!" 𝑢 = 1 − 𝑢! !_! !!

!!!𝑃!(𝑢) (1.9)

Se il fattore di normalizzazione è definito tale che: 𝑁_!"! ₌ !!!!! !!!! !!! !

!!! ! (1.10)

e il Polinomio di Legendre Associato viene normalizzato attraverso il prodotto:

𝑃_!" = 𝑁_!"𝑃_!"       (1.11) la relazione dei coefficienti normalizzati di armoniche sferiche con la distribuzione della massa diventa:

𝐶_!" 𝑆_!" =   ! !!!! !_!∙ ! !_! !

!"#$%"& 𝑃!"(sin 𝜑) cos 𝑚 𝜆_{sin 𝑚𝜆} 𝑑𝑀 (1.12)

dove r, ϕ, e λ sono le coordinate dell’elemento di massa dM

sull’intera massa del sistema che costituisce la Terra, includendo la componente solida e fluida.

1.2 Il potenziale anomalo T e il geoide

Volendo modellizzare le principali deviazioni della Terra dalla forma ellissoidale, si utilizza comunemente il potenziale anomalo T, cioè la differenza tra il potenziale gravitazionale reale e quello normale

T=V−V0.

Il potenziale anomalo è espresso in termini di armoniche sferiche come:

𝑇 𝑟, 𝜗, 𝜆 = !"_! ! !_! !!!

!!! !!!!!𝑇!"𝑌!" 𝜗, 𝜆 (1.13)

Più informazioni dettagliate del campo gravitazionale si ricercano, più termini sono richiesti in questa espansione in serie per un’adeguata rappresentazione; in altre parole, la serie è troncata al massimo grado l che può essere visto come un’approssimazione di una corrispondente scala spaziale D, espressa in chilometri, tale che:

𝐷 =!""""

! (1.14)

Supponendo di conoscere il potenziale anomalo T e conseguentemente il potenziale V è possibile invertire le equazioni (1.7), (1.13) e stimare i coefficienti della serie senza conoscere la densità ρ della Terra. Si noti che la stima di questi coefficienti dipende dalla qualità e precisione delle misurazioni; s’introduce così un limite superiore del massimo grado calcolabile con un errore accettabile.

Il secondo contributo importante alla gravità è la forza centrifuga con

il potenziale del suo campo Φ espresso come:

dove ω è la velocità angolare della Terra, assunta costante, e d la

distanza tra il punto P e l’asse di rotazione della Terra. Sommando la forza centrifuga al campo gravitazionale definiamo il potenziale di

gravità W:

W=V + _Φ (1.16) Per definire la posizione di un oggetto rispetto alla Terra è necessaria la scelta di una superficie di riferimento che abbia una forma molto vicina a quella della Terra stessa. Proiettando un punto su questa superficie, si potrebbe stabilire un valore di deviazione, cioè un numero che descriva la sua altitudine. Non è possibile usare direttamente la superficie della Terra come riferimento poiché essa è molto complessa ed è chiaramente impossibile recuperarne misurazioni omogenee e precise. In altre parole, il campo di gravità, come ogni vettore di campo, ammette una rappresentazione geometrica e infinite superfici equipotenziali; quindi, sfruttando la nozione di potenziale di gravità possiamo definire un riferimento standard chiamato geoide W0 [3] cioè la superficie equipotenziale al

livello medio dei mari di un ipotetico oceano a riposo (figura 1.1).

Figura 1.1: Geoide con le sue anomalie [metri].

Più semplice da utilizzare rispetto al geoide è l’ellissoide oblato; il

gravitazionale invece dell’espansione in serie (1.7) e definito in un punto P dalla relazione:

𝑉_! = !"_! 1 − !_!!!  𝐽_! !_! !𝑃_! sin 𝛿 (1.17) dove r è la distanza del punto P dal centro di massa dell’ellissoide, m e

R sono la massa ed il raggio equatoriale dell’ellissoide, 𝛿 è la declinazione di P, i 𝐽_! sono le armoniche zonali, ed infine 𝑃_! sin 𝛿 rappresenta il polinomio di Legendre di ordine l in sin 𝛿:

Il potenziale di gravità diventa:

U = V0 + Φ (1.18)

Il modulo del potenziale è misurato in [𝑚! _𝑠!_{] mentre la}

corrispondente accelerazione gravitazionale è tipicamente misurata in

gal (1 gal= 1 cm/s2); la gravità media della Terra è all’incirca 981 gal

(il ben conosciuto 9.81 m/s2) con una variazione dovuta

all’appiattimento, alla disomogeneità della densità, alla rotazione e alle escursioni della Terra, da 978.1 gal a 983.2 gal muovendosi dall’equatore ai poli.

Figura 1.2: Schema della Terra e delle sue principali superfici di riferimento.

1.Geoide, 2.Ellissoide, 3.Topografica. La retta con il pallino indica la direzione del filo di piombo, connessa alla direzione radiale diretta nel centro della Terra.

In base al tipo di superficie di riferimento considerato abbiamo differenti definizioni di altezza (figura 1.3). Mentre le altezze ellissoidale e ortometrica sono usate come misure dell’altitudine del punto rispetto al riferimento relativo, rispettivamente l’ellissoide e il geoide, l’altezza del geoide è appunto la differenza tra l’ellissoide e il geoide:

N= h– H (1.19)

Figura 1.3: Definizione di altezza relativa basata sulla scelta della superficie di riferimento. h = altezza ellissoide, H = altezza ortometrica, N = altezza geoide.

Le escursioni in termini di altezza del geoide N variano da circa +90 ad un massimo di −105 [m]; queste sono le caratteristiche di grande lunghezza d’onda (molte migliaia di chilometri). Le variazioni di piccola estensione (decine di migliaia di chilometri) vanno dall’ordine dei centimetri a pochi metri.

1.3 Determinazione del campo di gravità dallo

spazio

È comunemente noto che le forze gravitazionali diminuiscono con l’aumentare della distanza tra le masse, quindi perché misurare il campo di gravità lontano dalla Terra? La risposta è data dalle limitazioni delle tecniche tradizionali usate per la determinazione del campo di gravità.

Figura 1.4: Misurazioni del campo di gravità antecedenti le missioni satellitari

dedicate.

Prima dell’avvento di missioni satellitari mirate, solo i tre classici metodi per la determinazione del campo di gravità (gravimetria terrestre e navale, altimetria satellitare [49]) e l’analisi orbitale dell’orbita da terra [59] sono stati usati dalla Geodesia Spaziale [49] per costruire i modelli del geopotenziale.

Unendo assieme i dati presi con differenti sistemi di riferimento, i metodi, gli strumenti e conseguentemente una differente precisione, essi non possono portare a risultati omogenei; inoltre ogni tecnica ha le sue limitazioni e di conseguenza solo le tecniche spaziali possono fornire un intervallo di dati globale, regolare, di alta e omogenea qualità.

1.3.1 Il Satellite Laser Ranging (SLR)

Il Satellite Laser Ranging è la misurazione della distanza del satellite con il laser, attraverso l’osservazione del tempo di volo dell’impulso laser quando quest’ultimo viaggia dalla stazione di terra al satellite [49]. La misurazione della distanza con il laser è tra le tecniche di osservazione più accurate nella geodesia satellitare, ragione per cui essa viene utilizzata in soluzioni a lungo termine per importanti obiettivi nella geo-scienza. Il satellite, o target, è dotato di appositi retro-riflettori. Alcuni satelliti sono stati lanciati con il solo obiettivo di servire come target di precisione nella loro orbita. Satelliti dedicati al laser di questo tipo sono lo STARLETTE, lo STELLA, il LAGEOS 1-2 (figura 1.3), l’AJISAI, l’ETALON 1-1-2, il GFZ e il WESTPAC.

Figura 1.5: Satellite LAGEOS 1. I retro riflettori sono diffusi su tutto il corpo del

satellite.

I progressi nella geodesia con questo tipo di tecnica sono stati possibili solo grazie ad una cooperazione internazionale e ad un uso dei dati dalle stazioni distribuite sull’intero globo; l’International Laser

Ranging Service (ILRS) raccoglie, archivia e distribuisce i dati del

SLR e del LLR (Lunar Laser Ranging) e usa questi per produrre i risultati cercati. Tra le stazioni che contribuiscono alla raccolta delle

misurazioni rientra anche la sede di Matera presso la quale è stata svolta parte della tesi.

Figura 1.6: I retro riflettori laser del GOCE.

1.3.2

Le missioni CHAMP e GRACE

Le missioni satellitari CHAMP (Challenging Mini-satellite Payload for

Geophysical Research and Application) [42] e GRACE (Gravity

Recovery and Climate Experiment) [52] sono le prime due dedicate alla gravità. Queste soddisfano insieme le necessità di avere:

1) un tracciamento orbitale interrotto nelle tre dimensioni;

2) un’orbita con un’altitudine più bassa possibile;

3) la misurazione delle forze di natura non gravitazionale.

Per il tracciamento orbitale è stato sufficiente installare un ricevitore GNSS (GPS o GLONASS). L’impossibilità di abbassare l’altitudine, dovuta alle forze non gravitazionali agenti sul satellite, è stata invece per anni il principale ostacolo al lancio delle missioni di gravità spaziali. La vera svolta nella nuova era della Geodesia Spaziale è stata la creazione dei cosiddetti “accelerometri statici” che permettono la misurazione delle forze non gravitazionali agenti sul satellite. Queste forze, come la resistenza atmosferica o la pressione solare, sono prese

in considerazione nel calcolo oppure possono essere compensate da un meccanismo di controllo drag-free [49]. Questo permette di abbassare la quota del satellite consentendo una migliore misurazione del campo gravitazionale della Terra.

Queste due missioni sono realizzazioni di approcci differenti alla stima della gravità dallo spazio, ed è interessante esplorarle in relazione alla loro struttura di funzionamento.

Per CHAMP l’approccio utilizzato è il diffuso Satellite-to-Satellite

Tracking nel high-low mode (SST-hl) [29]: questo consiste in un

tracciamento continuo da satelliti in orbita alta a satelliti in orbita LEO. L’intero satellite, visto come una massa di prova, include un accelerometro triassiale posto nel centro di massa del satellite per misurare le forze non gravitazionali. Lanciato nel 2000, ha volato ad una quota media di 400 km con un’inclinazione orbitale di 87°, seguito da 12 satelliti che forniscono la sua posizione tridimensionale con una precisione del centimetro. CHAMP viene considerata come una missione-prova poiché è la prima volta che l’SST-hl è combinato con un accelerometro triassiale. Il principale limite della missione è costituito dalla bassa sensibilità alle anomalie della Terra che permettono la costruzione di modelli del geopotenziale solo dai bassi gradi.

Figura1.7: Schema di Satellite-to Satellite Tracking nel high-low mode. Il GPS in

Per ottenere una maggiore risoluzione e accuratezza è necessario un principio basato sulla differenziazione. Per sfruttare questo principio la soluzione più immediata è quella di usare due satelliti nella stessa orbita LEO che controllino la loro posizione relativa. Questo sistema chiamato Satellite-to-Satellite Tracking in low-low mode è implementato nella missione GRACE. Lanciata nel 2002, comprende una coppia di satelliti che adottano un sistema STT-ll e montano un accelerometro triassiale; la distanza tra i due satelliti è misurata con alta precisione (dell’ordine del micron) impiegando ricevitori microonde. I due satelliti volavano ad una quota media di 400 km con un’inclinazione di 89° e una distanza nominale di 220 km. Conoscendo questa distanza è possibile differenziare le forze gravitazionali agenti su ogni satellite, ottenendo le derivate seconde del campo.

Figura 1.8: Schema del Satellite-to-Satellite Trackin nel low-low mode. La

distanza tra la coppia di satelliti è misurata da un collegamento inter-satellitare di alta precisione.

   

1.3.3 Il GOCE

Un approccio migliore alla differenziazione si ottiene con l’uso di un gradiometro, ossia uno strumento che comprende tre coppie di accelerometri piazzati su tre assi ortogonali. Questo strumento chiamato Electrostatic Gravity Gradiometer (EGG) misura il gradiente della componente di accelerazione gravitazionale, cioè la derivata seconda spaziale del potenziale gravitazionale. La prima missione che utilizza questa tecnica, conosciuta anche come Satellite Gravity

Gradiometry (SGG) [45] [15], è la missione europea GOCE (Gravity

field and steady-state Ocean Circulation Explorer) [12] [16] [17].

Figura 1.9: GOCE spacecraft.

Il GOCE, lanciato nel 2009, vola ad una quota media di 250 km in un’orbita eliosincrona (dash-down) con un’inclinazione di 96.7°. La sua posizione è monitorata ogni istante, attraverso il concetto di SST-hl, anche simultaneamente da 12 satelliti del GPS.

Figura 1.10: Schema della Gradiometria Satellitare. Il GOCE utilizza tale modello

(SST-hl) per la misurazione delle anomalie.

Il GOCE rappresenta un capolavoro di tecnologia perché include un controllo di drag-free, un propulsore elettrico, un gradiometro gravitazionale elettrostatico, celle solari a tripla giunzione (GaAs) e una struttura largamente realizzata in honeycomb carbonio-carbonio. La richiesta di volo basso implica che la struttura minimizzi la forza di resistenza dell’aria, i momenti e i disturbi meccanici. Il risultato è un satellite molto snello, con un’area trasversale di 1.1 [𝑚!_{], 5.3 [m] di}

lunghezza e un peso di 1000 [kg]. Il satellite è all’incirca simmetrico lungo la direzione di volo e possiede due alette che promuovono una stabilità aerodinamica ulteriore. Una volta in orbita il satellite rivolge sempre la stessa faccia verso il sole. La sua struttura consiste di un cilindro cavo con sette scompartimenti interni che supportano gli equipaggiamenti e l’unità elettronica.

Figura 1.11: Struttura ed elementi interni del GOCE.

Due degli scompartimenti contengono il gradiometro montato in corrispondenza del centro di massa del satellite [5]. Il riflettore laser (LRR) è montato sulla parte superiore nella direzione di volo, mentre nella parte inferiore si trova il propulsore a ioni necessario per mantenere il satellite in “freefall” e per compensare, con una spinta continua, l’effetto della resistenza atmosferica e degli altri effetti di disturbo che altrimenti altererebbero le forze gravitazionali sulle masse del gradiometro. Questo sistema genera una spinta tra 1 e 20 [mN] in funzione di quanta resistenza il satellite incontri nel suo moto; è questo il sistema più vincolante in termini di durata della missione.

Il GOCE è stato costruito da un consorzio industriale Europeo [4]: il primo appaltatore è la Thales Alenia Spazio Italia seguita dall’Astrium Friedrichshafen responsabile della piattaforma; la Thales Alenia Space Francia e ONERA (Spagna) si sono occupate del gradiometro; a queste si aggiungono più di quaranta appaltatori minori.

1.3.3.1 Il Gradiometro Elettrostatico di Gravità (EGG)

Il Gradiometro Elettrostatico di Gravità (EGG) del GOCE consiste di tre paia di accelerometri capacitivi montati su una struttura ultra-stabile di honeycomb carbonio-carbonio.

Figura1.12: Accelerometro disassemblato e complessivo del Gradiometro.

Il funzionamento degli accelerometri consiste di una massa di prova, sospesa in una gabbia, mantenuta nel centro di quest’ultima da forze elettrostatiche; in altre parole viene applicata una tensione tra la gabbia e le varie facce delle masse con forma di parallelepipedo (4x4x1 [cm]). Questa tensione è rappresentativa dell’accelerazione che subisce la massa di prova ed è l’input iniziale di una lunga catena di analisi dei dati. La forma della masse non è casuale ma è stata scelta appositamente per semplificare i test in laboratorio. Nonostante la complessità degli strumenti utilizzati durante i test, non è stato possibile raggiungere la completa verifica della sensibilità degli accelerometri. Questa verifica è stata completata in orbita nei due mesi successivi al lancio con rilevante successo e con la generazione dei dati Level 1a [13]. Lo svantaggio nell’utilizzare masse di quella geometria è rappresentato dalla bassa sensibilità in una direzione di misurazione. Questo deriva dal fatto che il gradiometro ha due assi ultra-sensibili e altri assi meno sensibili. La direzione in-line (direzione definita da due accelerometri che costituiscono un braccio

del gradiometro) di ogni accelerometro è quella più importante e costituisce un asse sensibile. La direzione degli altri assi ultra-sensibili giace nel piano XZ per massimizzare la ultra-sensibilità della determinazione dell’accelerazione angolare attorno all’asse Y, dove X è orientato in direzione del moto, Y trasversalmente al moto e Z nella direzione radiale.

Figura 1.13: Disposizione degli accelerometri. Le direzioni tratteggiate

rappresentano le direzioni di osservazione meno sensibili.

La rotazione angolare attorno all’asse Y è invece la più importante nella determinazione del gradiente di gravità, poiché essa potrebbe contenere un grande contributo dovuto alla rotazione del satellite.

Gli accelerometri del GOCE sono circa 100 volte più sensibili di qualunque altro accelerometro che abbia mai volato [9]. Due accelerometri dello stesso paio sono montati a 50 cm di distanza l’uno dall’altro (figura 1.12).

Figura 1.14: Due accelerometri costituenti un braccio del gradiometro.

Le due masse di prova dello stesso paio hanno la tendenza ad avvicinarsi o allontanarsi tra di loro sotto l’influenza del campo gravitazionale della Terra: il gradiometro misura questo movimento. Sottoposta all’attrazione della Terra, ossia accelerando, la massa risente di una forza molto debole e soggetta al rumore di natura non gravitazionale; per questo viene utilizzato il metodo differenziale. Il risultato di due accelerometri in un braccio è sottratto dagli altri, rimuovendo il rumore e le forze di disturbo ai quali sono sottoposti entrambi gli accelerometri. Quello che resta è il valore di accelerazione dovuto alla Terra, misurato nelle due posizioni dello stesso braccio. Questa differenza è il gradiente di gravità, principale prodotto scientifico del GOCE. In aggiunta alla misura differenziale di accelerazione viene misurata la posizione media delle due masse in un braccio. L’EGG non è solo lo strumento principale per analizzare il campo di gravità ma fornisce anche informazioni base per il funzionamento del Drag-Free and Attitude Control System (DFACS).

Capitolo 2

Dati iniziali

2.1 Principio dinamico e dati del gradiometro

Il principale obiettivo del GOCE è sicuramente la misurazione del campo gravitazionale del pianeta consentendo la stima dei coefficienti del potenziale gravitazionale di basso grado con l’SST−hl e dando il massimo con le misurazioni del gradiometro. Questo strumento misura direttamente le derivate del secondo ordine del potenziale, il cosiddetto tensore di Marussi, essendo la componente radiale quella contenente più informazioni. Partendo dalla (1.7) possiamo scrivere:

!" !" 𝑟, 𝜗, 𝜆 = − !" !! !!!! 𝑙 + 1 ! ! !!! 𝑉_!" ! !!!! 𝑌!"(𝜗, 𝜆) (2.1)

la sua derivata seconda sarà:

!!! !!! 𝑟, 𝜗, 𝜆 = !" !! !!!! 𝑙 + 1 (𝑙 + 2) ! ! !!! 𝑉_!" ! !!!! 𝑌!"(𝜗, 𝜆) (2.2)

dove r è il raggio dell’orbita del satellite.

Guardando l’ultima equazione, la ragione per cui la derivata seconda può contenere i gradi alti può essere vista con la seguente spiegazione: il “fattore differenziale” (l+1)(l+2) contrasta il “fattore di

attenuazione” 𝑅 𝑟 !!! _{permettendo la determinazione di un modello}

di gravità di alta risoluzione.

Per mostrare come il gradiometro lavori è bene partire dai suoi accelerometri poiché allo stato di fatto esso usa le misurazioni registrate da ogni accelerometro su un braccio e, come già menzionato,

differenziandole, produce le sue misurazioni. Chiamando A la massa di prova, possiamo dire che la derivata seconda del tempo della sua

posizione 𝑋 A, ovvero l’accelerazione 𝑋A, corrisponda alla forza

specifica 𝐹A su di A, in un sistema di riferimento inerziale:

𝑋A = 𝐹! (2.3)

in accordo con la seconda legge della dinamica.

Figura 2.1: Sistema di riferimento inerziale, solidale alla Terra, del satellite e del

Gradiometro.

Assumendo che il centro del gradiometro (l’intersezione dei suoi tre assi) sia il centro di massa del satellite O, in accordo con il teorema di

Coriolis si ottiene che:

𝑋A = 𝑋O + Q  Ω𝑥A + Q  Ω!  𝑥A + Q 2Ω𝑥A + Q  𝑥A (2.4)

dove Q è la matrice di rotazione tra il sistema di riferimento locale

(XGRF, YGRF, ZGRF) del satellite (Gradiometer Reference Frame, GRF),

e il sistema di riferimento quasi−inerziale (IRF) centrato nel baricentro della Terra (XIRF, YIRF, ZIRF) (figura 2.1); Ω  è la matrice della velocità

angolare, Ω è la matrice dell’accelerazione angolare e Ω! _{è la matrice} dell’accelerazione centrifuga: Ω =   0 −𝜔_! 𝜔_! 𝜔_! 0 −𝜔_! −𝜔_! 𝜔_! 0 (2.5) Ω =   0 −𝜔_! 𝜔_! 𝜔_! 0 −𝜔_! −𝜔_! 𝜔_! 0 (2.6) Ω! ₌ −𝜔_!!_{− 𝜔} !! 𝜔!𝜔! 𝜔!𝜔! 𝜔_!𝜔_! −𝜔_!! _{− 𝜔} !! 𝜔!𝜔! 𝜔_!𝜔_! 𝜔_!𝜔_! −𝜔_!!_{− 𝜔} !! (2.7)

Sulle masse di prova, considerate nel GRF, agiscono due principali tipi di forza: la prima è la forza gravitazionale data dalla Terra, contenente piccole componenti di Sole e Luna, 𝑓gA; la seconda è la

forza elettrostatica 𝑓accA applicata dall’accelerometro per mantenere A bloccata in una posizione fissa rispetto al gradiometro. Possiamo scrivere:

Q (𝑓gA + 𝑓accA) = 𝐹A (2.8)

e quindi usando le relazioni (2.3), (2.4) e moltiplicando per 𝑄!

otteniamo:

dove si considera 𝑥A = 𝑥A = 0 poiché le masse di prova sono mantenute

ferme rispetto al GRF.

Considerando ora due accelerometri A e B, appartenenti allo stesso braccio, otteniamo:

(𝑓gA − 𝑓gB) + (𝑓accA − 𝑓accB) = (Ω + Ω!)(𝑥A − 𝑥B) (2.10) Si definisce M il tensore di Marussi; scrivendo le derivate seconde nella forma 𝑉_!" = _!"!#!!! esso è:

𝑀 =

𝑉_!! 𝑉_!" 𝑉_!" 𝑉_!" 𝑉_!! 𝑉_!" 𝑉_!" 𝑉_!" 𝑉_!!

(2.11)

Scrivendo il termine (𝑓gA − 𝑓gB) come una funzione del potenziale gravitazionale terrestre (1.3) e trascurando tutti gli altri effetti gravitazionali che possono essere tenuti in conto attraverso opportune correzioni, si ricava:

(𝑓gA − 𝑓gB) = ∇VA − ∇VB ≅M(𝑥A − 𝑥B) (2.12) Possiamo ora riorganizzare l’equazione (2.10) ed ottenere:

(𝑓accB − 𝑓accA) = (M − Ω − Ω!)(𝑥A − 𝑥B) (2.13) dove (𝑓accB − 𝑓accA) rappresenta l’osservazione del gradiometro.

Figura 2.2: Immagini del campo di gravità della Terra, in termini di derivata del

secondo ordine del potenziale anomalo. 1E (𝐸𝑜𝑡𝑣𝑜𝑠) = 10!!_{gal/cm = 10}!!_𝑠!!

Prendendo in considerazione le tre direzioni, definiamo il tensore

dell’osservabile 𝛤 come una matrice 3x3:

Γ = (!!""#  !  !!""#)_! !" (!!""#  !  !!""#) !!" (!!""#  !  !!""#) !!" = 𝑀 − Ω − Ω !   _(2.14)

dove LAB , LCD , LEF sono le distanze tra due accelerometri lungo ogni

asse del gradiometro.

Poiché 𝛺T _{≡ −𝛺, il contributo di Ω può essere eliminato calcolando:}

!

! Γ + Γ

! _{= 𝑀 − Ω}! _(2.15)

Si può osservare che il termine più rilevante di Ω! _{è 𝜔}

! , cioè quello

legato alla rotazione del satellite attorno alla Terra. Questo termine può essere stimato da 𝜔_!, calcolato dall’espressione !_! Γ_!,! + Γ_!,! e successivamente integrato lungo l’orbita usando le informazioni sull’assetto dai sensori di stella. Rimuovendo il contributo di Ω!_{, ed}

dell’accelerometro, è possibile ottenere un’osservazione diretta del

tensore di Marussi. Poiché gli accelerometri elettrostatici hanno un

asse meno sensibile, le derivate del secondo ordine che usano le sole osservazioni dagli assi più sensibili sono 𝑉_!! , 𝑉_!! , 𝑉_!!  e 𝑉_!" [51]. I dati ricevuti da GOCE attraversano un certo numero di passaggi prima di arrivare alla soluzione finale [53]; dal 2009 al 2012 sono stati raggruppati in diciassette cicli. Questi sono i dati di Level 1b [19] che contengono oltre alle misurazioni dell’EGG quelle istantanee del GPS. Le misurazioni dell’EGG sono state acquisite ogni secondo; il tempo nell’istante di misurazione è conteggiato dall’orologio a bordo del GOCE mentre i dati del GPS relativi alla posizione del satellite sono stati rilevati ogni 10 secondi conteggiati dall’orologio del ricevitore GPS. I cicli coprono l’intervallo che va da novembre 2009 a novembre 2012. La suddivisione in cicli è dovuta all’interruzione delle misurazioni durante le fasi di “shaking” quando il gradiometro viene fatto letteralmente “vibrare” per portare le masse di prova nella loro posizione di progetto, perduta a causa di errori sistematici. Altre interruzioni sono dovute a malfunzionamenti come è accaduto ad esempio al computer di bordo [10] nel 2010 quando l’intera missione ha rischiato di fallire. I dati mancanti (EGG e GPS) saranno simulati per ottenere un intervallo di dati continuo; in seguito viene illustrata la procedura seguita per lo scopo (Capitoli 5 e 6).

2.2 I dati del GPS

Oltre alle misurazioni del GPS contemporanee alle misurazioni dell’EGG, acquisite cioè dal GOCE, sono disponibili anche quelle acquisite dalla costellazione del GPS durante quasi tutta la missione (anche quando il gradiometro non funziona). Il GPS fornisce le coordinate del satellite nel sistema di riferimento WGS84 (World Geodetic System) [60] e si basa sul tempo UTC. Le interruzioni in questi dati sono dovute o al mal funzionamento della costellazione o a quello del ricevitore GPS a bordo del GOCE. Per la simulazione dei

dati orbitali mancanti è stato utilizzato il propagatore SGP4 (capitolo 5). I dati GPS saranno a loro volta utilizzati per la simulazione del segnale del potenziale mancante nei cicli del gradiometro.

2.3 Soluzioni mensili di GRACE

Le soluzioni mensili dei coefficienti di GRACE [11] si trovano in file di testo scaricabili dalla rete [22]. Tre sono i centri che si occupano dell’analisi dei dati del GRACE, in particolare le soluzioni utilizzate in questo calcolo sono state prodotte dal “GFZ Helmholtz-Zentrum

POTSDAM”; i coefficienti delle armoniche raggiungono il grado

massimo di novanta. Un esempio di file di testo contenente il valore dei coefficienti di gennaio 2012 è presente in Appendice (1).

2.4 Il modello GOCO03S di campo gravitazionale globale

Il GOCO03S è un modello di geopotenziale, rilasciato nel 2012, che proviene da una combinazione dei risultati di valutazione della gravità (coefficienti fino al grado 250) derivati esclusivamente da missioni satellitari e dall’elaborazione congiunta d’Istituzioni Europee di Geodesia [18]. Il GOCO03S è un modello statico globale e non tiene quindi conto degli effetti di variazione ciclica del geoide. Le seguenti missioni contribuiscono alla soluzione:

-­‐ GOCE (18 mesi) dati SST e gradiometria; -­‐ GRACE (7 anni);

-­‐ CHAMP (8 anni) dati SST; -­‐ SLR (5 anni, 5 satelliti).

2.5 Soluzioni mensili del SLR

Le soluzioni numeriche mensili dei coefficienti di basso grado delle armoniche provengono dal Centro di Geodesia Spaziale di Matera. I coefficienti (di ordine zero) sono le armoniche zonali 𝐽_!, 𝐽_! e 𝐽_! calcolate da gennaio 1984 a maggio 2012. Vengono considerate solo le soluzioni appartenenti al periodo di funzionamento del GOCE.

Capitolo 3

L’analisi dei dati GOCE

3.1 L’HPF e differenti approcci all’analisi dei dati

GOCE

L’High-Level Processing Facility (HPF) [6] [44] [21] avviene sotto il controllo dell’ESA e consiste di dieci università europee e centri di ricerca che hanno conoscenze complementari nella gravità e nei campi scientifici della geodesia; questi centri si sono uniti per operare nel HPF lungo tutta l’operatività del GOCE. Lo scopo principale di questi centri è la generazione dei dati di Level 2 [23] [20] elaborando quelli di Level 1b. Tra tutti i differenti metodi proposti per l’analisi del campo di gravità del GOCE, tre sono stati selezionati dall’ESA e portati avanti parallelamente da tre gruppi all’interno del HPF; una validazione finale di questi ultimi assicurerà l’alta qualità del prodotto GOCE del campo gravitazionale. Tali metodi sono chiamati: direct

method, time-wise e space-wise.

Il direct method [7] consiste in una soluzione ai minimi quadrati, molto pesante dal punto di vista del calcolo per la grande quantità di dati e incognite, per questo anche chiamato “brute force”.

L’approccio time-wise [38] sfrutta i vantaggi del flusso temporale entrante di dati e, dopo l’esecuzione di una trasformata di Fourier delle equazioni di osservazione che legano il potenziale lungo l’orbita (relazione di Kaula) con i coefficienti armonici, considera la struttura prevalentemente diagonale a blocchi di quest’ultima per stimare i coefficienti delle armoniche sferiche del campo di gravità (stima congiunta di coefficienti dello stesso ordine). Questo riduce considerevolmente i problemi di calcolo, anche con l’aiuto di una

procedura iterativa. La soluzione time-wise ufficialmente rilasciata è in realtà una soluzione ibrida tra l’approccio time-wise (come descritto) e il direct method.

L’approccio space-wise [32] è quello “più recente” e meno collaudato, allo stato di fatto esso può essere eseguito grazie alla piccola distanza tra gli accelerometri appartenenti allo stesso braccio del gradiometro. La piccola distanza fa si che la lettura dell’accelerazione sui due accelerometri, ovvero la derivata seconda del potenziale, può essere collocata nel punto centrale del braccio, ovvero nel baricentro del satellite. La derivata seconda del potenziale gravitazionale può essere vista come un’informazione puntuale, visto che la gravità può essere considerata costante spostandosi di qualche centimetro, ed è quindi trattata con tecniche statistiche di interpolazione come ad esempio la collocazione [35].

3.2. L’approccio space-wise

L’idea base dell’approccio space-wise [40] ai dati di gradiometria satellitare è quella di prendere i vantaggi di una correlazione spaziale delle misurazioni, ereditata da quella del potenziale gravitazionale, allo scopo di filtrare il rumore e calcolare i coefficienti delle armoniche sferiche del modello di geo-potenziale.

Teoricamente il migliore dei modi per implementare quest’approccio sarebbe quello di applicare una soluzione di collocazione globale [46] [36] unica a tutti i dati osservati, assumendo che la funzione di covarianza del potenziale T sia conosciuta. Sfortunatamente questo metodo non è fattibile, poiché il numero di osservazioni è molto grande rispetto alle capacità delle macchine di elaborare una grande quantità di dati; questo si traduce in tempi di calcolo molto ampi. Un metodo per processare i dati, basato su una strategia step-wise, è stato selezionato: prima viene eseguita un’interpolazione su griglia

sferica regolare all’altezza media del satellite (circa 250 km) per

questi dati della griglia, viene utilizzato un algoritmo di analisi armonica per stimare i coefficienti del campo.

Tra tutti i differenti metodi per implementare una griglia [55] [34] è stato dimostrato da test numerici che una tecnica basata sulla collocazione [54] sarebbe preferibile. Per la stessa ragione precedente, una collocazione unica globale non è fattibile e di conseguenza viene utilizzata un’analisi di approccio locale su un sottoinsieme sovrapposto [41]. Il primo passo di grigliatura (o gridding) è la chiave dell’approccio space-wise: esso permette di connettere i dati vicini nello spazio ma lontani nel tempo, riducendo gli effetti dei rumori tempo-correlati.

Il secondo passo dell’approccio è l’analisi armonica che può essere implementata usando differenti metodi, ad esempio: la spherical

collocation [47] che sfrutta la distribuzione regolare dei dati per

ridurre la complessità del calcolo; l’analisi di Fourier [14] sulla sfera che tuttavia richiede una griglia che raddoppi la soluzione nella direzione della latitudine; un’integrazione numerica che sfrutta le proprietà di ortogonalità delle armoniche sferiche. La soluzione implementata è quest’ultima.

Da un punto di vista teorico, i coefficienti delle armoniche sferiche Vlm

possono essere ottenuti usando la formula: 𝑉_!" =_!!!!_!! ! ! 𝑉!! 𝜗, 𝜆 𝑌!" 𝜗, 𝜆 𝑑𝜎 (3.1) dove: 𝑎_! = !" !! (𝑙 + 1)(𝑙 + 2) ! ! !!! (3.2) ed S è la sfera di raggio r. Questo integrale può essere approssimato sommando i valori grigliati:

𝑉_!" = !

!!!!_!

dove 𝑆_!" è l’area della superficie del blocco equiangolare Sij , in cui la

“sfera di riferimento” viene suddivisa.

Muovendosi dalla teoria alla pratica, l’approccio space-wise deve essere adattato per considerare le limitazioni della missione, come i rumori della strumentazione, l’intervallo ai poli e le trasformazioni tra i vari sistemi di riferimento.

Il problema dell’intervallo ai poli proviene dall’inclinazione dell’orbita eliosincrona del GOCE, ovvero il satellite non vola oltre le due calotte polari causando un buco nella copertura della sfera. Se non correttamente trattato, questo problema potrebbe introdurre errori inaccettabili quando integrato sulla sfera. Sono possibili diverse soluzioni: in questa analisi è stato utilizzato un modello (GRACE) per coprire i buchi ai poli, anche se questo implica una dipendenza dal modello scelto e introduce una frequenza artificiale alta nel modello stimato dovuta alla non perfetta “contiguità” dei dati osservati e da quelli generati dal modello GRACE.

3.2.1 La grigliatura dei dati

L’operazione di grigliatura consiste nello sviluppare una matrice G che moltiplicata per 𝑌t (il vettore osservato T o 𝑇!!) dia il valore

grigliato dello stesso funzionale:

G ⋅ 𝑌t = 𝑌!"#$% (3.4)

𝐾  ×  𝑁 𝑁  ×  1 𝐾  ×  1

dove N è il numero delle osservazioni e K è il numero di punti nella griglia; da notare che 𝑌_!"#$% è un vettore di dimensioni  𝐾  ×  1, ma formalmente è una matrice le cui dimensioni sono quelle della griglia.

3.2.2 Il calcolo dei coefficienti delle armoniche

Il calcolo del valore dei coefficienti delle armoniche sferiche avviene attraverso l’analisi armonica dei dati grigliati. Questo si ottiene riscrivendo la formula per 𝑇_!" con dati grigliati:

𝑇_!" = _!!!!_!! ! ! !𝑌!"#!$(𝜗!, 𝜆!)𝑌!"(𝜗!, 𝜆!)∆𝜎 (3.5) o nella forma: 𝐶_!" 𝑆_!" =   ! !!!!_!! ! !𝑌!"#!$(𝜗!, 𝜆!)𝑃!"(𝜗!) cos 𝑚 𝜆_! sin 𝑚𝜆_! ∆𝜎 (3.6)

dove 𝐶_!" e 𝑆_!" sono le componenti di seno e coseno di 𝑇_!" se si

scompone 𝑌_!" (armoniche sferiche di grado l e ordine m) come:

𝑌_!" 𝜗, 𝜆 = 𝑃_!"(𝜗) cos 𝑚𝜆

sin 𝑚𝜆 (3.7) e dove Ygrigl è il generico funzionale grigliato (T o 𝑇!!) e Δσ è l’area

sferica di dimensioni: ∆𝜎 = !!! 𝑑𝜆 ! ! !_!!  ! ! 𝑐𝑜𝑠𝜗𝑑𝜗 = 2Δ𝑠𝑖𝑛 !_! !_!!! ! !_!!! ! 𝑠𝑖𝑛 𝜗_! ≅ ∆!_{𝑠𝑖𝑛 𝜗} ! (3.8)

in cui Δ è l’intervallo angolare della griglia. La relazione (3.6) è implementata in Matlab nella funzione “analisi.m”. Quest’ultima basa il calcolo dei coefficienti sull'integrazione (numerica) di dati definiti su un grigliato sferico e su una discretizzazione basata sul calcolo delle armoniche sferiche nel punto centrale di ogni cella del grigliato con un limite massimo pari al grado 300. Dato limite non crea problemi in questa soluzione.

3.3 L’Error Degree Variances e l’Error Degree

Median

Assumendo che i coefficienti delle armoniche sferiche Tlm siano

variabili casuali con media nulla, stocasticamente indipendenti l’una dall’altra e con una varianza dipendente solo dal grado l , si ha:

𝐸 𝑇_!" =0 (3.9)

𝐸 𝑇_!"𝑇_!! = 𝛿_!"𝛿_!!𝜎_!! _(3.10)

Considerando (𝑘 = 𝑙) e (ℎ = 𝑚) la covarianza della stessa variabile casuale è la varianza. Si stima la Degree Variances [56] (del singolo coefficiente) come: 𝜎_!! ₌ ! !!!! 𝑇!" ! ! !!!! (3.10)

E’ interessante notare che, poiché essa si ottiene da una media di l valori, la precisione di stima della degree variances cresce linearmente con il grado. Si definisce per ragioni più pratiche la degree variances

DV (full power) come:

𝑐_! = 𝜎_!! _{2𝑙 + 1 = 𝑇} !"! ! !!!! (3.11) o in componenti: 𝑐_! = ! 𝐶_!"! !!! + !!!!𝑆!"! (3.12)

Da qui si considera l’Error Degree Variances (EDV) come differenza tra i coefficienti armonici provenienti da un modello di riferimento, in questo caso il GOCO03S (Clm0 e Slm0), e quelli calcolati a valle del grigliatore o in qualunque altro modo:

𝐸𝐷𝑉 = 𝑒_! = ! 𝐶_!"!− 𝐶_!" !

L’Error Degree Variances può essere visto come la sommatoria per righe (grado l costante) su un grafico dove le componenti seno e coseno dei coefficienti sono rappresentati in ordine e grado crescenti (figura 3.1).

Figura 3.1: Diagramma di rappresentazione dei coefficienti delle armoniche. A

sinistra le componenti del coseno (Clm), a destra quelle del seno (Slm).

Se invece della media dei coefficienti al quadrato, come in formula 3.10, si calcola la mediana e se ne fa la radice quadrata si ottiene l’Error Degree Median (EDMedian) ovvero:

𝐸𝐷𝑀 = 𝑒_! = 𝑚𝑒𝑑𝑖𝑎𝑛𝑎[ 𝐶_!"!− 𝐶_!" !_{, 𝑆}

!"! − 𝑆!" !] (3.14)

Questa media è più idonea nel caso di mancanza dei dati nei poli che provoca un forte degrado dei coefficienti di ordine basso.

Capitolo 4

Realizzazione e test del grigliatore

4.1 Introduzione

Nel paragrafo 3.3 sono state elencate tutte le operazioni che costituiscono il metodo space-wise. In questo capitolo si descrivono e si implementano le operazioni dal punto di vista matematico, valutandone la capacità dell’intero algoritmo di ottenere le soluzioni dei coefficienti con l’utilizzo di un modello di potenziale già esistente, il GOCO03S. L’implementazione della procedura in Matlab è stata eseguita in prima persona sotto la guida dell’Ing. Andrea Gatti.

4.2 Interpolazione con spline bilineare

Per ridurre il numero delle misurazioni, si calcola una media pesata dei valori di 𝑇_!! in un intervallo di superficie pari alla grandezza di una cella della griglia. A tale scopo si usa una spline del primo ordine e bidimensionale: questa viene considerata come il prodotto cartesiano di due spline del primo ordine e monodimensionali, e il suo dominio va da -1 a 1 in ogni direzione, con i vertici di valore nullo.

Figura 4.1: Spline Lineare e Spline Bilineare.

Le spline lineari sono matematicamente definite come:

𝑓_! 𝑡 = 1 + 𝑡       − 1 < 𝑡 < 01 − 𝑡      0 ≤ 𝑡 < 1 0      𝑎𝑙𝑡𝑟𝑜𝑣𝑒

(4.1)

quindi la formula per la spline bilineare è data da:

𝑓_! 𝑡 = (1 − 𝑥 )(1 − 𝑦 )      (−1 < 𝑥 < 1) ∧ (−1 < 𝑦 < 1)

0      𝑎𝑙𝑡𝑟𝑜𝑣𝑒 (4.2)

dove in questo caso x ed y rappresentano rispettivamente le coordinate

angolari (𝜗, _λ) della griglia, accettando una piccola distorsione quando

si va dall’equatore ai poli. Si normalizzano ora le distanze tra due

successive spline al valore unitario: chiamando con (𝜗_!, 𝜆_!) le

coordinate del centro della spline con dimensioni della base di ∆𝜗, ∆𝜆 e con (𝜗_!, 𝜆_!) le coordinate dell’osservazione, è possibile ottenere la distanza normalizzata punto-spline usando le espressioni:

𝜗 = (!!!!!)

∆!      𝜆 =

(!_!!!_!)

in questo modo si calcola il “termine di peso” nella relazione della media W:

𝑊 = 1 − 𝜗 1 − 𝜆 (4.4) per ottenere infine il valore mediato come:

𝑇_!! = !!!!"!!

!_!

! (4.5)

Questo è il valore inserito nella celletta della griglia con punto centrale di coordinate (𝜗_!, 𝜆_!).

4.3 Approssimazione del segnale alla quota media

del satellite

Come già anticipato, nella procedura space-wise è necessario interpolare i dati dell’EGG alla quota media di 250 km, ovvero realizzare l’idealizzazione che questi siano la proiezione su di una “orbita sferica” di raggio pari a 250 km. Per velocizzare questo passaggio si è utilizzata un’espansione di Taylor al primo ordine di 𝑇_!!:

𝑇_!! 𝑟_!"#$%& = 𝑇_!! 250 + 𝑇_!!!(𝑟_!"#$%& − 250) (4.6) dove 𝑇_!!(𝑟_!"#$%&) è la derivata seconda (lungo r) del potenziale anomalo nei punti reali dell’orbita in coordinate geocentriche (colatitudine 𝜗, latitudine 𝜆 e quota radiale r). 𝑇_!!(250) è la derivata seconda del potenziale anomalo alla quota costante di 250 chilometri

(r = 250 km) rispetto al raggio r. La variabile 𝑇_!!! è la derivata terza

del potenziale anomalo (di r) stimato in due modi differenti: il primo attraverso il calcolo dell’usuale sviluppo in armoniche sferiche (figura 4.2), il secondo come risultato del rapporto (figura 4.2):

∆!!!

∆!

=

(!!!"!#$%&!!!!!"#)

(!_!"#$%&!!!"#) (4.7)

La relazione che definisce la derivata terza di r del potenziale anomalo (𝑇_!!!) è simile a quella che definisce il 𝑇_!! a meno di un termine nella sommatoria dovuto alla derivata:

!!_!

!!! 𝑟, 𝜗, 𝜆 =

−!"_!! !_!!! 𝑙 + 1 𝑙 + 2 𝑙 + 3 !_! !!! !_!!!!𝑇_!"𝑌_!" 𝜗, 𝜆 (4.8)

Per la stima degli errori nell’interpolazione, tutte le derivate del potenziale anomalo sono state calcolate dai coefficienti del modello GOCO03S e nei punti delle posizioni occupate dal GOCE relative ad un periodo di funzionamento di due mesi (circa 6.5 milioni di dati). I valori delle derivate del potenziale anomalo sono stati ottenuti con il software “MANIPULATOR” sviluppato dall’Ing. Andrea Gatti del Politecnico di Milano. Il software fornisce come risultato un vettore riga contenente i valori puntuali del potenziale, o delle sue derivate, assegnando le coordinate della posizione occupata dal satellite e il modello da sintetizzare. Un esempio del file d’inizializzazione è contenuto in Appendice (2).

I risultati sono stati plottati su Matlab ottenendo i seguenti grafici:

Figura 4.2: Segnale del 𝑇_!!! sintetizzato dal MANIPULATOR (verde), 𝑇_!!! dalla differenza tra il segnale 𝑇_!!(𝑟_!"#$%&) e 𝑇_!!(250) (blu) calcolato dalla relazione (4.7), differenza tra i due segnali (rosso).

Figura 4.3: segnale di 𝑇!!250 sintetizzato (blu); segnale di 𝑇!!(𝑟!"#$%&) (rosso);

segnale di 𝑇_!!250 calcolato come differenza tra 𝑇_!!(𝑟_!"#$%&) e 𝑇_!!!. sintetizzato (magenta); segnale di 𝑇_!!250 calcolato come differenza tra 𝑇_!!𝑂𝑟𝑏𝑖𝑡𝑎 e 𝑇_!!! calcolato dalla 4.7 (nero); questo coincide con il primo segnale per definizione.

Figura 4.4: Particolare dei picchi della figura 4.3.

Dalla figura 4.2 si noti che l’errore tra il 𝑇_!!! sintetizzato e quello

calcolato dalla differenza tra 𝑇_!! 𝑟_!"#$%& e 𝑇_!! 250 è molto piccolo, assumendo i valori massimi in prossimità dei picchi di ampiezza del segnale. Dalla figura 4.3, e meglio dalla 4.4, dove si considera il particolare di alcuni picchi, si noti come la differenza tra il segnale interpolato alla quota media (magenta) e quello sintetizzato alla quota media (blu), mostri il massimo discostamento nei picchi di un valore di circa 0.1 ∗  10!!! _{; il valore quindi del 𝑇}

!!! calcolato con uno o

l’altro metodo ha un effetto trascurabile sul segnale di 𝑇_!!(250); il segnale sintetizzato di quest’ultimo (verde) ha un andamento molto casuale. L’errore che si commette è accettabile perché di per sé è molto inferiore rispetto ad altri introdotti da fenomeni non modellati all’interno del sistema. L’ultima considerazione che deriva dai picchi dei segnali è l’amplificazione tra il 𝑇_!! 𝑟_!"#$%&  (rosso) e il 𝑇_!!(250) dovuta alla diminuzione di quota a quella media o viceversa all’attenuazione dovuta all’allontanamento se il satellite si trova al di sotto della quota media.

4.4 Il problema dei poli

Quando l’operatore di grigliatura è pronto, viene applicato al

funzionale 𝑌_! ottenendo cosi 𝑌_!"#! . Sfortunatamente, a causa

dell’inclinazione dell’orbita del GOCE pari a circa 96.7°, non si hanno osservazioni ai poli [50]. Per rimediare a questa mancanza e arrivare alla determinazione dell’efficacia del nostro grigliatore, i valori di 𝑌_!"#$ mancanti vengono rimpiazzati con quelli calcolati servendosi dei coefficienti delle armoniche del modello GOCO03S con una griglia

delle stesse dimensioni di quella utilizzata per 𝑌_!. Anche il calcolo dei

valori mancanti ai poli viene effettuato con il Manipulator in quanto, oltre che nei punti dell’orbita, è in grado di sintetizzare i valori del potenziale nelle celle di una griglia.

4.5 Test del grigliatore

Il grigliatore finale è costituito dalla sequenza dei passaggi elencati in precedenza e dall’utilizzo finale della funzione “analisi.m” per il calcolo dei coefficienti. L’intero algoritmo implementato in Matlab è presente in Appendice (3). Per il test le celle della griglia hanno dimensioni di 0.5 per 0.5 gradi, poiché non è richiesta una risoluzione di rappresentazione molto alta ma un’elaborazione più rapida. Per ragioni legate alla rappresentazione dei risultati, al posto della latitudine si utilizza la colatitudine _ϑ uguale in gradi a:

𝜗 = 90 − 𝜑

                                                                     

(4.9)

 

Le rappresentazioni della EDV e della EDM forniscono una valutazione della “capacità” del grigliatore di calcolare i coefficienti delle armoniche, in particolare mostrano il grado massimo raggiunto da questi. Le curve dell’errore vengono confrontate con quella del segnale. Quando le due curve (EDV o EDM con il segnale) si

intersecano, l’errore che si commette è pari al segnale da stimare determinando il grado massimo; per gradi superiori risulta più conveniente stimare coefficienti nulli ovvero non effettuare alcuna stima. Nelle figure che seguono si confrontano i risultati al variare del metodo di calcolo del valore medio di 𝑇_!! da attribuire alla cella e i

diversi andamenti con o senza dati ai poli.

Figura 4.5: Le Error Degree Variances dei coefficienti calcolati con il grigliatore,

senza segnale ai poli (nero, blu) e con segnale ai poli (ciano, verde, giallo); coefficienti del modello di riferimento GOCO03S (rosso).

Figura 4.6: Le Error Degree Meridian dei coefficienti calcolati con il grigliatore,

senza segnale ai poli (nero, blu) e con segnale ai poli (ciano, verde, giallo); coefficienti del modello di riferimento GOCO03S (rosso).

Dalla figura 4.5 si risalta l’oscillazione dell’EDV dovuta alla mancanza di dati ai poli, comportamento che non è presente nella

figura 4.6 per l’EDMedian. Tuttavia entrambi concordano che il grado massimo raggiungibile dai coefficienti calcolati si avvicina a 210 e che il valore medio di 𝑇_!! valutato con la spline bilineare permette di

raggiunge il grado più elevato.

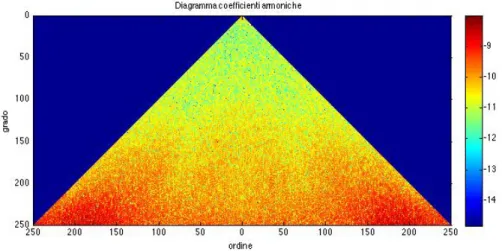
Di seguito sono mostrati i diagrammi della differenza tra i coefficienti valutati dal grigliatore e quelli originali del modello GOCO03S. Il primo diagramma è costituito dai coefficienti valutati senza dati ai poli; questo è informalmente definito come Diagramma a Farfalla per la particolare conformazione: al centro sembra esserci il corpo di una farfalla con le ali spiegate. Questo risultato evidenzia come la mancanza delle misurazioni da parte del GOCE nelle calotte polari causi una scarsissima valutazione dei coefficienti di basso ordine.

Figura 4.7: Diagramma “a farfalla”. Differenza tra i coefficienti valutati con il

grigliatore e i coefficienti del modello GOCO03S. L’errore massimo è nelle zone rosse.

Figura 4.8: Diagramma dei coefficienti con dati ai poli. Differenza tra i

coefficienti valutati con il grigliatore e i coefficienti del modello GOCO03S.

Dalla figura 4.8 si può notare come il degrado dovuto alla mancanza di dati nei poli è stato corretto. Mostra anche come la differenza dei coefficienti valutati dal grigliatore e quelli del GOCO03S presentano valori elevati nella parte bassa del grafico partendo all’incirca dal grado 200. Questo è un limite del grigliatore sviluppato, probabilmente dovuto allo spostamento dei dati in quota e all’interpolazione con le spline.

Continuando con i risultati, nella figura che segue è rappresentata la distribuzione della funzione “peso” W (relazione 4.4) che rappresenta un indice della densità di dati acquisiti dal satellite in un particolare punto della Terra.

Figura 4.9: Distribuzione della funzione peso (relazione 4.4)

Le fasce superiore e inferiore di colore blu evidenziano ancora una volta la completa assenza di dati nelle calotte polari. Seguono poi due fasce in rosso indicanti il maggior numero di passaggi che man mano diminuiscono avvicinandosi all’equatore.

L’ultimo risultato riguarda la differenza tra i valori medi di 𝑇_!!

calcolati da una semplice media aritmetica e quelli calcolati con una media pesata.

Si può ben vedere dalla figura 4.9 come la media pesata riesca a conservare in maniera migliore i valori di 𝑇_!! , specie nei punti in cui il

segnale è particolarmente forte, come si vedrà in seguito.

È importante ricordare che questi test sono stati effettuati partendo da un segnale privo di errori poiché calcolato da un modello con le stesse caratteristiche; quando l’analisi sarà condotta sul segnale originale si vedranno quelli che saranno gli ulteriori limiti legati alla semplicità del grigliatore.