Analysis of structural systems with interval uncertainties under deterministic and stochastic excitations

(1)

Università degli studi di Messina

Dipartimento di Ingegneria

Dottorato in Ingegneria e Chimica dei Materiali e delle

Costruzioni XXXII ciclo (2016-2019)

Analysis of structural systems with

interval uncertainties under

deterministic and stochastic excitations

PhD Student: Filippo Giunta

Tutor: Prof. Eng. Giuseppe Muscolino

(2)

(3)

To Margherita

“May we meet again in a better and safer place”

(4)

(5)

Acknowledgments

I would first like to thank my supervisors Professor Giuseppe Muscolino and Professor Alba Sofi for all the support and the teachings that they gave me during these three years. They suggested this research project giving me critical comments and continuous support and contributed to my professional growth, making me to become a “lover” of research. An important thank goes to Dr. Alice Cicirello, who supported, supervised and motivated me in my great experience at the Oxford University. I also thank the members of the “DVU LAB” for the beautiful moments spent together.

A special thank goes to my parents and my grandmother, who patiently took care of me. Finally, but not least, thanks to the old and new friends and colleagues that I made along the way.

(6)

(7)

“Uncertainties appear everywhere in the model. When using a

mathematical model, careful attention must be given to the

uncertainties in the model.”

(8)

(9)

Analysis of structural systems with interval uncertainties under deterministic and stochastic excitations

Index

Chapter 1. Introduction ... 1

Chapter 2. Fundamentals of Interval Analysis ... 7

2.1 Introduction ... 7

2.2 Fundamentals of Interval Analysis ... 10

2.2.1 Interval variable definition... 10

2.2.2 Basic notation ... 10

2.2.3 Basic operations of Interval Arithmetic ... 15

2.2.4 Algebraic properties ... 17

2.2.5 Interval functions ... 20

2.2.6 Dependency phenomenon ... 22

2.3 System of linear interval equations ... 25

2.3.1 Interval vectors ... 25

2.3.2 Interval matrices ... 27

2.3.3 Solution of linear interval equations ... 29

2.4 Mitigation of the dependency phenomenon ... 33

2.4.1 Affine Arithmetic ... 34

2.4.2 Parameterized Interval Analysis ... 36

2.4.3 Improved Interval Analysis via Extra Unitary Interval ... 37

2.4.4 Example 1: interval multiplication ... 38

(10)

2.5 Solution of systems of linear interval equations in structural engineering ... 45

2.5.1 Introduction ... 45

2.5.2 Monte Carlo Combination Method and Vertex method ... 46

2.5.3 Example 3: Solution for non-monotonic functions ... 49

2.5.4 Example 5: asymmetric two bar truss structure with uncertain axial stiffness subjected to a deterministic static load ... 52

Chapter 3. Static interval analysis of truss structures with uncertain axial stiffness .. 65

3.2 Problem statement ... 67

3.3 Interval Rational Series Expansion plus IIA via EUI ... 68

3.4 Bounds of the solution: approach based on the affine form of the IRSE-1 ... 74

3.5 Bounds of the solution: sensitivity approach ... 78

3.6 Higher-order terms of the IRSE by sensitivity approach ... 81

3.7 Numerical application ... 85

3.8 Overall considerations ... 108

Chapter 4. Static interval analysis of finite element modelled structures with uncertain parameters ... 111

4.2 Interval finite element method based on the IIA via EUI ... 115

4.3 Bounds of the solution based on the affine form of the IRSE ... 129

4.4 Numerical application ... 133

Chapter 5. Dynamic interval analysis of structures with uncertain parameters ... 167

(11)

5.1.1 Problem statement ... 171

5.1.2 Interval free vibrations ... 173

5.1.3 Pseudo-static sensitivity analysis ... 177

5.1.4 Generalized interval modal analysis ... 181

5.1.5 Bounds of free vibrations ... 183

5.1.6 Bounds of the interval response time-history ... 184

5.2 Numerical applications ... 187

5.2.1 3D truss structure with uncertain Young’s modulus under impulsive load .. 187

5.2.2 Grid structure with uncertain Young’s modulus under impulsive load ... 192

5.2.3 Shell corner with uncertain Young’s modulus under seismic excitation ... 203

Chapter 6. Failure interval analysis of truss structures with uncertain axial stiffness under stochastic stationary Gaussian excitations ... 209

6.2 Preliminary definitions ... 209

6.2.1 Random variables and random processes ... 209

6.2.2 Stationary Gaussian random processes ... 213

6.2.3 Stationary spectral moments ... 216

6.2.4 Failure due to random vibrations ... 219

6.2.4.1Distribution of extreme values for Gaussian stationary random process .. 220

6.2.4.2 Expected fatigue life of linear structures under stationary stochastic excitations ... 227 6.2.4.3 Frequency domain approach for the evaluation of fatigue life of linear

(12)

6.3 Truss structures with interval axial stiffness under multi-correlated stationary

Gaussian stochastic excitations ... 237

6.3.1 Problem statement ... 238

6.3.2 Model of turbulent wind excitation acting on truss structures ... 241

6.3.3 Interval stochastic response ... 244

6.4 Interval Reliability Analysis ... 251

6.4.1 Interval reliability function... 251

6.4.2 Bounds of the interval reliability function via sensitivity analysis ... 254

6.4.3 Interval fractiles ... 259

6.4.4 Numerical application ... 263

6.5 Interval fatigue analysis... 273

6.5.1 Interval expected fatigue life ... 273

6.5.2 Bounds of the expected fatigue life via sensitivity analysis ... 274

6.5.3 Numerical application ... 279

Chapter 7. Conclusions ... 293

Appendix 1. First-order Interval Perturbation Method……….…. 299

Appendix 2. Rational Series Expansion (RSE) of the stiffness matrix….……… 303

Appendix 3. Rational Series Expansion (RSE) of the FRF matrix…….………...309

Appendix 4. Dynamic first-order Interval Perturbation Method……….. 315

(13)

Chapter 1. Introduction

Equation Chapter (Next) Section 1

Structural engineering problems are tackled by using mathematical models which are based on appropriate simplifying hypotheses. The calibration of these models requires the definition of input parameters related to geometry, material properties and external loads. Usually, input parameters are estimated using experimental data, which, are inevitably affected by uncertainties. Indeed, the quality of experimental data is affected by many factors, e.g. the experimental design, the reliability of measurement devices and the data post-processing carried out by the analysts. Within the engineering context, the presence of these uncertainties often does not allow safe design of structures, because it is not possible to identify in a clear manner the most unfavourable conditions. It follows that it is crucial to develop efficient procedures that allow one to consider the non-deterministic nature of the input parameters, in such a way to identify the most unfavourable conditions and, therefore, achieve safe design.

Over the last decades, the quantification and propagation of uncertainties have attracted growing research interest in many engineering fields, e.g. biomedical, mechanic, civil, automotive and aerospace engineering.

Relying on their intrinsic nature, uncertainties are mainly classified into two categories, that is, aleatory (or stochastic) and epistemic. The word “aleatory” has an ancient origin, related to the Latin word “alea”, which refers to a kind of dice game. For instance, a typical aleatory uncertainty is flipping a coin and predicting either

heads or tails. An engineering example in which the effects of aleatory uncertainties

can be observed is the industrial production of materials. Indeed, different samples of the same material deriving from different factories are not the same, and thus do not show the same mechanical properties, due to different production environmental conditions, manufacturing tolerances and other unpredictable circumstances.

(14)

or the intrinsic variability of a physical quantity. Instead, the word “epistemic”

derives from the Greek word “επιστημη” (episteme), which means “knowledge”.

Indeed, the epistemic uncertainty comes from the lack of either knowledge or data, which lead to the inability to fully understand and predict a phenomenon. As an example, a source of epistemic uncertainty is represented by the drag in an experiment designed to measure the acceleration of gravity near the Earth’s surface.

The commonly used gravitational acceleration _{g =}_9.806m/s2_{actually ignores the}

effects of air resistance, but the air resistance for the object could be measured and incorporated into the experiment to reduce the resulting uncertainty in the calculation of the gravitational acceleration. It follows that, in this case, the uncertainty related to the value taken by g could be reduced by considering additional data and information. In general, epistemic uncertainties are uncertainties that may be reduced by the knowledge of additional data or information, or by increasing the accuracy of the estimates of parameters involved within mathematical models or by choosing more appropriate models for the analysed problem.

The most widespread approach is to handle uncertainties by means of the classical probability and random process theory, by describing uncertainties as random

variables or random fields. As widely recognized by the scientific community, this

approach turns out to be satisfactory only if enough statistical data is available to define the probability density function (PDF) of the uncertain parameters. However, in real situations, experimental data available to characterize probabilistically the uncertain parameters are often quite limited, especially in the early design stages. Therefore, among the scientific community some criticism has arisen on the use of traditional probabilistic approaches when available data is not enough to define accurately the PDFs of uncertain parameters or when information is ambiguous, vague or imprecise (Elishakoff, 2000). In this regard, Freudenthal (1961), who was one of the pioneers of the use of probabilistic methods in engineering stated that “…ignorance of the cause of variation does not make such variation random”. This statement is very meaningful; indeed, it suggests that, when crucial information on a variability is missing, it is not good practice to model an uncertain parameter as a probabilistic quantity described by a single PDF. Moreover, as highlighted by

(15)

Ben-Analysis of structural systems with interval uncertainties under deterministic and stochastic excitations

Haim and Elishakoff (1990), even small changes in the PDF of the input parameters may produce large changes in the failure probability. Thus, when available data is not enough to define accurately the PDF describing the uncertain parameters, in order to obtain conservative results, it is advisable either to carry out many probabilistic analyses by using different PDFs, so as to examine the effects of the chosen distribution, or to use an alternative uncertainty model.

Over the last few decades, several non-probabilistic approaches have been introduced in the literature. Within this framework, it is worth mentioning fuzzy sets theory (Zadeh, 1978), convex models (Ben-Haim and Elishakoff, 1990), and the interval model (Moore 1966; Moore et al., 2009). Such approaches, which do not need a full probabilistic characterization of uncertainty, can be alternatively used to model the input uncertain parameters when only fragmentary or incomplete experimental data is available (Moens and Vandepitte, 2005; Elishakoff and Ohsaki, 2010).

Elishakoff (1995) stated that: “Convex modeling of uncertainty, and in general the

set-theoretic modeling of it (the constraints should not necessarily be treated as convex), do not support probabilistic ideas. Convex modelling rather complements both the probabilistic approach and the fuzzy subsets-based treatment”. Elishakoff

(1995) with the beforementioned statement, suggests the use of a generalized framework which includes both probabilistic and non-probabilistic methods for modelling the uncertain parameters. For instance, in the preliminary stage of design, when the available data is not enough to define accurately the PDF describing the uncertain parameters, a non-probabilistic approach can be reasonably used. On the contrary, if more details on the uncertain parameters are available, the probabilistic approach can be reasonably used.

Within the framework of non-probabilistic approaches, the interval model is nowadays one of the most widespread used. The interval model is mainly based on the Classical Interval Analysis (CIA) introduced by Moore (1966). By using the interval model, the uncertain parameters are described by interval variables. Each interval variable is fully described once its Lower Bound (LB) and Upper Bound (UB) are known. For this reason, the interval model is an effective analytical tool to

(16)

only the knowledge of their range of variability, without requiring any information regarding the distribution within it. Despite its straightforward mathematical background (see Moore et al., 2009), the CIA suffers from the so-called dependency

phenomenon (Moore et al., 2009), which leads to overestimation of the results, that

may become pointless from the engineering point of view. In order to limit the conservatism due to the dependency phenomenon, several strategies have been introduced in the literature, such as: the Generalized Interval Analysis (Hansen, 1975), the Affine Arithmetic (AA) (Comba and Stolfi, 1993; Stolfi and De Figueiredo, 2003), the Parameterized Interval Analysis (PIA) (Elishakoff and Miglis, 2012a,b) and the Improved Interval Analysis via Extra Unitary Interval (IIA via EUI) (Muscolino and Sofi, 2012a).

The present PhD thesis is organized as follows. After this Introduction, in Chapter 2 the interval model of uncertainty is described along with some strategies to mitigate the dependency phenomenon affecting the CIA; some numerical examples aimed to clarify important issues arising in engineering applications are also presented. In Chapter 3, a method to perform the static interval analysis of truss structures with uncertain axial stiffnesses under deterministic loads is presented. In particular, the system of linear interval equations governing the equilibrium of truss structures is solved by taking advantage of the Interval Rational Series Expansion (IRSE) (Muscolino and Sofi, 2012b). Moreover, a comparison with the results provided by describing the uncertain parameters as random variables is carried out. In this regard, in order to examine the effects of the chosen PDFs on the results, the uncertain parameters are described by random variables with uniform and truncated Gaussian

PDFs, respectively. In order to demonstrate the effectiveness of the presented

method and to show the effects of the chosen PDFs on the response within the stochastic context, numerical results are provided. In Chapter 4, the Interval Finite

Element Method (IFEM) developed by Sofi and Romeo (2016) is first described.

Then, the system of linear interval equations governing the equilibrium of the Finite Element (FE) model of a structure with interval uncertainties subjected to static loads is solved by adopting three different decompositions of the interval stiffness matrix, that is: the column decomposition (Muscolino and Sofi, 2012b), the global spectral

(17)

decomposition (Giunta, 2016) and the element spectral decomposition (Sofi and

Romeo, 2016). Finally, a comparison with the results obtained by describing the uncertain parameters as random variables with uniform PDFs is carried out. In Chapter 5, the dynamic interval analysis of structures with uncertain parameters is addressed. A procedure based on the combination of the so-called pseudo-static

sensitivity analysis (Muscolino, Sofi and Giunta, 2018) with classical modal

superposition method is presented. Specifically, a pseudo-static sensitivity analysis is performed to seek the combinations of the endpoints of the uncertain parameters which give the lower bound and upper bound of the selected response of interest at each time instant. Among these, two combinations are selected as the most common ones over the time interval of interest, in order to avoid the onerous updating of the uncertain parameters at each time instant. Then, the bounds of the response time-history are evaluated by performing two parallel deterministic modal analyses associated to the most common combinations of the extreme values of interval uncertainties. Numerical applications are provided with the aim of demonstrating both the feasibility and accuracy of the presented method. In Chapter 6, the failure analysis, both in terms of reliability and fatigue, of linear truss structures with uncertain axial stiffnesses modelled as interval variables subjected to stationary multi-correlated stochastic Gaussian excitations, is addressed. Specifically, the classical spectral method to perform reliability analysis (see e.g., Lutes and Sarkani, 2004) and the empirical spectral approach developed by Benasciutti and Tovo

(2006), called α_0.75−method, are extended to the interval framework. Within the

interval context, the range of both the interval reliability function and the interval

expected fatigue life can be significantly overestimated by using the CIA due to the dependency phenomenon, which strongly affects stress-related quantities. To limit

the overestimation, a sensitivity-based approach, relying on the combination of the

IRSE with the IIA via EUI, is first presented and then applied perform interval

reliability and interval fatigue analysis. Through this procedure it is possible to obtain the combinations of the bounds of the interval axial stiffnesses which yield the

LB and UB of the interval expected fatigue life and the interval reliability function.

(18)

uncertain parameters on the expected fatigue life and reliability function. In order to demonstrate the feasibility and accuracy of the proposed methods, the reliability and fatigue analysis of truss structures with uncertain axial stiffness under wind excitation is carried out. Finally, a conclusive chapter summarizes meaningful results and highlights the main novelties introduced in the literature.

(19)

Chapter 2. Fundamentals of Interval Analysis

Equation Chapter (Next) Section 1

2.1 Introduction

Engineering problems are addressed by using mathematical models once appropriate hypotheses have been introduced. The calibration of these models requires the definition of input parameters related to the geometry, material properties and external actions. Input parameters are using estimated using experimental data and are inevitably affected by uncertainties. Hence, the deterministic models may provide unsatisfactory results. Moreover, although nowadays computers are very powerful, they are still discrete and finite machines; therefore, they cannot fully face up with some of the continuous and infinite aspects of mathematics (Hayes, 2003). Indeed, as

an example, a fractional number as 1/10 has no exact representation in the binary

code. Indeed, it can be represented just in an approximated form. However, those approximations may have severe consequences. On February 25, 1991, during the Gulf War, a Patriot missile defence system failed to intercept a Scud missile launched against the U.S. military installation at Dhrahn, Saudi Arabia (Elishakoff and Ohsaki, 2009). This malfunction caused the death of twenty-eight people and the injury of other ninety-eight. The cause of such a disaster was the wrong conversion of the time counted in tenths of a second into full seconds due to the roundoff error pertaining to the control system of the Patriot. Indeed, the algorithm implemented in the Patriot’s control system, multiplied many times the time expressed in tenths of a second by the decimal fraction 1/10, which has no finite representation in binary notation; consequently, the computer had to approximate. After four days, the roundoff errors, together with other peculiarities of the Patriot’s software, led to a miscalculation of almost 700 meters in the predicted incoming missile position, caused by a wrong assessment of about a third of a second on the expected ground impact time. After this event, the necessity to consider the sources of

(20)

non-Analysis of structural systems with interval uncertainties under deterministic and stochastic excitations

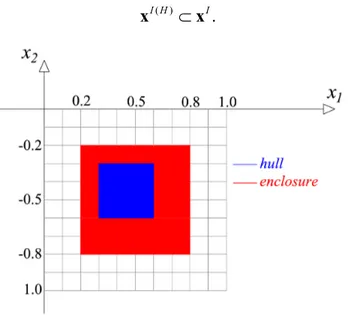
The easiest way to consider uncertainties without introducing any approximation is the identification of the confidence bounds that enclose the sought exact solution. In the mathematical context, such a quantity can be represented by using closed intervals (Moore et al., 2009).

One of the most famous and old examples of interval enclosure has been given by Archimedes (Alefeld and Mayer, 2000). Archimedes (287-212 B.C.E.) derived the

bounds of the transcendent number π (the exact value cannot be known) by

calculating the perimeter of a n-side polygon inscribed and circumscribed by a unitary diameter circle (see Figure 2-1). As the side number n of the polygon

increases, the value of πcan be enclosed within an increasingly smaller interval.

Considering n =96, Archimedes showed that the value of π is within the interval

(Elishakoff and Ohsaki, 2009)

10 1

3 3 .

71 π 7

+ < < + (2.1)

Figure 2-1 Bounds of π (circle with a unitary diameter) provided by the Archimede’s approach considering a regular polygon with a) 4 b) 10 and c) 96 sides .

According to Neumaier (1990), the first paper where an arithmetic was described for calculations with sets of numbers was published by Young (1931). Then, Dweyer (1951), in the context of error control in numerical analysis, focused his attention to the case of closed intervals referring to them as range numbers. Another important contribution was given in 1958 by the Japanese scientist Sunaga (Alefeld and Mayer, 2000). In his paper, Sunaga (1958) described the algebraic rules for the basic operations with intervals together with a systematic investigation of the properties

(21)

which they satisfy. Moreover, he introduced interval vectors as multidimensional intervals, discussing also the corresponding operations and focused his attention on the general principle of bounding the range of a rational function over an interval by using only the endpoints via interval arithmetic evaluation. However, the first nontrivial applications of interval analysis can be found in works by Moore and co-workers. Indeed, Moore and Yang (1959) and successively Moore (1962) analysed the initial value problem for ordinary differential equations in the context of the interval analysis. In the same works, the implementation of the interval arithmetic on digital computers was also discussed. In 1966, Moore collected and expanded his works and wrote the first monograph entirely devoted to interval analysis (Moore, 1966). In 2009, together with Kearfott and Cloud, Moore (Moore et al., 2009) revisited and extended his first monography including new trends in the context of interval analysis (Moore et al., 2009). In the same book, many numerical examples are carried out by using INTLAB (INTerval LABoratory), which is a MATLAB toolbox for reliable computing capable of performing interval calculations developed by Rump and his research group (Rump, 1999).

This chapter is organized as follows: in Section 2.2 an introduction of the Classical

Interval Analysis (CIA), mainly based on the book of Moore et al. (2009), is

presented. In the same section the dependency phenomenon is also discussed. The latter is the main drawback related to the use of the CIA, which generally leads to an overestimation of interval results, making them not useful from a practical engineering point of view. In Section 2.3, systems of linear interval equations and their solution are discussed, while different strategies able to mitigate the effects of the dependency phenomenon are presented in Section 2.4. Section 2.5 focuses on the use of the interval analysis as a tool to solve structural engineering problems.

(22)

2.2 Fundamentals of Interval Analysis

2.2.1 Interval variable definition

The set of all closed real interval numbers, herein indicated with , represents a

closed and connected subset of real numbers , such that a real interval variable

[ ]

, I x = x x _{∈ }_{ is defined by:}

[ ]

,

{

| ,

}

I x ≡ x x = x x x x x≤ ≤ _{∈ } (2.2)

where the superscript I, denotes interval variables, while

{

x P x denotes “ the set |

( )

}

of x such that the proposition P x

( )

holds”. Moreover in Eq. (2.2), the lower bound

(LB), x, and the upper bound (UB), x, of the interval _xI_{are real numbers. The}

bounds xand x of a generic interval variable _{x must satisfy the following}I

inequalities , , . x x x x ≤ > −∞ < +∞ (2.3)

The interval variable _xI ₌

[ ]

_{x x}, _{is said to be positive,} _{x >}I ₀_{, if}_x_{> ∀ ∈}₀ _{x x}I_{, or}

alternatively if x >0; while, it is said to be negative, _{x <}I 0_{, if} _x_{< ∀ ∈}₀ _{x x}I_or

alternatively if x <0.

2.2.2 Basic notation

A real interval variable _xI ₌

[ ]

_{x x}, _{can be alternatively represented in the following}

form:

{ }

mid

I I I

x = x + ∆x e (2.4)

where mid • is an operator which provides the midpoint of the interval quantity

{ }

enclosed by the curly brackets, defined as:

{ }

mid

mid ,

2

I x x

(23)

while ∆xis the deviation amplitude or radius of the interval _xI ₌

[ ]

_{x x}, _{, defined as:}

2

x x x −

∆ = (2.6)

and _eI _

[

_{− +}1, 1

]

_{is the Classical Unitary Interval (CUI), which is basically an}

interval whose LB and UB are equal to -1 and +1, respectively.

By introducing the operator w • , which provides the width of the interval, defined

{ }

as the absolute value of the difference between the UB and the LB of the interval quantity enclosed by the curly brackets, i.e.:

{ }

I ,

w x = −x x (2.7)

Eq. (2.4) can be rewritten as:

{ }

mid mid 1₂ , 1₂ mid 1₂ .

I I I I I I

x =x + ∆x e =x + −_ w x + w x _=x + w x e

  (2.8)

By inspection of Eq. (2.8), it appears that if _{w x =}

{ }

I 0_{, then, the LB,} _x_{, of the}

interval variable _xI_{, is equal to its UB,} _x_{. It follows that the interval contains a}

single real number and it is said to be degenerate or thin. The definition of

degenerate intervals allows us to consider the set of closed intervals,, as an

extension of the real number set . Indeed, real numbers can be viewed as

degenerate intervals, that is

[ ]

x x, ⇔

{

x x_{∈ }

}

. (2.9)

Moreover, the absolute value or modulus of an interval variable _xI_{, indicated as} _xI

is the maximum of the absolute values of its endpoints:

{

}

max ,

I

x = x x (2.10)

(24)

In order to clarify the meaning of the quantities introduced so far, the absolute value,

I

x , the width, _{w x , the midpoint,}

{ }

I _mid

{ }

_{x , and the radius,}I _∆_x_{, of the interval} I

x are shown in Figure 2-2.

Figure 2-2. Absolute value, width, midpoint and radius of the interval _xI_.

If the endpoints of two intervals _xI ₌

[ ]

_{x x}, _and_yI __{y y}_, _

=   are equal, it is said that

the two intervals are equal, i.e., they represent the same set:

if and .

I I

x = y x y= x y= (2.11)

An important typology of interval variables is the symmetric one. The interval

variable _xI_{is symmetric if:}

,

x= −x (2.12)

therefore, mid

{ }

_{x =}I 0_{. Considering Eq. (2.4) and Eq. (2.8), any symmetric interval}

variable _xI_{can be expressed as:}

{ }

[

]

{ }

1 _1,1 1 _.

2 2

I I I I I

x = w x − = w x e = ∆xe (2.13) As known, the real numbers are ordered by the relation “<”. The same relation “<” can be used for ordering interval variables with the inequality:

I I

(25)

meaning that x y< . For instance, let us assume that _{x =}I [0,1]_and _{y =}I _[2,3]_{, then}

we can write, _xI _< _yI_{, i.e.}_{[0,1] [2,3]}_< _{, since x y}_< _{. Moreover, given three real}

numbers a b c ∈, , , the relation “<” is said to be transitive if:

and < .

a b< b c a c⇒ < (2.15)

Analogously, given three interval variables , ,_{a b c ∈ }I I I _{ , the relation “<” is said to}

be transitive if:

and < .

I I I I I I

a <b b c ⇒a <c (2.16)

Besides, in the context of intervals, another transitive order relation, called set

inclusion, can be defined:

and .

I I

x ⊆ y ⇔ ≤y x x y≤ (2.17)

Given two intervals, _xI ₌

[ ]

_{x x}, _and _yI __{y y}_, _

=  , we can define their intersection,

union and interval hull.

The intersection of two interval variables _{x and}I _{y which do not have any common}I

point, that is if either y x< or x y< , is empty and by denoting with ∅ the empty

set, it can be written as:

.

I I

x ∩y = ∅ (2.18)

Moreover, when Eq. (2.18) holds the two interval variables, _xI_and_yI_{are said to be}

disjoint.

Otherwise, the intersection of two intervals, _xI _∩ _yI_{, is defined as the interval:}

{

| and |

}

max , ,min ,

{ }

.

I I I I

x _∩y ₌ z z x_∈ z z y_∈ _{= } x y x y 

 (2.19)

The union between two intervals _xI _∪ _yI_{, which in the general case is not an}

interval, is defined as:

{

| or |

}

.

I I I I

(26)

In the particular case where the intersection among two intervals is not empty,

I I

x ∩y ≠ ∅ , using the definition in Eq. (2.20) the union between _xI_and _{y is the}I

interval obtained as follows:

{

| or |

}

min , ,max ,

{ }

.

I I I I

x _∪y ₌ z z x_∈ z z y_∈ _{= } x y x y _ _(2.21)

The interval hull of two intervals, _xI _∪_yI_{, is always an interval defined as:}

{ }

min , ,max ,

I I

x ∪y _{= } x y x y _ (2.22)

Moreover, it can be observed that, for any two intervals, the result provided by the union is either equal or included within the interval hull, i.e.:

.

I I I I

x ∪y ⊆ ∪x y (2.23)

To clarify the concept of intersection, union and interval hull, let us first consider

two interval variables, namely _xI ₌

[ ]

3,9 ,_yI ₌

[

7,11

]

_{. Since} _xI_and _{y have}I

common points (i.e. _xI _∩_yI _{≠ ∅}_{), by taking into account Eq. (2.19), Eq. (2.21) and}

Eq. (2.22) it follows:

{ }

[

]

{ }

[

]

{ }

[

]

max 3,7 ,min 9,11 7,11 , min 3,7 ,max 9,11 3,11 , min 3,7 ,max 9,11 3,11 . I I I I I I x y x y x y ∩ =_ _= ∪ =_ _= ∪ =_ _= (2.24)

By inspection of Eq. (2.24), it can be noticed that _xI _∪_yI ₌_xI _∪_yI_{as the}

consequence that _xI _∩_yI _{≠ ∅}_{. Now, let us consider}_{x =}I

[ ]

_2,5 _and _{y =}I

[

_0.2,1

]

_{. In}

this case, _xI_and_yI_{do not have common points, therefore:}

{

}

[ ] [

]

{

}

{ }

[

]

, | or | 2,5 0.2,1 , min 2,0.2 ,max 5,1 0.2,5 . I I I I I I I I x y x y z z x z z y x y ∩ = ∅ ∪ = ∈ ∈ = ∪ ∪ =_ _= (2.25)

Eq. (2.25) shows that the union _xI _∪_yI_{is not represented by an interval, instead, it}

(27)

[ ] [

]

(

2,5 ∪ 0.2,1

)

⊆

[

0.2,5

]

(2.26)

2.2.3 Basic operations of Interval Arithmetic

For the set of interval variables , in analogy to the set of real numbers , the

elementary arithmetic operations can be defined. Let us consider two intervals,

[ ]

,

I

x = x x and _yI _{= }__{y y}, _

 ∈  . A generic elementary arithmetic operation

{

, , , /

}

∈Ω = + − ×

 between _xI_and_{y is defined as follows:}I

{

| ,

}

I I I I I I

x _y = x _y x x y y∈ ∈ (2.27)

with the assumption that 0_∉_yI_{in the case of division. Eq. (2.27) means that the}

resulting interval is a set which contains the results from the application of the considered numerical elementary arithmetic operation to all possible combinations of

the pairs of numbers, one belonging to _xI_{and the other one to} _{y . Based on Eq.}I

(2.27), it is possible to define the elementary operations between two interval variables by using their endpoints. Let us start considering the addition between two interval variables _xI _and_yI _{∈ }_ _{, such that}

I x x∈ ⇒ ≤ ≤x x x (2.28) and: . I y y∈ ⇒ ≤ ≤y y y (2.29)

Carrying out the addition between the previous inequalities, it follows that the

numerical sum _{x y x}_{+ ∈ +}I _yI_{must satisfy the relationship:}

x y x y x y+ ≤ + ≤ + (2.30)

Therefore, in terms of intervals:

, .

I I

x +y =_x y x y+ + _ (2.31)

(28)

Analysis of structural systems with interval uncertainties under deterministic and stochastic excitations ( ) I I I I x −y =x + −y (2.32) where: I y y∈ ⇒ ≤ ≤ ⇒ − ≤ − ≤ −y y y y y y (2.33)

Considering Eq. (2.28) and Eq. (2.33), it follows that: .

x y x y x y− ≤ − ≤ − (2.34)

Hence, in terms of intervals:

, .

I I

x −y =_x y x y− − _ (2.35)

The multiplication of two intervals _{x y}I_× I_{is given in terms of the minimum and}

maximum of four products of endpoints. Basing on the signs of the endpoints, x,

x,yand y , the formula for the interval product by exploiting the endpoints can be

particularized into nine special cases (Moore et al., 2009) reported in Table 2-1.

Table 2-1 Endpoint formulas for the interval multiplication.

Case x y× _{x y}_× 0≤x and 0≤y x y× x y× 0 and 0 x< < x ≤ y x y× x y× 0 and 0 x ≤ ≤ y x y× x y× 0≤ x and y< <0 y x y× x y× 0 and 0 x ≤ y< < y _{x y}× x y× 0≤x and y ≤0 x y× x y× 0 and 0 x< < x y≤ x y× x y× 0 and 0 x ≤ y≤ x y× x y× 0 and 0 x< <x y< < y _min

{

_{x y x y}_× _, _×

}

_max

{

_{x y x y}_× _, _×

}

(29)

Generalising the concept of division between real numbers, the interval division xI_I

y

can be written as the following product:

1 . I I I I x _x y = × y (2.36)

where, considering Eq. (2.29):

1 1 I 1 1_, _{if 0} I_. I y y y y y y y     = ∈ =  ∉   _ _ (2.37)

By using the endpoints of the intervals _xI_and _{y , the four elementary arithmetic}I

operations can be expressed as (Moore et al., 2009):

(

)

(

)

[

]

, ; , ; min , , , ,max , , , ; 1 1 , , if 0 . I I I I I I I I I x y x y x y x y x y x y x y xy xy xy xy xy xy xy xy x _{x x} _y y y y   + =_ + + _   − =_ − − _   × _{= } _   = ×  ∉     (2.38)

2.2.4 Algebraic properties

Since in the context of interval evaluations, it is implicit that interval variables are independent one from each other, the algebraic rules that hold for real numbers do not always hold for interval variables. Often, they just hold in a weaker form. Let us

consider three interval variables, _{x y z}I, ,I I_{. As in the context of real numbers, the}

interval addition, as well as the interval multiplication, is commutative, i.e.: ; . I I I I I I I I x y y x x y y x + = + × = × (2.39)

and associative, i.e.:

(

) (

)

;

I I I I I I

x + y +z = x +y +z

(30)

In the system of intervals, the degenerate intervals

[ ]

0,0 0= and

[ ]

1,1 1= are additive

and multiplicative identity elements, indeed, for any _{x ∈ }I _{ the following relations}

hold true: 0 0 , 1 1 , 0 0. I I I I I I I I x x x x x x x x + = + = × = × = × = × (2.41)

It can be noticed that, in the interval algebra, if we subtract the interval variable _xI

to itself:

( )

[ ] [

, ,

] [

,

]

,

I I

x + −x = x x + − − =x x x x x x− − (2.42)

it is equal to

[ ]

0,0 0= only if x x= , or, in other words, if the interval _{x is}I

degenerate (i.e. it represents a real number) since its width _{w x =}

{ }

I 0_{. Otherwise, if}

{ }

I 0

w x ≠ , according to Eq. (2.42):

( ) { }

[

1,1 .

]

I I I

x + −x =w x × − (2.43)

Similarly, if we divide the interval variable _xI _{by itself, the degenerate interval}

[ ]

1,1 1= is obtained only when_{w x =}

{ }

I 0_{. Otherwise, if}_{w x ≠}

{ }

I ₀_:

, if 0< , , if 0. I I x x _x x x x x _{x x} x x x          =     _<       (2.44)

The additive inverse, i.e. the difference between an interval variable and itself, as well as the multiplicative inverse, i.e. the multiplication between an interval variable not including the zero and its reciprocal, exists only for degenerate intervals (i.e. to

real numbers). However, in the system of intervals, the inclusions 0_{∈ −}_xI _xI_and

1 xI_I

x

(31)

Considering three real numbers , ,x y z∈ , the full distributive law of ordinary

arithmetic:

(

)

x y z+ =xy xz+ (2.45)

does not hold for the system of intervals. In order to prove it, let us consider the following three interval variables, _{x =}I

[ ]

1,2 _,_{y =}I

[ ]

_1,1 _and_{z = −}I

[ ]

_1,1 _.

The quantity _xI_×

(

_yI ₊_zI

)

_{is equal to}

[ ]

_{0,0 :}

(

)

[ ] [ ] [ ]

1,2

(

1,1 1,1

)

[ ] [ ] [ ]

1,2 0,0 0,0 ,

I I I

x × y +z = × − = × = (2.46)

whereas, the quantity _{x y}I_× I _{+ ×}_{x z}I I_{is equal to}

[

₋_1,1

]

_:

[ ] [ ] [ ] [ ]

( )

[ ] [ ] [

]

1,2 1,1 1,2 1,1

min 1,2 ,max 1,2 min 1,2 ,max 1,2

1,2 1,2 1,1 . I I I I x y× + ×x z = × − × =_  _{ }− _ = − = − (2.47) The comparison between Eq. (2.46) and Eq. (2.47) leads to:

(

)

.

I I I I I I I

x × y +z ≠x y× + ×x z (2.48)

However, in the system of intervals the subdistributive law holds:

(

)

I I I I I I I

x × y +z ⊆x y× + ×x z (2.49)

Indeed, considering the previous example

[ ] [

0,0 ⊆ −1,1

]

.

The full distributive law holds in the interval algebra only in a few special cases:

a) when a real number a ∈ multiplies the sum of two interval variables, i.e.

for any a ∈:

(

I I

)

I I

a y +z =ay +az (2.50)

b) for any interval variable _{x y z ∈ }I, ,I I _{ , involved in the expression}

(

)

I I I

(32)

(

)

.

I I I I I I I

x × y +z =x y× + ×x z (2.51)

It is noteworthy that in the context of interval algebra, the cancellation law holds only for the interval addition:

.

I I I I I I

x +z = y +z ⇒x = y (2.52)

Considering three symmetric intervals, _xI_, _{y and}I _{z , the interval operations}I

defined in Eq. (2.38), can be expressed in a simpler form:

(

)

, . I I I I I I I I I I I I x y x y x y e x y x y e + = − = + × = (2.53)

Moreover, the distribution of the interval multiplication over a sum can be expressed as:

(

)

(

)

I I I I I I I I I I I

x × y ±z = × − × =x y x z x y + z e (2.54)

where, • is the absolute value of an interval variable (see Eq.(2.10)) and _eI_{is the}

CUI (see Section 2.2.2).

If _xI_{is a generic interval, while}_{y is a symmetric one, then}I

.

I I I I

x y = x y (2.55)

It follows that considering a generic interval _xI_{and two symmetric intervals}_yI_and

I

z , the subdistributive law defined in Eq. (2.49) holds as equality:

(

)

I I I I I I I

x y +z =x y +x z (2.56)

2.2.5 Interval functions

Let us consider a real-valued function f of a single variable x . The range of values

assumed byf x as the argument x varies through a specified interval

( )

_xI_{is given}

(33)

( )

I

{

( )

| I

}

.

f x = f x x x∈ (2.57)

In other words, Eq. (2.57) provides the image of the set _xI _{under the mapping}_f _.

More generally, considering a multivariable function f x

(

1,...,xn

)

, where each of the

variables

(

x1,...,xn

)

varies through the associate intervals

(

x1I,...,x , the image set is nI

)

given by:

(

1I,..., nI

)

{

(

1,...., n

)

| 1 1I,...., n nI

}

.

f x x = f x x x x∈ x ∈x (2.58)

Let us consider the case in which f x is a monotonic function. If

( )

f x is an

( )

increasing monotonic function with increasing x , then it maps an interval _{x into}I

the interval:

( )

I

( ) ( )

, ,

f x = _f x f x _ (2.59)

while, if f x is a decreasing monotonic function with increasing x , then it maps

( )

an interval _xI_{into the interval:}

( )

I

( ) ( )

, .

f x = _f x f x _ (2.60) As a first example, let us consider the monotonically increasing function:

( )

log

( ) (

, 0 ;

)

f x = x x> (2.61)

applied to the interval _xI ₌

[ ]

_{x x}, _{. The function increases from} _{log x to}

( )

log x as x increases from x to x . As a result, the image set can be defined as:

( )

log _xI _{= }log _x ,log _x _.

  (2.62)

Instead, considering the monotonically decreasing function

( )

log 1 ,

(

0 ;

)

f x x x   = _{ } >   (2.63)

(34)

which decreases from log 1

x       to 1 log x    

  as x increases from x to x , the image

set is given by:

1 1 1

log _I log ,log .

x x x        =                (2.64)

As Eq. (2.64) shows, in the case of monotonically decreasing functions it is

important to correctly identify the LB and UB of the interval _xI_{in the evaluation of}

( )

I

f x .

As a second example let us consider the function:

( )

sin

( )

with .

f x = x x_{∈ } (2.65)

The function in Eq. (2.65), in general, is non-monotonic. However, its restriction f _A

to the set , 2 2 I A = −_ π +π_   is increasing, thus:

( )

sin _xI ₌_sin _x ,sin _x _|_xI _⊆_AI

  (2.66)

In the evaluation of the image set of a non-monotonic function _{f x}

( )

I _{, the considered}

range of values is a crucial point and needs to be dealt with before doing the

evaluation of the function. In particular, the image set _{f x}

( )

I _{can be obtained}

considering the endpoints of the interval _xI ₌

[ ]

_{x x}, _{together with the so-called}

critical points. The critical points within the interval _xI_{are those points where the}

monotonicity of the function changes direction. As an example, for the sine function

in Eq.(2.65), the critical points are at 1

2 n π

 ₊ 

 

  with n∈ (being  the set of all

integer numbers), whose function value can be only −1 or 1.

2.2.6 Dependency phenomenon

The Interval Analysis mainly based on the book of Moore et al. (2009), known as

(35)

applications since it suffers from the so-called dependency phenomenon. This phenomenon, often causes a strong overestimation of the range of the interval quantity of interest, thus leading to very conservative results pointless for engineering applications. The dependency phenomenon occurs because according to

CIA when multiple occurrences of the same intervals are involved within an

expression, they are considered as independent variables which vary within the same

range. As an example, let us consider the interval _xI ₌

[ ]

_{a b}, _{and to apply the CIA to}

the subtraction of the variable _xI_{to itself, i.e.:}

[

,

]

.

I I

x −x = a b b a− − (2.67) Since the two given intervals denote the same ideal quantity, the exact result is the

interval

[ ]

0,0 . However, since the CIA treats the two given intervals as independent,

its use provides, as a result, an interval (see Eq. (2.67)) much wider than the exact

solution. More generally, if the arguments of an interval operation _zI ₌ _{f x y}

(

I, I

)

are somewhat related, the interval result I

CIA

z obtained through the CIA may be

significantly wider than the exact one. Let us define the CIA overestimation factor σ

of an interval operation as the width of the interval I

CIA

z computed by using the CIA

divided by the width of the exact range of z, I

Exact z , i.e.:

{ }

. I CIA I Exact w z w z σ = (2.68)

As reported by Stolfi and De Figueiredo (2003), the overestimation factor σ

depends on the amount and the sign of correlation, on the derivative of the operation

f , but it is roughly independent of the width of the operands. In order to show the

low dependency of the overestimation factor from the width of the intervals involved in the operation, let us apply the rules of the CIA to evaluate the following expression (Stolfi and De Figueiredo, 2003)

(

10

)

I I I

(36)

considering two different values of the interval _xI_{, say}

[ ]

1I 3,5

x = and

[

]

2I 3.9,4.1

x = . As the results in Table 2-2 show, although the width of the interval

2I

x is much smaller than the one of _x₁I_{, the respective overestimation factors}_σ_are

the same; in both cases, the results provided by the CIA are intervals five times wider than the respective exact solutions.

Table 2-2 Solution of Eq. (2.69) for two values of the interval variable_xI I x _{w x}

{ }

I I CIA z

{ }

I CIA w z I Exact z

{ }

I Exact w z σ

[ ]

1I 3,5 x = 2

[

15,35

]

20

_[

21,25

_]

4 5

[

]

2I 3.9,4.1 x = 0.1

[

23.01,25.01

]

2

[

23.79,24.19

]

0.4 5

Another interesting example where is possible to notice the effects of the dependency phenomenon, is the evaluation of the following expression (Moore et al., 2009):

( ) ( )

2

.

I I

f x = x (2.70)

The solution set is

( ) {

I 2_| I

}

f x = x x x∈ (2.71) which can be expressed as

( )

{

}

2 2 2 2 2 2 , , 0 , , , 0, 0,max , , 0 . I x x x x f x x x x x x x x x _ _ < <    =_ _ ≤ ≤    < <    (2.72)

Assuming _{x = −}I

[

1,1

]

_{, Eq. (2.72) leads to:}

( ) ( )

2

[ ]

0,1 .

I I

f x = x = (2.73)

By following the rules of the CIA, the square of _xI _{can be expressed by the}

(37)

( )

2

[

] [

]

1,1 1,1 1,1 .

I I I

x =x x× = − × − = − (2.74)

However, the direct comparison between Eq. (2.73) and Eq. (2.74), shows that, in the context of the CIA, the definition of

( )

_{x is not the same as the one of}I 2 _{x x}I_× I_.

Moreover, it can be observed that the solution provided by the CIA encloses the correct solution:

[ ] [

0,1 ⊆ −1,1 .

]

(2.75)

Also in this case, the overestimation of the interval solution when

( )

_xI 2_{is computed}

as _{x x}I _× I_{is due to the dependency phenomenon. Indeed, in the interval product}

I I

x x× evaluated by using the CIA, the interval variables involved in the operation

are treated as independent. In other words, when we form the product _{x x}I _× I_{, it is}

assumed that the values in the second factor and the first factor vary independently, although the exact solution is given when the two factors vary at the same time since they represent the same quantity.

2.3 System of linear interval equations

2.3.1 Interval vectors

An interval vector _xI _∈_{ is an ordered n-tuple of intervals:}_n

1, ,...,2 T I I I I n x x x   =   x (2.76)

where the apex “T” means transpose, while __n_{denotes the set containing the}

interval vectors of order n . With appropriate modifications, most of notations used for ordinary intervals can be extended to interval vectors, i.e.:

• considering the case in which

[

1, ,...,2

]

T _n n

x x x

= ∈

x  is a real vector and

1, ,...,2 I I I I T n n x x x   =_ _ ∈

x  is an interval vector then it is possible to write:

; 1,2,...,

I _{x x i}I _n

∈ ⇔ ∈ =

(38)

• considering two interval vectors, I ₁I, ,...,₂I I T

n x x x   =   x and 1, ,...,2 I I I I T n y y y   =  

y , their intersection is empty if the intersection of any of

their corresponding components is empty; i.e. if I I

i i

x ∩y = ∅ for some i, then

I _∩ I _{= ∅}

x y . Otherwise, the intersection between two interval vectors is

defined as the following vector:

1 1, 2 2,..., . T I I I I I I I I n n x y x y x y   ∩ =_ ∩ ∩ ∩ _ x y (2.78)

• if xI = x x1I, ,...,2I xnITand yI = y y1I, ,...,2I ynIT are two interval vectors, then

it is possible to write: , 1,2,..., . I I I I i i x y i n ⊆ ⇔ ⊆ = x y (2.79)

The concepts of width, midpoint and absolute value defined for interval variables, can be extended to interval vectors as follows.

•_{the width of an interval vector}_w

{ }

_xI _{, where}

1, ,...,2 I I I I n x x x   =   x , is defined

as the operator which provides the largest of the widths of any of the

component intervals belonging to _{x :}I

{ }

I max

{ }

I .

i i

w _x = w x (2.80)

• the midpoint of an interval vector mid

{ }

_xI _{is an operator which provide a}

real number vector defined as:

{ }

1

{ }

2

{ }

mid I mid I ,mid I ,...,mid I T

i

x x x

 

=  

x (2.81)

•_{the norm of an interval vector} I ₁I, ,...,₂I I T

n

x x x

 

=  

x (which is a generalization

of the absolute value defined for interval variables) is:

max . I I i i x = x (2.82)

(39)

In order to clarify the meaning of width, midpoint and norm of an interval vector, let us consider a two-dimensional vector I ₌__{x x}₁I, ₂I_T _

[

_{x x}₁, , ,₁

] [

_{x x}₂ ₂

]

_T

=  

 

x . As shown

in Figure 2-3, such a vector is graphically represented by a rectangle in the x x _{1 2}

plane.

Figure 2-3 Width, norm and midpoint of a two-dimensional interval vector _xI_.

Considering two interval vectors, 1, , ,2

T I I I n u u u   =   u  and 1, , ,2 T I I I n v v v   =   v  , their

addition and inner product are respectively given by:

( )

1 1 2 2 1 1 2 2 , , , , , , . T I I I I I I I I n n T I I I I I I I I n n u v u v u v u v u v u v   ± =_ ± ± ± _ × = + u v u v   (2.83)