1 Coordinate di Fenchel-Nielsen complesse 4
1.1 Geometria di H3 e notazione . . . . 4
1.2 Distanza complessa . . . 4
1.3 Esagoni retti . . . 6
1.4 Alcuni fatti sulle rappresentazioni . . . 8
1.5 Strutture quasifuchsiane . . . 10
1.6 Parametri di mezza lunghezza . . . 11
1.7 Parametri di bending . . . 11
1.8 Condizioni per la fedelt`a delle rappresentazioni . . . 13
2 Rappresentazioni di π1(Π0) 15 2.1 Pantaloni etichettati . . . 15
2.2 Costruzione di una superficie data un’etichettatura . . . 17
2.3 Il fibrato normale unitario di una geodetica γ ∈ Γ . . . 17
2.4 Trasporto di misure . . . 20
2.5 Misure su skew pants e l’operatore ˆ∂ . . . 22
3 Misure su skew pants e il flusso geodetico 26 3.1 Funzione affinit`a . . . 26
3.2 Geometria dei bipodi ben connessi . . . 29
3.3 Geometria dei tripodi ben connessi . . . 30
3.4 L’operatore ˜∂ . . . 33
3.5 Dimostrazione del teorema 2.5.4 . . . 36
La dimostrazione della congettura di geometrizzazione di Thurston ha fornito un potentissimo strumento per lo studio delle 3-variet`a. In particolare ora sembra pos-sibile la risoluzione di una congettura detta di Haken virtuale. Tale congettura afferma che ogni 3-variet`a compatta, orientabile, irriducibile, con gruppo fondamen-tale infinito ha un rivestimento finito che contiene una superficie incompressibile1.
Assumendo la congettura di geometrizzazione di Thurston, la congettura di Haken virtuale rimane aperta solo per le 3-variet`a iperboliche.
Lo scopo di questa tesi `e ripercorrere i passi fatti da Jeremy Kahn e Vladimir Markovic nella risoluzione della congettura del sottogruppo di superficie. Tale con-gettura, formulata da Friedhelm Waldhausen, afferma che il gruppo fondamentale di ogni 3-variet`a iperbolica chiusa contiene un sottogruppo isomorfo al gruppo fon-damentale di una superficie diversa dalla 2-sfera. Questo sembra essere un risultato che pu`o portare alla risoluzione della congettura di Haken virtuale.
Nel capitolo 1 verranno introdotte le coordinate di Fenchel-Nielsen complesse per le rappresentazioni del gruppo fondamentale di una superficie S0 negli elementi
lossodromici di PSL(2, C) (tali coordinate sono un’estensione delle coordinate di Fenchel-Nielsen per lo spazio di Teichm¨uller).
Fissata una 3-variet`a iperbolica chiusa M3 = H3/G, dove G `e un gruppo
Klei-niano, e data una superficie S0 con una decomposizione in pantaloni C, `e dato il
seguente teorema, che sar`a enunciato in maniera pi`u precisa dopo le premesse fatte nel capitolo 1:
1Una superficie immersa i : S ,→ M si dice incompressibile se `e diversa dalla 2-sfera e se
i∗: π1(S) → π1(M ) `e iniettiva
Teorema 0.0.1. Siaε > 0. Supponiamo che una rappresentazione ρ : π1(S0) −→ G
soddisfi, per ogniC ∈ C e per qualche R > R(ε) > 0, le seguenti diseguaglianze: |hl(C) − R2 |< ε
|s(C) − 1| < ε R
dove hl(C) e s(C) sono i parametri di Fenchel-Nielsen complessi, detti rispettiva-mente di mezza lunghezza e bending. Si ha allora cheρ `e iniettiva.
Notiamo che data tale ρ, `e possibile costruire f : S0 −→ M3 che sia localmente
(1 + K(ε))-quasigeodetica, per qualche K(ε) > 0 e tale che f? = ρ.
Nel capitolo 2 saranno studiate le rappresentazioni ρ : π1(Π0) −→ G a meno di
coniugio in G (dette skew pants), dove Π0 `e un paio di pantaloni topologico. Dato
un insieme finito di skew pants L e un’involuzione σ : L −→ L sar`a mostrato come costruire una superficie S0 e una rappresentazione ρ
L,σ : π1(S0) −→ G. Saranno
date poi delle condizioni su L e σ affinch´e ρ soddisfi le ipotesi del teorema 0.0.1. Successivamente verr`a mostrato come costruire L e σ a partire da una misura µ a supporto finito nello spazio degli skew pants. Saranno dunque date delle condizioni sufficienti su µ per ottenere L e σ con le propriet`a richieste.
Infine, nel capitolo 3, verr`a costruita una tale µ grazie alla propriet`a di mixing esponenziale del flusso geodetico.
Coordinate di Fenchel-Nielsen
complesse
1.1
Geometria di H
3e notazione
Con H3 indicheremo lo spazio iperbolico, ovvero l’unica variet`a riemanniana
sem-plicemente connessa, completa, con curvatura gaussiana costante pari a −1. Iden-tificheremo il bordo geometrico di H3 con la sfera di Riemann ˆ
C. Detta γ(t), t∈ R una geodetica orientata diremo che γ = (u, v) dove u e v sono punti distinti di ˆC ottenuti facendo tendere t rispettivamente a −∞ e +∞.
Avremo inoltre bisogno di indicare particolari sottoinsiemi di C: • C+ = {z ∈ C, Re(z) > 0}
• C++ = C+∪ {it, t ≥ 0}
• Σ = {w ∈ C, −π < Im(w) ≤ π} ∩ C++
Inoltre, con r, s, t indicheremo una qualsiasi permutazione ciclica di 1, 2, 3
1.2
Distanza complessa
Definizione 1.2.1. Date a1, a2due geodetiche orientate e β una loro perpendicolare
comune (orientata), sia B l’isometria che preserva l’orientazione tale che B(β) = 4
(0, ∞). Allora B(a1) = (−u, u) e B(a2) = (−p, p) La distanza complessa tra la
coppia ordinata di geodetiche (a1, a2) lungo la perpendicolare β `e σ(a1, β, a2) ∈ C
mod 2πiZ, ed `e tale che
eσ(a1,β,a2)u = p
Lemma 1.2.2. σ(α, β, γ) `e invariante per isometrie che preservano l’orientazione e valgono inoltre le seguenti propriet`a in C 2πiZ:
• σ(α, β, γ) = −σ(γ, β, α) • σ(α, β, γ) = −σ(α, −β, γ) • σ(α, β, γ) = σ(−α, β, γ) + iπ
Lemma 1.2.3. Dati due geodetiche orientate perpendicolari α e c in H3 e λ ∈
C 2πiZ, esiste un’unica geodetica orientata β tale che λ = σ(α, c, β)
Dimostrazione. A meno di coniugio possiamo supporre che α = (−1, 1) e c = (0, ∞). Allora β = (−eλ, eλ)
Date due geodetiche con supporto distinto a1, a2 in H3 esiste ed `e unica la
geo-detica non orientata β perpendicolare comune ad a1, a2. Diamo di seguito un modo
canonico di assegnare un’orientazione alla perpendicolare tra due geodetiche: Definizione 1.2.4. La perpendicolare canonica tra le geodetiche orientate con sup-porto distinto a1, a2 `e κa1a2 ed `e l’unica geodetica orientata tale che σ(a1, κa1a2, a2)
abbia un rappresentante mod 2πiZ in Σ
Osservazione 1.2.5. Notiamo che se a1 e a2 non hanno punti di intersezione
l’orientazione di κa1a2 `e scelta in modo che a1∩ κa1a2 venga prima di a2∩ κa1a2
Definizione 1.2.6. Con σ(a1, a2) indicheremo σ(a1, κa1a2, a2)
Definizione 1.2.7. Siano u, v, p, q quattro punti distinti in ˆC. Il birapporto `e [u, p, q, v] = (u−q)(p−v)
(u−p)(q−v)
Il birapporto `e invariante per trasformazioni in SL(2, C). Si ottiene poi questo risultato:
Proposizione 1.2.8. Siano α = (u, v) e β = (p, q) due geodetiche orientate in H3.
Allora vale:
cosh σ(α, β) = [u,p,q,v]+1 [u,p,q,v]−1
1.3
Esagoni retti
Definizione 1.3.1. Un esagono retto `e il dato di 6 geodetiche orientate {a1, a2, a3, c1, c2, c3}
tali che cr sia perpendicolare a as e at
Date 3 geodetiche orientate a1, a2, a3, queste determinano in modo canonico
l’esagono retto {a1, a2, a3, κa2a3, κa3a1, κa1a2}
Definizione 1.3.2. Un esagono retto {a1, a2, a3, c1, c2, c3} `e positivamente orientato
se ct= κaras e at= κcrcs
Proposizione 1.3.3. Regola del coseno iperbolico: Sia {a1, a2, a3, c1, c2, c3} un esagono retto. Allora:
cosh σ(c2, a1, c3) sinh σ(a3, c2, a2) sinh σ(a1, c3, a2) =
cosh σ(a2, c1, a3) − cosh σ(a3, c2, a1) cosh σ(a1, c3, a2)
Dimostrazione. Notiamo innanzitutto che entrambi i membri dell’equazione non di-pendono dall’orientazione dei ci, quindi possiamo supporre che l’esagono sia
positiva-mente orientato. Inoltre, a meno di isometrie supponiamo a1 = (0, ∞), a2 = (u, v),
a3 = (p, q). Allora, per la proposizione 1.2.8:
cosh σ(a2, c1, a3) − cosh σ(a3, c2, a1) cosh σ(a1, c3, a2) = (v−u)(q−p)−2(uv+pq)
Se c2 = (−t, t) abbiamo che t2 = pq e sinh σ(a3, c2, a1) = q−p−2t. Analogamente,
se c3 = (−s, s) abbiamo che s2= uv e sinh σ(a1, c3, a2) = v−u2s . Si ricava inoltre che
cosh σ(c2, a1, c3) = s
2+t2
2st (da prop 1.2.8). Allora:
Enuniciamo ora un’altra relazione riguardante gli esagoni retti, che per`o non useremo nel resto della tesi:
Proposizione 1.3.4. Regola del seno iperbolico sinh σ(c1, a3, c2) sinh σ(a1, c3, a2) = sinh σ(c2, a1, c3) sinh σ(a2, c1, a3) = sinh σ(c3, a2, c1) sinh σ(a3, c2, a1)
Vediamo ora come date 3 distanze complesse queste possano determinare a meno di coniugio un esagono retto:
Proposizione 1.3.5. Dati λ1, λ2, λ3 in Σ \ {0, iπ}, esiste una tripla (a1, a2, a3) di
geodetiche orientate che soddisfano
λr = σ(as, at)
Inoltre, ogni altra tripla di geodetiche orientate(x1, x2, x3) che soddisfi:
λr = σ(xs, xt)
`e congruente tramite un’isometria che preserva l’orientazione a
(a1, a2, a3) o (−a1,−a2,−a3)
Inoltre le triple(λ1, λ2, λ3), (λ1, λ2+iπ, λ3+iπ), (λ1+iπ, λ2, λ3+iπ) e (λ1+iπ, λ2+
iπ, λ3) determinano tutte la stessa tripla di geodetiche con orientazioni diverse. Tra
gli otto esagoni che si ottengono in questo modo (il modo canonico) esattamente uno `e positivamente orientato.
Dimostrazione. C’`e un unico µ1∈ Σ che soddisfa:
cosh(µ1) = cosh(λsinh(λ1)−cosh(λ2) sinh(λ2) cosh(λ3) 3)
Fissiamo a1 = (0, ∞) e γ2= (−1, 1). Allora γ3= (−eµ1, eµ1) `e l’unica geodetica tale
che σ(γ2, a1, γ3) = µ1. Per il lemma 1.2.3 esistono uniche geodetiche a2 e a3 tali che
σ(a1, γ3, a2) = λ3 e σ(a3, γ2, a1) = λ2. Rimane da verificare che λ1 = σ(a2, a3): si
a2 = (eµ1tanh(λ23), eµ1coth(λ23))
a3 = (−tanh(λ22), −coth(λ22))
cosh(σ(a2, a3)) =
[eµ1tanh(λ32 ),−tanh(λ22 ),−coth(λ22 ),eµ1coth(λ32 )]+1 [eµ1tanh(λ32 ),−tanh(λ22 ),−coth(λ22 ),eµ1coth(λ32 )]−1 =
cosh(λ2) cosh(λ3) + cosh(µ1) sinh(λ2) sinh(λ3) = cosh(λ1)
1.4
Alcuni fatti sulle rappresentazioni
Definizione 1.4.1. Un elemento c ∈ PSL(2, C) si dice lossodromico se tr(c)2 6∈
[0, 4], dove tr(c) ∈ C `e la traccia di c.
Le isometrie lossodromiche si possono anche caratterizzare come le isometriche che non hanno punti fissi in H3 e hanno esattamente 2 punti fissi in ˆ
C.
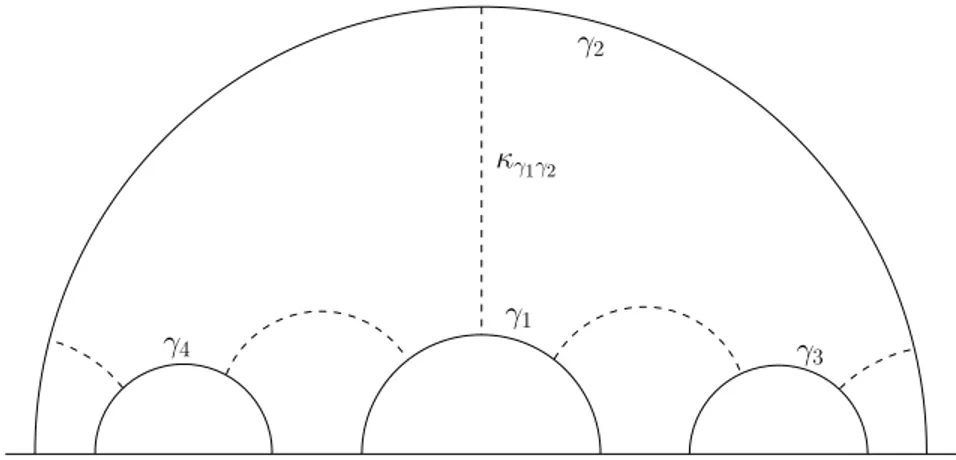
Definizione 1.4.2. Sia f un’isometria lossodromica di H3 e sia β una geodetica perpendicolare all’asse di f. L’asse orientato di f `e la geodetica orientata axis(f) = κβf (β). Il complex displacement `e l(f) = σ(β, f(β)).
Si verifica che l’asse orientato di un’isometria lossodromica `e la geodetica indi-viduata dai punti fissi dell’isometria in ˆC.
Proposizione 1.4.3. Sianoc1 ec2 due isometrie lossodromiche di H3. Supponiamo
che axis(c1) = axis(c2) e l(c1) = l(c2). Allora c1= c2.
Lemma 1.4.4. Siano c1, c2 ∈ PSL(2, C) lossodromiche senza punti fissi in comune
(in ˆC) e assumiamo che c2c1 e c1c2 siano lossodromiche. Siano γ1, γ2, γ3, γ4 gli
assi orientati di c1, c2, c3 = (c1c2)−1 e c4 = c2c1 rispettivamente. Allora si ha che
gli esagoni retti determinati da (γ1, γ2, γ3) e da (−γ1,−γ2, γ4) sono positivamente
orientati e la rotazione di π attorno a κγ1γ2 porta un esagono nell’altro.
Sia Π il gruppo con generatori c1, c2, c3 e relazioni c1c2c3 = id. Le
rappresen-tazioni del gruppo Π ci interesseranno particolarmente. Possiamo associare a una rappresentazione di Π dei parametri di mezza lunghezza:
γ1
γ2
γ3
γ4
κγ1γ2
Figura 1.1: situazione descritta nel lemma 1.4.4, nel modello del semispazio superiore per H3
Definizione 1.4.5. Sia ρ : Π −→ PSL(2, C) una rappresentazione. Siano a1, a2, a3
rispettivamente gli assi di ρ(c1), ρ(c2), ρ(c3) e sia {a1, a2, a3, γ1, γ2, γ3} l’esagono retto
individuato dai 3 assi. Si possono allora definire i parametri di mezza lunghezza: hlcr(ρ) = σ(γs, ar, γt) − iπ mod 2iπZ
Notiamo che tali parametri dipendono solo dalla classe di coniugio di ρ in PSL(2, C) Osservazione 1.4.6. Dal lemma 1.4.4 segue che 2hlci(ρ) = lci(ρ) = l(ρ(ci)) per
ogni i = 1, 2, 3.
Vediamo ora un risultato di unicit`a della rappresentazione assegnati i parametri di mezza lunghezza:
Proposizione 1.4.7. Per ogni λ = (λ1, λ2, λ3) ∈ (C+ 2πiZ)3 esiste un omomor-fismo φλ : Π −→ PSL(2, C) tale che hl(φλ(cr)) = λr mod 2πiZ. Se λ non soddisfa
ε1λ1 + ε2λ2 + ε3λ3 = πi mod 2πiZ per qualche εi ∈ {+1, −1} allora
l’omomorfi-smo `e unico a meno di coniugio in PSL(2, C). Inoltre, se coniughiamo φλ in modo
che axis(φλ)(c3) = (0, ∞) e il punto fisso repulsivo di φλ(c2) sia 1, allora, ponendo
Cj = cosh λj e Sj = sinh λj, si ha
φλ(c1) = S13 −C1
S3+ C1C3+ C2 −(C1+ C2C3− S2S3)(C3+ S3)
(C1+ C2C3+ S2S3)(C3+ S3) −C1S3− C1C3− C2
φλ(c2) = S13 −C2 S3+ C2C3+ C1 −C1− C2C3+ S2S3 C1+ C2C3+ S2S3 −C2S3− C2C3− C1 ! φλ(c3) = −C 3− S3 0 0 −C3+ S3 !
1.5
Strutture quasifuchsiane
Definizione 1.5.1. Sia Γ ⊂ PSL(2, R) un sottogruppo. Diremo insieme limite di Γ l’insieme dei punti z ∈ ˆC tali che z ∈ Γp per qualche p ∈ H3 e dove la chiusura `e
fatta in H3∪ ˆ
C.
Definizione 1.5.2. Un sottogruppo discreto Γ ⊂ PSL(2, R) si dice fuchsiano del primo tipo se ogni elemento diverso dall’identit`a `e lossodromico e se il suo insieme limite `e ˆR
Definizione 1.5.3. Un sottogruppo discreto Γ ⊂ PSL(2, C) si dice quasi-fuchsiano se `e quasiconformemente equivalente a un gruppo fuchsiano del primo tipo, cio`e se esiste un omeomorfismo quasiconforme g : ˆC−→ ˆC tale che g−1Γg sia fuchsiano del primo tipo
Osservazione 1.5.4. Valgono i seguenti fatti su un gruppo Γ quasi-fuchsiano: • L’insieme limite Λ di un Γ `e una curva di Jordan
• Γ agisce in modo propriamente discontinuo sull’insieme H(Λ), il convessificato di Λ in H3
• H(Λ) Γ `e omeomorfo a una superficie S se Γ `e fuchsiano, o a S × [0, 1] se Γ `e quasifuchsiano
• ˆC\Λ ha due componenti connesse Ω1e Ω2su cui Γ agisce in modo propriamente
discontinuo, e si ha che Ω1 Γ e Ω2 Γ sono superfici omeomorfe a S
Sia ora S una superficie chiusa orientabile di genere g ≥ 2 e sia Γ il suo gruppo fondamentale. Sia R ⊂ Hom(Γ, PSL(2, C)) costituito da tutti gli omomorfismi iniettivi che hanno come immagine un gruppo quasifuchsiano.
Definizione 1.5.5. L’insieme delle strutture quasifuchsiane su S `e Q(S) = R Int(PSL(2, C))
dove Int(PSL(2, C)) indica gli automorfismi interni di PSL(2, C).
1.6
Parametri di mezza lunghezza
Sia S una superficie orientabile chiusa di genere g ≥ 2. Fissiamo k = 3g − 3 e l = 2g− 2. Decomponiamo S nel seguente modo: scegliamo k curve semplici chiuse disgiunte C = {γ1, ..., γk} tali che S \Ski=1γi `e una collezione di l pantaloni S1, ..., Sl
Per semplicit`a, considereremo solo decomposizioni tali che ogni γi sia bordo di
due pantaloni distinti.
Ricordiamo che l’insieme delle curve chiuse su S a meno di omotopia libera si identifica con le classi di coniugio del gruppo fondamentale.
Per ogni Sj sia ∂Sj = {γj1, γj2, γj3}. Si pu`o scegliere (la scelta non `e unica) un
sottogruppo Γj ⊂ Γ che ammette una presentazione con generatori cj,1, cj,2, cj,3 tali
che cj,1cj,2cj,3= Id e ogni cj,m sia nella classe di coniugio individuata da γjm.
Sia ora ρ : π1(S) −→ PSL(2, C) una rappresentazione tale che ρ(cj,m) sia
lossodromica per ogni j, m (una rappresentazione in R soddisfa questa propriet`a). Definizione 1.6.1. Fissiamo Γj, cj,m come sopra. Definiamo hlρ(γjm) = hl(cj,m)
(nel senso della definizione 1.4.5).
Osserviamo che ρ|Γj `e unica a meno di coniugio in PSL(2, C) (in virt`u della
proposizione 1.4.7), dunque i parametri di mezza lunghezza risultano ben definiti (non dipendono dalla scelta di Γj).
1.7
Parametri di bending
Fissate le mezze lunghezze delle curve γi si determinano le rappresentazioni dei Γj.
Ora bisogna capire come queste sono combinate per ottenere la rappresentazione di tutto il gruppo Γ. Serviranno dei parametri di bending per ogni geodetica γi
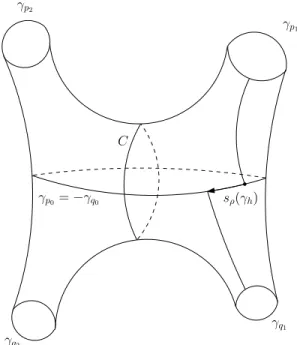
Consideriamo due pantaloni Sp e Sq tali che ∂Sp = {γp0 = γh, γp1, γp2} e ∂Sq=
{γq0 = −γh, γq1, γq2}, dove ora abbiamo orientato i bordi in base all’orientazione
del pantalone. Assumiamo inoltre che il parametro di mezza lunghezza associato al bordo in comune sia lo stesso.
Scegliamo una curva chiusa orientata C in Sp∪ Sq∪ γh in modo che C intersechi
γh esattamente due volte e C, γp1, γq1 individuino un pantalone orientato (questo
pantalone non fa parte della decomposizione). La scelta di una curva C con queste propriet`a `e detta marking
Fissiamo cj,0, cj,1, cj,2 ∈ π1(Sj) < π1(S) che siano nelle classi di coniugio
indivi-duate da γj0, γj1, γj2, per j = p, q e tali che:
• cj,0cj,1cj,2 = id per j = p, q
• cp,0= (cq,0)−1
• cp,1cq,1f = id per qualche f nella classe di coniugio individuata da C
Siano:
• ψ l’asse orientato di ρ(cp,0) = ρ(cq,0)−1
• η l’asse orientato di ρ(cp,1)
• θ l’asse orientato di ρ(cq,1)
Il parametro di bending associato a γh `e:
sρ(γh) = σ(κηψ, ψ, κψθ) = σ(κθψ,−ψ, κψη)
La seconda uguaglianza deriva dal fatto che il parametro di mezza lunghezza di γh sia lo stesso per entrambi i pantaloni e dunque abbiamo che il parametro di
bending risulta ben definito. I parametri di mezza lunghezza e bending sono detti parametri di Fenchel-Nielsen complessi. Vale questo risultato sulle rappresentazioni quasi-fuchsiane:
Teorema 1.7.1. (l, s) : Q(S) −→ Ck+× Ck `e un biolomorfismo (con la struttura complessa quoziente su Q(S)).
γp1 γq1 γq2 γp2 γp0=−γq0 C sρ(γh)
Figura 1.2: Idea della costruzione per il parametro di bending tra due pantaloni
1.8
Condizioni per la fedelt`
a delle rappresentazioni
Siamo ora pronti a enunciare un teorema ottenuto nel capitolo 2 di [1] grazie a delle tecniche sviluppate da Caroline Series in [5]:
Teorema 1.8.1. Esiste ˆε > 0 che soddisfa le seguenti affermazioni. Sia 0 < ε < ˆε. Allora dataS0 una superficie topologica chiusa con una decomposizione in pantaloni
C0 siaρ : π
1(S0) −→ PSL(2, C) una rappresentazione tale che ρ(c) sia lossodromica
per ogni c nella classe di coniugio di una curva inC0 e:
|hl(c) − R2 |< ε |s(c) − 1| < ε
R
per qualcheR > R(ε) > 0. Allora ρ `e iniettiva e il gruppo ρ(π1(S0)) `e K-quasifuchsiano
K = ˆε + ε ˆε − ε
Nei successivi capitoli verr`a dimostrata l’esistenza di una superficie S0 e una
Rappresentazioni di
π
1
(Π
0
)
Un po’ di notazione:
• Γ e Γ? indicano la collezione delle geodetiche chiuse rispettivamente non
orien-tate e orienorien-tate in M3
• sia γ?∈ Γ?, −γ? `e la geodetica con orientazione opposta
2.1
Pantaloni etichettati
Sia Π0 un pantalone (topologico) con un punto base e un’orientazione fissati.
Fis-siamo un omeomorfismo ω : Π0 −→ Π0 che preserva l’orientazione di ordine 3 che
permuta i bordi e tale che il punto base sia un punto fisso per ω. Detta C una com-ponente connessa del bordo del pantalone sia c ∈ π1(Π0) un elemento nella classe di
coniugio di C tale che cω(c)ω2(c) = id.
Definizione 2.1.1. Sia ρ : π1(Π0) −→ PSL(2, C) una rappresentazione fedele.
Diremo che ρ `e ammissibile se ρ(ωi(c)) `e lossodromica e
hl(ωi(C))) = l(ωi(c))
2
dove l(ωi(c)) `e scelto in modo che −π < Im(l(ωi(c))) ≤ π
Definizione 2.1.2. Sia ρ : π1(Π0) −→ G ammissibile. Uno skew pant Π `e la classe
di coniugio Π = [ρ]. L’insieme di tutti gli skew pant sar`a indicato con Π 15
Sia ρ : π1(Π0) −→ G con [ρ] = Π e sia Ai = ρ(ωi(c)). Definiamo ρ0(ω−i(c)) =
A−1i . Definisco allora la mappa R : Π −→ Π tale che R(Π) = [ρ0]. Osserviamo
che R `e un’involuzione senza punti fissi. Sia Π ∈ Π con Π = [ρ]. Indicheremo con γ?(Π, ωi(c)) la geodetica in Γ? che rappresenta la classe di coniugio di ρ(ωi(c)).
Vale l’identit`a γ?(R(Π), ωi(c)) = −γ?(Π, ω−i(c)). L’insieme delle coppie (Π, γ?) con
γ? = γ?(Π, ωi(c)) sar`a indicato con Π?.
Definiamo R : Π? −→ Π?data da R(Π, γ?(Π, ωi(c))) = (R(Π), γ?(R(Π), ω−i(c))).
Si definisce inoltre rot : Π? −→ Π?data da rot(Π, γ?(Π, ωi(c))) = (Π, γ?(Π, ωi+1(c))
Osservazione 2.1.3. Le mappe R e rot hanno un’interpretazione geometrica: Sia R0: Π0−→ Π0 la riflessione rispetto a un piano che passa per C e per il punto base.
La mappa R si ottiene semplicemente precomponendo la rappresentazione con R0 ?.
Allo stesso modo rot si ottiene precomponendo la rappresentazione con ω?.
Definizione 2.1.4. Sia L un insieme finito. Diremo che lab : L −→ Π?`e un’etichettatura legale se sono soddisfatte:
• esiste un’involuzione RL : L −→ L tale che R(lab(a)) = lab(RL(a)) per ogni
a∈ L
• esiste una bigezione rotL : L −→ L tale che rot(lab(a)) = lab(rotL(a)) per
ogni a ∈ L
Definizione 2.1.5. Sia σ : L −→ L un’involuzione. σ si dice ammissibile rispetto all’etichettatura legale lab se la seguente condizione `e soddisfatta: sia a ∈ L con lab(a) = (Π1, γ?). Allora lab(σ(a)) = (Π2,−γ?), con Π2 ∈ Π un qualche altro
pantalone.
Osservazione 2.1.6. RL`e un’involuzione ammissibile
Esempio 2.1.7. Denotiamo con NΠ l’insieme delle somme formali finite di skew pants a coefficienti interi non negativi. Supponiamo di avere W ∈ NΠ. Diremo che W `eR-simmetrica se W = n1(Π1+ R(Π1)) + ... + nm(Πm+ R(Πm)) con ni ∈ N e
Π ∈ Π. Vediamo ora come data W si possa costruire un’etichettatura legale. Questa costruzione ci servir`a in seguito: Sia L = {(j, k) ∈ N × N : 1 ≤ j ≤ 2 Pm
i=1ni; 0 ≤
lab(j, k) =
(Πs, γ?(Πs, ωk(c))) 2 Pi=1s−1ni< j ≤ 2Psi=1ni j dispari
(R(Πs), γ?(R(Πs), ω−k(c))) 2 Pi=1s−1ni< j ≤ 2Psi=1ni j pari
Definiamo ora le bigezioni: RL(j, k) = (j + 1, k) j dispari (j − 1, k) j pari rotL(j, k) = (j, k + 1 mod 3)
2.2
Costruzione di una superficie data un’etichettatura
Supponiamo di avere un’etichettatura legale lab : L −→ Π? e un’involuzione
am-missibile σ : L −→ L. Costruiamo una superficie topologica chiusa S0: ad ogni
elemento di L/rotL assegniamo una copia del pantalone Π0 e a ogni elemento di L
facciamo corrispondere un bordo orientato del pantalone corrispondente. σ d`a un modo di attaccare questi pantaloni, a formare una superficie S0. Questa costruzione
permette di definire una rappresentazione ρlab,σ : π1(S0) −→ G.
Osservazione 2.2.1. S0 `e connessa se e solo se l’azione del gruppo generato dalle
bigezioni (RL, rotL, σ) `e minimale su L (cio`e L `e il pi`u piccolo insieme invariante
sotto l’azione del gruppo)
Dato a ∈ L, sia lab(a) = (Π, γ?(Π, ωi(c))). Possiamo definire hl(a) = hl
Π(ωi(c)).
Si verifica che le condizioni di ammissibilit`a implicano che hl(a) = hl(σ(a)).
2.3
Il fibrato normale unitario di una geodetica
γ
∈ Γ
Fissiamo γ? ∈ Γ? e indichiamo il suo fibrato normale unitario con N1(γ). Gli
elementi di N1(γ) sono coppie (p, v) dove p ∈ M3 e v `e un vettore unitario normale
a γ in p. Indichiamo inoltre con N1(Γ) l’unione disgiunta dei fibrati delle geodetiche
di M3.
Fissiamo un’orientazione γ?su γ e sia ζ ∈ C. Definiamo la mappa A
ζ : N1(γ) −→
N1(γ) data da A(p, v) = (p
1, v1) dove p1 e v1 sono definiti come segue: sia ˜γ?
˜
γ? = (0, ∞). Sia A
ζ ∈ PSL(2, C) data da Aζ(w) = eζw per w ∈ ∂H3. Definiamo
( ˜p1, ˜v1) = Aζ(˜p, ˜v). Imponiamo che ( ˜p1, ˜v1) sia un sollevamento di (p1, v1).
Questa costruzione pu`o essere fatta scegliendo una qualsiasi orientazione su γ e la mappe che si ottengono sono l’una l’inversa dell’altra.
Osserviamo che C (considerato come gruppo additivo) agisce transitivamente su N1(γ). Sia l(γ) la complex translation length di γ, tale che −π < Im(l(γ)) ≤ π. Si
ha allora che Al(γ) = id su N1(γ). Questo implica che Al(γ) 2
`e un’involuzione che ci permette di definire N1(√γ) = N1(γ)/A
l(γ) 2
. Indicheremo con N1(√Γ) l’unione
disgiunta di questi fibrati al variare delle geodetiche in M3.
C agisce transitivamente su N1(√γ). Inoltre c’`e un’unica struttura complessa su N1(√γ) tale che A
ζ sia un biolomorfismo. Con questa struttura complessa si ha
che:
N1(√γ) ≡ C/(l(γ)
2 + 2πiZ)
Questa identificazione permette di definire una distanza euclidea su N1(√γ) che
sar`a indicata con dis. Notiamo che per |ζ| piccolo si ha dis((p, v), Aζ(p, v)) = |ζ|.
Sia (Π, γ?) ∈ Π? e sia γ?
k tale che (Π, γk?) = rotk(Π, γ?) per k = 1, 2. Sia poi
δ?
k una geodetica orientata in M3 perpendicolare comune tra γ? e γk? tale che un
sollevamento di δ?
k sia un lato dell’esagono retto che determina Π. L’orientazione di
δ?
k `e scelta in modo che il punto δk?∩ γk? venga dopo δk?∩ γ?. Siano ora pk= δ?k∩ γ?
e vk il vettore tangente unitario in pk che abbia lo stesso verso di δk?. Poich´e Π `e
nela classe di coniugio di una presentazione ammissibile, notiamo che Al(γ) 2
scambia (p1, v1) e (p2, v2).
Osservazione 2.3.1. `e qui che serve la condizione di ammissibilit`a, poich´e si vede che Al(γ)
2
= Ahl(γ) manda il sollevamento di δ1? in δ?2.
Questo significa che la classe [(pk, vk)] ∈ N1(√γ) non dipende da k. Ne segue
che si pu`o definire la funzione:
f oot : Π?−→ N1(√Γ)
data da
f oot(Π, γ?) = [(p k, vk)]
Osserviamo che foot(Π, γ?) = foot(R(Π, γ?)).
Sia ora S0 una superficie con una decomposizione in pantaloni data da C0.
Fis-siamo ρ : π1(S0) −→ G tale che ristretta al gruppo fondamentale di ogni paio
di pantaloni sia ammissibile. Consideriamo due pantaloni Π0
i, i = 1, 2 che
abbia-no in comune un arco C ∈ C0 nel loro bordo. Chiamiamo (Π
1, γ) e (Π2,−γ) i
corrispondenti skew pants marcati in Π?.
Consideriamo ora l’azione Aζ su N1(√γ) che corrisponde all’orientazione di γ?.
Fissiamo ζ0 tale che:
Aζ0(foot(Π1, γ
?)) = foot(Π 2,−γ?)
Definiamo:
˜s(C) = ζ0− iπ, mod (l(γ)2 + 2πiZ)
˜s(C) `e detto parametro di bending ridotto. Spiegheremo ora il perch´e di questo nome.
Osservazione 2.3.2. Si verifica che scegliendo dei rappresentanti ρi ∈ Πi tali che
ρ1(c) = ρ2(c)−1 e un qualsiasi marking si ottiene un parametro di bending s(c) tale
che
s(c) = ˜s(C) mod (l(γ)
2 + 2πiZ)
Inoltre, al variare di tutti i possibili marking si ottengono per il parametro di bending tutti i valori del tipo s(c) + khl(c), k ∈ Z
Enunciamo ora il teorema che andremo a dimostrare:
Teorema 2.3.3. Esistono costanti q > 0 e K > 0 tali che per ogni ε > 0 e per ogni R > 0 abbastanza grande si ha che: esistono un insieme finito di etichette L, un’etichettatura legale lab :L −→ Π e un’involuzione ammissibile σ : L −→ L tali che per ogni a∈ L si abbia:
|hl(a) − R 2| < ε
Questo teorema implica il teorema 1.8.1. Grazie all’osservazione 2.3.2 si ve-de infatti che `e possibile costruire una superficie S e una rappresentazione ρlab,σ :
π1(S) −→ G che soddisfi le relazioni richieste nel teorema 1.8.1. (basta notare che
per R → ∞ si ha che KRe−qr = o(1 R)).
2.4
Trasporto di misure
Sia (X, d) uno spazio metrico. Denotiamo con M(X) lo spazio delle misure di Borel positive e a supporto compatto. Dati A ⊂ X e δ > 0 indichiamo con
Nδ(A) = {x ∈ X : ∃a ∈ A tale che d(x, a) ≤ δ}
il δ-intorno di A.
Definizione 2.4.1. Siano µ, ν ∈ M(X) due misure tali che µ(X) = ν(X) e fissiamo δ > 0. Supponiamo che per ogni A⊂ X di Borel si abbia µ(A) ≤ ν(Nδ(A)). Diremo
allora che µ e ν sono δ-equivalenti.
Vediamo innanzitutto che questa definizione `e in realt`a simmetrica in µ e ν: per ogni A ⊂ X Boreliano si ha ν(A) ≤ ν(X) − ν(Nδ(X \ Nδ(A))) ≤ µ(X) − µ(X \
Nδ(A)) = µ(Nδ(A))
Le seguenti proposizioni vengono direttamente dalla definizione di misure equi-valenti:
Proposizione 2.4.2. Supponiamo che µ e ν siano δ-equivalenti. Allora per ogni K > 0 si ha che Kµ e Kν sono δ-equivalenti. Inoltre, se supponiamo che ν e η sianoδ1-equivalenti, allora µ e η sono (δ + δ1)-equivalenti
Proposizione 2.4.3. Sia (T, Λ) uno spazio di misura e consideriamo due mappe fi : T −→ X i = 1, 2 tali che d(f1(t), f2(t)) ≤ δ per quasi ogni t ∈ T . Allora le
misure (f1)]Λ e (f2)]Λ sono δ-equivalenti
Ora consideriamo un teorema che `e il contrario della precedente proposizione nel caso particolare in cui le misure siano discrete:
Teorema 2.4.4. Supponiamo che A e B siano due insiemi finiti aventi la stessa cardinalit`a muniti delle rispettive misure standard che contano i punti ΛA e ΛB.
Supponiamo di avere delle mappe f : A −→ X e g : B −→ X tali che le misure f]ΛA e g]ΛB siano δ-equivalenti per qualche δ > 0. Allora esiste una bigezione
h : A−→ B tale che d(g(h(a)), f(a)) ≤ δ per ogni a ∈ A. Ci servir`a il teorema del matrimonio di Hall che dice:
Teorema 2.4.5. Supponiamo di avere una relazioneRel⊂ A × B. Per ogni Q ⊂ A indichiamo con
Rel(Q) ={b ∈ B : ∃a ∈ Q|(a, b) ∈ Rel}
Se |Rel(Q)| ≥ |Q| per ogni Q ⊂ A allora esiste una funzione iniettiva h : A −→ B tale che(a, h(a)) ∈ Rel per ogni a ∈ A.
Dimostriamo ora il teorema 2.4.4:
Dimostrazione. Definiamo la relazione Rel in questo modo: (a, b) ∈ Rel se d(f(a), g(b)) ≤ δ. Si vede quindi che |Rel(Q)| = (g?ΛB)(N (f(Q))) ≥ (f?ΛA)(f(Q)) = |Q|. Il
teo-rema di Hall ci d`a quindi un’iniezione h : A −→ B tale che d(g(h(a)), f(a) ≤ δ per ogni a ∈ A. Poich´e A e B sono finiti e hanno la stessa cardinalit`a si ha che h `e una biiezione.
Enunciamo ora un risultato di equivalenza di misure su un toro complesso: Siano z, w ∈ C due numeri complessi tali che T (z, w) = C/(zZ+wZ) sia un toro. Indicheremo con d(., .) la distanza indotta dalla distanza euclidea e con λ la misura indotta dalla misura di Lebesgue su T (z, w).
Teorema 2.4.6. Sia µ∈ M(T (z, w)) tale che esistano K > 0 e δ > 0 con K≤ |∂µ∂λ| ≤ K(1 + δ) quasi ovunque su T (z, w)
dove |∂µ∂λ| `e la derivata di Radon-Nikodym. Allora µ `e 2δ(|z| + |w|)-equivalente a K0λ, dove µ(T (z, w)) = K0λ(T (z, w)).
2.5
Misure su skew pants e l’operatore ˆ
∂
Definizione 2.5.1. Indichiamo con MR0(Π) lo spazio delle misure positive di Borel a supporto finito sull’insieme degli skew pants orientati che sono invarianti per l’in-voluzione R. Indichiamo inoltre con M0(N1(
√
Γ)) lo spazio delle misure positive di Borel a supporto compatto sulla variet`a N1(√Γ)
Andremo ora a definire l’operatore ˆ ∂ :MR 0 (Π) −→ M0(N1( √ Γ)) Sia Π ∈ Π e siano γ?
i ∈ Γ?, i = 0, 1, 2 le geodetiche corrispondenti tali che
(Π, γ?
i) ∈ Π?. Denoteremo con αΠi ∈ M0(N1(
√
Γ)) la misura atomica supportata nel punto foot(Π, γ?
i) e di massa totale pari a 1.
Definizione 2.5.2. Sia
αΠ= P2 i=0αΠi
allora definiamo l’operatore ˆ ∂µ =P
Π∈Πµ(Π)αΠ
La sommatoria ha senso poich´e µ(Π) `e diverso da 0 solo per un numero finito di Π ∈ Π. Osserviamo che la massa totale di ˆ∂µ `e 3 volte la massa totale di µ. Definizione 2.5.3. Sia α ∈ M0(N1(
√
Γ)). Indichiamo con (Aζ)?α il push-forward
di α tramite la mappa Aζ : N1(
√
Γ) −→ N1(√Γ). Diremo che α `e δ-simmetrica se
α e (Aζ)?α sono δ-equivalenti per ogni ζ ∈ C.
Questo teorema ci permetter`a di dimostrare il teorema 2.3.3:
Teorema 2.5.4. Esistono q > 0 e D1, D2 > 0 tali che per ogni 0 < ε ≤ 1 e per
ogni R > 0 sufficientemente grande, esiste una misura µ∈ MR
0 (Π) che soddisfa le
seguenti propriet`a. Se µ(Π) > 0 per qualche Π∈ Π allora si ha che |hl(ωi(C)) − R
dove hl(ωi(C)) `e la lunghezza che corrisponde alla classe di equivalenza Π.
Inoltre, esiste una misuraβ∈ M0(N1(
√
Γ)) tale che le misure ˆ∂µ e β siano D1e−
R 8
-equivalenti e tale che per ogni toroN1(√γ) esista una costante K
γ≥ 0 tale che quasi
ovunque su N1(√γ) si abbia
Kγ ≤ |dβdλ| ≤ Kγ(1 + D2e−qR)
doveλ `e la misura di Lebesgue su N1(√γ)
Dimostreremo questo teorema nel 3. Ora, assumendo questo risultato, proveremo il teorema 2.3.3:
Proposizione 2.5.5. Esistono q > 0, D > 0 tali che per ogni 0 < ε ≤ 1 e per ogni R > 0 abbastanza grande, esista una misura µ∈ MR
0(Π) che abbia le seguenti
propriet`a:
1. µ(Π)∈ Q per ogni Π ∈ Π
2. Se µ(Π) > 0 per qualche Π∈ Π allora si ha che |hl(ωi(C)) − R
2| ≤ ε
dove hl(ωi(C)) `e la lunghezza che corrisponde alla classe di equivalenza Π
3. Le misure ˆ∂µ e (A1+iπ)]∂µ sono DReˆ −qR-equivalenti
Dimostrazione. Assumiamo le notazioni e le conclusioni del teorema 2.5.4. Mo-striamo prima che ˆ∂µ e (A1+iπ)] e ˆ∂µ sono DRe−qR-equivalenti. Dato che β
ˆ
∂µ sono D1e−
R
8-equivalenti basta mostrare questo fatto su ogni N1(√γ) tale che
β(N1(√γ)) > 0. Fissiamo dunque γ ∈ Γ con questa propriet`a. Abbiamo che, per
il teorema 2.4.6 e dato che λ `e invariante per l’azione di Aζ, le misure (Aζ)]β e
K0λ sono (2π +|l(γ)|2 )D2e−qR-equivalenti per qualche K
0
> 0 e per ogni ζ ∈ C. Poich´e |l(γ)| < R + 1 possiamo dire che (Aζ)]β e K
0
λ sono C1Re−qR-equivalenti
per qualche C1 > 0. D’altra parte, (Aζ)]β e ˆ∂µ sono D1e−
R 8-equivalenti. Ne segue che (Aζ)]∂µ e Kˆ 0 λ sono D2(Re−qR+ e− R
8)-equivalenti per qualche D2 > 0 e per
ogni ζ ∈ C. Ne segue che esiste una costante D > 0 tale che ˆ∂µ e (A1+iπ)]∂µ sonoˆ
numero finito di atomi, grazie alla procedura di razionalizzazione standard (vedere proposizione 4.2 in [2]), possiamo supporre gli atomi abbiano peso razionale. La proposizione `e dunque dimostrata.
Ora siamo pronti per
Dimostrazione del teorema 2.3.3. Siano Π+e Π−due insiemi disgiunti tali che Π+∪ Π− = Π e R(Π+) = Π−. Notiamo che esistono pi`u decomposizioni con queste propriet`a, ma per il resto della dimostrazione ne fissiamo una. Se ν ∈ MR
0 allora
indichiamo con ν+ e ν− le restrizioni di ν rispettivamente a Π+ e Π−. Poich´e
f oot(Π, γ?= foot(R(Π), −γ?) otteniamo che ˆ∂ν+= ˆ∂ν− e 2 ˆ∂ν+= ˆ∂ν.
Consideriamo ora la misura µ data dalla proposizione 2.5.5. Poich´e µ ha supporto finito e valori razionali, possiamo moltiplicarla per un fattore in modo da ottenere una misura ψ = Kµ tale che i pesi ψ(Π) siano numeri interi pari. Si ha ancora che
ˆ
∂ψ e (A1+iπ)]∂ψ sono DReˆ −qR-equivalenti.
Notiamo che ψ ∈ NΠ `e una somma formale R-simmetrica. Sia lab : L −→ Π?
l’etichettatura descritta nell’esempio 2.1.7. Ci resta da definire un’involuzione σ : L −→ L.
Fissiamo γ?∈ Γ?. Definiamo:
X+= {a ∈ L|lab(a) = (Π, γ?) per qualche Π ∈ Π+}
Definiamo X− in modo analogo, e indicheremo con f+/− : X+/− −→ Π? la
restri-zione della mappa lab a X+/−.
Sia inoltre α+la restrizione di ˆ∂µ+a M
0(N1(√γ)) (definiamo α− in modo
ana-logo). Osserviamo che α+= α− Allora, dalla definizione di L abbiamo che:
α+= (foot)
](f+)]ΛX+
(A1+iπ)]α−= (A1+iπ)](foot)](f−)]ΛX−
Dove ΛX+/− sono le misure che danno la cardinalit`a di un sottoinsieme di X+/−
Chiamiamo f = foot ◦ f+ e g = A
1+iπ◦ foot ◦ f−.Poich´e α+ e (A1+iπ)] sono
DRe−qR-equivalenti abbiamo che il teorema 2.4.4 ci d`a una bigezione h : X+ −→ X−
Possiamo quindi definire σ : X+∪ X− −→ X+∪ X− data da σ(x) = h(x) per
x ∈ X+ e σ(x) = h−1(x) per x ∈ X−. Al variare di γ? ∈ Γ? questa costruzione ci
d`a un’involuzione σ : L −→ L ammissibile. Si verifica che la coppia (lab, σ) verifica le assunzioni del teorema 2.3.3.
Misure su skew pants e il flusso
geodetico
3.1
Funzione affinit`
a
Definizione 3.1.1. Sia F(H3) l’insieme dei 2-frame unitari F = (p, u, n) dove p ∈ H3, u, n ∈ TpH3 ortogonali.
Abbiamo che PSL(2, C) agisce in modo naturale su F(H3). Dati (p
i, ui, ni) ∈
F(H3) definiamo una funzione distanza:
D((p1, u1, n1), (p2, u2, n2)) = d(p1, p2) + Θ(u1@p2, u2) + Θ(n1@p2, n2)
dove u1@p2 e n1@p2 indicano il trasporto parallelo di u1 e n1 lungo la geodetica che
collega p1 a p2. Osserviamo che D `e invariante per l’azione di PSL(2, C). Denotiamo
con Nε(F ) ⊂ F(H3) l’insieme dei punti di F(H3) che hanno distanza minore di ε da
F .
Indichiamo con gt : T (H3) −→ T (H3), t ∈ R il flusso geodetico standard.
L’a-zione del flusso si estende a F(H3) in modo naturale: g
r(p, u, n) = (p1, u1, n1) dove
((p1, u1) = gr(p, u) e n1 = n@p1 `e il trasporto parallelo di n lungo la geodetica tra
p e p1. Dotiamo lo spazio F(H3) della misura di Liouville Λ, invariante per il flusso
geodetico e per l’azione di PSL(2, C).
Ricordiamo che M3 = H3/G `e una 3-variet`a iperbolica chiusa e G `e un gruppo
Kleiniano. Identifichiamo F(M3) con il quoziente F(H3). Il flusso geodetico agisce
su F(M3) tramite la proiezione al quoziente. Denotiamo ancora con Λ la misura di
Liouville su F(M3) indotta dalla proiezione al quoziente.
La seguente proposizione afferma che il flusso geodetico su F(M3) ha la propriet`a
di mixing esponenziale:
Teorema 3.1.2. Esiste una costanteq > 0 che dipende solo da M3 tale che valgano
le seguenti affermazioni. Siano φ, ψ : F(M3) −→ R due funzioni C1. Allora per
ogni r∈ R vale la diseguaglianza: |Λ(F(M3)) Z F (M3) (g? rψ)(x)φ(x)dΛ(x)− Z F (M3) ψ(x)dΛ(x) Z F (M3) φ(x)dΛ(x)| ≤ Ce−qr
DoveC > 0 dipende solo dalla norma C1 delle funzioni ψ e φ.
Date due funzioni ψ, φ : F(M3) −→ R poniamo:
(ψ, φ) =Z
F (M3)
ψ(x)φ(x)dΛ(x)
D’ora in poi r >> 0 sar`a un numero reale positivo molto grande e ε > 0 un numero positivo pi`u piccolo del raggio di iniettivit`a di M3. Questo ci assicura che
la proiezione F(H3) −→ F(M3) `e iniettiva su ogni palla N
ε⊂ F(H3).
Fissiamo F0 ∈ F(H3). Scegliamo una funzione fε(F0) : F(H3) −→ R di classe
C1, positiva, con supporto in N
ε(F0) e tale che:
Z
F (H3)
fε(F0)(x)dΛ(x) = 1
Per un generico F ∈ F(H3) definiamo f
ε(F ) come il pullback di fε(F0) tramite
l’applicazione di PSL(2, C) corrispondente. Per F ∈ F(M3) f
ε)(F ) sar`a definito
tramite la proiezione (`e ben definita poich´e la proiezione `e iniettiva su ogni palla Nε(F ).
Definizione 3.1.3. Siano Fj = (pj, uj, nj) ∈ F(H3), j = 1, 2 due frame e poniamo
gr
4(pj, uj, nj) = ( ˆpj, ˆuj, ˆnj). Definiamo
aH3(F1, F2) = (g?r
2fε( ˆp1, ˆu1, ˆn1), fε( ˆp2, ˆu2, ˆn2)).
Osservazione 3.1.4. Si pu`o verificare che a soddisfa le seguenti propriet`a: 1. a(F1, F2) = a(F2, F1) per ogni F1, F2 ∈ F(H3)
2. a(A(F1), A(F2)) = a(F1, F2) per ogni A ∈ PSL(2, C)
3. Se a(F1, F2) > 0 con F1= (p, u, n) e F2 = (q, v, m) allora
|d(p, q) − r| < ε Θ(n@q, m) < ε
Θ(u, v(p, q)) < Ce−r4 Θ(v, v(q, p)) < Ce−r4
dove Θ(x, y) `e l’angolo non orientato tra i vettori x e y. Indichiamo con γ il segmento geodetico da p a q. Dunque v(p, q) ∈ TpH3 `e il vettore tangente a γ in p.
Definizione 3.1.5. Siano Fj = (pj, uj, nj) ∈ F(M3), j = 1, 2 due frame e γ un
seg-mento geodetico che connette p1 e p2. Sia ˜p1∈ H3un sollevamento di p1e ˜p2 il
solle-vamento di p2lungo γ. Denotiamo con ˜Fj = ( ˜pj, ˜uj, ˜nj) ∈ F(H3) i corrispondenti
sol-levamenti. Abbiamo che `e ben definita la funzione aγ(F1, F2) = aH3( ˜F1, ˜F2). Diremo
che F1 e F2 sono (ε, r) ben connessi lungo il segmento geodetico γ se aγ(F1, F2) > 0.
Osservazione 3.1.6.Siano Fj = (pj, uj, nj) ∈ F(M3), j = 1, 2 e poniamo gr
4(pj, uj, nj) =
(pj0, u0
j, n0j). Possiamo definire la funzione:
a(F1, F2) = (g?r 2 fε(p01, u01, n01), fε(p02, u02, n02)) Allora si ha che: a(F1, F2) = X γ aγ(F1, F2)
dove la somma `e fatta su tutti i segmenti geodetici γ che connettono p1 a p2 (solo
un numero finito degli addendi `e diverso da 0).
Lemma 3.1.7. Fissiamo ε > 0. Allora per ogni r abbastanza grande e per ogni F1, F2 ∈ F(M3) abbiamo che:
a(F1, F2) = Λ(F (M1 3))(1 + O(e
−qr 2))
3.2
Geometria dei bipodi ben connessi
Sia ω : F(H3) −→ F(H3) dato da ω(p, u, n) = (p, ωn(u), n), dove ωn(u) `e il vettore
ortogonale a n ottenuto ruotando u di 2π
3 in senso antiorario (il piano ortogonale a
n `e orientato da n stesso). L’omeomorfismo ω commuta con l’azione di PSL(2, C), dunque la sua azione `e ben definita anche su F(M3). Osserviamo che la funzione
distanza D `e invariante per l’azione di ω.
Il seguente lemma si dimostra con tecniche di geometria iperbolica elementare: Lemma 3.2.1. Siano F1 = (p, u, n), F2 = (q, v, m), F3 = (p1, u1, n1) ∈ F(H3).
Supponiamo che le coppie (F1, ω(F2)) e (F2, ω(F3)) siano (ε, r) ben connesse. Sia
A ∈ PSL(2, C) la trasformazione tale che A(F1) = F3. Allora per r abbastanza
grande, la trasformazioneA `e lossodromica e |l(A) − 2r + 2 log(4
3)| ≤ Dε
per qualche costanteD > 0. Inoltre, detto α l’asse di A, d(p, α), d(q, α), d(p1, α)≤ log(
√
3) + Dε
Ad ogni frame F = (p, u, n) ∈ calF (M3) associamo il bipodo B = omegai(F ) =
(p, ωi
n(u), n), i = 0, 1.
Definizione 3.2.2. Dati due frame F1 = (p, u, n), F2 = (q, v, m) ∈ F(M3) siano
B1 e B2 i bipodi corrispondenti. Sia γ = (γ0, γ1) una coppia di segmenti geodetici
in M3 che collegano p a q. Diremo che i bipodi B
1 e B2 sono (ε, r) ben connessi
lungo la coppia di segmenti γ se le coppie (F1, ω(F2)) e (ω(F1), F2) sono (ε, r) ben
connesse lungo i segmenti γ0 e γ1 rispettivamente.
Lemma 3.2.3. Siano F1 = (p, u, n), F2 = (q, v, m) ∈ F(M3) due frame e siano
B1 eB2 i bipodi corrispondenti. Supponiamo che B1 eB2 siano (ε, r) ben connessi
lungo la coppia di segmenti γ = (γ0, γ1). Allora, per r abbastanza grande, la curva
chiusaγ0∪ γ1 `e omotopa a una geodetica chiusa δ(B1, B2, γ)∈ Γ(M3) e vale inoltre
la seguente diseguaglianza
|l(δ(B1, B2, γ))− 2r + 2log(43)| ≤ Dε
Dimostrazione. Sia (p(0), u(0), n(0)) ∈ F(H3) un sollevamento di F1.
Denotia-mo poi con (q(0), v(0), m(0)) ∈ F(H3) il sollevamento di F
2 lungo γ0. Sia poi
(p(1), u(1), n(1)) il sollevamento di F1 a partire da (q(0), v(0), m(0)) lungo γ1. Sia
A∈ G l’isometria tale che A((p(0), u(0), n(0))) = (p(1), u(1), n(1)). Dal lemma 3.2.1 segue che A `e lossodromica. Allora l’asse di A si proietta su M3 ad una geodetica
δ(B1, B2, γ) che `e omotopa a γ0∪ γ1 e l(δ(B1, B2, γ)) = l(A). Il lemma 3.2.1 fornisce
anche la stima voluta.
3.3
Geometria dei tripodi ben connessi
Fissiamo P, P1, P2 ∈ F(H3) con P1, P2 ∈ Nε(P ). Sia F1 ∈ F(H3) e r >> 0.
Definiamo ora il frame F2 = L(F1, P1, P2, r):
Sia ˜F1= gr
4(F1). Sia ˆF1 ∈ Nε( ˜F1) il frame tale che per qualche M1∈ PSL(2, C)
si abbia M1(P ) = ˜F1 e M1(P1) = ˆF1. Sia poi (ˆq, −ˆv, ˆm) = gr
2( ˆF1) e poniamo
ˆ(F2) = (ˆq, ˆv, ˆm). Sia ora ˜F2 il frame tale che per qualche M2 ∈ PSL(2, C) si abbia
M2(P ) = ˜F2 e M2(P2) = ˆF2. Poniamo infine F2 = g−r
4( ˜F2) = L(F1, P1, P2, r).
Osserviamo che F2= L(F1, P1, P2, r) non dipende da P .
F1 ˜ F1 ˆ F1 ˆ F2 ˜ F2 F2 Figura 3.1: Costruzione di L(F1, P1, P2, r)
Osservazione 3.3.1.Se F2= L(F1, P1, P2, r), `e facile mostrare che F1 = L(F2, P2, P1, r)
Ricordiamo che con Π0 indichiamo un paio di pantaloni topologico e con ω 0 :
Π0 −→ Π0 denotiamo un omeomorfismo di ordine 3 che permuta le componenti
connesse del bordo del pantalone. Indichiamo quindi con ωi(C), i = 0, 1, 2 dove C `e
una componente connessa del bordo di Π0 orientata. Fissiamo inoltre c ∈ π
1(Π0) la
cui classe di coniugio corrisponde a C. Ne segue che ω0
Sia ora P ∈ F(H3) e fissiamo sei frame Pj
i ∈ Nε(P ) i = 0, 1, 2, j = 1, 2. Data la
sestupla (Pj
i) definiremo una rappresentazione
ρ(Pij) : π1(Π0) −→ PSL(2, C)
come segue:
Scegliamo F2 ∈ F(H3) e siano F1i, i = 0, 1, 2 i frame tali che ω−i(F2) = L(ωi(F1i), Pi1, Pi2, r).
Essi sono univocamente definiti in virt`u dell’osservazione 3.3.1.
Siano ora Ai ∈ PSL(2, C) date da A0(F10) = F11, A1(F11) = F12 e A2(F12) = F10.
Osserviamo che A2A1A0= id. Possiamo ora definire ρ(Pij) = ρ data da ρ(ω0i(c)) =
Ai. Osserviamo che a meno di coniugio in PSL(2, C) la rappresentazione ρ dipende
solo dalla sestupla (Pj
i) e da r. Si verifica inoltre che se per ogni i, j si ha P j i = P ,
allora le mezze lunghezze associate alla rappresentazione ρ sono tutte reali positive e uguali fra loro.
Lemma 3.3.2. SiaP ∈ F(H3) e fissiamo Pj
i ∈ Nε(P ) i = 0, 1, 2, j = 1, 2. Poniamo
ρ(Pij) = ρ. Allora per ogni k = 0, 1, 2 la trasformazione ρ(ωk(c)) `e lossodromica e
|hl(ωk
0(c)) − r + log43| ≤ Dε
per qualche D > 0, dove hl(ωk
0(c)) `e il parametro di mezza lunghezza associato alla
rappresentazioneρ.
Dimostrazione. Dal lemma 3.2.1 segue che: |l(ωk
0(c)) − 2r + 2 log43| ≤ Dε
Sappiamo inoltre che hl(ωk 0(c)) =
l(ωk0(c))
2 + mπi per qualche m ∈ {0, 1}. Rimane da
mostrare che k = 0: Sia Pj
i(t) un cammino continuo in H3tale che P j i(0) = P e P j i(1) = P j i. Poniamo
ρt = ρ(Pij(t)). Per ogni t ∈ [0, 1] otterremo il corrispondente m(t) ∈ {0, 1}. Poich´e
abbiamo osservato che m(0) = 0 e data la continuit`a di m(t) ne deriva che m(1) = m = 0.
Per ogni frame F ∈ F(M3) consideriamo il tripodo associato T = ωi(F ), i =
Definizione 3.3.3. Siano Fj = (pj, uj, nj) ∈ F(M3), j = 1, 2 e siano Tj, j = 1, 2,
i rispettivi tripodi associati. Sia γ = (γ0, γ1, γ2) una tripla di segmenti geodetici in
M3, ognuno dei quali connette p
1 a p2. Diremo che la coppia di tripodi T1 e T2 `e
(ε, r) ben connessa lungo la tripla di segmenti γ se per ogni i = 0, 1, 2 abbiamo che ωi(F
1) e ω−i(F2) sono (ε, r) ben connessi lungo il segmento γi.
Ora vedremo come a ogni coppia di tripodi ben connessa `e possibile associare uno skew pant nel senso della definizione 2.1.2.
Chiamiamo θ-grafo l’1-complesso formato da due 0-celle, p e q, e tre 1-celle, h0, h1, h2, ciascuna che connette p a q. Sia Tj = (pj, ωnij(uj), nj), i = 0, 1, 2 j = 1, 2
una coppia di tripodi ben connessa lungo γ = (γ0, γ1, γ2) costruiamo una mappa
φ dal θ-grafo a M3 tale che φ(p) = p
1, φ(q) = p2 e φ : hi −→ γi sia un
qual-siasi omeomorfismo. Si pu`o vedere che θ-grafo `e un retratto di deformazione di Π0. Questo ci permette di estendere la mappa φ : Π0 −→ M3. Indicheremo con
ρ(T1, T2, γ) = φ?: π1(Π0) −→ G la rappresentazione indotta da tale φ.
Tale rappresentazione pu`o rivelarsi banale, ma poich´e T1 e T2 sono ben connessi
lungo γ abbiamo dimostrato che ρ(T1, T2, γ) `e ammissibile e che la classe di coniugio
in G data da [ρ(T1, T2, γ)] `e uno skew pant.
Osservazione 3.3.4. Sia γ = (γ0, γ1, γ2). Poniamo −γ = (−γ0,−γ1,−γ2)). Allora
vale che:
R([ρ(T1, T2, γ)]) = [ρ(T2, T1,−γ)]
Lemma 3.3.5. SianoT1 eT2 due tripodi ben connessi lungo la tripla di segmenti γ
e poniamoρ = ρ(T1, T2, γ). Allora ρ(ω0i(C)), i = 0, 1, 2 `e lossodromica e si ha:
|hl(ωi
0(C)) − r + log43| ≤ Dε
per qualche costanteD > 0. Dimostrazione. Sia (P, ωi
n(u), n) = T1. Basta osservare che esistono Pij ∈ Nε(P )
tali che ρ(Pj
i) = ρ(T1, T2, γ). Il resto viene dal lemma 3.3.2
Definizione 3.3.6. Siano Tj = ωi(Fj), i = 0, 1, 2 j = 1, 2 due tripodi ben connessi
bγ(T1, T2) = 2 Y i=0 aγi(ω i(F 1), ω−1(F2))
Poich´e la coppia di tripodi `e ben connessa lungo la tripla γ abbiamo che bγ(T1, T2) > 0
.
Sia ν(T1, T2, γ)∈ M0(Π) la misura supportata sullo skew pant [ρ(T1, T2, γ)] con
peso pari a bγ(T1, T2). Poniamo:
ν(T1, T2) =
X
γ
ν(T1, T2, γ)
dove la somma `e fatta su tutte le triple di geodetiche γ lungo le quali i tripodi T1 e
T2 sono ben connessi. Siamo ora in grado di definire la misura µ del teorema 2.5.4
Definizione 3.3.7. Sia µ ∈ MR0 (Π) data da: µ(Π) = Z F2(M3) ν(T1, T2)(Π)d(Λ2) dove F2(M3) = F(M3) × F(M3) e Λ2= Λ × Λ. Poniamo R = r − log4
3. Dalla definizione di µ e dal lemma 3.3.5 segue che se
µ(Π) > 0 per qualche Π∈ Π, allora: |hl(ωi
0(C)) − R| ≤ Dε
dove hl(ωi
0(C)) indica le mezze lunghezze associate alla rappresentazione ρ.
Rimane ora da costruire la misura β ∈ M0(N1(
√
Γ)) e dimostrare le sue pro-priet`a.
3.4
L’operatore ˜
∂
Siano F1 = (p, u, n) e F2 = (q, v, m) due frame in F(M3), tali che i tripodi associati
Tj = ωi(Fj) siano ben connessi lungo una tripla di segmenti γ = (γ0, γ1, γ2). Sia
q0 ∈ H3un sollevamento di q e siano pi∈ H3, i = 0, 1, 2 i sollevamenti di p lungo γ−1i .
Indicheremo poi con (pi, ui, ni) i corrispondenti sollevamenti di F1 e con (q0, v0, m0)
Fissiamo Ai∈ G tali che A0(p0, u0, n0) = (p1, u1, n1), A1(p1, u1, n1) = (p2, u2, n2),
A2(p2, u2, n2) = (p0, u0, n0). Sia poi ρ : π1(Π0) −→ G definita da ρ(ωi0(c)) = Ai.
Sia hj ∈ N1(axis(A0)), j = 1, 2 il piede della perpendicolare tra axis(A0) e
axis(Aj) che punta verso Aj (questa costruzione `e la stessa fatta nella sezione 2.3
per definire poi la mappa foot). Ricordiamo che vale Aζ(h1) = h2 con ζ = hl(ρ(c)).
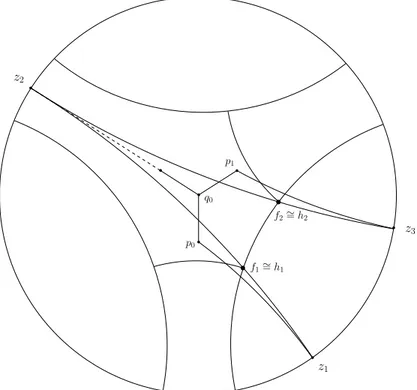
Siano ora: • z1 = lim t→∞gt(p0, ω 2(u 0)) ∈ ∂H3 • z2 = lim t→∞gt(q0, ω −2(v 0)) ∈ ∂H3 • z3 = lim t→∞gt(p1, ω 2(u 1)) ∈ ∂H3
Definiamo le geodetiche α = (z1, z2) e β = (z3, z2). Siano ora f1 il piede della
perpendicolare tra α e axis(A0) che punta verso α e f2 il piede della perpendicolare
tra β e axis(A0) che punta verso β.
La seguente proposizione si dimostra con tecniche di geometria iperbolica ele-mentare:
Proposizione 3.4.1. Usando la notazione appena introdotta, abbiamo che per r abbastanza grande e ε abbastanza piccolo vale la diseguaglianza:
dis(fj, hj) ≤ De
r 4
per qualche costanteD > 0. Inoltre si ha che Aζ(f1) = f2 con ζ = hl(ρ(c)).
Dunque, dato uno skew pant Π = [ρ(T1, T2, γ)], consideriamo (Π, δ?) ∈ Π? per
qualche geodetica orientata δ. Indichiamo con fδ?(T1, T2, γ)∈ N1(
√
δ) la proiezione dei vettori corrispondenti f1 e f2 appena definiti.
Proposizione 3.4.2. Siano T1 e T2 due tripodi ben connessi lungo le triple γj =
(γj 0, γ
j 1, γ
j
2), j = 1, 2 tali che, per qualche i ∈ {0, 1, 2}, si abbia γi1= γi2eγi+11 = γi+12 .
Siaδ? la geodetica inM3 omotopa a γ
i∪ γi+1. Allora si ha:
fδ?(T1, T2, γ1) = fδ?(T1, T2, γ2)
z1 z3 z2 f1∼= h1 f2∼= h2 p0 p1 q0
Figura 3.2: Costruzione di hj e fj nel modello della palla per H3
Proposizione 3.4.3. SiaΠ = [ρ(T1, T2, γ)] e (Π, δ?) ∈ Π. Allora per r abbastanza
grande e ε abbastanza piccolo abbiamo
dis(f ootδ?(Π), fδ?(T1, T2, γ))≤ De− r 4
per qualche D > 0.
Dimostrazione. Segue dalla proposizione 3.4.1 Sia ˜∂δ?(T1, T2, γ)∈ M0(N1(
√
δ)) la misura supportata nel punto fδ?(T1, T2, γ))
con peso pari a bγ(T1, T2). Poniamo:
˜ ∂(T1, T2, γ) = 2 X i=0 ˜ ∂δ?i(T1, T2, γ)
dove ([ρ(T1, T2, γ)], δi?) ∈ Π? sono i tre skew pant marcati che corrispondono a
Proposizione 3.4.4. Le misure ˜∂(T1, T2, γ) e ˆ∂ν(T1, T2, γ) sono De−
r
4-equivalenti,
per qualche costanteD > 0.
Dimostrazione. Segue dalla proposizione 2.4.3 e dalla proposizione 3.4.1 Poniamo: ˜ ∂(T1, T2) = X γ ˜ ∂(T1, T2, γ)
dove la somma `e fatta su tutte le triple di geodetiche γ lungo le quali i tripodi T1 e
T2 sono ben connessi. Definiamo ora la misura β del teorema 2.5.4
Definizione 3.4.5. Sia β ∈ M0(N1( √ Γ)) data da: β(Π) = Z F2(M3) ˜ ∂(T1, T2)(Π)d(Λ2) dove F2(M3) = F(M3) × F(M3) e Λ2= Λ × Λ.
Segue dalle precedenti proposizioni che la misure β e ˆ∂µ sono De−r4 equivalenti.
Rimane ora da stimare la derivata di Radon-Nikodym di β rispetto a quella euclidea su ogni toro in N1(√Γ).
3.5
Dimostrazione del teorema 2.5.4
Fissiamo δ ∈ Γ e sia βδ la restrizione della misura β a N1(
√
δ). Andiamo dunque a stimare la derivata di Radon-Nikodym di βδrispetto alla misura euclidea su N1(
√ δ). Sia Aδ ∈ G l’isometria che corrisponde a δ. Sia Tδ = H3/ < Aδ >. Denotiamo
poi con F(Tδ) = F(H3)/ < Aδ>. Siano F1 = (p, u, n) e F2 = (q, v, m) due frame in
F(Tδ). Denoteremo ancora con F1 e F2 le rispettive proiezioni in F(M3). Diremo
che F1 e F2 sono ben connessi lungo il segmento γ ⊂ Tδ se questo succede per le
rispettive proiezioni in F(M3).
Definizione 3.5.1. Siano F1 e F2 due frame in F(Tδ) e siano B1 e B2 i bipodi
associati. Diremo che (F1, F2) ∈ S(δ) ⊂ F2(Tδ) se esiste una coppia di segmenti
γ = (γ0, γ1) tali che i bipodi B1 e B2 siano ben connessi lungo γ e γ0∪ γ1`e omotopo
Osserviamo che S(δ) `e aperto in F(Tδ). Inoltre, dato (F1, F2) ∈ S(δ) esiste
un’unica coppia di segmenti γ = (γ0, γ1) lungo la quale i corrispondenti bipodi B1 e
B2 sono ben connessi e γ0∪ γ1 `e omotopo a δ.
Fissiamo F1, F2 ∈ S(δ) e la corrispondente coppia γ = (γ0, γ1). Sia ˜δ ⊂ H3
un sollevamento di δ.Sia Aζ ∈ PSL(2, C) la trasformazione che ha come asse ˜δ e
complex translation length pari a ζ ∈ C. Siano Fj(ζ) ∈ F(Tδ) tali che Fj(ζ) =
Aζ(Fj), j = 1, 2. Poniamo poi γ0(ζ) = Aζ(γ0) e γ1(ζ) = Aζ(γ1).
Osserviamo che aγ0(ζ)(F1(ζ), F2(ζ)) e aγ1(ζ)(ω(F1(ζ)), ω
−1(F
2(ζ))) non
dipen-dono da ζ. Questo implica che l’intera orbita di (F1(ζ), F2(ζ)) `e contenuta in
S(δ).
Siano (F1, F2) ∈ S(δ) indichiamo con Tj = ωi(Fj) i corrispondenti tripodi.
Fis-siamo ~n ∈ N1(√δ) e sia S(~n, δ)⊂ S(δ) l’insieme di tutte le coppie (F
1, F2) tali che
fδ(T1, T2, γ) = ~n, per qualche tripla di segmenti γ. Poich´e l’azione di C/hl(δ) + 2πiZ
non ha punti fissi e poich´e C/hl(δ)+2πiZ `e abeliano, possiamo definire la corrispon-dente misura sezionale su S(~n, δ) indotta dalla misura di Liouville Λ, che denoteremo con Λ~n
Calcoliamo la derivata di Radon-Nikodym di βδ nel punto ~n ∈ N1(
√ δ): |dβδ dλ(~n)| = Z S(~n,δ) (X γ bγ(T1, T2))dΛ~n
dove la somma `e fatta su tutte le triple γ lungo le quali T1 e T2 sono ben connessi.
Osserviamo che X γ bγ(T1, T2) = X γ0,γ1 ( X γ2(γ0,γ1) bγ(T1, T2))
dove γ2(γ0, γ1) denota tutti i possibili segmenti tali che T1 e T2 siano ben connessi
lungo (γ0, γ1, γ2(γ0, γ1). Scriviamo ora
X
γ2(γ0,γ1)
bγ(T1, T2) = aγ0(F1, F2)aγ1(ω(F1), ω
−1(F
2))a(ω2(F1), ω−2(F2))
Dal lemma 3.1.7 sappiamo che: a(ω2(F
1), ω−2(F2)) = Λ(M1 3(1 + O(e
−qr 2))
X γ2(γ0,γ1) bγ(T1, T2) = 1 Λ(M3(1 + O(e −qr 2))aγ 0(F1, F2)aγ1(ω(F1), ω −1(F 2))
Sia ora ~n(ζ) = Aζ(~n). Allora si ha:
|dβδ dλ(~n(ζ))| = 1 Λ(M3(1 + O(e −qr 2))X(ζ) dove X(ζ) = Z S(~n,δ) X γ0(ζ),γ1(ζ) aγ0(ζ)(F1(ζ), F2(ζ))aγ1(ζ)(ω(F1(ζ)), ω −1(F 2(ζ)))dΛ~n(ζ)
Poich´e X(ζ) non dipende da ζ ∈ C e poich´e Aζ agisce transitivamente su N1(
√ δ), concludiamo che la derivata di β rispetto a un certo multiplo della misura euclidea `e esponenzialmente vicina a 1 su ogni toro in N1(√Γ). Questo prova il teorema 2.5.4.
[1] Jeremy Kahn, Vladimir Markovic, “Immersing almost geodesic surface in 3-hyperbolic manifold” arXiv:0910.5501
[2] Jeremy Kahn, Vladimir Markovic “The Weil-petersson distance bet-ween finite degree covers of punctured Riemann surfaces and random ideal triangulations” arXiv:0806.2304
[3] C.Kourouniotis “Complex length coordinates for quasi-fuchsian groups” Mathematika, 41 (1994), 173 − 188
[4] C.Moore, “Exponential decay of correlation coefficients for geodesic flows.” Group representations, ergodic theory, operator algebras, and mathematical physics (Berkeley, Calif., 1984), 163 − 181, Math. Sci. Res. Inst. Publ., 6, Springer, New York, (1987)
[5] C.Series, “An extension of Wolpert’s derivative formula.”Pacific J. Math. 197 (2001), no. 1, 223 − 229