Formazione di immagini ISAR 3D con configurazioni radar interferometriche e bistatiche

UNIVERSITÀ DI PISA

FACOLTÀ DI INGEGNERIA

CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI

TESI DI LAUREA MAGISTRALE

FORMAZIONE DI IMMAGINI ISAR 3D CON

CONFIGURAZIONI RADAR INTERFEROMETRICHE E

BISTATICHE

Relatori:

Candidato:

Prof. Fabrizio Berizzi Emiliano Casalini

Prof. Marco Martorella

Ing. Daniele Staglianò

Ing. Elisa Giusti

i

I

NDICE

Introduzione ...1

1. ISAR: Inverse Synthetic Aperture Radar ...3

1.1 Il moto ...4

1.2 La geometria ...7

1.3 Il segnale ricevuto ...8

1.4 La costruzione dell’immagine ISAR ...11

1.5 Point Spread Function (PSF) ...14

1.6 Tecnica Range-Doppler (RD) ...17

1.7 Compensazione del moto ...19

2. B-ISAR: Bistatic ISAR ...23

2.1 Il segnale ricevuto...25

2.2 Point Spread Function ...26

2.3 Distorsioni bistatiche ...28

2.4 Vettore di rotazione effettivo bistatico ...31

3. 3D-ISAR: Three Dimensional ISAR ...36

3.1 Monostatico: caso non-squinted ...37

3.2 Monostatico: caso squinted H/V ...43

3.3 Monostatico: caso squinted H&V ...51

3.4 Monostatico: metodo phase compensation ...55

3.5 Bistatic ISAR ...62

4. Analisi delle prestazioni ...69

4.1 Monostatico: configurazione non-squinted ...71

4.2 Monostatico: configurazione squinted ...74

4.3 Monostatico: al variare dell’angolo di squinted ...77

4.4 Monostatico: a parità di baseline efficace ...80

4.5 Bistatico: configurazione non-squinted ...84

4.6 Bistatico: configurazione squinted ...87

4.7 Bistatico: al variare dell’angolo bistatico ...90

ii 4.9 Confronto: Monostatico vs BEM ...96 5. Conclusioni ...100 Bibliografia ...102

1

I

NTRODUZIONE

L’ISAR (Inverse Synthetic Aperture Radar), in italiano “Radar ad Apertura Sintetica Inverso”, è una tecnica di elaborazione del segnale che consente di ottenere l’immagine elettromagnetica ad alta risoluzione di un bersaglio non cooperante. Tale tecnica, ampliamente trattata nella letteratura recente, viene frequentemente utilizzata sia in contesto civile che militare ai fini – per esempio – della classificazione (Automatic

Target Classification, ATC) e del riconoscimento (Automatic Target Recognition, ATR)

dei target non cooperanti. Molteplici sono le configurazioni proposte e consolidate nel corso degli anni: ad oggi esistono sistemi ISAR di tipo monostatico e multistatico, siano essi attivi o passivi, capaci di utilizzare segnali con diverse polarizzazioni. Quale che sia la configurazione in esame, adottando la tecnica ISAR classica conseguiamo al più una immagine bidimensionale del target, ovvero la stima della sua funzione di riflettività proiettata sul cosiddetto piano immagine. Ciò rappresenta una indubbia limitazione in quanto l’interpretazione di una immagine ISAR bidimensionale non è mai semplice: potenzialmente posizione e moto relativo potrebbero essere tali per cui non sia possibile riconoscere dall’immagine il target in esame. V’è quindi la necessità di realizzare 3D-ISAR, ovvero ricostruire la funzione di riflettività tridimensionale del target, risultato che può essere conseguito utilizzando i concetti propri dell’interferometria.

La fase interferometrica porta l’informazione sulla quota degli scatteratori componenti il target in quanto – a meno di ambiguità di fase – esiste una relazione univoca fra fase interferometrica e quota stessa. In questa tesi viene allora studiato teoricamente ed implementato un sistema ISAR multicanale progettato affinchè ricostruisca l’immagine 3D del target adottando un approccio interferometrico. I diversi canali possono lavorare sia in configurazione monostatica, problema già trattato in [1] e [2], che in configurazione bistatica grazie alla quale riusciamo a risolvere il problema rappresentato dalle traiettorie ad angolo di vista costante. Inoltre, la configurazione bistatica permette di rivelare la presenza di target di tipo stealth capaci di riflettere

2 l’energia elettromagnetica in una direzione diversa da quella che individua il trasmettitore. L’analisi del caso bistatico rappresenta un primo passo verso lo studio e l’implementazione di sistemi 3D-ISAR multistatici per mezzo dei quali aumenta la capacità di riconoscimento del target non cooperante.

La presente tesi è organizzata come segue: nel capitolo 1 vengono richiamati i concetti di base della tecnica ISAR focalizzando l’attenzione sulla configurazione monostatica, per la quale si calcolano Point Spread Function (PSF) ed annesse risoluzioni. Nel capitolo 2 viene esposta una generalizzazione della tecnica ISAR al caso bistatico, ed analogamente al caso monostatico se ne valuta la PSF mettendo in risalto talune delle distorsioni introdotte dalla diversa geometria. Quindi, nel capitolo 3, viene riproposta la tecnica di ricostruzione 3D-ISAR per sistemi in configurazione monostatica e la si generalizza in un secondo momento al caso bistatico. Nel capitolo 4, invece, sono illustrati i risultati ottenuti in ambiente Matlab dove è stata testata la suddetta tecnica. Infine, il lavoro di tesi termina con le conclusioni di capitolo 5.

3

C

APITOLO

1

ISAR:

I

NVERSE

S

YNTHETHIC

A

PERTURE

R

ADAR

L’ISAR è una tecnica che permette di ricostruire immagini elettromagnetiche di target non cooperanti dove, se la cella di risoluzione è sufficientemente piccola, siamo in grado di apprezzare le proprietà di retrodiffusione dei singoli scatteratori. La risoluzione in range di un radar che implementa la tecnica della compressione di impulso è legata alla banda occupata dal segnale trasmesso secondo la seguente legge:

∆

_𝑅

_{= c 2B}

_(1.1)

dove c è la velocità della luce nel vuoto mentre B è la banda del segnale trasmesso. Una elevata risoluzione in range viene quindi ottenuta trasmettendo segnali a banda molto larga, quali per esempio i segnali modulati in fase e frequenza, e realizzando un’opportuna compressione di impulso. Nelle telecomunicazioni, ed in particolare nelle applicazioni radar, il segnale comunemente utilizzato è il segnale chirp dove la frequenza istantanea varia linearmente nel tempo di trasmissione e la sua escursione totale è approssimativamente la banda del segnale stesso. D’altro canto, una spinta risoluzione in cross-range può essere conseguita usando una antenna il cui angolo di apertura sul piano azimutale sia sufficientemente piccolo:

∆

_𝐶𝑅

= 𝑅𝜗

_𝐴𝑍 (1.2)

E' allora evidente come la risoluzione in cross-range migliori al diminuire dell'angolo d'apertura di antenna, ma tanto più è piccolo tale angolo tanto maggiore è la dimensione dell'antenna, e laddove desiderassimo risoluzioni dell’ordine del metro se non inferiori, tale dimensione risulterebbe essere enorme. Per questa ragione l’ISAR ripropone il concetto di base della tecnica SAR (Synthetic Aperture Radar): nel SAR, sfruttando il

4 movimento della piattaforma su cui è posto il radar ed elaborando coerentemente gli echi ricevuti, è possibile definire una antenna sintetica di dimensione molto grande e raggiungere di conseguenza la risoluzione in cross-range desiderata. Nell’ISAR si ricorre alla versione “inversa” della tecnica SAR: il radar è fisso mentre il target è in movimento, ed elaborando coerentemente gli echi ricevuti è possibile conseguire la risoluzione voluta. In realtà, un processing corretto del segnale ricevuto non è condizione sufficiente tale da garantire l’elevata risoluzione in cross-range. Difatti, come si dimostra nei paragrafi successivi tale risoluzione risulta essere funzione della variazione totale dell'angolo di vista la quale è data dal moto relativo fra il radar ed il

target non cooperante. Di conseguenza, solo se nel tempo di integrazione l’angolo di

vista con il quale il radar illumina il bersaglio varia sufficientemente otteniamo l’immagine elettromagnetica alla risoluzione desiderata.

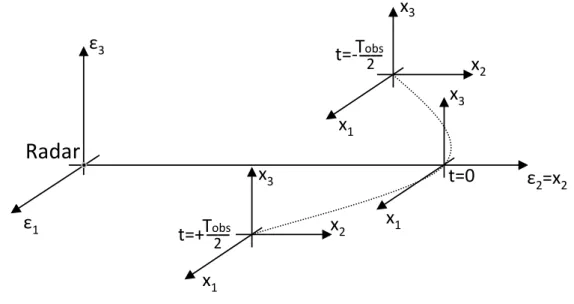
Di seguito è riportato un semplice scenario di riferimento:

Figura 1.1 – Scenario di riferimento

1.1 IL

MOTO

Il moto del target rispetto al radar durante il tempo di osservazione veste un ruolo di basilare importanza ai fini del successo della tecnica ISAR. Difatti, il moto interviene fissando il piano immagine e definisce la variazione totale dell’angolo di vista direttamente legata alla risoluzione che si ottiene nella direzione di cross-range. Il moto del target può essere sempre scomposto come somma di due diversi contributi:

 moto di traslazione del baricentro O;  moto di rotazione attorno al baricentro O.

Bersaglio

Traiettoria

5 Questo secondo moto può essere ulteriormente suddiviso in due diversi moti di rotazione:

 moto di rotazione traslazionale: Ωtr;

 moto di rotazione proprio: Ω.

Per semplicità di rappresentazione grafica si prenda in esame un target in moto su traiettoria rettilinea e planare in (ε1,ε2) dove per il momento si trascurano eventuali moti

propri di rotazione:

Figura 1.2 – Target con moto di rotazione traslazionale

L’angolo evidenziato in fig. 1.2 è l’angolo di vista mentre la linea tratteggiata individua la Line of Sight (LoS). Si noti come nonostante non vi sia alcun moto di rotazione proprio, il solo moto di traslazione del target si traduce in una variazione dell’angolo di vista. Possiamo quindi interpretare il moto come somma fra un primo moto di traslazione del baricentro (ad angolo di vista costante) ed un secondo moto di rotazione (traslazionale) che provoca la variazione dell’angolo di vista. Nell’esempio specifico il vettore di rotazione totale è coincidente con il vettore di rotazione traslazionale ed è ortogonale al piano (ε1,ε2):

Ω

_𝑻

= Ω

_𝒕𝒓

⊥ (Ԑ

₁

, Ԑ

₂

)

(1.3) Nel caso più generale il target, oltre a sperimentare moto di rotazione traslazionale, può anche essere caratterizzato da moto di rotazione proprio causato – per esempio – da fenomeni oscillatori intorno all’asse longitudinale (roll), trasversale (pitch) e verticale (yaw).

Si prenda in esame lo stesso identico esempio appena esposto dove, a parità di traiettoria, introduciamo un generico moto di rotazione proprio attorno all’asse verticale passante per il baricentro del target (yaw). In fig. 1.3 è illustrato lo scenario proposto:

ε₁ ε₂

Radar

t=-T

__

obs₂ t=+T

__

obs₂ t=0

6 Figura 1.3 – Target con moto di rotazione traslazionale e proprio

La rotazione complessiva non è più solo quella data dal moto traslatorio ma abbiamo un secondo contributo relativo alla rotazione del target attorno all’asse verticale passante per il baricentro. Analogamente all’esempio precedente, il vettore di rotazione totale è ortogonale al piano (ε1,ε2):

Ω

_𝑻

= (Ω

_𝒕𝒓

+ Ω) ⊥ (Ԑ

₁

, Ԑ

₂

)

(1.4) Quanto visto fino al momento ci induce a pensare che la variazione totale dell’angolo di vista nel tempo di osservazione sia data dal vettore di rotazione totale ma questo non è necessariamente vero. Negli esempi riportati il vettore di rotazione totale risulta giacere sul piano ortogonale alla LoS e per questa ragione produce una variazione dell’angolo di vista. Nel caso più generale la traiettoria del target può essere tridimensionale ed il vettore di rotazione totale potenzialmente può essere orientato in una qualsiasi direzione. In tal contesto, il vettore di rotazione totale è scomponibile in due diversi contributi:

Ω

_𝑻 =

Ω

_𝒆𝒇𝒇

+ Ω

_𝑳𝑶𝑺 (1.5)

dove Ωeff è la proiezione sul piano ortogonale alla LoS mentre ΩLOS è la proiezione sulla

LoS, contributo che risulta essere del tutto irrilevante ai fini del processo di imaging in quanto non provoca una variazione dell’angolo di vista. Infatti, il radar riesce a discriminare i diversi scatteratori nella coordinata di cross-range solo e soltanto se il moto del target genera un cambiamento dell’angolo di vista. Ciò significa che al variare del tempo lento la distanza tra il generico scatteratore ed il radar deve necessariamente cambiare, ma laddove vi fosse una rotazione attorno all’asse parallelo alla LoS, pur essendo presente un movimento rotatorio degli scatteratori, la distanza che intercorre fra il generico scatteratore ed il radar risulterebbe essere costante nel tempo. Quindi si

ε₁ ε₂

Radar

t=-T

__

obs₂ t=+T

__

obs₂ t=0

7 conclude che la variazione dell’angolo di vista nel tempo di integrazione è data dal solo vettore di rotazione effettivo. Inoltre, ed è stato dimostrato in [3], il vettore di rotazione effettivo definisce il piano immagine, Image Plane Projection (IPP), rispetto al quale si forma l’immagine che risulta essere ortogonale al vettore stesso.

1.2 LA

GEOMETRIA

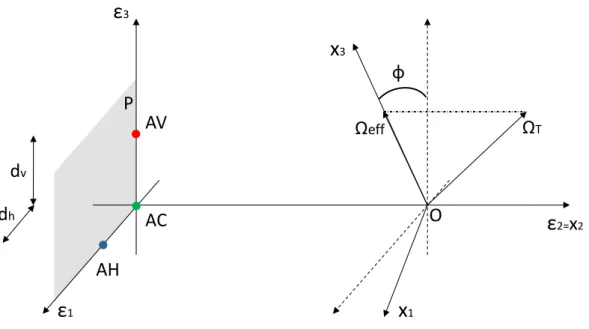
In fig. 1.4 viene riportata la geometria che è stata adottata nel prosieguo della tesi:

Figura 1.4 – Geometria del sistema

In primis si definisce il sistema di riferimento Tε di assi (ε1, ε2, ε3) nella cui origine è

collocato il radar. Si introduce quindi un secondo sistema di riferimento, Tx, di assi (x1,

x2, x3), la cui origine è coincidente con O, punto di riferimento posto sul target: l’asse x3

è preso parallelo al vettore di rotazione effettivo, l’asse x2 parallelo alla LoS relativa

all’istante temporale t=0 mentre l’asse x1 ortogonale al piano individuato da (x2, x3). Al

variare del tempo lento, indipendentemente dalla traiettoria intrapresa dal target, gli assi di questo sistema di riferimento sono sempre egualmente orientati. Adottando il sistema di riferimento Tx appena descritto, il piano (x1, x2) risulta essere coincidente con il

piano immagine ed i due assi identificano rispettivamente la direzione di cross-range e

range. Infine, introduciamo un terzo sistema di riferimento, Ty, di assi (y1, y2, y3),

centrato sul target, la cui origine è ancora il punto di riferimento O ed è definito come coincidente con il sistema di riferimento Tx solo e soltanto per l’istante temporale t=0.

Al fine di comprendere meglio la differenza fra i due sistemi di riferimento si prenda in esame il caso di un target composto da due scatteratori puntiformi ..

ε₁ ε₂=x₂ ε₃ x₁ x₂ x₃ x₁ x₁ x₂ x₃ x₃ t=-T

__

obs 2 t=0 t=+T

__

obs₂

Radar

8 Figura 1.5 – Tempo varianza dei sistemi di riferimento

Come si apprezza valutando fig. 1.5, la posizione relativa degli scatteratori rispetto al sistema di riferimento Ty è la stessa durante l’intero intervallo di osservazione; d’altro

canto, la posizione relativa degli stessi scatteratori rispetto al sistema di riferimento Tx

varia in funzione del tempo.

1.3 IL

SEGNALE

RICEVUTO

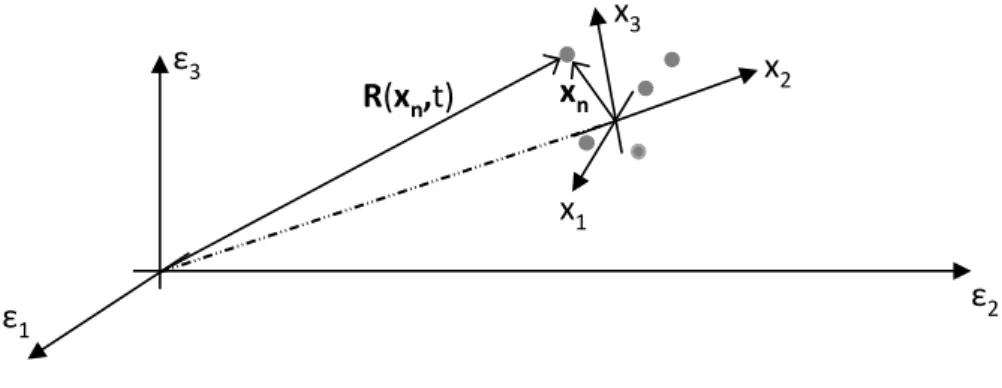
La trattazione che segue è indipendente dal tipo di segnale che è stato utilizzato in trasmissione. Si ipotizzi, per semplicità, che il target illuminato sia costituito da un insieme finito di punti di scattering come raffigurato in fig. 1.6:

Figura 1.6 – Target composto da un insieme finito di scatteratori

Si indichi con sTX(α) il segnale utilizzato in trasmissione. Nell'ipotesi semplificativa in

cui vi fosse un singolo scatteratore, il segnale ricevuto risulterebbe essere semplicemente una versione attenuata e ritardata del segnale trasmesso. Viceversa, nel caso in cui avessimo un target definito da N scatteratori puntiformi, in prima

x₁=y₁ x₁ x₂=y₂ x₂ y₁ y₂ x₃=y₃ t=0 t=t* x₃ ε₁ ε2 x₂ x₁ ε₃ x_n R(x_n,t)

9 approssimazione possiamo utilizzare il principio della sovrapposizione degli effetti. Ciò significa che il segnale ricevuto è dato dalla somma di N repliche del segnale trasmesso, ciascuna opportunamente attenuata e ritardata:

𝑠

_𝑅𝑋

(𝛼) =

𝜍

_𝑛

𝑠

_𝑇𝑋

(𝛼 − Ƭ

_𝑛

(𝛼))

𝑁

𝑛=1

(1.6) dove σn è un coefficiente moltiplicativo complesso dato dalle caratteristiche

elettromagnetiche dello scatteratore mentre Τn(α) è il ritardo di propagazione funzione

della distanza Rn(α) che intercorre fra lo scatteratore in esame ed il radar per il generico

istante temporale α. Esplicitando in eq. 1.6 il round-trip delay (RTD) si ottiene il seguente segnale:

𝑠

_𝑅𝑋

(𝛼) =

𝜍

_𝑛

𝑠

_𝑇𝑋

6𝛼 −

2𝑅

𝑛

(𝛼)

𝑐

7 =

𝑁 𝑛 =1

=

𝜍

_𝑛

𝑠

_𝑇𝑋

𝛼 −

2𝑅(𝒙

𝒏

, 𝛼)

𝑐

𝑁 𝑛=1 (1.7)

dove xn è la posizione dell’n-esimo scatteratore rispetto al sistema di riferimento Tx. Sia

inoltre pari a Tobs secondi il tempo di osservazione, intervallo temporale durante il quale

il radar “osserva” il target. Questo intervallo è suddivisibile in N sweep successive della durata di TR secondi cadauna per ciascuna delle quali il radar trasmette il segnale e

riceve l'eventuale eco. Possiamo quindi calcolare il segnale ricevuto per la k-esima

sweep come segue:

𝑠

_𝑅𝑋

(𝛼, 𝑘𝑇

_𝑅

) =

𝜍

_𝑛

𝑠

_𝑇𝑋

𝛼 − 𝑘𝑇

_𝑅

−

2𝑅(𝒙

𝒏

, 𝛼)

𝑐

𝑁 𝑛=1

(1.8) con 𝛼 ∈ ,𝑘𝑇_𝑅, (𝑘 + 1)𝑇_𝑅-. Per semplicità di trattazione si supponga che sia verificata l'approssimazione stop and go, ovvero si ipotizzi che lo scatteratore si trova nella stessa identica posizione durante l'intera sweep e si muova rispetto al radar a scatti di TR in TR.

Sotto tale ipotesi, la distanza in eq. 1.8 può essere approssimata come segue:

𝑅(𝒙

_𝒏

, 𝛼) ≈ 𝑅(𝒙

_𝒏

, 𝑘𝑇

_𝑅

)

(1.9) Sostituendo eq. 1.9 in eq. 1.8 siamo quindi in grado di esprimere il segnale ricevuto nel formato “tempo veloce - tempo lento”:

𝑠

_𝑅𝑋

(𝜏, 𝑘𝑇

_𝑅

) =

𝜍

_𝑛

𝑠

_𝑇𝑋

𝜏 −

2𝑅(𝒙

𝒏

, 𝑘𝑇

𝑅

)

𝑐

𝑁

𝑛=1

(1.10) con 𝜏 ∈ ,0, 𝑇_𝑅-. Il segnale ottenuto lo possiamo inoltre pensare come risultato del campionamento realizzato nel tempo lento di un segnale continuo sia nel tempo veloce che nel tempo lento. Tale campionamento viene realizzato a passi di TR con frequenza

10

𝑠

_𝑅𝑋

(𝜏, 𝑡) =

𝜍

_𝑛

𝑠

_𝑇𝑋

𝜏 −

2𝑅(𝒙

𝒏

, 𝑡)

𝑐

𝑁

𝑛=1 (1.11)

con 𝜏 ∈ ,0, 𝑇_𝑅- e 𝑡 ∈ ,− 𝑇_𝑜𝑏𝑠 , 𝑇2 _𝑜𝑏𝑠 -.2 Esprimiamo ora il segnale ricevuto di eq. 1.11 esplicitando la cosiddetta funzione di riflettività, la quale è una funzione complessa espressa nel dominio spaziale che definisce le proprietà elettromagnetiche del target. Specificatamente al bersaglio puntiforme trattato nel paragrafo, la funzione di riflettività sarà una sommatoria di delta di Dirac tridimensionali opportunamente pesate:

𝑓(𝒙) =

𝜍

_𝑛

𝜕(𝒙 − 𝒙

_𝒏

)

𝑁

𝑛=1

(1.12) Sostituendo 1.12 in eq. 1.11 il segnale ricevuto assume la seguente forma:

𝑠

_𝑅𝑋

(𝜏, 𝑡) = 𝑓(𝒙)

𝑉

𝑠

_𝑇𝑋

𝜏 −

2𝑅(𝒙

𝒏

, 𝑡)

𝑐

𝑑𝒙

(1.13)

con 𝜏 ∈ ,0, 𝑇_𝑅-, 𝑡 ∈ ,− 𝑇_𝑜𝑏𝑠 , 𝑇2 _𝑜𝑏𝑠 - e dove V è la regione spaziale “coperta” dalla 2 funzione di riflettività ovvero quella regione nella quale è presente il bersaglio. Infine, usando la proprietà campionatrice della delta di Dirac si ottiene ..

𝑠

_𝑅𝑋

(𝜏, 𝑡) = 𝑓(𝒙)

𝑉

𝑠

_𝑇𝑋

𝜏 −

2𝑅(𝒙, 𝑡)

𝑐

𝑑𝒙

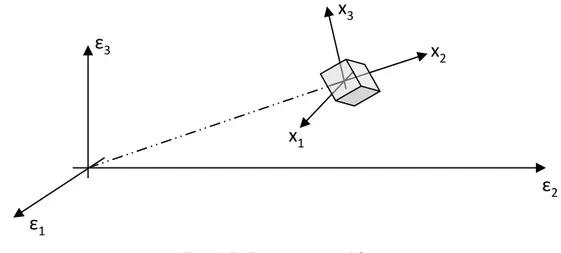
(1.14)

Il modello di segnale ricevuto di eq. 1.14 è stato ottenuto partendo dall’ipotesi di target puntiforme ma ciò nonostante tale modello è valido anche per target estesi spazialmente come quello rappresentato in fig. 1.7:

Figura 1.7 – Target esteso spazialmente

La differenza sostanziale sta nel fatto che la funzione di riflettività di eq. 1.14 non è più definita da un numero finito di delta di Dirac tridimensionali quanto è una funzione tridimensionale continua nello spazio che possiamo interpretare come una sorta di

Radio Cross Section (RCS) per unità di volume.

ε

₁

ε

₂

ε

₃

x

₁

x

₂

x

₃

11

1.4 COSTRUZIONE

DELL’IMMAGINE

ISAR

Nel presente paragrafo vengono discusse le operazioni necessarie per conseguire l’immagine ISAR partendo dal segnale ricevuto di eq. 1.14. In primis viene realizzato un opportuno pre-processing che consiste in un’analisi spettrale rispetto al tempo veloce τ ed in un filtraggio adattato rispetto all’inviluppo complesso del segnale trasmesso. Realizzando la trasformata di Fourier del segnale ricevuto rispetto alla variabile di tempo veloce τ si ottiene il seguente risultato

:

𝑆

_𝑅𝑋

(𝑓, 𝑡) = 𝑆

_𝑇𝑋

(𝑓) 𝑓(𝒙)𝑒

−𝑗 2𝜋𝑓 (2𝑅(𝒙,𝑡)𝑐 ) 𝑉

𝑑𝒙

(1.15)

Eseguiamo quindi il filtraggio adattato all’inviluppo complesso del segnale trasmesso:

𝑆

_𝑅𝑋′

(𝑓, 𝑡) = 𝑆

_𝑅𝑋

(𝑓, 𝑡)𝑆

_𝑇𝑋∗

_{(𝑓) = |𝑆}

𝑇𝑋

(𝑓)|

2

𝑓(𝒙)𝑒

−𝑗 2𝜋𝑓 ( 2𝑅(𝒙,𝑡) 𝑐 ) 𝑉

𝑑𝒙

(1.16) dove il termine |𝑆_𝑇𝑋(𝑓)|2 _{può essere compensato dal segnale ricevuto poiché è un}

termine noto. Ricordando inoltre che il segnale trasmesso ha banda limitata e che il

target è osservato per un intervallo temporale finito, modifichiamo il segnale di eq. 1.16

ottenendo il seguente risultato:

𝑆

_𝑅𝑋′

(𝑓, 𝑡) = 𝑟𝑒𝑐𝑡

𝑓 − 𝑓

0

𝐵

𝑟𝑒𝑐𝑡

𝑡

𝑇

_𝑜𝑏𝑠

𝑓(𝒙)𝑒

−𝑗 2𝜋𝑓 2𝑅(𝒙,𝑡)_𝑐 𝑉

𝑑𝒙 =

= 𝑊(𝑓, 𝑡) 𝑓(𝒙)𝑒

−𝑗 2𝜋𝑓 2𝑅(𝒙,𝑡) 𝑐 𝑉

𝑑𝒙

(1.17)

dove 𝑓0 è la frequenza portante mentre 𝑊(𝑓, 𝑡) è la finestra entro la quale è noto il

segnale ricevuto. Concentriamoci ora sul termine 𝑅(𝒙, 𝑡) che rappresenta la distanza fra il generico punto posto sul target ed il centro di fase dell’antenna per l’istante di tempo lento in esame. Sia D la massima estensione del target: se ..

𝐷 ≪ 𝑅

₀

(𝑡)

(1.18)

.. allora si commette un errore trascurabile approssimando il modulo del vettore 𝑹(𝒙, 𝑡) con il modulo della sua proiezione lungo la LoS:

𝑅(𝒙, 𝑡) ≈ 𝑅

₀

(𝑡) + 𝒙 • 𝒊

_𝑳𝑶𝑺

(𝑡)

(1.19) Questa ipotesi prende il nome di Straight Iso-Range Approximation ed è spesso verificata poiché negli scenari tipici di utilizzo della tecnica ISAR la dimensione del

12 Calcoliamo la distanza fra il focusing-point e la proiezione dello scatteratore sulla LoS:

𝒊

_𝑳𝑶𝑺

(𝑡) = 𝑠𝑖𝑛 𝜗(𝑡) 𝒊

_𝟏

+ 𝑐𝑜𝑠 𝜗(𝑡) 𝒊

_𝟐 (1.20a)

𝒙 = 𝑥

₁

𝒊

_𝟏

+ 𝑥

₂

𝒊

_𝟐

+ 𝑥

₃

𝒊

_𝟑 (1.20b)

𝒙 • 𝒊

_𝑳𝑶𝑺

(𝑡) = 𝑥

₁

𝑠𝑖𝑛 𝜗(𝑡) + 𝑥

₂

𝑐𝑜𝑠 𝜗(𝑡)

(1.20c) dove 𝜗(𝑡) è l’angolo di vista per il generico istante temporale mentre ik è il versore che

individua la direzione associata all’asse xk del sistema di riferimento Tx. Utilizzando

l’approssimazione 1.19 in eq. 1.17, e sostituendo al prodotto scalare il risultato ottenuto in 1.20c, il segnale ricevuto assume la seguente forma:

𝑆

_𝑅𝑋′

(𝑓, 𝑡) = 𝑊(𝑓, 𝑡)𝑒

−𝑗 2𝜋𝑓 2𝑅0(𝑡) 𝑐

_{𝑓(𝒙)𝑒}

−𝑗 2𝜋𝑓 6 2 𝒙•𝒊_𝑳𝑶𝑺(𝑡) 𝑐 7 𝑉

𝑑𝒙 =

= 𝑊(𝑓, 𝑡)𝑒

−𝑗 4𝜋𝑓𝑅0𝑐(𝑡)

_{𝑓(𝒙)𝑒}

−𝑗 4𝜋𝑓 𝑥1𝑠𝑖𝑛 𝜗 (𝑡) +𝑥2𝑐𝑜𝑠 𝜗 (𝑡) 𝑐 𝑉

𝑑𝒙

(1.21) Si noti ora che la sola funzione di riflettività dipende dalla coordinata x3 che rappresenta

la quota dello scatteratore rispetto al piano immagine. Ciò significa che integrando rispetto a x3 interveniamo solo e soltanto sulla funzione 𝑓(𝒙):

𝑆_𝑅𝑋′ (𝑓, 𝑡) = 𝑊(𝑓, 𝑡)𝑒−𝑗 4𝜋𝑓𝑅0𝑐(𝑡) _{𝑔(𝑥1, 𝑥2})𝑒−𝑗 4𝜋𝑓

𝑥1𝑠𝑖𝑛 𝜗 (𝑡) +𝑥2𝑐𝑜𝑠 𝜗 (𝑡)

𝑐 𝑆

𝑑𝑥1𝑑𝑥2 (1.22)

dove 𝑔(𝑥1, 𝑥2) è la proiezione della funzione di riflettività sul piano immagine:

𝑔(𝑥

₁

, 𝑥

₂

) ≜ 𝑓(𝑥

₁

, 𝑥

₂

, 𝑥

₃

)𝑑𝑥

₃ 𝑥3

(1.23) E' quindi evidente come, disponendo del solo segnale bidimensionale di eq. 1.14, dopo un opportuno processing riusciamo ad ottenere al più una stima della proiezione della funzione di riflettività sul piano immagine. Allo stato attuale non è possibile stimare la funzione di riflettività del target poiché non è possibile ricostruire una funzione tridimensionale partendo da un segnale bidimensionale.

Terminato il pre-processing si realizza la costruzione vera e propria della immagine ISAR: di seguito si elencano le operazioni fondamentali.

Compensazione del Moto (Motion Compensation): questa operazione consiste nella

rimozione del termine 𝑒−𝑗 4𝜋𝑓𝑅0(𝑡)𝑐 _{che introduce una vera e propria modulazione di fase} sul segnale ricevuto. Questo termine di fase è da ricondursi al moto radiale del punto di riferimento posto sul target e deve necessariamente essere compensato poiché in caso contrario otterremmo una immagine ISAR non focalizzata. Perché sia possibile

13 compensare il moto è obbligatorio stimare con cura il termine 𝑅₀(𝑡) e ciò viene fatto utilizzando tecniche parametriche o non parametriche. Nel prosieguo del capitolo verrà analizzata con cura una precisa tecnica di compensazione del moto chiamata Image

contrast based-technique (ICBT). Per il momento si ipotizzi che sia stata realizzata una

perfetta compensazione del moto: rimuovendo il termine di fase dal segnale di eq. 1.22 si ottiene il seguente risultato:

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡) = 𝑊(𝑓, 𝑡) 𝑔(𝑥

₁

, 𝑥

₂

)𝑒

−𝑗 4𝜋𝑓 𝑥1𝑠𝑖𝑛 𝜗 (𝑡) +𝑥𝑐 2𝑐𝑜𝑠 𝜗 (𝑡) 𝑆

𝑑𝑥

₁

𝑑𝑥

₂ (1.24)

Mappatura delle Frequenze Spaziali (Spatial Frequency Mapping): il risultato di eq.

1.24 può essere interpretato come la trasformata di Fourier bidimensionale della proiezione della funzione di riflettività sul piano immagine. Perché sia più evidente, si realizzino le seguenti trasformazioni di coordinate:

8

𝑋

1

= (2𝑓 𝑐

)𝑠𝑖𝑛 𝜗(𝑡)

𝑋

₂

= (2𝑓 𝑐

)𝑐𝑜𝑠 𝜗(𝑡)

(1.25) Così facendo ogni singolo campione del segnale 𝑆_𝑅𝑋𝐼 (𝑓, 𝑡) viene mappato in un punto del piano delle frequenze spaziali (𝑋₁, 𝑋₂), ed il segnale ricevuto può essere quindi riscritto come segue:

𝑆

_𝑅𝑋𝐼𝐼

(𝑋

₁

, 𝑋

₂

) = 𝑊(𝑋

₁

, 𝑋

₂

) 𝑔(𝑥

₁

, 𝑥

₂

)𝑒

−𝑗 2𝜋𝑓 (𝑋₁𝑥₁+𝑋₂𝑥₂) 𝑆

𝑑𝑥

₁

𝑑𝑥

₂ (1.26) dove:

𝑊(𝑋

₁

, 𝑋

₂

) = 1, (𝑋

₁

, 𝑋

₂

) ∈ D

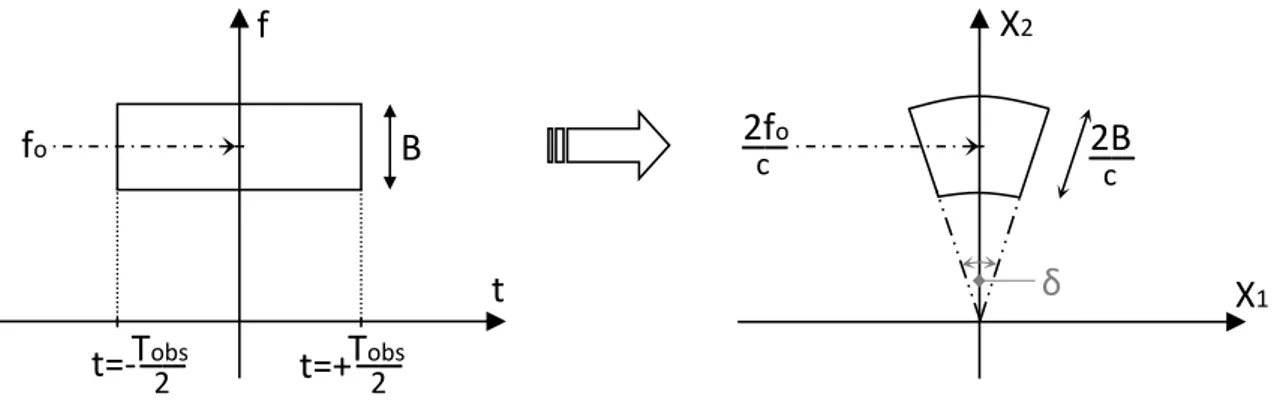
.. che rappresenta il dominio Cartesiano all'interno del quale conosciamo la trasformata di Fourier bidimensionale della funzione 𝑔(𝑥₁, 𝑥₂). In fig. 1.8 viene rappresentata la regione D prima in funzione di frequenza e tempo lento, e poi in funzione delle frequenze spaziali:

Figura 1.8 – Dominio entro il quale è nota la TF del segnale ricevuto

f t B t=-T

__

obs₂ t=+T

__

obs₂ 2B

__

c 2fo

__

c X1 X2 δ fo

14 dove δ rappresenta la variazione totale dell’angolo di vista nel tempo di osservazione e può essere calcolata come segue:

𝛿 = θ +Tobs

2 − θ − Tobs

2

Trasformata inversa di Fourier bidimensionale: la ricostruzione della proiezione

della funzione di riflettività sul piano immagine può essere ottenuta calcolando la 2D-IFT del segnale di eq. 1.26 ottenendo il seguente risultato:

𝑔 (𝑥

₁

, 𝑥

₂

) = 𝑤(𝑥

₁

, 𝑥

₂

) ⊗⊗ 𝑔(𝑥

₁

, 𝑥

₂

)

(1.27) dove la funzione 𝑤(𝑥₁, 𝑥₂) prende il nome di Point Spread Function (PSF) e rappresenta a tutti gli effetti la risposta impulsiva del sistema ISAR che può essere schematizzato come segue:

Figura 1.9 – Schematizzazione sistema ISAR

Il sistema di imaging può allora essere interpretato come un sistema lineare e spazio invariante con risposta impulsiva 𝑤(𝑥1, 𝑥2) che viene alimentato dall’esterno dalla

funzione di riflettività proiettata sul piano immagine 𝑔(𝑥1, 𝑥2).

Valore assoluto: l’immagine ISAR viene infine ottenuta realizzando il valore assoluto

della funzione di riflettività ricostruita di eq. 1.27:

𝐼 (𝑥

₁

, 𝑥

₂

) = 𝑔 (𝑥

1

, 𝑥

2

)

(1.28)

1.5 POINT

SPREAD

FUNCTION

(PSF)

Nel paragrafo precedente abbiamo visto come la PSF del sistema ISAR si calcoli facendo la trasformata di Fourier bidimensionale inversa della funzione “finestra” entro la quale è nota la trasformata del segnale ricevuto. Tale PSF veste un ruolo di basilare importanza poiché definisce la risoluzione spaziale del sistema. Si ipotizzi, per semplicità, che tale funzione sia una delta di Dirac bidimensionale. Come sappiamo, la delta di Dirac è una funzione neutra all’operazione di convoluzione e di conseguenza la ricostruzione della funzione di riflettività proiettata risulterebbe essere perfettamente coincidente con la funzione stessa. In tal contesto la risoluzione spaziale del sistema sarebbe infinita sia lungo la coordinata di range che lungo la coordinata di cross-range e saremmo in grado di discriminare scatteratori anche infinitamente vicini. Nella realtà,

g(x

^ 1

,x

2

)

15 però, la risposta impulsiva non è una delta di Dirac e la risoluzione sperimentata lungo le due direzioni risulta essere limitata. Di seguito calcoliamo la PSF e le risoluzioni spaziali supponendo verificate talune ipotesi semplificative:

Ω

_𝐞𝐟𝐟

(𝑡) = Ω

_𝐞𝐟𝐟

Δ = Ω

_eff

T

_obs

≪ 1 rad

𝑓

_𝑜

𝐵 ≫ 1

(1.29)

dove l’invarianza nel tempo del vettore di rotazione effettivo è una approssimazione tanto più valida quanto più è breve l’intervallo di osservazione. Valori tipici del tempo di osservazione necessari per acquisire una immagine ISAR sono inferiori al secondo ed in tal contesto è ragionevole assumere il vettore di rotazione totale (e quindi quello effettivo) come costante. Queste ipotesi semplificative ci permettono di approssimare il settore di corona circolare di fig. 1.8 con un settore rettangolare facilitando il calcolo della PSF.

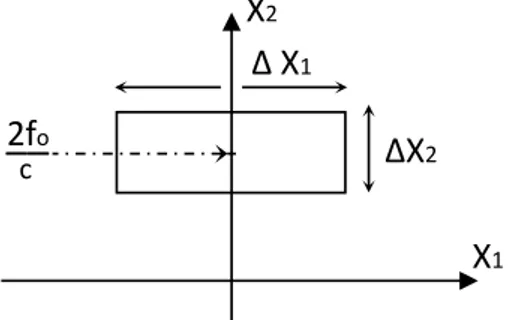
Figura 1.10 – Dominio approssimato entro il quale è nota la TF del segnale ricevuto

La funzione “finestra” assume la seguente espressione analitica:

𝑊(𝑋

₁

, 𝑋

₂

) = 𝑟𝑒𝑐𝑡

𝑋

1

𝛥𝑋

₁

𝑟𝑒𝑐𝑡

𝑋

₂

− 𝑋

₀

𝛥𝑋

₂

(1.30)

con 𝑋0 = 2𝑓0 e dove 𝛥𝑋𝑐 1 e 𝛥𝑋2 si calcolano come segue:

8

𝑋

1

=

(

2𝑓 𝑐

)

𝑠𝑖𝑛

𝜗

(

𝑡

)

≅ (2𝑓

0

/𝑐)Ω

𝑒𝑓𝑓

𝑡

𝑋

2

=

(

2𝑓 𝑐

)

𝑐𝑜𝑠

𝜗

(

𝑡

)

≅ 2𝑓/𝑐

⇓

𝛥𝑋

₁

= (4𝑓

₀

)(𝛿 2

𝑐

) = (2𝑓

₀

)𝛿

𝑐

𝛥𝑋

₂

= 2𝐵 𝑐

(1.31)

Antitrasformando la funzione di eq. 1.30 si ottiene la PSF del sistema di imaging:

𝑤(𝑥

₁

, 𝑥

₂

) = 𝛥𝑋

₁

𝑠𝑖𝑛𝑐(𝑥

₁

𝛥𝑋

₁

) ∙ 𝛥𝑋

₂

𝑠𝑖𝑛𝑐(𝑥

₂

𝛥𝑋

₂

) ∙ 𝑒

+𝑗4𝜋𝑓𝑐0𝑥2 (1.32) Calcolata la PSF del sistema siamo in grado di valutare la risoluzione sperimentata nella direzione di range e cross-range. Presa in esame la generica direzione quanto possono essere ravvicinati due diversi scatteratori perché sia possibile discriminarli? Per

2fo

__

c Δ X1 ΔX2 X1 X2

16 esempio, potremmo usare come criterio di risoluzione la larghezza a -3dB del lobo principale della sinc bidimensionale di eq. 1.32. Nel caso in cui vi fossero due scatteratori la cui distanza è inferiore, i rispettivi lobi principali si sovrapporrebbero parzialmente o totalmente, e non sarebbe possibile riconoscere come differenti i due scatteratori. D’altro canto, se il criterio fosse rispettato, i due lobi principali non si sovrapporrebbero e nell’immagine ISAR spiccherebbero due picchi, permettendoci di discriminare i due scatteratori. Sapendo che la larghezza a -3dB della sinc bidimensionale è circa pari alla distanza che intercorre fra l’origine della stessa ed il primo nullo, otteniamo le seguenti risoluzioni:

∆

_𝑅

_{= 1 𝛥𝑋}

2

∆

_𝐶𝑅

_{= 1 𝛥𝑋}

1

(1.33)

Infine, sostituendo 1.31 in eq. 1.33 si ottiene ..

∆

_𝑅

=

𝑐

2𝐵

∆

_𝐶𝑅

=

𝑐

2𝑓

₀

𝛿

=

𝜆

2𝛿

(1.34)

Si noti allora come la risoluzione lungo la coordinata di range risulti essere inversamente proporzionale alla banda del segnale trasmesso, come avviene in un qualsiasi radar che utilizza la tecnica della compressione di impulso. D’altro canto, la risoluzione in cross-range risulta essere inversamente proporzionale al termine δ che rappresenta la variazione totale dell’angolo di vista nel tempo di integrazione: tanto più è grande δ, tanto più è spinta la risoluzione in cross-range. Ma se da un lato siamo in grado di imporre la risoluzione in range poiché decidiamo in prima persona la banda del segnale che si intende trasmettere, dall’altro non possiamo definire la risoluzione in

cross-range poiché è funzione del moto relativo fra target (non cooperante) e radar. Ciò

nonostante, sebbene non sia possibile gestire il termine δ, è comunque utile notare come anche piccole variazioni dell’angolo di vista si traducano in risoluzioni particolarmente spinte.

Esempio. Si supponga di utilizzare in trasmissione una 𝑓₀ = 10𝐺𝐻𝑧: quale variazione dell’angolo di vista garantisce una risoluzione in cross-range pari ad un metro?

𝜆 =

𝑐

𝑓

₀

= 0.03 𝑚 ⇒ 𝛿 =

𝜆

2

= 0.015 𝑟𝑎𝑑 = 0.8594°

Con una variazione totale dell’angolo di vista inferiore al grado otteniamo comunque un’ottima risoluzione in cross-range.

17

1.6 TECNICA

RANGE-DOPPLER

(RD)

Quanto visto nel paragrafo precedente può essere schematizzato come segue. Sia 𝑆_𝑅𝑋𝐼 (𝑓, 𝑡) il segnale ricevuto dopo la rimozione del moto (vedi eq. 1.24) ..

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡)

𝑀𝑎𝑝𝑝𝑖𝑛𝑔

𝑆

_𝑅𝑋𝐼𝐼

(𝑋

₁

, 𝑋

₂

)

2𝐷−𝐼𝐹𝑇

𝑔 (𝑥

₁

, 𝑥

₂

)

.. tramite l’operazione di mappatura delle frequenze spaziali e dopo la trasformata bidimensionale di Fourier inversa si ottiene la ricostruzione della funzione di riflettività proiettata sul piano immagine. Supposte valide le ipotesi semplificative riportate in 1.29, è possibile dimostrare come si raggiunga lo stesso identico risultato adottando la seguente elaborazione del segnale:

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡)

2𝐷−𝐼𝐹𝑇

𝑔 (𝜏,

𝜈

)

𝐴𝑥𝑖𝑠 𝑆𝑐𝑎𝑙𝑖𝑛𝑔

𝑔 (𝑥

₁

, 𝑥

₂

)

L’algoritmo riportato schematizza quella che in letteratura è comunemente chiamata tecnica Range-Doppler la quale – come vedremo – ci permette di conseguire gli stessi identici risultati ottenuti nel paragrafo precedente. In primis si realizza una trasformata bidimensionale di Fourier inversa che rimappa il segnale dal dominio “frequenza-tempo lento” a quello “range-doppler”. Quindi, dopo un opportuna scalatura degli assi, si ricava la funzione desiderata.

Il segnale ricevuto rappresentato nel formato “frequenza – tempo lento”, dopo perfetta compensazione del moto, assume la seguente forma:

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡) = 𝑊(𝑓, 𝑡) 𝑔(𝑥

₁

, 𝑥

₂

)𝑒

−𝑗 2𝜋𝑓 2.𝒙(𝑡)•𝒊𝑳𝑶𝑺 𝒙 _(𝑡)/ 𝑐 𝑆

𝑑𝑥

₁

𝑑𝑥

₂

=

= 𝑊(𝑓, 𝑡) 𝑔(𝑦

₁

, 𝑦

₂

)𝑒

−𝑗 2𝜋𝑓 2.𝒚•𝒊𝑳𝑶𝑺 𝒚 _(𝑡)/ 𝑐 𝑆

𝑑𝑦

₁

𝑑𝑦

₂ (1.35) dove i due diversi sistemi di riferimento rispetto ai quali esprimiamo il segnale ricevuto sono quelli definiti nel par. 1.2. Quando la risoluzione spaziale richiesta non è enormemente spinta, e considerando valori tipici della velocità angolare di imbarcazioni ed aerei, il prodotto scalare di eq. 1.35 può essere approssimato come suggerito in [4]:

𝒚 • 𝒊

_𝑳𝑶𝑺𝒚

(𝑡) = 𝑦

2

+ Ω

𝑒𝑓𝑓

𝑦

1

𝑡

(1.36) Il segnale di eq. 1.35 può allora essere riscritto come segue:

𝑆_𝑅𝑋𝐼 (𝑓, 𝑡) = 𝑟𝑒𝑐𝑡 𝑓 − 𝑓0 𝐵 𝑟𝑒𝑐𝑡 𝑡 𝑇𝑜𝑏𝑠 𝑔(𝑦1, 𝑦2)𝑒−𝑗 4𝜋𝑓 𝑐 𝑦2+Ω𝑒𝑓𝑓𝑦1𝑡 𝑆 𝑑𝑦1𝑑𝑦2 (1.37)

18 Per semplicità di trattazione, nel calcolo della PSF si prenda in esame un target composto da un singolo scatteratore puntiforme posizionato rispetto al sistema di riferimento Ty in (y1, y2, y3). Conseguentemente, il segnale ricevuto assume la seguente

forma:

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡) = 𝑟𝑒𝑐𝑡

𝑓 − 𝑓

0

𝐵

𝑟𝑒𝑐𝑡

𝑡

𝑇

_𝑜𝑏𝑠

𝑒

−𝑗4𝜋𝑓_𝑐 𝑦2+Ω𝑒𝑓𝑓𝑦1𝑡 _(1.38)

Realizzando la trasformata inversa di Fourier rispetto alla frequenza si ottiene il seguente risultato: 𝑆_𝑅𝑋∗ (𝜏, 𝑡) = 𝐵𝑠𝑖𝑛𝑐 𝐵 𝜏 −2𝑦2 𝑐 𝑒 𝑗 2𝜋 𝑓0.𝜏−2𝑦_𝑐2/_{𝑟𝑒𝑐𝑡} 𝑡 𝑇_𝑜𝑏𝑠 𝑒 −𝑗 2𝜋 2𝑓0Ω_𝑐𝑒𝑓𝑓𝑦1 𝑡 (1.39)

Quindi, si realizza la trasformata rispetto al tempo lento: 𝑔 (𝜏, 𝜈) = 𝐵𝑠𝑖𝑛𝑐 𝐵 𝜏 −2𝑦2 𝑐 𝑒 𝑗 2𝜋𝑓0.𝜏−2𝑦_𝑐2/_𝑇 𝑜𝑏𝑠𝑠𝑖𝑛𝑐 6𝑇𝑜𝑏𝑠4𝜈 − 2𝑓₀Ω_𝑒𝑓𝑓 𝑐 𝑦157 (1.40) Per esprimere il segnale in funzione delle coordinate spaziali di range e cross-range è ora necessaria l’opportuna scalatura degli assi:

𝜈 =

2𝑓

𝑜

Ω

𝑒𝑓𝑓

𝑐

𝑥

1

𝜏 =

2

𝑐

𝑥

2

(1.41)

⇓

𝑔 (𝑥

₁

, 𝑥

₂

) = 𝐵𝑠𝑖𝑛𝑐 6

(𝑥

2

− 𝑦

2

)

∆

_𝑅

7 𝑒

+𝑗4𝜋𝑓_𝑐 0(𝑥₂−𝑦2)

_𝑇

𝑜𝑏𝑠

𝑠𝑖𝑛𝑐 6

(𝑥

₁

− 𝑦

₁

)

∆

_𝐶𝑅

7

(1.42)

⇓

𝑤(𝑥

₁

, 𝑥

₂

) = 𝐵𝑠𝑖𝑛𝑐

𝑥

2

∆

_𝑅

𝑒

+𝑗4𝜋𝑓_𝑐 0𝑥2

_𝑇

𝑜𝑏𝑠

𝑠𝑖𝑛𝑐

𝑥

₁

∆

_𝐶𝑅

(1.43) La funzione di eq. 1.43 descrive analiticamente la sinc bidimensionale spazio invariante che rappresenta la risposta impulsiva del sistema ISAR: il risultato ottenuto è del tutto analogo a quanto riportato in eq. 1.32 a meno del coefficiente moltiplicativo. Definendo la risoluzione spaziale per la generica coordinata come la distanza che intercorre fra l’origine della funzione sinc ed il rispettivo primo zero, si ottengono le stesse identiche risoluzioni riassunte in 1.34.

Ora, si tenga presente come – spesse volte – nella pratica possa non essere disponibile a priori il vettore di rotazione effettivo, ovvero potenzialmente potremmo ignorare sia il modulo che la direzione del vettore di rotazione effettivo. Ciò comporta talune problematiche che vengono accennate di seguito:

19  non è nota a priori la variazione totale dell’angolo di vista e di conseguenza non

conosciamo la risoluzione nella coordinata di cross-range;

 non è possibile realizzare l’operazione di scalatura di eq. 1.41 che prende il nome di cross-range scaling. Questo ci “costringe” a lavorare con una immagine ISAR che non è funzione delle coordinate spaziali quanto è espressa in funzione di range e Doppler. Quindi, la funzione che viene ricostruita è la seguente:

𝑔 (𝜏,

𝜈

) = 𝑔(𝜏,

𝜈

) ⊗

_𝜏

⊗

_𝜈

𝑤(𝜏,

𝜈

)

(1.44) dove la relazione che lega tempo veloce e range è nota. Possiamo dunque apprezzare la forma del bersaglio, ma non è possibile dedurre la sua reale dimensione lungo la coordinata di cross-range.

Infine, è bene sottolineare come i risultati ottenuti siano validi solo e soltanto per piccoli intervalli di osservazione per i quali è verificata l’approssimazione di eq. 1.36: in tal contesto la frequenza Doppler che caratterizza il segnale retrodiffuso da un dato scatteratore risulta essere costante nel tempo lento e di conseguenza la tecnica RD ha successo. Nel caso in cui, viceversa, il tempo di osservazione fosse di svariati secondi perché – per esempio – v’è la necessità di raggiungere risoluzioni dell’ordine dei centimetri, l’approssimazione di eq. 1.36 non è più verificata ed il segnale ricevuto dal dato scatteratore presenta una frequenza Doppler tempo variante: la tecnica RD fallisce e si deve utilizzare per forza di cose un altro tipo di approccio.

1.7 COMPENSAZIONE

DEL

MOTO

Uno dei passaggi critici della tecnica ISAR è la focalizzazione dell’immagine che viene realizzata eseguendo l’operazione comunemente chiamata “Compensazione del Moto”. Come evidenziato in eq. 1.22, il segnale ricevuto risulta essere moltiplicato per un termine di fase tempo variante funzione dell’evoluzione nel tempo lento della distanza che intercorre fra il focusing point, punto di fuoco, ed il centro di fase dell’antenna. Perché si parla di “focalizzazione dell’immagine”? Nel caso in cui il termine di fase non fosse opportunamente compensato, il segnale ricevuto risulterebbe caratterizzato da una modulazione di fase residua che comporta una sorta di “spanciamento” della risposta impulsiva del sistema di imaging. Ciò significa che l’immagine ISAR risultante non è composta da un insieme di picchi ben definiti, uno per ogni scatteratore, quanto è caratterizzata da un background uniforme: l’immagine non è focalizzata.

20 Quindi, per ottenere una immagine correttamente focalizzata dobbiamo compensare il termine di fase già citato, e per compensare tale termine dobbiamo stimare con cura la distanza 𝑅₀(𝑡).

Le tecniche di autofocalizzazione presenti in letteratura sono principalmente suddivise in parametriche e non parametriche dove i parametri in questione sono i coefficienti che definiscono il polinomio che descrive la distanza 𝑅₀(𝑡):

𝑅

₀

(𝑡) =

𝑎

𝑛

𝑡

𝑛

𝑛!

∞ 𝑛=0 (1.45) Adottando una tecnica parametrica stimiamo il termine 𝑅₀(𝑡) stimando un numero finito di coefficienti 𝑎_𝑛, dove ciascuno rappresenta una precisa grandezza fisica:

𝑎

_𝑛

=

𝑑

𝑛

𝑑𝑡

𝑛

𝑅

0

(𝑡)

𝑡=0 (1.46)

⇓

𝑎₀ = 𝑅₀(0) = 𝑑𝑖𝑠𝑡𝑎𝑛𝑧𝑎 𝑟𝑎𝑑𝑎𝑟 − 𝑡𝑎𝑟𝑔𝑒𝑡; 𝑎1 = 𝑅 0(0) = 𝑣𝑒𝑙𝑜𝑐𝑖𝑡à 𝑟𝑎𝑑𝑖𝑎𝑙𝑒; 𝑎₂ = 𝑅 ₀(0) = 𝑎𝑐𝑐𝑒𝑙𝑙𝑒𝑟𝑎𝑧𝑖𝑜𝑛𝑒 𝑟𝑎𝑑𝑖𝑎𝑙𝑒; 𝑎₃ = 𝑅₀(0) = 𝑗𝑒𝑟𝑘; ⋮

Come è ovvio, nella pratica è possibile stimare al più un numero limitato di parametri e di conseguenza la stima della funzione distanza nel tempo assume la seguente forma:

𝑅

₀

(𝑡) =

𝑎

𝑛

𝑡

𝑛

𝑛!

𝑁 𝑛=0 (1.47) dove N è il numero di parametri utilizzati e 𝑎 _𝑛 è la stima dell’n-esimo parametro. La scelta del numero di parametri che debbono essere stimati è funzione del moto relativo fra target e radar. Per piccoli intervalli di osservazione è lecito supporre il moto sufficientemente regolare e di conseguenza la distanza 𝑅₀(𝑡) può essere approssimata attorno all’istante temporale centrale con il rispettivo sviluppo in serie di Taylor bloccato al secondo ordine:

𝑅

₀

(𝑡) ≅ 𝑅

₀

(𝑡) =

𝑎

𝑛

𝑡

𝑛

𝑛!

2 𝑛=0

= 𝑎

₀

+ 𝑎

₁

𝑡 +

𝑎

2

2

𝑡

2 (1.48) Sotto tali ipotesi l’errore commesso sulla stima della distanza tende a zero e l’effetto di sfocamento dato dalla modulazione di fase residua sul segnale è del tutto trascurabile. Infine, è utile notare come il primo parametro dello sviluppo, ovvero la distanza fra

21 trascurato poiché la sua effettiva compensazione non porta alcun contributo ai fini della focalizzazione dell’immagine. Per valutare l’effetto del parametro 𝑎₀ si supponga di aver stimato perfettamente gli infiniti parametri successivi:

𝑅

₀

(𝑡) =

𝑎

𝑛

𝑡

𝑛

𝑛!

∞ 𝑛=1

=

𝑎

𝑛

𝑡

𝑛

𝑛!

∞ 𝑛=1 (1.49) Il segnale ricevuto prima della compensazione del moto assume la seguente forma:

𝑆

_𝑅𝑋′

(𝑓, 𝑡) = 𝑊(𝑓, 𝑡)𝐺(𝑓, 𝑡)𝑒

−𝑗 4𝜋𝑓𝑅0𝑐(𝑡) (1.50)

⇓

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡) = 𝑆

_𝑅𝑋′

_{(𝑓, 𝑡)𝑒}

+𝑗 4𝜋𝑓𝑅 0_𝑐(𝑡)

_{= 𝑊(𝑓, 𝑡)𝐺(𝑓, 𝑡)𝑒}

−𝑗 2𝜋𝑓 .2𝑎_𝑐0/ _(1.51) Infine, realizzando la 2D-IFT si ottiene il seguente risultato:

𝑔 (𝜏, 𝜈) = 𝑔(𝜏, 𝜈) ⊗

_𝜏

⊗

_𝜈

𝑤 𝜏 −

2𝑎

0

𝑐

, 𝜈

(1.52) Come è evidente, la non compensazione del parametro 𝑎₀ si traduce banalmente in uno

shift dell’immagine range-doppler lungo la coordinata del tempo veloce (ovvero in range) e non v’è alcuna distorsione della PSF del sistema di imaging. Concludendo, ai

fini della focalizzazione della immagine ISAR il parametro in esame può essere trascurato. Quindi, la funzione temporale che deve essere stimata non è più 𝑅₀(𝑡) quanto ..

𝛥𝑅

₀

(𝑡) = 𝑅

₀

(𝑡) − 𝑅

₀

(0) =

𝑎

𝑛

𝑡

𝑛

𝑛!

∞ 𝑛 =1 (1.53)

⇓

𝛥𝑅

₀

(𝑡) =

𝑎

𝑛

𝑡

𝑛

𝑛!

𝑁 𝑛=1 (1.54) dove N tipicamente è pari a 2÷3.

Image contrast based-technique (ICBT): tale tecnica è di tipo parametrico e stima i

parametri introdotti nel paragrafo corrente andando a massimizzare il contrasto dell’immagine. Come già accennato precedentemente, la non compensazione del termine di fase dato dal moto radiale del target comporta una non focalizzazione dell’immagine e di conseguenza il contrasto della stessa assume piccoli valori. Esiste dunque una diretta relazione fra la bontà della stima dei parametri dello sviluppo polinomiale ed il contrasto dell’immagine: all’aumentare della precisione di stima, aumenta il contrasto e quindi migliora la focalizzazione.

22 Sia 𝐼(

𝜏,

𝜈) l’intensità della immagine ISAR ottenuta operando il valore assoluto dell’immagine complessa, la funzione contrasto è definita come segue:

𝐼𝐶(𝒂

) ≝

𝜍(𝒂

)

𝜂(𝒂

)

=

𝐸*,𝐼(𝜏, 𝜈; 𝒂

) − 𝐸*𝐼(𝜏, 𝜈; 𝒂

)+-

2

₊

𝐸*𝐼(𝜏, 𝜈; 𝒂

)+

(1.55) dove 𝒂 = ,𝑎 ₁, 𝑎 ₂, ⋯ , 𝑎 _𝑁- è un vettore di prova contenente le stime dei parametri utilizzati per la compensazione del moto, mentre 𝐸*⋅+ rappresenta l’operatore di media spaziale. La stima finale dei parametri di focalizzazione è ottenuta risolvendo il seguente problema di ottimizzazione:

𝒂

= 𝑎𝑟𝑔 2max

𝒂

,𝐼𝐶(𝒂

)-3

(1.56)

Di seguito sono elencati i problemi principali della tecnica in esame:

 non esiste una soluzione analitica del problema in forma chiusa, quindi siamo “costretti” a utilizzare metodi numerici di ottimizzazione;

 𝐼𝐶(𝒂 ) non è una funzione convessa ed è quindi caratterizzata da diversi minimi e massimi.

Ne segue che è necessaria una valida tecnica di inizializzazione dell’algoritmo numerico di massimizzazione poiché in caso contrario potremmo ottenere una soluzione non coincidente con il massimo globale della funzione contrasto. La stima iniziale dei parametri di prova è un passaggio fondamentale della tecnica ICBT poiché la convergenza al massimo globale può essere raggiunta solo e soltanto innescando l’algoritmo di massimizzazione nell’intorno del massimo globale. In fig. 1.11 si riporta lo schema a blocchi della ICBT:

Figura 1.11 – Schema a blocchi della tecnica ICBT

Lo stop del processo di ottimizzazione può avvenire quando è stato raggiunto un numero massimo di iterazioni o quando la differenza fra il contrasto misurato su due iterazioni successive è inferiore ad una certa soglia.

a~k Inizialization Motion Compensation IC Image Recon. (2D-IFT) S‘RX(f,t) a~ini g^k(τ,ν) g(τ,ν)^

23

C

APITOLO

2

B-ISAR:

B

ISTATIC

ISAR

Un radar in configurazione bistatica è un sistema dove trasmettitore e ricevitore risultano essere disposti spazialmente ad opportuna distanza, e si differenzia da un radar in configurazione monostatica dove trasmettitore e ricevitore sono colocati, ovvero posti nello stesso identico punto. Ovviamente, possiamo parlare di radar in configurazione bistatica purché la diversità spaziale sia considerevole. Taluni sistemi radar possono utilizzare due diverse antenne, una per la trasmissione ed una per la ricezione, sebbene trasmettitore e ricevitore siano colocati. In tal contesto l’angolo bistatico, ovvero l’angolo sotteso dalla terna trasmettitore-target-ricevitore, risulta essere tendente allo zero e di conseguenza non ha senso parlare di radar in configurazione bistatica quanto di radar pseudo-monostatici.

La diversità geometrica che sussiste fra trasmettitore e ricevitore ci permette di risolvere talune problematiche che si incontrano adottando il caso monostatico. Per esempio, se da un lato il trasmettitore osserva il target con bassa RCS, dall’altro il ricevitore potrebbe osservare lo stesso target con un angolazione tale da sperimentare una RCS ben maggiore. Più in generale, possiamo affermare che il radar in configurazione bistatica, ed a maggior ragione un sistema multistatico, ci permette di acquisire una quantità maggiore di informazioni riguardante il target.

Inoltre, adottando un sistema bistatico risolviamo il problema dato dalle traiettorie ad angolo di vista costante. Difatti, come visto nel capitolo precedente, perché sia possibile acquisire una immagine ISAR risoluta anche nella direzione di cross-range è necessario che vi sia una variazione dell’angolo di vista nel tempo di integrazione. Quindi, in presenza di un target privo di moti indotti che si muove lungo la LoS, non v’è alcuna variazione dell’angolo di vista e di conseguenza non otterremo una immagine ISAR risoluta lungo entrambe le direzioni, range e cross-range, quanto un profilo in range del

24

target. D’altro canto, ponendo il ricevitore a distanza opportuna, risolviamo tale

problema poiché la LoS del ricevitore differisce da quella del trasmettitore e conseguentemente il ricevitore sperimenta una variazione dell’angolo di vista potenzialmente tale da garantire una immagine ISAR sufficientemente risoluta anche nella direzione di cross-range.

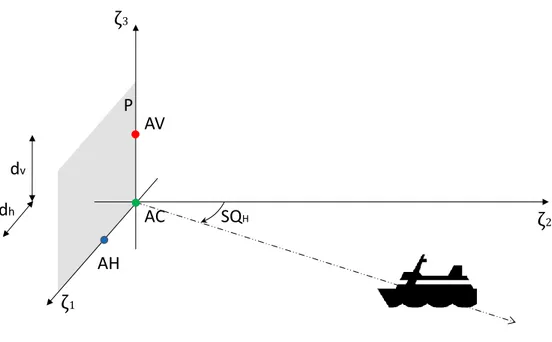
In fig. 2.1 è riportata la geometria bistatica:

Figura 2.1 – Geometria bistatica

Siano 𝑅𝑎𝑑𝑎𝑟 𝐴 e 𝑅𝑎𝑑𝑎𝑟 𝐵 due radar che trasmettono e potenzialmente possono ricevere il segnale riflesso dal target e generato in un primo momento sia dall’uno che dall’altro radar. 𝑅_𝐴(𝑡) e 𝑅𝐵(𝑡) sono le distanze individuate da 𝑅𝑎𝑑𝑎𝑟 𝐴-target e

𝑅𝑎𝑑𝑎𝑟 𝐵-target, mentre 𝑖_𝑀𝐴(𝑡) e 𝑖_𝑀𝐵(𝑡) sono le rispettive LoS che individuano l’angolo bistatico 𝜃. In tal contesto possiamo adottare una qualsiasi configurazione di lavoro fra le tre possibili:

 𝑅𝑎𝑑𝑎𝑟 𝐴 in configurazione monostatica: 𝑅𝑎𝑑𝑎𝑟 𝐴 trasmette e riceve;  𝑅𝑎𝑑𝑎𝑟 𝐵 in configurazione monostatica: 𝑅𝑎𝑑𝑎𝑟 𝐵 trasmette e riceve;

 due equivalenti monostatici, 𝑅𝑎𝑑𝑎𝑟 𝐵𝐼, definiti utilizzando il 𝑅𝑎𝑑𝑎𝑟 𝐴 (𝑅𝑎𝑑𝑎𝑟 𝐵) come trasmettitore ed il 𝑅𝑎𝑑𝑎𝑟 𝐵 (𝑅𝑎𝑑𝑎𝑟 𝐴) come ricevitore.

Vedremo nel prosieguo del capitolo come la configurazione bistatica produca un radar equivalente in configurazione monostatica posizionato a distanza opportuna lungo la bisettrice dell’angolo bistatico. Inoltre, valuteremo sotto quali condizioni l’elaborazione del segnale classica usata per l’acquisizione di immagini ISAR con radar monostatici, ovvero la tecnica RD combinata alla compensazione del moto radiale, sia applicabile al caso bistatico.

25

2.1 IL

SEGNALE

RICEVUTO

Coerentemente con quanto dimostrato nel capitolo precedente, dopo opportuno

pre-processing il segnale ricevuto espresso nel formato “frequenza-tempo lento” per la

generica configurazione radar assume la seguente forma:

𝑆

_𝑅𝑋′

(𝑓, 𝑡) = 𝑟𝑒𝑐𝑡

𝑓 − 𝑓

0

𝐵

𝑟𝑒𝑐𝑡

𝑡

𝑇

_𝑜𝑏𝑠

𝑓(𝒙)𝑒

−𝑗𝜑 (𝒙,𝑓,𝑡) 𝑉

𝑑𝒙 =

= 𝑊(𝑓, 𝑡) 𝑓(𝒙)𝑒

−𝑗𝜑 (𝒙,𝑓,𝑡) 𝑉

𝑑𝒙

(2.1)

dove 𝑊(𝑓, 𝑡) è la finestra entro la quale è noto il segnale ricevuto, 𝑓(𝒙) è la funzione di riflettività del target che “copre” la regione V mentre 𝜑(𝒙, 𝑓, 𝑡) è la fase del segnale ricevuto. L’espressione di eq. 2.1 è valida per una qualsiasi delle tre diverse configurazioni introdotte, ciò che cambia è il termine di fase

𝑒

−𝑗𝜑 (𝒙,𝑓,𝑡):

𝜑

_𝑀𝐴

(𝒙, 𝑓, 𝑡) =

4𝜋𝑓

𝑐

,𝑅

𝐴

(𝑡) + 𝒙 • 𝑖

𝑀𝐴

(𝑡)-

(2.2a)

𝜑

_𝑀𝐵

(𝒙, 𝑓, 𝑡) =

4𝜋𝑓

𝑐

,𝑅

𝐵

(𝑡) + 𝒙 • 𝑖

𝑀𝐵

(𝑡)-

(2.2b)

𝜑

_𝐵𝐼

(𝒙, 𝑓, 𝑡) =

2𝜋𝑓

𝑐

,𝑅

𝐴

(𝑡) + 𝒙 • 𝑖

𝑀𝐴

(𝑡) + 𝑅

𝐵

(𝑡) + 𝒙 • 𝑖

𝑀𝐵

(𝑡)- =

=

4𝜋𝑓

𝑐

6

𝑅

_𝐴

(𝑡) + 𝑅

𝐵

(𝑡)

2

+ 𝒙 • 4

𝑖

_𝑀𝐴

(𝑡) + 𝑖

𝑀𝐵

(𝑡)

2

57 =

=

4𝜋𝑓

𝑐

6

𝑅

_𝐴

(𝑡) + 𝑅

𝐵

(𝑡)

2

+

𝑖

𝑀𝐴

(𝑡) + 𝑖

𝑀𝐵

(𝑡)

2

𝒙 • 4

𝑖

_𝑀𝐴

(𝑡) + 𝑖

𝑀𝐵

(𝑡)

𝑖

_𝑀𝐴

(𝑡) + 𝑖

_𝑀𝐵

(𝑡)

57 =

=

4𝜋𝑓

𝑐

,𝑅

𝐵𝐼

(𝑡) + 𝐾(𝑡)𝒙 • 𝑖

𝐵𝐼

(𝑡)-

(2.2c) Come evidenziato in eq. 2.2c, il termine di fase del segnale ricevuto dal radar in configurazione bistatica può essere manipolato affinché assuma – a meno del termine 𝐾(𝑡) – una forma del tutto analoga al termine di fase duale del caso monostatico. Con riferimento a fig. 2.1, indipendentemente dalla configurazione bistatica adottata (𝑅𝑎𝑑𝑎𝑟 𝐴 trasmette e 𝑅𝑎𝑑𝑎𝑟 𝐵 riceve, o viceversa), possiamo pensare che il segnale sia ricevuto da un radar posto lungo la bisettrice dell’angolo bistatico a distanza 𝑅_𝐵𝐼(𝑡) rispetto al target. Difatti, il termine di fase generato dal moto radiale del target assume la forma 𝑒−𝑗4𝜋𝑓𝑐 𝑅𝐵𝐼(𝑡)_{, risultato del tutto analogo al caso in cui si lavorasse con un radar}

26 in configurazione monostatica ed il target fosse posto effettivamente a distanza 𝑅_𝐵𝐼(𝑡). La differenza sostanziale rispetto al caso monostatico è rappresentata dal termine 𝐾(𝑡) che porta l’informazione relativa alla variazione nel tempo della geometria bistatica, e – come vedremo – introduce delle distorsioni sull’immagine ISAR:

𝐾(𝑡) =

𝑖

𝑀𝐴

(𝑡) + 𝑖

𝑀𝐵

(𝑡)

2

=

= 𝑐𝑜𝑠 4

𝑎𝑟𝑐𝑐𝑜𝑠 𝑖

𝑀𝐴

(𝑡) • 𝑖

𝑀𝐵

(𝑡)

2

5 = 𝑐𝑜𝑠 4

𝜃(𝑡)

2

5

(2.3)

dove 𝜃(𝑡) è l’angolo bistatico al variare del tempo lento.

E’ allora evidente come in presenza di angolo bistatico iniziale tendente allo zero e variazione dello stesso trascurabile, 𝐾(𝑡) → 1 ed il termine di fase del segnale ricevuto sia pressoché identico a quello del caso monostatico. Di conseguenza, per quei sistemi radar dove si utilizzano due diverse antenne poste in punti diversi seppur a distanza contenuta, è lecito utilizzare un approccio di tipo monostatico tant’è che si parla di radar pseudo-monostatici.

2.2 POINT

SPREAD

FUNCTION

(PSF)

Nel calcolo della PSF supponiamo verificate le stesse ipotesi riportate in 1.29 per il calcolo della PSF del caso monostatico, fra cui vettore di rotazione effettivo Ωeff

costante nel tempo che è una condizione tanto più verificata quanto minore è il tempo di osservazione. Ipotizzando realizzata una perfetta compensazione del moto, operazione che può essere realizzata nel caso bistatico usando una qualsiasi delle tecniche proposte per il caso monostatico, il segnale ricevuto assume la seguente forma:

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡) = 𝑊(𝑓, 𝑡) 𝑔(𝑥

₁

, 𝑥

₂

)𝑒

−𝑗4𝜋𝑓𝑐 𝐾(𝑡) 𝑥1𝑠𝑖𝑛 𝜗 (𝑡) +𝑥2𝑐𝑜𝑠 𝜗 (𝑡) 𝑆

𝑑𝑥

₁

𝑑𝑥

₂

=

= 𝑊(𝑓, 𝑡) 𝑔(𝑥

₁

, 𝑥

₂

)𝑒

−𝑗4𝜋𝑓𝑐 𝐾(𝑡) 𝑥1𝑠𝑖𝑛 Ω𝑒𝑓𝑓𝑡 +𝑥2𝑐𝑜𝑠 Ω𝑒𝑓𝑓𝑡 𝑆

𝑑𝑥

₁

𝑑𝑥

₂ (2.4) dove il sistema di riferimento utilizzato, Tx, è centrato sul target ed orientato in maniera

tale che l’asse x3 sia parallelo al vettore di rotazione effettivo. Ancora una volta,

𝑔(𝑥₁, 𝑥₂) rappresenta la funzione di riflettività proiettata sul piano di imaging mentre Ωeff è il modulo del vettore di rotazione effettivo, anch’esso costante nel tempo. Per

27 semplicità di calcolo pensiamo che il target sia composto da un singolo scatteratore ideale di coordinate (𝑥₁₀, 𝑥₂₀, 𝑥₃₀). Il segnale di eq. 2.4 assume la seguente forma:

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡) = 𝑊(𝑓, 𝑡)𝑒

−𝑗4𝜋𝑓𝑐 𝐾(𝑡) 𝑥10𝑠𝑖𝑛 Ω𝑒𝑓𝑓𝑡 +𝑥20𝑐𝑜𝑠 Ω𝑒𝑓𝑓𝑡 (2.5) Supponendo inoltre di lavorare con tempi di integrazione brevi perché – per esempio – la risoluzione desiderata non è eccezionalmente alta, la variazione nel tempo di integrazione dell’angolo bistatico risulta essere piccola. Ciò significa che il termine 𝜃(𝑡) può essere ben approssimato con uno sviluppo in serie di Taylor (Maclaurin) bloccato al primo ordine:

𝜃(𝑡) ≅ 𝜃(0) + 𝜃 (0)𝑡

(2.6) dove ..

𝜃 (0) =

𝑑

𝑑𝑡

𝜃(𝑡)

_𝑡=0

, 𝑡

∈

−

𝑇

_𝑜𝑏𝑠

2

,

𝑇

_𝑜𝑏𝑠

2

Analogamente, lo stesso termine 𝐾(𝑡) può essere approssimato con uno sviluppo in serie di Taylor (Maclaurin) bloccato al primo ordine:

𝐾(𝑡) ≅ 𝐾(0) + 𝐾 (0)𝑡 =

= 𝑐𝑜𝑠 4

𝜃(0)

2

5 −

𝜃 (0)

2

𝑠𝑖𝑛 4

𝜃(0)

2

5 𝑡 = 𝐾

0

+ 𝐾

1

𝑡

(2.7) Quindi, sostituendo 2.7 in eq. 2.5 si ottiene il seguente risultato:

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡) ≅ 𝑊(𝑓, 𝑡)𝑒

−𝑗4𝜋𝑓𝑐 (𝐾0+𝐾1𝑡) 𝑥10𝑠𝑖𝑛 Ω𝑒𝑓𝑓𝑡 +𝑥20𝑐𝑜𝑠 Ω𝑒𝑓𝑓𝑡 (2.8) Infine, avendo ipotizzato piccoli intervalli di integrazione e piccole variazioni dell’angolo di vista è possibile approssimare il segnale di eq. 2.8 come segue:

𝑆

_𝑅𝑋𝐼

(𝑓, 𝑡) ≅ 𝑊(𝑓, 𝑡)𝑒

−𝑗4𝜋𝑓𝑐 (𝐾0+𝐾1𝑡) Ω𝑒𝑓𝑓𝑡 𝑥10+𝑥20

₌

= 𝑊(𝑓, 𝑡)𝑒

−𝑗4𝜋𝑓𝑐 (𝐾0+𝐾1𝑡)Ω𝑒𝑓𝑓𝑡 𝑥10+(𝐾0+𝐾1𝑡)𝑥20

_≅

≅ 𝑊(𝑓, 𝑡)𝑒

−𝑗4𝜋𝑓𝑐 0 (𝐾0+𝐾1𝑡)Ω𝑒𝑓𝑓𝑡 𝑥10

_𝑒

−𝑗4𝜋𝑓_𝑐 , (𝐾0+𝐾1𝑡)𝑥20 - _(2.9)

Analogamente al caso monostatico, la formazione dell’immagine viene conseguita adottando la tecnica RD a patto che siano verificate talune condizioni che analizzeremo in seguito. La compressione in range viene allora ottenuta realizzando la trasformata di Fourier rispetto alla frequenza:

𝑆_𝑅𝑋∗ (𝜏, 𝑡) = 𝑊(𝑓, 𝑡)𝛿(𝑥₁− 𝑥₁₀, 𝑥₂ − 𝑥₂₀)𝑒−𝑗 𝜑𝐵𝐼(𝑥10,𝑥20,𝑓,𝑡)_𝑒−𝑗 2𝜋𝑓𝜏_𝑑𝑥

1𝑑𝑥2𝑑𝑓 =

= 𝑒−𝑗4𝜋 𝑓𝑐 0 (𝐾0+𝐾1𝑡)𝛺𝑒𝑓𝑓𝑡𝑥10 𝛿 𝜏 −2

𝑐(𝐾0 + 𝐾1𝑡)𝑥20 ⊗𝜏 𝑊