Applicazione della ISO 11929 2010 a misure di radioattività ambientale

(1)

POLITECNICO DI MILANO

III Facoltà di Ingegneria

Corso di Laurea in Ingegneria Nucleare

APPLICAZIONE DELLA ISO 11929:2010 A MISURE DI

RADIOATTIVITA’ AMBIENTALE

Relatore: Dott. Marco Caresana

Tesi di Laurea di:

Chiara Boccingher

Matricola 725608

(2)

Per te mamma, che mi hai sopportato e supportato, sempre. Questa laurea è anche un po’ tua.

(3)

Indice

INDICE

Introduzione………...1

Capitolo 1

Definizioni metrologiche fondamentali nell’analisi degli errori…………...3

1.1 Concetto di misura e miglior stima……….3

1.2 Definizione di incertezza…………..………5

1.3 Conferma metrologica e taratura dello strumento………..………….……10

Capitolo 2

Determinazione dei limiti caratteristici per la misurazione delle radiazioni

con stima dell’incertezza “classica”………...11

2.1 Definizioni……….………..11

2.2 Simboli utilizzati nella trattazione………..12

2.3 Modello di calcolo……….13

Capitolo 3

Determinazione dei limiti caratteristici per la misurazione delle radiazioni

ionizzanti in approccio ISO 11929:2010………23

3.1 Simboli utilizzati nella norma ISO 11929:2010………...23

3.2 Modello di calcolo………...24

3.3 Confronto dei limiti caratteristici ottenuti tramite l’approccio “classico” e quello della norma ISO 11929:2010……….28

Capitolo 4

Approccio Bayesiano dell’ISO 11929:2010………...33

(4)

Indice

II

4.2 Esempio di misura di attività specifica di un radionuclide con ISO 11929:2010 in approccio Bayesiano……….…40

Capitolo 5

Determinazione della concentrazione di attività alfa e beta totale in

campioni di acque prelevati dall’ARPA……….…………...45

5.1 Cenni sull’attività del Centro per la Radioprotezione di ARPA Lombardia…..………...45 5.2 Concetti di base della scintillazione liquida e di taratura della sorgente………...46 5.3 Calcoli della concentrazione di attività e definizione dei limiti caratteristici…50 5.4 Confronto dei risultati ottenuti per i campioni di acqua seguendo i due approcci………...52 5.4.1 Dati concentrazione di attività alfa………52 5.4.2 Dati concentrazione di attività beta………...55

Capitolo 6

Determinazione della concentrazione di attività beta totale con smear

test……….59

6.1 Modalità di analisi Smear test del Laboratorio di Radioprotezione del Politecnico di Milano………...59 6.2 Determinazione dell’attività presente su uno smear test………60 6.3 Determinazione della curva di efficienza del rivelatore e del limite di rivelazione………..62 6.4 Confronto dei limiti di rivelazione ottenuti con i due approcci su dati simulati e incidenza sull’incertezza sull’attività………63

Conclusioni………...69

(5)

Introduzione

INTRODUZIONE

Nel Capitolo 1 vengono richiamati i concetti fondamentali relativi alla valutazione delle incertezze, attraverso la definizione di misurando ed incertezza ad esso associata. Si passa quindi ai concetti statistici di media e varianza ed al loro significato come stimatori del risultato di una misurazione e dell’incertezza associata.

Il risultato di una misura, infatti, è definito non solo dalla migliore stima del misurando, ma anche dalla distribuzione dei valori che possono essere ragionevolmente attribuiti al misurando stesso. Solo in questo modo è possibile confrontare misure effettuate da laboratori diversi o con tecniche diverse e valutarne la compatibilità.

In accurata analisi delle incertezze si deve considerare tutto il processo di misura, incluso il metodo di taratura.

Nel Capitolo 2 viene introdotto il concetto di limite caratteristico, nello specifico, per la misurazione delle radiazioni ionizzanti. In particolare viene descritto un approccio, proposto per la prima volta da Lloyd A. Currie, che di seguito verrà chiamato “metodo classico”. Nel Capitolo 3 il metodo classico viene confrontato con quanto proposto dalla ISO 11929:2010.

Nel Capitolo 4 prosegue lo studio della norma ISO 11929:2010. Questa infatti non si limita a modificare il calcolo dei limiti caratteristici, ma propone un approccio di tipo Bayesiano all’analisi dei dati sperimentali. Questo tipo di approccio impatta sia sulla migliore stima del misurando sia sull’incertezza ad essa associata.

Il Capitolo 5 descrive un metodo di misura della radioattività alfa e beta totali con il metodo della scintillazione liquida. Questa tecnica di misura è normalmente usata dall’ARPA Lombardia per le misure di routine in matrici ambientali.I dati sperimentali sono stati forniti da ARPA già analizzati secondo il loro metodo che sostanzialmente coincide con quello descritto del Capitolo 1. Nell’ambito di questa tesi i dati grezzi sono stati elaborati con l’approccio Bayesiano descritto nel Capitolo 4 e confrontati con il risultato dell’analisi del metodo ARPA. Dal confronto si cerca di individuare le situazioni in cui l’approccio Bayesiano si discosta dall’analisi standard.

(6)

Introduzione

2

È stata effettuata una simulazione di dati in particolare per Ni-63 e Cs-137, analizzati con approccio classico e con quello proposto in ISO 11919:2010. Dal conforonto si cerca di individuare come questi incidano in maniera diversa sull’incertezza sull’attività.

(7)

Capitolo 1 Definizioni metrologiche fondamentali nell’analisi degli errori

CAPITOLO 1

DEFINIZIONI METROLOGICHE FONDAMENTALI

NELL’ANALISI DEGLI ERRORI

1.1 Concetto di misura e miglior stima

Secondo la definizione del VIM (Vocabolario Internazionale di Metrologia) [1] il misurando è la grandezza che si intende misurare. L’operazione di misura quindi è diretta a fornire la migliore stima di una grandezza oggetto della misura stessa. Salvo casi particolari, una misura avviene per confronto con un campione di riferimento della specifica grandezza oggetto della misura. Ciò implica che la strumentazione deve essere tarata a fronte di detta grandezza.

In generale il misurando non è descritto da un singolo valore ma piuttosto da una distribuzione di valori che possono essere attribuiti al misurando secondo una determinata probabilità. La definizione di questa distribuzione di probabilità è, di fatto, l’operazione che sottende alla stima dell’incertezza. Esistono varie cause che concorrono alla definizione dell’incertezza. Alcune sono intrinseche alla grandezza fisica in misura. Se si pensa ad esempio alla misura di attività di una sorgente radioattiva si deve considerare che il decadimento radioattivo è un fenomeno probabilistico, che è ben approssimato da una distribuzione di Poisson, e quindi anche il misurando assumerà valori in accordo con questo tipo di distribuzione.

Particolarmente interessante è il caso in cui la misura può essere ripetuta più volte. Risulta che la miglior stima sia il valor medio dei valori misurati. La giustificazione a tale affermazione è che, quando il numero delle misure si avvicina all’infinito, la loro distribuzione si avvicina a una curva continua e definita chiamata distribuzione limite f(x).

(8)

Figura 1: Distribuzione limite: i tre istogrammi mostrano le frazioni (f) di misure che cadono nei rispettivi

intervalli x nei casi in cui siano state effettuate 10, 100 e 1000 misure della stessa grandezza. All’aumentare del numero delle misure la distribuzione dei dati si avvicina a una curva continua e definita.

Se f(x) fosse nota, si potrebbe calcolare sia la media sia la deviazione standard ottenute dopo infinite misure e per la distribuzione normale, conoscere il valore vero X. Non conoscendo mai la distribuzione limite, però, si parte dal presupposto che si voglia arrivare alla miglior stima di X possedendo in pratica un numero finito di valori misurati x1, x2, …, xN. Se le

misure seguissero, per ipotesi, una distribuzione normale, cioè una curva simmetrica a campana come distribuzione limite e se si conoscesse il parametro X assieme alla sua deviazione standard, allora la probabilità di ottenere i valori x1 e x2 realmente ottenuti

sarebbe: ! !_! ∝! !! ! !!!! ! !!!_{, ! !} ! ∝_!!! ! !!!!! !!!₍₁₎

definita come probabilità di ottenere una lettura vicino a x1 e vicino a x2, con σ deviazione

standard.

Analogamente, tutte le probabilità possono essere scritte allo stesso modo terminando con quella per xN, data da:

(9)

! !_! ∝ !

!!

! !!!! !

!!!_{. (2)}

La probabilità di osservare l’intero insieme di N letture è il prodotto di queste probabilità separate:

! !!, … , !! = ! !! × ! !! × … × ! !! ∝_!!!!

! !!!!!

!!!₍₃₎

con incogniti X (valore vero) e σ (larghezza della distribuzione).

Attraverso il principio di massima verosimiglianza [2] si può affermare che la migliore stima di X è data da quei valori per cui P x!, … , x! è massima; questo avviene se la somma

nell’esponente è minima. Così la miglior stima per X è quel valore di X per cui x_!− X ! _σ!

!

!!! è minima. La condizione di minimo è data dalla (4), ottenuta

differenziando l’argomento dell’esponenziale dell’equazione (3) rispetto a X e ponendo la derivata uguale a zero:

!_! − ! = 0

!

!!! o ! = _!!!. (4)

Si è dimostrato che la migliore stima per il valore vero X è la media delle N misure x.

Un’analisi delle incertezze basate su misure ripetute viene chiamata valutazione delle incertezze di categoria A. Tuttavia può accadere che non sia agevole effettuare misure ripetute, in questo caso la stima dell’incertezza viene fatta sfruttando altre tecniche. In modo residuale vengono definite incertezze di categoria B quelle valutate con tecniche diverse dalla ripetizione delle misure.

1.2 Definizione di incertezza

In generale le incertezze di misura possono essere significative rispetto all’accuratezza richiesta alla misura. La loro valutazione è, quindi, di estremo interesse per valutare se una

(10)

La definizione di incertezza proposta da UNI CEI 9 è la seguente:

incertezza (di misura): parametro, associato al risultato di una misurazione, che

caratterizza la dispersione dei valori ragionevolmente attribuibili al misurando.

In pratica esistono molte fonti di incertezza per una misura, come ad esempio una definizione incompleta del misurando, l’inadeguata conoscenza degli effetti delle condizioni ambientali sulla misurazione, la distorsione nella lettura dello strumento di misura, i valori non esatti dei parametri di misurazione e infine, la presenza di campioni non trattati o in numero non adeguato.

Dato il gran numero di sorgenti, si applica la divisione già vista in due categorie a seconda del metodo di valutazione, “A” e “B”. Queste categorie vengono applicate all’incertezza e non sostituiscono i termini “casuale” e “sistematico” utilizzati per le sue componenti, talune valutate dalla distribuzione statistica dei risultati e caratterizzate mediante scarti tipo sperimentali, altre, sempre caratterizzabili mediante scarti tipo, sono valutate da distribuzioni di probabilità ipotizzate sulla base dell’esperienza o di informazioni di altro tipo.

In particolare, un’incertezza di categoria A è ottenuta da una densità di probabilità derivata da una distribuzione di frequenza osservata da una serie di misure effettuate, mentre quella di categoria B è ottenuta da una densità di probabilità ipotizzata sulla base del grado di credenza nel verificarsi di un evento.

Per la valutazione di tali categorie di incertezza tipo, occorre definire un modello di misurazione e visto che nella maggior parte dei casi il misurando, definito con Y, non viene misurato direttamente, esso è determinato attraverso altre N grandezze X1, X2,…, XN

mediante una relazione funzionale f specificata nella (5):

! = ! !!, !!, … , !! . (5)

Le grandezze Xi, dette di ingresso, sono esse stesse misurandi e possono a loro volta

dipendere da altre, come ad esempio da fattori di correzione per gli effetti sistematici. Essendo f usualmente complicata, può essere valutata in maniera generale mediante un algoritmo numerico.

(11)

In questa trattazione, la relazione funzionale è interpretata come funzione contenente ogni grandezza che possa originare sul risultato della misurazione una componente di incertezza significativa.

Da specificare che le incertezze delle grandezze Xi sono determinate sia in modo diretto

nella misurazione, da osservazioni singole o ripetute, sia da fonti esterne, da campioni di misura tarati o da dati di riferimento ottenuti dai manuali.

Dall’equazione per il modello si ricava una stima del misurando Y, denotata y, usando stime di ingresso x1, x2, …, xN per i valori delle N grandezze X1, X2,…, XN. La stima d’uscita, che

è il risultato della misurazione, è data da:

! = ! !!, !!, … , !! . (6)

Lo scarto tipo stimato associato con la stima d’uscita y è denominato incertezza tipo composta uc(y); questa è determinata dallo scarto stimato associato a ciascuna delle stime di

ingresso xi, che è definito u(xi) e detto incertezza tipo.

Ogni stima di ingresso xi e ogni incertezza tipo associata u(xi) sono ricavate da una

distribuzione di valori possibili della grandezza Xi, che è basata su frequenze empiriche

(osservate) nel caso di valutazioni di categoria A oppure è una distribuzione iniziale se è base per le valutazioni di categoria B.

Nella maggior parte dei casi di valutazione di categoria A dell’incertezza tipo, la migliore stima dei valori attesi, μq, di una grandezza q aleatoria di cui sono ottenute n osservazioni

indipendenti qk in uguali condizioni sperimentali è il valor medio q:

! =!_! ! !_!

!!! . (7)

Quindi, per una grandezza di ingresso Xi stimata da n osservazioni a dare Xi,k, il valor medio

!! è usato come stima di ingresso xi nel modello f per determinare il risultato della

misurazione y; ne risulta che x! = X!.

Le osservazioni qk differiscono dalle grandezze di influenza a causa di effetti aleatori; la

(12)

La radice quadrata positiva di questa quantità, cioè s(qk), è denominata appunto scarto tipo

sperimentale e assieme alla stima della varianza caratterizza la dispersione dei valori osservati intorno alla media q.

La varianza sperimentale della media è data da

!! _{! =}!! !!

! . (9)

La radice di tale quantità è lo scarto tipo sperimentale della media s q e quantifica quanto bene q stimi il valore atteso μq; sia lo scarto tipo sperimentale, sia la varianza sperimentale

sono adottati come valutazione quantitativa dell’incertezza di q.

Pertanto, per una grandezza di ingresso Xi, l’incertezza tipo della sua stima xi è data da:

! !_! = ! !_! (10) chiamata specificatamente incertezza tipo di categoria A, definita come radice quadrata positiva di u! x! = s! X! e calcolata dall’equazione della varianza sperimentale della

media con la sostituzione di X! a q.

Al contrario, per una stima xi di una grandezza di ingresso Xi non ottenuta da osservazioni

ripetute, la varianza stimata u! x! e l’incertezza tipo u x! , definita di categoria B, sono

valutate attraverso un giudizio scientifico basato su tutte le informazioni possibili su Xi,

come:

• dati di misurazioni precedenti; • specifiche tecniche;

• dati ottenuti da certificati di taratura;

• incertezze assegnate a valori di riferimento presi da manuali.

L’incertezza di xi non è necessariamente data da uno scarto tipo, ma potrebbe essere definita

per esempio da un intervallo avente un certo livello di fiducia. Ipotizzando che sia adottata una distribuzione normale, da questo può essere ricostruita l’incertezza tipo dividendo quella dichiarata per il fattore appropriato per la distribuzione normale.

Ora, se le grandezze di ingresso sono tutte indipendenti tra loro, l’incertezza tipo di y (e quindi il risultato della misurazione) è ottenuta con la composizione opportuna delle

(13)

incertezze tipo delle stime x1, x2, …, xN a dare l’incertezza tipo composta definita come

segue: !_!! _{! =} !" !!! ! !! _! ! ! !!! (11)

che è la radice quadrata della varianza composta. Nella precedente relazione, f è la funzione già definita in precedenza e ciascuna u x! è un’incertezza tipo di valutazione di categoria A

o B. Attraverso questa equazione viene caratterizzata la dispersione dei valori ragionevolmente attribuiti al misurando Y.

Le derivate parziali _!!!!

!, valutate per x! = X!, sono chiamate coefficienti di sensibilità e

descrivono il variare della stima di uscita rispetto al variare dei valori delle stime di ingresso. Se questa variazione è generata dall’incertezza tipo della stima x!, la variazione in y è

appunto _!!!!

! u x! ; la varianza composta risulta, quindi, una somma dei termini, ognuno

rappresentante la varianza associata alla stima di uscita y generata dalla varianza associata ad ogni stima di ingresso x!. L’equazione diventa, quindi

!!! ! = _!!!" ! ! !! _! ! ! !!! = !!!! !!! !! ! = !!!!!!! ! (12) con c! = _!!!! ! .

Fino ad ora si è visto come u!(y) possa essere usata per esprimere l’incertezza del risultato

di una misurazione, ma nelle applicazioni usuali e in alcune normative è necessario dare una valutazione quantitativa dell’incertezza che definisca un intervallo intorno al risultato che comprenda una gran parte della distribuzione di valori ragionevolmente attribuiti al misurando; è per questo motivo che viene definita l’incertezza estesa U, ottenuta dalla moltiplicazione dell’incertezza composta per un fattore di copertura k

(14)

1.3 Conferma metrologica e taratura dello strumento

La conferma metrologica consta di tutte le operazioni da effettuare prima della misurazione per assicurare che la funzione di ogni apparecchio usato sia in stato di conformità ai requisiti per l’utilizzazione specifica prevista. In particolare, per un centro di taratura essa consiste nell’assicurare che gli strumenti campione forniscano il livello di incertezza ipotizzato nelle procedure di taratura che li impiegano, per tutto il tempo di validità della conferma in modo da potersi sempre riportare alle grandezze fondamentali del Sistema Internazionale (SI). Le operazioni fondamentali effettuate dal sistema di conferma sono:

• taratura dello strumento, attraverso dei punti di misura che tengano in considerazione le variabili di influenza, come le condizioni ambientali di riferimento, le impostazioni, l’impiego e la messa a punto dello strumento, in modo che la misura non si discosti entro una certa incertezza dal riferimento;

• esame dei risultati di taratura per la verifica dell’adeguatezza dello strumento, che consiste nel confronto tra il valore della misura dato dalla taratura con il limite di accettazione, definito dalla sua incertezza associata. Il campione di riferimento serve solo per le misure di controllo di taratura e può essere, per esempio, una sorgente di laboratorio.

È necessario, infine, valutare che lo strumento campione assicuri il livello di incertezza previsto fino alla taratura successiva. Questo è fatto attraverso delle procedure interne, con le quali si accetta che la misura si discosti da quello di riferimento fino a un certo valore o con delle norme, che fissano le incertezze entro cui lo strumento sia reputato adatto alla misura.

(15)

Capitolo 2 Determinazione dei limiti caratteristici per la misurazione delle radiazioni ionizzanti con stima dell’incertezza “classica”

CAPITOLO 2

DETERMINAZIONE DEI LIMITI CARATTERISTICI

PER LA MISURAZIONE DELLE RADIAZIONI

IONIZZANTI CON STIMA DELL’INCERTEZZA

“CLASSICA”

ANALISI QUALITATIVA E QUANTITATIVA (LLOYD A. CURRIE) [3]

2.1 Definizioni

Le definizioni dei limiti caratteristici per un processo di misurazione sono riportati in seguito, assieme ad una descrizione qualitativa, mentre il modello quantitativo segue nel paragrafo 2.3:

limite di decisione (decision limit): estimatore del misurando, valore per cui si decide se il

risultato di una misura indica rivelazione. Se la migliore stima della misura è inferiore al limite di decisione, allora la probabilità di falsi negativi (mancata rivelazione dell’effetto fisico laddove questo è in realtà presente) è inferiore ad una specifica probabilità α. In genere si utilizza α=0.05. Un falso negativo viene anche detto errore di prima specie.

limite di rivelazione (detection limit): più piccolo valore vero del misurando che assicura

una probabilità specifica di rivelazione con la procedura di misura utilizzata. Se la migliore stima della misura è superiore al limite di rivelazione, allora la probabilità di falsi positivi

(16)

2.2 Simboli utilizzati nella trattazione

Il processo di misura è definito in modo completo attraverso il metodo di osservazione, l’apparato di misura e la natura del campione stesso.

Come già visto la quantità di interesse Y non è in generale misurata direttamente, ma è derivata dalla grandezze di ingresso X secondo un modello di misurazione. Allo stesso modo l’incertezza associata a Y è derivata dalle incertezze stimate per le grandezze di ingresso e composte secondo la legge di propagazione descritta nel capitolo precedente.

In Tabella 1 sono riportate le definizioni e i simboli adottati nella trattazione, dove le quantità fisiche sono denotate con lettere maiuscole, mentre i loro valori con lettere minuscole:

Simbolo Descrizione

m Numero di quantità in ingresso

Xi Quantità in ingresso (i=1,….,m)

xi Stima delle quantità in ingresso Xi

u(xi) Incertezza standard della quantità in ingresso Xi a cui è

associata la stima xi

G Funzione modello

Y Variabile random come stima del misurando, usata anche

come vero misurando che quantifica l’effetto fisico di interesse

y Valore determinato dello stimatore Y, stima del misurando,

risultato della prima misurazione del misurando

u(y) Incertezza standard del misurando associata al risultato di misura primaria y

Lc, y* Limite di decisione, sopra il quale il segnale osservato può

essere riconosciuto come “rivelato” LD, y

#

Limite di rivelazione, più piccolo valore vero del misurando che assicura a priori la rivelazione

(17)

Capitolo 2 Determinazione dei limiti caratteristici per la misurazione delle radiazioni ionizzanti con stima dell’incertezza “classica” B, X2 Valore osservato del fondo

σB, u(x2) Deviazione standard del fondo, incertezza del segnale di

fondo

μS+B, x1 Stima del segnale lordo

S+B, X1 Valore lordo osservato

σS+B, u(x1) Deviazione standard del segnale lordo, incertezza del

segnale lordo

μS= μS+B-‐ μB Media del segnale netto

S=S+B -‐ B = X1-‐X2

Valore di segnale netto derivato

!_!

= !_!!!! _{+ !} !! ! !

Deviazione standard del segnale netto

α, β Probabilità dell’errore di prima e seconda specie

Tabella 1: Simboli e definizioni: sono riportate entrambe le notazioni usate nell’articolo del Currie e nella

norma ISO 11929:2010 (grassetto) per permettere una più facile lettura e una più chiara corrispondenza dei modelli di calcolo

Il bianco (background, B), detto anche fondo, è definito come risultato di misura di un campione identico al campione di interesse, con l’eccezione che la sostanza da misurare è assente.

2.3 Modello di calcolo

Preso un misurando Y, funzione di diversi valori di input Xi, il modello di valutazione è

il seguente:

! = !(!_!, … … , !_!) (15) Sostituendo le stime xi delle quantità in entrata nella funzione modello G, si ottiene y,

(18)

Se le quantità in input sono misurate in modo indipendente e se sono date le singole incertezze standard u(xi) associate alle stime xi, allora l’incertezza standard del misurando

associata a y risulta: !! _{! =} !" !"! ! !(!_!) ! !!! (17)

a questo punto le stime xi possono essere sostituite nella formula alle quantità in input Xi,

all’interno delle derivate parziali di G.

Nel modello specifico per le misure delle radiazioni ionizzanti, il misurando Y si riferisce a un campione di materiale radioattivo determinato dal conteggio del segnale lordo e di quello del fondo.

Y può essere, quindi, il tasso di conteggio netto o l’attività del campione che viene misurato. Il modello è specificato come segue:

! = ! !_!, … … , !_! = !_! − !_!!_!− !_! ∙ !!!!…

!!!!…= !!− !!!!− !! ∙ ! (18)

con

! =!!!!…

!!!!… (19)

Le quantità presenti nell’equazione (18) sono, nello specifico, X1, segnale di conteggio

lordo, X2, segnale di conteggio del fondo. Le altre quantità di input, Xi, rappresentano i

fattori di taratura, conversione e correzione; in particolare, X3 è il fattore di schermo e X4 la

correzione addizionale al fondo.

Come accennato prima, sostituendo le stime xi nel modello, la stima principale y del

misurando Y risulta:

! = ! !_!, … … , !_! = !_!− !_!!_!− !_! ∙ !!!!…

!!!!…= !!− !!!!− !! ∙ ! (20)

(19)

! =!!!!…

!!!!… (21)

Per il calcolo dell’incertezza standard, si sviluppano le derivate:

!" !!! = !; !" !!! = −!!!; !" !!!= −!!!; !" !!! = −!; !" !!! = ± ! !! (! ≥ 5, !"# !!"# ! ) (22)

A questo punto, attraverso la formula vista in precedenza, si ottiene l’incertezza standard del misurando associata a y:

! ! = !!_{∙ !}! _!

! + !!!!! !! + !!!!! !! + !! !! + !!!!"#! (!) (23)

Per semplificare la trattazione viene utilizzato in seguito un modello di misurazione semplificato, nel quale X3=1 e X4=0, ottenendo

! = !!− !! ∙ !_!!!!…

!!!… = !!− !! ∙ ! (24)

e sostituendo le rispettive stime

! = !_!− !_! ∙ !!!!…

!!!!…= !!− !! ∙ !. (25)

La stima dell’incertezza è calcolata come segue, tenendo in considerazione che in questo caso u x! = u(x!) sono entrambe poste a 0

! ! = !!_{∙ !}! _!

! + !! !! + !!!!"#! (!). (26)

Supponendo a priori che l’effetto fisico sia assente, il valore atteso di x1 coincide con quello

(20)

Di particolare interesse è il caso in cui la variabile aleatoria y segua una distribuzione Poissoniana. Questa è una distribuzione di probabilità discreta, definita anche come legge degli eventi rari, perché una singola prova ha probabilità di successo bassissima.

Tipico esempio di distribuzione di Poisson è appunto il decadimento radioattivo, dove in un dato intervallo di tempo, sapendo che mediamente si verifica un numero λ (tasso medio di conteggi) di eventi, la probabilità di registrare n eventi è data dala (28):

! ! = !!! !!

!! (28)

per ogni ! ∈ ℤ!.

La caratteristica importante è data dalla definizione di media e varianza; se Y è una variabile aleatoria di distribuzione di Poisson,

!"#$% ! = ! ; !"# ! = !. (29) I segnali lordo e di fondo, entrambi in forma digitale e quindi per la maggior parte dei casi governati dalla distribuzione di Poisson sono misurati come specificato in precedenza nel modello per rivelare l’attività in un campione.

Se il numero di conteggi è sufficientemente grande, la distribuzione è normale; si possono calcolare quindi i limiti caratteristici attraverso la stima della varianza del segnale σ2

data da

!! _{= !}

!!!! + !!! (30)

dove σ è evidentemente dipendente dal livello del segnale.

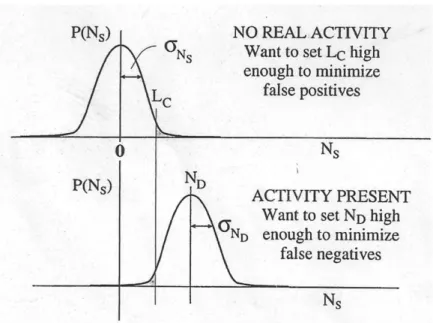
Ogni decisione in seguito a un’osservazione sperimentale sulla presenza o meno del segnale è affetta da due tipi di errori casuali vista la natura ripetibile delle misure: α (del primo tipo), legato alla possibilità di decisione che la sostanza sia presente quando in realtà non lo è e β (del secondo tipo), riguardante l’errata decisione che non sia presente quando in realtà lo è. Il limite di decisione Lc è stabilito attraverso il massimo valore di α accettabile assieme a σ0,

deviazione standard del segnale netto quando μs=0; superato Lc si può affermare che il

segnale osservato S è rivelato. Allora

(21)

con kα ascissa della distribuzione normale standardizzata che corrisponde al livello di

probabilità 1-α, riferito alla decisione corretta di non rivelazione.

Una volta definito Lc viene specificato un valore a priori, LD, limite di rivelazione, attraverso

lo stesso livello di accettabilità, β e σD, deviazione standard caratterizzante la distribuzione

di probabilità del segnale netto quando μS, cioè la media del valore vero, è uguale a LD.

!_! = !_!+ !_!!_! (32)

con kβ ascissa della distribuzione normale standardizzata che corrisponde al livello di

probabilità 1-β, cioè al valore di decisione corretto di possibile rivelazione.

Figura 2: Errori di primo e secondo tipo

Peculiarità della distribuzione di Poisson è data dal fatto che σ0=0 e quindi LC=0 solo se la

media dei conteggi del fondo è pari a zero. A questo punto, avendo !_!! sia quando μS=0 che

quando μS=LC, ne risulta

(22)

Se i conteggi netti sono inferiori a LC, si conclude che la sostanza sia priva di attività, mentre

se la soglia viene superata si assume che ci sia qualche attività presente.

Come visto in precedenza, se non è presente attività nel campione i valori medi dei conteggi del fondo e del segnale lordo risultano equivalenti e il conteggio del segnale netto è zero; l’effetto cercato non c’è e, avendo y=0, si ottiene x1=x2.

A questo punto, l’incertezza è data da

! 0 = !!_{∙ 2!(!}

!) = !!∙ 2!!! (35)

e LC dipende solo dall’incertezza della misura di fondo x2, secondo la formula

!_! = !_!!(0) = !_!!_!. (36) Sotto queste condizioni la deviazione standard del segnale lordo è uguale a quella del fondo; applicando alla formula della varianza

!_!! _{= 2!}

!!. (37)

e se le uniche fluttuazioni che entrano nella misura sono quelle date dalla statistica di conteggio, secondo la distribuzione di Poisson risulta

!_! = !_!. (38) Supponendo che il rischio di errore casuale accettabile sia del 5%, tenendo presente che questo presenta una distribuzione normale, la costante k nella formula (31) assume il valore 1.645 di segno positivo dato l’interesse solo per la deviazione positiva dalla media. In altre parole, esiste la probabilità del 95% che il campione casuale stia al di sotto della media più 1.645σ.

(23)

Se è presente dell’attività nel campione, μS ha valore positivo. Se in questo caso la media dei

conteggi fosse posta uguale a LC, il tasso dei falsi negativi sarebbe pari al 50% vista la

simmetria della distribuzione Gaussiana proprio rispetto alla media. Ecco che viene definita la MDA (minima attività rilevabile) dell’attività di un campione misurato, necessaria a produrre un valore medio dei conteggi netti abbastanza alto da ridurre il tasso di errore e renderlo accettabile. Usualmente la probabilità scelta per i falsi negativi è del 5%.

LD rappresenta il minimo valore che soddisfa questi criteri di decisone, definito come stima

della media dei conteggi netti che corrisponde alla MDA.

Per assicurare che il 95% dell’area sotto la distribuzione LD sia sopra LC si richiede che

!_! = !_!+ 1.645!_!_! (40)

e tramite l’approssimazione data dal fatto che tutti i segnali sono piccoli rispetto al fondo,

!_! = !_!+ 1.645 2!_! = !_!+ 2.326!_! = !_!+ 2.326 !_!. (41)

Con una derivazione più accurata si trova [4] che !!! = 2!!+ 1.645 e sostituendo il

valore di LC, risulta infine

!_! = 4.653!_!+ 2.706 (42) chiamata equazione di Currie.

(24)

Figura 3: Distribuzioni dei conteggi netti Ns=CN nel caso di assenza di attività (a) e quando c’è una vera

attività presente nel campione

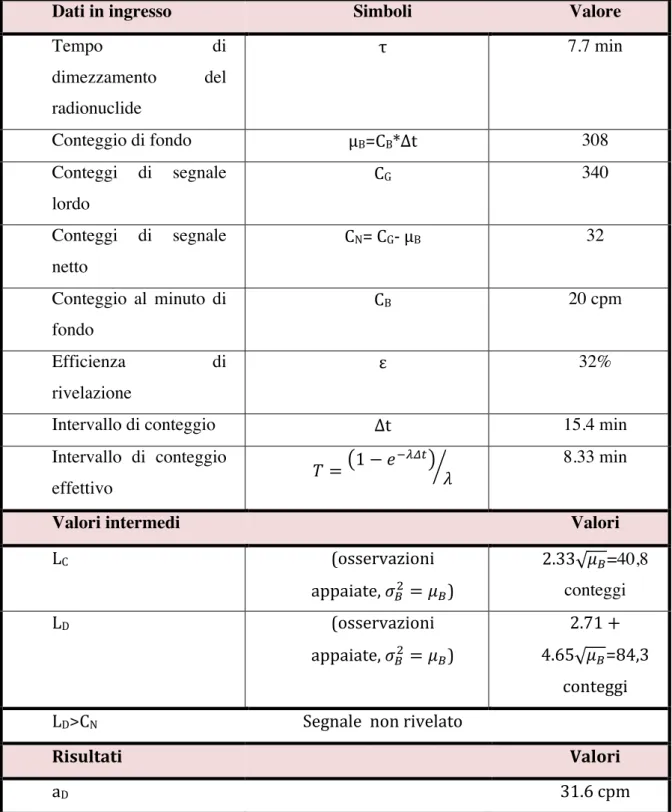
In Tabella 2 è riportato un esempio di misura di radioattività di un campione elaborato con il metodo specificato dal Currie.

Si vuole misurare la radiazione prodotta da un emettitore di positroni, 38_{K. Usando un}

cristallo di iodide di sodio la misura avviene attraverso la rivelazione dei quanti di annichilazione del positrone di energia 0.511 MeV.

Si procede con il calcolo dei limiti in termini di attività, cioè specificandone il tasso di disintegrazione.

L’intervallo di conteggio deve essere stabilito approssimativamente due volte il tempo di dimezzamento del radionuclide in modo che ci sia il limite di rivelazione.

La minima attività rivelabile, denominata con aD, segue dall’espressione (42)

!_! _{= 1 ! !}_! (43)

(25)

Dati in ingresso Simboli Valore

Tempo di dimezzamento del radionuclide τ 7.7 min Conteggio di fondo μB=CB*Δt 308 Conteggi di segnale lordo CG 340 Conteggi di segnale netto CN= CG-‐ μB 32 Conteggio al minuto di fondo CB 20 cpm Efficienza di rivelazione ε 32%

Intervallo di conteggio Δt 15.4 min

Intervallo di conteggio

effettivo ! =

1 − !!!"#

! 8.33 min

Valori intermedi Valori

LC (osservazioni appaiate, !_!! _{= !} !) 2.33 !!=40,8 conteggi LD (osservazioni appaiate, !_!! _{= !} !) 2.71 + 4.65 !!=84,3 conteggi LD>CN Segnale non rivelato

Risultati Valori

aD 31.6 cpm

Tabella 2: Calcolo dei limiti caratteristici e dell’attività di un campione contenente 38_K

(26)

Se ad esempio, l’osservazione di un campione assieme al fondo da un totale di 340 conteggi e si assume che il fondo sia di 308 conteggi, allora il segnale netto è dato dalla differenza, cioè vale 32 conteggi. Con una deviazione standard stimata di 25.4 conteggi, LC risulta dal

calcolo in tabella 40.8 conteggi, cioè si può affermare che il segnale non è rivelato essendo 32<40.8 conteggi.

(27)

Capitolo 3 Determinazione dei limiti caratteristici con l’approccio ISO 11929:2010

CAPITOLO 3

DETERMINAZIONE DEI LIMITI CARATTERISTICI

CON L’APPROCCIO ISO 11929:2010 [5]

L’ISO (International Organization for Standardization) è un’organizzazione mondiale il cui scopo principale è la preparazione di regole standard internazionali.

In particolare, l’ISO 11929:2010 riguarda la definizione delle soglie che definisco la presenza o meno di materiale radioattivo all’interno di un campione analizzato.

Questo norme specificano una procedura per il calcolo della “decision threshold”, soglia di decisione, del “detection limit”, limite di rivelazione, e degli intervalli di confidenza per un misurando non negativo di radiazione ionizzante.

I campi di applicazione dell’ISO 11929:2010 sono: • misure di conteggi fatti con un rateometro;

• misure di conteggi ripetute con influenza casuale o non conosciuta; • misure di attività;

• misure di conteggi su un filtro durante l’accumulo di materiale radioattivo; • misure spettrometriche multi-canali.

3.1 Simboli utilizzati nella norma ISO 11929:2010

Per la determinazione delle soglie vengono utilizzati alcuni simboli per descrivere le variabili di interesse in aggiunta a quelli già specificati nel Capitolo 2, riportati in Tabella 3:

(28)

Simbolo Descrizione

! Valore vero del misurando; se l’effetto fisico non è presente, è zero, altrimenti è sempre positivo

!(!) Incertezza standard dell’estimatore Y come una funzione del valore vero del misurando

! Migliore stima del misurando

y* Soglia di decisione del misurando y# _{Limite di rilevamento del misurando}

!⊲_{, !}⊳ _{Limiti inferiore e superiore dell’intervallo di confidenza del}

misurando

1-‐γ Probabilità per l’intervallo di confidenza del misurando

kp, kq Quantili della distribuzione normale standardizzata per le

probabilità p e q

ϕ(t) Funzione di distribuzione di una distribuzione normale standardizzata; si applica ϕ(kp)=p

Tabella 3: Simboli e definizioni in aggiunta

3.2 Modello di calcolo

Partendo da un sistema fisico che si vuole studiare, si assegna un valore non negativo al misurando, che ne quantifica l’effetto. Viene assunto che, nel caso particolare in cui non ci sia questo effetto, il valore vero definito con ! sia uguale a zero.

Al misurando viene assegnato uno stimatore Y, ed una quantità y, valore dello stimatore, cioè stima del misurando.

In generale, il fatto che il misurando sia non negativo non è preso in considerazione, quindi y può avere valori negativi, specialmente in un intorno di zero.

Seguendo il modello già specificato nella trattazione “classica” e sostituendo come prima le quantità xi nel modello, la stima principale y del misurando Y risulta:

! = ! !_!, … … , !_! = !_!− !_!!_!− !_! ∙ !!!!…

!!!!…= !!− !!!!− !! ∙ !. (44)

(29)

! ! = !!∙ !! !_! + !_!!!! !_! + !_!!!! !_! + !! !_! + !!!_!"#! ! . (45)

L’incertezza relativa, somma delle incertezze standard relative delle quantità da x5 a xm è

definita

!_!"#! _{(!) =} !!(!!)

!_!! !

!!! . (46)

Le stime xi assieme alle loro incertezze standard u(xi) (i=3,…… m) sono conosciute da

investigazioni precedenti o sono valori basati su esperienza in accordo con altre informazioni sul sistema. Ad esempio, xi potrebbe essere determinata come media aritmetica

e u2_(x

i) come varianza empirica o come varianza di una distribuzione rettangolare sulla

regione dei possibili valori di xi di larghezza Δxi. Questo porterebbe a u 2

(xi)=(Δxi) 2

/12. Tenendo in conto delle semplificazioni specificate nel capitolo precedente (24), l’espressione dell’incertezza diventa

! ! = !!_{∙ !}! _!

! + !! !! + !!!!"#! ! . (47)

In accordo con il modello, può essere generalmente eliminata la variabile x1, tasso di

conteggio, ridefinendola come

!! = _!! + !! (48)

che sostituita nella formula della sua incertezza, data come funzione standard h! x! , porta

all’espressione

!! _!

! = ℎ!! !_!+ !! . (49)

(30)

! ! = !!_{∙ !}! _!

! + !! !! + !!!!"#! ! =

= !!∙ ℎ_!! !_!+ !_! + !! !_! + !!!_!"#! ! (50)

essendo h! x! = x! t, definito t tempo di misura del segnale lordo, si arriva infine a

! ! = !!_∙ !

!" + 2!! !! + !!!!"#! ! . (51)

Dalla (51), imponendo y=0, ovvero ipotizzando l’assenza dell’effetto considerato, si ricava la (52), che rappresenta la soglia di decisione. Si nota che il risultato è identico a quello ricavato nel Capitolo 2

!! = !∗ = !!!!!(0). (52)

Il limite di rivelazione può essere ricavato seguendo un ragionamento analogo a quello usato nel capitolo precedente. Ciò porta a scrivere la (53).

!! = !# = !∗+ !!!!!(!#). (53)

Esplicitando l’espressione dell’incertezza, risulta !#_{= !}∗_{+ !} !!! !!∙ ! # !" + 2!! !! + !#!!!"# ! _{! (54)}

dove si nota la dipendenza del limite di rivelazione dall’incertezza relativa associata a w. La (54) può essere risolta per iterazione o per interpolazione.

Seguendo il primo metodo, si mette a sistema l’equazione (54) con la retta y = y e si ottiene una soluzione grafica come evidenziato in Figura 4.

In particolare, partendo da un valore iniziale y! < y#, si ottiene un valore approssimato y!!!

sempre migliore attraverso la (55)

!_!!! = !∗_{+ !}

!!!!(!!) (55)

(31)

Come scelta iniziale si può prendere il valore !_! = 2!∗.

Figura 4: Calcolo del limite di rivelazione con iterazione Punti indicati in figura: 1) retta ! = ! 2)

curva ! = !∗_{+ !}

!!!!(!); ! è il valore vero del misurando; y è la stima del misurando

Con l’iterazione, partendo da un’approssimazione di partenza, la sequenza di approssimazioni successive migliorate (con i=1,2,……) converge a y#, che è l’ascissa del punto di intersezione tra la retta e la curva.

Il secondo metodo è basato sull’interpolazione; se lineare, l’approssimazione risulta:

!# _{= ! + !}!_{+ (!} !!!! − !!!!! )!!(0) (56) con ! = !_!!!! 0 + 1/2 !!!!! !! ! ! _! ! − !!(0) (57)

Se α=β, come da ipotesi, segue che !#= 2!.

Può anche essere scelta un’approssimazione polinomiale del secondo ordine del tipo u! _{y = c}

(32)

!

#

₌

!!∗!!!!!

!!!!_!_! . (59)

Questo risultato è in accordo con quanto proposto dal Currie dove L! = k!+ 2L! a patto

che i coefficienti siano rispettivamente posti c1=1 e c2=0, quindi secondo

un’approssimazione del primo ordine.

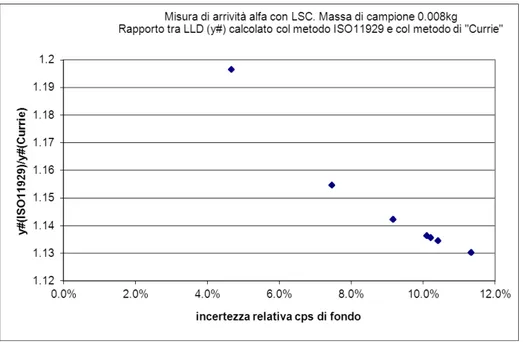
3.3 Confronto dei limiti caratteristici ottenuti tramite l’approccio “classico” e quello della norma ISO 11929:2010

Alla luce di quanto detto, vengono confrontati i limiti caratteristici calcolati con i due diversi metodi ISO 11929:2010 e classico del Currie. Il loro rapporto varia in funzione della variazione di incertezza relativa.

In Figura 5 è rappresentato quanto detto; l’esempio è quello di una misura di attività alfa di un campione ottenuto per scintillazione liquida. Il procedimento è descritto in dettaglio nel Capitolo 5.

Figura 5: Rapporto tra i limiti di rivelazione dell’ISO 11929:2010 e del Currie

Dal grafico si vede che, per un’elevata incertezza dei conteggi di fondo, il limite di rivelazione “ISO 11929:2010” sovrastima di circa il 13% il corrispondente limite “Currie”.

(33)

Diminuendo l’incertezza associata ai conteggi di fondo, l’incertezza associata a w assume un peso percentuale più importante nell’incertezza composta. Questo comporta un aumento del rapporto riportato in ordinata nel grafico di Figura 5.

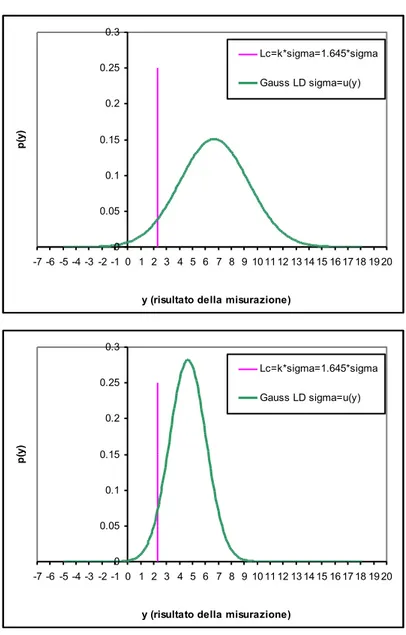
In Figura 6 si presenta l’interpretazione grafica del risultato:

Figura 6: Dipendenza del limite di rilevazione da !!"#! (!): grafico superiore, distribuzione gaussiana

ottenuta con un’incertezza elevata; grafico inferiore, gaussiana ottenuta con piccola incertezza

Dalla figura risulta evidente l’allargamento della distribuzione gaussiana del limite di

0 0.05 0.1 0.15 0.2 0.25 0.3 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

y (risultato della misurazione)

p( y) Lc=k*sigma=1.645*sigma Gauss LD sigma=u(y) 0 0.05 0.1 0.15 0.2 0.25 0.3 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

y (risultato della misurazione)

p(

y)

Lc=k*sigma=1.645*sigma Gauss LD sigma=u(y)

(34)

A seguire viene riportato un esempio di applicazione dell’ISO 11929:2010 per la misura di attività con un rateometro [6]: viene specificata in modo sperimentale l’analogia e la differenza di questo metodo con quello del Currie per la determinazione dei due limiti caratteristici.

Si utilizza un rateometro, che registra il tasso degli impulsi che arrivano all’ingresso dello strumento, contatore analogico e lineare con segnale di uscita che cresce bruscamente (costante di tempo di salita trascurabile) durante l’arrivo del segnale in entrata e poi che decresce esponenzialmente (costante di tempo di rilassamento τ), fino all’arrivo dell’impulso successivo. τ è indipendente dal tasso di conteggio.

I valori di aspettazione rg e r0 delle quantità in ingresso X1 e X2 per il calcolo dei limiti

caratteristici sono i segnali di uscita del rateometro in caso di misura rispettivamente del segnale lordo e del fondo. I valori delle quantità in ingresso sono, quindi:

!! = !!; !! = !! (60)

con le loro incertezza standard associate:

!! _! ! =_!!!! !; ! ! _! ! = _!!!! ! (61)

La costante del tempo di rilassamento influenza fortemente la soglia di decisione ed il limite di rilevamento, ma la sua incertezza standard non è necessaria.

Il semplice modello è nella forma ! = !!− !! = !!− !! , quindi prendendo in

considerazione le stime del misurando:

! = !!− !! (62) con ! ! = !! !!!+ !! !!! (63)

Di seguito viene riportato un esempio numerico, nel quale la costate del tempo di rilassamento è presa di valore τg=τ0=120 s.

(35)

DATI IN INGRESSO

Quantità Simboli Valori

Conteggi lordi: Numero di eventi registrati ng 2591 Durata di misura tg 360 s Conteggi di fondo: Numero di eventi registrati n0 41782 Durata di misura t0 7200 s

Misure di segnale lordo con il rateometro: Tasso di conteggio rg 7,2 s -1 Costante di tempo di rilassamento τ_g 120 s

Misure di fondo con il rateometro: Tasso di conteggio r0 5,8 s -1 Costante di tempo di rilassamento τ0 120 s Volume V 0,5 l Efficienza di rivelazione ε 0,3 Fattore di auto-assorbimento F 0,6

Incertezza sul volume u(V) 0,005 l

Incertezza sull’efficienza

u(ε) 0,015

Incertezza sul fattore di u(f) 0,4

(36)

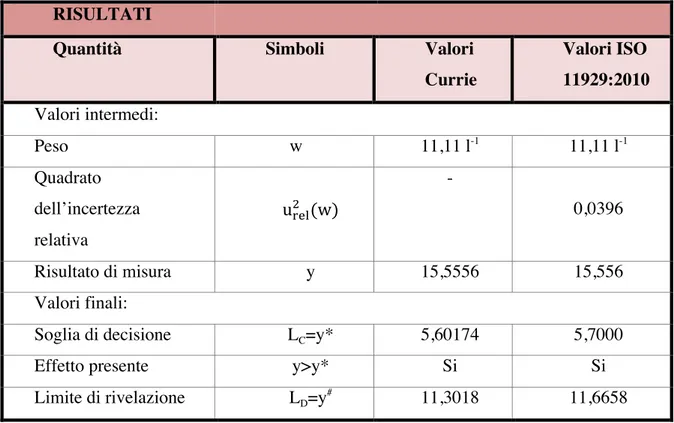
RISULTATI

Currie Valori ISO 11929:2010 Valori intermedi: Peso w 11,11 l-1 11,11 l-1 Quadrato dell’incertezza relativa u_!"#! _(w) - 0,0396 Risultato di misura y 15,5556 15,556 Valori finali:

Soglia di decisione LC=y* 5,60174 5,7000

Effetto presente y>y* Si Si

Limite di rivelazione LD=y

#

11,3018 11,6658

Tabella 5: Calcoli di misura, soglie e limiti caratteristici

Nella Tabella 4 sono specificati i dati in entrata, mentre nella Tabella 5 vengono definite le quantità calcolate assieme ai limiti di interesse.

In Allegato B è presente il foglio di calcolo che ha portato a tale risultato.

Come risulta dal confronto, il valore del limite di rivelazione calcolato con l’ISO 11929:2010 si discosta da quello ottenuto utilizzando il metodo di calcolo descritto dal Currie, in particolare ha valore maggiore.

Questa differenza deriva, infatti, dal fatto che venga presa in considerazione o meno l’incertezza relativa associata al volume, all’efficienza e al fattore di auto-assorbimento, che modifica il calcolo dell’incertezza complessiva.

(37)

Capitolo 4 Approccio Bayesiano dell’ISO 11929:2010

CAPITOLO 4

APPROCCIO BAYESIANO DELL’ISO 1929:2010

4.1 Statistica Bayesiana e confronto con il modello “classico”

Seppur sviluppati per definire e calcolare gli stessi limiti caratteristici per la misura delle radiazioni ionizzanti, i due modelli presentano una fondamentale differenza nell’approccio con cui la teoria viene sviluppata. In entrambi le misure fisiche sono trattate come casuali e indipendenti, cioè il verificarsi di un evento aleatorio non ha effetto su quello di un altro, ma mentre nell’articolo del Currie la valutazione delle misure segue una distribuzione Poissoniana, nell’ISO 11929 le formule di definizione sono basate sulla statistica Bayesiana. Quest’ultima si differenzia da quella convenzionale per il suo diverso uso del termine probabilità, che non viene interpretato con frequenza ma come livello di fiducia nel verificarsi di un dato evento.

L’inferenza bayesiana rappresenta una formalizzazione del metodo scientifico, che implica la raccolta di dati che verificano o confutano una precedente ipotesi; con l’aumentare della disponibilità dei dati cambia il grado di fiducia. Tramite tale approccio viene usata la stima del grado di confidenza in una data ipotesi prima dell’osservazione dei dati al fine di associarne successivamente un valore numerico. In altre parole, la statistica bayesiana possiede la caratteristica addizionale di richiesta di un set di distribuzioni a priori per i parametri sconosciuti, oltre a quella per i dati che derivano dalla semplice osservazione. Il teorema di Bayes generale è enunciato come segue:

! !_! ! =! ! !! !(!!)

!(!) (64)

con !(!_!) probabilità a priori;

(38)

Considerando la misura di attività in un campione, la statistica convenzionale descrive la distribuzione di probabilità f(y|η), cioè la distribuzione condizionale della stima y dato il valore vero η del misurando Y.

La statistica bayesiana permette il calcolo di f(η|y), la distribuzione del vero valore η del misurando Y data una sua stima y, che è il risultato della misura.

Graficamente i due approcci sono rappresentati in Figura 7:

Figura 7: Approccio classico e bayesiano: diversa interpretazione della variabile indipendente (in asse x) e di

quella dipendente (in asse y) Approccio classico 0 0.05 0.1 0.15 0.2 0.25 0.3 -10 -5 0

y

5 10

f(y

|η

)

Approccio Bayesiano 0 0.05 0.1 0.15 0.2 0.25 0.3 -10 -5 0 5

η

10

f(

η

|y)

(39)

Si nota come siano presi i valori di y sull’asse x nell’approccio classico e come siano presi i valori di η sempre sull’asse x nell’approccio bayesiano.

I limiti caratteristici e gli intervalli di confidenza, calcolati tenendo conto di tutte le sorgenti di incertezza, sono basati sulle distribuzioni f(y|η) e f(η|y).

Per stabilire f(η|y) vengono separate le informazioni sulle misure ottenute dall’esperimento da quelle già disponibili in precedenza per il misurando; ne risulta

! ! ! = ! ∙ !_!(!|!) ∙ !(!) (65) con c, costante di normalizzazione;

!_!(!|!) distribuzione di probabilità per cui il misurando Y ha vero valore η solo se vengono date y e la sua incertezza u(y);

!(!) che raccoglie tutte le informazioni disponibili prima dell’esperimento, funzione indipendente da y.

Se il misurando è una concentrazione di un elemento o una attività di sorgente di radiazione, si è a conoscenza del fatto che sia positivo η ≥ 0 prima di effettuare la misurazione; sebbene y possa essere negativo, si sa per certo a priori senza analisi sperimentale che il vero valore è non-negativo. Da qui si può definire f(η) come segue:

f η =!"#$₀ η ≥ 0_{η < 0} (66)

A questo punto la funzione di distribuzione di probabilità f(η|y) risulta essere una Gaussiana troncata N(y,u(y)) come si evidenza nella figura che segue:

(40)

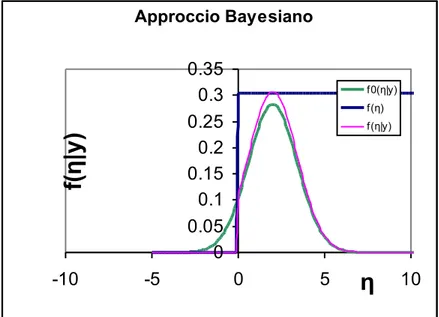
Figura 8: Funzione distribuzione di probabilità f(η|y): prodotto di !(!) e di una Gaussiana troncata

N(y,u(y))

Si osserva, quindi, che l’approccio Bayesiano si scosta da quello classico quando l’area sottesa dalla guassiana a sinistra dell’origine è significativa. Infatti, se tutta la campana della distribuzione gaussiana si trova a destra dell’origine, non c’è differenza tra le due e quindi neanche tra i due approcci.

Approccio Bayesiano 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 -10 -5 0 5

_η

10

f(

η

|y

)

f0(η|y) f(η) f(η|y) Approccio Bayesiano 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 -10 -5 0 5

_η

10

f(

η

|y

)

f(η|y)

(41)

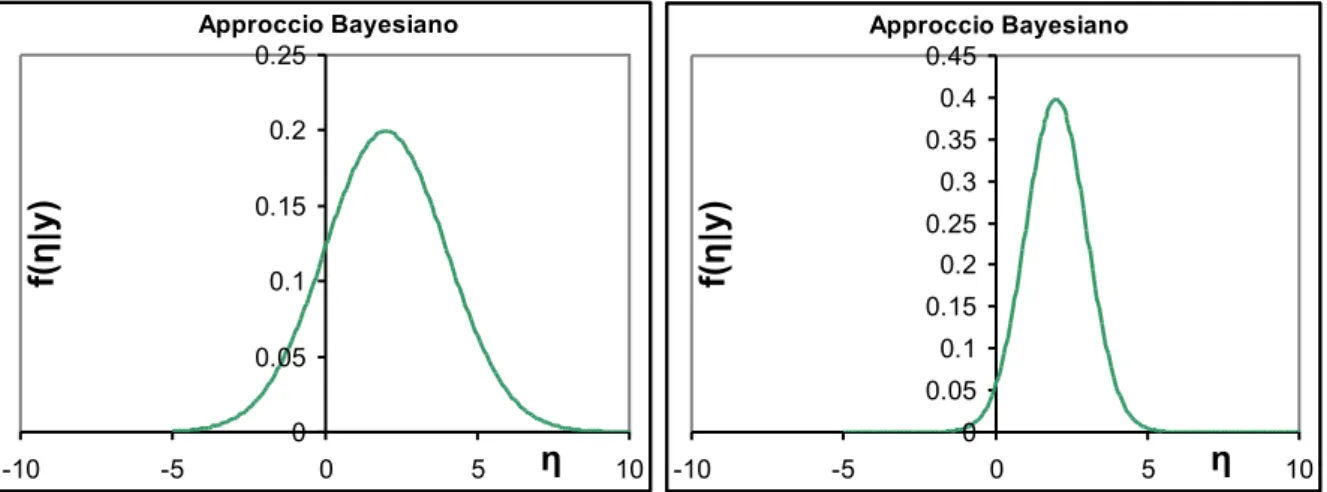
Figura 9: Variazione della distribuzione di probabilità: area sottesa calcolata noto il rapporto y/u(y).

Grafico superiore sinistro, y/u(y)=1, area sottesa 16%; grafico superiore destro, y/u(y)=2, area sottesa 2.3%; grafico inferiore sinistro, y/u(y)=3, area sottesa 0.13%; grafico inferiore destro, y/u(y)=4, area sottesa

0.0032%.

Dopo aver ottenuto f(η|y), il calcolo di f(y|η), anch’esso attraverso il teorema di Bayes, può essere ottenuto dalla formula seguente:

! ! ! ∙ ! ! = !(!|!) ∙ !(!) (67) che è la distribuzione di probabilità gaussiana per un vero valore η del misurando con incertezza standard u η (visto che u! y = u! η , cioè la varianza della distribuzione di

Approccio Bayesiano 0 0.05 0.1 0.15 0.2 0.25 -10 -5 0 5 η 10 f( η |y) Approccio Bayesiano 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 -10 -5 0 5 η 10 f( η |y) Approccio Bayesiano -0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 -10 -5 0 5 _η 10 f( η |y) Approccio Bayesiano -0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -10 -5 0 5 η 10 f( η |y)

(42)

standard che serve per la determinazione è calcolata come funzione u(η) del valore vero η del misurando.

Come nell’approccio classico, la soglia di decisione è quel valore superato il quale, si decide che l’elemento o il radionuclide sia presente; nulla si può dire della presenza o meno se la soglia non viene superata. Segue:

!_! = !∗ _{= !}

!!!!(0) (68)

dove u(0) è l’incertezza del misurando quando il suo valore vero è zero.

Allo stesso modo, il limite di rivelazione è definito come il più piccolo valore vero del misurando rilevabile con il metodo di misura utilizzato. Quindi,

!_! = !∗ _{= !}∗_{+ !}

!!!!(!∗). (69)

Per concludere la trattazione, manca da definire l’intervallo di confidenza; quando l’effetto fisico è dato come presente, questo contiene il valore vero del misurando, preso non negativo, con la probabilità specifica 1-γ.

Il limite dell’intervallo di confidenza inferiore !⊲ e quello superiore !⊳ sono definiti in modo generale come segue:

!⊲ _{= ! − !} !!(!) (70) con ! = ! ⋅ (1 −!_!) (71) e !⊳ _{= ! + !} !!(!) (72) con ! = 1 − !!_! (73) dove ! = ! ! !(!) (74)

(43)

In Allegato A è presente l’andamento della funzione di distribuzione ϕ(t).

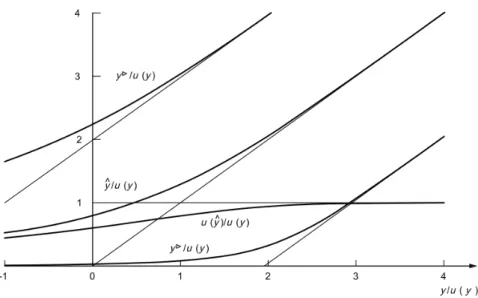
Figura 10: Stima migliore e limiti dell’intervallo di confidenza ! _{!(!) rapporto tra il risultato di misura}

principale del misurando e l’incertezza standard associata alla miglior stima. Per ! ≥ 4!(!), valgono le approssimazioni ! = ! e ! ! = !(!).

Nel caso particolare in cui ! ≥ 4!(!) , allora può essere scelto il valore ω=1; l’approssimazione simmetrica rispetto a y è adottata per gli intervalli di confidenza, che appaiono nella forma:

!⊲ _{= ! − !}

!!!_!! ! (75)

e

!⊳ _{= ! + !}

!!!_!! ! (76)

Vengono illustrati in Figura 11 gli intervalli di confidenza ηl e ηu assieme alla migliore stima

(44)

Figura 14: Illustrazione dei limiti di confidenza ηl e ηu e della migliore stima z

4.2 Esempio di misura di attività specifica di un radionuclide con ISO 11929:2010 in approccio Bayesiano

Viene effettuata la misura della attività specifica di un campione di materiale contenente un radionuclide dopo la separazione chimica di quest’ultimo.

Il misurando Y è definito in questo caso come l’attività specifica a; per questa quantità sono calcolate le grandezze caratteristiche tenendo presente l’influenza casuale data dal trattamento del campione a seguito della separazione chimica.

Il modello risulta:

! = ! = !!!!!

!!!!!! =

!!!!!

!"# (77)

dove !! = !! è il tasso medio di conteggio del campione lordo, !! = !! è il tasso medio di

conteggio del fondo, M definisce la massa del campione, k l’efficienza di rivelazione dello strumento e infine ε, fattore collegato alla separazione chimica.

Le medie degli eventi registrati per il campione e per il fondo, !! e !!, sono calcolate dalle

misure di conteggio sui campioni testati per un tempo di misura della durata di tg e t0

(45)

Una volta passati alle stime delle quantità in esame, essendo, x1=rg e x2=r0 rispettivamente i

tassi di conteggio lordi e di fondo, ne deriva:

! = ! !!, … … , !! = !!− !!!!− !! ∙ ! = !_!! ! − !! !!!!− !! ∙ ! (78) con !_! = !! _! ! ; !! = ! ! !_!. (79) Per i valori x1 e x2 le incertezze associate sono:

!! _! ! = !! !!! = !! !! ; ! ! _! ! =!_!! !! = !! !! (80)

e trovate le varianze empiriche !!! e !!! si hanno i dati necessari al calcolo

!! _! ! =!! ! (!!!!)! ; ! ! _! ! = !! ! (!!!!)! (81)

con !! e !! numero di misurazioni del campione e del fondo.

Avendo a disposizione tutti i dati necessari si procede con il calcolo di u(y) secondo il modello.

Per il calcolo della soglia di decisione e del limite di rilevamento, l’incertezza standard del misurando deve essere espressa come funzione u(y) del valore vero y ≥ 0 del misurando; questa deve essere definita, unica e continua per tutti i valori di y ≥ 0 e non deve assumere valori negativi.

In accordo con il modello di cui sopra, l’incertezza standard u(x1) del rateo di conteggio

lordo x1=ρg è data come funzione h! x! = x! t_!= x! _n

! a seconda che sia espressa

(46)

A questo punto, sostituendo x1, tenendo in considerazione che l’incertezza è calcolata come

funzione h, cioè u! x! = h!!(y w + x!x!+ x!), il risultato è il seguente:

! ! = !!_{∙ ℎ} ! ! ! !+ !!!!+ !! + !! !_!! _! ! + !!!!! !! + !! !! + !!!"#! (!) (82)

Adesso, sostituendo h1, x1, x2 e le loro incertezze standard u(x1) e u(x2) nella formula

precedente, si arriva all’equazione che segue:

! ! = !!_∙ ! !!!!!!!!! ! !! + !! ! !!! !!+ !! !_!! _! ! + !! !! + !!!"#! (!). (83)

L’incertezza standard nell’esempio di applicazione non è disponibile come funzione di h_!(x_!), quindi può essere utilizzato il metodo dell’interpolazione.

Ponendo y = y = 0, risulta u! 0 = w!∙ u! x! + u! x! . Ora per y =0 può avvenire la

sostituzione di s!

!

t_!! con s! !

t_!! e tendendo presente le formule precedenti

!! _{0 = !}!_{∙ !}!!

!_!! ∙ 1 !_! + 1 !_! . (84)

Nella Tabella 6 sono specificati i dati in ingresso e le quantità calcolate assieme ai limiti di interesse

In Allegato C è presente la tabella di calcolo che ha portato al risultato per la definizione dei limiti di rivelazione.

(47)

DATI IN INGRESSO

Numero di campioni mg 5 Numero di bianchi m0 5 Numero di eventi registrati: Campioni (segnale lordo) ng,i 1832, 2259, 2138, 2320, 1649

Bianchi (fondo) n0,i 966, 676, 911,

856, 676 Durata di misura: Dei campioni tg 30000 s Del fondo t0 30000 s Massa M 0,100 Kg Efficienza di rivelazione k 0,51 Campo chimico di separazione di 90 Sr ε 0,57

Incertezza sulla massa u(M) 0,001 Kg

Incertezza sull’efficienza u(k) 0,02 Incertezza sulla separazione u(ε) 0,04

(48)