Misura del rapporto dei calori specifici dell'aria mediante video-monitoraggio di oscillazioni di pressione

Università degli studi di Roma

“La Sapienza”

Facoltà di Scienze Matematiche Fisiche e Naturali

Dissertazione di laurea triennale in fisica

Anno Accademico 2006-2007

Misura del rapporto dei calori specifici

dell’aria mediante video-monitoraggio di

oscillazioni di pressione

Indice

Introduzione………..

1. Il pistone adiabatico

2. Onde sonore in aria.

3. Esperimento di Rüchardt.

Un metodo di misura alternativo……….24

Conclusioni

Appendice A

Appendice B.

Bibliografia………...

Introduzione

In questa dissertazione ci proponiamo di riprodurre un famoso esperimento, ideato da Rüchardt, si tratta in breve di misurare il periodo di oscillazione di una pallina metallica che oscilla in un tubo di vetro innestato su un contenitore pieno d’aria che permette di misurare, nel modo che descriveremo, il valore del rapporto dei calori specifici di un gas. L’aspetto innovativo di questa dissertazione consiste nell’ utilizzare un sistema di elaborazione delle immagini digitali che ci ha permesso di ottenere, con una buona risoluzione, la posizione della pallina in funzione del tempo. La descrizione dell’esperimento è preceduta da due brevi sezioni introduttive volte ad illustrare la fisica alla base dell’esperimento: nella prima viene analizzato il problema della determinazione dello stato di equilibrio di un pistone adiabatico che si muove in un contenitore chiuso e con pareti adiabatiche, mostrando come la termodinamica classica non è in grado di predire uno stato finale in maniera univoca in quanto restano indeterminate le temperature finali di equilibrio. Il problema è stato risolto in letteratura in modo approssimato con un modello cinetico in cui si tiene in conto l’effetto della velocità finita del pistone nel computo degli scambi di quantità di moto tra il pistone e le molecole del gas [1]; come vedremo con questo modello è possibile ottenere equazioni, risolvibili numericamente, per le variabili dinamiche temperatura dei due sottosistemi e posizione del pistone in grado di predire univocamente lo stato finale del sistema date le condizioni iniziali. La seconda parte consiste di una breve trattazione riguardante le oscillazioni di un gas in mezzi infiniti e confinati con particolare attenzione alla classificazione dei regimi di oscillazioni adiabatiche ed isoterme.

La terza sezione presenta l’esperimento che abbiamo condotto e si conclude con un’analisi dell’esperimento di Ruchadt condotto da De Lange e Pierrus con un metodo di misura elettronico; i cui risultati vengono messi a confronto con quelli ottenuti con la nostra tecnica, discutendo i diversi regimi di oscillazione di un gas confinato. In appendice è riportato un approfondimento sul calore specifico di un gas biatomico ed uno sui dettagli della nostra tecnica di misura basata sull’ elaborazione di immagini digitali.

Capitolo 1

Pistone adiabatico.

1.1 Presentazione del problema e soluzione con modello cinetico. Dinamica verso l’equilibrio con stati intermedi definiti.

La predizione dello stato di equilibrio in un sistema composito isolato con pareti interne adiabatiche è un problema complesso, la cui soluzione non è univocamente determinata nel quadro della termodinamica elementare. Questa è in grado di predire solamente il valore della pressione di equilibrio del sistema, mentre le altre variabili, rimanendo indeterminate, danno luogo ad una degenerazione dei possibili stati finali. Mostreremo come questa indeterminazione possa essere rimossa attraverso un modello cinetico in cui la presenza di una velocità finita del pistone nel bilancio dello scambio di quantità di moto con le molecole del gas gioca un ruolo essenziale, ovvero introducendo una forza di attrito che permette al pistone di raggiungere l’equilibrio.

Si consideri un cilindro adiabatico chiuso alle estremità contenente due sottosistemi separati da un pistone mobile senza attrito e anch’esso adiabatico (fig 1). Chiamiamo i due sottosistemi A e B, entrambi contenenti una mole del medesimo gas perfetto. All’istante t=0 , quando il pistone è tenuto fermo da vincoli i sistemi A e B sono caratterizzati dalle temperature T₁(t= )0 ≡T_A, T₂(t= )0 ≡T_B e dai volumi V_A =SX(0) e

)] 0 ( [L X S

V_B = − dove S e L sono rispettivamente la sezione e la lunghezza del cilindro. Immaginiamo ora di rimuovere i due vincoli dal pistone: la differenza di pressione tra i due sottosistemi eserciterà una forza sul pistone che ne determina il moto. Come anticipato, da un punto di vista strettamente termodinamico, possiamo predire una relazione univoca solo per la pressione finale (cioè quella di equilibrio meccanico tra A e B), ma i valori delle temperature e dei volumi finali (che sono diverse, cioè quando il pistone si ferma non abbiamo un completo equilibrio termodinamico) restano indeterminati: si presenta una degenerazione dei possibili stati finali.

Seguiamo l’approccio termodinamico per verificare quanto affermato.

Poiché per ipotesi l’energia interna totale è U =U_A+U_B =c_vT_A+c_vT_B allora dal primo principio segue la relazione sulle temperature finali T_1f, T_2f:

B A f

f T T T

T₁ + ₂ = + (1)

mentre l’uguaglianza delle pressioni finali produce:

f f f f V V T T 1 2 1 2 _{= (2)}

dove V_1f ,V_2f indicano i volumi finali. In definitiva le equazioni (1) e (2) consentono di determinare la pressione finale:

B A B A f f f f f f f f f f f f f V V T T R V V T T R V V V T T T R V RT P + + = + + = + + = = 2 1 2 1 1 2 1 1 2 1 1 1 ) / 1 ( ) / 1 ( (3)

la pressione finale dipende quindi univocamente dalle variabili termodinamiche dello stato iniziale, mentre le temperature ed i volumi finali dipendono da parametri che esulano dal dominio di una descrizione puramente termodinamica del sistema.

Mostriamo come queste possano invece essere determinate, sotto opportune condizioni, tramite il modello cinetico, in altre parole cerchiamo le equazioni che governano le evoluzioni temporali delle variabili T₁,T₂,X verso l’equilibrio (X

essendo la posizione del pistone).

Nel seguito indicheremo con N il numero di Avogadro, con M la massa del pistone, con M_g il valore della massa del gas dai due lati del pistone che assumiamo comune senza perdere di generalità.

Come già detto facciamo l’ipotesi di gas ideale (U=nc_vT); ed assumiamo, affinché le temperature T₁(t) e T₂(t) in A e B siano ben definite ad ogni istante (i due gas passano per stati di equilibrio), che le molecole del gas obbediscano alla distribuzione delle

pistone (condizione che può essere ottenuta scegliendo la massa del pistone sufficientemente grande).

Otteniamo le due equazioni per le temperature imponendo separatamente la conservazione dell’energia in A e in B sotto le ipotesi adiabatiche, ed esprimendo il lavoro compiuto dai gas in termini della variazione di quantità di moto associata alle collisioni molecolari con il pistone in moto.

dt dt dX S dt dX v m dL dU dT c_{v x} 2 2 1 2 1 1 1 ρ     ₋ − = − = = dt dt dX dt dX v v dt dX S m _{x x}               + − − = 2 2 1 2 ρ dt dt dX S m dt dt dX X T RM dt dt dX X RT g 3 1 2 1 1 8 _      −       + − = ρ π (4) analogamente per T₂(t): dt dt dX S m dt dt dX X L T RM dt dt dX X L RT dT c_v g 3 2 2 2 2 2 8       +       − + − = ρ π (5) dove SX N = 1 ρ , ) ( 2 _{S L X} N − =

ρ sono le densità molecolari in A e B, L1è il lavoro

compiuto dal gas in A sul pistone,

N M m₌ g _{la massa molecolare,} 2 x v = m T k_{b 1,2} la velocità quadratica media delle molecole ottenuta dalla distribuzione di Maxwell e

m T k v b x _π 2 , 1

= la velocità molecolare media anch’essa ottenuta con la distribuzione di Maxwell.

E’ importante notare come l’introduzione dell’effetto della velocità finita del pistone sulla variazione della quantità di moto delle molecole, che è tenuto in conto sostituendo v_x con dt dX v_x − nell’equazione (4) e dt dX v_x + nella (5), abbia prodotto in queste equazioni termini proporzionali a

2       dt dX _{ed a} 3       dt dX _{che come}

vedremo giocheranno un ruolo decisivo nello studio della dinamica verso l’equilibrio. Per ottenere l’equazione X(t) imponiamo la conservazione dell’energia totale:

= + +             2 1 2 2 dt cT cT dX M v v costante

che differenziata rispetto al tempo diventa:

0 2 1 2 2 = + +             dt dT c dt dT c dt X d dt dX M _{v v}

sostituendo in questa equazione le (4) e (5) troviamo: 2 2 1 2 1 2 2 _{1 1 8 1 1}             − − +               − + −       − − = dt dX X L X M M dt dX X L T X T RM M X L RT X RT M dt X d g g π (6)

Osserviamo che trascurando nelle (4) e (5) i termini di ordine superiore al primo in

dt

dX _{e integrando per separazione di variabili otteniamo le equazioni di}

trasformazioni adiabatiche reversibili per i due sottosistemi: −1=

1Xγ

T costante e

=

− −1

2(L X)γ

T costante , queste ultime si riflettono nell’ equazione (6) con la presenza del solo primo termine del secondo membro, che essendo proporzionale alla differenza di pressione tra la parte 1 e la parte 2 produce una forza di richiamo. Avremo quindi in questa approssimazione un moto periodico non smorzato.

I termini in x•2 al secondo membro delle (4) e (5) (entrambi positivi e molto maggiori dei termini inx•3) producono nella (6) un termine proporzionale alla velocità che rappresenta lo smorzamento delle oscillazioni del pistone verso la posizione di equilibrio.

Il tempo caratteristico di smorzamento decresce al crescere di

M M_g

π

δ = 8 ; ricordiamo a tal proposito che alla base del nostro modello c’è l’assunzione di masse del pistone molto grandi, cioè piccolo smorzamento (che è proprio l’ipotesi che useremo in seguito per stimare il γ del gas con l’esperimento di Ruchardt quando considereremo lineare la relazione tra il volume e il periodo al quadrato delle oscillazioni, cfr. cap 3). Il precedente set di equazioni può essere più convenientemente riscritto in forma adimensionale: ξ ξ δ γ π ξ ξ θ γ δ ξ ξ θ γ θ 3 2 2 1 1 1 ( 1) 8 ) 1 ( ) 1 ( • • • • − − − + − − = (7) ξ ξ δ γ π ξ ξ θ γ δ ξ ξ θ γ θ − − + − − + − − = • • • • 1 ) 1 ( 8 1 ) 1 ( 1 ) 1 ( 3 2 2 2 2 2 ; (8) 2 2 2 1 2 1 1 1 1 8 1 1 • • • •       − − +         − − − − − = ξ ξ ξ δ π ξ ξ θ ξ θ δ ξ θ ξ θ ξ ; (9)

In questo modo il nostro modello permette di determinare univocamente il valore di equilibrio (che è il valore asintotico) di T_1,2e X una volta noti i corrispondenti valori

iniziali, mentre la termodinamica standard predice, come abbiamo visto, solamente il comune valore delle pressioni finali; ovviamente questa uguaglianza può essere riottenuta come caso particolare del nostro modello come si vede ponendo dX/dt=0 e

0 / 2 2_{X dt =}

d nell’equazione (6) in corrispondenza della posizione finale di equilibrio

f

X .

Tipiche soluzioni numeriche delle equazioni (7)-(8)-(9) sono riportate in figure 3.2,3.3,3.4,3.5 [1] nel caso di gas monoatomico, cioè γ =5/3. Sottolineiamo che i grafici in figura si riferiscono a piccoli valori del coefficiente di smorzamento

2 / 1 ) / 8 ( M_g πM

δ = , cioè a grandi valori di M in accordo con l’assunzione iniziale del nostro modello. Come ci si aspetta le soluzioni sono puramente periodiche per δ =0 (questo non implica che la massa del pistone M sia infinita, ma solamente che i termini superiori all’ordine zero in δ a secondo membro delle equazioni (7)-(9) vengono trascurati), mentre per δ ≠0abbiamo oscillazioni smorzate con tempo di

smorzamento decrescente all’aumentare di δ .

Sfrutteremo nel seguito questi risultati per delineare un modello elementare del moto della pallina nell’esperimento di Ruchardt e per trovare una relazione utilizzabile sperimentalmente per la misura di γ . Osserviamo che nel modello cinetico presentato il pistone si muove tra due sottosistemi isolati entrambi caratterizzati da pressione e temperatura funzioni del tempo. Questa situazione conduce ad un sistema di equazioni differenziali non risolvibili analiticamente. Il caso dell’esperimento di Ruchardt è invece meno complesso in quanto, come sarà accuratamente descritto nel seguito, uno dei due sottosistemi, quello sovrastante la pallina, ha volume infinito e pressione costante. In questo caso è possibile determinare un’equazione risolvibile analiticamente per il moto della pallina mediante la quale, nell’ipotesi di oscillazioni adiabatiche e debole smorzamento, potremo determinare γ .

Capitolo 2

Onde sonore in aria

In questo capitolo ci proponiamo di dare una sintetica descrizione dei principali fenomeni fisici riguardanti la propagazione delle onde sonore in un mezzo infinito per poi specializzare la discussione al caso di un gas contenuto in un volume finito e porre le basi per una interpretazione dei risultati ottenuti da Pierre e De Lange con l’esperimento di Ruchardt (cfr. cap. 3, par 4).

2.1 Mezzi infiniti

Il suono è una perturbazione (prodotta da una sorgente sonora) che, propagandosi in un mezzo elastico, provoca una variazione di pressione ed uno spostamento di particelle, tale da poter essere rilevata da uno strumento acustico. Mentre questa perturbazione, che trasporta sia informazione che energia, si propaga in regioni estese dello spazio, le singole particelle del gas rimangono sempre in prossimità della loro posizione originale. Si hanno cioè delle vibrazioni locali (compressione e rarefazione) di particelle: nel caso di gas e liquidi, che non possono trasmettere sforzi di taglio, tali vibrazioni sono sempre parallele alla direzione di propagazione dell’onda, per cui si parla di onde longitudinali.

Le caratteristiche di spostamento delle particelle intorno alle posizioni di equilibrio dipendono dalle caratteristiche della sorgente che ha prodotto la perturbazione.

Le onde sonore si propagano con velocità caratteristica del mezzo di trasmissione: mentre la frequenza delle vibrazioni locali dipende dalla sorgente, la velocità di propagazione dipende esclusivamente dal mezzo di trasmissione.

Nel caso di gas perfetti (quale può essere considerata anche l’aria nelle condizioni standard di temperatura, ₂₅oC_{, e pressione, 1 atm) la velocità di propagazione del}

suono, che indicheremo con c, può essere espressa, considerando adiabatiche le oscillazioni del mezzo, mediante la seguente relazione:

0 0 ρ γp c= dove v p c c =

γ , p0 è la pressione di equilibrio del gas (in assenza di

perturbazione sonora), ρ₀ la densità del gas anch’essa in condizioni statiche.

Come avremo modo di dire in seguito, il considerare trasformazioni adiabatiche deriva dal fatto che la velocità di propagazione del suono nel mezzo è talmente elevata rispetto alla velocità con cui avvengono i processi di scambio termico da poter ritenere tali processi nulli.

Considerando l’equazione di stato dei gas perfetti (in cui M è la massa del gas e M_m

la massa molecolare) _{0 0} R₀T₀ M M V p m = otteniamo m M R T

c₌ γ 0 0 da cui possiamo dire che

la velocità di propagazione del suono è indipendente dalla pressione del gas mentre è proporzionale a _T1\2_.

Nel fenomeno sonoro, oltre alla velocità di propagazione (che misura la rapidità con cui il segnale si sposta da un punto ad un altro del mezzo di trasmissione) occorre considerare altre proprie caratteristiche delle onde quali la frequenza, il periodo e la lunghezza d’onda.

La frequenza, legata alla rapidità con cui le particelle oscillano in ogni singolo punto, è il numero di oscillazioni nell’unità di tempo, si misura in cicli per secondo, ossia in Hertz (Hz).

L’inverso della frequenza prende il nome di periodo: si tratta del tempo necessario affinché le particelle compiano una oscillazione completa.

La lunghezza d’onda è la distanza percorsa dall’onda durante un’oscillazione completa (o anche il cammino percorso dall’onda mentre localmente avviene un’oscillazione completa).

Le tre proprietà sono legate dalla relazione: cT f c =

=

λ .

Abbiamo detto che, durante la propagazione del fenomeno acustico in un gas, le particelle del mezzo vibrano intorno alla loro posizione di equilibrio. Tali vibrazioni non avvengono in tutti i punti con la stessa fase (la legge di variazione della pressione nel mezzo è sinusoidale, e quindi in alcuni punti le particelle vibrano in opposizione di fase), con la conseguenza che in alcune zone le particelle tenderanno ad addensarsi, in altre a rarefarsi. Nel mezzo di propagazione si avranno dunque variazioni di densità e di pressione, entrambe funzioni del tempo e dello spazio. Possiamo allora scrivere la pressione P dell’aria nella forma P(xr,t)= p₀+ p(xr,t) dove

0

p è il valore della pressione in condizioni statiche (assenza di perturbazione, ovvero

equilibrio) considerata omogenea, mentre p r( tx, ) rappresenta la cosiddetta pressione sonora, ossia la variazione di pressione dovuta appunto al fenomeno acustico. In generale risulta p(xr,t)<< p₀ ed è perciò possibile trascurare i termini di ordine superiore al primo nel computo della pressione totale.

E’ importante osservare che le variazioni della pressione sonora (vale a dire della differenza tra la pressione istantanea e quella atmosferica) prodotte nel gas dall’onda

sonora, avvengono in generale così rapidamente da non permettere scambi di calore tra volumi adiacenti.

Soffermiamoci adesso sulla questione della natura adiabatica delle onde sonore. E’ noto da quasi due secoli che i fenomeni fisici associati alle oscillazioni in un gas dipendono dalla natura dei flussi di calore al suo interno. Nella seconda edizione dei

Principia, Newton comparò il valore misurato della velocità del suono in aria con

quello da lui stesso calcolato, trovando una discrepanza dell’ordine del 17%. In seguito emerse dal lavoro di Lagrange, Poisson, Laplace, e altri, che il valore calcolato da Newton si applica a vibrazioni isoterme: in cui la temperatura del gas è mantenuta costante dalla conduzione termica al suo interno, mentre le vibrazioni sonore in aria avvengono adiabaticamente (senza scambio interno di calore). La relazione tra le velocità del suono in questi due limiti è stata mostrata essere c_a = γc_i. Studi successivi focalizzarono l’attenzione su questioni generali riguardanti i diversi regimi di propagazione sonora, come ad esempio, sotto quali condizioni si ottengono i limiti di oscillazioni adiabatiche e isoterme, e quali sono le proprietà delle oscillazioni tra questi due estremi. Oggi sappiamo che in un mezzo infinito le onde sonore di basse frequenza sono adiabatiche e divengono isoterme solo a frequenze molto alte (alte o basse si intende rispetto alla frequenza caratteristica del sistema). Questo deriva dalla competizione di due effetti contrapposti: (i) il tempo disponibile per il flusso di calore tra regioni vicine cresce al diminuire della frequenza ,(ii) la scala delle distanze per cui questo calore deve essere condotto è fissata dalla lunghezza d’onda, che cresce col decrescere della frequenza. In altre parole si ha un processo competitivo tra la velocità con cui il calore viene trasportato dall’onda e il tasso di diffusione del calore per conduzione. A causa dell’effetto i) il tempo disponibile va come 1/ω, mentre per l’effetto ii) la lunghezza da compiere va come

2

/

1 ω (processo diffusivo con costante di tempo _{τ =}4_π2_λ2/D_).

Qui alte e basse frequenze sono dunque relative alla frequenza caratteristica del sistema πκ 2 2 a c c f = dove p C ρ λ

κ = è la “diffusività” termica (λeρ indicano rispettivamente la conduttività termica e la densità di equilibrio del gas). Per gas in condizioni standard la frequenza caratteristica è relativamente alta, per esempio per l’aria f_{c ≅10}9Hz_{, motivo per cui le oscillazioni in aria (in assenza di vincoli) sono}

sempre adiabatiche.

2.2 Mezzi confinati

Consideriamo adesso un gas confinato in un volume finito, e che la frequenza di oscillazione (o le dimensioni del contenitore, o entrambi) sia abbastanza piccola così che la relativa lunghezza d’onda sia molto più grande del contenitore (ad esempio la

grandezza per la diffusione termica è fissata dalle dimensioni del volume in cui è racchiuso il gas, e non più dalla lunghezza d’onda delle sue oscillazioni.

Se l’oscillazione del gas è puramente adiabatica allora la temperatura del gas oscillerà uniformemente intorno al suo valore di equilibrio. Ma a causa della finita conduttività termica del gas e poiché, come abbiamo visto, la scala della conduzione termica è ora fissata dalle dimensioni del contenitore (il che vuol dire che al di sopra di una certa lunghezza d’onda uno dei due effetti antagonisti di cui sopra svanisce, cioè la distanza tipica che il flusso deve percorrere affinché ci sia scambio di calore è sempre la stessa indipendentemente dalla frequenza; rimarrà a questo punto il solo contributo del periodo, cioè il tempo disponibile per lo scambio di calore prima che “passi” la perturbazione) ci sarà, sovrapposto all’oscillazione adiabatica della temperatura, un contributo dipendente dal tempo che tenderà a portare le oscillazioni verso una situazione isoterma (per il calcolo dettagliato di questo spostamento dalle condizioni di pura adiabaticità, che esula dagli scopi di questa dissertazione, si rimanda all’articolo originale [2]).

Approfondiremo nel secondo capitolo, sezione un metodo alternativo di misura, questi aspetti delle oscillazioni in un gas confinato da un punto di vista prettamente sperimentale .

Capitolo 3

Esperimento di Rüchardt.

3.1 Presentazione dell’esperimento

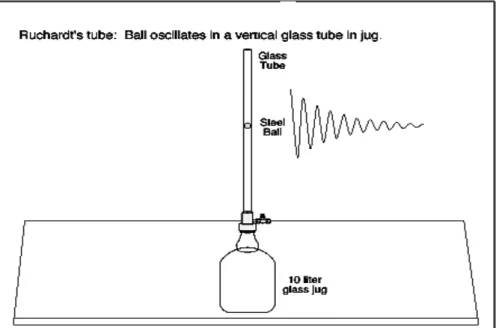
Fig 3.1 Apparato sperimentale dell’esperimento di Ruchardt.

L’apparato consiste di un serbatoio di vetro con una capacità di 10 litri; un tappo attraverso cui passa un tubo di vetro ad alta precisione (la sua sezione interna, a tutti

effettuare un moto armonico debolmente smorzato. Come vedremo il quadrato del periodo di oscillazione è in relazione lineare (con coefficiente di proporzionalità legato al rapporto dei calori specifici) con il volume di gas all’interno del serbatoio; misurando il periodo di oscillazione al variare del volume del gas (per variare il volume si inserisce dell’acqua nel serbatoio) saremo in grado di estrapolare, tramite fit lineare, il valore del rapporto dei calori specifici.

Sia m la massa della pallina, x lo spostamento dalla posizione di equilibrio, A la sezione del tubo, V il volume occupato dal gas e γ il rapporto dei calori specifici. La pallina è in equilibrio se la pressione p all’interno del serbatoio è uguale alla

somma della pressione atmosferica p₀ e della pressione dovuta al peso della pallina: A

mg p

p= ₀+ (1)

Quando la pallina si sposta di una distanza x dall’equilibrio, la pressione cambia di

∆p, e quindi su di essa si esercita una forza A∆p imprimendole una accelerazione: p A dt x d m 2₂ = ∆ (2) Assumiamo le oscillazioni quasi-statiche e adiabatiche†, perciò:

= γ pV costante (3) e differenziando: 0 1 ₌ +_{p V} −_dV dp Vγ γ γ (4) da cui dV V p dp=−(γ ) (5)

Per uno spostamento infinitesimo dx della pallina si ha una variazione di volume pari a:

Adx

dV = (6) sostituendo la (6) nella (5) si ottiene

V pAdx

dp=−γ (7)

considerando variazioni finite in (7) e sostituendo (7) in (2) si ha:

0 ) ( 2 2 2 = + x mV pA dt x d γ ₍₈₎

che è l’equazione del moto di un oscillatore armonico con frequenza

mV pA2 2 0 γ ω = .

Osserviamo che si perviene allo stesso risultato utilizzando la dinamica del pistone adiabatico sviluppata nel primo capitolo tramite una semplice operazione di limite. Consideriamo l’equazione (1.6) trascurando i termini proporzionali alla velocità del pistone; abbiamo a secondo membro un termine proporzionale alla differenza di pressione dei due sottosistemi che produce quindi una forza di richiamo:

(

)

dove A è la sezione del cilindro, L la sua lunghezza, M la massa del pistone, R la costante dei gas e X la posizione del pistone.

usando l’equazione delle trasformazioni adiabatiche quasi-statiche PVγ =costante _e

differenziando otteniamo: dV V p A dp       − = γ (16)

considerando ora variazioni finite di pressione e volume e sostituendo la (16) nella (15) otteniamo per l’equazione del moto del pistone:

      ∆       + ∆       − = ₂ 2 2 1 1 1 2 2 ₁ V V P A V V P A M dt X d γ γ ₍₁₇₎

Nel caso dell’esperimento di Ruchardt uno dei due volumi (quello sovrastante la pallina) è infinito, quindi facendo il limite V₂ →∞ l’equazione (17) diventa:

      ∆       − = ₁ 1 1 2 2 ₁ V V P A M dt X d γ ₍₁₈₎

Ora tenendo conto che ad una variazione di volume ∆V₁ corrisponde uno spostamento X del pistone e sostituendo in (18):

              − = X V P A M dt X d 1 1 2 2 2 _{1 γ} (19)

Ancora dalla teoria con il modello molecolare discussa nel capitolo precedente possiamo assumere che nell’equazione del moto (8) ci sia un termine di smorzamento β proporzionale

m M_g

π

δ = 8 (vedi capitolo 1) dovuto agli urti della pallina con le molecole del gas, e che questo sia proporzionale alla velocità:

0 2 2 2 = + + x mV pA dt dx m dt x d β γ ₍₉₎

soluzione di questa equazione differenziale è:

) cos( ) exp( ) ( ₀ ω ϕ τ + − = A t t t x (10)

doveA0 è la posizione iniziale e τ _β

2

m

= il tempo di rilassamento; per ricavare il periodo

ω π

2 =

T facciamo riferimento alla soluzione generale delle equazioni

differenziali del secondo ordine a coefficienti costanti da cui

2 2 2 0 4m β ω ω = − (11) con mV pA2 2 0 γ

ω = frequenza dell’oscillatore non smorzato, otteniamo per il periodo: 2 _{2 2)}4 2 ₂ 16 1 ( pA mV pA mV T γ π τ γ + = (12)

Poiché (come sarà evidente dai dati sperimentali) tau è una funzione di V, la dipendenza di T da V non è, in linea di principio, semplice; si può tuttavia tentare una prima approssimazione della (12) considerando il limite di debole smorzamento richiamandoci ancora al modello cinetico: _{mV << pA}2_τ2_{, trascuriamo dunque la}

correzione alla frequenza dell’oscillatore libero introdotto nella (10) ovvero la correzione dipendente da β ‡ e ridurci all’espressione:

V pA m T ₂ 2 2 4 γ π = (13) considerando il nostro apparato sperimentale V=V0−Vl,

con V₀ e V_l rispettivamente volumi di aria e liquido nel serbatoio, avremo dunque:

2 4 2₂ pA m T γ π = (V₀−V_l) (14)

Generalmente questa risulta essere un’approssimazione sufficientemente buona come verificheremo dai risultati sperimentali.

3.2 Procedimento Sperimentale

La misura del periodo delle oscillazioni può essere fatta in linea di principio con un semplice cronometro contando le oscillazioni. Un’ analisi più completa del moto richiede invece la determinazione dell’equazione oraria. De Lange e Pierrus hanno utilizzato a questo fine un sistema di rilevamento basato una tecnica elettronica (come vedremo nel paragrafo 3.4) [2].

In questa tesi, posti di fronte al problema di come fare ad ottenere una traccia del moto pallina con buona risoluzione spaziale e temporale senza avere a disposizione sofisticati mezzi elettronici abbiamo pensato di riprendere le oscillazioni con una videocamera digitale per poi analizzare il video in formato avi attraverso il programma Matlab al fine di estrarre la posizione della pallina in funzione del tempo. A tale scopo è necessario preparare l’esperimento in modo tale che una volta acquisita l’immagine della pallina oscillante, questa sia chiaramente distinguibile dal resto dell’immagine. Abbiamo quindi operato nel modo seguente.

Si è posizionato un foglio di carta semiopaco aderente al tubo di vetro e si è illuminato l’apparato sperimentale in modo da produrre un fondo bianco sul quale far risaltare l’immagine della pallina che appare nera (vedi foto); a questo punto si è registrato il moto della pallina oscillante con la videocamera digitale e importando il video attraverso Matlab, ed analizzando la matrice dei pixel dell’immagine fotogramma per fotogramma si è ricostruita la posizione della pallina in funzione del tempo (si rimanda all’appendice B per ulteriori dettagli).

Al variare del volume del gas all’interno del recipiente si osservano diverse traiettorie ognuna caratterizzata da un periodo di oscillazione, da un’ampiezza delle oscillazioni

3.3 Risultati Sperimentali

Si riportano qui di seguito alcuni grafici delle equazioni orarie per diversi valori di

l V . V_l=2 litri V_l= 3 litri. V_l = 4 litri.

V_l=8 litri. V_l=9 litri.

L’analisi delle equazioni orarie rivela le seguenti caratteristiche:

• La posizione intorno alla quale la pallina oscilla varia nel tempo riflettendo un leggero abbassamento della posizione di equilibrio. Riteniamo che tale effetto possa essere attribuito ad una lieve perdita di aria all’interfaccia tra la pallina ed il tubo di vetro durante la fase di compressione. Si può tenere in conto questo effetto nel modello utilizzato per analizzare l’equazione oraria inserendo nella funzione di fit un termine lineare nel tempo.

• Nella coda a tempi lunghi dei grafici si osserva un andamento leggermente dissimile da quello del fit. La ragione è che nella reale dinamica dell’esperimento, quando la pallina raggiunge velocità sufficientemente basse intorno alla posizione di equilibrio, l’effetto dell’attrito statico, non tenuto in conto nel fit, dovuto alle pareti del tubo su di essa supera quello dell’attrito

ragionevolmente buona, ai fini della misura che ci siamo proposti di effettuare, pur non tenendo in conto questo effetto.

Per ottenere i valori del quadrato del periodo per ogni valore del volume di liquido abbiamo operato in due modi diversi.

Il primo metodo è quello di un fit con una funzione oscillante smorzata da un esponenziale reale decrescente e un termine lineare nel tempo che tiene in conto le perdite.

Il secondo metodo consiste nel misurare la distanza di ogni cresta dalla successiva e farne la media. Per ogni valore del volume di acqua possiamo ottenere un altro set di dati _T2 _vs

l

V . Facendo la media aritmetica dei due set di dati otteniamo i valori di _T2

riportati in tabella.

I rispettivi errori sono stati ottenuti mediante propagazione degli errori assumendo nel caso della misura cresta per cresta 1 frame come incertezza, nell’altro caso l’incertezza è fornita da fit (algoritmo di….).

l V (litri) _T2 _(s^2) ) (_T2 σ (s^2) 2 1.052 0.085 3 0.966 0.077 4 0.864 0.068 5 0.705 0.055 7 0.498 0.039 8 0.368 0.030 9 0.222 0.016

TAB 1.Il periodo è stato ottenuto come media tra i valori ottenuti da fit e quelli ottenuti mediando cresta per cresta

Con i dati del periodo in funzione del volume, sfruttando la relazione lineare tra quadrato del periodo e volume in regime di debole smorzamento (14) possiamo stimare il rapporto dei calori specifici (

v p

c c

=

γ ) dal coefficiente angolare della retta di

miglior fit (minimi quadrati) : 2 4 2₂

pA m T

γ π

= (V₀−V_l) il cui grafico è riportato di seguito. Ricordiamo che nella formula precedente p è la pressione di equilibrio del gas che abbiamo considerato essere la somma della pressione atmosferica s.l.m. 101325 Pa , della pressione esercitata dalla pallina 811 Pa, meno il contributo della pressione di vapore dell’acqua (con cui è riempito l’aspiratore) che a 20 gradi centigradi è 2200 Pa.

Fig. 2: andamento del quadrato del periodo delle oscillazioni in funzione del volume di liquido nel contenitore in regime di debole smorzamento.

Otteniamo:

γ_aria. V₀

Valore aspettato 1.4 10.10 litri

Valore misurato 1.376±0.050 (10.30±0.30) litri

Il valore ottenuto per il rapporto dei calori specifici corrisponde entro gli errori a quello di un gas biatomico: che evidentemente rappresenta l’aria con sufficiente accuratezza.

Il valore aspettato del volume a vuoto del serbatoio (V₀) è quello fornito dalla casa

produttrice (10 litri) a cui abbiamo sommato il volume di gas nel tubo sottostante la pallina da noi misurato (riteniamo trascurabile l’errore su questa misura).

Come possiamo notare i valori ottenuti sono in buon accordo, entro gli errori sperimentali ( in particolare nel caso del γ_aria abbiamo una deviazione di circa l’ 1%), con quelli aspettati.

Verifichiamo ora la validità dell’ipotesi di debole smorzamento _{mV << pA}2_τ2 _(si

ricorda che m è la massa della pallina, A la sezione del tubo, p la pressione di equilibrio del gas e V il volume di aria nel serbatoio; i rispettivi valori sono stati forniti nella fase di presentazione dell’esperimento. Si ha:

• Per Vl=3 litri

2 2_τ

pA

Come si vede l’approssimazione risulta particolarmente buona per volumi di liquido fino a 8 litri (corrispondenti a volumi di aria da 10 a 2 litri), mentre per un volume di aria pari ad 1 litro la validità dell’approssimazione è sotto al 10%.

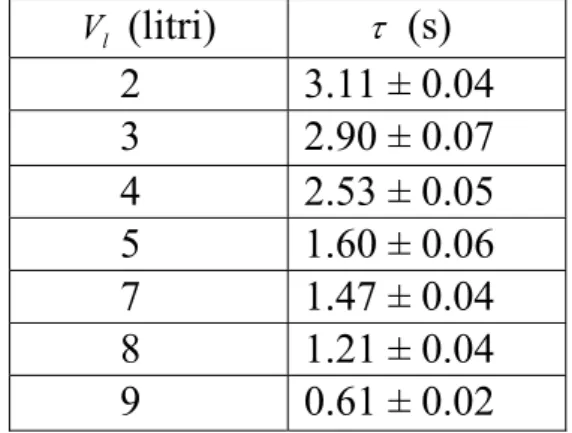
Riportiamo per completezza i valori del tempo di smorzamento in funzione del volume di liquido nel contenitore:

V_l (litri) τ (s) 2 3.11 ± 0.04 3 2.90 ± 0.07 4 2.53 ± 0.05 5 1.60 ± 0.06 7 1.47 ± 0.04 8 1.21 ± 0.04 9 0.61 ± 0.02

Tab. 2 Tempo di smorzamento in funzione del volume di liquido nel serbatoio.

E’ importante a questo punto porsi la questione della validità dell’approssimazione adiabatica: a causa della finita conduttività termica del gas e delle pareti del serbatoio ci si può aspettare che il gas scambi calore con l’esterno ed anche che ci siano flussi di calore al suo interno durante le oscillazioni, con l’effetto che il profilo di temperatura di oscillazioni adiabatiche risulti tanto più modificato quanto più aumenta il numero delle oscillazioni (cioè tanto maggiore è il tempo di oscillazione); nel nostro esperimento questo aspetto sembra non influire dato l’accordo del valore misurato di γ con quello aspettato per un gas biatomico e quindi abbiamo concluso che il regime di oscillazione è effettivamente adiabatico. Nel prossimo paragrafo descriveremo un metodo alternativo di misura utilizzato in letteratura, basato su effetti elettromagnetici, che sembra invece evidenziare la presenza di un regime di oscillazione non adiabatico.

3.4 Un metodo di misura alternativo

Discuteremo in questa sezione i risultati di alcuni lavori di O.L. de Lange e J. Pierrus sull’esperimento di Ruchardt [2] ed alcune sue implicazioni interessanti collegate alla discussione sulle onde sonore in mezzi confinati del capitolo precedente.

L’apparato sperimentale è identico al nostro salvo che il volume dell’aspiratore è

0

V ≅23 litri.

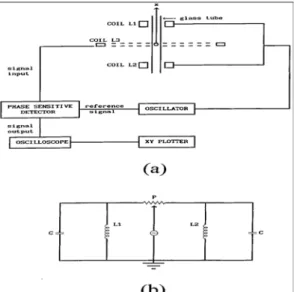
Un diagramma a blocchi dell’apparato di misura è riportato in figura 2.1(a), L₁ e L₂

rappresentano due bobine (bobine di eccitazione) avvolte in sensi opposti, ma altrimenti identiche. Sono montate coassialmente al tubo di vetro. Una terza bobina

3

L (la bobina collettrice), anch’essa montata coassialmente, è posizionata a metà

strada tra L₁ e L₂. Le bobine di eccitazione sono connesse attraverso un

potenziometro in alternata a frequenza variabile come mostrato in figura 2.1(b). Il campo magnetico oscillante prodotto dalle bobine di eccitazione è nullo nel piano mediano di L₃, ed è proporzionale alla coordinata x per piccoli valori di x. La

bobina collettrice è connessa ad un amplificatore lock-in (rivelatore phase-sensitive(PSD)) usato come rivelatore. L’uscita del PSD è mostrata su un oscilloscopio digitale e registrata su un grafico XY.

L’uscita del PSD è nulla con la pallina in zero (all’equilibrio). Con la pallina in una posizione x, il PSD fornisce una risposta in continua con due caratteristiche fondamentali: (i) la sua polarità è determinata dal verso dello spostamento dall’equilibrio della pallina. (ii) è proporzionale ad x se |x| ≤5 cm e diventa non-lineare altrimenti.

Per ottenere il massimo di sensibilità, la frequenza f dell’oscillatore è fissata alla frequenza di risonanza dei due circuiti LC mostrati in figura 2.1(b).

La componente P rappresenta un potenziometro usato per aggiustare la calibrazione del PSD (necessario per compensare i piccoli errori dovuti al posizionamento di L₃

esattamente a metà strada tra L₁eL₂).

Fig 2.1.(a)Diagramma a blocchi del circuito usato per misurare la posizione x(t) della pallina. L’origine di x è nel piano mediano della bobina L₃. (b)Circuito per le bobine di eccitazione L₁ e

2

L che mostra i due cicli Lc ed il potenziometro P.

Facciamo notare che la precisione ottenibile con questo metodo di misura sulla determinazione della x(t), e quindi del periodo è dell’ordine del ms: più di un ordine di grandezza superiore alla nostra risoluzione temporale (0.04 s). Una simile

Nel nostro esperimento sono due i fattori strumentali per cui crediamo di non aver potuto osservare il comportamento del periodo che descriveremo nel seguito (come osservato da Pierre e De Lange): (i) quanto già detto sulla risoluzione temporale. (ii) il fatto che il nostro aspiratore ha un volume massimo di 10 litri che permette di andare poco oltre i 0.9 secondi di periodo (limite per la chiara osservabilità del fenomeno).

In fig. 2.2 riportiamo i valori del periodo misurato come distanza picco-picco.

Nei lavori di De Lange e Pierrus il set di punti etichettato (a) corrisponde ad un volume di aria =0.71 litri; i punti etichettati (b) si riferiscono ad un volume di aria=13.21 litri. E’ chiaro che i due set differiscono considerevolmente. Il periodo delle oscillazioni a frequenza più alta è essenzialmente costante, T=0.300 s (nella risoluzione dell’oscilloscopio, circa 2 ms) per tutti e 22 i cicli. Al contrario il grafico delle oscillazioni con periodo più lungo mostra quattro caratteristiche distinte, segnate con I,II,III,IV in fig 2.2:

I. Il primo ciclo ha il periodo più basso, T_a=1.25 s. Periodo che aumenta lentamente

nei due cicli successivi a 1.26 e 1.27 s. II. Plateau di 4 cicli con T_m=1.27 s.

III. Alla fine del sesto o settimo ciclo c’è un rapido cambiamento, lungo approssimativamente 3 cicli, verso un secondo plateau.

IV. Il secondo plateau consiste di cinque cicli a T_i=1.50 s. Il plateau persiste fino alla

cessazione delle oscillazioni.

Il rapporto tra il valore più alto e quello più basso del periodo è 1.50/1.25=1.20.

Uno studio sistematico siffatto per ogni valore del volume porta alle seguenti conseguenze.

(i) Quando il volume del gas V=V₀-V_l è minore di 2 litri, corrispondente a T≤0.5 s, i valori di T misurati sono del tipo (a) (costanti).

(ii) per T≥0.9 s i valori di T seguono chiaramente un andamento del tipo (b).

(iii)Tra questi due estremi c’è un insieme di valori per cui queste zone non sono chiaramente distinguibili.

Fig 2.2. Plot dei valori del periodo delle oscillazioni per ogni ciclo Per due valori indicativi del volume. Sono evidenziati, per il set di punti etichettato (b), i quattro regimi descritti nel testo. T_i,T_m,T_a sono rispettivamente i periodi di oscillazioni isoterme, adiabatiche e intermedie.

Seguendo ancora de Lange e Pierrus, consideriamo una possibile interpretazione di questi risultati.

Abbiamo già avuto modo di dire come la finita conduttività termica del gas e del serbatoio possano alterare il profilo di temperatura delle oscillazioni adiabatiche e che gli scambi di calore all’interno del gas possano far transire verso un regime di oscillazioni dapprima intermedio tra adiabatico ed isotermo e poi puramente isotermo. Ricordiamo che nell’esperimento di Ruchardt la lunghezza d’onda delle oscillazioni è tipicamente molto maggiore delle dimensioni del serbatoio, e, per quanto detto nel secondo capitolo a proposito delle oscillazioni in mezzi confinati, la questione della non-adiabaticità, a differenza delle oscillazioni in mezzi infiniti, gioca un ruolo essenziale.

Come abbiamo visto, il rapporto tra la velocità del suono in un gas nei limiti di oscillazioni adiabatiche ed isoterme è c_a = γc_i (dove γ è il rapporto dei calori specifici) e quindi T_i = γT_a : ora nel caso in esame il rapporto tra i valori estremi del periodo è molto prossimo a γ_aria =1.18, questo suggerisce l’ipotesi che il primo ciclo in (b) sia adiabatico, ed i cicli nel plateau IV isotermi: le altre oscillazioni formando un regime intermedio tra i due estremi.

Per testare queste idee sono stati estratti dal plot in fig 2.2 i valori di

i

T(isotermo),T_m(intermedio),T_a(adiabatico) per un intervallo di volumi tra 23(=V₀) e

0.13 litri ( il volume più piccolo per cui si ha ancora una traccia discernibile sull’oscilloscopio). Sono stati quindi riportati in un grafico 2

i T , 2 a T , 2 m T in funzione del volume di liquido V_l. Questi grafici sono riportati in fig (2.3). I valori del coefficiente

angolare, dell’intercetta, e di γ_aria nei casi adiabatico ed isotermo sono riportati in tabella 2.1§.

L’equazione (12) in questo caso è stata usata nella forma 4 ₂ ( ₀ )

, 2 2 , l a i a i V V A K m T = π − con il modulo di bulk nei casi adiabatico e isotermo dato rispettivamente da =1

P

K_{i e} K

Valore sperimentale Valore teorico

K_i/P 0.976±0.007 1.000

K_a/P 1.395±0.006 1.400

Tabella 2.1 Valori ottenuti per il modulo di bulk adiabatico ed isotermo.

. Fig 2.2. Grafico del periodo per oscillazioni adiabatiche, intermedie e isoterme in funzione del volume di acqua nell’aspiratore

Come appare evidente l’accordo tra i valori teorici e quelli misurati è molto buono per il caso adiabatico, mentre nel caso isotermo il valore misurato è leggermente inferiore rispetto a quello aspettato, la ragione di questa leggera discrepanza, come affermano gli stessi esecutori dell’esperimento, non è chiara.

Possiamo concludere questa sezione osservando che l’analisi di questo esperimento, realizzato con una tecnica un po’ più sofisticata della nostra (come abbiamo visto l’accuratezza nella determinazione della posizione della pallina è di un ordine di grandezza superiore), ha messo in luce una risposta del gas alla variazione della frequenza delle oscillazioni simile a quella predetta dalle analisi di Stokes sulle transizioni tra oscillazioni adiabatiche e isoterme nei gas**, e si potrebbe quindi pensare, sostengono gli autori, alla frequenza al di sotto della quale si osservano oscillazioni isoterme come il “limite di Stokes”.

Conclusioni

La termodinamica da sola non fornisce la soluzione univoca del problema del moto di un pistone adiabatico oscillante tra due gas perfetti identici contenuti in due sottosistemi con pareti adiabatiche

Abbiamo visto come con l’adozione di un semplice modello cinetico sia possibile ricavare equazioni deterministiche per la dinamica di un tale sistema e attraverso queste ottenere la forma funzionale del coefficiente di smorzamento dalle masse del gas e del pistone. Tramite questo modello dunque possiamo scrivere un’equazione differenziale del secondo ordine per la posizione della pallina in moto nel cilindro del nostro esperimento che tenga conto del termine di smorzamento proporzionale alla velocità della pallina e che giustifichi l’approssimazione di debole smorzamento adottata per ottenere una relazione lineare tra il periodo delle oscillazioni e il volume di aria all’interno del contenitore, da cui stimare il valore del rapporto dei calori specifici dell’aria. Come si vede il valore ottenuto è pienamente in accordo con quello aspettato per un gas biatomico, possiamo asserire a posteriori la validità delle ipotesi di lavoro: debole smorzamento ed adiabaticità delle oscillazioni.

Abbiamo infine analizzato lo stesso esperimento condotto da De Lange e Pierrus con un metodo di misura elettronico e le interessanti implicazioni di questo in relazione ai diversi regimi di oscillazione di un gas confinato; è emerso il seguente comportamento: per volumi di gas maggiori di 8 litri, corrispondenti a periodi maggiori di 0.9 secondi, a causa della finita conduttività termica del recipiente, vengono osservate transizioni nel regime delle oscillazioni: da adiabatiche a isoterme.

Appendice A

Calore specifico di un gas biatomico non interagente.

Per un gas biatomico non interagente (H_tot =

∑

molecola (nell’approssimazione di trattare il gas costituito da atomi puntiformi, ovvero di trascurare i contributi all’hamiltoniana dovuti all’eccitazione elettronica) è

data da (| |) 2 2 ₂ 1 2 2 2 1 2 1 _{U r r} m p m p

H_i = r + r + r−r dove U(|rr −₁ rr₂|) è il potenziale interatomico ed i

pedici 1 e 2 si riferiscono ai due atomi costituenti la molecola. Se ci mettiamo nel sistema del centro di massa otteniamo: (| |)

2 2 2 2 r U p M P H tot i r r r + + = µ avendo definito

l’impulso totale Pr_tot, l’impulso relativo pr, la massa totale M, la massa ridotta µ e la

coordinata relativa rr.

Passando in coordinate sferiche l’ hamiltoniana diventa:

) ( sin 2 2 2 2 2 2 2 2 2 2 2 r U r p r p p M P H tot r i = + _µ + _µ + _{µ θ} + ϕ θ r

Ora facendo l’approssimazione di potenziale interatomico armonico, il che vuol dire che il sistema è vicino al minimo dell’energia, cioè i due atomi compiono piccole oscillazioni intorno alle posizioni di equilibrio, abbiamo che 2

2 1 )

(r r

U = α e quindi i gradi di libertà canonici che compaiono quadratici nell’ hamiltoniana sono sette, dal teorema di equipartizione quindi segue che in queste condizioni l’energia totale del sistema è U Nk_BT

2 7

= , di conseguenza il calore specifico è _v Nk_B dT dU c 2 7 =       = . Se

invece abbassiamo la temperatura al punto di congelare i gradi di libertà vibrazionali fissando la coordinata relativa, il sistema si comporterà come una bacchetta rigida (nel senso che U(r)=costante e pr_r=0) ed i gradi di libertà quadratici nell’

hamiltoniana scendono a 5, per cui in questo caso c_v Nk_B

2 5

Appendice B

Determinazione della legge oraria mediante acquisizione video.

Abbiamo mostrato in questa tesi come sia possibile ottenere una buona risoluzione spaziale e temporale senza avere a disposizione sofisticati mezzi elettronici attraverso le immagini delle oscillazioni acquisite con una videocamera digitale e successivamente analizzate con il programma Matlab.

Il programma di calcolo scientifico Matlab fornisce la possibilità di leggere un video in formato avi tramite la funzione aviread(‘nome file.avi’ ). Una volta caricato il video ed assegnato alla variabile matriciale mov(f), dove f è un indice che rappresenta il frame (per ogni frame, mov contiene tre matrici di pixel: una per l’intensità del rosso, una per quella del giallo,un’altra per il blu), facciamo un ciclo su tutti i fotogrammi del video per individuare la posizione della pallina in funzione del tempo (la risoluzione temporale ovviamente è 1 frame cioè 0.04 s). A tale scopo operiamo nel seguente modo.

Concentriamoci su un certo fotogramma. Per come abbiamo preparato l’esperimento (cfr. 3.2) avremo che l’unica zona dell’immagine con un’alta intensità del nero è quella in cui è situata la pallina, le altre appariranno bianche. Ora però bisogna tenere in conto il fatto che la pallina sulla scala dei pixel non appare come un oggetto puntiforme, ma occupa una regione estesa della matrice dei pixel: occorre calcolare il baricentro della posizione della pallina come media pesata dei pixel con peso il valore del nero associato. Calcoliamo per ogni pixel l’intensità del nero come somma dei tre colori fondamentali (stando attenti al fatto che il nero è associato al valore zero mentre il bianco al valore 255 che è l’intensità massima). Con un ciclo su ogni colonna della matrice dei pixel dell’immagine individuiamo il baricentro delle zone associate al nero più intenso (cioè il baricentro della pallina).

Con un ciclo su tutti i fotogrammi si ottiene l’ equazione oraria.

Riportiamo in figura B.1 l’intensità associata al nero per un certo fotogramma in funzione della posizione x, in pixel, all’interno del tubo.

Fig B.1. Intensità del nero per f fissato in funzione

della posizione nel tubo in pixel. La distribuzione

è fortemente piccata in un punto. La posizione della pallina è stata ricavata come media pesata dei pixel con peso il valore del nero

Riportiamo di seguito il codice utilizzato in Matlab per estrarre la posizione della pallina in funzione del tempo.

mov=aviread('nome_file.avi'); /* importo il filmato */ nframes=250; /* numero_frames */ for f=[1:nframes]; /* ciclo sui frames */ x=[1:576];

i=[1:160];

a=mov(f).cdata(:,i,1);

b=mov(f).cdata(:,i,2); /* valore di R. G. B. (rosso, giallo,blu) per ogni pixel */ c=mov(f).cdata(:,i,3);

g=a+b+c; /* sommo intensità di R. G. B. */ tot=0 for h=1:160 gg=g(:,h); ggnor=-(double(gg)-255); ggnor=ggnor(300:400)'; x=[300:400]

cmass=sum(ggnor.*x)/sum(ggnor); /* calcolo baricentro della pallina */ tot=tot+cmass;

plot(ggnor) /* plot del baricentro */ end

Bibliografia

[1] B. Crosignani, P. Di Porto, M. Segev Approach to thermal equilibrium in a

system with adiabatic constrains, Am. J. Phys. 64 (1996)

[2] J. Pierrus e O.L. de Lange Experimental and thorethical study of adiabatic,

intermediate, and isothermal oscillations in air, Phys. Rew. E 56, 3 (1996)

[3] J. Pierrus e O.L. de Lange Measurement of bulk moduli and ratio of specific

heats of gases using Ruchardt’s experiment, Am. J. Phys. 68 (3), March 2000

[4] C.Mencuccini V.Silvestrini Fisica I, Liguori Editore

[5] S. Focardi I.Massa A. Uguzzoni Fisica Generale, Meccanica e Termodiamica ,

Casa Editrice Ambrosiana

[6] K. Huang Meccanica Statistica, Zanichelli

[7] Leybold didactic GMBH Apparatus for determining the ratio of specific heats,