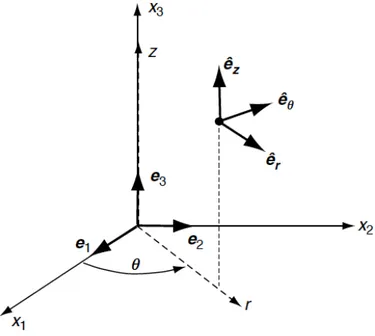
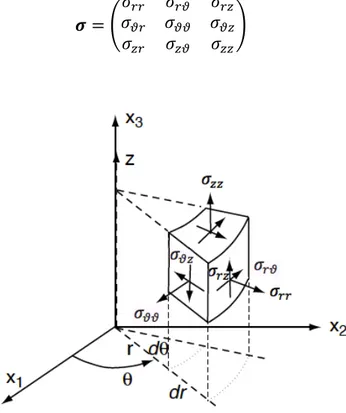
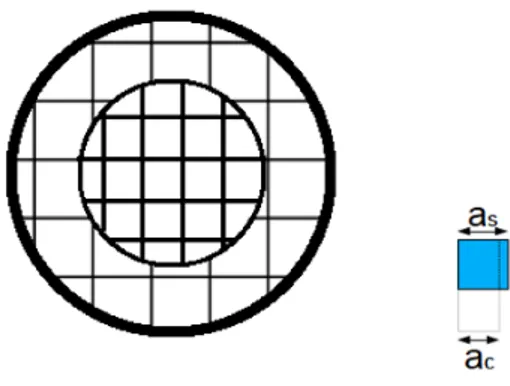
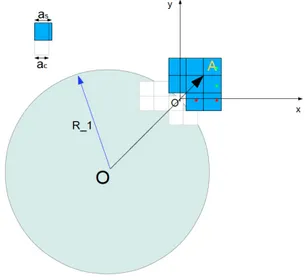
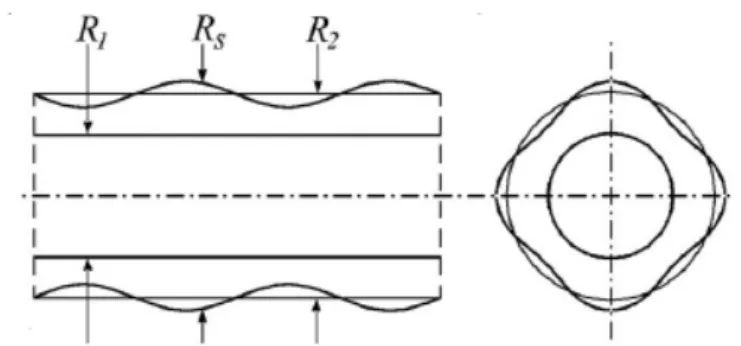
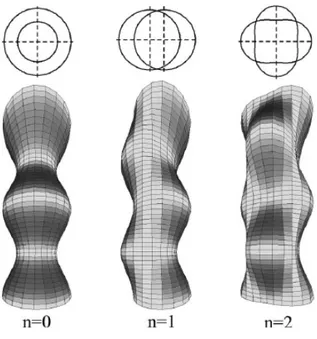
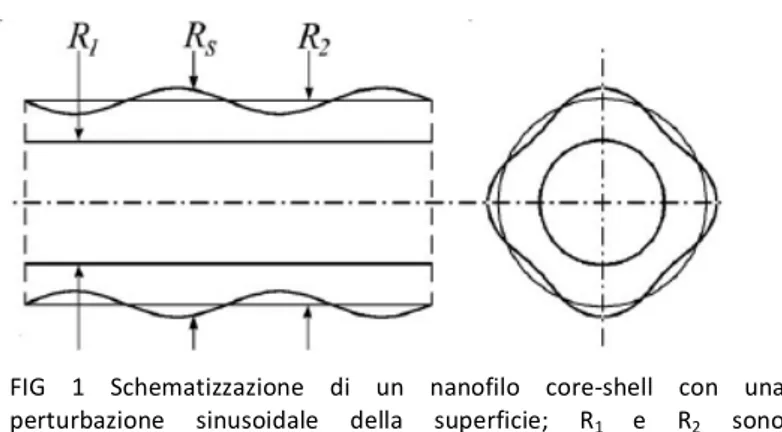
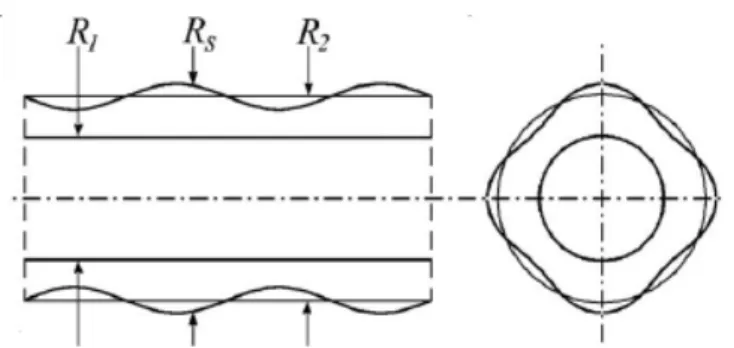
Morphological instability analysis of a misfit strained core-shell nanowire for the growth of quantum dots
Testo completo
Figura
Documenti correlati
[r]
The Greek Islands are generally subdivided into two groups, according to the location: the Ionian Islands (including Kerkira, Cephalonia, Lefkas, Zakinthos,
The prob lems re lated with the cal i bra tion of the ra dio car bon dates of the pre his toric shell mid - dens of the north-west ern Ara bian Sea have been long de bated with
MARIA GRAZIA FOLLI Prof..
The study of the review was taken on after having singled out some recurring themes: analysis of mediums and the centrality of photography (not only with reference to
The former consisted in the absolute phase measurement of a voltage, with respect to the cosine waveform with positive peak aligned with the PPS signal (see Fig. The
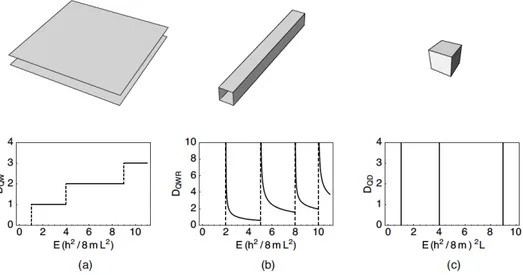
On successful completion of this course the student should understand the fundamental concepts of both quantum and classical statistical mechanics and their applications to the
On successful completion of this course the student should understand the fundamental concepts of both quantum and classical statistical mechanics and their applications to the