LEZIONI ED ESERCITAZIONI DI MATEMATICA
Prof. Francesco Marchi
1
Esercitazione per l’esame di saldo debito formativo
27 febbraio 2010
1Per altri materiali didattici o per contattarmi:
Blog personale: http://francescomarchi.wordpress.com/
Indirizzo email: [email protected]
http://francescomarchi.wordpress.com
Indice
1 Limiti che non presentano forme indeterminate 2
1.1 Limiti per semplice sostituzione . . . 2
1.1.1 Funzioni algebriche . . . 2
1.1.2 Funzioni goniometriche . . . 2
1.1.3 Funzioni esponenziali e logaritmiche . . . 2
1.2 Algebra degli infiniti . . . 2
1.2.1 Funzioni algebriche . . . 2
1.2.2 Funzioni goniometriche . . . 2
1.2.3 Funzioni esponenziali. . . 3
1.3 Limiti di funzioni composte . . . 3
2 Limiti che presentano forme indeterminate 4 2.1 Forma ∞∞ . . . 4
2.1.1 Per funzioni razionali fratte . . . 4
2.1.2 Per funzioni irrazionali fratte . . . 4
2.2 Forma 00 . . . 4
2.2.1 Per funzioni razionali fratte . . . 4
2.2.2 Tramite limite notevole sin 𝑥𝑥 → 1 . . . 4
2.2.3 Tramite limite notevole 𝑒𝑥𝑥−1 → 1. . . 4
2.3 Forma 1∞ . . . 5
2.3.1 Tramite limite notevole (1 +1𝑥)𝑥→ 𝑒 . . . 5
3 Dominio e segno di una funzione 6 3.1 Esercizi di teoria . . . 6
3.2 Impostazione dei calcoli relativi a dominio e segno . . . 6
3.3 Determinazione del dominio e segno di funzioni date . . . 6
3.4 Abbinamento grafici-funzioni . . . 6
3.4.1 Esercizio 1 . . . 6
4 Limiti, continuit`a, asintoti 7 4.1 Determinazione del grafico di funzioni che soddisfano date condizioni . . . 7
4.1.1 Esercizio 1 . . . 7
4.1.2 Esercizio 2 . . . 7
4.2 Abbinamento grafici-funzioni . . . 9
4.2.1 Esercizio 1 . . . 9
4.3 Individuazione del grafico di una funzione . . . 9
4.3.1 Esercizio 1 . . . 9
4.4 Esercizi vari . . . 11
4.4.1 Asintoti verticali . . . 11
4.4.2 Asintoti orizzontali . . . 11
5 Derivate 12 5.1 Linearit`a dell’operatore derivata . . . 12
5.2 Derivata del prodotto . . . 12
5.3 Derivata di un rapporto . . . 12
5.4 Derivata di funzioni composte . . . 12
5.4.1 Composizione di due funzioni . . . 12
5.4.2 Composizione di tre o pi`u funzioni . . . 12
http://francescomarchi.wordpress.com
1
Limiti che non presentano forme indeterminate
1.1
Limiti per semplice sostituzione
1.1.1 Funzioni algebriche lim 𝑥→02 2𝑥2−1 = 1 2 (1) 𝑥→lim𝜋 3 𝑥 + 4 3 − 𝑥 = 𝜋 + 12 3 − 𝜋 (2) 1.1.2 Funzioni goniometriche lim 𝑥→𝜋 3 2 sin 𝑥 + 𝑥2=9 √ 3 + 𝜋2 9 (3) lim 𝑥→𝜋 tan 𝑥 − 3 tan 𝑥 + 1 = −3 (4) lim 𝑥→𝜋 3 −2 cos(3𝑥) + 1 = 3 (5) lim 𝑥→1cos 𝜋𝑥 3𝑥 − 1= 0 (6)
1.1.3 Funzioni esponenziali e logaritmiche
lim 𝑥→𝑒ln 𝑥 2+ 3 + 𝑥 = 5 + 𝑒 (7) lim 𝑥→1 ( 2𝑥 3𝑥 − 2 )𝑥−1 = 1 (8) lim
𝑥→4log4𝑥 + 3 + sin 𝑥 = 4 + sin 4 (9)
lim 𝑥→0 𝑒𝑥+ 𝑒−𝑥 3 = 2 3 (10)
1.2
Algebra degli infiniti
1.2.1 Funzioni algebriche lim 𝑥→−∞ ( 𝑥2+1 𝑥 ) = +∞ (11) lim 𝑥→+∞ √ 1 +𝑥32 2𝑥 + 1 = 0 (12) lim 𝑥→1− 𝑥2+ 𝑥 + 1 𝑥 − 1 = −∞ (13) lim 𝑥→0+ (4 𝑥+ 𝜋 𝑥7 ) = +∞ (14) lim 𝑥→5− 𝑥 𝑥 − 5 = −∞ (15) lim 𝑥→1+ 3𝑥√𝑥 𝑥2− 3𝑥 + 2 = −∞ (16) lim 𝑥→2− 𝑥 − 3 √ 2 −√𝑥= −∞ (17) lim 𝑥→−∞(4𝑥 2− 𝑥 + 3) = +∞ (18) 1.2.2 Funzioni goniometriche
http://francescomarchi.wordpress.com
http://francescomarchi.wordpress.com
lim 𝑥→𝜋 4+ 𝑥2 tan 𝑥 − 1 = +∞ (19) lim 𝑥→𝜋− sin 2𝑥 cos 𝑥 + 7 = 0 (20) lim 𝑥→𝜋+ cos 𝑥 + 2 sin 𝑥 = −∞ (21) lim 𝑥→0+ 3 + 𝑥3+ cos 𝑥 sin 𝑥 = +∞ (22) lim 𝑥→𝜋− 𝑥2 cos 𝑥 + 1= +∞ (23) lim 𝑥→𝜋 6+ tan +3 √ 3 − 2 cos 𝑥= +∞ (24) 1.2.3 Funzioni esponenziali lim 𝑥→+∞ 5 𝑥𝑒𝑥 = 0 (25) lim 𝑥→+∞𝑥 3(1 − 2𝑥) = −∞ (26) lim 𝑥→+∞ 1 + 𝑒−𝑥 𝑥2+ 1 = 0 (27) lim 𝑥→+∞ 𝑒𝑥− 1 1 − 𝑒−𝑥 = +∞ (28)
1.3
Limiti di funzioni composte
lim 𝑥→+∞arctan ln 𝑥 = 𝜋 2 (29) lim 𝑥→3−log1/2(9 − 𝑥 2) = +∞ (30) lim 𝑥→−∞sin(𝑒 𝑥) = 0 (31) lim 𝑥→𝜋 2− 𝑒tan 𝑥= +∞ (32) lim 𝑥→+∞𝑒 −√𝑥= 0 (33) lim 𝑥→+∞ln 3𝑥 2 + 𝑥3 = −∞ (34)
http://francescomarchi.wordpress.com
http://francescomarchi.wordpress.com
2
Limiti che presentano forme indeterminate
2.1
Forma
∞∞2.1.1 Per funzioni razionali fratte
lim 𝑥→+∞ 1 − 10𝑥2 4𝑥2− 1 = − 5 2 (35) lim 𝑥→+∞ (𝑥 + 1)2 𝑥 + 4 = +∞ (36) lim 𝑥→−∞ 𝑥2+ 6𝑥 + 5 𝑥5+ 4 = 0 (37) lim 𝑥→+∞ 𝑥2 𝑥 + 1− 𝑥3+ 1 𝑥2− 1 = −1 (38)
2.1.2 Per funzioni irrazionali fratte
lim 𝑥→+∞ √ 𝑥 − 1 − 1 √ 𝑥 − 1 + 1 = 1 (39) 𝑥→+∞lim √ 𝑥2− 1 − 𝑥 √ 𝑥2− 1 + 𝑥 = 0 (40)
2.2
Forma
002.2.1 Per funzioni razionali fratte
lim 𝑥→2 4𝑥 − 𝑥3 𝑥 − 2 = −8 (41) lim 𝑥→−2− 2𝑥2+ 4𝑥 𝑥2+ 4𝑥 + 4 = −∞ (42) lim 𝑥→5 𝑥3− 25𝑥 𝑥 − 5 = 50 (43) lim 𝑥→0− 𝑥5− 𝑥 2𝑥2+ 3𝑥3 = +∞ (44)
2.2.2 Tramite limite notevole sin 𝑥𝑥 → 1
lim 𝑥→0 sin 7𝑥 𝑥 = 7 (45) lim 𝑥→0− sin 𝑥2 𝑥3 = −∞ (46) lim 𝑥→0 sin2𝑥 𝑥 = 0 (47) lim 𝑥→0 4 sin 3𝑥 5𝑥 = 12 5 (48)
2.2.3 Tramite limite notevole 𝑒𝑥𝑥−1 → 1
lim 𝑥→0 𝑒3𝑥− 1 𝑥 = 3 (49) lim 𝑥→0 𝑒3𝜋𝑥 − 1 4𝑥 = 1 12𝜋 (50) lim 𝑥→0 𝑒4𝑥− 1 2𝑥 = 2 (51)
http://francescomarchi.wordpress.com
http://francescomarchi.wordpress.com
2.3
Forma 1
∞2.3.1 Tramite limite notevole (1 + 1 𝑥) 𝑥→ 𝑒 lim 𝑥→+∞ ( 1 + 1 𝑥 )2𝑥 = 𝑒2 (52) lim 𝑥→−∞ ( 1 − 𝜋 𝑥 )3𝑥 = 𝑒−3𝜋 (53) lim 𝑥→−∞ ( 1 + 1 7𝑥 )𝑥 =√7𝑒 (54) lim 𝑥→+∞ ( 1 −51 𝑥 )𝑥 = 𝑒−51 (55)
http://francescomarchi.wordpress.com
http://francescomarchi.wordpress.com
3
Dominio e segno di una funzione
3.1
Esercizi di teoria
Dire se le seguenti affermazioni sono vere o false: 1. Il dominio delle due funzioni seguenti `e lo stesso
𝑓 (𝑥) = 5 +√3
6 + 𝑥 − 2√𝑥7− 5 sin 𝑥; 𝑔(𝑥) = √
𝑥7− 5 sin 𝑥 +√54 + 𝑥
8 2. Si consideri la funzione ℎ(𝑥) = 6+𝑥5−𝑥2 + log(𝑥 + 3).
(a) Il punto 𝑥 = −3 appartiene al dominio. (b) Il punto 𝑥 = 0 appartiene al dominio. (c) La funzione non `e definita per 𝑥 = 0.13 − 𝜋.
3.2
Impostazione dei calcoli relativi a dominio e segno
Impostare il sistema relativo alla determinazione del dominio delle seguenti funzioni, senza risolverlo. 1. 𝑓1(𝑥) =√cos(4 + 𝑥6 3) +log(𝑥−4)5
2. 𝑓2(𝑥) = tan( √
𝑥 + 7) − 𝑥3+ 8
3.3
Determinazione del dominio e segno di funzioni date
Per le seguenti funzioni ℎ(𝑥) e 𝑔(𝑥):
ℎ(𝑥) =cos 𝑥 − √ 2/2 𝑥2+ 4𝑥 + 4 𝑔(𝑥) = √ 𝑥2− 4 ∙ Determinare il dominio e scriverlo sotto forma di intervallo.
∙ Studiare il segno e rappresentare sotto forma di intervallo i valori di 𝑥 per cui le funzioni sono positive.
3.4
Abbinamento grafici-funzioni
3.4.1 Esercizio 1
Con opportune considerazioni sul dominio, stabilire le corrispondenze fra le funzioni elencate qui di seguito e i grafici riportati in figura1.
1. 𝑎(𝑥) = 5 √ 𝑥3−5𝑥2+3𝑥+1 2𝑥−1 2. 𝑏(𝑥) = 4 tan(4𝑥 + 3) 3. 𝑐(𝑥) = 𝑒cos 𝑥+√4 − 𝑥2+ sin 𝑥 4. 𝑑(𝑥) = 351𝑒𝑥+√4 𝑥2− 4 5. 𝑒(𝑥) = 15log(7 − 𝑥) + 4 cos 𝑒𝑥 6. 𝑓 (𝑥) =(6 7 )𝑥 + 3 log 𝑥 +√9 𝑥3− 5
http://francescomarchi.wordpress.com
http://francescomarchi.wordpress.com
(a) (b)
(c) (d)
(e) (f)
Figura 1: Grafici relativi all’esercizio3.4.1.
4
Limiti, continuit`
a, asintoti
4.1
Determinazione del grafico di funzioni che soddisfano date condizioni
4.1.1 Esercizio 1
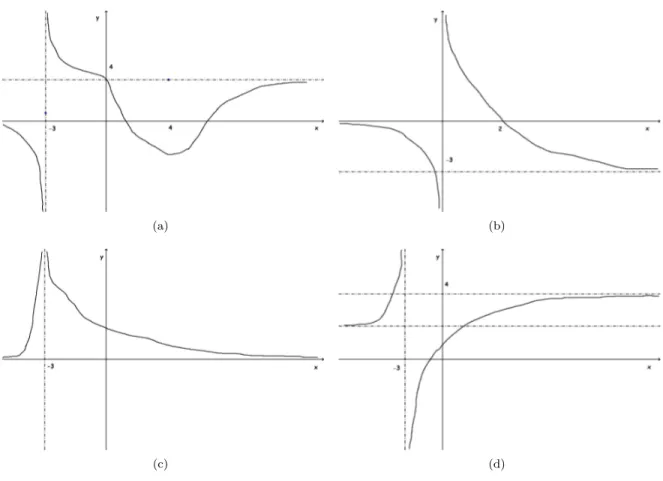
Di una certa funzione 𝑓 (𝑥) si sa che: ∙ lim𝑥→−3+𝑓 (𝑥) = +∞
∙ 𝑓 (4) > 0
∙ lim𝑥→+∞𝑓 (𝑥) > lim𝑥→−∞𝑓 (𝑥)
Determinare quale fra i grafici proposti in figura2rappresenta la funzione 𝑓 (𝑥). 4.1.2 Esercizio 2
Di una certa funzione 𝑓 (𝑥) si sa che: ∙ 𝑓 (−4) = −𝑓 (4)
http://francescomarchi.wordpress.com
(a) (b)
(c) (d)
Figura 2: Grafici relativi all’esercizio4.1.1.
http://francescomarchi.wordpress.com
(a) (b)
(c) (d)
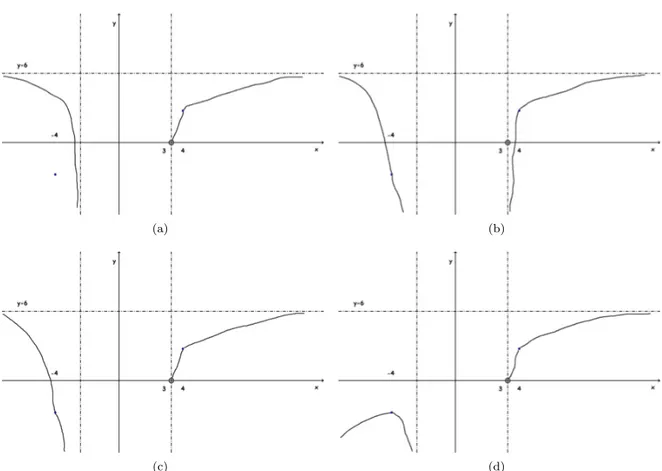
Figura 3: Grafici relativi all’esercizio4.1.2.
∙ la retta di equazione 𝑦 = 6 `e un asintoto orizzontale
∙ la funzione ha nel punto 𝑥 = 3 una discontinuit`a eliminabile
Determinare quale fra i grafici proposti in figura3rappresenta la funzione 𝑓 (𝑥).
4.2
Abbinamento grafici-funzioni
4.2.1 Esercizio 1
Mediante opportune considerazioni sugli asintoti, associare a ciascuna delle funzioni seguenti il grafico corrispondente, fra quelli proposti in figura4:
𝑓1(𝑥) = 1 4 − 𝑥2; 𝑓2(𝑥) = 𝑥2 4 − 𝑥2; 𝑓3(𝑥) = 𝑥 2 − 𝑥; 𝑓4(𝑥) = 𝑥 4 − 𝑥2;
4.3
Individuazione del grafico di una funzione
4.3.1 Esercizio 1
Determinare a quale delle funzioni elencate di seguito corrisponde il grafico rappresentato in figura5.
http://francescomarchi.wordpress.com
(a) (b)
(c) (d)
Figura 4: Grafici relativi all’esercizio4.2.1.
http://francescomarchi.wordpress.com
Figura 5: Grafico relativo all’esercizio4.3.1. 𝑓 (𝑥) =𝑥 2− 1 𝑥2− 4 (56) 𝑓 (𝑥) = ln ( 𝑥2− 1 𝑥2− 4 ) (57) 𝑓 (𝑥) = 𝑒 𝑥2 −1 𝑥2 −4 (58) 𝑓 (𝑥) = √ 𝑥2− 1 𝑥2− 4 (59)
4.4
Esercizi vari
4.4.1 Asintoti verticaliQuali tra le funzioni elencate qui di seguito ha almeno un asintoto verticale?
𝑓 (𝑥) = 1 𝑥2− 1 (60) 𝑓 (𝑥) = 1 𝑥2+ 1 (61) 𝑓 (𝑥) =√𝑥2− 1 (62) 𝑓 (𝑥) = ln(1 + 𝑥2) (63) 𝑓 (𝑥) = ln 𝑥 (64) 4.4.2 Asintoti orizzontali
Quali tra le funzioni elencate qui di seguito ha almeno un asintoto orizzontale?
𝑓 (𝑥) =√1 − 𝑥2 (65) 𝑓 (𝑥) = 𝑥 𝑥2+ 𝑥 + 1 (66) 𝑓 (𝑥) =𝑥 2+ 𝑥 + 1 𝑥 (67) 𝑓 (𝑥) = ln 𝑥 (68)
http://francescomarchi.wordpress.com
http://francescomarchi.wordpress.com
5
Derivate
5.1
Linearit`
a dell’operatore derivata
𝑓 (𝑥) = 𝑥3 (69) 𝑓 (𝑥) = 3𝑥5 (70) 𝑓 (𝑥) = 4𝑥2+1 3𝑥 4− 1 𝑥 (71) 𝑓 (𝑥) = 2 tan 𝑥 − arctan 𝑥 (72) 𝑓 (𝑥) = ln 𝑥 − 3 arctan 𝑥 +√𝜋 (73) 𝑓 (𝑥) = 𝑥1/7+√5𝑥 (74)
5.2
Derivata del prodotto
𝑓 (𝑥) = 𝑥 ln 𝑥 − 2𝑥 + 1 (75) 𝑓 (𝑥) = 𝑒𝑥(𝑥4− 6𝑥2+ 𝑥 + 7) (76) 𝑓 (𝑥) = 𝑥4𝑒𝑥 (77) 𝑓 (𝑥) = sin 𝑥 cos 𝑥 (78)
5.3
Derivata di un rapporto
𝑓 (𝑥) = 𝑥 + 1 𝑥 − 2 (79) 𝑓 (𝑥) = 1 + 𝑥 2 𝑒𝑥 + 4𝑒 (80) 𝑓 (𝑥) = 3 ln 𝑥 2𝑥2− 3 (81) 𝑓 (𝑥) = 1 − cos 𝑥 1 + cos 𝑥 (82) 𝑓 (𝑥) = 1 sin 𝑥− 1 5 (83) 𝑓 (𝑥) = 6 sin 𝑥 + cos 𝑥 𝑒𝑥+ sin 𝑥 (84)5.4
Derivata di funzioni composte
5.4.1 Composizione di due funzioni
𝑓 (𝑥) = ln 2𝑥 (85)
𝑓 (𝑥) = sin4𝑥 (86)
𝑓 (𝑥) = 𝑒3𝑥+ 7 (87)
𝑓 (𝑥) = 𝑒3𝑥+7𝑥2 (88)
𝑓 (𝑥) = 𝑥 + sin 2𝑥 − 4 cos 3𝑥 (89)
5.4.2 Composizione di tre o pi`u funzioni
http://francescomarchi.wordpress.com
𝑓 (𝑥) = ln sin 2𝑥 (90) 𝑓 (𝑥) =√7ln sin 𝑥 (91) 𝑓 (𝑥) = cos arctan 𝑒𝑥 (92) 𝑓 (𝑥) =√4 sin(𝑥3+ 2𝑥 − 4) (93)