2 - I quarzi

2 - I quarzi

2.1 Introduzione

I dispositivi elettronici che forniscono un’oscillazione stabilizzata in frequenza, utilizzano spesso alcuni componenti che sono in grado di fissare in modo preciso e stabile la frequenza di lavoro. Questi dispositivi sono i risonatori al quarzo o semplicemente quarzi che in virtù delle loro proprietà di piezoelettricità, se sottoposti ad una tensione elettrica oscillano ad una frequenza precisa dovuta alle loro caratteristiche fisiche. Il quarzo (SiO2) è un minerale appartenente alla classe degli

ossidi. E' uno dei minerali più comuni della crosta terrestre, essendo presente nelle rocce magmatiche e ricche in silice e nella maggior parte delle sabbie. Esistono diversi tipi di quarzo: latteo, ialino, affumicato, azzurro, citrino, rosa, rutilato, occhio di tigre e di gatto, avventunirato. Può assumere colorazione bianca, trasparente, gialla o nera; ha lucentezza vitrea, il suo abito cristallino può essere prismatico, esagonale, alquanto allungato secondo l'asse verticale terminato in piramidi. Non è soggetto a sfaldatura, la sua durezza è pari a 7 e il suo peso specifico è 2.65. E’ insolubile in acqua ed è attaccabile dall’acido fluoridrico (HF).

2.2 L’effetto piezoelettrico

Nel 1880, Jacques e Pierre Curie scoprirono che uno stress meccanico applicato a materiali cristallini come il quarzo (SiO2), il sale di Rochelle (NaKC4H4O6٠ 4H2O) e la

tormalina, produceva in risposta un potenziale elettrico tra le superfici del cristallo, di ampiezza proporzionale allo stress applicato. Questo comportamento è oggi noto come effetto piezoelettrico, termine che deriva dal greco piezein (premere) [1]. Questa proprietà si manifesta in quei materiali cristallini privi di un centro di simmetria. Tale asimmetria fa sì che il cristallo presenti un asse polare dovuto ai dipoli elettrici associati all’orientazione degli atomi del reticolo cristallino.

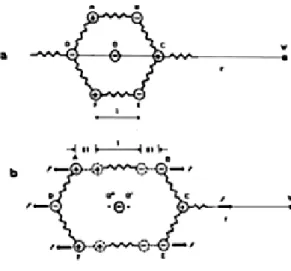
Un modello [2] che può spiegare il comportamento del cristallo piezoelettrico a livello reticolare, è costituito da un esagono i cui vertici sono occupati alternativamente da cariche elettriche positive e negative q+ e q- collegate da molle meccaniche di lunghezza l che ne costituiscono i lati (figura 2.1):

Figura 2.1 Modello del reticolo cristallino per lo studio dell’effetto piezoelettrico

Si suppone che i dipoli AB, CD e EF non interagiscano tra loro (dalla figura i dipoli si vedono male). In questo modello il reticolo non possiede una simmetria centrale, dato che la proiezione di ogni carica attraverso il centro O, ad esempio B- ed F+, cade sulla carica di polarità opposta.

Ci sono 21 sistemi cristallografici che non possiedono un centro di simmetria, 20 dei quali presentano l’effetto piezoelettrico. Inoltre alcune ceramiche PXE (come PbTiO3 e

PbZrO3) ed alcuni polimeri sottoposti a stress (come il PVF2) presentano una eccellente

piezoelettricità. In questi materiali, l’effetto piezoelettrico ha origine in quelle regioni del cristallo in cui il dipolo elettrico è stato “fissato” in sede di fabbricazione in seguito all’applicazione di un forte campo elettrico in presenza di uno sforzo meccanico.

Il campo elettrico E dovuto ad un dipolo in un punto dell’asse congiungente le due cariche ad una distanza r, con r >> l, vale:

3 0 2 r E πε χ = (2.1)

Nel punto W, posto ad una distanza r dalla carica C, il campo elettrico è pari alla somma dei contributi dei dipoli AB,CD e EF:

( ) (

)

( )

Quando due forze uguali in modulo e opposte in verso vengono applicate al cristallo lungo la direzione OW, ogni carica subirà uno spostamento δl (figura 1.2b) ed in questo caso la somma di tutti i contributi nel punto W sarà più nulla ma data da:

3 0 2 2 r l q E πε δ ⋅ ⋅ = (2.3)

Il momento di dipolo generato dallo spostamento è χ =2qδl =2qlψ, dove ψ è la deformazione longitudinale che vale δl/l.

Per un cristallo reale formato da N atomi per unità di volume, la polarizzazione è la somma di tutti i momenti di dipolo di tutti gli atomi che hanno subìto uno spostamento, cioè:

ψ

χ_E =2qlN (2.4)

La carica q, la distanza interatomica l e il numero di atomi N, sono tipiche di ogni cristallo e vengono perciò incorporate nell’espressione del tensore di stress _{σ = 2qlN,} per cui avremo:

σψ

χE = qN = (2.5)

Analogamente si può verificare che un cristallo che ha un centro di simmetria, se sottoposto a stress meccanico, non produce campo elettrico.

La relazione tra forza applicata (sforzo) T, deformazione S, campo elettrico E e vettore polarizzazione D, è rappresentata dalle equazioni costitutive:

E d S c T _{= ⋅ −} t_{⋅ (2.6)} E S d D= ⋅ +ε⋅ (2.7)

dove c è la matrice dei coefficienti di rigidezza, d la matrice dei coefficienti piezoelettrici, ε la costante dielettrica del materiale.

2.3 Il quarzo come risuonatore elettromeccanico

Le caratteristiche del quarzo permettono di generare una risonanza meccanica all’interno del cristallo, che possono essere pensate come onde acustiche periodiche che si propagano in direzioni specifiche.

A tal fine vengono impiegate delle fette sottili (slices) di quarzo monocristallino tagliate seguendo particolari direzioni rispetto agli assi cristallografici (figura 2.2).

Figura 2.2 Orientazione del taglio del quarzo AT-cut

I quarzi più diffusi nelle varie applicazioni elettroniche, e in particolare nello studio di questa tesi, sono gli AT-cut, ottenuti tagliando il quarzo con un angolo di 35° 25’ rispetto all’asse cristallografico z. Il vantaggio principale di questo taglio è l’ottenimento di quarzi aventi caratteristiche poco sensibili alla temperatura, almeno in un intervallo che va da 10 a 50° C. Il tipico risuonatore di quarzo a disco con due elettrodi d’oro, uno per faccia, è riportato in figura 2.3, assieme ad uno dei sistemi di montaggio più usati (mollette).

Figura 2.3 Risuonatore al quarzo discoidale con elettrodi d’oro e contatti metallici

2.4 Propagazione dell’onda acustica nel quarzo

Immaginiamo [3] di applicare al tempo t = 0 un impulso di tensione nel centro del disco, provocando quindi un certo spostamento u delle particelle. A causa delle proprietà viscoelastiche del quarzo, tale spostamento avrà un certo ritardo rispetto all’impulso. Questo spostamento fa immagazzinare energia meccanica al materiale che viene poi convertita in energia cinetica rendendo possibile l’innesco di un’onda di risonanza meccanica.

L’ampiezza dello spostamento e la sua velocità massima dipendono dalle caratteristiche del cristallo nella direzione del campo elettrico applicato. Il quarzo è infatti un materiale fortemente anisotropo, per cui le sue caratteristiche fisiche variano rispetto alla direzione spaziale considerata.

Questo moto viene smorzato dalla viscosità del materiale per cui l’onda decade rapidamente dal centro verso la periferia. Anche la piezoelettricità gioca un ruolo fondamentale in questo smorzamento, in quanto la separazione della carica dovuta alla deformazione induce una variazione del campo elettrico tale da contribuire al ritorno alle condizioni iniziali.

Si forma così un potenziale elettrico variabile nel tempo praticamente in fase all’onda meccanica. Il centro del disco non è meccanicamente isolato e questo comporta che lo spostamento u, che qui è massimo, si propaghi radialmente con intensità decrescente.

Questa è l’onda acustica che si propaga dal punto di stimolazione. Poiché l’impulso iniziale ha generato un potenziale variabile nel tempo, quest’ultimo può essere prelevato, amplificato e riapplicato al dispositivo in fase col segnale e di conseguenza con l’onda acustica, ottenendo così un sistema che risuona, che sostiene, cioè, l’oscillazione. E’ interessante vedere come il cristallo piezoelettrico possa essere usato per generare un segnale elettrico in modo tale da essere utilizzato come sensore fisico o chimico.

Si è detto che l’applicazione per mezzo di un elettrodo superficiale di un impulso di tensione nel centro del disco genera un’onda acustica che si propaga con una certa velocità. La direzione e le modalità di propagazione, ovvero trasversale verticale, trasversale orizzontale o longitudinale, dipendono dall’orientamento del campo elettrico rispetto agli assi cristallografici.

L’onda così generata si propagherà fino a trovare un vincolo, tipicamente il bordo fisico del quarzo , in corrispondenza del quale subisce una riflessione e un’attenuazione a causa degli attriti viscosi presenti nel mezzo di propagazione. Trascurando momentaneamente questa attenuazione, l’onda riflessa genera grazie all’effetto piezoelettrico inverso un potenziale elettrico agli elettrodi e quindi una corrente nel circuito esterno. A sua volta tale potenziale genera un’onda acustica grazie all’effetto piezoelettrico diretto.

Se queste onde sono tra loro in fase, l’interferenza che si genera è costruttiva e si forma quindi un’onda stazionaria, altrimenti l’interferenza è distruttiva e si ha cancellazione dell’onda. Per sostenere quest’onda stazionaria deve essere fornita energia dall’esterno, in particolare energia elettrica che viene convertita in energia cinetica.

Una condizione affinché si instauri un’onda stazionaria, è che la sua lunghezza d’onda sia uguale a 2tq, dove tq è lo spessore del disco di quarzo.

La frequenza dell’onda acustica alla condizione di risonanza è data dall’equazione:

q q q q tr t t f /2 ( / 1/2)/2 0 2 / 1 ρ µ υ = = (2.8)

2.5 L’ Equazione di Sauerbrey

Nel 1959 Sauerbrey [4] ricavò per primo la relazione tra la frequenza e la massa depositata su un disco di quarzo. Nel suo lavoro, Sauerbrey assunse che, per piccole variazioni, l’aumento di massa poteva essere visto come l’effetto provocato da uno strato sottile aggiuntivo.

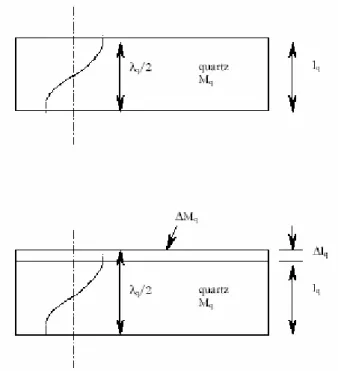
Figura 2.3 Rappresentazione schematica del modello di Sauerbrey di un quarzo, per piccole variazioni di massa sulla superficie

La figura 2.3 mostra il modello di Sauerbrey, che rappresenta un quarzo oscillante di massa Mq e spessore lq. La frequenza di risonanza (fq), in questo modello è:

l V V f q q q q 2 = = λ ( 2.9)

dove λq è la lunghezza d’onda dell’onda acustica che si propaga nel quarzo, pari al doppio dello spessore del quarzo (lq); Vq è la velocità di propagazione di tale onda (λqfq). Nel caso di deposizione di massa sulla superficie del quarzo, si ha un aumento dello spessore l che causa una variazione della frequenza di risonanza fq. Un aumento di

spessore e di massa, provoca una diminuzione della frequenza di risonanza, in accordo con le equazioni (2.10) e (2.11): q q q q l l f f ∆ − = ∆ (2.10) q q q q M M f f ∆ − = ∆ (2.11)

L’equazione fondamentale (2.12) per applicazioni microgravimetriche, derivata da Sauerbrey durante esperimenti di deposizione di films sulla superficie del quarzo, è ottenuta dalla combinazione delle equazioni (2.9) e (2.11):

q q q q q q M A V f f f ∆ − = ∆ ) 2 ( ρ (2.12)

dove A è l’area del cristallo espressa in cm2. Sostituendo i valori di ρq con la densità del quarzo (2.648 g٠cm-3) e Vq con la velocità di propagazione dell’onda acustica nel quarzo (3.336٠105 _cm٠s-1_{), si ottiene l’equazione (2.13):}

A M f

f =− ⋅ _q ∆

∆ _{2,26 10}−6 2 _(2.13)

Lo spessore del cristallo determina la frequenza di risonanza e quindi la sensibilità nei confronti della massa depositata. Il limite inferiore allo spessore è imposto dalla fragilità meccanica del disco di quarzo. La relazione di Sauerbrey mette in evidenza il fatto che la variazione di frequenza è dovuta ad una variazione di massa che viene a formarsi sull’elettrodo indipendentemente dalla distanza radiale dal centro. Comunque, l’effettiva risposta in frequenza del quarzo ad una variazione di massa è espressa attraverso la costante di sensibilità differenziale cf, che rappresenta la variazione

differenziale di frequenza a fronte di una variazione differenziale di massa, nella zona dell’elettrodo, ed è data da:

S dm df

c_f = / = (2.14)

La sua integrazione sulla superficie dell’elettrodo, fornisce la costante di sensitività integrale:

∫∫

dove r e Ф sono la distanza e l’angolo del sistema di coordinate polari posto al centro dell’elettrodo mentre Cf , corrisponde al termine 2f02/(µqρq)1/2 dell’equazione di

Sauerbrey.

Tale equazione (Sauerbrey) assume che il film depositato sulla regione attiva del quarzo abbia uno spessore omogeneo, in quanto cf dipende dallo spessore.

Alcuni studi hanno evidenziato che cf ha valore massimo al centro dell’elettrodo e

decresce con il raggio seguendo un andamento pressoché gaussiano fino a diventare trascurabile oltre il bordo dell’elettrodo. Questo comportamento può essere spiegato anche dal fatto che solamente la porzione del quarzo che si trova tra gli elettrodi sperimenta il campo elettrico responsabile dell’oscillazione.

La zona non ricoperta dall’elettrodo serve a smorzare le oscillazioni che restano confinate all’interno della zona ricoperta dall’elettrodo, realizzando così una sorta di intrappolamento dell’energia. Come conseguenza, le due zone suddette hanno due frequenze di taglio sotto le quali le onde non si possono propagare senza subire uno smorzamento, e sono we e wq, relative rispettivamente alla zone ricoperta o meno

dall’elettrodo. L’energia associata al modo fondamentale dell’oscillazione è confinata nella regione dell’elettrodo, con ampiezza massima al centro e via via decrescente fino ad annullarsi ai bordi.

Il moto armonico del quarzo è analogo a quello di una corda vibrante, di un pendolo e di un sistema massa-molla (figura 2.4).

Figura 2.4 Sistemi meccanici; a) massa-molla; b) pendolo; c) corda vibrante

In tali sistemi, l’ampiezza dell’oscillazione è fissata dalla quantità di energia meccanica fornita inizialmente e la frequenza di risonanza è determinata da caratteristiche fisiche come la massa e la lunghezza. Le proprietà risonanti del quarzo, come per questi sistemi, possono essere dedotte dall’equazione del moto delle onde. Per il quarzo, la condizione iniziale è spostamento nullo alla superficie nell’istante iniziale nel quale viene fornito il campo elettrico.

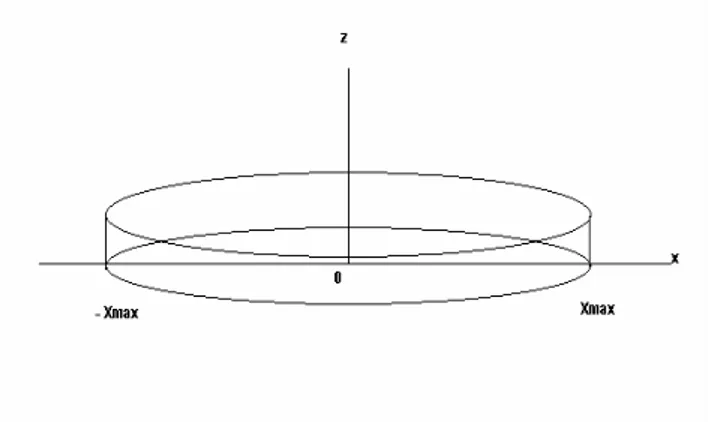
Il moto trasversale del cristallo si svolge tra due limiti, per cui -xmax < x < +xmax , dove

l’ampiezza massima xmax dipende dalla tensione applicata alle facce del quarzo.

Come negli altri sistemi meccanici, l’energia potenziale ha un massimo per x = ± xmax

ed è nulla per x = 0, mentre l’energia cinetica è trascurabile in x = ± xmax ed è massima

in x = 0, facendo riferimento alla figura 2.5.

Per comprendere il ruolo della massa nel determinare la frequenza di risonanza, si può fare un paragone con la corda vibrante.

In essa la frequenza di oscillazione è data da: l

m S

f₀ =( / _l)/2 (2.16)

dove S è la tensione applicata alla corda, ml la massa per unità di lunghezza ed l la

lunghezza della corda vibrante. Analogamente, incrementando lo spessore del quarzo si ottiene una diminuzione della frequenza di oscillazione:

q

t

f₀ ∝1/ (2.17)

La differenza principale tra il quarzo e gli altri sistemi meccanici oscillanti, è che esso è capace di oscillare con una minima perdita di energia.

Il rapporto tra il massimo dell’energia immagazzinata e l’energia dissipata, durante un ciclo, è conosciuto col nome di fattore di merito Q:

dissipata Energia ata immagazzin Energia Q _ _ 2_π = (2.18)

Per i quarzi Q può superare il valore di 100˙000.

Questa proprietà è una delle ragioni principali del largo utilizzo dei quarzi nei sistemi di controllo della frequenza e di generazioni di riferimenti temporali.

Le basse perdite di energia permettono una precisa determinazione del periodo e quindi della frequenza di oscillazione. Questo fa dei quarzi i candidati ideali per applicazioni di controllo della frequenza e di misurazioni in sistemi QCM.

2.6 Circuito equivalente del quarzo nel vuoto

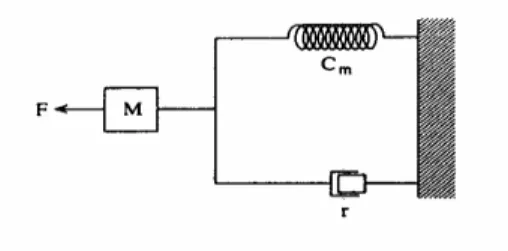
Come dispositivo elettroacustico, il quarzo può essere rappresentato con un modello meccanico a parametri concentrati costituito da una massa, una molla e un pistone.

Essi sono rappresentati (figura 2.6) da una massa M collegata alla serie di una molla di cedevolezza Cm, uguale a 1/k, dove k è la costante di Hooke, e di un pistone con

coefficiente di attrito r.

Figura 2.6 Modello meccanico equivalente del quarzo

A tale modello meccanico corrisponde un analogo modello elettrico a parametri concentrati, costituito da componenti con caratteristiche induttive, capacitive e resistive (figura 2.7).

Figura 2.7 Modello elettrico equivalente del quarzo

Le componenti del ramo serie corrispondono al modello meccanico nel seguente modo: • L1 è la componente inerziale associata alla massa M durante l’oscillazione. • C1 è la cedevolezza del quarzo (Cm) e rappresenta l’energia accumulata.

• R1 rappresenta la dissipazione di energia dovuta agli attriti interni, alle perdite meccaniche dovute al sistema di sostegno del quarzo e alle perdite acustiche dovute all’ambiente circostante.

Il modello è completato dal condensatore C0 in parallelo, che rappresenta la capacità

statica degli elettrodi del quarzo. Il ramo serie, detto anche cinetico, si comporta come un circuito LCR. Se R fosse nulla, l’energia del campo elettromagnetico si palleggerebbe all’infinito tra la capacità C1 e l’induttanza L1, ma il fatto che R sia

diversa da zero comporta che l’oscillazione sia smorzata, come avviene ovviamente nel quarzo a causa degli attriti interni. Concettualmente, quando lo spostamento della superficie del quarzo è massimo, cioè x = ± xmax, è come avere, nell’equivalente

elettrico LCR, il condensatore carico. In questa situazione l’energia potenziale è massima e quella cinetica è nulla. Quando x = 0, situazione in cui si ha spostamento nullo e velocità massima, nell’equivalente elettrico è come avere il condensatore completamente scarico e il massimo campo magnetico attorno all’induttore con la massima corrente, che rappresenta la massima energia cinetica.

Per meglio comprendere l’equivalenza tra i due modelli equivalenti, è utile confrontare le equazioni che descrivono il circuito LC (R = 0) e il sistema massa-molla riportate nella tabella 1.

Sistema massa-molla Circuito LC

2 2 2 2 1 2 1 2 1 kA kx mv + = ( ) 2 1 ) ( 2 1 2 1 2 2 2 C Q C q Li + = 2 2 _x A m k v= − 1 _Q2 _q2 LC i= − dt dx v= dt dq i= t m k A x _      = sin t LC Q q _      = sin 1

( )

( )

a _{m = massa; v = velocità; k = costante di Hooke; x = spostamento; A = ampiezza o} spostamento massimo; ω = velocità angolare; f = frequenza; t = tempo; L = induttanza; i = corrente; q = carica; C = capacità; Q = carica massima.

Si nota la corrispondenza di L con m e di k = 1/Cm con 1/C. La presenza del fattore di

smorzamento nel modello meccanico. L’equivalenza può essere espressa anche attraverso le due seguenti equazioni:

F x Cm dt dx r dt x d M  =      +       +     1 2 2 (2.19) V C q dt dq R dt q d L =     +       +     1 1 2 2 1 (2.20)

dove F è la forza applicata alla massa e V la tensione applicata ai contatti del quarzo. Alcuni studi [5,6] hanno mostrato come sia possibile calcolare i parametri elettrici RLC, risolvendo l’equazione del moto, applicando le opportune condizioni al contorno, calcolando la deformazione, la polarizzazione, la densità di carica e il potenziale in ciascun punto della superficie.

Da questo tipo di analisi sono stati trovati i seguenti valori: • C D_q A t_q 12F 0 = ε / ≈10− (2.21) • C A 2 2t_qc 14F 1=8 ε /π ≈10− (2.22) • = 3 /8 2 ≈100Ω 1 t r Aε R _q (2.23) • L t_q3 A 2 3H 1= ρ/8 ε ≈75×10− (2.24)

dove Dq è la costante dielettrica del quarzo, ε0 la permittività del vuoto, r il coefficiente

di attrito del pistone, A l’area dell’elettrodo, ε la costante piezoelettrica di stress e c la costante elastica. La capacità statica C0 non dipende da ε e quindi questo elemento non

partecipa alla piezoelettricità, mentre C1, L1, R1 dipendono invece fortemente da ε. C1

dipende inoltre dalla costante elastica c che tiene conto delle forze elastiche del reticolo cristallino del quarzo, L1 dipende dalla densità del risuonatore; la quantità tq3ρ/A

rappresenta una massa per unità di area e non è altro che il termine ∆m/A dell’equazione di Sauerbrey.

Quindi ad un aumento della costante elastica corrisponde una diminuzione di C1, ad un

aumento dell’energia dissipata un aumento di R1 ed infine, ad un aumento della massa

contatto di film polimerici o fluidi viscoelastici. E’ interessante inoltre notare che C0 e

C1 aumentano con la superficie A dell’elettrodo, mentre R1 e L1 diminuiscono con essa.

2.7 Modi di oscillazione del cristallo e armoniche superiori

La frequenza di risonanza dei cristalli dipende dallo spessore del disco, sia dal modo di vibrazione. La gamma delle frequenze di risonanza ottenibili va da 400 Hz fino a 125 Mhz.

Ad un maggiore spessore del disco corrisponde una minore frequenza.

In quanto al limite superiore di banda, esso resta limitato dallo spessore minimo ottenibile tale da non provocare la rottura del quarzo stesso.

In un cristallo di quarzo la vibrazione può avvenire in tre modi diversi: flessorio, longitudinale e trasversale, come illustrato in figura 2.8:

Figura 2.8 Modi vibrazionali

La vibrazione flessoria consiste in un movimento di curvatura e inarcatura; la vibrazione longitudinale avviene tramite uno spostamento in larghezza delle dimensioni della piastrina, partendo dal centro, mentre la vibrazione trasversale consiste nello spostamento delle due facce in senso opposto, pur conservando il loro parallelismo. Ogni modo di vibrazione produce una gamma di frequenze ben distinta:

• modo flessorio: da 400 Hz a 100 Khz • modo longitudinale: da 40 Khz a 15 Mhz • modo trasversale: da 100 Khz a 125 Mhz

I cristalli possono vibrare in uno dei due seguenti modi: fondamentale o armonica superiore. La frequenza fondamentale è la più bassa frequenza in corrispondenza della quale il cristallo risuona, quindi non è possibile ottenere frequenze più basse della fondamentale. Se ciò accade, si tratta di una oscillazione del circuito non vincolata al cristallo e quindi di un segnale privo di utilità. Tale frequenza è inversamente proporzionale allo spessore della piastrina e poiché non è possibile ottenere spessori piccoli oltre un certo limite, essa è limitata superiormente. Tale limite è inferiore a 20 Mhz.

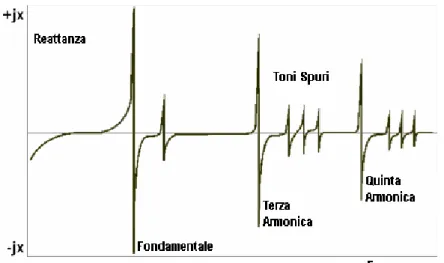
Per ottenere frequenze superiori il cristallo deve essere stimolato in modo tale da farlo oscillare in corrispondenza delle armoniche superiori che tipicamente sono di ordine dispari. Un tipico andamento delle frequenze di oscillazione di un quarzo, inteso come un circuito RLC e considerando solamente la parte immaginaria dell’impedenza equivalente, è rappresentato in figura 2.9.

Figura 2.9 Rappresentazione delle armoniche di un quarzo

2.8 I quarzi nei liquidi

Tipicamente un quarzo, per applicazioni classiche come sistemi di controllo della frequenza, orologi, oscillatori etc., viene mantenuto dentro una capsula metallica contenente gas inerte e quindi opera in condizioni paragonabili a quelle ideali del vuoto.

Per applicazioni QCM, il quarzo viene ricoperto da un sottile film polimerico e/o da altri strati che servono per specializzarlo ad un gas o ad un’analita; nel caso dei biosensori, oggetto di questa tesi, il bersaglio è una molecola biologica (DNA o RNA) che è presente in una soluzione che viene portata sull’elettrodo attraverso un opportuno circuito idraulico. Queste particolari condizioni modificano il comportamento del quarzo rispetto al caso del vuoto discusso finora. Nel caso di immersione di un elettrodo in un liquido, alla variazione di frequenza dovuta all’aumento di massa (equazione 8.7), deve essere sommata una variazione di frequenza dovuta alla densità e viscosità del liquido [Kanazawa e altri], espressa dall’equazione 2.25:

q q L L f f µ πρρ η 3 0 − = ∆ (2.25)

dove ρl e ηl sono rispettivamente la densità e la viscosità del liquido.

2.8.1 Effetti fisici all’interfaccia.

I risuonatori al quarzo possono essere descritti meccanicamente con un modello monodimensionale in cui tutte le quantità fisiche come spostamento, stress e potenziale elettrico sono funzioni di una sola variabile, lo spessore. (Per una descrizione rigorosa monodimensionale [7,8]). In questo modello ogni strato è descritto da una matrice 8×8 i cui coefficienti sono le costanti elastiche, piezoelettriche, dielettriche, la densità e lo spessore. Il risuonatore nella sua interezza è descritto dal prodotto delle singole matrici. In figura 2.10, è raffigurato il caso di quarzo avente un elettrodo (ortogonale all’asse y, in y=0) a contatto con un film viscoelastico di spessore df immerso, a sua volta, in uno

strato sottile di un liquido newtoniano (liquido viscoso in cui la resistenza allo scorrimento di uno strato sull'altro è proporzionale alla velocità di scorrimento, ad esempio l’acqua), e l’altro elettrodo (y= - dq), a contatto con l’aria. A causa

dell’accoppiamento elettromeccanico che si ha all’interfaccia, le proprietà viscoelastiche del fluido si riflettono sulle proprietà elettriche del quarzo.

Figura 2.10 Risuonatore composito, costituito da un disco di quarzo con depositato un film viscoelastico, a contatto con uno strato di liquido (newtoniano)

Lo strato semi-infinito di liquido newtoniano, è caratterizzato da una densità ρl e una

viscosità ηl mentre il film viscoelastico, dalla sua densità ρf, dal modulo elastico di

immagazzinamento G’f (shear storage modulus [9]) e dalla viscosità ηf.

Il coefficiente di viscosità, nello studio dei materiali viscoelastici, può essere espresso in forma complessa:

η η

η∗= ′−i ′′ (2.26)

Analogamente, anche il modulo elastico di taglio G, può essere espresso come coefficiente complesso:

G i G

G∗= ′+ ′′ (2.27)

Nelle due equazioni 2.26 e 2.27, la parte reale tiene conto dell’energia immagazzinata (storage modulus, comportamento elastico), mentre la parte immaginaria, tiene conto dell’energia dissipata (loss modulus, comportamento viscoso).

Per il quarzo, si ha:

q i e c G ωη ε + + = 22 2 26 66 (2.28)

dove c66 è il modulo di taglio (shear modulus), e26 la costante piezoelettrica ed ε22 la

costante dielettrica a deformazione costante. mentre, per il film viscoelastico, si ha:

f f i

G

G= + ωη (2.29)

dove ω rappresenta la pulsazione dell’onda acustica che si propaga all’interno del risuonatore composito. Il comportamento del risuonatore, in termini di spostamento lungo l’asse x, è descritto dall’equazione:

2 2 2 2 y u G t u_{x x} ∂ ∂ = ∂ ∂ ρ (2.30)

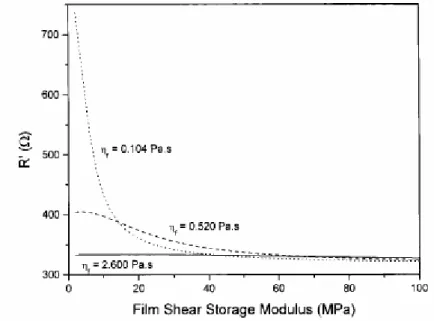
dove ρ è la densità del quarzo o del film, a seconda del mezzo in cui viene studiato il moto dell’onda acustica. In letteratura, sono presenti studi [10] che mostrano l’influenza delle caratteristiche viscoelastiche dei film sottili, sulle proprietà elettriche del quarzo [11]. Un risultato interessante, è mostrato in figura 2.11.

Figura 2.11 Curve della resistenza elettrica R del quarzo, in funzione di G (shear storage modulus) di un film viscoelastico a contatto con un elettrodo del quarzo

Le curve mostrano l’andamento della resistenza elettrica del quarzo, espressa in Ω (qui indicata come R’) in funzione del modulo G del film, espressa in MPa (megapascal), per diversi valori della viscosità ρf del film stesso (spessore 1 µm, densità 1 g/cm3). Il

comportamento viscoelastico del film è abbastanza complesso, e dipende dall’interazione tra le proprietà meccaniche del materiale costituente il film, dal suo spessore e dalla lunghezza d’onda dell’onda acustica propagantesi. Per valori elevati di G (80 MPa), la resistenza diventa praticamente indipendente dalla viscosità del film: il suo valore di 320 Ω, è vicino a quello dovuto al solo strato di liquido newtoniano. Questo significa che il film, molto rigido, oscilla in modo solidale al quarzo [12]. Per valori di G compresi tra 2 e 10 MPa, la resistenza varia fortemente con G, in quanto l’effetto della frizione interna al film, è dominante.

Quindi, un film viscoelastico a contatto con un liquido, varia l’impedenza acustica del cristallo, espressa dall’equazione 2.31:

v

Z_A =τ (2.31)

essendo τ lo shear stress applicato e v la velocità di spostamento della superficie. La corrispondente impedenza elettrica del quarzo, può essere calcolata con l’equazione 2.32:

2

k Z

Z ₌ A _(2.32)

dove k è la costante elettromeccanica del cristallo [12].

Come mostrato in [13], la variazione di impedenza del QCM, è data, in modo approssimato, dalla somma delle impedenze acustiche del film e del liquido, ognuna moltiplicata per un termine che tiene conto della variazione di fase e dell’attenuazione dell’ampiezza.

2.8.2 Andamento dell’impedenza del quarzo nel vuoto.

La possibilità di esprimere le proprietà elettromeccaniche del quarzo mediante un circuito elettrico equivalente è di fondamentale importanza in quanto i parametri elettrici possono essere calcolati mediante strumenti come gli analizzatori di

impedenza. L’analisi dell’impedenza (o ammettenza) può descrivere quindi le proprietà di un particolare quarzo ed in particolare le interazioni che esso ha col mezzo circostante.

Gli analizzatori di impedenza come ad esempio il 4192, il 4194A o il più sofisticato 4294A, tutti della Hewlett Packard, sono in grado di fornire la misura dell’impedenza Z, fase θ, ammettenza Y, conduttanza G, suscettanza B e di altri parametri. Questi strumenti compiono una misura di tensione imponendo una corrente nel bipolo da misurare, su un certo intervallo di frequenza, che negli strumenti più sofisticati può andare dalla continua fino a 100 Mhz.

Le proprietà del ramo RLC serie sono facilmente descrivibili mediante l’ammettenza, espressa nell’equazione :

jB G

Y = + (2.33)

Tali proprietà possono essere rappresentate sul grafico dell’ammettenza, che riporta in ascissa la parte reale dell’ammettenza ed in ordinata la sua parte immaginaria.

Ogni componente ha una ammettenza rappresentata in figura 2.12:

Figura 2.12 Luogo dell’ammettenza del bipolo LCR serie

Il modulo dell’ammettenza |Y| è dato dalla:

(

)

B G

e può essere determinata dalla risultante dei vettori della parte reale e immaginaria, definita come il valore del luogo dell’ammettenza ad una certa frequenza.

Tale luogo si ricava facendo il quadrato della (2.34), che fornisce l’equazione di un cerchio con centro nell’origine e raggio G/2. Incrementando la frequenza dal valore nullo, la componente immaginaria dell’ammettenza (jB) raggiunge un massimo per f = f1; qui, il modulo di B è massimo.

Incrementando ancora la frequenza, si arriva all’asse delle ascisse dove la componente reale dell’ammettenza (G) è massima. Questo punto si trova a frequenza fr, che è la

frequenza di risonanza della rete RLC. Alla frequenza fr l’impedenza raggiunge il suo

minimo. Inoltre in questo punto la fase θ = 0, per rispettare la condizione di onda stazionaria. Alla frequenza f2, B ha modulo minimo. L’ammettenza di un quarzo si

comporta in accordo al luogo dell’ammettenza di figura 2.13, a causa del contributo della capacità C0 in parallelo.

Figura 2.13 Luogo dell’ammettenza della rete equivalente del quarzo

La presenza di C0 introduce un offset il luogo dell’ammettenza di una quantità ωC0,

introducendo altre importanti frequenze. Il massimo e il minimo di B si trovano ancora rispettivamente alle frequenze f1 e f2, ma il punto di massimo dell’ammettenza non si

Inoltre si nota che la frequenza fYmax per cui l’ammettenza è massima è minore della

frequenza fYmin cui si ha il minimo dell’ammettenza (il luogo è percorso in senso

orario). In modo duale, l’impedenza presenta prima un minimo e poi un massimo. La risonanza è qui soddisfatta in corrispondenza di due frequenze, fs e fp, che sono

rispettivamente la frequenza di risonanza serie e parallelo.

Per f = fs, la parte reale dell’ammettenza (G) è di poco minore rispetto al suo valore

massimo alla frequenza fGmax, mentre alla frequenza fp, G è di poco maggiore di zero.

Il luogo dell’ammettenza fornisce utili informazioni per interpretare alcuni comportamenti del quarzo in applicazioni QCM.

Ad esempio, se R aumenta, il diametro del cerchio diminuisce e fs ed fp convergono. Se

C0 aumenta, il luogo dell’ammettenza si sposta ancora più in alto ottenendo similmente

la suddetta convergenza.

Infine, grandi valori di R e di C0 fanno sì che il luogo non attraversi l’asse reale. In

questo caso la fase non si annulla mai e quindi non si ha oscillazione.

In ogni caso fs, che è la frequenza che viene misurata nella maggior parte delle

applicazioni QCM, varia R. Queste considerazioni sono molto utili per la scelta del quarzo per misure in sistemi QCM che lavorano in liquido o con film sottili depositati, in quanto questi contribuiscono al valore effettivo di R. In figura 2.14 è rappresentato il grafico dell’ammettenza in coordinate cartesiane, in funzione della frequenza.

Figura 2.14 Grafico di Y in coordinate cartesiane

Le proprietà del risuonatore al quarzo possono essere raffigurate anche sul diagramma dell’impedenza, modulo Z e fase θ (figura 2.15 ).

Figura 2.15 Diagramma Z-θ in coordinate cartesiane

Il diagramma contiene le due frequenze fZmin e fZmax in cui il modulo dell’ammettenza è

rispettivamente massimo e minimo. Alle basse frequenze, domina la reattanza capacitiva ω(C0+C1) e la fase vale θ = 90°. Salendo in frequenza, in prossimità della

zona di risonanza, il contributo della reattanza induttiva ωL1 aumenta, opponendosi a

quella capacitiva, e in fZmin si raggiunge il minimo dell’impedenza.

Si raggiunge poi la frequenza fp in corrispondenza della quale si ha il massimo

dell’impedenza. Per f > fp , il valore dominante dell’impedenza è 1/ωC0, e quindi si

ritorna ad un comportamento induttivo. La fase θ passa per zero alle due frequenze fs e

fp , in cui le reattanze serie e parallelo si annullano. Il quarzo presenta quindi un

comportamento capacitivo per f < fs e f > fp, con θ = -90°, ed un comportamento

Figura 2.16 Comportamento dell’impedenza equivalente del quarzo

Nella seguente tabella sono riportate le espressioni delle grandezze di interesse nello studio dell’impedenza Z del quarzo.

Reattanza Serie 1 1 1 C L X X X_{serie L c} ω ω − = − = (2.35) Reattanza parallelo 0 1 1 1 C L X_parallelo ω ω − = (2.36) Impedenza serie

(

)

( )

Frequenza di risonanza serie

1 1 2 1 C L f_s π = (2.38) Frequenza di risonanza parallelo

1 0 1 0 1 2 1 C C C C L f_p + = π (2.39)

Come si vede dal confronto dei due grafici di Z-θ e G-B, le due frequenze fBmax e fBmin

coincidono con le frequenze f1 e f2 , che sono le frequenze in corrispondenza delle quali

la curva raggiunge la metà del suo valore massimo. La corrente scorre più facilmente attraverso il risuonatore in corrispondenza delle frequenze vicine a fGmax, in cui è

massima la conduttanza, e questo mette in evidenza il comportamento di filtro passa-banda del quarzo. La passa-banda di tale filtro è:

1

2 f

f

BW = − (2.40)

In genere i quarzi hanno bande molto strette, il che li rende i dispositivi ideali nella realizzazione di sistemi di controllo della frequenza e di orologi. Questa proprietà è stata ampiamente studiata fin dagli anni 20 quando Cady [14] dimostrò che l’effetto piezoelettrico inverso poteva essere utilizzato nella realizzazione di circuiti oscillatori molto stabili.

Anche le applicazioni QCM richiedono che il quarzo oscilli ad una frequenza precisa e stabile. Molti oscillatori pilotano il quarzo facendo uso di un anello di reazione che garantisce una corrente massima attraverso il quarzo rispettando la condizione dell’annullamento della fase. Questa condizione si ha in f = fs , frequenza molto vicina

a fGmax. L’angolosità del picco della conduttanza G fa sì che l’anello di retroazione si

“agganci” in una banda molto stretta di frequenze. La banda e la frequenza di risonanza determinano il fattore di merito Q:

1 2 max 1 2 f f f f f f Q s G − ≈ − = (2.41)

fGmax, può essere usata solo per i quarzi con fattori Q molto alti. Il fattore di merito

dipende anche da R e L, come mostrato nella relazione:

R L f

L’alto valore di Q ( > 105), può essere attribuito ad un alto valore di L e un basso valore di R. Dalle relazioni 2.41 e 2.42, si vede che un aumento di R fa diminuire il Q e di conseguenza aumentare la banda e quindi la stabilità dell’oscillazione.

A titolo di esempio, un tipico quarzo AT-cut da 10 Mhz, come quelli utilizzati in questo lavoro di tesi, presenta un andamento dell’impedenza come in figura 16.2:

Figura 2.17 Grafico dell’impedenza, modulo e fase, di un tipico quarzo AT-cut da 10 Mhz

Valori tipici dei parametri elettrici del circuito equivalente, delle frequenze di risonanza serie e parallelo e di Q possono essere:

• L1 = 0.0149 H • C1 = 0.017 pF • R1 = 20 Ω • C0 = 4 pF • fs = 10000058 Hz • fp = 10021268 Hz • Q = 2πfsL1/R = 46803

2.8.3 Quarzi Nuova Mistral

I quarzi utilizzati in questo lavoro di tesi sono quarzi AT-cut da 10 Mhz, acquistati presso la ditta Nuova Mistral di Latina e aventi le caratteristiche riassunte nella seguente tabella:

Caratteristica Unità di misura Valore

Frequenza nominale Mhz 10.000 Modo fondamentale Tolleranza a 25°C % ± 0.5 (50 Khz) Stabilità termica ppm ± 10 Intervallo di temperatura °C 10 ÷ 40 Capacità di carico C1 pF --- Resistenza R Ω ≤ 22 Capacità di shunt C0 pF 12.8 ± 0.9 Capacità cinematica C1 pF 55.5 ± 20 % Induttanza cinematica mH 4.6 ± 20 % Drive Level (10 Ω) 1 mW Diametro elettrodo mm 7.36 Diametro disco mm 13.97 Spessore disco mm 0.18

Substrato elettrodo Ni/Cr

Elettrodo oro

Bibliografia capitolo 2

[1] Daniel A. Buttry, Michael D. Ward, “Measurement of Interfacial Processes at Electrode Surfaces with the Electrochemical Quartz Crystal Microbalance”, Chem. Rev., 1992, pp. 1355-1379.

[2] Jiří Janata, “Principles of Chemical Sensors”, University of Utah, Salt Lake City, Utah, Plenum Press, New York and London.

[3] Dr. D.C. Stone, “Piezoelectric Sensor”, CHM414, Lecture Notes: http://www.chem.utoronto.ca/coursenotes/CHM414/notes/Section3a.pdf [4] Sauerbrey G. Z., Phys., 1959, pp. 155 – 206.

[5] Cady, W.G., “Piezoelectricity”, Dover: New York, 1964.

[6] Bottom, V.G.. “Introduction To Quartz Crystal Unit Design”, Van Nostrand Reinhold, New York, 1982.

[7] H. Nowotny, E. Benes, General one-dimensiontreatment of the layered piezoelectric resonator with two electrodes, J. Acoust. Soc. Am. 82 (2) 1987, pp. 513-521

[8] E. Benes, M. Groschl, W. Burger, M. Schmid, Sensors based on piezoelectric resonators, Sensors and Actuators A, 48, 1995, pp. 1-21

[9] http://www.vilastic.com/tech3.htm

[10] Physical Acoustic – Principles and Method, edited by W. P. Mason, Vol.1-Part A, Academic Press, New York, 1964

[11] M. A. Tenan, D. M. Soares, The quartz cristal microbalances: a tool for probing viscous/viscoelastic properties of thin films, Brasilian J. Of Physics, 28, (1998), 405 [12] D. M. Soares, M. A. Tenan, S. Walse, Electrochim. Acta, 44, 263 (1998) [13] V. E. Grandstaff, S. J. Martin, J. Appl. Phys., 75, 1319, (1994)