Capitolo 3 Codici di Spreading

(1)

esaminate le sequenze di

1. Walsh-Hadamard (WH), [8];

2. Complementary (CP), [8];

3. Orthogonal Gold (OG), [9];

4. Small Kasami (SK), [10];

5. Shapiro-Rudin (SR), [11].

Le sequenze esaminate sono state modificate secondo la definizione: γ_m(k)=∆

(

c(k)m 0 ≤ m ≤ N/2 − 1

c(k)_m+N −N/2 ≤ m ≤ −1 (3.1)

dove k indica il k-esimo codice. Queste sequenze sono state ottenute scambiando le pri-me N

2 colonne della matrice dei codici con le ultime N

2. La funzione di autocorrelazione

aperiodica per le sequenze di codice modificate é rappresentata dalla seguente espressione A(k)_µ =∆

N/2−1−µ

X

ν=−N/2

(2)

dove l’indice k indica il codice scelto e 0 ≤ µ ≤ N − 1.

Si definisce la funzione di cross-correlazione aperiodica per le sequenze di codice modifi-cate come Xµ(k,k′) ∆ = N/2−1−µ X ν=−N/2 γν(k)γ (k′₎ ν+µ (3.3)

dove k e k′indicano i codici scelti.

3.1 Codici di Walsh-Hadamard (W-H)

I codici di Walsh-Hadamard si ottengono dalle righe (o dalle colonne) di opportune matrici dette di Hadamard. Una matrice di Hadamard di ordine 2n_{con n > 0 si costruisce}

con la seguente procedura ricorsiva:

H₁ ₌h₁i H₂ ₌ " 1 1 1 −1 # H₄ ₌       1 1 1 1 1 −1 1 −1 1 1 −1 −1 1 −1 −1 1       H₂n = " H2n₋₁ H₂n₋₁ H2n₋₁ H¯₂n₋₁ # (3.4) dove ¯H2n₋₁ indica la matrice ottenuta da H₂n₋₁ cambiando il segno di tutti i suoi

ele-menti. L’ordine 2n_{della matrice indica la lunghezza della sequenza di codice. Ad esempio}

le sequenze di codice di lunghezza 4 sono quelle estratte dalle righe (o dalle colonne) della matrice H4. Le quattro sequenze sono quindi

c1 = {+1, +1, +1, +1}

(3)

Figura 3.1: Matrice dei codici di Walsh-Hadamard.

Si possono fare alcune considerazioni riguardo ai codici di W-H:

• hanno lunghezza pari a potenza di 2 e sono in numero pari alla loro lunghezza; • queste sequenze per costruzione hanno tutte un numero di 1 pari al numero di −1 (ad

eccezione della sequenza di tutti 1 ottenuta dalla prima riga della matrice);

• sono utili quando si ha un sistema perfettamente sincrono. I principali inconvenienti di questi codici sono:

• numero limitato di sequenze, pari a 2n_;

• cross-correlazione tra due di esse che può assumere valori significativamente diversi

da 0 quando i due codici non sono allineati;

• non buone proprietà di autocorrelazione di alcune sequenze.

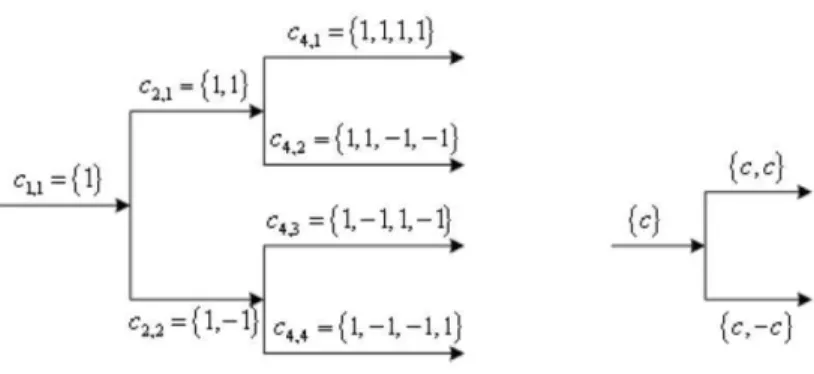
Le sequenze di Walsh appartengono alla famiglia dei codici OVSF (Orthogonal Variable Spreading Factor), cioè a fattore di spreading variabile che consentono di trasmettere a bit-rate diversi cambiando il valore dello spreading factor. Tali codici sono costruiti tramite una struttura ad albero, come quella mostrata in Fig. 3.2 in cui sono rappresentati i codici

(4)

Figura 3.2: Albero per la costruzione dei codici a fattore di spreading variabile.

ci,j, dove i é la lunghezza della sequenza e j é l’indice del codice.

I codici sul grafo ad albero sono gli stessi di quelli della matrice di W-H; le sequenze composte dallo stesso numero di simboli sono quindi ortogonali. Riscrivendo i codici in questo modo si mette in evidenza un’altra importante proprietà che é quella di ortogonalità tra sequenze di lunghezza diversa. Due sequenze di lunghezza diversa, per esempio una pari a 4 e l’altra pari a 2, sono ortogonali tra di loro se dividendo la sequenza più lunga in sottosequenze di lunghezza pari a quella più corta i prodotti interni tra ciascuna delle sottosequenze e la sequenza corta sono nulli. Prendendo una qualunque sequenza ci,j di

lunghezza L, questa é ortogonale a:

• tutte le sequenze della stessa lunghezza L;

• tutte le sequenze di lunghezza L′ _{> L che non sono state generate da essa;}

• tutte le sequenze di lunghezza L′′ _{< L che non sono sul percorso da essa alla radice.}

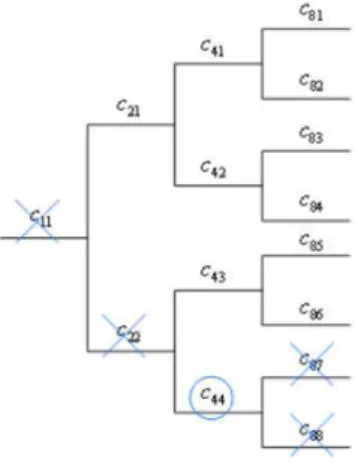
Quindi riferendoci alla Fig. 3.2 e considerando ad esempio la sequenza c4,4 si ha che le

sequenze non ortogonali di lunghezza minore sono c2,2 e c1,1, mentre quelle di lunghezza

maggiore sono c8,7e c8,8 e tutte le sequenze da esse generate. Le rimanenti sequenze sono

ortogonali a c4,4.

(5)

Figura 3.3: Sequenze ortogonali alla c4,4.

3.1.1 Codici di W-H modificati

Le sequenze di codice modificate si ottengono scambiando le prime N

2 colonne della

matrice di Walsh con le ultime N

2. Bisogna tener presente comunque che tutte le proprietà

rimangono invariate anche per le sequenze modificate. Di seguito é rappresentata la matri-ce dei codici per N = 8 modificata secondo la definizione sopra data:

Figura 3.4: Matrice dei codici di W-H modificati.

Si nota che le prime N

2 righe della matrice modificata coincidono con le prime N

2 righe

della matrice di partenza mentre le ultime N

2 coincidono con le ultime N

2 della matrice di

partenza ma scambiate di segno.

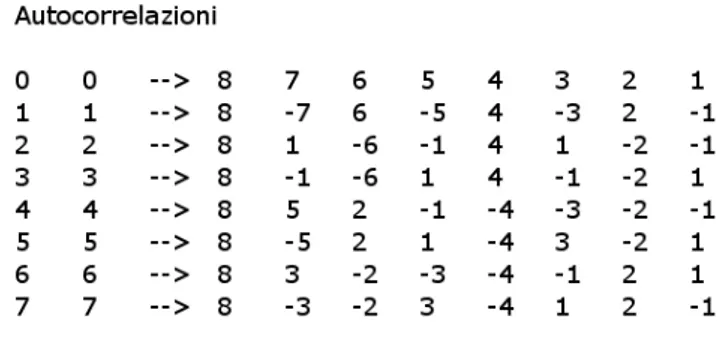
Di seguito é invece riportata la funzione di autocorrelazione aperiodica di tutte le sequenze contenute nella matrice dei codici modificati di dimensione N = 8.

(6)

Figura 3.5: Autocorrelazione aperiodica tra le sequenze di W-H modificate.

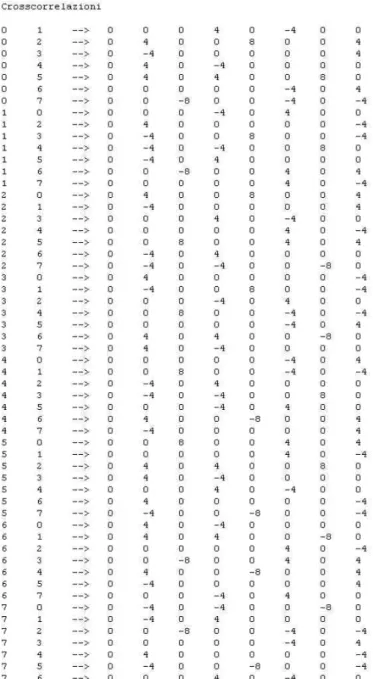
Le autocorrelazioni aperiodiche calcolate in 0 producono il valore massimo che é pari alla dimenzione N della matrice, 8 nel caso rappresentato. Solo la prima sequenza di codice, che é composta da tutti 1, ha un’autocorrelazione aperiodica con valori tutti positivi e decre-scenti fino al valore minimo pari a 1. In Fig. 3.6 é riportata la funzione di cross-correlazione tra tutte le sequenze contenute nella matrice dei codici modificati di dimensione N = 8. É bene mettere in evidenza che:

• tutte le cross correlazioni aperiodiche calcolate in 0 tra due codici differenti sono

nulle in accordo con l’ortogonalità tra due sequenze;

• la cross correlazione aperiodica tra due generiche sequenze i e j é scambiata di segno

(7)

(8)

3.2 Complementary Sequences (CP)

Le sequenze CP si ottengono dalle righe (o dalle colonne) di opportune matrici dette di Golay. Una matrice di Golay di ordine 2n_{, con n > 0, si costruisce secondo la seguente}

procedura ricorsiva: H₁ ₌h₁i H₂ ₌ " 1 1 1 −1 # H₄ ₌       1 1 1 −1 1 −1 1 1 1 1 −1 1 1 −1 −1 −1       H_N ₌ " HN/2 H˜N/2 HN/2 − ˜HN/2 # (3.6) dove ˜HN rappresenta la matrice commutata di HN secondo la seguente regola:

H_N ₌ " A B # ˜ H_N ₌ " B A # (3.7) Per ottenerla é sufficiente scambiare le prime N

2 righe con le seconde N

2 della matrice. É

possibile anche ottenere una forma ricorsiva per la definizione di ˜HN partendo da HN e

dalla matrice commutata:

˜ H_N ₌ " HN/2 − ˜HN/2 HN/2 H˜N/2 # (3.8) Di seguito é riportata la matrice dei codici modificata per N = 8 secondo la definizione data:

Si può verificare facilmente che la matrice di Golay gode della seguente proprietà:

(9)

Figura 3.7: Matrice dei codici CP.

dove HT

N é la trasposta della matrice HN ed IN é la matrice identità di ordine N. Tale

proprietà garantisce l’ortogonalità tra tutte le righe e tra tutte le colonne della matrice, quindi i codici di uguale lunghezza sono ortogonali tra di loro. Si possono fare ulteriori considerazioni riguardo ai codici di Golay:

• hanno lunghezza pari a potenze di 2 e sono in numero pari alla loro lunghezza; • queste sequenze per costruzione non hanno un numero di 1 uguale al numero di −1

come abbiamo visto per le sequenze di Walsh;

• sono utili quando abbiamo un sistema perfettamente sincrono.

I principali inconvenienti per questi codici sono invece:

• il numero limitato di sequenze, pari a 2n_;

• non consentono di usare un bit-rate variabile.

Lo svantaggio di non poter usare un bit-rate variabile pone molti vincoli sull’allocazione degli utenti, infatti, nel caso in cui un utente utilizzi un fattore di spreading pari a 2 si ha che tutti i codici con SF maggiore di 2 non sono ortogonali a quello usato e pertanto l’allocazione massima di utenti é pari a 2. Questo rappresenta il principale vincolo che ci porta a preferire le sequenze di Walsh anche se hanno proprietà di auto e cross-correlazione peggiori rispetto alle complementari.

(10)

3.2.1 Sequenze CP modificate

2 colonne della

matrice di Golay con le ultime N

2. Bisogna tener presente comunque che tutte le proprietà

rimangono invariate anche per le sequenze modificate. Di seguito é rappresentata la matrice dei codici per N = 8 modificata secondo la definizione data precedentemente:

Figura 3.8: Matrice dei codici CP modificati.

Nella Fig. 3.9 é riportata la funzione di autocorrelazione aperiodica di tutte le sequenze contenute nella matrice dei codici modificati di dimensione N = 8.

Figura 3.9: Autocorrelazione aperiodica dei codici CP modificati.

Le autocorrelazioni calcolate in 0 producono il valore massimo pari alla dimensione N della matrice che nel nostro caso é 8.

In Fig. 3.10 é riportata la funzione di cross correlazione aperiodica tra tutte le sequenze contenute nella matrice dei codici modificati di dimensione N = 8.

(11)

(12)

3.3 Codici Orthogonal Gold

Andiamo ora ad analizzare i codici di Gold.

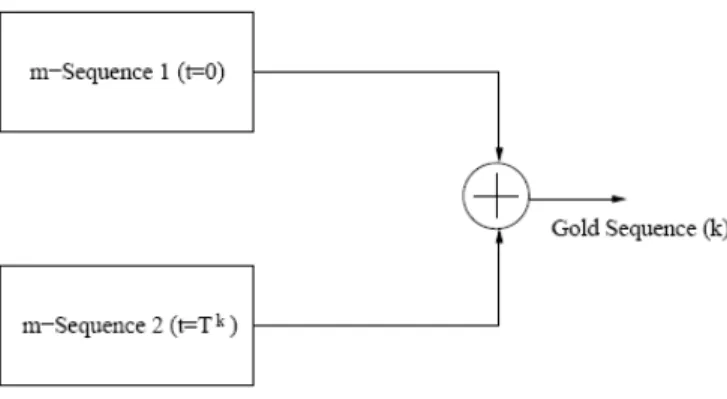
Le sequenze di Gold sono generate tramite l’operazione di somma modulo 2 di due diffe-renti m-sequences della stessa lunghezza [10]. In Fig. 3.11 é rappresentato il diagramma a blocchi del generatore di una sequenza di Gold.

Figura 3.11: Diagramma a blocchi di un tipico generatore di sequenze di Gold.

Le due m-sequences sono in grado di generare una famiglia di codici a prodotto non mas-simo, ma una sequenza maximal length preferita può solo produrre codici di Gold [12]. Quindi é necessario trovare una coppia di sequenze maximal length preferite per definire un set di sequenze di Gold.

Siccome entrambe le m-sequences hanno la stessa lunghezza N, anche la sequenza di Gold generata é di lunghezza N. Data una coppia di sequenze preferite, le sequenze di Gold sono generate tramite la somma modulo 2 della prima con la versione shiftata della secon-da o vice versa. Per un periodo di N = 2n_{− 1 ci sono N possibili spostamenti circolari.}

Così facendo si possono ottenere N sequenze partendo da due sequenze maximal length preferite, che vengono chiamate sequenze di Gold.

Consideriamo una m-sequence rappresentata da un vettore binario u di lunghezza N, e una seconda sequenza v ottenuta prelevando ogni q-esimo simbolo di u. In altre parole, v = u [q], dove q é dispari e uguale a q = 2k_{+ 1.}

Due m-sequences u e v sono chiamate la coppia preferita se

(13)

G_{(u, v) =}_{©u, v, u ⊕ v, u ⊕ T · v, u ⊕ T}2_{· v, . . . , u ⊕ T}N −1_{· v}ª

(3.12) dove T é l’operatore di shift ciclico e ⊕ é l’operazione di XOR.

Le proprietà di autocorrelazione dei codici di Gold non sono tanto buone quanto quelle delle sequenze maximal length. A parte le due sequenze originali, tutte le altre non sono m-sequences; quindi la funzione di autocorrelazione non assume solo due valori.

Il set di sequenze di Gold ha tre valori per lo spettro dell’autocorrelazione, ma queste sequenze forniscono maggiore sicurezza paragonate alle m-sequences.

La funzione di autocorrelazione rxx(τ ) e la funzione di cross-correlazione rxy(τ ) per le

sequenze di Gold possono essere definite come rxx(τ ) =    1 per τ = 0 n −t(n)_N , −_N1,t(n)−2_N o per τ 6= 0 (3.13) rxy(τ ) = ½ −t(n) N , − 1 N, t(n) − 2 N ¾ (3.14) dove t(n) = ( 1 + 2n+1 2 per n dispari 1 + 2n+22 per n pari (3.15) Il valore di picco per la correlazione delle sequenze di Gold é t(n)

N e dalle precedenti

equa-zioni, sequenze di Gold con valori dispari della lunghezza LFSR hanno valori di correla-zione minori paragonati a quelli ottenuti con valori pari di n, nonostante il valore di t(n) per valori pari di n é minore.

Un problema nell’utilizzare le sequenze di Gold é quello che la loro lunghezza é pari a N = 2n_{− 1. Per rendere tali sequenze di lunghezza pari ad una potenza di 2 si inserisce}

(14)

codici Orthogonal Gold.

I valori e le proprietà di correlazione di queste sequenze di Gold ortogonali sono molto simili a quelli dei codici di Gold originali.

Di seguito é riportata la matrice dei codici di Gold per N = 8:

Figura 3.12: Matrice dei codici di Gold.

3.3.1 Codici Orthogonal Gold Modificati

2 colonne della

matrice dei codici Orthogonal Gold con le ultime N

2. Bisogna tener presente comunque

che tutte le proprietà rimangono invariate anche per le sequenze modificate. Di seguito é rappresentata la matrice dei codici per N = 8 modificata secondo la definizione 3.1.

Figura 3.13: Matrice dei codici di Gold modificati.

(15)

(16)

3.4 Codici Kasami

Le sequenze Kasami sono sequenze Pseudo Noise (PN) di lunghezza N = 2n_{− 1, dove}

n é il grado del polinomio primitivo usato per generare le sequenze di Kasami e queste sequenze sono definite per valori pari di n [10].

Ci sono due classi di sequenze di Kasami:

1. il set Small Kasami;

2. il set Large Kasami.

3.4.1 Small Set delle Sequenze di Kasami

Il set Small Kasami é ottimo nel senso di uguagliare il lower bound di Welch per quanto riguarda le funzioni di correlazione. Un set di sequenze Small Kasami é un set di 2n

2

sequenze binarie ognuna di lunghezza N = 2n_{− 1, dove n é il grado più alto del polinomio}

primitivo usato per generare il set ed é di lunghezza pari. Il grado del polinomio di secondo ordine usato per generare il set Small Kasami é n

2. Sia u una m-sequence di lunghezza N

generata da un polinomio primitivo di lunghezza n, e sia w la sequenza ottenuta decimando u per 2n

2 + 1. Il set Small Kasami é quindi definito come:

K_s_{(u) =}n_{u, u ⊕ w, u ⊕ T · w, u ⊕ T}2_{· v, . . . , u ⊕ T}2

n 2₋₂

· vo (3.16)

La sequenza w ottenuta decimando la m-sequence u per 2n

2 + 1 é ancora una m-sequence di

lunghezza 2n

2 − 1, generata da un polinomio primitivo di grado n

2. In modo simile ai codici

di Gold, la funzione di correlazione può assumere tre valori. La funzione di correlazione per le sequenze assume i valori {−1, −s(n), s(n) − 2}, dove s(n) = 2n

2 + 1.

La funzione di autocorrelazione per il set di sequenze Small Kasami é definita come:

rxx(τ ) =    1 per τ = 0 n −s(n)_N , −_N1,s(n)−2_N o per τ 6= 0 (3.17)

(17)

relazione delle sequenze. Il nuovo set di sequenze così ottenuto é chiamato Large Kasami. Questo contiene un alto numero di sequenze paragonato ai codici di Gold, ma allo stesso tempo queste sequenze hanno molti valori di correlazione rispetto a quelli assunti dalle sequenze di Gold. Il set Large Kasami contiene tutte le sequenze del set Small Kasami insieme ai codici di Gold. Per mod(n, 4) = 2 i codici Large Kasami sono definiti come segue.

Sia v la sequenza ottenuta decimando la sequenza u per t(n). Il set dei codici Large Kasami é allora definito come:

La funzione di correlazione per tali sequenze assume i valori

{−t(n), −s(n), −1, s(n) − 2, t(n) − 2}. Il valore massimo della funzione di correlazione é t(n) che é uguale a quello per sequenze di Gold per valori pari di n, mentre per valori dispari di n le sequenze di Gold assumono valori di correlazione più bassi rispetto a quelli assunti dalle sequenze Large Kasami.

Nella tabella in Fig. 3.16 sono riportati il numero di sequenze appartenenti ad un set e la lunghezza di queste sequenze [14].

Le matrici di codici usate sono state ricavate dal set Small Kasami estraendo dalla matrice rettangolare originale una matrice quadrata dove il numero di sequenze e la loro lunghezza sono uguali e pari ad una potenza di 2. É di seguito riportata la matrice dei codici di dimensione 8 × 8.

(18)

Figura 3.16: Numero di sequenze per i due set di codici Kasami.

Figura 3.17: Matrice dei codici di Kasami.

3.4.3 Codici di Kasami Modificati

2 colonne della

matrice dei codici di Kasami con le ultimeN

2. Bisogna tener presente comunque che tutte le

proprietà rimangono invariate anche per le sequenze modificate. Di seguito é rappresentata la matrice dei codici per N = 8 modificata secondo la definizione 3.1.

(19)

Figura 3.18: Matrice dei codici di Kasami modificati.

(20)

(21)

11 111 − 1 111 − 111 − 11

111 − 111 − 11111 − 1 − 1 − 11 − 1

111 − 111 − 11111 − 1 − 1 − 11 − 1111 − 111 − 11 − 1 − 1 − 1111 − 11 (3.19) Siamo però interessati ad ottenere non una singola sequenza di una data lunghezza, ma piuttosto un set di sequenze di numero pari alla loro lunghezza, così da avere una matrice quadrata del tipo 2j _{× 2}j _{con j = 1, 2, 3, . . . . Per ottenere quanto detto utilizziamo la}

trasformata simmetrica di Shapiro-Rudin (SRT) [11]. Per costruire tale matrici si utiliz-za sempre un processo iterativo che ha inizio dalla conoscenutiliz-za della matrice minima di dimensioni 2 × 2 qui di seguito riportata.

"

1 1

1 −1 #

(3.20) Il processo per ottenere la matrice di dimensioni 4 × 4 é di seguito spiegato:

• Copiare la prima riga della matrice 2 × 2 nelle prime 2 colonne delle prime 2 righe e nelle ultime 2 colonne delle ultime 2 righe della matrice 4 × 4;

• Copiare la seconda riga della matrice 2 × 2 nelle ultime 2 colonne della prima riga e nelle prime 2 colonne della terza della matrice 4 × 4;

• Copiare la seconda riga della matrice 2 × 2 cambiata di segno nelle ultime 2 colonne della seconda riga e nelle prime 2 colonne della quarta della matrice 4 × 4.

(22)

Così facendo otteniamo:       1 1 1 −1 1 1 −1 1 1 −1 1 1 −1 1 1 1       (3.21)

Per generalizzare il processo di costruzione iterativo bisogna applicare lo stesso procedi-mento descritto in precedenza a tutte le altre righe della matrice 2j _{× 2}j _{fin quando non}

vengono prese tutte in considerazione. Tali righe vengono inserite, in modo sequenzia-le e con meccanismo analogo a quello descritto, nelsequenzia-le righe ancora vuote della matrice 2j+1_{× 2}j+1_{. Il numero di iterazioni che bisogna compiere é pari ad un quarto dell’ordine}

della matrice che si vuole costruire: ad esempio per la matrice 8 × 8 bisogna ripetere il processo iterativo 2 volte. Avendo generalizzato così il processo di costruzione, si possono ottenere matrici di Shapiro-Rudin della dimensione voluta. É riportata di seguito la matrice 8 × 8:                  1 1 1 −1 1 1 −1 1 1 1 1 −1 −1 −1 1 −1 1 1 −1 1 1 1 1 −1 −1 −1 1 −1 1 1 1 −1 1 −1 1 1 −1 1 1 1 1 −1 1 1 1 −1 −1 −1 −1 1 1 1 1 −1 1 1 1 −1 −1 −1 1 −1 1 1                  (3.22)

Tutte le righe (e le colonne) nelle matrici simmetriche ottenute sono mutualmente ortogo-nali

3.5.1 Codici di Shapiro-Rudin Modificati

2 colonne della

matrice dei codici di Shapiro-Rudin con le ultime N

2. Bisogna tener presente comunque

che tutte le proprietà rimangono invariate anche per le sequenze modificate.

Di seguito é rappresentata la matrice dei codici per N = 8 modificata secondo la definizione 3.1.

(23)

Figura 3.21: Matrice dei codici di Shapiro-Rudin modificati.

Nella Fig. 3.22 é riportata la funzione di autocorrelazione aperiodica di tutte le sequen-ze contenute nella matrice dei codici modificati di dimensione N = 8.

Figura 3.22: Autocorrelazione aperiodica dei codici di Shapiro-Rudin modificati.

(24)