Capitolo 1 Monitoraggio delle prestazioni

 

Capitolo 1 

 

Monitoraggio delle prestazioni 

 

1.1  Problematiche generali 

 

1.1.1  Monitoraggio dei sistemi controllati 

 

Il  monitoraggio  automatico  delle  prestazioni  dei  sistemi  controllati  (CLPM,  Control  Loop  Performance  Monitoring),  è  una  problematica  importante  per  ottimizzare le operazioni di un processo industriale. Vista la crescente complessità  e automazione dei moderni impianti, il numero degli anelli di regolazione che gli  operatori  devono  monitorare  è  considerevolmente  aumentato.  Il  tempo  che  un  operatore  può  dedicare  ad  ogni  loop  di  controllo  è  limitato,  per  cui  è  utile  poter  eseguire  un  monitoraggio  automatico  per  vedere  di  quanto  le  prestazioni  si  discostano dall’ottimale. 

Il  monitoraggio  automatico  consente,  inoltre,  di  realizzare  una  manutenzione  preventiva, che permette di ridurre i costi di esercizio dell’impianto. 

 

Un  impianto  dovrebbe  essere  gestito  in  modo  ottimale  per  poter  effettuare un  controllo  sulla  qualità  dei  prodotti  finali,  per  minimizzare  i  consumi  energetici  e  per  ridurre  le  emissioni  di  inquinanti.  A  livello  accademico  ci  sono  ancora  degli  aspetti non risolti, come la definizione e l’efficienza di indici di prestazione, utili a  determinare in modo  chiaro gli anelli di regolazione caratterizzati da prestazioni  scarse,  l’identificazione  dei  processi  e  dei  disturbi  e  l’estensione  dei  problemi  di  ottimizzazione a sistemi più complessi. 

Un  deterioramento  delle  prestazioni  nel  controllo  di  processo  si  manifesta  spesso  con  delle  oscillazioni  della  variabile  controllata.  Un  sistema  si  può  comportare  in  modo  non  ottimale  per  cause  diverse:  progetto  o  sintonizzazione  non  corretta  dei  regolatori,  presenza  di  attrito  negli  attuatori,  perturbazioni  esterne,  presenza  di  interazione  tra  gli  anelli  di  controllo.  Sugli  impianti  è  tipico  trovare dei regolatori sintonizzati, in modo cautelativo, rispetto alla situazione più  critica in cui possono trovarsi, così da avere un controllo eccessivamente robusto.  Un approccio di questo tipo è sicuramente lontano dall’ottica di ottimizzazione in  cui si vorrebbe lavorare, dato che si ottiene una risposta troppo lenta. Al contrario,  se  un  regolatore  è  sintonizzato  in  modo  da  fornire  un’azione  di  controllo  troppo  aggressiva  si  otterrà  una  risposta  eccessivamente  oscillante  con  eventuale  usura  degli  attuatori.  La  causa  più  comune  di  una  prestazione  scarsa  degli  anelli  di  regolazione  è  comunque  dovuta  alla  presenza  di  attrito  negli  attuatori  (generalmente  valvole  di  regolazione).  Questo  fenomeno  causa  ritardo  e  rallentamento  nell’attuazione  delle  modifiche  richieste  dal  regolatore,  con  possibilità  di  blocco  dell’azione  correttiva.  Per  esempio  si  ritiene  che  circa  il  30%  degli  anelli  di  regolazione  presenti  negli  impianti  di  produzione  della  carta  oscillino per problemi alle valvole ([6], [7]). 

 

Il monitoraggio automatico delle prestazioni dei sistemi di controllo ha quindi  l’obiettivo di scoprire quali anelli di regolazione lavorano lontano dalle condizioni  ottimali,  perché  caratterizzati  da  una  risposta  troppo  oscillante  o  troppo  lenta,  capirne  le  cause  analizzando  i  dati  provenienti  dagli  impianti  e  fornire  agli  operatori dei suggerimenti per migliorarne il comportamento. 

 

1.1.2  Sistemi di controllo 

 

Per  controllare  i  processi  di  una  larga  tipologia  di  impianti,  dove  ci  possono  essere centinaia di anelli di regolazione, vengono utilizzati dei Sistemi di Controllo  Distribuiti  (DCS)  commerciali.  Esistono  vari  produttori  che  offrono  DCS  con  diverse  caratteristiche,  tra  questi:  la  Bailey,  la  Emerson‐Fisher,  la  Foxboro  e  la  Honeywell.  Un  generico  sistema  di  controllo  distribuito  deve  essere  flessibile,  ovvero facile da configurare e da modificare, e deve essere in grado di comandare  un numero elevato di anelli di controllo. Un DCS comprende un numero elevato  di anelli di regolazione operanti sulle singole variabili di processo, che sono gestiti  da  sistemi  di  controllo  a  livello  superiore  con  funzione  di  supervisione  e  ottimizzazione.  Tra  i  diversi  componenti  viene  realizzato  un  intenso  scambio  di  dati,  trasferendo  informazioni  sullo  stato  del  processo  e  sulle  modifiche  da  effettuare  (set‐point,  parametri  del  regolatore,  ecc…).  Da  un  punto  di  vista  prettamente  informatico  un  DCS  consiste  in  un  certo  numero  di  nodi  basati  su 

microprocessori  che  sono  interconnessi  da  una  rete  di  comunicazione  digitale,  spesso chiamata autostrada dei dati (Field Bus). Le funzioni di controllo dei processi  possono essere distribuite funzionalmente e/o geograficamente. Una distribuzione  funzionale permette di raggruppare e implementare funzioni di controllo collegate  in  un  singolo  nodo.  Una  distribuzione  geografica,  invece,  permette  ai  nodi  del  controllo di processo di essere fisicamente posizionati vicino alle apparecchiature  messe  sotto  controllo.  Dato  che  i  nodi  all’interno  del  DCS  sono  collegati  tra  loro  attraverso  una  connessione  veloce,  questi  possono  essere  fisicamente  separati  da  centinaia di metri. 

 

Gli elementi di un generico DCS sono illustrati in figura 1.1. Un numero elevato  di  computer  locali  sono  connessi  al  processo:  ognuno  di  essi  è  responsabile  del  rilevamento di alcuni processi e di una parte dell’azione di controllo locale. Questi  riportano  i  risultati  delle  misurazioni  e  dell’azione  di  controllo  imposta  ad  altri  computer  attraverso  l’autostrada  di  dati.  L’autostrada  rende  poi  disponibili  le  informazioni agli schermi delle varie postazioni di controllo degli operatori, invia  nuovi  dati,  richiama  dati  storici  dall’archivio  e  connette  il  computer  di  controllo  principale  alle  altre  parti  della  rete.  Un  computer  di  supervisione  è,  invece,  responsabile di funzioni ad alto livello, come l’ottimizzazione delle operazioni di  processo su vari orizzonti di tempo (giorni, settimane o mesi) e lo svolgimento di  speciali  procedure  di  controllo  all’avviamento  e  alla  fermata  degli  impianti.  Il  collegamento  dati  tra  il  computer  di  supervisione  e  il  computer  di  controllo  principale  ha  generalmente  prestazioni  inferiori  rispetto  a  quello  dell’autostrada,  perché qui vengono trasferiti dati con scansione meno frequente.        fig. 1. 1: Elementi di un generico sistema di controllo distribuito.       

Normalmente su un DCS è prevista una certa ridondanza. Infatti esistono due  autostrade dei dati indipendenti, ovvero due nodi vicini sono collegati da due cavi  diversi. Questo per evitare di non poter effettuare un trasferimento di dati in caso  di  interruzione  sull’autostrada  dei  dati.  Un  alternativa  è  quella  di  avere  un’autostrada di dati fatta ad anello, in modo che l’informazione possa passare in  entrambe le direzioni, sopperendo così ad una possibile interruzione. 

Sono  anche  previste  più  postazioni  di  controllo  operatore  in  modo  da  ridurre  l’impatto del malfunzionamento di una di queste. 

 

Un DCS come quello mostrato in figura 1.1 permette agli operatori un accesso  immediato  ad  una  grande  quantità  di  informazioni  dall’autostrada  di  dati  e  consente  di  visualizzare  le  vecchie  condizioni  di  un  processo  richiamando  i  dati  dall’archivio.  Si  possono,  perciò,  utilizzare  i  dati  provenienti  dagli  impianti  per  decidere  la  strategia  di  controllo,  andando  ad  aggiustare  i  parametri  dei  controllori. 

 

1.1.3  Implementazione 

 

L’implementazione  di  una  tecnica  di  monitoraggio  assume  differenti  caratteristiche  in  base  al  tipo  di  funzionamento  adottato.  In  caso  di  applicazione  sul DCS (sul computer principale o su quello di supervisione) c’è la possibilità di  mettere  sotto  controllo  in  tempo  reale  gli  anelli  di  regolazione;  in  questo  caso  si  parla di applicazione on‐line. Esistono, però, dei vincoli restrittivi legati al tempo  di  calcolo,  allo  spazio  occupato  sulla  memoria,  al  traffico  di  dati  generato  e  alle  interazioni con l’operatore. L’alternativa è quella di utilizzare un sistema applicato  in  modo  off‐line,  in  cui  i  dati  dei  loop  da  monitorare  vengono  acquisiti  su  un  computer  esterno  per  poi  essere  analizzati  in  seguito.  In  questo  caso  i  risultati  dell’analisi sono disponibili con un certo ritardo rispetto al tempo in cui sono stati  registrati, ma sono ottenuti con vincoli meno restrittivi. 

 

In generale, comunque, è desiderabile che un’applicazione per il monitoraggio  delle prestazioni sia semplice da capire, rapida da applicare, non intrusiva e dotata  di  una  certa  flessibilità,  che  permetta  di  poterla  applicare  a  diverse  tipologie  d’impianto.         

 

1.2 Indici di prestazione 

 

Per  individuare  i  circuiti  di  controllo  caratterizzati  da  scarsa  prestazione  è  necessario stabilire opportuni criteri basati su indici, generalmente normalizzati su  un  intervallo.  Gli  indici  di  prestazione  hanno  lo  scopo  di  rendere  questa  analisi  oggettiva,  sfruttando  i  dati  disponibili  sul  sistema  di  controllo  e  fornendo  dei  criteri  di  valutazione  della  risposta  non  qualitativi.  L’obiettivo  è  quello  di  individuare  le  risposte  troppo  lente,  caratterizzate  da  un  tuning  del  regolatore  troppo  blando,  e  le  risposte  eccessivamente  oscillanti,  indice  della  possibile  presenza di fenomeni di attrito, di disturbi esterni o di interazione tra gli anelli, o  dovute ad una sintonizzazione del regolatore troppo aggressiva. 

 

In  seguito  verranno  illustrati  un  indice  per  individuare  una  risposta  eccessivamente lenta [8] e una tecnica di analisi per individuare risposte oscillanti  [9],  entrambi  utili  a  caratterizzare  sollecitazioni  deterministiche  in  ingresso  al  sistema.  Considerando,  invece,  una  sollecitazione  di  tipo  stocastico  è  possibile  definire  un  indice  di  prestazione  che  ha  come  obiettivo  la  minimizzazione  della  varianza della variabile controllata [10]. 

 

1.2.1  Idle Index 

 

In generale si vorrebbe che un regolatore riuscisse a realizzare risposte veloci e  poco  oscillanti.  Il  tuning  dei  parametri  viene  fatto  in  base  allo  scopo  per  cui  è  progettato il regolatore: si cerca di ottimizzare o l’inseguimento del riferimento o  l’abbattimento dei disturbi in ingresso al sistema. Dato che durante la marcia di un  impianto  le  variazioni  di  set‐point  sulle  variabili  principali  sono  meno  frequenti  rispetto  alle  perturbazioni  esterne  è  utile  analizzare  il  comportamento  dei  regolatori sulla base della risposta ad un disturbo. 

 

Al fine di valutare la velocità di abbattimento di un disturbo è stato proposto da  Hägglund (1999) un indice di prestazione denominato Idle Index, ovvero un indice  di  lentezza.  Questo  indice  si  basa  sull’andamento  del  gradiente  della  variabile  controllata y

( )

t e del segnale di controllo u

( )

t . 

 

Assumiamo che il guadagno del processo sia conosciuto e che, per semplicità,  sia  positivo.  Per  prima  cosa  è  necessario  definire  due  parametri:  ,  somma  di  tutti  gli  interavalli  di  tempo  in  cui  il  prodotto  tra  i  gradienti  della  variabile  controllata  e  di  quella  manipolata  è  positivo,  e  ,  somma  degli  interavalli  di 

pos

t

neg

tempo  in  cui  tale  prodotto  è  negativo.  Indicando  con    il  tempo  di  campionamento è possibile calcolare i due tempi caratteristici ad ogni istante:  h   ⎩ ⎨ ⎧ + = pos pos pos _t h t t     se se 0 0 ≤ ∆ ∆ > ∆ ∆ u y u y        (1.1)    ⎩ ⎨ ⎧ + = neg neg neg t h t t     se se 0 0 ≥ ∆ ∆ < ∆ ∆ u y u y        (1.2)    L’Idle Index viene quindi definito come:    neg pos neg pos I t t t t I + − =       (1.3)   

Il  termine  al  denominatore  è  necessario  per  normalizzare  l’indice,  per  cui  è 

compreso nell’intervallo [‐1,1] essendo   e   compresi tra zero e +∞. Per una 

risposta  molto  lenta  e  quindi  l’Idle  Index  assume  valori  prossimi  ad  1. 

Per una risposta molto veloce, invece,   e l’indice assume valori prossimi 

a  ‐1.  Hägglund  propone  di  accettare  risposte  con  un  Idle  Index  compreso  nell’intervallo [‐0.4,0.4] perché sopra il limite superiore la risposta è troppo lenta e  sotto  il  limite  inferiore  la  risposta  è  molto  veloce  e  quindi  in  genere  molto  oscillante.  pos t t_neg neg pos t t >> pos neg t t >>   La valutazione di questo indice è problematica nel caso di presenza di rumore  di  fondo,  poiché  esso  causa  variazione  del  gradiente  sia  dell’azione  di  controllo  che della variabile controllata. Inoltre, essendo il rumore della strumentazione di  tipo probabilistico, la sua influenza sull’Idle Index non è facilmente determinabile  e  modellizzabile.  Infatti,  il  prodotto  del  gradiente  della  variabile  controllata  e  di  quello  del  segnale  di  controllo  subisce  un  continuo  cambio  di  segno  per  effetto  della  componente  probabilistica  legata  al  rumore.  Questo  fenomeno  influenza  pesantemente  il  calcolo  dei  due  tempi  caratteristici  necessari  alla  valutazione  dell’indice,  fornendo  un  risultato  falsato.  Questo  indice,  quindi,  è  ritenuto  poco  utile ed è necessario ricercare un indice più affidabile.         

 

1.2.2  Test di Hägglund 

 

Questo  test  [9]  permette  di  caratterizzare  le  oscillazioni  di  una  risposta  con  l’obiettivo di individuare le oscillazioni significative, andando poi a vedere quali  tra queste sono anche persistenti. Questa tecnica è stata costruita al fine di ottenere  una procedura automatizzata per individuare quando le prestazioni di un circuito  di controllo si stanno deteriorando per l’insorgere di pendolazioni persistenti. 

 

Le  ragioni  per  cui  un  circuito  di  controllo  può  causare  una  forte  oscillazione  sulla  variabile  controllata  sono  sostanzialmente  tre.  La  prima  causa  è  legata  al  tuning errato dei parametri del regolatore, che così viene spinto verso un’eccessiva  azione  di  controllo.  Una  sintonizzazione  inadeguata  può  essere  dovuta  ad  una  errata identificazione del processo, ad errori dovuti all’operatore stesso oppure a  cambiamenti  nella  dinamica  del  processo.  La  seconda  causa,  invece,  è  legata  alla  presenza  di  attrito  sullo  stelo  dell’attuatore.  Questo  fenomeno  genera  tipici  andamenti non lineari e la forma d’onda dell’oscillazione è molto lontana da una  sinusoide. La terza ed ultima causa, infine, è legata all’ingresso di un disturbo nel  sistema.  Accanto  a  queste  cause  risulta  importante  rilevare  la  presenza  di  interazione  tra  gli  anelli  di  controllo:  a  causa  dell’interazione,  infatti,  si  possono  osservare oscillazioni nell’andamento di una variabile controllata anche se l’anello  a cui appartiene non è direttamente affetto dalla causa di cattiva prestazione. 

 

Si  può  considerare  significativa  una  oscillazione  in  base  a  quanto  la  variabile  controllata  PV  si  discosta  dal  set‐point  SP  e  per  quanto  tempo  dura  tale  scostamento.  Per  poter  valutare  la  significatività  di  una  oscillazione  è  opportuno  anche  fissare  l’entità  degli  scostamenti  ritenuti  accettabili,  facendo  riferimento  al  range  di  controllo  della  valvola  che  va  ad  attuare  le  modifiche  calcolate  dal  regolatore. La procedura si basa sul valore assoluto dell’errore e=SP−PV ; viene  valutato lo IAE tra due tempi successivi ti e ti+1 in cui si attraversa lo zero: 

 

( )

t dt e IAE i i t t

∫

+ = 1        (1.4)    Per utilizzare l’indice riportato nell’equazione 1.4 è necessario che il regolatore  abbia azione integrale in modo tale che l’errore oscilli intorno allo zero.    Si considerano significative quelle oscillazioni il cui IAE supera un certo limite, 

indicato  con    che  ora  andremo  a  definire.  Si  suppone  che  l’errore  abbia  le 

caratteristiche di onda puramente sinusoidale con ampiezza a e frequenza w. Con 

questa  scelta  l’errore  commesso  per  ogni  oscillazione  della  risposta  deve  essere 

lim

paragonato  a  quello  di  metà  periodo  dell’onda  sinusoidale  descritta.  Il  valore  di  riferimento è perciò:   

( )

u a dt t asen IAE ω ω ω π/ ₂ 0 lim =

∫

=       (1.5)   

Con  questa  procedura  devono  essere  individuate  oscillazioni  che  hanno  frequenza  bassa  o  media  ma  non  elevata,  così  da  escludere  tutte  le  oscillazioni  legate  al  rumore  della  strumentazione.  Come  possibile  limite  si  può  considerare  quello  della  frequenza  ultima  del  sistema  ω_u,  in  modo  da  rilevare  tutte  le  oscillazioni con frequenza minore. 

La  scelta  dell’ampiezza  dell’onda  sinusoidale  di  riferimento,  invece,  dipende  dal  range  di  controllo  del  sistema,  in  modo  tale  da  pesare  l’oscillazione  da  analizzare. L’errore limite, quindi, diventa:    u aRangeCTRL IAE ω 2 lim =        (1.6)    L’unico parametro da scegliere per questo test rimane l’ampiezza a; Hägglund  propone come scelta ragionevole un valore dell’1%.   

La  frequenza  ultima  del  sistema  è  sconosciuta  a  meno  che  non  si  abbia  a  disposizione  un  modello  del  sistema.  Se  il  regolatore  è  sintonizzato  in  base  a  regole  che  non  richiedono  la  conoscenza  di ω   l’unica  informazione  sul  tempo _u caratteristico  del  sistema  è  l’azione  integrale  τ_i  del  regolatore  stesso.  Di  conseguenza,  se  il  regolatore  PI(D)  è  sintonizzato  adeguatamente,  la  costante  di  tempo integrale deve essere dello stesso ordine di grandezza (si ricordino le regole  di  sintonizzazione  di  Zigler‐Nichols)  della  pulsazione  ultima  ,  che  può  essere  riportata in funzione di  u P i ω :    i u P ω π 2 =        (1.7)   

È quindi possibile dare una stima dello IAE_lim:    i aRangeCTRL IAE ω 2 lim =        con  i i _τ π ω = 2        (1.8)         

Per ogni oscillazione, quindi, si calcola il valore di IAE e si confronta col valore 

di  riferimento  :  se    si  ha  un’oscillazione  anomala,  mentre  se 

  l’oscillazione  rientra  nella  norma  ed  è  associabile  alla  presenza  di  rumore  sulla  strumentazione.  Naturalmente  quando  l’errore  cambia  segno  inizia  una nuova oscillazione e lo IAE parte nuovamente da zero. 

lim

IAE IAE >IAE_lim

lim

IAE IAE <

 

A  noi,  però,  interessa  individuare  quelle  oscillazioni  anomale  che  sono  persistenti, così da evitare la segnalazione di anomalie isolate. Si fissa, perciò, un  intervallo di tempo di supervisione Tsup nel quale eseguire l’analisi. Se il numero 

di  oscillazioni  supera  un  determinato  limite    durante  questo  periodo,  la  prestazione  dell’anello  di  regolazione  è  considerata  scadente  per  la  presenza  di  una  risposta  troppo  oscillante.  E’  necessario  stabilire  un  tempo  di  supervisione  adeguato, sufficientemente lungo da permettere la stabilizzazione della risposta in  modo da individuare tutte le oscillazioni significative che la compongono:  lim n   2 lim sup u P n T ≥        (1.9)   

La  pulsazione  ultima  del  sistema    viene  divisa  per  due  poiché  con  questa  analisi si considera una oscillazione per ogni mezzo periodo dell’onda sinusoidale. 

Hägglund  ha  proposto  come  scelta  adeguata  un  valore  di  .  In  questo 

modo il tempo di supervisione risulta essere cinque volte la pulsazione ultima del  sistema.  Per  essere  sicuri  di  identificare  anche  oscillazioni  con  un  periodo  significativamente  più  grande  di    si  utilizza  un  tempo  di  supervisione  dieci  volte maggiore, per cui:  u P 10 lim = n u P   u P Tsup =50       (1.10)    Anche in questo caso, se la pulsazione ultima del processo non è conosciuta il  tempo  di  supervisione  viene  legato  alla  costante  di  tempo  di  integrale  del  regolatore: 

 

i

Tsup =50τ       (1.11)   

La  procedura  così  descritta  è  di  difficile  applicazione,  poiché  non  si  hanno  informazioni sulla durata di ogni oscillazione. Si introduce, quindi, un parametro  γ , legato al tempo di campionamento h e al tempo di supervisione:    sup 1 T h − = γ        (1.12) 

In  questo  modo  è  possibile  utilizzare  una  procedura  ad  ogni  istante  di  campionamento k, andando a calcolare una variabile x:   

(

k

)

x

( )

k load x +1 =γ +       (1.13)    dove il parametro load assume valore uno se l’oscillazione è anomala (e quindi se  ),  mentre  ha  valore  zero  in  caso  contrario.  E’  da  sottolineare  che  se  una  oscillazione  è  anomala,  load  assume  valore  uno  solo  al  tempo  di 

campionamento in cui si scopre  , e per il resto dell’oscillazione torna  ad avere valore zero. Il parametro  lim IAE IAE > lim IAE IAE > γ , sempre minore di uno, smorza il parametro  x, così da mettere in conto la durata di ogni oscillazione. Questa analisi si esegue 

per  la  durata  del  tempo  di  supervisione.  Se  alla  fine  di  questo  la  variabile  x  ha  superato il numero limite di oscillazioni, ovvero se    10 ≥ x       (1.14)    allora si è individuata una oscillazione anomala (fig. 1.2). Se, invece, alla fine del  tempo  di  supervisione  si  conclude  senza  che  x  abbia  superato  il  valore  di  10  si  inizia  una  nuova  analisi  per  un  altro  tempo  di  supervisione,  facendo  ripartire  la  variabile x da zero (fig. 1.3).        fig. 1.2: Oscillazione anomala: la variabile x supera il valore 10 nel tempo di supervisione.   

    fig. 1.3: Oscillazione non anomala: la variabile x non supera il valore 10 nel tempo di  supervisione e viene riazzerata   

 

1.3 Attrito 

 

Facciamo riferimento allo schema di un anello di regolazione a singolo ingresso  e  singola  uscita  (fig.  1.4)  e  indichiamo  il  set‐point  con  SP,  il  segnale  di  controllo  con OP, la variabile manipolata con MV e la variabile controllata con PV.        fig. 1.4: Schema di riferimento per un circuito SISO.    L’unica parte in movimento di un loop di controllo è la valvola e la presenza di  attrito  si  può  manifestare  soltanto  in  questa  apparecchiatura.  Le  valvole  di  regolazione possono essere di tipo Elettrico o Pneumatico, cioè comandate da un  motore elettrico nel primo caso, o da un segnale di aria compressa nel secondo. Le  valvole  pneumatiche  risultano  le  più  veloci  nell’intervento  e  per  questa  ragione  sono  le  più  diffuse  nei  processi  industriali,  quando  è  necessaria  una  variazione  continua  della  portata.  Dato  che  il  segnale  del  regolatore  è  di  tipo  elettrico  o  digitale,  è  necessaria  un’interfaccia  di  conversione  elettro/pneumatica.  Gli 

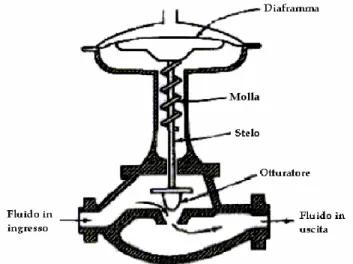
elementi  che  costituiscono  una  valvola  e  il  suo  principio  di  funzionamento  sono  schematizzati in figura 1.5.      fig. 1.5: Struttura di una valvola di controllo pneumatica.       

Il  flusso  del  fluido  è  modificato  andando  ad  agire  sulla  posizione  dell’otturatore,  determinata  da  un  bilancio  tra  la  forza  elastica  e  quella  della  pressione.  L’otturatore  è  collegato  allo  stelo,  che  viene  mosso  dal  diaframma.  L’attrito  si  può  manifestare  tra  lo  stelo  e  la  guarnizione  che  impedisce  la  fuoriuscita  del  fluido.  Il  principio  di  funzionamento  resta  lo  stesso  anche  in  valvole  aventi  aspetti  costruttivi  diversi:  a  farfalla  (fig.  1.6(a)),  a  membrana  (fig.  1.6(b)), a doppia sede bilanciata (fig. 1.6(c)). 

 

 

(a) A farfalla  (b) A membrana  (c) A doppia sede  bilanciata   

1.3.1  Conseguenze del fenomeno 

 

La presenza di attrito in un attuatore introduce un ritardo e un comportamento  non lineare tra il segnale di controllo OP e la variabile manipolata MV, generando  delle oscillazioni in uscita al processo.    Nel caso di valvola perfetta la curva caratteristica (grafico MV vs. OP) dovrebbe  essere una retta con pendenza di 45°, sia per la fase di apertura che per quella di  chiusura (fig. 1.7(a)).   

In  caso  di  attrito,  invece,  si  verifica  un  ciclo  di  isteresi  perché  in  un  certo  intervallo di tempo la valvola non si muove. Infatti, fino a che la forza attiva  ,  proporzionale all’uscita del controllore, è minore della forza di attrito statico   la  valvola  rimane  bloccata  in  una  posizione  che  può  generare  un  offset  tra  la  variabile  controllata  PV  e  il  set‐point  SP.  Un  errore  costante,  in  presenza  di  una  componente integrale sul regolatore, porta ad un aumento della OP e quindi ad un  aumento  di  .  Una  volta  superata  la  forza  di  attrito  statico  la  valvola  si  sblocca  compiendo  un  salto  e  nella  successiva  fase  di  movimento  è  rallentata  dalla 

componente di attrito dinamico  . Nel movimento della valvola l’errore tra SP e  PV cambia segno. Il controllore riduce l’azione di controllo, la forza attiva torna ad  essere minore dell’attrito statico e la valvola si blocca in una nuova posizione.  a F s F a F d F  

Questa  sequenza  è  nota  come  “stick‐slip  motion”  ed  è  costituita  da  quattro  componenti (fig. 1.7(b)): deadband (tratto AB), stickband (tratto BC), salto (tratto CD)  e movimento (DE). I tratti AB e BC rappresentano il comportamento della valvola  quando  non  si  muove  (MV  è  costante)  sebbene  OP  stia  cambiando;  il  tratto  CD  rappresenta il rilascio improvviso di energia potenziale, accumulata nella camera  dell’attuatore  a  causa  dell’elevato  attrito  statico,  nella  forma  di  energia  cinetica  appena  la  valvola  comincia  a  muoversi.  Compiuto  il  salto,  la  valvola  comincia  a  muoversi fino a bloccarsi di nuovo (punto E in fig. 1.7(b)). 

   

  (a) Assenza di attrito  (b) Presenza di attrito    fig. 1.7: Curva caratteristica di una valvola.    La conoscenza della variabile MV permetterebbe una identificazione più facile  della  presenza  di  attrito  tramite  un  semplice  confronto  diretto  con  OP,  ma  dovrebbe  essere  fatto  in  automatico.  In  più  la  variabile  manipolata  non  è  generalmente  registrata  dal  sistema  di  controllo.  Questo  punto,  comunque,  sarà  ripreso in seguito. 

 

1.3.2  Modello fisico 

 

Diversi  modelli  di  attrito  sono  stati  proposti  in  letteratura.  Una  rassegna  può  essere trovata in [11]. 

Per  una  valvola  pneumatica  l’equazione  di  bilancio  delle  forze  basata  sulla  seconda legge di Newton si può scrivere come:    f r a F F F Forze dt x d M ₂ =

∑

= + + 2 ,      (1.15)   

dove  M  è  la  massa  delle  parti  in  movimento,  x  è  la  posizione  dello  stelo, 

Au F_a =  è la forza applicata dall’attuatore (A è l’area del diaframma e u è il segnale  in ingresso alla valvola), F_r =−kx è la forza della molla (k è la costante elastica) e   è la forza dovuta all’attrito ([12], [13], [14]).  f F  

La  forza  di  attrito,  il  cui  modello  è  dovuto  a  Karnopp  [15],  ripreso  da  Olsson  [16]) e usato anche da Horch&Isaksson [17], è espressa come: 

( )

(

)

(

)

⎪ ⎩ ⎪ ⎨ ⎧ + ⋅ − + − − ⋅ − = r a s r a v c f F F sgn F F F vF v sgn F F     if if if 0 0 0 = = ≠ v   v , v e e s r a s r a F F F , F F F > + ≤ +        (1.16)    La prima riga dell’equazione (1.16) rappresenta l’attrito dinamico e comprende  un  termine  ,  indipendente  dalla  velocità  v  della  valvola  e  conosciuto  come  attrito  di  Coulomb,  e  un  termine    che  dipende  linearmente  dalla  velocità:  entrambi  si  oppongono  al  movimento  della  valvola,  come  si  vede  dai  segni  negativi.  c F v vF  

La  seconda  riga  dell’equazione  (1.16)  rappresenta  il  caso  in  cui  la  valvola  è  bloccata;    è  il  massimo  attrito  statico.  La  velocità  è  nulla  e  non  cambia  e,  di  conseguenza, anche l’accelerazione è nulla. Quindi, essendo  s F 0 2 2 = dt x d M , risulta che  . 

(

_{a r}

)

f F F F =− +   La terza riga del modello rappresenta il momento in cui la valvola si sblocca: la  somma delle forze è 

(

F_a+F_r

)

−F_s⋅sgn

(

F_a+F_r

)

, che è diversa da zero se  F_a+F_r >F_s.  L’accelerazione diventa non nulla e la valvola comincia a muoversi.   

Nonostante  la  sua  semplicità,  questo  modello  è  di  difficile  implementazione  perché richiede la conoscenza di una serie di parametri, che spesso non si riescono  a valutare. 

 

1.3.3  Modello basato sui dati d’impianto 

 

Di facile implementazione risulta, invece, il modello proposto da Choudhury et al  [18]:  si  basa  su  parametri  che  si  ricavano  direttamente  dai  dati  d’impianto,  ottenendo  gli  stessi  risultati  del  modello  fisico.  Supera,  perciò,  la  difficoltà  di  quest’ultimo  di  conoscere  necessariamente  la  massa  delle  parti  in  movimento  dell’attuatore, la costante elastica e le forze di attrito. 

 

Nei processi industriali, l’attrito è generalmente misurato come una percentuale  del  cammino  dello  stelo  della  valvola  oppure  del  range  del  segnale  di  controllo  [19].  Per  esempio,  un  2%  di  attrito  significa  che,  quando  la  valvola  si  è  bloccata,  comincerà  a  muoversi  solo  dopo  che  il  cambio  cumulativo  del  suo  segnale  di  controllo sarà maggiore o uguale al 2%. Se il range del segnale di controllo è 4‐20  mA, allora il 2% di attrito significa che un cambio del segnale di controllo minore  di 0.32 mA non riesce a sbloccare la valvola. 

Il  modello  prevede  la  conversione  del  segnale  di  controllo  in  percentuale  del  cammino dello stelo della valvola e si base su due parametri: S che è una misura  dell’attrito  statico  (tratti  AB  e  BC  della  figura  1.  7(b))  e  J  che  rappresenta  il  salto  compiuto  dalla  valvola  dopo  che  si  sblocca  (tratto  CD  della  fig.  1.7(b)).  Da  sottolineare  che  S  è  una  differenza  tra  due  valori  di  OP  (segnale  in  ingresso  alla  valvola),  mentre  J  una  differenza  tra  due  valori  di  MV  (segnale  in  uscita  dalla  valvola). Segue una breve descrizione dell’algoritmo del modello: 

 

• Indicando con k un istante generico, OP(k), espresso in mA, viene convertito in  percentuale x(k) del cammino dello stelo della valvola. 

 

• Se  x(k)  è  minore  dello  0%  o  maggiore  di  100%,  la  valvola  è  saturata  (completamente chiusa o completamente aperta). 

 

• Se x(k) è compresa nell’intervallo 0‐100%, l’algoritmo ne calcola la pendenza tra  l’istante k e quello precedente k‐1. 

 

• Nell’istante  in  cui  tale  pendenza  cambia  segno,  si  assume  che  la  valvola  si  blocca  e  il  corrispondente  valore  del  segnale  in  ingresso  alla  valvola  si  indica  con xss.    • Per il caso in cui il segno della pendenza non cambia, se risulta che:   

( )

k x S x − _ss > ,       (1.17)   

questa  compie  il  salto  e  comincia  a  muoversi,  altrimenti  continua  a  rimanere  bloccata.    • Sempre per il caso in cui il segno della pendenza non cambia, ma passa da un  valore positivo o negativo al valore nullo o viceversa, se risulta che:   

( )

k x J x − _ss > ,       (1.18)   

questa  compie  il  salto  e  comincia  a  muoversi,  altrimenti  continua  a  rimanere  bloccata.    • Il segnale y(k) in uscita dalla valvola è calcolato usando l’equazione (1.19):   

( )

( )

(

)

2 ) (pendenza S J sgn k x k y = − ⋅ − ,      (1.19)   

dove il termine sgn(pendenza) è pari a +1 se la pendenza di x(k) è positiva, a –1  se è negativa e, infine, a zero se è nulla. L’andamento di y(k) dipende dal tipo  di attrito presente nella valvola: 

 

o _{Deadband  puro:  in  questo  caso  J=0,  per  cui  non  si  osserva  alcun  salto  nella}  valvola (fig. 1.8(a)). 

 

o Undershoot:  in  questo  caso  J <   e  il  segnale  in  uscita  dalla  valvola  non S

raggiunge mai quello in ingresso (fig. 1.8(b)), per cui è sempre presente un  offset. 

 

o _{Assenza  di  offset:  in  questo  caso  J =   e  non  c’è  un  offset  tra  il  segnale  in S} ingresso  e  in  uscita  dalla  valvola.  Una  volta  che  il  segnale  in  ingresso  alla  valvola supera l’attrito, quello in uscita lo raggiunge esattamente. Questo è  il ben noto caso di “stick‐slip” (fig. 1.8(c)). 

 

o Overshoot:  in  questo  caso  J >   e  il  segnale  in  uscita  dalla  valvola  supera S

sempre il segnale in ingresso (fig. 1.8(d)) a causa del forte attrito.   

• Infine, y(k) viene convertito nel segnale MV(k), espresso in mA, sulla base della  curva  caratteristica  della  valvola,  e  viene  riportata  la  nuova  posizione  della  valvola.                         

  (a) J=0  (b) J <S    (c) J =S  (d) J >S    fig. 1.8: Tipologie di attrito in una valvola.   

 

1.4 Tecniche di individuazione dell’attrito 

 

Per  l’individuazione  dell’attrito  in  letteratura  sono  state  proposte  molte  tecniche. Come analisi preliminare, ne consideriamo tre, di facile implementazione  e  specifiche  per  sistemi  SISO  :  la  Cross‐Correlazione  [2],  la  Bicoerenza  [3],  la  tecnica del Relay [4]. 

 

1.4.1  Cross‐Correlazione 

 

L’idea  di  base  è  quella  di  utilizzare  le  informazioni  ottenute  correlando,  attraverso una funzione, il segnale di controllo u(t) con la variabile controllata y(t).  Questa  analisi  può  essere  fatta  su  processi  che  non  hanno  azione  integrale  e  che  hanno un controllore di tipo PI. Possono essere scoperte soltanto oscillazioni con  un’ampiezza significativa. 

Si possono fare le seguenti osservazioni (fig. 1.9):   

• in  presenza  di  attrito  nella  valvola,  il  segnale  di  controllo  e  la  variabile  manipolata  sono  sfasati  approssimativamente  di 

2 π

  e  la  cross‐correlazione  è  una funzione dispari;    • in presenza di un disturbo esterno lo sfasamento è approssimativamente di π  e  la cross‐correlazione è una funzione pari;    • un loop instabile che oscilla con ampiezza costante dà origine ad una funzione  di cross‐correlazione pari.      (a) Attrito (funzione dispari)  (b) Disturbo esterno o loop instabile  con saturazione (funzione pari)    fig. 1.9: La funzione di cross‐correlazione (in basso) e dei tipici set  di dati (in alto).   

La funzione di cross‐correlazione r_uy, in funzione del ritardo aggiuntivo τ  e per  un set di dati con N campioni, si ottiene come segue (equazione 1.20):   

( )

τ =

∑

−τ−

( ) (

+τ = k y k u r N k uy 1 0

)

       (1.20)   

Con  riferimento  alla  fig.  1.10,  si  indicano  con τ_r  e  con −   rispettivamente  il τ_l ritardo  positivo  e  quello  negativo  in  corrispondenza  di  due  attraversamenti  consecutivi  dello  zero  e  con    il  valore  della  funzione  di  cross‐correlazione  a  ritardo nullo. Inoltre si definiscono:  0 r  

( )

_{[ ]}

( )

τ τ τ τ ruy r sgn r r l, 0 max = ⋅ _∈max₋        (1.21)      r l r l τ τ τ τ τ + − = ∆        (1.22)      max 0 max 0 r r r r + − = ∆ρ        (1.23)          fig. 1.10: Definizione delle variabili chiave per la funzione di cross‐correlazione.   

Si  indica  con ∆   lo  sfasamento  tra  i  segnali  u(t)  e  y(t).  Dato  che  l’obiettivo  è φ quello di distinguere tra uno sfasamento di  2 π  e uno di  π , si possono formulare le  seguenti regole:    •interpretare  6 2 π π φ = ± ∆  come  2 π φ = ∆     •interpretare  6 π π φ = ± ∆  come ∆φ =π  

Nel  caso  in  cui  ∆ ∈_⎢⎣⎡ + − _⎥⎦⎤ 6 , 6 2 π π π π

φ   non  può  essere  fatta  alcuna  diagnosi,  per 

evitare  di  fornire  indicazioni  errate.  Le  regole  possono  poi  essere  riportate  in  termini di  τ∆  e ∆ : ρ   ⎪⎭ ⎪ ⎬ ⎫ ≤ ∆ < ≤ ∆ < 3 1 0 072 . 0 0 τ ρ Disturbo ⇒ = ∆ ⇒ φ π     ⎪ ⎭ ⎪ ⎬ ⎫ ≤ ∆ < ≤ ∆ < 3 2 3 1 3 1 072 . 0 τ ρ decisione   Nessuna ⇒     ⎪ ⎭ ⎪ ⎬ ⎫ < ∆ < < ∆ < 1 3 2 1 3 1 τ ρ Attrito ⇒ = ∆ ⇒ 2 π φ    

Quindi,  calcolando  ∆τ   e  ∆ ,  si  riesce  a  definire  se  la  funzione  di  cross‐ρ correlazione  è  dispari  o  pari,  e  quindi  se  siamo  in  presenza  di  attrito  o  di  un  disturbo  esterno.  L’algoritmo  è  facilmente  implementabile  ed  ha  un  carico  computazionale  basso;  ha  lo  svantaggio  di  presentare  un’ampia  zona  di  indecisione.  In  più  è  stato  dimostrato  [5]  che,  in  caso  di  disturbo  sinusoidale,  la  frequenza  delle  oscillazioni  influisce  sul  risultato  dell’analisi:  per  valori  di 

2 . 0 < u w w

, con   frequenza del disturbo e   frequenza ultima del sistema, questa 

tecnica  indica  erroneamente  la  presenza  di  attrito,  per  cui  i  suoi  risultati  devono  essere scartati. 

w w_u

 

1.4.2  Bicoerenza 

 

Questa  tecnica  [3]  si  basa  su  statistiche  di  ordine  elevato.  Un  segnale  non‐ lineare, infatti, presenta accoppiamenti di fase che causano caratteristiche spettrali  di  ordine  elevato  che  possono  essere  individuate  dalla  Bicoerenza,  definita  come  (equazione 1.24):   

(

)

(

)

( ) ( )

[

]

[

(

)

2

]

2 1 2 2 1 2 2 1 2 1 2 , , f f X E f X f X E f f B f f bic + =       (1.24)   

dove B

(

f₁, f₂

)

 è il Bispettro alle frequenze 

(

f₁, f₂

)

 dato dall’equazione (1.25):   

(

f1,f2

)

E

[

X

( ) ( ) (

f1 X f2 X f1 f2

)

]

B = ∗ +       (1.25)   

( )

f₁

X   è  la  trasformata  discreta  di  Fourier  del  segnale  nel  tempox

( )

k   alla  frequenza f1,   è il suo complesso coniugato e l’operatore E calcola il valore 

di  aspettazione.  Il  Bispettro  ha  valore  non‐nullo  se  tra  le  frequenze f

( )

f1

X∗

1  e f2  ci  sono 

accoppiamenti  di  fase  nel  segnale  x

( )

k .  La  Bicoerenza  dà  la  stessa  informazione  del Bispettro, ma è normalizzata assumendo valori compresi tra 0 e 1.     In [3] sono definiti due indici: l’indice di Non‐Linearità (NLI) e l’indice di Non‐ Gaussianità (NGI):   

( )

2 2 2 crit bic bic NGI= −       (1.26)   

( )

_⎜

( )

_{( ) ⎟⎠}⎞ ⎝ ⎛ ₊ − = 2 22 2 2 max 2 2 bic bic bic NLI σ        (1.27)   

dove 

( )

bic2 2 , 

( )

bic2 2max  e σ_{( )bic}22  sono  rispettivamente  il  valore  medio,  il  valore 

massimo  e  la  deviazione  standard  del  quadrato  della  bicoerenza  valutati  per  frequenze tali che 0< f₁ <0.5,f₂ < f₁ e 2f1+ f2 <1. Il termine 

2 crit

bic  rappresenta un 

valore limite ottenuto dalla distribuzione χ2 del quadrato della bicoerenza.  

Per  un  anello  di  regolazione,  il  calcolo  di  tali  indici  è  effettuato  sull’errore 

PV SP

e= − ,  essendo  più  stabile  di  PV  e  di  OP.  Se  entrambi  gli  indici  sono  maggiori  dei  rispettivi  valori  limite,  il  segnale  è  ritenuto  non‐gaussiano  e  non‐ lineare  e,  di  conseguenza,  viene  attribuita  una  non‐linearità  alla  valvola  di  controllo che, nella maggior parte dei casi, coincide con la presenza di attrito, sotto  le seguenti assunzioni:    − si assume che il processo sia localmente lineare;    − si assume che nessun disturbo non‐lineare entri nell’anello.    Se il segnale è lineare (gaussiano o non‐gaussiano), le possibili cause di scarsa  prestazione  dell’anello  di  controllo  possono  essere  un  disturbo  oscillante  esterno  oppure una sintonizzazione non adeguata del regolatore. 

     

Si  può  visualizzare  l’andamento  di  bic2

(

f₁, f₂

)

  rispetto  a f1  e f2  in  un  grafico  tridimensionale, dove la presenza di picchi indica la presenza di una non‐linearità  nel segnale (fig. 1.11(a)), mentre l’assenza di picchi indica che il segnale è lineare  (fig. 1.11(b)).      (a) Presenza di attrito  (b) Assenza di attrito    fig. 1.11: Grafico tridimensionale della funzione di Bicoerenza.   

 

1.4.3  Relay 

 

L’idea  di  base  del  metodo  [4]  nasce  dall’osservazione  che  le  oscillazioni  generate da una valvola affetta da attrito sulla variabile controllata PV presentano  una  forma  d’onda  simile  a  quelle  generate  da  un  processo  del  primo  ordine  più  ritardo (FOPTD) posto in circuito chiuso con un relay (fig. 1.12).        fig. 1.12 : Schema di un circuito a Relay    Se, invece, l’oscillazione è generata da un problema di tuning o da un disturbo  esterno la forma d’onda ha un andamento sinusoidale. 

Ogni semiciclo significativo dell’errore e=SP−PV  viene approssimato usando  tre  modelli  differenti:  la  risposta  ad  un  FOPTD  con  relay,  un’onda  triangolare  e  un’onda sinusoidale.    L’approssimazione sinusoidale CS è:   

(

_{S S}

)

S S A sen t C = ⋅ ω +φ        (1.28)   

dove AS, ω_S e φ_S sono calcolati attraverso il metodo del simplesso. Il punto di 

partenza è calcolato sulla base dei dati registrati: ampiezza e frequenza sono prese  uguali a quelle delle oscillazioni registrate; la fase iniziale è scelta uguale a zero.    L’approssimazione triangolare CT è:   

(

)

(

)

( )

(

)

⎩ ⎨ ⎧ + − + ⋅ + ⋅ = 1 2 1 2 1 1 q n t m m t m A q t m A C T T T n n n n > ≤         (1.29)   

dove n   è  il  vertice  del  triangolo  e  AT  è    un  fattore  di  scala.  Per  i  punti n_i ≤n 

l’approssimazione  è  una  linea  con  coefficiente  m₁>0  e  per  i  punti  n_i >n  l’approssimazione  è  una  linea  con  coefficiente  m₂ <0.  L’intercetta  della  seconda  linea è scelta per avere lo stesso valore delle due linee al vertice del triangolo. Tutti  i  parametri AT  , m1, m2  e q1  sono  facilmente  ottenibili  utilizzando  la  tecnica  di 

regressione dei minimi quadrati lineari (LLS, Linear Least Squares). 

 

Più  complessa  è  l’approssimazione  con  onda  a  relay.  Per  prima  cosa  si  divide  l’oscillazione registrata in tre parti  ( )1 re y ,  ( )2 re y  e  ( )3 re

y  definendo due numeri n1 e n2. La 

divisione in tre intervalli permette di costruire un buon algoritmo per ottenere la  migliore approssimazione: 

 

1. Si sceglie un valore per n1 e n2 con n >₂ n₁. 

 

2. Il  modulo  di  ottimizzazione,  basato  sul  metodo  del  simplesso,  ad  ogni  iterazione  fissa  un  valore  per  i  due  parametri  che  caratterizzano  l’onda  a  relay: la costante di tempo τ  e il ritardo θ .    3. L’uso dei parametri permette di ottenere la curva di approssimazione, con  ampiezza unitaria, nel primo intervallo:    τ θ − − ∧ − = e t y₁ 1       (1.30)   

4. L’ampiezza  A1,  che  permette  di  ottenere  la  migliore  curva  di  approssimazione nel primo intervallo y1, è calcolata con la tecnica LLS:   

(

)

( ) 1 1 1 1 1 1 1 1 1 yˆ yˆ yˆ y y A yˆ A = T − _re ⇒ = ⋅       (1.31)   

5. La curva di approssimazione del secondo intervallo ha la stessa  τ  di y1. Il 

ritardo  θ₂,  invece,  è  valutato  in  modo  da  ottenere  yˆ₂

( )

n₁ ≡yˆ₁

( )

n₁ ;  con  questa  imposizione  la  seconda  parte  dell’approssimazione,  con  ampiezza  unitaria, è:    τ θ₂ 1 ˆ₂ − − + − = e t y        (1.32)    6. Il calcolo dell’ampiezza ottimale di fittaggio A2, in questo caso, deve essere 

soggetta  all’imposizione  y₂

( )

n₁ ≡y₁

( )

n₁ .  Il  problema  è  risolto  con  le  equazioni 1.33 e 1.34, mentre il valore di A2 è valutato ancora con il metodo  LLS (equazione 1.35):   

( )

1 2 2 2 ˆ ˆ ~ _{y y n} y = −       (1.33)    ( ) ( ) ( )

( )

1 2 2 2 ~ _{y y n} yre = re − re       (1.34)   

(

)

( ) 2 2 2 2 2 1 2 2 2 y~ ~y ~y y~ y A yˆ A = T − _re ⇒ = ⋅        _(1.35)    7. La terza parte dell’approssimazione è valutata nello stesso modo: si fissa il  valore θ3 come al punto 5 e l’ampiezza A3 come al punto 6, ottenendo y3.  

 

8. La  curva  di  approssimazione  globale  è  l’unione  delle  tre  parti  approssimate: y_ap =

[

y1T yT2 yT3

]

T. Un fattore di scala globale ATot è valutato 

con tecnica LLS tra yap e la curva registrata, in modo da ottenere la migliore 

approssimazione possibile.   

9. Se il nuovo yap genera un errore minore rispetto a yap valutato all’iterazione 

precedente,  il  sistema  utilizza  la  nuova  curva  come  migliore  approssimazione CR, altrimenti si mantiene l’approssimazione precedente. 

 

10. Il modulo della tecnica del simplesso esegue poi un primo controllo: se non  ha  raggiunto  la  convergenza  viene  cambiato  il  valore  di  τ   e  θ   e  la  procedura riparte dal punto 3. 

11. Se  il  metodo  del  simplesso  è  andato  a  convergenza  o  si  è  raggiunto  il  massimo  numero  di  iterazioni  possibile,  la  procedura  esegue  un  secondo  controllo:  se n1  e n2  non  hanno  assunto  tutti  i  possibili  valori  la procedura 

riparte  dal  punto  1,  altrimenti  è  stata  trovata  la  miglior  curva  di  approssimazione CR. 

 

Confrontando  l’errore  tra  i  dati  reali  e  quelli  approssimati  si  può  valutare  l’accuratezza  dell’approssimazione  e  dare  un’indicazione  sul  fenomeno  che  dà  origine alle oscillazioni: se è migliore il seno (errore ES) l’oscillazione è associata ad  un disturbo esterno (fig. 1.13(b)); se è migliore l’onda a relay o l’onda triangolare  (errore ERT ) l’oscillazione è associata all’attrito (fig. 1.13(a)).      (a) Presenza di attrito  (b) Presenza di un disturbo    fig. 1.13: Andamento dei dati reali (in nero), dell’approssimazione con seno (in rosso) e  dell’approssimazione migliore tra relay e triangolo (in blu) per un ciclo.      Mediando i due errori su tutti i semicicli esaminati si ottengono rispettivamente  ES,m e ERT,m con cui è possibile definire un indice di attrito SI:    m RT m S m RT m S I E E E E S , , , , + − =       (1.36)   

L’indice  di  attrito  è  compreso  nell’intervallo  [‐1,1]  e  assume  valori  negativi  quando  l’approssimazione  sinusoidale  risulta  migliore,  mentre  assume  valori  positivi in caso di attrito. Valori vicini a zero indicano che le due approssimazioni  hanno  errori  simili  e  la  procedura  dà  una  risposta  incerta;  considerando  che  il  rumore può cambiare la forma della curva, è stata definita una zona di incertezza  per valori di SI <0.21. Ciò corrisponde al rapporto  0.66 , , ₌ m RT m S E E , in analogia con il  valore limite  3 2 ≤ ∆τ  della tecnica della cross‐correlazione.  

Viene anche calcolato un indice di attrito per i soli semicicli positivi (S ) e un _I+

indice di attrito per i  soli semicicli negativi (S ). Se, infatti, soltanto uno dei due _I−

indici S   e _I+ S   assume  un  valore  superiore  a  0.21,  siamo  in  presenza  di  attrito I−

asimmetrico. 

 

1.5 Effetto dei principali parametri sulle oscillazioni 

registrate 

 

In  questa  sezione  si  analizzano  le  principali  caratteristiche  del  fenomeno  dell’attrito, osservando gli andamenti allo stazionario delle variabili del processo  (segnale  di  controllo  OP,  variabile  manipolata  MV,variabile  controllata  PV)  al  variare di alcuni parametri importanti, cioè i parametri del processo, dell’attrito e  del regolatore. In particolare questa analisi è finalizzata a verificare l’effetto della  variazione  del  guadagno  del  regolatore  sulla  frequenza  delle  oscillazioni  registrate:  si  tratta  di  un  test,  già  proposto  in  [5],  per  confermare  la  presenza  di  attrito nel caso di anelli di regolazione SISO. 

 

L’analisi si basa su alcune semplici simulazioni, eseguite con MATLAB®, nelle  quali si  considera  come  esempio  illustrativo  un  processo  del  primo  ordine  più  ritardo  (FOPTD,  First  Order  Plus  Time  Delay)  controllato  in  retroazione  da  un  regolatore  PI  la  cui  valvola  è  affetta  da  attrito.  Si  tratta,  quindi,  di  un  classico  anello di controllo di tipo SISO (Single Input Single Output) ): in fig. 1.14 si riporta  lo schema SIMULINK® impiegato per le simulazioni. Per simulare l’attrito si usa il  modello di Choudhury descritto precedentemente (paragrafo 1.3.3).    Lo schema SIMULINK® prevede l’uso di uno switch, che permette di simulare,  a seconda della posizione, l’attrito nella valvola oppure l’ingresso nell’anello di un  disturbo  sinusoidale.  In  tutte  le  simulazioni  il  set‐point  è  costante  ed  è  sempre  uguale a zero. 

     

    fig. 1.14: Schema SIMULINK® di un sistema SISO   

 

1.5.1  Variazione dei parametri del processo 

 

Si  vuole  studiare  l’influenza  dei  parametri  del  processo  sulle  oscillazioni  generate  dalla  presenza  di  attrito  nella  valvola  e  registrate  nelle  variabili  di  processo ( lo switch è posizionato in modo da simulare l’attrito nella valvola,  

fig. 1.14). 

In fig. 1.15 si riportano gli andamenti di OP, MV e PV al variare dei parametri  del processo, in particolare del ritardo  θ  e della costante di tempo  τ , e fissando  quelli dell’attrito e del regolatore: il modello del processo, il tuning del regolatore  e i parametri dell’attrito impiegati sono riportati in tab. 1.1. 

     

Processo  Regolatore  Parametri dell’attrito 

    S  J  1 3 + − s e s τ θ   ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + s s 10 1 10 2 . 0   1  1    tab. 1.1: Modello del processo, tuning del regolatore e parametri dell’attrito        Sono stati analizzati tre casi, utilizzando i seguenti valori:    a) θ =10; τ =1;    b) θ =10; τ =5;    c) θ =10; τ =10. 

  a)  =10 τ θ   b)  =2 τ θ   c)  =1 τ θ   fig. 1.15: Andamenti di OP, MV e PV al variare di  τ θ     Si osserva che in tutti e tre i casi la variabile manipolata MV mantiene il tipico  andamento  ad  onda  quadra,  indice  di  una  marcata  non‐linearità  mentre  l’andamento  del  segnale  di  controllo  OP  è  ad  onda  triangolare.  La  variabile  controllata PV mostra anche la presenza del ciclo limite ma l’effetto del processo  modifica il tipico andamento ad onda quadra osservato nella MV. Al diminuire di 

τ θ

  la  forma  delle  onde  cambia  da  quadra  a  triangolare,  confondibile  con  una  sinusoide.  

Infatti,  al  diminuire  di  τ θ

,  è  maggiore  l’effetto  di  filtrazione  esercitato  dal 

processo su MV, con il risultato che in PV la tipica onda quadra mostrata da MV  scompare per essere sostituita da una forma triangolare. 

Inoltre l’ampiezza delle oscillazioni non è influenzata da θ  e τ ; la frequenza di  oscillazione, invece, diminuisce al diminuire di  τ θ . 

 

1.5.2  Variazione dei parametri dell’attrito 

 

Fissando i parametri del processo e del regolatore e variando quelli dell’attrito,  è stato possibile analizzare come le oscillazioni cambiano a seconda della tipologia  di  attrito  che  le  genera.  Il  modello  del  processo,  il  tuning  del  regolatore  e  i  parametri  dell’attrito  usati  nelle  simulazioni  sono  riportati  in  tab.  1.2.  I  risultati 

ottenuti  dalle  simulazioni  sono  riportati  in  fig.  1.16  e  in  fig.  1.17,  adottando  la  seguente simbologia:    1. Deadband: colore magenta    2. Undershoot: colore blu    3. No offset: colore rosso    4. Overshoot: colore verde     

Processo  Regolatore    Attrito 

    Deadband  Undershoot  No offset  Overshoot 

    S  J  S  J  S  J  S  J  1 10 3 10 + − s e s   ⎜_⎝⎛ + ⎟_⎠⎞ s s 10 1 10 2 . 0   5  0  5  2  5  5  5  7    tab. 1.2: Modello del processo, tuning del regolatore e parametri dell’attrito            a) Grafico MV vs OP  b) Grafico PV vs OP    fig. 1.16: Variazione dei parametri dell’attrito   

   

fig. 1.17: Andamenti di OP, MV e PV   

Nei tre casi di attrito (Undershoot, No offset e Overshoot) gli andamenti di OP, MV 

e  PV  mostrano  dei  cicli  limite,  mentre  la  sola  presenza  di deadband  non  causa 

oscillazioni ma aggiunge soltanto un ritardo al processo. 

In  presenza  di  cicli  limite,  il  segnale  di  controllo  OP  assume  un  andamento  oscillatorio  ad  onda  triangolare  e  la  variabile  manipolata  MV,  invece,  il  tipico  andamento ad onda quadra. Per quanto riguarda la PV, al diminuire del rapporto 

J S

  la  forma  delle  onde  cambia  da  quadra  a  triangolare.  Inoltre,  per  tutte  e  tre  le  variabili,  al  diminuire  del  rapporto 

J S

  sia  l’ampiezza  che  la  frequenza  delle  oscillazioni aumentano.    La fig. 1.16a mostra il grafico di MV vs OP, il cui andamento indica chiaramente  la presenza di attrito nella valvola, mentre il grafico PV vs OP (fig. 1.16b), che ha  un andamento ellittico, non sempre può essere impiegato per l’individuazione dei  problemi di attrito. Ciò è dovuto al fatto che il grafico PV vs OP include non solo  la caratteristica non lineare dalla valvola, ma anche la dinamica del processo, P

( )

s ,  che in questo caso è del primo ordine più ritardo. 

Quindi,  se  la  MV  è  disponibile  nei  dati  di  impianto,  si  usa  direttamente  il  grafico di MV vs OP per l’individuazione dell’attrito nella valvola; il grafico di PV  vs  OP  si  può  usare  soltanto  per  gli  anelli  di  controllo  di  flusso,  dove  il  flusso  attraverso  la  valvola,  cioè  la  PV,  si  può  considerare  proporzionale  all’apertura  della valvola, cioè la MV. 

     

1.5.3  Variazione del guadagno del regolatore 

 

Si  vuole  studiare  ora  l’effetto  del  guadagno  del  regolatore  sul  ciclo  limite  generato  dalla  valvola:  si  eseguono,  pertanto,  alcune  simulazioni  variando  il  guadagno  del  regolatore, KC,  e  fissando  tutti  gli  altri  parametri.  Il  modello  del 

processo, il tuning del regolatore e i parametri dell’attrito sono riportati in tab. 1.3.   

Processo  Regolatore  Parametri dell’attrito 

    S  J  1 10 3 10 + − s e s   ⎜_⎝⎛ + ⎟_⎠⎞ s s K_C 10 1 10   3  1    tab. 1.3: Modello del processo, tuning del regolatore e parametri dell’attrito      Sono stati analizzati tre casi in cui si è scelto:    a) 3 2 max , = C C K K     b) 2 1 max , = C C K K     c) 3 1 max , = C C K K    

dove  KC,max =0.524  è  il  guadagno  del  regolatore  in  corrispondenza  del  quale  il  processo raggiunge le condizioni di stabilità marginale. 

In  fig.  1.18  si  riportano  gli  andamenti  di  OP,  MV  e  PV:  si  osserva  che  la 

diminuzione di KC causa sia una diminuzione dell’ampiezza che una diminuzione 

della frequenza delle oscillazioni. 

In  particolare  la  frequenza  w0  diminuisce  nelle  stesse  proporzioni  in  cui 

diminuisce KC. 

 

Una spiegazione intuitiva di questo comportamento è che un basso valore di KC 

causa  una  bassa  velocità  di  aumento  della  forza  attiva    (paragrafo  1.3.1);  ciò  vuol dire che ci vuole più tempo affinché   raggiunga la forza di attrito statico    e, di conseguenza, la frequenza di oscillazione è più bassa (la frequenza e il tempo  sono grandezze inversamente proporzionali).  a F a F F_S

Una spiegazione più accurata si trova in [20], dove l’effetto della variazione del  guadagno  del  regolatore  sulla  frequenza  di  oscillazione  a  causa  dell’attrito  nella  valvola è analizzato attraverso la tecnica della funzione descrittiva.      a)  3 2 max , = C C K K   b)  2 1 max , = C C K K   c)  3 1 max , = C C K K     fig. 1.18: Effetto della variazione del guadagno del regolatore sulle oscillazioni generate da una  valvola affetta da attrito    La variazione del guadagno del regolatore, sulla base degli effetti che produce,  può  rappresentare  un  valido  test  per  confermare  la  presenza  di  attrito  in  una  valvola [5], quando, per esempio, le tecniche di individuazione dell’attrito danno  risultati incerti e cioè che la causa delle oscillazioni registrate nei dati di impianto  può  essere  o  la  presenza  di  attrito  nella  valvola  o  l’ingresso  nell’anello  di  un  disturbo.    A tale proposito, si simula l’ingresso di un disturbo sinusoidale (cambiando la  posizione dello switch, fig. 1.14), variando il guadagno del regolatore e fissando i  parametri del processo.  Essendo la valvola in assenza di attrito, è simulata come un guadagno unitario,  per cui la variabile manipolata MV coincide con il segnale di controllo.  Il disturbo al generico tempo t è dato da:   

(

w t

)

sen A d= ⋅ _d⋅        (1.37)   

dove A è l’ampiezza e w_d è la frequenza. 

Il modello del processo, il tuning del regolatore e i parametri del disturbo sono  riportati in tab. 1.4. 

 

Processo  Regolatore  Parametri del disturbo 

    A  wd (rad/sec)  1 10 3 10 + − s e s   ⎜_⎝⎛ + ⎟_⎠⎞ s s 10 1 10 4 . 0   1  0.2    tab. 1.4: Modello del processo, tuning del regolatore e parametri del disturbo 

In fig. 1.19a si riportano gli andamenti di OP e di PV al diminuire di KC: le curve 

di  colore  verde  rappresentano  il  caso  base,  per  quelle  di  colore  rosso KC  è  stato 

dimezzato e, infine, per quelle di colore blu KC è stato diviso per 4. Si osserva che 

la frequenza di oscillazione non cambia nei tre casi: calcolando tale frequenza sulla  base  del  semiperiodo  di  oscillazione,  inteso  come  l’intervallo  di  tempo  entro  il  quale  la  variabile  in  esame  assume  sempre  lo  stesso  segno  (da  notare  che  le  variabili del processo oscillano sempre intorno a zero), risulta che questa coincide  con la frequenza di oscillazione del disturbo. 

 

Osservando, invece, il grafico PV vs OP in fig. 1.19b, si nota che le ampiezze dei  due  segnali  e  l’inclinazione  dell’ellisse  (l’andamento  è  ellittico  come  nel  caso  di  attrito nella valvola) diminuiscono al diminuire di KC.    a)  b)      fig. 1.19: a) Andamenti di OP e PV; b) Grafico PV vs OP   

Quindi,  se  la  causa  delle  oscillazioni  registrate  nei  dati  di  impianto  è  dovuta  all’ingresso di un disturbo lineare, la variazione del guadagno del regolatore non  influenza affatto la frequenza di oscillazione. 

 

Per cui, se l’indicazione fornita da una tecnica per l’individuazione dell’attrito è  incerta  e  si  cambia  il  guadagno  del  regolatore,  la  variazione  della  frequenza  di  oscillazione  dimostra  che  la  causa  delle  oscillazioni  è  l’attrito  nella  valvola,  altrimenti è dovuta all’ingresso nell’impianto di un disturbo lineare.