Capitolo 2

Strutture torsionali in silicio-germanio:

struttura e metodi di misura

Come già citato nel capitolo 1, questa tesi si occupa dell’analisi di microrisonatori torsionali in silicio-germanio, con lo scopo di caratterizzarne il comportamento piezoresistivo.

In particolare, si studierà una struttura (progettata all’Università di Pisa1 e realizzata all’istituto di ricerca IMEC2) formata da quattro risonatori: ciascun risonatore è un diaframma rettangolare sospeso e collegato ad una struttura fissa, tramite due molle3; l’insieme formato dal diaframma e dai sostegni è composto da silicio-germanio e manifesta un comportamento piezoresistivo, se sollecitato a torsione. Si è scelto di collegare a ponte di Wheatstone i quattro risonatori, perché questo permette di estrarre direttamente la variazione di resistenza, con la tensione di uscita del ponte (si faccia riferimento alla figura 1.4 del capitolo 1).

La modalità di misura con cui si ricava la ∆R dei risonatori citati differisce dalle usuali tecniche di sensing piezoresistivo: sensori del genere vengono di solito realizzati integrando piezoresistori in punti della struttura dove ci si aspetta un elevato valore di deformazione. In questa tesi, invece, si è scelto di considerare l’intera struttura come un piezoresistore, anziché integrarvi opportune resistenze in punti strategici.

Nella prima parte di questo capitolo si descrive il silicio-germanio come materiale per fabbricare MEMS (sistemi microelettromeccanici). Nella seconda parte sarà descritto il layout della struttura a quattro risonatori e sarà discusso il modello elettrico

1

Dipartimento di Ingegneria dell’Informazione, laboratorio di tecnologie microelettroniche.

2

Interuniversity Microelectronics Center, Leuven, Belgio.

3

equivalente e la configurazione dei segnali di attuazione e di misura. Nel capitolo 1 (paragrafo 1.1) si è detto che la relazione fra l’angolo θ di torsione di un risonatore e la sua variazione di resistenza ∆R è di tipo quadratico: ∆ ≅_R αθ2

. Questa tesi sarà ampiamente discussa e dimostrata nei capitoli 3 e 4; in questo capitolo sarà assunta come vera e si studieranno le tensioni applicate, confrontando diverse configurazioni, per scegliere quella più adatta, in termini di minimizzazione degli errori di matching. Tale studio sarà completato nel capitolo 6, dove la struttura analizzata in questo capitolo sarà simulata con il programma ad elementi finiti ANSYS.

2.1 Il silicio-germanio come materiale per fabbricare

MEMS

Le tecnologie microelettroniche attuali sono orientate allo sviluppo della fabbricazione di sensori con tecnologia CMOS, che permette di integrare nello stesso wafer sia la parte di sensing, che il circuito di elaborazione dei segnali. Una migliore alternativa è rappresentata dalla tecnica del postprocessing, che consiste nel realizzare la parte elettromeccanica sopra un substrato CMOS già pronto; questo permette di conservare i vantaggi dell’integrazione monolitica (minor spazio occupato, costi inferiori, maggiore affidabilità e riproducibilità), evitando di dover modificare i processi CMOS di fonderia [7]. L’unico rilevante difetto del postprocessing è la massima temperatura di deposizione che si può utilizzare, per non danneggiare i contatti della struttura; spesso si fa uso di silicio policristallino per fabbricare MEMS (sistemi microelettromeccanici), ma questo comporta una temperatura di lavorazione di 800o C, mentre non si dovrebbero superare i 500o C. Il silicio-germanio policristallino drogato con boro, invece, è più adatto per la fabbricazione di MEMS su una base CMOS, perché può essere deposto a 450o C; inoltre, questo tipo di materiale presenta eccellenti qualità meccaniche ed elettriche ed un basso valore di tensione residua di deposizione (10 MPa, comprimente).

2.1.1 Il silicio-germanio idrogenato

Nell’istituto di ricerca IMEC si fa attualmente uso di silicio-germanio microcristallino idrogenato (µcSiGe:H) [8], [9], depositato a temperature comprese fra 300 e 400o C: questi sono i più bassi valori di temperatura mai ottenuti per realizzare strati di SiGe policristallino per applicazioni MEMS.

Nel processo di deposizione di un materiale microcristallino idrogenato (solitamente deposto con tecnologia PECVD4) si regola la quantità di idrogeno presente nel plasma, per ottenere una struttura cristallina a temperature relativamente basse e per ridurre i difetti, che si creano durante la crescita. La variazione nel rapporto di diluizione dell’idrogeno5 può influenzare la struttura dei cristalli, cambiando il profilo di deformazione dello strato. Aumentare la quantità di idrogeno favorisce il processo di cristallizzazione dei grani di silicio-germanio, pertanto si è scelto di variare il rapporto di diluizione durante la deposizione dello strato [10]: ad un graduale decremento di tale rapporto è associata, infatti, una iniziale crescita di grani a forma di V che si trasformano, con l’aumento dello spessore, in grani colonnari; la regolazione della forma e delle dimensioni di questi ultimi permette di controllare i gradiente di deformazione del materiale. La figura 2.1 riporta un’immagine TEM di una sezione di µcSiGe:H, deposto su SiO2 con la tecnica del decremento graduale dell’idrogeno: vi è raffigurata la parte inferiore dello strato, che presenta grani a forma di V e zone parzialmente amorfe all’interfaccia con l’ossido.

4

Plasma Enhanced Chemical Vapor Deposition.

5

H2/(SiH4+GeH4); è il rapporto fra la quantità di idrogeno e i gas che trasportano il silicio ed il

FIGURA 2.1: Immagine TEM di uno strato di silicio-germanio microcristallino di spessore 0.84 µm.

2.1.2 Proprietà piezoresistive del silicio-germanio

Il silicio-germanio è un materiale adatto per la fabbricazione di MEMS. Tuttavia, la possibilità di poter estenderne l’uso a dispositivi piezoresistivi è ancora oggetto di studio: è noto, infatti, che il SiGe abbia un buon comportamento piezoresistivo, ma non sono ancora noti con precisione i valori degli omonimi coefficienti, indispensabili per la realizzazione di eventuali sensori. La difficoltà di questo tipo di misura è dovuta al processo di crescita del silicio-germanio: quando si cresce uno strato di Si1-xGex su silicio, la costante reticolare del primo rimane uguale a quella del silicio, nel piano parallelo all’interfaccia fra i due materiali; lungo la direzione perpendicolare si ha, invece, una dilatazione del cristallo, con un conseguente aumento della costante reticolare [10]. Pertanto la simmetria cristallina cambia e l’entità del cambiamento dipende sia dal rapporto percentuale fra silicio e germanio, sia dalla distribuzione casuale con cui gli atomi dei due elementi si posizionano nei siti del cristallo: questo modifica la matrice delle piezoresistività, con un effetto che

dipende anche dal drogaggio. Una prima valutazione teorica e sperimentale dei coefficienti di piezoresistività, è stata fatta nel 2004: se ne citano i risultati e si rimandano eventuali approfondimenti al riferimento [10]. A causa della simmetria reticolare del silicio-germanio, la matrice delle piezoresistività del silicio germanio ha la stessa configurazione di quella del silicio, ma con sei coefficienti indipendenti (π₁₁, π₁₂, π13, π33, π44, π66) e, ovviamente, con diversi valori.

Le ricerche attuali stanno ancora lavorando, per relazionare questi coefficienti alla struttura delle bande del materiale. Sono stati fatti esperimenti con il Si0.9Ge0.1, ed è stato ricavato il valore di π66, per due diversi drogaggi: con cm

18 10 = A N -3 si è ottenuto 66 136 10 11 Pa − ⋅ = π -1 ; con N_A =1019 cm-3 si ha 66 87 10 11 Pa − ⋅ = π -1 .

Non è stato ricavato il valore degli altri coefficienti, tuttavia, da un’analisi teorica, sembra che in generale il SiGe abbia maggiori proprietà piezoresistive, rispetto al silicio; questo importante aspetto aprirebbe nuove strade di ricerca per il silicio-germanio, rendendolo un materiale ideale per la fabbricazione di MEMS piezoresistivi.

Le strutture discusse in questa tesi sono state simulate con un programma ad elementi finiti, nel quale si sono dovuti specificare, ovviamente, i valori dei coefficienti di piezoresistività del materiale; poiché, per il silicio-germanio, tali valori non sono ancora disponibili, si è deciso di usare quelli del silicio. Naturalmente, questo tipo di scelta conduce ad un modello fisico diverso da quello reale; tuttavia, lo scopo della tesi è scoprire che tipo di relazione c’è fra lo spostamento del dispositivo (in termini di angolo di torsione) e la quantità elettrica misurata (in termini di variazione di resistenza). Tale relazione non dipende dai valori dei coefficienti di piezoresistività, pertanto si possono usare quelli del silicio, in attesa di conoscerli anche per il silicio-germanio.

2.2 Microrisonatori torsionali in silicio-germanio

Segue ora uno studio di una particolare struttura a microrisonatori torsionali, già citata nell’introduzione di questo capitolo: se ne riportano il layout, i parametri tecnologici ed un’analisi delle tensioni da applicare al modello elettrico equivalente.

2.2.1 Layout

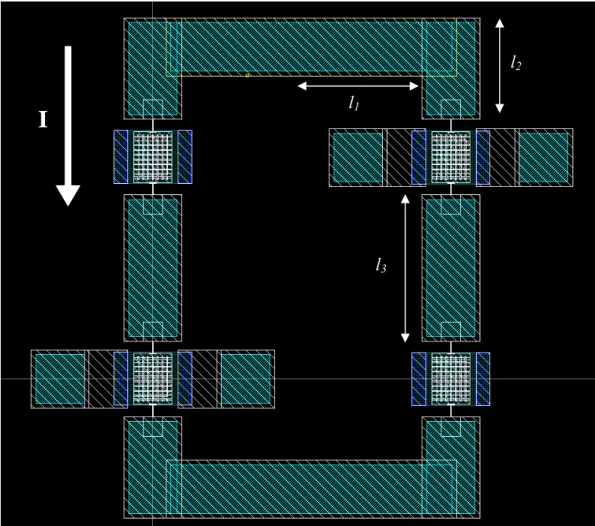
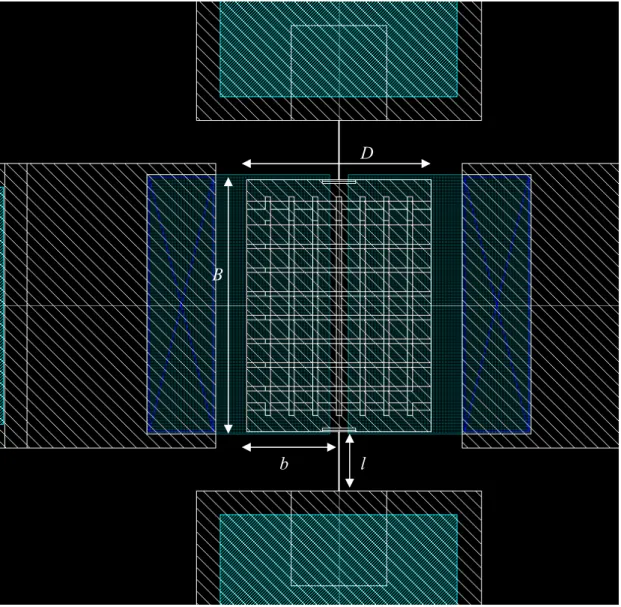
Si riportano due immagini, dimensionate, del layout della struttura sotto osservazione [11]:

l1

l3

I

l2

D

B

b l

FIGURA 2.3: Ingrandimento del layout, contenente un singolo risonatore.

La figura 2.2 mostra l’intera struttura: i quattro risonatori in SiGe (in bianco) sono collegati fra loro con delle piste di SiGe sormontate da alluminio (celeste). Ciascun risonatore è formato da un piatto e da due molle di sostegno che, con il loro comportamento elastico, permettono la torsione (si osservi la figura 2.3); il diaframma presenta due fessure in corrispondenza degli estremi, che hanno il compito di assorbire eventuali deformazioni compressive o tensili delle molle: queste, infatti, devono funzionare solo in maniera torsionale. Il piatto è sospeso, un gap di aria lo separa dal substrato di silicio (drogato p) sottostante, e con questo forma un

condensatore: più precisamente, si hanno due zone di silicio n separate (in verde) che assieme alle superfici sovrastanti del piatto, formano due condensatori.

Ciascuna zona di silicio è collegata tramite un contatto (blu/viola) con una pista di SiGe sormontata da alluminio, che porta il segnale dall’esterno. A riposo, scorre una corrente I nel ponte di Wheatstone e i risonatori non subiscono deformazione; se si applica un segnale ad una delle zone di silicio p, che rappresentano le armature inferiori dei condensatori, si varia la tensione ai capi del relativo condensatore, facendo inclinare il piatto verso destra o verso sinistra e provocando la torsione delle molle di sostegno; la direzione dello spostamento angolare dipende da dove è stata applicata tensione, se al condensatore di destra, oppure a quello di sinistra. Si noti che solo due dei quattro risonatori presentano la parte di attuazione, mentre gli altri sono immobili: il motivo di questa scelta sarà spiegato nel paragrafo 2.2.2. Il diaframma presenta anche una serie di buchi di forma rettangolare che, dalle immagini di layout, forse non si distinguono: essi servono a far penetrare meglio l’attacco sotto lo strato di SiGe (il risonatore è, infatti, una struttura sospesa, realizzata con tecniche di microfabbricazione superficiale).

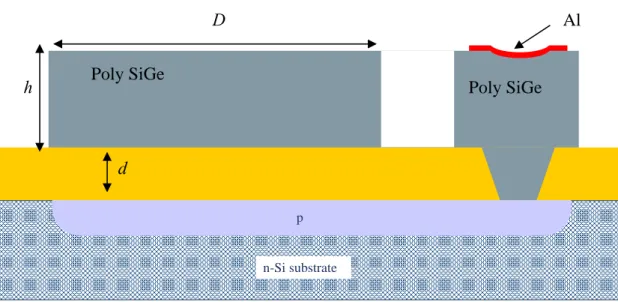
La figura 2.4 [12] mostra una sezione laterale della struttura, esplicitando la posizione dei due condensatori:

D

SiGe

Si p

h

In figura 2.6 [13] sono rappresentati i vari strati che formano la struttura: vi è raffigurata una parte della sezione del risonatore e il silicio-germanio ancorato, con il contatto di alluminio (in rosso). Si nota il diaframma (in grigio) di Si-Ge, con sotto lo strato sacrificale (giallo), che sarà eliminato per liberare la struttura.

D Al

FIGURA 2.5: Sezione laterale di un risonatore e della parte ancorata che porta il segnale.

Si riportano i dati di progetto che interessano questo studio: le dimensioni citate nelle figure 2.2, 2.3, 2.4 e 2.5, il modulo di Young, il coefficiente di Poisson, la densità e la resistività del SiGe usato per realizzare i risonatori.

Quantità Valore Descrizione

l 25 µm Lunghezza di una molla

B 106.2 µm Lunghezza del piatto di un risonatore

h 4 µm Altezza del piatto di un risonatore

d 1 µm Distanza fra le armature del condensatore

D 78 µm Larghezza del piatto

b 39 µm Metà larghezza del piatto, corrispondente alla distanza fra l’asse della molla ed il termine del piatto

Al Al Al Poly SiGe h Poly SiGe d p n-Si substrate

a 4 µm Distanza fra l’asse della molla e l’inizio della superficie di silicio drogato p. È risultato impossibile indicare questa distanza sulla figura 2.3

b-a 35 µm Larghezza della superficie del condensatore

(b-a)*D 3717 µm2

Larghezza della superficie del condensatore

TABELLA 2.1 Inoltre, si ha che:

(

)

d B a b

C =ε₀ − , capacità del condensatore6.

La struttura analizzata è formata da silicio –germanio finemente policristallino, con grani colonnari; i dati relativi alla densità ed alle costanti elastiche riportano i seguenti valori [14]:

Densità ~ 3.4-3.46 g*cm-3

Modulo di Young7 (teorico): 146-148 GPa Rapporto di Poisson (teorico): ~ 0.23

Percentuale di germanio nella lega SiGe: 62-65 %

Poiché i dati disponibili forniscono solo due valori di costanti elastiche, si ipotizza che il silicio-germanio realizzato con il processo dell’IMEC sia isotropo.

6 2 12 0 2 C 8.859 10 m ×N ε _{= ⋅} − ⎡ ⎤ ⎢

⎣ ⎦⎥, costante dielettrica nel vuoto. 7

Si considerino le relazioni fra stress e deformazione (capitolo 1, paragrafo 1.2.1): si definisce modulo di Young _i ij ij c E S = , rapporto di Poisson _ij ii jj S S ν = − , modulo di taglio _ij ij ij G S τ =

2.2.2 Modello elettrico e metodi di misura

Si procede presentando il modello elettrico equivalente del layout di figura 2.2; esso è un ponte di Wheatstone, in cui due resistori (due risonatori) subiscono deformazione, mentre gli altri rimangono fermi. Sia il valore a riposo della resistenza di tali strutture, e sia

0

R

0

R + ∆ il valore dopo l’applicazione del momento torcente. Ciascun R

risonatore soggetto a torsione può essere schematizzato con due semi-resistenze in serie del valore 1

(

₀

2 R + ∆ ; dal punto di contatto di queste resistenze (che si trova a R

)

metà lunghezza del piatto) si fanno partire i due condensatori (citati nel paragrafo 2.2.1), che collegano il diaframma al substrato di silicio. Ne deriva lo schema elettrico illustrato nella figura 2.5, a cui sono state aggiunte le varie tensioni che regolano il funzionamento del dispositivo. Sono state calcolate (con il metodo analitico di Grabel) le frequenze di polo dei condensatori e si sono ottenuti valori dell’ordine di 1010 Hz; tali valori sono molto maggiori rispetto alle frequenze con le quali sarà pilotato il circuito (per approfondimenti sui valori delle frequenze utilizzate, consultare il secondo paragrafo del capitolo 6), pertanto le capacità possono essere considerate come circuiti aperti e si fanno agire solo le resistenze ed i generatori di tensione. Si è scelto, inoltre, di trascurare le resistenze delle piste di alluminio, perché molto inferiori ad . Il circuito deve fornire in uscita una tensione proporzionale all’angolo di torsione dei due risonatori (si impone la condizione di uguaglianza fra i due angoli di torsione); la tensione E polarizza il circuito, facendo scorrere corrente nella maglia e fissando il valore di che, assieme a , fissa la tensione ai capi del condensatore. è la tensione sul piatto del risonatore, mentre è la tensione del sottostante strato di silicio. Si prende, come uscita, la differenza di potenziale

0 R x V V_d c x V =V −V_d b x V d V u a

0 2 2 R ∆R + 0 R C Vx C Va 0 2 2 R ₊∆R _{0 Vd} 2 2 R ₊∆R E Vb Vx C C 0 R 0 2 2 R ₊∆R _Vd

FIGURA 2.6: Schema elettrico equivalente del dispositivo completo.

Si applica E come differenza di due tensioni, che chiamiamo V_p e −V_p: E=2V_p. Dall’analisi del circuito, si ottiene la tensione di uscita a riposo:

0 =

u

V ,

e si ottiene la stessa tensione, in seguito all’applicazione di una torsione:

R R R V V_{u p} ∆ + ∆ = 0 2

Si fa la ragionevole ipotesi che la variazione di resistenza sia molto inferiore a , quindi si ottiene: 0 R 0 u p R V V R ∆ ≅ (2.1)

La (2.1) mostra che la tensione di uscita è proporzionale alla variazione di resistenza, pertanto, assumendo come vera l’ipotesi che ∆ ≅R αθ2, si osserva che il dispositivo sotto osservazione permette di conoscere l’angolo θ di torsione, attraverso una misura piezoresistiva di tensione.

Un risonatore torsionale analizzato in maniera piezoresistiva è un sistema elettromeccanico che collega il momento torsionale m t( ) all’angolo θ e l’angolo alla variazione di resistenza. Lo schema a blocchi del sistema è il seguente (figura 2.7):

FIGURA 2.7: Schema a blocchi del sistema elettromeccanico torsionale

L’angolo di torsione è legato al momento, attraverso l’equazione del moto [12]:

2 2 ( ) ( ) ( ) t t ( ) m t I k t t t θ θ _β θ _θ ∂ ∂ = + + ∂ ∂

Dove I è il momento di inerzia della struttura a cui si applica il momento torcente,

β è il coefficiente di smorzamento, mentre k_θ è la costante elastica torsionale della molla (questa quantità sarà analizzata nel dettaglio nel capitolo 3, paragrafo 3.2). Se si lavora in frequenza, si ottiene la seguente funzione di trasferimento:

( )

2 0 0 ( ) 1 1 ( ) 1 j H j M j k j Q θ ω ω ω _{ω ω} ω ω Θ = = ⋅ ⎛ ⎞ −_{⎜ ⎟} + ⎝ ⎠ , m(t) θ(t) h(t) θ2(t) αθ2(t)=∆R Vu(t) (.)2 α h1(t)

dove ω₀ è la frequenza di risonanza, mentre Q è il fattore di qualità del filtro. Si ha:

( )

1 0 H k_θ = Valore in continua

(

0

)

Q H j k_θ

ω = Valore alla frequenza ω₀

La funzione di trasferimento è costante alle basse frequenze, presenta un picco in ω₀ e reietta le frequenze superiori, con una selettività tanto maggiore, quanto più elevato è il Q . ω₀ è la prima frequenza di risonanza del sistema e lo fa oscillare attorno all’asse delle molle di sostegno: esistono altre frequenze ω_0i, con i relativi modi di risonanza (si consulti il capitolo 6 per approfondimenti); in generale, la funzione di trasferimento del sistema può essere schematizzata con uno spettro a righe centrate nelle varie ω0i, in cui è presente anche la continua.

Si può scegliere, a questo punto, di sollecitare il risonatore con un angolo statico, oppure di aggiungere una componente dinamica: nel primo caso si ottiene, in uscita, una tensione continua, che può essere disturbata dal rumore a bassa frequenza e da eventuali offset introdotti dalla catena di misura. È preferibile, pertanto, che il segnale di uscita abbia uno spettro a righe e filtrare la componente frequenziale più adatta. Si fa lavorare lo specchio alla frequenza di risonanza più bassa (torsione attorno all’asse delle molle di sostegno), e si fa in modo che tale oscillazione sia sovrapposta ad una torsione statica trascurabile rispetto a quella dinamica, cioè vogliamo:

1cos( 0 )

o t

θ θ θ= + ω , dove θo θ1.

Si impone, inoltre, che il valore dell’angolo dinamico θ₁ sia vicino a quello di pull-in (massimo angolo di torsione possibile, in corrispondenza del quale il piatto giunge a toccare il substrato di silicio). Sia θ_pin tale angolo; il suo valore è stato calcolato [6] e risulta essere:

0.65o 0.0112

pin rad

θ = = ,

dove θpin ≈ . θ1

Si ottiene, infine, la relazione fra il momento applicato e l’angolo di torsione, che servirà per ricavare un’espressione per θ :

( ) k m Q θ θ = θ a frequenza ω₀. ( )mθ =k_θθ in continua.

Si assumono le seguenti ipotesi:

• Il risonatore si muove solo in corrispondenza delle frequenze di risonanza, per cui:

( )

(

0

)

Q H j H j k_θ

ω = ω = alla frequenza di risonanza

H(0) 1

k_θ

= in continua.

H j

( )

ω = per tutte le altre frequenze. 0 • Si trascura il contributo di R∆ nel calcolo di , per cui: V_x

2

p x

V

V = .

(

2 2 1 1 ( ) 2 c 2 x C C mθ V V θ θ Vd

)

∂ ∂ = ⋅ = − ∂ ∂ (2.2) Poiché 2 p x V V = , si ottiene: 2 1 ( ) 2 2 p d V C mθ θ ⎛ ⎞ ∂ = _⎜ − ∂ ⎝ V ⎟ (2.3) ⎠

La capacità C è una funzione non lineare dell’angolo di inclinazione ed è stata espressa come [12]: 0 ( ) B lnd a C d b ε θ θ θ θ − = ⋅ − , (2.4)

dove si ricorda che θ presenta una parte statica ed una dinamica. A causa dei piccoli valori degli angoli in gioco, si fa l’ipotesi che la variazione di capacità in funzione di θ sia costante e pari al suo valore calcolato in θ =0. Si scrive, quindi:

0 C θ θ ₌ ∂ = ∂ C , dove:

(

2 2

)

2 0 2 o b a B C d θ ε θ ₌ − ∂ ₌ ∂ (2.5)

Tutti i parametri presenti al secondo membro dell’equazione (2.5) sono stati definiti nel paragrafo 2.2.1. Dalle (2.2), (2.3) e (2.5) si ottiene:

(

)

2 2 2 2 2 1 ( ) 2 2 4 2 o p d b a B V V m V d ε θ = ⎛_⎜ − ⎞_⎟ = − ⎛_⎜ − ⎞_⎟ ⎝ ⎠ ⎝ ⎠ C p V_d (2.6)

Si osserva che il momento (e, conseguentemente, l’angolo) dipende dalle tensioni e . È necessario, quindi, uno studio di tali funzioni, per ricavare la configurazione più adatta al nostro scopo.

p

V

d

V

Si scelgono tre diverse configurazioni:

1) 1 0 ( ) cos( ) p po d d V V V t V ω t = = 2) 1 1 1 0 ( ) cos( ) ( ) cos( ) p po p d d V t V V t V t V t ω ω = + = 3) p( ) p1cos( 0 ) d do V t V t V V ω = =

Per quanto riguarda il secondo caso, si sceglie di applicare anche una frequenza ω₁, lontana da tutte le frequenze di risonanza, il cui scopo è permettere l’estrazione del segnale di uscita ad una frequenza intermedia (in questo capitolo sarà dettagliatamente spiegato il motivo di questa scelta).

Si analizzano i 3 casi e si sviluppano i conti, per ricavare un’espressione di R∆ e . V_u

Caso 1): 1 0 ( ) cos( ) p po d d V V V t V ω t = =

Poiché, in questo caso,

2 po x V V = , e considerando la (2.6), si ricava:

[

]

2 1 0 1 ( ) cos( ) 2 x d mθ = C V −V ω t =

2 2 2 1 1 0 1 0 1 cos(2 ) 2 cos( ) 2 2 2 d d x x d V V V ω t V V ω ⎡ ⎤ = _⎢ + + − _⎥ ⎣ ⎦ C t = 2 2 2 1 1 0 1 1 cos(2 ) cos( ) 2 4 2 2 po d d po d V V V t V V t ω ω ⎡ ⎤ = _⎢ + + − _⎥ ⎢ ⎥ ⎣ ⎦ C ₀ , Poiché ( )mθ =k_θθ in continua e ( )m k Q θ

θ = θ a frequenza ω₀, anche l’angolo θ

presenta una componente continua ed una sinusoidale: 2 2 1 1 0 1 1 ( ) cos( ) 2 4 2 po d po d V _{V Q} t V k_θ k_θ θ = ⎡⎢ ⎛⎜_⎜ + ⎞⎟_⎟− V ω t ⎤⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦ C

Si ha, quindi, che:

1 0 ( )t _o cos( t) θ =θ θ+ ω , dove 2 2 1 0 1 2 4 2 po d V V kθ θ = ⎛_⎜⎜ + ⎞_⎟⎟ ⎝ ⎠ C e ₁ 1 ₁ 2 po d Q V V kθ θ = − C .

La componente a 2ω₀ è stata eliminata dal filtro del risonatore.

Poiché ∆ =R αθ2, la variazione di resistenza presenta, come l’angolo ed il momento, una parte statica ed una dinamica ed è:

2 2 2 2 1 1 0 2 ₂ 2 ₂ 2 2 2 2 1 1 0 1 1 1 ( ) cos( ) 4 4 2 1 cos(2 ) 2 cos( ) 4 2 2 po d po d po po d d po d V V Q R t V V t k k V V Q Q Q V V t V V k k k θ θ θ θ θ α ω α η ω η ω ⎡ ⎛ ⎞ ⎤ ∆ = ⎢ ⎜_⎜ + ⎟_⎟− ⎥ = ⎢ ⎝ ⎠ ⎥ ⎣ ⎦ ⎡ _{⎛ ⎞ ⎛ ⎞} ⎤ ⎢ ⎥ = +_{⎜ ⎟} +_{⎜ ⎟} − ⎢ ⎝ ⎠ ⎝ ⎠ ⎥ ⎣ ⎦ C C ₀t

dove η 2 2 1 1 4 2 po d V V k_θ ⎛ ⎞ = ⎜_⎜ + ⎟_⎟ ⎝ ⎠ Dalla (2.1) si ricava: 2 ₂ 2 ₂ 2 2 2 2 1 1 0 1 0 0 ( ) ( ) ( ) cos(2 ) 2 cos( ) 4 2 2 po po po u p d d po d V V V R t Q Q Q V t V t V V t V V t R R kθ kθ kθ α ⎡η ⎛ ⎞ ⎛ ⎞ ω η ω₀ ⎤ ∆ _{⎢ ⎥} = = +_{⎜ ⎟} +_{⎜ ⎟} − ⎢ ⎝ ⎠ ⎝ ⎠ ⎥ ⎣ ⎦ C

Si osserva che la tensione di uscita presenta una parte in continua e due componenti frequenziali, rispettivamente a frequenza ω₀ e 2ω₀.

Caso 2): 1 1 1 0 ( ) cos( ) ( ) cos( ) p po p d d V t V V t V t V t ω ω = + = Si ottiene: 1 1 ( ) cos( ) 2 2 po p x V V V t = + ωt

Si sceglie una frequenza intermedia ω1, che sia abbastanza più grande di ω0 da non far oscillare il risonatore, e che sia lontana dalle altre frequenze di risonanza. Questo permette di poter considerare V t_x( ) costante nel calcolo dell’angolo di torsione. L’espressione di ∆R t( ) è stata ricavata nel caso precedente, mentre la tensione di uscita diventa: 2 ₂ 2 ₂ 2 2 2 2 1 1 0 1 0 0 1 1 ( ) 1 ( ) ( ) cos(2 ) 2 cos( ) 4 2 2 cos( ) po po u p d d po d po p V V R t Q Q Q V t V t V V t V V t R R k k k V V t θ θ θ α η ω η ω ω 0 ⎡ _{⎛ ⎞ ⎛ ⎞} ⎤ ∆ _{⎢ ⎥} = = +_{⎜ ⎟} +_{⎜ ⎟} − ⋅ ⎢ ⎝ ⎠ ⎝ ⎠ ⎥ ⎣ ⎦ ⎡ ⎤ ⋅_⎣ + _⎦= C

[

2 3 2 3 2 2 2 2 2 1 1 0 1 0 2 ₂ 2 2 1 1 1 cos(2 ) 2 cos( ) 4 2 2 cos( 2 po po po d d po d po d p V V Q Q Q V V V t V V R k k k V Q V V k θ θ θ θ α η ω η ω η ω ⎛ ⎞ ⎛ ⎞ = +_{⎜ ⎟} +_{⎜ ⎟} − ⎝ ⎠ ⎝ ⎠ ⎡ _{⎛ ⎞} ⎤ ⎢ ⎥ + _{+ ⎜ ⎟} ⎢ ⎝ ⎠ ⎥ ⎣ ⎦ C ₀t +

[

]

[

]

2 ₂ 2 1 1 1 0 1 0 1 1 1 1 0 1 0 ) cos((2 ) ) 4

cos((2 ) ) cos(( ) ) cos(( ) )

po d p po d p V Q t V V t k Q t t V V V t t k θ θ ω ω ω ω η ω ω ω ω ⎛ ⎞ + _{⎜ ⎟} + ⎝ ⎠ + − − + + − +

Adesso la tensione di uscita presenta una componente continua e 7 componenti frequenziali: ω₀, 2ω₀, ω₁, 2ω₁, 2ω ω₀+ , ₁ 2ω ω₀− , ₁ ω ω₁+ ₀ e ω ω₁− ₀. Caso 3): 1 0 ( ) cos( ) p p d do V t V t V V ω = = 1 0 ( ) cos( ) 2 p x V V t = ω t

È un caso analogo al primo:

2 1 0 0 1 ( ) cos( ) 2 2 p d V mθ = ⎡_⎢ ω t −V ⎤_⎥ = ⎣ ⎦ C 2 2 1 2 1 0 0 1 0 1 cos(2 ) cos( ) 2 8 8 p p d p d V V V ω t V V ω ⎡ ⎤ = _⎢ + + − _⎥ ⎢ ⎥ ⎣ ⎦ C ₀t

L’angolo θ( )t diventa: 2 1 2 0 1 0 1 1 ( ) cos( ) 2 8 p d p d V _Q t V V V k_θ k_θ θ = ⎡⎢ ⎛⎜_⎜ + ⎞⎟_⎟− ω₀t ⎤⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦ C 2 ₂ 2 ₂ 1 1 2 2 2 2 0 0 0 1 0 1 ( ) cos(2 ) 2 cos( ) 4 2 2 p p d d p d V V Q Q Q 0 R t V V t V V k_θ k_θ k_θ α ⎡⎢γ ⎛ ⎞ ⎛ ⎞ ω γ ω ⎤⎥ ∆ = +_{⎜ ⎟} +_{⎜ ⎟} − ⎢ ⎝ ⎠ ⎝ ⎠ ⎥ ⎣ ⎦ C t , dove γ = 2 1 2 0 1 8 p d V V kθ ⎛ ⎞ + ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

Si ottiene la seguente tensione di uscita:

0 ( ) ( ) ( ) u p R t V t V t R ∆ = = 2 ₂ 2 ₂ 1 2 2 1 2 1 2 0 0 0 0 1 0 0 0 3

cos( ) cos(3 ) (1 cos(2 ))

4 4 4 p p p d d p d V Q V Q V Q V t V t V V R α γ k_θ ω k_θ ω γ k_θ ω ⎡⎛ _{⎛ ⎞} ⎞ _{⎛ ⎞} ⎤ ⎢⎜ ⎟ ⎥ = +_{⎜ ⎟} +_{⎜ ⎟} − + ⎜ ⎟ ⎢_{⎝ ⎝ ⎠ ⎠ ⎝ ⎠} ⎥ ⎣ ⎦ C t Osservazioni:

Fra i tre casi, qual è il migliore? È preferibile usare la seconda configurazione, che permette di prelevare il segnale di uscita ad una frequenza intermedia. È pericoloso, infatti, sintonizzarsi su una frequenza multipla di ω₀, dove possono finire componenti indesiderate, a causa della non perfetta linearità del termine k_θθ nell’equazione del moto.

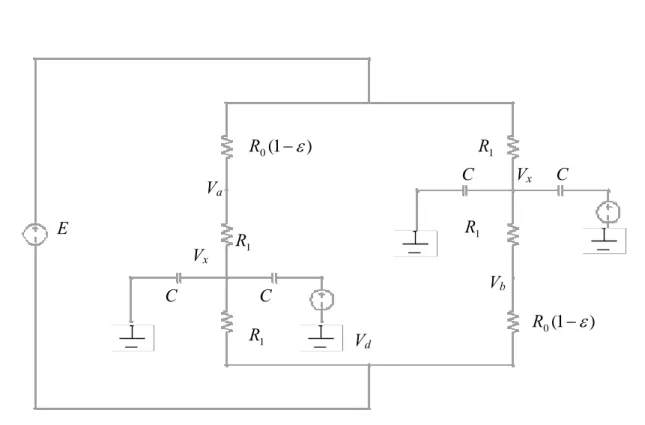
Analisi del mismatch:

Le resistenze a riposo non sono, in valore, perfettamente uguali al valore nominale 0

R . Si genera, perciò, un errore di matching che si somma ad altri eventuali disturbi

nel calcolo di R∆ , e . V_x V_u

Si riporta il ponte di Wheatstone della figura 2.6, in cui sono presenti disturbi di matching sulle resistenze, nel caso peggiore, cioè quando tali errori si sommano in uscita: ) 1 ( 0 −ε R R₁ C Vx C Va 1 R E 1 R Vx Vb C C ) 1 ( 0 −ε R 1 R _Vd

FIGURA 2.8: Schema circuitale del ponte di Wheatstone, in cui sono stati esplicitati gli errori dovuti al mismatch.

Il parametro ε rappresenta l’errore percentuale di matching, mentre ) 1 ( 2 2 0 1 ⎟ +ε ⎠ ⎞ ⎜ ⎝ ⎛ ₊∆ = R R R .

Le funzioni , e diventano, rispettivamente, , e . Tali funzioni devono essere, dunque, ricalcolate:

) (t R ∆ V t_x( ) V t_u( ) ∆R'(t) V_x'(t) V_u'(t) 2 ' =λθ ∆R , dove )λ =α(1+ε . Si ottiene: R R = + ∆ ∆ ' (1 ε) 2 ) ( ) 1 ( ) ( ' _t V t V_x = +ε p ' ' 0 0 0 0 2 ( ) ( ) ( ) ( ) 2 ( ) u p p p p R R R R V t V t V t V t V t R R R ε _{ε ε} ∆ + ∆ ∆ ≅ = + + Si definiscono: ( ) ( ) 2 p x V t

v t =ε errore di matching riportato sulla tensione V_x

0 ( ) 2 ( ) u R v t V t R ε⎛ ∆ ⎞ = _⎜ + _⎟

⎝ ⎠ p errore di matching riportato sulla tensione Vu

Si è ipotizzato che l’ordine di grandezza di ε sia 10-2; i valori di e di che ne conseguono, pertanto, possono essere significativi, superando il segnale utile.

( )

x

v t v t_u( )

Analizzando di nuovo il caso 2), si ottiene:

1 1 ' 1 1 ( ) cos( ) cos( ) 2 2 2 2 po p po p x V V V V V t =⎡_⎢ + ωt ⎤_⎥+ε_⎢⎡ + ωt ⎤_⎥ ⎣ ⎦ ⎣ ⎦

2 _{2 2 2}

' 2 1 1

1 0 0 1 0

1 1

( ) (1 ) cos( ) (1 ) cos(2 ) (1 ) cos( )

2 2 2 4 2 2 po po d d d po d V V V V m θ = _⎢⎡ + −ε V ω t ⎤_⎥ = _⎢⎡ +ε + + ω t −V V +ε ω t _⎥⎤ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ C C 2 2 ' 2 1 ' 1 0 1 1 1 ( ) (1 ) (1 ) cos( ) cos( ) 2 4 2 po d po d o V V Q t V V t kθ kθ ' 0t θ = ⎢⎡ _⎜⎜⎛ +ε + ⎞⎟_⎟− +ε ω ⎤⎥=θ − ⎢ ⎝ ⎠ ⎥ ⎣ ⎦ C θ ω 2 ' 2 1 0 2 ₂ 2 ₂ 2 2 2 2 2 2 1 1 ( ) (1 ) (1 ) cos( ) 4 (1 ) (1 ) (1 ) cos(2 ) 4 2 2 2 po d po po d d po Q R t V V t k V V Q Q V V k k Q V V k ε θ ε θ θ ε θ α _{ε η ε ω} α 0t ε η ε ε η ⎡ ⎤ ∆ = + _⎢ − + _⎥ = ⎣ ⎦ ⎡ _{⎛ ⎞ ⎛ ⎞} ⎢ = + +_{⎜ ⎟} + +_{⎜ ⎟} + ⎢ ⎝ ⎠ ⎝ ⎠ ⎣ − C C 1(1 ) cos( 0 ) d ε ω t ⎤ + _⎥ ⎦ ω dove 2 ₂ 2 1 1 (1 ) 4 2 po d V V k ε θ η = ⎡_⎢ +ε + ⎤_⎥ ⎢ ⎥ ⎣ ⎦

Si ottiene un nuovo valore di V t_u( ):

[

2 ₂ ' ' 2 2 2 1 0 0 2 ₂ 2 2 1 0 1 0 1 2 (1 ) (1 ) 4 2 (1 ) cos(2 ) 2 2 (1 ) cos( ) 2 po u p p d po d po d po V R Q V V V V R R k V Q V t k Q V V t V k ε θ θ ε θ ε α ε η ε ε ω η ε ω ε ⎧ ⎡ _{⎛ ⎞} ∆ ⎪ _⎢ = + =_⎨ + +_{⎜ ⎟} + + ⎢ ⎝ ⎠ ⎪ _⎣ ⎩ ⎛ ⎞ +_{⎜ ⎟} + − ⎝ ⎠ ⎫ ⎤ ⎪ − + _⎥+ _⎬ ⎪ ⎦ ⎭ C

]

1cos( 1 ) p V ωt + 2 (2.7)

Osservazioni:

L’errore di matching si riporta su tutte le frequenze presenti in uscita, e vi si riporta in maniera non lineare, pertanto non è possibile eliminarlo. È però possibile toglierlo dall’espressione di θ, cambiando la configurazione delle tensioni applicate, per annullare l’effetto della V_x ( che contiene il disturbo).

Infatti, poiché (1 ) 2 p x V V = +ε e ( ) 1

[

2 2 x d mθ = C V −V

]

, l’errore contenuto in θ dipende solo da V_x (V_d è imposto dall’esterno).

La seguente configurazione: 1 1 1 0 ( ) cos( ) ( ) cos( ) p p d do d V t V t V t V V t ω ω = = +

permette di rendere minimo l’effetto del matching, eliminando il contributo di in questo modo (per semplicità, sono stati omessi gli apici):

x V

[

]

2

[

]

2 1 0 2 2 2 1 1 0 1 1 1 ( ) ( ) cos( ) 2 2 1 cos(2 ) 2 cos( ) 2 2 2 d do d d d do do d m V t V V t V V V t V V θ ω ω ω = = + = 0t ⎡ ⎤ = _⎢ + + + _⎥ ⎣ ⎦ C C C

Quindi l’angolo di torsione diventa:

2 2 1 1 0 1 0 1 1 2 cos( ) cos( 2 2 d do do d o V Q V V V t k_θ k_θ t) θ = ⎡_⎢ ⎛_⎜ + ⎞_⎟+ ω ⎤_⎥=θ θ+ ω ⎝ ⎠ ⎣ ⎦ C

Adesso l’angolo non dipende più dalla tensione , ma solo da . Si osserva, inoltre, che e sono inversamente proporzionali: possiamo aumentare l’uno e diminuire l’altro e viceversa.

p

V V_d

do

V V_d1

Ovviamente non è possibile cancellare del tutto il disturbo, perché questo è presente nel termine che moltiplica α . Infatti:

2 2 1 1 0 1 0 1 1 ( ) 2 cos( ) cos( ) 2 2 d do do d o V Q t V V V t k_θ k_θ t θ = ⎡_⎢ ⎛_⎜ + ⎞_⎟+ ω ⎤_⎥=θ θ+ ω ⎝ ⎠ ⎣ ⎦ C

Per cui la variazione di resistenza diventa:

2 2 2 2 1 1 0 2 2 2 2 2 2 2 2 1 1 0 1 2 2 1 (1 ) 1 ( ) 2 cos( ) 4 2 (1 ) 2 2 cos(2 ) 4 cos( ) , 4 1 dove 2 d do do d do d do d do d d do V Q R t V V V t k k Q Q Q V V V V t V V t k k k V V k θ θ θ θ θ θ α ε _ω α ε _{ζ ω ζ} ζ ⎡ ⎛ ⎞ ⎤ + ∆ = _{⎢ ⎜} + _⎟+ _⎥ = ⎝ ⎠ ⎣ ⎦ ⎡ _{⎛ ⎞ ⎛ ⎞} ⎤ + _{⎢ ⎥} = + _{⎜ ⎟} + _{⎜ ⎟} + ⎢ ⎝ ⎠ ⎝ ⎠ ⎥ ⎣ ⎦ ⎛ ⎞ = _⎜ + _⎟ ⎝ ⎠ C C ω₀

2 2 2 2 2 2 2 2 1 1 0 0 ( ) (1 ) ( ) 2 ( ) 2 2 cos(2 ) 4 u p do d do d R t Q Q V t V t V V V V t R R kθ kθ α ε ε ⎧ ⎡ζ ⎛∆ ⎞ ⎪ + _⎢ ⎛ ⎞ ⎛ ⎞ =_⎜ + _⎟ =_⎨ + _{⎜ ⎟} + _{⎜ ⎟} ⎢ ⎝ ⎠ ⎪_⎩ C _⎣ ⎝ ⎠ ⎝ ⎠ ω0 + 1 0 1 1 2 2 2 2 2 1 1 1 0 4 cos( ) 2 cos( ) (1 ) 2 cos( ) 4 do d p do d p Q V V t V t k Q V V V t R k θ θ ζ ω ε ω α ε _{ζ ω} ⎫ ⎤ ⎪ + _⎥+ _⎬ = ⎪ ⎦ ⎭ ⎧⎡ _{⎛ ⎞} ⎤ + _{⎪⎢ ⎥} = _⎨ + _{⎜ ⎟} + ⎢ ⎝ ⎠ ⎥ ⎪⎣ ⎦ ⎩ + C

[

]

[

]

2 2 2 1 1 0 1 0 1 1 1 1 0 1 0 1 1 cos((2 ) ) cos((2 ) )

2 cos(( ) ) cos(( ) ) 2 cos( )

do d p do d p p Q V V V t t k Q V V V t t V t k θ θ ω ω ω ω ζ ω ω ω ω ε ⎛ ⎞ + + − + ⎜ ⎟ ⎝ ⎠ ⎫ + + + − _⎬+ ⎭ ω Osservazioni:

Non è possibile eliminare completamente i disturbi di matching, perché il fattore )

1

( + moltiplica la Rε ∆ , quindi accompagna tutte le componenti frequenziali della tensione di uscita. Tuttavia, la forma della è migliore in questo ultimo caso (rispetto alla (2.6)): il parametro

( )

u

V t

ε è, infatti, presente in maniera lineare. Si può, dunque, misurare la tensione di uscita, a meno di un errore del 1%; è, inoltre, consigliabile, eliminare le componenti a frequenza ω₁, per togliere 2εV_p1cos(ω₁t) dalla sommatoria. Ovviamente, nel sistema studiato sono presenti altri disturbi, oltre al mismatch, di cui non si è tenuto conto; nel capitolo 6 sarà fatto un breve studio sul rumore introdotto dalle resistenze, per valutare quali sono i valori di tensione più

adatti per polarizzare il circuito, evitando che il segnale in uscita sia coperto dal rumore.

2.3 Conclusioni

In questo capitolo è stata presentata una struttura micromeccanica torsionale, formata da quattro microrisonatori, utilizzabile per la caratterizzazione piezoresistiva del silicio-germanio. È stato successivamente studiato il circuito equivalente ed è stata trovata la configurazione di tensioni più adatta per polarizzare il circuito e per minimizzare i disturbi dovuti al mismatch.