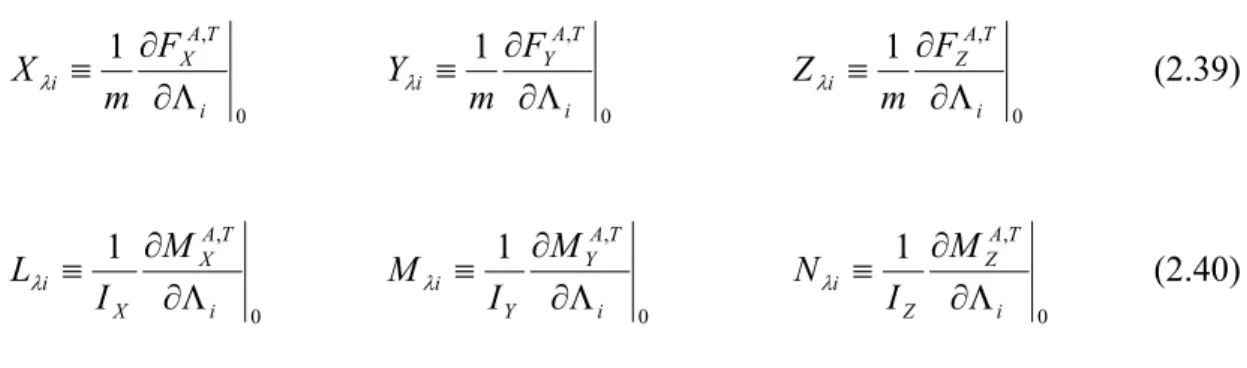1. 6

2. MODELLO MATEMATICO PER LO STUDIO DELLA

DINAMICA DEL VELIVOLO.

2.1 - INTRODUZIONE.

In questo capitolo vengono definiti il modello matematico utilizzato nell’ambito dello studio della dinamica del volo atmosferico e le ipotesi alla base delle equazioni del moto del velivolo esplicitate in forma completa. Questo è costituito da equazioni differenziali non lineari, non risolubili in forma chiusa. Al fine di facilitare la trattazione, sono utilizzate nella loro forma linearizzata, riferite ad una terna cartesiana in assi stabilità. La tecnica adottata per la linearizzazione, fa uso di un approccio in variabili di stato che può essere impiegato per affrontare un’ampia tipologia di problemi

2.2 - EQUAZIONI DEL MOTO NELLA TERNA ASSI CORPO.

Per la valutazione dell’andamento temporale dei carichi su un velivolo, in risposta ad una generica manovra cui esso sia sottoposto, si considerano le equazioni del moto che descrivono la dinamica completa di un corpo rigido con massa costante o lentamente variabile. Il sistema di riferimento adottato per la scrittura delle equazioni, è quello “assi corpo”, in cui coincide con l’asse longitudinale della fusoliera del velivolo, è rivolto verso il ventre del velivolo, edY è diretto secondo l’apertura alare in modo tale da rendere la terna levogira. L’origine del sistema è nel centro di massa del velivolo ed il piano

B

X Z_B

B

(

XB,ZB

)

è assunto coincidente con il piano longitudinale di simmetria per lo stesso.

Le equazioni d’equilibrio dinamico delle forze si ricavano dalle equazioni cardinali della meccanica newtoniana, valide per qualunque corpo rigido soggetto ad un sistema di forze e momenti. Per un velivolo, tale sistema di forze e momenti dipende complessivamente dalle seguenti forze agenti:

• Forze legate all’apparato propulsivo (_FrT)_.

• Forza di natura gravitazionale dovuta alla massa del velivolo(_FrW)_.

Le forze di natura aerodinamica e le coppie da queste generate,

(

_FA_,MA

)

_{, dipendono dal}

moto relativo del velivolo rispetto all’atmosfera mediante espressioni del tipo:

F A _SV2_C 2 1_ρ = F M A _SV2_C 2 1_ρ = M

I coefficienti aerodinamici C e sono dipendenti da numerose variabili, tra cui il numero di mach, gli angoli di incidenza e di derapata, le componenti di velocità lineare ed angolare del velivolo e le rispettive derivate temporali. Per quanto detto, risulta conveniente valutare ed

F CM

A

F _{M con riferimento ad una terna solidale al velivolo.} A

Considerazioni analoghe valgono anche per le forze e coppie di natura propulsiva

(

_{F ,}T _MT

)

_{, per cui è vantaggioso scrivere le equazioni del moto con riferimento ad una}

terna assi corpo. Definite

(

U,V,W

)

e

(

P ,,Q R

)

le componenti dei vettori, valutati rispetto alla terna inerziale, rispettivamente, della velocità lineare Vr e della velocità angolare Ωr del centro di massa del velivolo sulla stessa terna assi corpo, le due equazioni cardinali della meccanica newtoniana forniscono 6 equazioni differenziali non lineari nelle incognite

. Per determinare il moto del velivolo, occorre aggiungere ulteriori equazioni di natura cinematica che leghino le derivate degli angoli di Eulero alle componenti di R Q, , Ω P W V U, , ,

(

Φ ,,Θ Ψ

)

r

. Inoltre, per determinare la posizione del centro di gravità del velivolo in funzione del tempo, si definiscono X_N, X_E, H rispettivamente la distanza percorsa verso

nord, verso est e la quota di volo. Si ottengono così 12 equazioni differenziali non lineari del primo ordine, che descrivono completamente il moto del velivolo. Queste sono riassunte nella tabella 2.1. Si indicano con

(

A,T

)

Z T A Y T _F , _F , _, A X F , ed

(

AT

)

Z T A Y T A X M M , , , _{, ,} M le componenti

propulsive )(_FrT _{, e delle coppie da queste generate rispetto al centro di massa del velivolo.}

Il termine rappresenta la massa del velivolo, mentre e la generica componente del tensore d’inerzia in assi corpo. Per completezza si introduce l’angolo di pendenza della traiettoria

m I_KH

γ , definito come l’angolo che il vettore Vr forma rispetto al piano orizzontale locale. U& + RU V&+ W& + T A, X I P& − T A Y, Y I Q& + T A, Z I R& − = Φ P& = Θ Q& = Ψ Q& Θ sin = X&_N sin

)

Θ Φ = X&_E

)

Ψ V U H& = Θ r (2.1) m F g RV QW AT X / sin_Θ+ , − = − (2.2) m F g PW AT Y / cos sin_{Φ Θ+} , = − (2.3) m F g QU PV AT Z / cos cos_{Φ Θ+} , = − (2.4)

(

Z Y

)

XZ X XZ QR I I PQI M I R& + − − =

(

IX IZ

)

R IXZ P IXZ M PR _{− −} 2 ₊ 2 _{= (2.5)} (2.6)

(

Y X

)

XZ Z XZ PQ I I QRI M I P& + − + = (2.7) Θ Φ + Θ Φ

+Qsin tan Rcos tan

(2.8) Θ − Φ sin cos R Θ Φ + Θ Φ cos cos cos sin R (2.9)

(

− Φ Ψ+ Φ Ψ

)

+ + Ψ

Θcos cos sin cos

cos V

U

(

Φ Ψ+ Φ Θ Ψ

+W sin sin cos sin cos (2.10)

(

Φ Ψ+ Ψ

)

+

+ Ψ

Θsin cos cos sin sin sin

cos V

U

(

− Φ Ψ+ Φ Θ

+W sin cos cos sin sin (2.11)

γ sin cos cos cos sin sinΘ−V Φ Θ−W Φ = (2.12)

Tab. 2.1: Sistema completo di equazioni differenziali non lineari del primo ordine che descrivono il moto del velivolo.

2.3 - EQUAZIONI DEL MOTO IN VARIABILI DI STATO.

Le equazioni differenziali (2.1) – (2.12) che descrivono il moto del velivolo possono essere espresse fondamentalmente attraverso una relazione del tipo:

(

X,X,U

)

=0

f &r r r (2.13)

dove Xr è il vettore degli stati, Ur rappresenta il vettore degli ingressi e le componenti di

Xr ed Ur sono, a loro volta, funzioni del tempo.

(2.14)

[

T E N X H X R Q P W V U X ≡ , , , , , ,Φ,Θ,Ψ, , _,

]

La (2.13) presuppone che le forze e le coppie aerodinamiche e propulsive siano esprimibili in funzione di Xr , Ur ed X&r . Il vettore Ur contiene le variabili di comando su cui può intervenire il pilota, direttamente o indirettamente, per modificare la dinamica del velivolo. Nel caso di velivoli convenzionali, Ur è tipicamente costituito dalla posizione dell’equilibratore, degli alettoni, del timone di direzione e dalla posizione della manetta del motore, oltre ad eventuali ulteriori variabili, quali tabs, flaps ed altre. È importante notare che, le componenti di U compaiono implicitamente nelle espressioni delle forze e coppie di natura aerodinamica e propulsiva.

r

2.4 - LINEARIZZAZIONE DELLE EQUAZIONI DEL MOTO.

Le 12 equazioni differenziali (2.1) – (2.12) non consentono di determinare soluzioni in forma chiusa al problema della valutazione della risposta dinamica del velivolo. Nei casi pratici è però importante studiare il comportamento del velivolo per piccoli scostamenti rispetto a traiettorie stazionarie: per questi casi è possibile semplificare il problema, linearizzando le equazioni del moto. Questa operazione consiste nel determinare un punto di equilibrio (ovvero condizione di trim) e scrivere le equazioni differenziali del moto, rispetto a tale punto, utilizzando uno sviluppo di Taylor arrestato al primo ordine.

Considerando le equazioni del moto espresse in forma compatta secondo la (2.13), il velivolo si trova in una condizione di trim quando è possibile determinare un vettore degli stati Xv₀ ed un vettore degli ingressi Ur₀ costanti, e tali che:

(

0,X₀,U₀

)

=0

f r r (2.15)

Matematicamente, l’espressione linearizzata della (2.13), rispetto alla condizione di equilibrio indicata con il pedice 0, assume la forma seguente:

(

, ,

)

(

)

(

)

(

₀

)

0 0 0 0 0 0 = − ∂ ∂ + − ∂ ∂ + − ∂ ∂ ≅ U U U f X X X f X X X f U X X f &r &r _r r r _r r r &r r r &r _(2.16)

dove le derivate parziali:

0 0 0 , , U f X f X f r r &r ∂ ∂ ∂ ∂ ∂ ∂ X

, sono matrici Jacobiane da valutare nella condizione di equilibrio corrispondente ad r = Xr₀ ed Ur =Ur₀.

x X

Xr ≡ r₀ +r Ur =Ur₀ +ur (2.17)

Introdotti i termini stazionari e le perturbazioni xr ed ur rispetto alle condizioni di equilibrio, tenuto conto della (2.15) e della precedente simbologia (2.17), la relazione (2.16) si trasforma semplicemente nella (2.18).

u B x A x_& = + ε (2.18) Si è posto: 0 X f A _r ∂ ∂ ≡ , 0 U f B _r ∂ ∂ ≡ , 0 X f &r ∂ ∂ − ≡ ε (2.19)

Infine, poiché la matrice ε è non singolare, potendo scrivere A_=ε−1A _{e B=ε}−1_{B, si}

ricava:

Bu Ax

La relazione (2.20) rappresenta il sistema delle equazioni linearizzate del moto, in cui prende il nome di matrice degli stati e

A B matrice degli ingressi. Il processo di

linearizzazione descritto, viene applicato alle 12 equazioni differenziali: in analogia alla (2.17), la generica componente del vettore degli stati Xr viene sempre scomposta nella somma di un contributo di trim (componente stazionaria legata alle condizioni di equilibrio) ed un contributo di perturbazione (componente che determina l’allontanamento del sistema dalla condizione di equilibrio); per le componenti della velocità lineare V e della velocità angolare Ω

r

r

del centro di massa del velivolo, risulta:

v V Vr= r₀+r (2.21) ωr r r + Ω = Ω _{0 (2.22)}

(

0 0 0

)

0 U ,V ,W Vr = Ωr₀ =

(

P₀,Q₀,R₀

)

_(2.23)

(

u v w

)

vv = , , ωv =

(

p ,,q r

)

_(2.24)

Analogamente, per la risultante delle forze aerodinamiche e propulsive agenti sul sistema, e per la risultante dei momenti conseguentemente generati, si può scrivere:

T A T A

_F

_F

F

, _{0 0} 0

r

r

r

+

=

_M

AT

_M

A

_M

T 0 0 , 0

r

r

r

+

=

(2.25) T A T A T A _{F F} F , , 0 , v r r ∆ + = _MAT _MA,T _MA,T 0 , r r r ∆ + = (2.26)

Le equazioni cardinali delle forze e dei momenti (2.1) – (2.12) possono essere linearizzate, utilizzando direttamente la loro forma vettoriale. Le due equazioni cardinali della meccanica newtoniana, relative alla risultante ed al momento risultante (rispetto al centro di massa) delle forze esterne agenti sul velivolo, con evidente significato dei simboli, divengono: W T A _F F V m v m v mv_&+ Ωr ∧r+ r∧ r =∆r , +∆r 0 0 ω (2.27)

( ) ( )

_{I I M}AT I , 0 0 r r r r r r &+Ω ∧ ⋅ + ∧ ⋅Ω =∆ ⋅ω ω ω (2.28)

Le componenti del vettore _∆FrW _{derivano dalle variazioni delle componenti della forza}

gravitazionale, dipendente dall’accelerazione, riferite alla terna assi corpo e dovute al moto del velivolo. La forza gravitazionale dipende dalla accelerazione di gravità e dalla massa del velivolo, la quale è pensata concentrata nel baricentro. Nelle precedenti relazioni sono stati trascurati i termini del secondo ordine mωr ∧vr ed ωr∧ I

( )

⋅ωr , e si è tenuto conto del fatto che in condizioni di trim si ha, per definizione:

W T A _F F V m , ₀ 0 0 0 r r r r + = ∧ Ω

( )

_{I M}A,T 0 0 0 r v r = Ω ⋅ ∧ Ω (2.29)

A questo stadio si assume l’ipotesi per cui la condizione di trim corrisponde ad una situazione di volo rettilineo orizzontale con ali livellate, vettore di velocità appartenente al piano longitudinale di simmetria per il velivolo ed angolo di imbardata nullo, ovvero:

0

0 =

Ωr Φ₀ =Ψ₀ =0 V₀ =0 γ₀ =0 (2.30)

La condizione Ωr₀ =0 implica che sia: P₀ =Q₀ =R₀ =0. In questo modo le (2.27) e (2.28) si semplificano nel modo seguente:

m F m F V v AT W r r r r v &+ ∧ = ∆ + ∆ , 0 ω (2.31) T A M I r r , & ∆= ⋅ω (2.32)

La linearizzazione delle forze e dei momenti risulta facilitata avendo separato la parte gravitazionale da quella aerodinamica e propulsiva. La variazione _∆FrW _{risulta funzione}

degli angoli Φ e Θ, pertanto, essendo per ipotesi Φ₀ =0, si ha:

          Θ − Θ Θ − =      ∆ θ ϕ θ 0 0 0 sin cos cos g g g m F B W r (2.33)

Per quanto riguarda le forze e coppie di natura aerodinamica e propulsiva, in generale si indica con _Λr _∈Rn _{il vettore contenente tutte le variabili da cui dipendono F}A,T _{ed M}A,T_.

Si fa notare che generalmente risulta Λr ≠ Xr . Ponendo λr =Λr −Λr₀ ed indicando con il pedice 0 le condizioni di trim, si ottiene:

( )

r _r λr 0 , 0 , , Λ ∂ ∂ + Λ = AT AT T A _F F F

( )

r _r λr 0 , 0 , , Λ ∂ ∂ + Λ = AT AT T A _M M M (2.34)

Dalle precedenti si riconosce che:

∑

= ∂Λ ∂ = Λ ∂ ∂ = ∆ n i i i T A T A T A F F F 1 ₀ , 0 , , _λr _λ r

∑

= ∂Λ ∂ = Λ ∂ ∂ = ∆ n i i i T A T A T A M M M 1 ₀ , 0 , , _λr _λ r (2.35) dove: 0 , 1 , 0 , ,..., _      Λ ∂ ∂ Λ ∂ ∂ = Λ ∂ ∂ n T A T A T A _{F F} F r 0 , 1 , 0 , ,..., _      Λ ∂ ∂ Λ ∂ ∂ = Λ ∂ ∂ n T A T A T A _{M M} M v (2.36)

Introducendo esplicitamente le derivate di stabilità, in termini di componenti rispetto alla terna assi corpo si ha:

[

]

n T i n i n i i i i i i i B T A _{X Y Z} m F m _     = ∆

∑

∑

∑

=1 =1 =1 , 1 _{, ,} 1 _{λ λ λ} λ λ λ (2.37) (2.38)

[

]

n T i n i n i i i Z i i Y i i X B T A _{I L I M I N} M _      ⋅ ⋅ ⋅ = ∆

∑

∑

∑

=1 =1 =1 , _{λ , λ , λ} λ λ λ

In questo modo, le variazioni delle forze e dei momenti _∆FA,T _{ed ∆M}A,T _risultano

dipendenti da tutte le possibili derivate aerodinamiche riferite ad un determinato velivolo in prefissate condizioni di volo: le loro espressioni più generali e complete, sono di seguito riportate: 0 , 1 i T A X i F m X Λ ∂ ∂ ≡ λ 0 , 1 i T A Y i F m Y Λ ∂ ∂ ≡ λ 0 , 1 i T A Z i F m Z Λ ∂ ∂ ≡ λ (2.39) 0 , 1 i T A X X i M I L Λ ∂ ∂ ≡ λ 0 , 1 i T A Y Y i M I M Λ ∂ ∂ ≡ λ 0 , 1 i T A Z Z i M I N Λ ∂ ∂ ≡ λ (2.40)

Sostituendo le (2.33), (2.37), (2.38) nelle (2.31), (2.32) ed esplicitando le dipendenze delle forze e coppie di natura aerodinamica e propulsiva, utilizzando tutti termini necessari per ottenere un modello matematico completo, si ottengono le 6 equazioni scalari seguenti:

∑

+ + + + + + Θ − = + i i q w w u uu X u X w X w X q X i X g q W

u_{& 0} cos ₀θ _{&& & & δ}δ (2.41)

∑

+ + + + + Θ = − + i i r p v vv Y v Y p Y r Y i Y g p W r U

v_{& 0 0} cos ₀ϕ _{&& δ}δ (2.42)

∑

+ + + + + + + Θ − = − i i q q w w u uu Z u Z w Z w Z q Z q Z i Z g q U

w_{& 0} sin ₀θ _{&& & & && δ}δ (2.43)

∑

+ + + + = − i i r p v v X XZ _{L v L v L p L r L i} I I r

p_{& & && δ}δ (2.44)

∑

+ + + + + + = i i q q w w u uu M u M w M w M q M q M i M

q_{& && & & && δ}δ (2.45)

∑

+ + + + = − i i r p v v Z XZ _{N v N v N p N r N i} I I p

r_{& & && δ}δ (2.46)

Nelle precedenti equazioni, δi rappresenta il generico ingresso di comando in termini di variazione rispetto al trim e le sommatorie che compaiono sono estese a tutti gli ingressi. Le espressioni delle forze e coppie aerodinamiche che compaiono presuppongono implicitamente l’esistenza di un campo aerodinamico non stazionario. Ciò equivale a ritenere le forze e coppie aerodinamiche dipendenti, non solo dalla velocità, lineare ed angolare, del velivolo relativa all’aria, ma anche dalle loro derivate temporali. In particolare, sono prese in considerazione le derivate di stabilità che dipendono dalle derivate temporali delle componenti della velocità (lineare ed angolare) relativa del velivolo rispetto all’aria, che l’esperienza ha dimostrato essere necessarie per ottenere un modello matematico sufficientemente significativo per descrivere la dinamica del velivolo, considerata pure la flessibilità della struttura.

È utile osservare che i termini in v e consentono di modellare l’effetto del ritardo aerodinamico sulla coda del velivolo (effetti di “sidewash” per v e di “dawnwash” per ). Le derivate aerodinamiche in sono generalmente trascurabili se le equazioni sono scritte in assi stabilità; in assi corpo generici, invece, diventano non trascurabili quando si considerano condizioni di trim di alta incidenza, dal momento che una variazione di u

induce una corrispondente variazione dell’incidenza. Infine, attraverso le derivate in si mettono in conto parte degli effetti legati all’elasticità strutturale del velivolo e dovuti essenzialmente alla superficie orizzontale di coda.

& w&

& w&

q& u&

Nelle equazioni in u, , compaiono tipicamente solo i comandi relativi al piano longitudinale (quali ad esempio

& w& q& e

δ e δt), mentre nelle equazioni di v_&, ed p& r& compaiono

solo i comandi relativi al piano latero-direzionale (quali ad esempio δa e δr). In tali ipotesi, si ha un completo disaccoppiamento tra le equazioni che descrivono la dinamica longitudinale del velivolo e le equazioni relative alla dinamica latero-direzionale. In questo modo è possibile risolvere separatamente le equazioni longitudinali del moto e valutare la relativa dinamica, indipendentemente dal comportamento dinamico del velivolo nel piano direzionale. Il vettore degli stati longitudinali ed il vettore degli stati latero-direzionali sono allora costituiti dalle seguenti variabili:

(2.47)

[

T LON u w q h X ≡ , , ,θ,

]

]

(2.48)

[

T LAT v p r X ≡ , , ,ϕ,ψ

2.5 - EQUAZIONI LONGITUDINALI DEL MOTO RISPETTO AD UNA TERNA ASSI STABILITÀ.

Le equazioni del moto linearizzate si semplificano ulteriormente se la terna assi corpo coincide con una terna assi stabilità che, per definizione è quella particolare terna assi corpo in cui la direzione di X_B coincide con la direzione della velocità del velivolo Vr in condizioni di trim. Ciò implica che sia W₀ =0. Inoltre, tenendo presente che la condizione di trim è di volo orizzontale (avente quindi γ₀ =0) con il vettore velocità appartenete al piano longitudinale di simmetria del velivolo, risulta anche Θ₀ =0 ed U₀ ≡Vr .

Nel proseguo di questo lavoro si analizza la dinamica del velivolo nel piano longitudinale, adottando le equazioni del moto riferite ad una terna assi stabilità in assenza di raffica. Esse sono riassunte nella tabella (2.3).

∑

+ + + + + + − = j j q w w u uu X u X w X w X q X j X g

u& θ && & & _δδ (2.49)

∑

+ + + + + + + = − j j q q w w u uu Z u Z w Z w Z q Z q Z j Z q U

w_{& 0 && & & && δ}δ (2.50)

∑

+ + + + + + = j ij q q w w u uu M u M w M w M q M q M j M

q_{& && & & && δ} δ (2.51)

(2.52) q = θ& (2.53) w U h&= ₀θ − VARIABILI AGGIUNTIVE α θ γ = − _(2.54) 0 U w = α (2.55) g q U w n_{z = &}− 0 (2.56)

Tab. 2.3: Modello matematico completo della dinamica longitudinale del velivolo in assi stabilità, in assenza di vento o raffica.

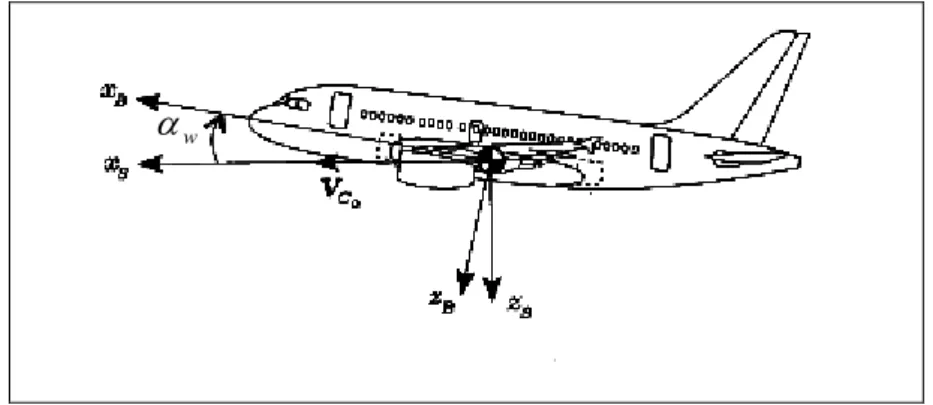
w

α

Fig. 2.1: Orientamento relativo delle terne assi corpo ed assi stabilità.

È bene precisare che le derivate aerodinamiche che compaiono nelle equazioni riportate nella tabella (2.3), sono numericamente diverse da quelle che compaiono nella precedente tabella (2.2) perchè riferite a terne diverse, anche se indicate con gli stessi simboli: infatti le equazioni del moto del velivolo riferite ad una terna assi corpo oppure ad una terna assi stabilità sono formalmente identiche, ma le derivate di stabilità e le componenti del tensore d’inerzia assumono valori diversi nei due casi. In particolare, sia le derivate aerodinamiche che i momenti d’inerzia, nel passaggio da una terna assi corpo ad una assi stabilità, si modificano mediante un’opportuna matrice di trasformazione.

2.6 - ANALISI DEL SISTEMA DI FORZE AGENTI SUL VELIVOLO.

Esplicitate le forze aerodinamiche in funzione delle forze di portanza e di resistenza generate sia dall’ala che dalla superficie orizzontale di coda, dipendenti da coefficienti aerodinamici, angoli geometrici e lunghezze geometriche caratteristiche del velivolo, la risultante lungo l’asse delle forze aerodinamiche, propulsive e di massa e la risultante

F Z_B

M intorno all’asse Y delle coppie aerodinamiche e propulsive, agenti complessivamente sul velivolo, sono costituite dai seguenti contributi (i simboli impiegati sono definiti nell’elenco simboli di pag. 1):

W T A _F F F = r , + r _(2.57) θ α α α α

α cos sin sin sin cos

cos L D D T W L F = _{wb w}+ _{t s} + _{wb w} + _{t s} + _{eng e} − (2.58) T A M M ₌ r , _(2.59)

(

)

(

t s t t

)

t

(

wb w wb w

)

a

(

t s t s t e eng a s t s t w wb w wb t wb Z D L Z D L X D L Z T X D L D L M M M α α α α α α

)

α α α α cos sin cos sin sin cos sin cos sin cos 025 025 − − − − + − + + + + + + = (2.60)

In corrispondenza di una generica condizione di trim per il velivolo, indicando con il simbolo di sopra-segno (–) le diverse grandezze nella condizione d’equilibrio considerata, le precedenti divengono: θ α α α α

α cos sin sin sin cos

cos L D D T W L F = _{wb w} + _{t s} + _{wb w} + _{t s} + _{eng e} − (2.61)

(

)

(

t s t t

)

t

(

wb w wb w

)

a

(

t s t s

)

t e eng a s t s t w wb w wb t wb Z D L Z D L X D L Z T X D L D L M M α α α α α α α α α α cos sin cos sin sin cos sin cos sin cos 0 _{025 025} − − − − + − + + + + + + = (2.62)

Per valutare in modo completo la forza di portanza generata nella condizione d’equilibrio in ala L ed in coda _wb L , occorre considerare il coefficiente di portanza dell’ala C e della _t

coda come funzioni di tutti i possibili contributi, compresa le rotazioni

wb

L

j Lt

C δ delle

possibili superfici di comando che consentono il controllo del moto del velivolo nel proprio piano longitudinale. Queste rotazioni determinano una variazione della pendenza della curva di portanza della superficie su cui il comando è montato. Per le posizioni delle

superfici di controllo nelle condizioni di trim si assume δ_j,δ_k =0. In questo modo i coefficienti di portanza relativi alla condizione di trim, C_Lwb, C , risultano funzioni note _Lt

come indicato nella tabella 2.4.

Lwb w w Lwb w w wb S V C q S C L = 2 = 2 1_ρ (2.63) Lt t t Lt t t t SV C qSC L = 2 = 2 1_ρ (2.64) ) , , , , , , ( _{w w j} Lwb f M h

C = α α& θ&θ&& δ TRIM → _{( , , , )} j w Lwb = f α M h δ C (2.65) ) , ( _{s k} Lt f C = α δ _TRIM_{ →} ( , ) k s Lt f C = α δ _(2.66)

Tab. 2.4: Forza di portanza e coefficiente di portanza dell’ala e della coda al trim.

Gli effetti di un comando esercitato dal pilota in una condizione di trim per compiere una determinata manovra, oltre ad una possibile perturbazione agente sul sistema, si traducono in una variazione dell’angolo compreso tra la direzione del flusso che investe le superfici portanti del velivolo e l’asse del sistema di riferimento. Ciò implica nuove espressioni per i coefficienti di portanza, dipendenti da tale variazione. La variazione dei coefficienti di portanza, rispettivamente del sistema ala-corpo e della coda, rispetto alla condizione di trim, dovuta all’effetto di un comando, è data da:

B X

( )

0 j Lwb wb L C C j δ δ _∂ ∂ =

( )

0 k Lt tail L C C k δ δ _∂ ∂ = (2.67)

Analogamente, le derivate dei coefficienti rispetto agli angoli d’attacco rispettivamente dell’ala e della coda (α_w,α_s), indicano come varia la portanza della superficie considerata al variare dell’incidenza, partendo dalla condizione di trim.

(

)

0 w Lwb wb L C C α α _∂ ∂ =

(

)

0 s Lt tail L C C α α _∂ ∂ = (2.68)

Indicando con il prefisso le relative variazioni a partire dalla condizione di trim, in corrisponedenza della quale il velivolo è in equilibrio avendo condizioni iniziali nulle per

∆

w

α_{& , , , complessivamente risulta:} θ& θ&&

ALA: CODA: w w w α α α = +∆ (2.69) α_s =α_s +∆α_s (2.74) w w α α_& =∆ _{& (2.70)} k k δ δ =∆ (2.75) (2.71) θ θ& ∆= & (2.72) θ θ&& ∆= && j j δ δ =∆ (2.73)

Ne derivano le seguenti espressioni complete del coefficiente di portanza del sistema ala-corpo e della coda:

) , , , , ( _{w w w j} Lwb f

C = α +∆α ∆α_& ∆θ& ∆θ&&∆δ (2.76)

) , ( _{s s k}

Lt f

A titolo di esempio si riporta l’espressione completa della forza portante dell’ala e della coda, proiettata secondo l’asse , conseguente l’azionamento di un comando ed un’eventuale perturbazione del sistema. I termini

B

Z

w

q

∆ e rappresentano,

rispettivamente, le variazioni dei valori assoluti delle velocità del flusso che investe l’ala e la coda, dovute alla perturbazione dell’intero sistema.

t q ∆

( )

Lwb Z_B =

(

Lwb +∆Lwb

)

cos

(

αw +∆αw

) (

= qw +∆qw

)

SwCLwbcos

(

αw +∆αw

)

(2.78)

( )

Lt Z_B =

(

Lt +∆Lt

)

cos

(

αs +∆αs

) (

= qt +∆qt

)

StCLtcos

(

αs +∆αs

)

(2.79)

Dalle precedenti, si ottiene l’espressione della variazione della forza di portanza del sistema ala-corpo e della coda, proiettata secondo l’asse , come differenza tra la risultante complessiva della stessa e la sola componente relativa alla condizione di trim.

B

Z

(

∆Lwb

)

Z_B =

(

Lwb+∆Lwb

)

cos

(

αw+∆αw

)

−

(

Lwbcosαw

)

≅∆Lwbcosαw−Lwb∆αwsinαw

(2.80)

( )

∆Lt ZB =

(

Lt +∆Lt

)

cos

(

αs+∆αs

)

−

(

Ltcosαs

)

≅∆Ltcosαs−Lt∆αssinαs

2.7 - ANGOLO DI INCIDENZA DELLA CODA.

Il valore dell’angolo α_s, in generale come indicato nel riferimento [3], è dato dai seguenti contributi:             +       +       + + − + − − = _z z s t t s t t s t z t w w w s _dn n d M dM d L dL d s V n g l α α α ε ε α α α _{α 0} ( ₂ 1) (2.82)

La precedente relazione mostra la dipendenza di α_s dall’angolo α_w di incidenza dell’ala, dall’angolo ε₀ di “downwash” generato dall’ala sulla coda orizzontale per incidenza dell’ala nulla, dalla variazione ε_αw di tale angolo con α_w e dall’angolo di calettamento dello stabilizzatore. Inoltre α_s dipende dall’effetto di “ritardo di scia” attraveros il termine

(

2

)

t V / ) 1 ( _z tg n

l − in cui la quantità

(

g(n_z −1)/V_t

)

rappresenta la velocità di “pitch” . Inoltre i termini θ&    t s dL dα  ,       ,   t s dM dα    z s dn dα   legano il valore di

 αs all’elasticità della struttura

del velivolo.

Per una generica condizione d’equilibrio in cui vale n_Z =1 si ha la seguente espressione:

              +       +       + + − − = trim z s t trim t s t trim t s w w w s dn d M dM d L dL d s α α α ε ε α α α _{α 0} (2.83)

I valori degli angoli sopra-segnati che compaiono nella precedente relazione, sono riferiti alla generica condizione di trim presa in considerazione. Per valutare la variazione ∆ α_s dell’angolo α_s, dovuta alle perturbazioni agenti, occorre considerarla come una funzione di tutte le possibili variabili. In generale risulta:

) (2.84) , , , , , ( θ θ

α = _{& &} ∆& ∆ &&

In particolare, chiamando la generica variabile di stato, l’espressione completa della suddetta variazione è data da:

i x i i i s x xf ∆ ∂ ∂ = ∆α

∑

(2.85)

I termini rappresentano la variazione di ciascuna variabile di stato dalla condizione di equilibrio. Con condizioni iniziali tutte nulle per le variabili di stato, le variazioni

i x ∆ i x ∆ coincidono con le stesse variabili di stato al generico istante di tempo. Per semplicità di scrittura, si pone: 6 5 4 3 2 1 A A A A A A s = + + + + + ∆α _(2.86)

In ogni termine compare la dipendenza delle diverse grandezze da tutte le variabili di stato considerate. Trascurando effetti di ordine superiore al primo, valgono:

j A θ θ α θ θ α α α α α _&& && & & & & & & ∂ ∆ ∂ + ∆ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ = w w w w _w w w w u u w w u u A₁ (2.87)       _∆ ∂ ∂ + ∆ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = θ θ α θ θ α α α α α ε_α && && & & & & & & w w w w w w w w w u u w w u u A₂ (2.88) +         − = g V V g l A t t t r 1 2 3

(

)

      _∆ ∂ ∂ + ∆ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂       − − + θ θ θ

θ& & && && & & & & t t t t t t t z t V V w w V u u V w w V u u V V n g l 1 2₃ (2.89)

      _∆ ∂ ∂ + ∆ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂       = θ θ θ θ α _&& && & & & & & & t t t t t t t s _w L L w L u u L w w L u u L dL d A₄ (2.90)       _∆ ∂ ∂ + ∆ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂       = θ θ θ θ α _&& && & & & & & & t t t t t t t s _w M M w M u u M w w M u u M dM d A₅ (2.91)         −       = g V dn d A t z s r 1 6 α (2.92)

Per i termini relativi alla flessibilità della fusoliera, si assume, in prima analisi, che non dipendano dalle variabili di stato.

Sostituendo nell’espressione dell’angolo α_s il carico L ed il momento complessivo _t M _t

agenti sulla coda del velivolo nella condizione di equilibrio, segue l’equazione completa per il calcolo del valore dell’angolo α_s, in corrispondenza del punto di equilibrio considerato (relazione (2.97)). Lt t t t qSC L = (2.93) t mt t t t qSC c M = _(2.94)

Il coefficiente di momento relativo alla coda, C , può essere scritto nella forma: _mt

            + = _Lt Lt mt t m mt C dC dC C C ₀ (2.95)

dove:

• Rappresenta il coefficiente di momento sulla coda per portanza della coda nulla, dipendente dalle caratteristiche geometriche ed aerodinamiche della stessa.

t m C ₀ • _      Lt mt dC dC

Rappresenta l’entità del contributo al C fornito dal coefficiente di portanza C .

mt

Lt

La relazione (2.94) diviene, dunque:

            + = _Lt Lt mt t m t t t t _dC C dC C c S q M ₀ (2.96)

ANGOLO D’ATTACCO DELLA CODA AL TRIM

( )

+       + + − − = _Lt t s t t w w w s C dL d S q s α ε ε α α α _{α 0}

( )

_      +       ⋅       +       + z s Lt Lt mt t m t s t t t dn d C dC dC C dM d c S q α ₀ α (2.97)

2.8 - CONSIDERAZIONI SULLA VELOCITÀ DEL FLUSSO CHE INVESTE LA CODA DEL VELIVOLO.

Il vettore velocità del flusso fluido che investe la coda

( )

Vr_t è costituito fondamentalmente da due contributi:

• La velocità Vr del flusso asintotico che investe anche l’ala.

• La velocità di perturbazione wr in prossimità del piano di coda del velivolo. _t

La componente di velocità wr è dovuta all’interferenza ala-fusoliera-coda e soprattutto al _t fenomeno di induzione della scia che segue l’ala, sulla coda stessa. Ipotizzando che la velocità indotta dalla scia sulla coda sia ortogonale al piano che contiene la scia, è ragionevole formulare l’ipotesi che wr sia ortogonale alla scia stessa. In generale si può _t

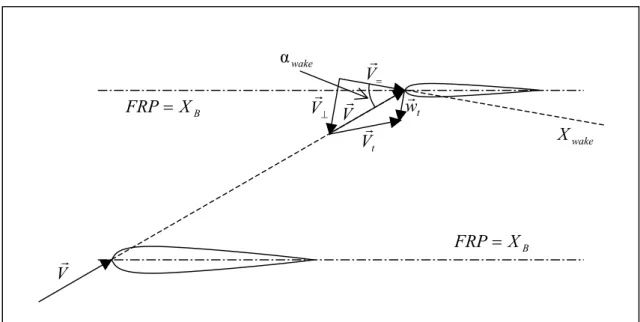
supporre per semplicità d’analisi che la scia rimanga piatta per il tratto in cui investe la coda e che la velocità di perturbazione presente lungo tutta l’apertura della superficie orizzontale del piano di coda sia ortogonale alla stessa e costante in intensità. Il valore della velocità può essere assunto pari al valore che assume in mezzeria in corrispondenza dell’asse longitudinale del velivolo. Tale situazione è schematizzata nella figura sottostante.

= Vr t wr t Vr ⊥ Vr _Vr Vr wake α B X FRP= B X FRP= wake X

Definite Vr₌ e Vr_⊥ le componenti del vettore velocità Vr rispettivamente parallela ed ortogonale alla direzione della scia X_wake, valgono le seguenti relazioni, definito α_wake l’angolo che la direzione del flusso indisturbato forma con la direzione della scia:

⊥ = + =V V Vr r r _(2.98) wake V Vr₌ = r cosα (2.99) wake V Vr_⊥ = r sinα (2.100)

Ne deriva per la velocità che investe la coda la seguente forma vettoriale:

(

t

)

t

t V w V V w

Vr = r+ r = v₌ + r_⊥ + r (2.101)

Il valore assoluto di tale velocità può derivarsi dal relativo prodotto scalare: introducendo le componenti del vettore V e trascurando termini di ordine superiore al primo, indicato con

il modulo del vettore velocità V , si ha:

t r V r       + = t _wake t V w V V2 2 1 2 sinα _(2.102)

In questo modo si ottiene il modulo della velocità che investe la coda come funzione del modulo della velocità del flusso indisturbato V , della velocità indotta wr e dell’angolo _t

wake

α . I valori di wr ed _t α_wake possono essere stimati adottando opportuni modelli di calcolo aerodinamici noti in letteratura. Tale teoria è alla base della stima dell’angolo di “downwash” per incidenza nulla dell’ala e della relativa variazione con il variare dell’angolo d’incidenza della stessa ala (ε₀,ε_αw).