CAPITOLO 1 FONDAMENTI DI ACUSTICA

(1)

CAPITOLO 1

FONDAMENTI DI ACUSTICA

In questo capitolo saranno presentati alcuni concetti base di acustica necessari a comprendere il significato dei parametri trattati nel presente lavoro. Inizialmente si definirà qualitativamente il modo in cui le onde sonore si propagano nei mezzi elastici e si definiranno le principali grandezze fisiche coinvolte, dopodichè si mostreranno le relazioni fondamentali che legano tra loro tali grandezze e le leggi che descrivono quantitativamente come esse variano nello spazio e nel tempo. L’attenzione sarà rivolta ai mezzi fluidi cosiddetti ideali, cioè omogenei, isotropi, perfettamente elastici e in cui le onde si propagano senza alcun effetto dissipativo.

1.1 Suono e rumore

Il Suono è una perturbazione di carattere oscillatorio prodotta da una sorgente sonora che, propagandosi in un mezzo elastico, provoca una variazione di pressione tale da essere percepita entro un certo campo di frequenza (20-20000 Hz) dall’orecchio umano.

In altre parole è una forma di trasporto di energia meccanica che avviene senza trasporto di materia, attraverso onde che si propagano in un mezzo elastico. Per esistere il suono deve esistere il mezzo elastico (gas, liquido, solido, terreno, cemento ecc…); quindi in assenza di questo non esiste alcuna propagazione sonora (quindi nel vuoto non si ha trasporto di energia acustica).

Tradizionalmente il termine “rumore“ si riferisce ad un suono non desiderato, non piacevole. Le persone, però, possono avere differenti opinioni a riguardo di suoni gradevoli o meno, tanto che un’emissione particolare può essere percepita come un rumore da un individuo e come un suono piacevole da un altro. Quindi in senso stretto il “rumore“ è solo un termine soggettivo e non tecnico.

In ogni caso qualsiasi suono non diventa un rumore finché non ci sia uomo o animale che venga da esso disturbato. Quindi, a riguardo del nostro caso, il traffico non genererà “rumore“ in quelle aree attorno al territorio stradale dove non si trovino esseri viventi che possano essere da esso disturbati.

(2)

Nel linguaggio di ogni giorno è diventata pratica comune usare il termine “rumore“ anziché “suono“ quando quest’ultimo è considerato fonte di disturbo, e quindi indesiderato. Questo è il motivo per cui nella seguente trattazione verrà usato quasi esclusivamente il termine “rumore“ riferendoci alle emissioni che provengono dalla pavimentazione stradale.

Verranno ora introdotti alcuni concetti fondamentali e definizioni concernenti il campo dell’acustica.

1.1.1 Il livello della pressione sonora

L’orecchio umano è in grado di percepire una pressione sonora minima di circa 20 μPa. All’estremo opposto, una pressione sonora dell’ordine di 60 Pa induce sensazione di panico, e valori ancora superiori producono danni uditivi immediati. Quindi, anche limitandosi agli aspetti della percezione, il campo dei valori entro il quale può variare la pressione sonora risulta esteso su oltre sei ordini di grandezza. Inoltre poiché la risposta soggettiva risulta maggiormente correlata alla densità di energia sonora, definita come l’energia contenuta in una unità di volume del mezzo ed equivalente al quadrato della pressione sonora efficace divisa per la densità dell’aria moltiplicata al quadrato della velocità del suono (p2/(ρ0·c2)), il campo di variazione diventa dell’ordine di 1012.

Due fondamentali ragioni, inducono allora a rappresentare le variazioni di tali grandezze, anziché su scala lineare, con una scala compressa, di tipo logaritmico: la prima è per evitare l’oggettiva difficoltà di trattare con numeri molto piccoli o molto grandi, dispersi in un campo eccessivamente esteso; la seconda, è che proprio l’enorme capacità dinamica dell’apparato uditivo suggerisce una risposta organizzata più in termini logaritmici che non lineari, più vicina alla sensibilità propria dell’orecchio.

L’uso della scala logaritmica consente di confrontare i valori della grandezza in esame con valori convenzionali assunti come riferimento. Il logaritmo decimale, moltiplicato per 10 (onde evitare un’eccessiva compressione della scala), del rapporto di questi valori rappresenta il livello della grandezza in esame ovvero rappresenta il livello rispetto al valore di riferimento della stessa grandezza. Il risultato viene espresso in decibel (dB); nonostante definisca una quantità adimensionale, nella pratica comune il dB viene trattato come una unità di misura vera e propria.

Si può quindi definire il livello della pressione sonora Lp (l’acronimo SPL dall’inglese Sound Pressure Level è preferito all’espressione intera), in accordo alla seguente equazione:

(3)

2 lg 10 _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ = ref p p p L [dB] dove:

pref è un valore di pressione sonora di riferimento standardizzato pari a 20*10-6 Pa alla

temperatura di 20°C e umidità relativa (UR) del 50%, che corrisponde alla soglia uditiva umana media alla frequenza di 1KHz.

Il valore di riferimento è stato scelto in modo da ottenere un livello della pressione sonora pari a 0 dB alla soglia dell’orecchio (cioè se la pressione misurata o percepita dall’orecchio è di 20*10-6 Pa, l’SPL è 0 dB). I valori della pressione sonora sono compresi quindi nell’intervallo tra lo 0 e i 120 dB, che permette ai tecnici del suono di lavorare con numeri pratici.

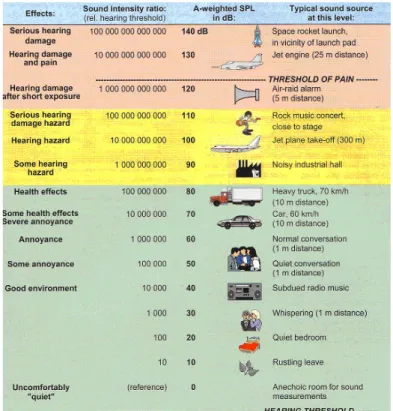
La figura 1.1 illustra la scala logaritmica del suono e dell’intensità sonora e mostra alcune sorgenti comuni che operano tipicamente in un certo intervallo. La seconda colonna illustra l’intensità del suono a paragone con l’intensità del suono alla soglia dell’orecchio. In particolare si osserva la soglia di udibilità (hearing threshold) corrispondente ad un livello di pressione sonora di 0 dB, e la soglia sopra la quale si manifestano effetti di panico (threschold of pain).

Fig. 1.1: illustrazione dei livelli sonori di differenti suoni su una scala che comprende l’intero campo di variabilità nella società. Zona rossa: area di danno, zona gialla: area di rischio; zona verde: area senza

(4)

1.1.2 Frequenza, lunghezza d’onda e spettro

Il suono è il movimento di un’onda o un’oscillazione nella pressione dell’aria. La variazione della pressione dell’aria, oltre alle caratteristiche sopra specificate, ha un altro importante fattore caratterizzante: la velocità alla quale si manifestano le oscillazioni o le variazioni di densità. La descrizione di questa caratteristica avviene attraverso la frequenza ( f ). Essa rappresenta il numero delle oscillazioni ( o periodi ) che avvengono in un secondo. La lunghezza in metri di un periodo prende il nome di lunghezza d’onda (λ ). L’unità della frequenza è l’Hz; 1 Hz è un’oscillazione per secondo. La relazione tra la frequenza f e la lunghezza d’onda è la seguente:

λ

c

f

=

[Hz]

dove:

c (m/s) è la velocità di propagazione del suono.

Ogni segnale può essere immaginato come una combinazione armonica o disarmonica di un numero finito o infinito di segnali a singola frequenza. La distribuzione per frequenza dell’energia (o del livello) associata ad ognuna di tale componente, si chiama spettro in frequenza. Come si può vedere nella sottostante figura 1.2, un’onda monocromatica sinusoidale (primi due grafici in alto a sinistra) composta quindi da un’unica frequenza, avrà un solo picco nel grafico del suo spettro in frequenza (primi due grafici in alto a destra) spostato verso le basse frequenze nel primo caso e verso le alte nel secondo. Se si ha un’onda dicromatica formata dalle due onde precedenti (grafico in basso a sinistra), nel suo spettro in frequenza non si troverà più un unico picco ma due picchi, ognuno dei quali corrispondente alle singole frequenze che compongono il segnale (grafico in basso a destra).

(5)

La larghezza e la forma della distribuzione in frequenza dei segnali sonori che ci accompagnano nella vita di tutti i giorni variano notevolmente e sono fondamentali per caratterizzare il tipo di segnale e la sua capacità di disturbo.

Quindi fare l’analisi in frequenza di un segnale significa scinderlo nelle sue componenti in frequenza e misurare il contenuto energetico di ognuna di esse; si ottiene così lo spettro in frequenza del segnale.

Un essere umano giovane e normoudente può percepire segnali che hanno frequenze comprese tra circa 20 Hz e 16-20 KHz. La percezione uditiva delle frequenze più elevate diminuisce gradualmente con l’età infatti, nelle persone anziane la frequenza massima di percezione può scendere fino ad un livello di circa 10-12 KHz [6]. I suoni che oscillano con frequenze superiori ai 20 KHz (chiamati ultrasuoni) hanno una lunghezza d’onda piccolissima al punto tale che il nostro apparato uditivo non riesce a percepirne la variazione.

Le oscillazioni con frequenze inferiori ai 20 Hz (chiamate infrasuoni) sono solitamente percepite dal corpo intero come una sorta di vibrazioni, e non come veri e propri suoni.

Analizzando il rumore del traffico in generale, incluso quello generato dall’interazione pneumatico-pavimentazione, è molto importante utilizzare non solo il modulo dell’energia associata alla pressione sonora, ma anche la sua distribuzione in funzione della frequenza.

In generale, quando si ha a che fare con suoni che si propagano per alcuni chilometri, bisogna tener presente che, alle basse frequenze, il suono non è influenzato dalla distanza; al contrario, alle elevate frequenze, il suono subisce una attenuazione. Nel nostro caso, poiché si acquisiscono i dati ad una distanza di massimo 7.5 m, si può tranquillamente trascurare questo fattore.

1.1.3 Il livello sonoro equivalente L

eq

Il rumore prodotto dal flusso di traffico varia nel tempo in funzione di numerosi parametri, come il numero di veicoli e la loro composizione, la velocità, le condizioni meteorologiche, la tipologia della superficie stradale. La fluttuazione può essere così ampia da richiedere un metodo che permetta di descrivere l’andamento dei livelli con pochi parametri statisticamente significativi.

Un metodo possibile per misurare il livello sonoro di un veicolo è di rilevare il livello sonoro massimo, Lmax, che è misurato dal microfono quando il veicolo passa davanti ad esso.

(6)

La localizzazione del picco dell’emissione e del suo valore avviene attraverso l’analisi della “time – history“ o storia temporale, che rappresenta l’andamento nel tempo del livello di pressione sonora.

Un altro modo per descrivere l’evento è quello di considerare l’energia media dell’evento stesso: dal momento che l’energia acustica è proporzionale al quadrato della pressione acustica prodotta nel tempo dalla sorgente, la media energetica equivale alla media temporale della pressione e se riferita al valore di riferimento si parla livello sonoro equivalente. Tale livello equivalente può essere visto come quel livello del suono costante che, durante un certo periodo di tempo, risulta avere la stessa energia sonora totale

dell’attuale livello oscillante. L’indicatore di questo valore mediato è Leq ed è dato dalla seguente formula:

]

[

2 1 2 0 2 1 2 10 , ) ( 1 10 dt p t p t t Log L t t A T eq

∫

− = [dB]

Si può immaginare questo livello del suono come una media dei segnali registrati durante un certo intervallo di tempo T, che deve essere specificato insieme all’indicatore connesso al valore.

La media non è aritmetica ma energetica; ciò implica che sia la potenza ad essere mediata. Quindi, poiché in questo calcolo la pressione sonora viene elevata al quadrato, le pressioni sonore più grandi avranno un’influenza maggiore e non proporzionale, rispetto alle pressioni più basse, sul livello equivalente.

Questo significa che, relativamente all’arco temporale su cui si calcola il livello equivalente, poiché il calcolo del livello complessivo è una somma logaritmica, due segnali che sono uno maggiore dell’altro, non incideranno sul valore finale in maniera proporzionale alla loro differenza ma il segnale più grande avrà un peso maggiore rispetto all’altro.

1.1.4 Relazioni tra i livelli

L’intensità di un’onda sonora (I), rappresenta la quantità di energia che fluisce, nell’unità di tempo, attraverso una superficie di area unitaria perpendicolare alla direzione di propagazione dell’onda. L’unità di misura è Watt per metro quadrato (W/m²). Come nel caso della pressione sonora, l’intensità del suono I è di solito convertita in una scala logaritmica, che calcola il livello dell’intensità sonora in accordo a questa equazione:

(7)

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ = ref I I I L 10 lg [dB] dove: Iref = 1 pW/m2 = 10-12 W/m2 .

Il livello di riferimento per l’intensità è stato scelto in modo che, in uno spazio acustico libero da fattori influenti, si potrebbe ottenere la stessa lettura in dB indipendentemente dall’avere misurato la pressione o l’intensità su di una superficie di 1 m2.

Si definisce potenza sonora (W) l’energia irradiata nell’unità di tempo da una sola sorgente acustica. L’unità di misura della potenza è il Watt.

Anche per questa grandezza è possibile parlare di livello di potenza sonora come segue:

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ = ref W W W L 10 lg [dB] dove:

Wref è la potenza sonora di riferimento assunta convenzionalmente uguale a 10-12 W.

Se si ipotizza una sorgente puntiforme e la presenza di una superficie S che circonda completamente la sorgente, tenendo presente la definizione di intensità, si può scrivere che:

∫

⋅

= Is dS

W [Watt]

dove:

IS è l’intensità sonora rilevata su un’area elementare dS della superficie immaginaria S. Se inoltre, si ipotizza che la sorgente irradi la stessa energia uniformemente in tutte le direzioni e se la superficie che circoscrive la sorgente è allora, per convenienza, una sfera di raggio r, la relazione precedente diventa semplicemente:

S I r W = ⋅ ⋅ 2 ⋅ 4 π [Watt] dove:

IS, per l’assunzione fatta, è l’intensità rilevata in una qualsiasi direzione a distanza r dalla sorgente.

(8)

Con questa relazione si stabilisce che tutta l’energia sonora irradiata dalla sorgente deve passare attraverso la superficie sferica immaginaria e, inoltre, che più estesa è tale superficie, cioè maggiore è il suo raggio r, minore è l’intensità su ogni area elementare. Con questo, è possibile dare anche una nuova definizione dell’intensità sonora, in termini di potenza sonora che fluisce attraverso l’unità di area. Sostituendo nell’ultima relazione, l’espressione dell’intensità valida per le onde piane (che è stato dimostrato essere valida anche per onde sferiche [7]) e cioè: c) · ( / p I₌ 2 _ρ₀ [Watt/m2] dove:

p2 è il quadrato della pressione sonora efficace;

ρ0 · C è l’impedenza acustica caratteristica (Z0) ossia l’opposizione al flusso di energia acustica in cui ρ0 = densità dell’aria e C = velocità dell’onda sonora; questa assume il valore di 400 Pa·s/m alla temperatura di 39°C (per cambiamenti della temperatura di circa 20°C, l’impedenza non subisce variazioni apprezzabili);

si ottiene: c) ( / p r 4 W ₌ _⋅

_π

_⋅ 2 _⋅ 2

_ρ

₀ _⋅ [Watt] potendo così ricondurre la potenza sonora alla pressione sonora e distinguendo meglio la potenza, che è la causa, dalla pressione del suono, che è l’effetto e dipende dalla distanza dalla sorgente.

E’ possibile ora prendere in analisi le relazioni che intercorrono tra i livelli di pressione, di intensità e di potenza sonora.

Ammettendo valida la relazione che lega la pressione e l’intensità attraverso la costante ρ0 · C si può mettere insieme le formule sopra scritte ed ottenere:

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ ⋅ ⋅ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ = ref ref I _I _c _I I L ο ρ 2 p lg 10 lg 10 _[dB]

Quando ρ0·C vale 400 Pa·s/m, poiché ρ0·C· IREF risulta essere uguale a pref2 , cioè a

(9)

P

I

L

=

.

Inoltre, se l’intensità sonora è uniforme su una superficie di area S, che circoscrive una sorgente di potenza W, poiché I = W/S, si può scrivere la seguente relazione tra i livelli di intensità e di potenza sonora:

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅ ref ref ref S S I I W W lg 10 lg 10 lg 10 _[dB] dove:

Sref è un’area di riferimento assunta uguale ad 1 m2; se anche S = 1 m2 , risulta esattamente LI = LW.

1.2 Equazione d’onda in aria libera

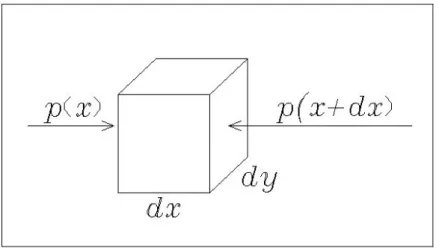
Il punto di partenza per descrivere la propagazione delle onde sonore nei gas e nei liquidi è rappresentato dalle due equazioni fondamentali dell’idrodinamica, l’equazione di Eulero e l’equazione di continuità, unitamente all’equazione di stato del fluido in esame. La regione elementare di mezzo cui guardare può essere rappresentata dal piccolo volume V0, di dimensioni dx, dy e dz, schematizzato in fig. 1.3.

1.2.1 Equazione di Eulero

L’equazione di Eulero deriva dal bilanciamento delle forze che agiscono sul singolo elemento di volume e definisce le condizioni di equilibrio dinamico delle forze che agiscono sull’elemento di fluido considerato, come si può apprezzare nella seguente figura:

(10)

Fig. 1.3: volume infinitesimo preso come riferimento.

Applicando la legge di Newton relativamente alla componente x della forza, e ricordando che F_x = p⋅dydz, si ottiene:

[

p x p x dx

]

dydz

dt dv

m_⋅ x ₌ ₍ ₎₋ ₍ ₊ ₎ _⋅ _[N]

La massa contenuta nel volumetto infinitesimo sarà invece espressa in funzione della densità, ottenendo: dydz dx x p dt dv dxdydz x _⋅ ∂ ∂ − = ⋅ ⋅ ρ [N] Riscrivendo opportunamente: t v x p _x ∂ ∂ ⋅ − = ∂ ∂ _ρ [Kg/m2 s2]

L’equazione precedentemente scritta può essere estesa in forma vettoriale, applicando la legge di Newton anche alle coordinate y e z. In definitiva:

t v p ∂ ∂ − = ∇ ρ [Kg/m2 s2]

(11)

1.2.2 Equazione di continuità

L’equazione di continuità esprime il fatto che al flusso di massa entrante o uscente nell’unità di tempo dall’interno di una superficie chiusa corrisponde una variazione di densità contenuta in tale superficie.

L’equazione viene pertanto scritta in forma differenziale, ricordando che per il teorema di Gauss la divergenza di un vettore è pari al flusso specifico per un volumetto infinitesimo. Si introduce la “corrente di materia”, definita come:

v

J =ρ⋅ [Kg/m2 s]

L’equazione di continuità assume dunque la forma caratteristica:

t J ∂ ∂ − = ⋅ ∇ ρ [Kg s/m3]

Assumendo che la variazione di densità all’interno del volumetto sia trascurabile rispetto alla variazione di velocità possiamo scrivere:

(

v

)

v t =−∇⋅ ⋅ ≈− ∇⋅ ∂ ∂ρ _ρ _ρ [Kg s/m3]

1.2.3 Equazione di stato

Nello scrivere l’equazione di stato per il gas in cui avviene il transito dell’onda acustica, assumiamo che la propagazione all’interno del mezzo avvenga con sufficiente rapidità, trascurando gli effetti di dissipazione di calore. Questo ci permette di scrivere un’equazione di stato adiabatica, della forma:

t V

p

pVγ = ₀ ₀γ =cos

Differenziando e introducendo la densità:

0 1 0 0 _ρ ρ ρ ρ γ γ d p dp − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = [Pa]

(12)

Essendo la variazione di densità tale da potersi ritenere agevolmente: 1 1 0 ≈ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ γ− ρ ρ [adimensionale]

derivando rispetto al tempo si ottiene, in definitiva:

t t p p ∂ ∂ = ∂ ∂ ρ ρ γ 0 0 1 1

1.2.4 Combinazione delle tre equazioni: equazione d’onda

Combinando l’ultima equazione ottenuta con l’equazione di continuità si ha che:

) ( 1 1 0 0 0 v t p p ∂ = − ∇⋅ ∂ _ρ ρ γ

Si deriva ulteriormente l’equazione precedente rispetto al tempo, e si applica l’equazione di Eulero: p p t v t p p 2 0 0 2 2 0 1 1 _≈ _∇ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∇ − ⋅ ∇ − = ∂ ∂ ⋅ ∇ − = ∂ ∂ ρ γ ρ γ γ

Da un’analisi dimensionale è facile riconoscere nel fattore γp0/ρ0 una grandezza pari al

quadrato di una velocità. L’equazione scritta prende dunque la forma:

0 1 2 2 2 2 ₌ ∂ ∂ − ∇ t p c p [Pa]

in cui riconosciamo nel fattore c la velocità di propagazione dell’onda acustica, definita come:

0 0

ρ γ p

(13)

1.3 Grandezze fisiche funzionali alla descrizione delle

proprietà acustiche dei materiali

Per la previsione delle proprietà acustiche dei materiali, e nella fattispecie dei conglomerati costituenti le pavimentazioni stradali, riveste un ruolo fondamentale la conoscenza della grandezza nota come impedenza acustica caratteristica di un mezzo. Questa si esprime mediante rapporto nel dominio spettrale tra la pressione dell’onda in tale mezzo e la conseguente velocità delle particelle all’interno di esso [8]:

v p

Z_c = [(MKS) rayls = N/s m3]

Si ricorda in proposito che tale grandezza rappresenta una proprietà intrinseca del materiale, indipendente dal suo spessore e dai meccanismi di propagazione che possono attuarsi negli eventuali strati contigui; per l’aria, ad esempio l’impedenza è esprimibile nella forma: 0 0 0 c Z =ρ [rayls] dove:

ρ0 rappresenta la densità dell’aria, pari a circa 1.25 kg/m3;

c è la velocità del suono in aria, e vale 343 m/s a TPS. L’impedenza caratteristica dell’aria è pari a circa 407 (mks) rayls.

Considerando invece una superficie che delimiti un dominio entro il quale si intende studiare la propagazione delle onde acustiche (superficie al contorno), si definisce impedenza acustica superficiale il rapporto tra il valore della pressione in prossimità della superficie e la componente della velocità normale a tale contorno:

⊥ =

v p

(14)

Tale definizione differisce dalla prima in quanto questa formulazione può essere usata per calcolare il campo acustico senza dover estendere lo studio alle condizioni di propagazione oltre la superficie definita come contorno, nella maniera che sarà precisata in seguito; in pratica in questo caso la pressione e la velocità delle particelle non sono relative ad un mezzo continuo, ma interessano la superficie di separazione tra due regioni di spazio contigue, anche nel caso in cui siano riempite dallo stesso materiale.

Solitamente il valore dell’impedenza acustica superficiale viene normalizzato rispetto all’impedenza caratteristica dell’aria:

0 0c

Z_s

s _ρ

ζ = [adimensionale]

La conoscenza dell’impedenza superficiale è fondamentale nella fattispecie ogni qualvolta si vogliano studiare gli effetti della propagazione sonora quando si incontra una superficie di separazione tra due mezzi (ad esempio aria e pavimentazione stradale).

In tal caso la presenza di una discontinuità porta in generale ad un effetto di riflessione, visualizzabile come un’onda regressiva.

Considerando ad esempio la propagazione in aria di un’onda piana sull’asse x, incidente normalmente ad una superficie di separazione tra due mezzi differenti, la pressione acustica associata a tale avanzamento potrà essere scritta:

) ( , 0 ) , ( ikx t in in x t p e p = ⋅ −ω [Pa] dove:

p0,in rappresenta l’ampiezza d’onda associata a tale propagazione;

k rappresenta il numero d’onda (in tre dimensioni vettore d’onda) [m-1]; ω è la pulsazione, direttamente proporzionale alla frequenza [s-1].

Per come è stata definita l’impedenza caratteristica dell’aria, l’espressione relativa alla velocità delle particelle di aria associata alla propagazione incidente è:

) ( 0 0 , 0 0 ) , ( ) , ( in in i kx t in _c e p Z t x p t x v ω ρ ⋅ − = = [m/s]

(15)

Data la superficie di contorno per la quale sia nota l’impedenza superficiale, il contributo di pressione nell’aria dovuto all’onda riflessa, e la relativa velocità di particelle, potranno essere scritte:

) ( , 0 ) , ( i kx t rif rif x t p e p ₌ _⋅ − −ω [Pa] ) ( 0 0 , 0 0 ) , ( ) , ( rif rif i kx t rif e c p Z t x p t x v ω ρ − − ⋅ − = = [m/s]

Per un’onda piana incidente normalmente ad una superficie l’ampiezza dell’onda riflessa è proporzionale a quella dell’onda incidente, mediante un coefficiente di riflessione (complesso) Rp: 0 , 0 , p in rif R p p = ⋅ [Pa]

Sommando i contributi di onda incidente e onda riflessa si arriva alla determinazione della pressione e della velocità totali in un punto generico:

[

( ) ( )

]

) , ( i kx t p t kx i in e R e p t x p ₌ −ω ₊ _⋅ − −ω [Pa]

[

]

0 0 ) ( ) ( ) , ( c e R e p t x v t kx i p t kx i in ρ ω ω − − − ₋ _⋅ = [m/s]

Se si pone per semplificare i calcoli l’origine dell’asse x in corrispondenza della superficie di separazione, si arriva alla determinazione dell’impedenza superficiale e dell’impedenza superficiale normalizzata:

p p s R R c t x v t x p Z − + = = 1 1 ) , ( ) , ( 0 0 ρ _[rayls] p p s R R − + = 1 1 ζ _{[adimensionale]}

(16)

Invertendo le precedenti relazioni, si vede la dipendenza esplicita del coefficiente di riflessione dall’impedenza acustica specifica:

1 1 + − = s s p R ζ ζ [adimensionale]

Naturalmente le equazioni precedenti sono valide per qualsiasi mezzo in cui si vogliano indagare i contributi dell’onda incidente e riflessa, avendo cura di utilizzare l’impedenza caratteristica del dato materiale in luogo di quella dell’aria, utilizzata per il caso in oggetto:

p p c s R R Z Z − + = 1 1 [rayls]

Nel caso in cui l’onda piana nel mezzo generico sia incidente con angolo θ rispetto alla superficie di separazione si può mostrare che valgono:

p p c s R R Z Z − + = 1 1 cosθ [rayls] 1 cos ) ( 1 cos ) ( + − = θ θ ζ θ θ ζ s s p R [adimensionale]

Nell’ultima equazione è stata esplicitata la dipendenza dell’impedenza superficiale dall’angolo, perché in generale il rapporto tra p e v sulla superficie dipende dall’angolo di incidenza dell’onda; ad ogni modo, per una particolare categoria di materiali, detti localmente reagenti, Zs non dipende da θ.

Definendo il coefficiente di assorbimento acustico α come la quota dell’energia non riflessa dalla superficie di separazione, è facile dimostrare che in generale vale:

(

cos( )

)

2Re( )cos( ) 1

) cos( ) Re( 4 ) ( ₂ + + = θ ζ θ ζ θ ζ θ α s s s [adimensionale]

(17)

1.4 Propagazione delle onde sonore nei mezzi

Consideriamo adesso la propagazione acustica in un mezzo differente dall’aria. Tale propagazione può avvenire in modo da non deformare la struttura stessa del mezzo, in tal caso si parla di materiali infinitamente rigidi, oppure in modo da trasferire parte dell’energia a vibrazioni strutturali; inoltre si parla di materiali dissipativi quando l’interazione acustica con il mezzo porta alla perdita di energia, quindi allo smorzamento dell’ampiezza dell’onda all’interno del materiale. In pratica tutti i materiali fibrosi o porosi possono essere considerati dissipativi.

Per descrivere la propagazione ondosa in un mezzo dissipativo occorre introdurre un termine immaginario puro al numero d’onda, tale da rappresentare lo smorzamento [9]:

d

c k ik

k = ₀+ [m-1]

In tal modo lavorando con i numeri complessi come conseguenza dell’elevamento a potenza si ottiene un termine che decade esponenzialmente:

x k x ik ikx e e d e = 0 ⋅ − [adimensionale]

In letteratura viene definito un parametro correlato al numero d’onda complesso, detto costante di propagazione, dato da:

c

c =ik

γ [m-1_]

Tipicamente per la descrizione acustica dei materiali si è soliti definire una densità complessa ρc e una velocità di fase complessa cc caratteristiche in modo che l’impedenza

caratteristica possa ancora essere definita come: ) ( ) (ω ω ρ_c _c c c Z = ⋅ [rayls]

Un altro parametro introdotto per descrivere le proprietà acustiche dei materiali è il cosiddetto modulo di comprimibilità Kg (bulk modulus), tale che:

(18)

) ( ) ( ω ρ ω c c c K c = [m/s] c c K k(ω)=ω ρ [m-1] ) ( ) (ω ω ρ_c _c c K Z = [rayls]

Nel caso di sovrapposizione di più strati propagativi, l’impedenza superficiale relativa all’i-esimo strato viene ricavata mediante la seguente legge di composizione:

) cot( ) cot( , , 1 , , , 1 , , , i i c i c i s i c i i c i s i c i s d k iZ Z Z d k iZ Z Z − + − = − − [rayls]

Tale legge è ricavabile esprimendo l’onda riflessa sullo strato i-1-esimo in funzione di Zs,i-1, ricordando che −icot(kd)=coth(ikd)e che in ogni punto vale:

[

( ) ( )

]

) , ( i kx t p t kx i in e R e p t x p = −ω + ⋅ − −ω [Pa]

[

]

i c t kx i p t kx i in Z e R e p t x v , ) ( ) ( ) , ( ω ω − − − ₋ _⋅ = [m/s]

1.5 Riflessione di onde sferiche su pavimentazioni

orizzontali

L’analisi della riflessione del suono fin qui svolta non è valida nel caso di onde sferiche. Si dimostra infatti che per un’incidenza radente delle stesse (onde che si propagano parallelamente alla superficie di separazione tra due mezzi) deve essere introdotto il coefficiente di riflessione sferica così definito [10]:

(19)

) ( ) 1 ( R F w R Q= _p + − _p _{[adimensionale]}

dove w è la cosiddetta “distanza numerica” relativa alla superficie di reazione, in questo caso estesa. Una soluzione approssimata del problema è data dalle equazioni seguenti [11]:

χ θ ζ χ θ ζ + − = cos cos s s p R [adimensionale] θ χ 2 2 0 _sin 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = k k _{[adimensionale]}

[

]

2 2 0 2 ₌₂ ₍₁₋ ₎− p s r R r ik w χ ζ [adimensionale] ) ( 1 ) ( ( 2) iw erfc e w i w F ₌ ₊ _⋅ _π _⋅ _⋅ −w ₋ _{[adimensionale]} r r d d ikr r in r ik in d e r p Q e p r p= 1 ₀_, ⋅ + ⋅ ₀_, 1 _[Pa]

dove i pedici d ed r si riferiscono rispettivamente ai percorsi dell’onda diretta e riflessa, quest’ultimo definito a partire dalla sorgente immagine posta oltre la superficie di separazione. Per il caso di una pavimentazione la situazione è descritta nella figura 1.4 seguente:

(20)

Nel caso in cui la pavimentazione presenti una discontinuità in termini di impedenza, la condizione di propagazione può essere ben descritta attraverso il metodo De Jong et al. [10], che applicato al caso esposto in Figura 1.5 si traduce:

Figura 1.5. Tecnica di de Jong per la propagazione sopra una pavimentazione con salto di impedenza.

(

)

[

(

) (

)

( )

]

2 1 2 1 1 2 1 1 4 1 2 ) ( 1 2 1 1 1 2 1 2 1 ( ) ( ) 1 ) ( ikr r i _F _k _s _r _F _k _s _r _eik r r s r e Q Q e Q r r p t p ₌ ₊ − ₊ ₋ − _⋅ ₋ ₊ ₋ − π π [Pa] dove:

p è la pressione totale al ricevitore;

p1 è la pressione di campo libero al ricevitore;

Q1 e Q2 sono i coefficienti di riflessione dell’onda sferica calcolati nel punto di

riflessione a distanza d0 rispettivamente per le impedenze Z1 e Z2 secondo la formula:

) ( ) 1 ( R F z R Q= _p + − _p ; ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ + = cosθ 2 1 0 2 Z Z kr i z ; ) ( 1 ) (z iz cerfe z F = + π dw e F x iw

∫

∞ = ( ) 2 2 ;

(21)

1.6 Introduzione ai modelli per la caratterizzazione

acustica dei materiali

Per la caratterizzazione acustica dei materiali in termini di impedenza caratteristica e costante di propagazione all’interno del mezzo sono stati implementati svariati modelli teorici che consentono di studiare l’influenza dei parametri fisici rilevanti per il comportamento di tali mezzi rispetto alla sollecitazione sonora. In particolare sono classificabili tre approcci:

¾ Modelli empirici;

¾ Modelli microstrutturali; ¾ Modelli fenomenologici.

I modelli empirici vengono implementati correlando risultati sperimentali ricavati per provini di materiali che presentano caratteristiche fisiche simili, ma differenti valori di alcuni parametri ritenuti influenti sulla variazione delle proprietà acustiche (ad esempio spessore, densità, resistenza al flusso, porosità ecc.); come modello viene quindi assunta la legge matematica che meglio approssima i risultati sperimentali.

Il primo modello empirico introdotto, funzionale alla descrizione dei materiali porosi e fibrosi, è stato proposto da Delany e Bazley [12] e permette di calcolare l’impedenza relativa ad uno strato di materiale omogeneo e isotropo in funzione dello spessore d e di una grandezza nota come “resistività al flusso d’aria” σ. Per uno strato di materiale tale grandezza è definita come il rapporto tra la differenza di pressione applicata alle due superfici dello strato e la portata d’aria defluente attraverso il materiale:

d v p_⋅1 Δ = σ [rayls/m]

Nel sistema M.K.S., dove p è espressa in Pa [N/m2] e v in m/s, la resistenza al flusso ha le dimensioni di Nsm-4.

Naturalmente le equazioni di Delany-Bazley contengono parametri dimensionali, che quindi sono differenti in funzione del sistema di unità di misura scelto, per cui si ricorda che:

(22)

σ σ σ 1000 1 ] [ ] [_kNsm−4 ₌ _gs−1_cm−3 ₌ [N s m-4]

Per come sono costruite le equazioni del modello di Delany-Bazley, questo è noto come modello a due parametri. Si sottolinea che l’articolo originale presenta i risultati nel sistema c.g.s. (in cui le dimensioni di σ sono gs-1cm-3).

Le equazioni originarie sono:

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⋅ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = = − −0,75 0,73 0 0 9 , 11 08 , 9 1 σ ω σ ω ρ f c i f c c Z W c [adimensionale] ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⋅ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = − −0,59 0,70 8 , 10 1 3 , 10 σ ω σ ω γ f c i f c [cm -1 ] ) coth( 0 0 l W c Z_s _γ ρ = ⋅ [adimensionale]

Le equazioni tradotte nel sistema MKS risultano invece:

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⋅ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = = − −0,75 0,73 0 0 077 , 0 051 , 0 1 σ ω σ ω ρ f c i f c c Z W c [adimensionale] ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⋅ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = − −0,59 0,70 086 , 0 1 17 , 0 σ ω σ ω γ f c i f c [m -1_]

Sulla base della forma delle equazioni di Delany-Bazley diversi autori hanno proposto modifiche ai coefficienti empirici introdotti, basandosi su prove sperimentali compiute su differenti categorie di materiali per le quali il modello presentava scostamenti significativi.

I modelli microstrutturali definiscono invece le proprietà acustiche dei mezzi in funzione delle geometrie locali e dei meccanismi di propagazione interni alle cavità, anche in relazione agli effetti dovuti alla viscosità dell’aria e alla dissipazione per scambio termico; possono essere inoltre implementati in tali modelli gli effetti dell’elasticità stessa del materiale, che portano a trasferimenti di energia per deformazione [13]; un esempio di

(23)

modello microstrutturale è quello proposto da Johnson-Champoux-Allard [14], ad oggi il più utilizzato per i materiali porosi di diversa natura; questo esprime la densità dinamica e la compressibilità in funzione di cinque parametri fisici che caratterizzano la struttura: resistività al flusso d’aria, porosità a cella aperta, la cosiddetta tortuosità acustica, lunghezza termica e lunghezza viscosa. Specificamente per il caso delle pavimentazioni stradali è stato sviluppato a partire dal modello di Johnson-Champoux-Allard il modello di Hamet-Bérengier [15], le cui equazioni vengono di seguito riassunte:

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = ∞ f f i c μ φ α ρ ω ρ ( ) 0 1 [kg/m3] 1 0 1 ) 1 ( 1 ) ( − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − + = θ γ γ ω f f i P Kc [N/m2] 2 / 1 2 / 1 0 1 1 1 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + − − ⋅ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⋅ = ∞ f f i f f i k k θ μ _γ γ α [m-1_] 2 / 1 2 / 1 0 1 1 1 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + − − ⋅ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + = ∞ f f i f f i c Zc θ μ _γ γ φ α ρ [rayls]

in cui le funzioni fμ e fθdescrivono rispettivamente la frequenza critica viscosa e la frequenza

critica termica, ricavabili dalle equazioni:

∞ ⋅ = α πρ σ φ μ 0 2 f _[Hz] pr N f 0 2πρ σ θ = [Hz]

(24)

Dove:

P0 è la pressione atmosferica, pari a circa 101325 Pa;

ρ0 è la densità dell’aria, pari a circa 1,2 kg/m3;

γ è il rapporto tra i calori specifici, pari a 1,4 [adimensionale]; Npr è il numero di Prandtl, pari a 0,7 [adimensionale];

σ è la resistività al flusso d’aria [rayls/m];

φè la porosità comunicante;

α∞ è un fattore di forma chiamato tortuosità [adimensionale], definito come limite per

frequenze che tendono all’infinito del rapporto tra la velocità del suono in aria e la velocità di fase all’interno del materiale:

2 0 lim ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ∞ → ∞ c c ω α [adimensionale]