CAPITOLO 2
Formulazione del metodo ibrido MM/FEM.
2.1
Geometria della FSS
Una possibile geometria di superfici selettive in frequenza, realizzata mediante uno schermo metallico spesso, è mostrata in Fig 2.1. Lo schermo è costituito da una piastra metallica spessa su cui vengono praticate aperture di forma arbitraria equispaziate lungo due direzioni di periodicità inclinate di un angolo α.
Per l’analisi presentata in seguito, ogni apertura è considerata come uno spezzone di guida d’onda di lunghezza pari allo spessore dello schermo stesso. Il piano di riferimento è scelto in modo da avere la superficie illuminata dello schermo sul piano xy mentre la direzione z risulta perpendicolare allo schermo con direzione opposta a quella di propagazione dell’onda.
Al fine dell’analisi si suppone che lo schermo sia infinito (non verranno presi in
onda
incidente
(θ,φ)
apertura con
forma
schermo metallico
spesso
x
y
z
Le aperture sono disposte in modo periodico lungo l’asse x con periodo dx mentre, lungo l’altro asse, che forma un angolo α con l’asse x, la spaziatura ha periodo dy sin α. Per questo motivo, nella maggior parte dei casi, è possibile definire delle celle elementari che suddividono l’array e che contengono una sola apertura. La geometria dello schermo sul piano x-y e le due direzioni di periodicità sono rappresentate in Fig 2.2.
Fig 2.2 Rappresentazione dello schermo sul piano xy con i due periodi di ripetizione.
Gli angoli che descrivono la direzione di incidenza dell’onda piana sulla superficie della FSS sono definiti come:
θ = angolo formato tra la direzione di incidenza e l’asse z
φ = angolo formato tra la proiezione della direzione di incidenza sul piano xy ed x
dy sinα
dx
2.2
Il metodo dell’accoppiamento modale (Mode Matching)
Il Mode-Matching è un metodo di analisi numerica di larga diffusione per lo studio e la progettazione di componenti a microonde, che produce risultati molto precisi. Il principale vantaggio di questa tecnica consiste nella possibilità di valutare l’interazione, non solo tra i modi fondamentali, ma tra tutti i modi in cui viene espanso il campo, anche tra quelli di ordine superiore. Per questo motivo il Mode-Matching (MM) è in grado di ricostruire l’andamento del campo elettromagnetico in modo completo; si tratta in altre parole di una tecnica “full-wave”. Nei paragrafi successivi viene ricavato l'accoppiamento modale, in termini di onde dirette e riflesse, che consente di ottenere la definizione della matrice di scattering generalizzata (Generalized Scattering Matrix GSM) relativa alla discontinuità aria-apertura, indispensabile per la determinazione della matrice di scattering generalizzata della FSS.
Formulazione in termini di onde dirette e riflesse
Nella analisi della discontinuità aria-apertura, si considerino lo sviluppo modale di Floquet per quanto riguarda la propagazione in aria e quello su di un set completo di funzioni modali in guida (ottenute con il metodo FEM full-wave) per quanto riguarda la propagazione guidata nello schermo. Considerando di porre entrambi i piani di riferimento alla coordinata z=0 con z perpendicolare alla superficie dello schermo si ottiene.
(
)
(
)
1 1 A t i i i i A t i i i i E a b E H a b H ∞ = ∞ = = + = − ∑
∑
ur ur uur uur (2.2.1)(
)
(
)
1 S t i i i i S t i i i E A B e H A B h ∞ = ∞ = + = − ∑
∑
ur r uur r (2.2.2)Nella (2.2.1) e (2.2.2) ai e bi sono i coefficienti complessi dello sviluppo modale di Floquet in aria, rispettivamente per l’onda incidente e per quella riflessa; Ai e Bi sono i coefficienti trasversi dello sviluppo modale in guida, rispettivamente dell’onda riflessa e trasmessa nel tratto guidato della apertura praticata nello schermo.
La geometria considerata è riportata in Fig 2.3.
Fig 2.3 Intensità d’onda entranti ed uscenti nello schermo per entrambi gli sviluppi modali.
Alle (2.2.1),(2.2.2) va ora applicata la condizione di continuità della componente trasversa dei campi sull’interfaccia tra aria e apertura data dalla relazione
' 0 ' S A t C t A S t t C E sull apertura S E sul pec H H sull apertura S = = ur ur uur uur (2.2.3) e sostituendo le (2.2.1) e (2.2.2)
(
)
(
)
(
)
(
)
1 1 1 1 i i i i i i i i i i i i i i i i a b E A B e a b H A B h ∞ ∞ = = ∞ ∞ = = + = + − = − ∑
∑
∑
∑
ur r uur r (2.2.4)Si noti che con SC viene indicata la superficie a comune delle due regioni in cui sono definiti rispettivamente le espansioni modali in aria e le espansioni modali in guida. Se ne deduce che SC corrisponde alla superficie dell'apertura.
ai
bi
Bi
1 , 2 1( ) 2 ( ) ˆ D
S
f f f t f ∗ t z dS
< >=
∫
× ⋅ (2.2.5)si proiettano l'equazione di continuità del campo elettrico sulle autofunzioni magnetiche e l'equazione di continuità del campo magnetico sulle autofunzioni elettriche. La proiezione si rende indispensabile al fine di imporre l'uguaglianza dei campi in media sull'intero dominio considerato e non su un numero finito e discreto di punti. In particolare proiettando la prima equazione sulle autofunzioni ∗
j
Hr e la seconda sulle autofunzioni *
j er si ottiene:
(
)
(
)
(
)
(
)
(
)
(
)
(
)
( )
* * 1 0 * * 1 1 ˆ ˆ ˆ ˆ A C C C i j j i i z i i i z i S i S i j i j i i z i i z i S i S a b E H i dS A B e H i dS a b H e i dS A B h e i dS ∞ ∞ = = ∞ ∞ = = + × ⋅ = + × ⋅ − × ⋅ = − × ⋅∑
∫∫
∑
∫∫
∑
∫∫
∑
∫∫
ur uur ur uur uur r r r (2.2.6)Si noti che nelle precedenti equazioni si sono indicate con SC la superficie definita precedentemente, e con SA la superficie su cui è definito lo sviluppo modale di Floquet in aria (corrispondente alla cella di periodicità). Passando ad una formulazione di tipo matriciale il sistema precedente risulta equivalente a:
(
)
(
)
(
)
(
)
H D H A P B A C b a C B A P b a − = − + = + (2.2.7) dove:(
)
(
)
( )
* * * ˆ ˆ ˆ A C C i j A ij z S j i ij z S i j S ij z S P E H i dS C e H i dS P e h i dS = × ⋅ = × ⋅ = × ⋅∫∫
∫∫
∫∫
ur uur r uur r r (2.2.8)Nelle relazioni precedenti S ij
P e A
ij
invece rettangolare con dimensioni date dal numero di modi in guida, per le righe, e da quello in aria, per le colonne. La matrice C è detta “matrice di accoppiamento” in quanto tiene conto dell'accoppiamento tra i modi in guida e quelli in aria.
Considerando che i vettori dei coefficienti dello sviluppo modale delle onde riflesse b ,B possono essere espressi in funzione di quelli delle onde incidenti a , A tramite definizione della matrice di scattering generalizzata:
= = A a S S S S A a S B b 22 21 12 11 (2.2.9)
si ottengono le definizioni delle quattro sottomatrici della matrice di scattering della discontinuità aria-apertura:
(
) (
)
(
)
(
)
(
)
⋅ − = ⋅ + ⋅ ⋅ = − ⋅ = − ⋅ ⋅ ⋅ + = − − 12 2 22 1 1 2 1 12 11 2 21 2 1 1 2 1 11 2 S M I S M I M M S S I M S I M M M M I S (2.2.10)avendo indicato con
( )
( )
1 1 1 * 2 A H SM
P
C
M
P
C
− −=
⋅
=
⋅
(2.2.11)Per ottenere la GSM svincolata dalla dipendenza dalle potenze associate ai modi nei due mezzi si effettua una normalizzazione secondo la regola:
1 1 1 1 1 1 1 1 11 11 12 12 21 21 22 22
'
'
'
'
A A S A A S S SS
P S P
S
P S P
S
P S P
S
P S P
− − − − − − − −=
=
=
=
(2.2.12)Criteri di convergenza
L’espressioni modali utilizzate per rappresentare i campi nella procedura del Mode Matching sono di infiniti termini. In pratica per realizzare codici numerici al calcolatore occorre troncare la serie ad un numero finito, tale operazione di troncamento può influire sui risultati finali. Per essere sicuri di effettuare l’analisi considerando tutti i modi necessari a descrivere esattamente i campi sulla discontinuità, occorre effettuare delle prove di convergenza, che consistono nel calcolare i parametri di interesse per numero crescente dei modi. Il valore a cui tende la soluzione rappresenta il valore esatto ed in pratica è sufficiente troncare la serie a quel valore per il quale il risultato non si discosta significativamente da quello finale.
Occorre inoltre considerare anche un altro fenomeno noto come “convergenza relativa”: i risultati ottenuti con l’espansione modale potrebbe convergere ad un valore non esatto, qualora non venga rispettato un determinato rapporto N1/N2 tra il numero di modi presenti
nelle due sezioni.
In particolare, il corretto rapporto fra il numero di modi considerati per l’espansione di Floquet ed il numero di modi dell’espansione in guida viene determinato come segue: tenendo conto che per eseguire un MM corretto si devono avere da entrambe le parti modi che variano con uguale velocità (criterio spettrale), si selezionano tutti quei modi che hanno un autovalore trasvero inferiore a un valore massimo prefissato MAX
t
K . Infatti, l’autovalore trasverso è un buon indice della velocità di variazione dei campi sulla sezione trasversale.
Fig 2.4 Rappresentazione grafica di Kt in termini di velocità della variazione dei campi trasversi in aria ed
in guida .
Operativamente, il primo passo da compiere è quello di scegliere un autovalore trasverso massimo: per mesh costituite da triangoli pseudo-equilateri, il valore di MAX
t
K è fissato in relazione alla lunghezza media degli spigoli lmed in accordo con la seguente regola:
max 0.5 0.7
t
med
k =α π con < <α
l (2.2.13)
Successivamente viene determinato il numero di modi dell’espansione FEM con autovalore trasverso minore di MAX
t
K . Infine vengono selezionati tutti i modi di Floquet che garantiscono la stessa variazione spaziale, sul piano trasverso nelle direzioni x e y, e che hanno autovalore trasverso inferiore a MAX
t
K .
Operando in questo modo è stato possibile applicare una sorta di criterio spettrale per la soluzione del problema della convergenza relativa dei parametri di scattering della discontinuità aria-apertura, in cui i campi sono rappresentati mediante due espansioni modali differenti.
2.3
Espansione dei campi in aria
Il campo elettromagnetico nei due semispazi delimitati dallo schermo deve soddisfare il teorema di Floquet. In accordo con quanto asserito dal suddetto teorema, il campo elettromagnetico totale, sia per la regione di provenienza dell’onda piana monocromatica, che per la regione "d’ombra", nella quale si ha la propagazione dell’onda monocromatica trasmessa, può essere espanso su di un set completo di funzioni modali di base di Floquet, con coefficienti di ampiezza complessi incogniti.
Considerando un sistema di riferimento cartesiano, in cui la superficie della FSS, su cui incide l’onda piana, giace sul piano xy alla coordinata z=0 e l’asse z è sulla perpendicolare a tale piano con direzione opposta a quella dell’onda, risulta possibile fornire un’espressione analitica dell’espansione modale di Floquet del campo elettrico relativo al modo i-esimo. Si noti che le formulazioni risultano differenti a seconda del tipo di polarizzazione con cui l’onda piana incide sullo schermo. A tale proposito è opportuno ricordare che si considera che un'onda abbia polarizzazione TE, nel caso in cui il campo elettrico risulti completamente contenuto su di un piano parallelo a quello dato dalla superficie dello schermo; si considera invece che un'onda abbia polarizzazione TM, nel caso in cui sia il campo magnetico ad essere interamente contenuto in un piano parallelo a quello dato dalla superficie dello schermo. Trascurando la dipendenza dal tempo, data dall’espressione e−jωt, i coefficienti di ampiezza
risultano: ( ) ( ) ( ) ( ) 1 ˆ ˆ ( sin( ) 1 ˆ ˆ ( sin( ) yi xi yi xi j k y j k x yi TE xi i x y ti ti h h j k y j k x yi TM xi i x y ti ti h h k k e i i e e k k a b k k e i i e e k k a b α α − − − − = − = + r r (2.3.1)
Nell’espressione precedente compare la costante di propagazione traversa kti che è definita come: 2 2 yi xi ti
k
k
k
=
+
(2.3.2)dove kxi e k rappresentano le proiezioni della costante lungo gli assi cartesiani yi x , y ed il loro valore è dato dalle espressioni:
0 0 2 cos( )sin( ) 2 2 sin( )sin( ) sin( ) tan( ) xi h yi h h m k k a n m k k b a π φ θ π π φ θ α α = + = + − (2.3.3)
A questo punto è opportuno evidenziare come, tra gli indici dell’espansione modale di Floquet m ed n, ed il modo i-esimo intercorra una corrispondenza biunivoca.
Nella (2.3.3) compaiono gli angoli θ e φ che rappresentano la direzione di incidenza dell’onda piana monocromatica sullo schermo. θ rappresenta l’angolo formato dalla direzione di propagazione con l’asse z e φ rappresenta l’angolo formato dalla proiezione della direzione di propagazione sul piano xy con l’asse x.Come inttrodotto nel paragrafo 2.2 α è invece l’angolo formato tra i due assi di periodicità. La geometria considerata è illustrata in Fig 2.2.
Il caso particolare, ma comunque frequente, di geometria axial in cui le direzioni di periodicità risultano ortogonali tra di loro, viene automaticamente considerato imponendo
2
π α = .
Per quanto riguarda i coefficienti relativi al modo i-esimo dell’espansione modale di Floquet del campo magnetico, possono essere ricavati da quelli relativi al campo elettrico, utilizzando la relazione che intercorre fra campo elettrico e magnetico per un’onda piana:
)
ˆ
(
z i i iY
i
e
h
r
=
×
r
(2.3.4)nella quale l'ammettenza modale Y assume espressioni differenti a seconda che sia riferita i alla polarizzazione TE oppure a quella TM
0 0 0 0 TE zi i TM i zi k Y k k Y k η η = = (2.3.5)
Nell’ espressione precedente va considerato che η0 ≅377Ω è l'impedenza caratteristica del vuoto e che la costante di propagazione lungo la direzione data da z e relativa al modo i-esimo kzi viene definita come:
2 2 2 2 0 0 2 2 0 zi zi zi
k
k
se k
k
j k
k
altrimenti
−
≥
−
−
(2.3.6)Applicando le definizioni (2.3.5) e (2.3.6) alla (2.3.4), se ne deduce che l’espressione analitica dei coefficienti dell’espansione modale di Floquet per il modo i-esimo del campo magnetico risultano: ( ) ( ) ( ) ( ) 0 0 0 0 1 ˆ ˆ ( sin( ) 1 ˆ ˆ ( sin( ) yi xi yi xi TE zi xi yi j k x j k y i x y ti ti h h TM yi xi j k x j k y i x y zi h h ti ti k k k h i i e e k a b k k k k k h i i e e k a b k k η α η α − − − − = + = − + ur ur (2.3.7) Si noti che il modo dato dai coefficienti m= n0 =0 risulta sempre il modo fondamentale per
l’espansione in aria, i modi di ordine superiore sono sempre evanescenti per le frequenze di interesse. Questo permette di descrivere la superficie selettive in frequenza in termini di coefficienti di riflessione e di trasmissione utilizzando i valori S11 ed S12 della matrice di
scattering generalizzata come è descritto in dettaglio nei capitoli successivi.
Incidenza normale
Di particolare interesse il caso particolare corrispondente a θ =0.
costante di propagazione traversa. Per la (2.3.2) risulta nulla anche la kti. Conseguentemente a quanto prima esposto risultano di difficile valutazione i rapporti kxi kti e kyi kti che compaiono nella definizione dei coefficienti moltiplicativi complessi dell'espansione modale (2.3.6). Sembra opportuno a tal proposito far notare che, facendo tendere l’angolo di incidenza alla normale (θ →0), kxi,kyi,kti risultano infinitesimi dello stesso ordine e quindi il loro rapporto tende ad un valore finito non necessariamente nullo.
Per superare il problema si consideri una incidenza non ortogonale (θ ≠0) e il modo fondamentale individuato dai coefficienti m= n0 =0. Con queste assunzioni le (2.3.3) assumono la forma 0 0 cos sin sin sin xi yi k k k k φ θ φ θ = = (2.3.8) Applicando le (2.3.8) alla (2.3.2) ed esplicando i rapporti kxi kti e kyi kti si ottiene
(
) (
)
(
) (
)
0 0 2 2 0 0 0 0 0 2 2 0 0 0cos sin cos sin
cos sin
cos sin sin sin
sin sin sin sin
sin sin
cos sin sin sin
xi ti yi ti k k k k k k k k k k k k k k φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ φ θ = = = + = = = + (2.3.9)
I risultati ottenuti risultano indipendenti dal valore di θ e quindi sono validi anche per incidenza normale. La costante di propagazione lungo la direzione di propagazione, risulta:
0
zi
k = (2.3.10) k
ed applicando quanto sopra alle (2.3.5)
0 1 TE TM i i Y Y η = = (2.3.11)
Il risultato appena ottenuto è particolarmente interessante se si pensa che la costante di propagazione e l’ammettenza modale del modo fondamentale di Floquet sono uguali a quelli di un’onda piana monocromatica che si propaga nello spazio libero.
Applicando i risultati appena ottenuti alle (2.3.1) ed (2.3.7), le costanti moltiplicative complesse del modo fondamentale dello sviluppo modale di Floquet per un’onda con incidenza normale sullo schermo, risultano:
0 ; m 0 n 0 θ = = = (2.3.12)
(
)
(
)
0 0 1 1 ˆ ˆ cos sin ( sin( ) 1 1 ˆ ˆ sin cos ( sin( ) TE i x y h h Tm i x y h h h i i a b h i i a b φ φ η α φ φ η α = + = − + ur ur (2.3.13)(
)
(
)
1 ˆ ˆ sin cos ( sin( ) 1 ˆ ˆ cos sin ( sin( ) TE i x y h h TM i x y h h e i i a b e i i a b φ φ α φ φ α = − = + r r2.4 Metodo agli Elementi Finiti
Per quanto concerne le superfici selettive in frequenza induttive spesse realizzate mediante siloni, la propagazione nelle aperture può essere considerata come la propagazione all’interno di guide d’onda in cui la guida ha la stessa geometria della apertura praticata nello schermo. In questo senso, per l’analisi modale del campo diretto e riflesso in apertura, è stato sfruttato un metodo agli elementi finiti sviluppato per consentire lo studio di guide d’onda caratterizzate da configurazioni che possono essere disomogenee. In tali dispositivi, in accordo con le leggi di Maxwell, si propagano modi ibridi per la cui valutazione si rende necessaria un’analisi di tipo full-wave. Lo sviluppo di tale metodo può essere presentato brevemente come segue:
“A partire dall’equazione d’onda (equazione di Helmoltz) in forma vettoriale, si rappresentano i campi trasversi e longitudinali come somme di funzioni base (rispettivamente Whitney function e polinomi di Lagrange) definite su un dominio computazionale (sezione della apertura) discretizzato in elementi finiti triangolari. Sfruttando alcune proprietà integrali e proiettando il set di equazioni ottenute su una base di funzioni test, scelte in questo caso uguali al quelle di interpolazione dei campi (metodo di Galerkin), si ricava la forma debole della equazione d’onda vettoriale, la quale, già in forma discretizzata, fornisce il sistema risolvente. Il problema si riduce dunque alla soluzione di un problema agli autovalori generalizzato (Generalized Eigenvalue Problem, GEP) la cui soluzione, tenuto conto anche della natura sparsa delle matrici involute nel metodo, è nota. Gli autovalori ricavati sono dunque le costanti di propagazione modale, mentre gli autovettori costituiscono le componenti di campo trasverso e longitudinale ricostruito in guida .”
Nelle pagine successive viene riportata la formulazione in termini di matrici locali (riferite al singolo elemento in cui viene discretizzato l’intero dominio dato dall’apertura) i cui elementi vengono inseriti nelle matrici globali tramite la corrispondenza tra la numerazione locale e quella globale.
Formulazione dell’equazione d’onda nella sua forma debole
Nella analisi full-wave della guide dielettriche, è necessario risolvere il seguente problema ai valori di confine (BPV Boundary Problem Value)
$ $ 2 1 2 1 0 r r E k E in E n su E n su ε µ ∇× ∇× − = Ω × Γ ∇× × Γ ur ur ur ur ur ur ur (2.4.1)
dove Ω Γ Γ rappresentano rispettivamente: la sezione della guida d’onda, le pareti PEC e , 1, 2 le pareti PMC della stessa. Per il campo elettrico dell’espressione precedente, è assunta una dipendenza dalla direzione di propagazione di tipo esponenziale (e−j zβ ) dove β è la costante
di propagazione. Considerando che è possibile esprimere sia il campo elettrico che l’operatore
∇ur in termini di componenti trasverse e longitudinali, come espresso nella (2.4.2),
( , ) ( , ) j z z E E x y E x y e z z z β τ τ − = + ∂ ∇ = ∇ + ∂ ur uur $ ur uur $ (2.4.2)
l’equazione di Helmotz diventa:
(
)
(
)
2 2 2 1 1 1 z r r r z r z r E j E E k E E j E k E τ τ τ τ τ τ τ τ τ β β ε µ µ β ε µ ∇ × ∇ × − ∇ − = − ∇ ⋅ ∇ + = uur uur uur uur uur uur
uur uur uur (2.4.3)
Esistono due differenti approcci alla risoluzione del precedente problema agli autovalori: uno risolve per k avendo fissato il valore della costante di propagazione 2 β ; l’altro consiste nel
fissare la frequenza di lavoro e risolvere per β . La formulazione presentata è riferita al secondo approccio.
Imponendo la frequenza di lavoro, l’equazione (2.4.3) diventa una equazione agli autovalori quadrati su β che risulta di difficile e complessa valutazione. Inoltre, essendo β reale per i modi in propagazione ed immaginaria per quelli evanescenti, l’approccio richiede la soluzione di un problema agli autovalori complessi. La complessità computazionale raggiunta a causa delle due problematiche sopra citate, può essere eliminata operando la trasformazione delle variabili:
x x y y z z
e =βE e =βE e = −jE (2.4.4)
Applicando la (2.4.4) alla (2.4.3) si ottiene:
(
)
(
)
2 2 2 2 2 2 1 1 z r r r z r z r e e e k e e e k e τ τ τ τ τ τ τ τ τ β β ε µ µ β β ε µ ∇ × ∇ × − ∇ − = ∇ ⋅ ∇ − = uur uur ur uur ur ur
uur uur ur (2.4.5)
Come si vede dalla (2.4.5) il problema risulta ridotto ad un problema agli autovalori reali di primo grado sulla variabile γ β= 2.
Il passo successivo è quello di definire un prodotto interno in cui si consideri la funzione di test Tur su cui vengono proiettate le due equazioni. Si ottiene
(
)
(
)
2 2 2 2 1 z r r r z z r z z r T e T e T e d k T e d T e e d k T e d τ τ τ τ τ τ τ τ τ τ τ τ τ γ ε µ µ β β ε µ Ω Ω Ω Ω ⋅ ∇ × ∇ × − ⋅ ∇ − ⋅ Ω = ⋅ Ω ∇ ⋅ ∇ − Ω = Ω ∫∫
∫∫
∫∫
∫∫
uur uur uur ur uur uur uur ur uur ur
uur uur ur (2.4.6)
(
) (
) (
)
$(
)
(
)
$ 2 0 2 0 1 1 1 1 z r r r C z z z r z z r z z z r C T e T e T e d k T e d T n e d T e T e d k T e d e T T n e d n τ τ τ τ τ τ τ τ τ τ τ τ τ τ τ τ τ τ γ µ ε µ γ γ ε µ γ µ Ω Ω Ω Ω ∇ × ⋅ ∇ × + ⋅ ∇ + ⋅ Ω = = ⋅ Ω − × ∇ × ∇ ⋅ ∇ + ∇ ⋅ Ω − Ω = = ∂ + ⋅ ∂ ∫∫
∫∫
∫
∫∫
∫∫
∫
ur ur ur r ur ur ur r ur r ur ur r l ur ur ur r r l (2.4.6)Nelle relazioni precedenti si è indicato con $n il versore ortogonale al contorno C della guida, con
n ∂
∂ la derivata lungo la direzione identificata da $n e con C
∫
dl l’integrale sul contorno della guida. Operando la trasversalizzazione dei campi e dell’operatore ∇ur anche per le condizioni al contorno si ottengono le relazioni:$
(
)
$ 0 . . . 0 0 . . . 0 z z z e n su pareti p e c e e e n su pareti p m c e τ τ τ τ × = = ∇ + ⋅ = ∇ × = uur uur uur uur (2.4.7)Si noti che l’integrale di linea residuo delle (2.4.6) risulta identicamente nullo sia per parete
PEC sia per parete PMC. Applicando le condizioni al contorno alle (2.4.6) si ottiene la forma debole dell’equazione
d’onda considerata:
(
) (
)
(
)
(
)
2 0 2 0 1 1 0 r z r z z z r z z r T e d k T e d T e T e d T e T e d k T e d τ τ τ τ τ τ τ τ τ τ τ τ τ τ ε γ µ γ ε µ Ω Ω Ω Ω Ω ∇ × ⋅ ∇ × Ω − ⋅ Ω = − ⋅ ∇ + ⋅ Ω = − ∇ ⋅ ∇ + ∇ ⋅ Ω − Ω ∫∫
∫∫
∫∫
∫∫
∫∫
ur ur ur r ur r ur ur ur r ur ur ur r (2.4.9)Discretizzazione del dominio mediante elementi finiti
Per risolvere l’equazione d’onda in forma debole ricavata precedentemente, si procede dividendo il dominio di indagine in sottodomini (elementi triangolari). Condizione necessaria al fine che il metodo risulti valido è quella di discretizzare il dominio in modo tale da ottenere tutti gli elementi triangolari caratterizzati da proprietà dielettriche costanti. Questo equivale a dire che, nel caso nel caso in cui il dominio di partenza sia riempito di dielettrici differenti, non è ammissibile avere un triangolo al cui interno coesistano i due materiali. La situazione ottenuta è rappresentata in Fig 2.5.
Fig 2.5 Rappresentazione del dominio discretizzato mediante elementi finiti.
Per quanto riguarda la scelta delle funzioni di base per l’espansione del campo elettrico sugli spigoli e sui nodi, è possibile dimostrare che lo spazio delle autofunzioni ammissibili per la soluzione del problema è individuato da funzioni vettoriali di spigolo, tangenzialmente continue fra gli elementi, e funzioni di nodo scalari continue sul dominio triangolare. Avendo scomposto l’equazione vettoriale di Helmotz in componente trasversa e componente longitudinale, le funzioni tangenziali vettoriali di spigolo (TVFE) possono essere utilizzate per approssimare i campi trasversi e le funzioni scalari polinomiali possono essere utilizzate per approssimare il campo longitudinale sui nodi della mesh. In particolare, sono state usate le funzioni TVFE di ordine 0 (Whitney) per la scomposizione del campo elettrico trasverso sugli
spigoli degli elementi e le funzioni polinomiali di Lagrange di ordine 1 per l’espansione del campo longitudinale sui nodi dei triangoli. Il campo elettrico si può pertanto scomporre in
3 3 1 m m z 1 zi i m i eτ E Wτ e e E L = = =
∑
=∑
ur uuur (2.4.9)dove E ed Eτm zi sono rispettivamente il valor medio della componente trasversa del campo
elettrico sullo spigolo m-esimo ed il valor medio della componente longitudinale del campo elettrico sul nodo i-esimo del generico elemento preso in considerazione.
Per il generico elemento considerato vengono considerate le numerazioni locali rappresentate in Fig 2.6.
Fig 2.6 Numerazione locale per l’elemento e-esimo
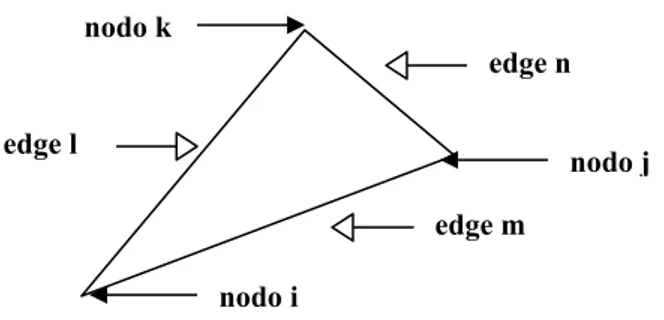
Utilizzando le due terne cicliche (m,n,l) per gli spigoli ed (i,j,k) per i nodi del generico elemento triangolare della mesh, è possibile scrivere
(
)
(
)
(
)
m m i j j i n n j k k j l l k i i k W l L L L L W l L L L L W l L L L L τ τ τ τ τ τ = ∇ − ∇ = ∇ − ∇ = ∇ − ∇uuur uur uur
uur uur uur
uur uur uur
(2.4.10)
dove le Wuuri sono le funzioni di Whitney definite sullo spigolo dell’elemento e-esimo ed L sono le funzioni interpolanti di Lagrange di ordine 1 definite sui nodi dello stesso elemento. Si noti che le due terne di numerazione non sono indipendenti ma sono tra loro collegate: lo
nodo k nodo j nodo i edge n edge m edge l
spigolo l-esimo si trova sempre tra i nodi k-esimo ed i-esimo come rappresentato nella precedente figura.
Le funzioni di Lagrange di ordine 1 sono le coordinate di area calcolate su di ogni punto del dominio triangolare per ogni nodo dello stesso. Si consideri la Fig 2.7, la coordinata di area per il nodo 1 è calcolata come il rapporto tra l’area del triangolo dato dai nodi (P,2,3) e l’area del triangolo dato dai nodi (1,2,3), per il nodo 2 è il rapporto tra le aree di (P,3,1) ed (1,2,3), per il nodo 3 è il rapporto tra le aree di (P,1,2) ed (1,2,3).
Fig 2.7 Rappresentazione delle coordinate di area del punto P(x,y).
In formule questo corrisponde a calcolare
1 1 1 2 2 2 2 3 3 3 3 1 1 1 / 1 1 1 x y x y L x y x y x y x y = (2.4.12)
e quindi, dopo alcune operazioni, si ottiene
2 3 3 2 2 3 3 2 1 2 2 2 x y x y y y x x L x y A A A − − − = + + (2.4.13)
Le funzioni di Whitney, sono funzioni vettoriali, il cui andamento è mostrato nella Fig 2.8, che assicurano la continuità della componente tangenziale del campo attraverso gli spigoli ed una variazione lineare della componente normale sugli stessi.
P(x,y)
1(x1,y1) 2(x2,y2)
Fig 2.8 Rappresentazione dell’andamento del modulo (a) e dell’andamento vettoriale (b) delle funzioni di Whitney per un triangolo rettangolo.
Applicando la procedura di Galerkin, secondo la quale le funzioni di test devono coincidere con le funzioni base scelte le funzioni di test trasverse coincidono con le funzioni di Whitney, mentre quelle longitudinali con le funzioni di Lagrange.
m
z i
T W per i tre spigoli
T L per i tre nodi
τ =
= uur uuur
(2.4.13)
Applicando la (2.4.13) alla (2.4.8) si ottiene: (a)
(b)
Dominio Triangolare
(
) (
)
(
)
3 2 0 1 3 3 1 1 3 2 0 1 1 1 1 1 1 n m r n m m m T r T n m m n j zj m m r T r T m j m j i i r T r W W d k W W d E W W d E W L d E L W d E L L k τ τ τ τ τ τ τ τ τ ε µ γ γ µ µ γ γ µ µ = = = = ∇ × ⋅ ∇ × Ω − ⋅ Ω = = − ⋅ Ω − ⋅ ∇ Ω − ∇ ⋅ Ω − ∇ ⋅ ∇ − ∑ ∫∫
∫∫
∑
∫∫
∑
∫∫
∑ ∫∫
ur uur ur uur uur uur
uur uur uur ur
ur uur 3
(
ur ur)
1 0 r r j i zj i T L L d E ε µ = Ω = =∑ ∫∫
(2.4.14)dove l’indice m identifica la numerazione dello spigolo locale al triangolo considerato, l’indice n scorre per le funzioni di test sugli spigoli del triangolo, l’indice i indica la numerazione locale dei nodi e l’indice j scorre per le funzioni di test sui nodi del triangolo. Le relazioni della (2.4.14) possono essere anche espresse in forma matriciale compatta:
0 0 0 T z z A e B C e e C D e τ τ γ = − (2.4.17)
dove eτ ed ez sono i vettori contenenti il valore medio del campo elettrico sui tre spigoli ed il
valore puntuale sui tre nodi. Le matrici sono definite come:
(
) (
)
2 0 1 ( , ) n m r n m r T T A m n τ W τ W d k ε W W d µ =
∫∫
∇ ×ur uur ⋅ ∇ ×ur uur Ω −∫∫
uur uur⋅ Ω (2.4.16) 1 ( , ) n m r T B m n W W d µ =∫∫
uur uur⋅ Ω (2.4.17) 1 ( , ) T m j r T C m j W τL d µ =∫∫
uur uur⋅ ∇ Ω (2.4.18) 1 ( , ) i n r T C i n = µ∫∫
∇τL W d⋅ Ω uur uur (2.4.19)(
2)
0 1 ( , ) j i r r j i r T D i j τL τL k ε µ L L d µ =∫∫
∇ur ⋅ ∇ur − Ω (2.4.20)Si noti che le matrici locali sono quadrate e con dimensioni
[
3 3×]
, eτ =[
eτ1 eτ2 eτ3]
ed[
1 2 3]
z z z z
e = e e e . Nelle definizioni precedenti è stato possibile portare fuori dal segno di integrale le costanti dielettriche in quanto costanti sul generico elemento.
Espressione esplicita delle matrici locali
Si considerino le terne cicliche già definite nella sezione precedente, una che scorre sugli spigoli (m,n,l) ed una che scorre sui nodi (i,j,k). Esplicitando la dipendenza delle funzioni polinomiali di Lagrange dalle coordinate cartesiane, si deduce il legame con il vettore perpendicolare allo spigolo, infatti, dalla (2.4.12):
(
) (
)
1 2 i j k k j j k k j L x y x y y y x x x y A = − + − + − (2.4.21)con ,x x e j k y y coordinate cartesiane dei nodi del triangolo ed A la sua area. j, k
Fig. 2.9 Numerazione degli spigoli, nodi e vettori perpendicolari ai lati per un elemento finito triangolare.
Il gradiente trasverso di L risulta: i
1 i n L V τ ∇uur = − uur (2.4.22) i j k m n l Vm Vn Vl
avendo indicato con Vuurn il vettore perpendicolare allo spigolo n-esimo, opposto al nodo i-esimo.
Dal legame fra la funzione di Whitney associata allo spigolo m-esimo e le funzioni di Lagrange associate ai nodi i-esimo ed i+1-esimo (estremi dello stesso spigolo) si ha:
(
)
2m(
)
m m i j j n i l l W l L L L V L V A τ τ = ∇ − ∇ = −uuur uur uur uur ur
(2.4.23)
In Tabella 1 sono riassunte le espressioni delle funzioni di Whitney, di Lagrange ed il loro legame mediante i vettori perpendicolari per un generico triangolo e con numerazione locale esplicita.
(
) (
)
1(
)
1 2 3 3 2 2 3 3 2 1 2 1 2 2 1 3 1 1 , , 2 2 2 l L x y x y x y y y x x L V W L V L V A τ A A= − + − + − ∇uur = − uur uur= uur− uur
(
) (
)
2(
)
2 3 1 1 3 3 1 1 3 2 3 2 3 3 2 1 1 1 , , 2 2 2 l L x y x y x y y y x x L V W L V L V A τ A A= − + − + − ∇uur = − uur uur= uur− ur
(
) (
)
3(
)
3 1 2 2 1 1 2 2 1 3 1 3 1 1 3 2 1 1 , , 2 2 2 l L x y x y x y y y x x L V W L V L V A τ A A= − + − + − ∇uur = − ur uur= ur− uur
Tab 1 Espressioni esplicite delle funzioni di Lagrange e Whitney in relazione ai vettori perpendicolari agli spigoli.
Al fine di evitare confusione nella numerazione delle funzioni di base si indica con l’apice T la numerazione relativa alle funzioni di test.
Matrice A
Gli elementi di questa matrice considerano le interazioni fra la funzione di base associata allo spigolo m-esimo e quella di test associata allo spigolo n-esimo. Si consideri il primo addendo della (2.4.16) e si sostituisca l’espressione (2.4.23) che lega la funzione di Whitney con i vettori perpendicolari agli spigoli; si ha:
(
) (
)
4(
)(
)
1 1 1 ( , ) 4 T T T T m T n m n l n l m r T r T l l A m n W W d V V V V d A τ τ µ µ=
∫∫
ur∇ ×uuur ⋅ ∇ ×ur uuur Ω =∫∫
uur ur uur uuur× × Ω (2.4.24) avendo espresso il rotore trasverso della funzione di Whitney come:(
)
2 2(
)
m m n l l W V V A τ ∇ × = × ur uuur uur ur (2.4.25)Si noti che i vettori perpendicolari agli spigoli non dipendono dalla variabile di integrazione e la funzione integranda risulta quindi costante; il risultato dell’integrale è l’area dell’elemento:
(
)(
)
3 1 1 ( , ) 4 T T T m T n n l l m r l l A m n V V V V d A µ= uur ur uur uuur× × Ω (2.4.26)
Applicando le medesime sostituzioni al secondo addendo della (2.4.23) si ottiene:
(
)
(
)
(
)
(
)
2 0 2 2 0 2 ( , ) 4 T T T T T T T T T T n m r T m n r k j l n k i l l j j m n j i m l T A m n k W W d l l k L L V V L L V V L L V V L L V V d A ε ε = ⋅ Ω = ⋅ − ⋅ − ⋅ + ⋅ Ω ∫∫
∫∫
uur uuruur uur uur ur uuur uur uuur ur (2.4.27)
Considerando le proprietà delle funzioni di Lagrange e dell’integrale del loro prodotto [3]
(
)
1 2 3 ! ! !2! 2 ! i j k T i j k L L L d i j k Ω = + + +∫∫
(2.4.28)è possibile definire la matrice LL:
1 1 1 2 1 3 2 1 2 2 2 3 3 1 3 2 3 3 2 1 1 1 2 1 12 1 1 2 T L L L L L L A LL L L L L L L d L L L L L L = Ω =
∫∫
(2.4.29)(
)
(
)
( )
(
)
(
)
(
)
( )
(
)
2 0 2( , ) 12 , , , , T T T T T m T n T T r l n l l T T n l m i m l l A m n k LL k j V V LL k i V V A LL j j V V LL j i V V ε = ⋅ − ⋅ − ⋅ + ⋅ uur uur uur ur
uuur uur uuur ur (2.4.30)
Operativamente si definiscono le matrici dei prodotti vettoriali (VEC) e scalari (SC) fra i vettori perpendicolari agli spigoli; in questo modo è possibile riscrivere in forma più compatta l’espressione per ricavare la matrice A.
1 1 1 2 1 3 2 1 2 2 2 3 3 1 3 2 3 3 V V V V V V SC V V V V V V V V V V V V ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ur ur ur uur ur uur uur ur uur uur uur uur
uur ur uur uur uur uur (2.4.31)
1 1 1 2 1 3 2 1 2 2 2 3 3 1 3 2 3 3 V V V V V V VEC V V V V V V V V V V V V × × × = × × × × × × ur ur ur uur ur uur uur ur uur uur uur uur
uur ur uur uur uur uur (2.4.32)
Il generico elemento della matrice A diventa pertanto:
( )
(
)
(
) ( )
( ) ( )
(
) (
)
( ) (
)
2 0 3 1 ( , ) , , , , 4 12 , , , , , , T m T m T n T T n T T r r T T T T T T l l l l A m n VEC n l VEC l m k LL k j SC l n A A LL k i SC l l LL j j SC m n LL j i SC m l ε µ = − + − − + (2.4.33) Matrice BLa matrice B differisce dal secondo addendo della matrice A per una costante. Quindi non sono necessari calcoli aggiuntivi, ma è sufficiente moltiplicare il risultato ottenuto per il secondo addendo della matrice A per un opportuno termine di scala.
(
) ( )
( ) ( )
(
) (
)
( ) (
)
1 ( , ) , , , , 12 , , , , T m T n T T T T r T T T T l l B m n LL k j SC l n LL k i SC l l A LL j j SC m n LL j i SC m l µ = − + − + (2.4.34) Matrice CTGli elementi di questa matrice considerano l’interazione fra le funzioni di test applicate ai nodi dell’elemento e le funzioni di base sugli spigoli dello stesso. Tenuto conto delle equazioni (2.4.22), (2.4.23) e della (2.4.18) si ottiene:
2 1 1 ( , ) 4 T T T T T m m j j n l i l l r T r T l C m j W L d L V V L V V d A τ µ µ
=
∫∫
uur uur⋅∇ Ω =∫∫
uur uur⋅ − ur uur⋅ Ω (2.4.35) I vettori perpendicolari agli spigoli sono costanti rispetto alle variabili di integrazione pertantola (2.4.37) può essere scritta come:
(
)
(
)
2 1 ( , ) 4 T T T T m n l j l l i r T T l C m j V V L d V V L d A µ = ⋅ Ω − ⋅ Ω ∫∫
∫∫
uur uur ur uur
(2.4.36)
Si deve adesso risolvere l’integrale della funzione di Lagrange sul dominio triangolare che vale
(
)
6 12 12 3 i i i j k i i i j i k T T T L d L L L L d L L L L L L d A A A A Ω = + + Ω = + + Ω = = + + =∫∫
∫∫
∫∫
(2.4.37)indipendentemente dalla funzione prescelta. Utilizzando la notazione già impiegata e descritta dalla (2.4.31), l’espressione cercata diventa:
Matrice C
Gli elementi di questa matrice tengono conto delle interazioni fra le funzioni definite sugli spigoli dell’elemento e le funzioni di espansione nodali. C è la matrice trasposta di CT
quindi non occorrono calcoli aggiuntivi.
Matrice D
Gli elementi della matrice tengono conto delle interazioni fra la funzione di base associata al nodo i-esimo e quella di test associata al nodo j-esimo, si ricavano come nel caso delle matrici precedenti.
( )
1( )
2( )
0 1 , , , 4 T T T r r D i j SC i j k LL i j A ε µ = − (2.4.39)Si noti che la matrice SC1 può essere ottenuta mediante cambiamenti di righe e colonne
effettuati sulla matrice SC spostando la prima colonna nella terza, la terza nella seconda e la prima nella terza
1 2 1 3 1 1 2 2 2 3 2 1 3 2 3 3 3 1 ' V V V V V V SC V V V V V V V V V V V V ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ur uur ur uur ur ur uur uur uur uur uur ur uur uur uur uur uur ur
ed effettuando lo stesso procedimento sulle righe
2 2 2 3 2 1 1 3 2 3 3 3 1 1 2 1 3 1 1 V V V V V V SC V V V V V V V V V V V V ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
uur uur uur uur uur ur uur uur uur uur uur ur
Riempimento delle matrici globali
Nel paragrafo precedente sono state ricavate le matrici locali definite su ogni elemento triangolare in cui viene discretizzato il dominio di analisi. Il passo successivo consiste nel disporre i valori trovati in una matrice che contenga le informazioni necessarie per la soluzione del problema agli autovalori. Per fare questo occorre la sola conoscenza della corrispondenza tra la numerazione locale e quella globale. Nella Fig. 2.9 viene rappresentato il generico elemento triangolare che compone la mesh e viene evidenziata la corrispondenza univoca esistente tra le due numerazioni. Nella figura la numerazione interna al triangolo corrisponde a quella locale, generata come spiegato nel paragrafo precedente; quella esterna all’elemento, corrisponde alla numerazione globale, generata in fase di lettura della mesh.
Fig 2.9 Rappresentazione della corrispondenza tra numerazione locale e globale
Si noti che il solito spigolo può essere in comune tra non più di due elementi triangolari; a titolo di esempio si consideri che lo spigolo caratterizzato dalla numerazione locale e1, corrispondente alla numerazione globale E21, è comune agli elementi 2 e 35. La procedura di riempimento della matrice globale consiste nel “copiare” i valori ottenuti per le matrici locali nelle corrispondenti posizioni della matrice globale. Per quegli spigoli comuni a più elementi, il valore nella matrice globale si ottiene sommando i risultati ottenuti per le matrici locali degli elementi triangolari a cui lo spigolo appartiene, debitamente moltiplicati per un fattore unitario, il cui segno deriva dal confronto tra i versi di percorrenza dello spigolo stesso nella
n3 n1 n2 e1 e2 e3 N15 N23 N20 E21 E18 E31 3 6 9 2 22 23 35
contributi senza dover considerare il verso di percorrenza. Nella Fig. 2.10 viene rappresentata in maniera intuitiva la procedura appena introdotta.
Fig 2.10 Riempimento della sottomatrice globale A in relazione alla numerazione di Fig. 2.9
Per rendere il codice più veloce si noti che solo i secondi termini della matrice A e della matrice B presentano una dipendenza dalla frequenza (in particolare da k0) e vanno calcolati
per ogni step in frequenza; le matrici B, CT e C vengono calcolate solo una volta. Inoltre il secondo termine della matrice A sono solo moltiplicati per k0 è quindi sufficiente calcolarli
una volta per poi moltiplicarli per il differente k0 ad ogni passo frequenziale.
Imposizione delle condizioni al contorno
Una volta ottenute le matrici globali, può essere affrontato il problema agli autovalori generalizzato dato dall’equazione:
− = e Kdme e Kme τ γ τ (2.4.41) E18 E18 E21 E21 E31 E31 … … …… …… e3 e3 - e1 - e1 e2 e2
dove le matrici KmeeKdme sono definite come = = D C C B Kdme ed A Kme T 0 0 0 (2.4.42)
Si ricordi che le matrici AeB sono matrici quadrate di dimensioni [n° spigoli x n° spigoli];
la matrice B ha dimensioni [n° nodi x n° nodi] e la matrice CT ha dimensioni
[n° spigoli x n° nodi]; i. Ne consegue che il problema ha dimensione [n° spigoli+ n° nodi x n° spigoli + n° nodi]. Nei nodi e negli spigoli compaiono anche
quelli di bordo il cui valore è forzato dalle condizioni al contorno. Prima di risolvere il problema agli autovalori generalizzato dato dalla (2.4.41) è necessario quindi imporre le condizioni al contorno sulle pareti PEC. Per le pareti perfettamente conduttrici il campo elettrico tangenziale risulta nullo sulla parete stessa. Questa condizione equivale ad annullare la componente traversa del campo elettrico sugli spigoli e quella longitudinale sui nodi PEC. In questo modo le righe e le colonne delle matrici KmeeKdme relative agli spigoli ed ai nodi sulle pareti perfettamente conduttrici risultano identicamente nulle e possono quindi essere cancellate. Le dimensioni del problema vengono quindi ridotte, dato che il valore dei campi sugli spigoli e sui nodi non devono essere calcolate perché noti a priori. Risolvendo ora il problema agli autovalori ridotto ottenuto si ricavano i valori medi della componente trasversa dei campi sugli spigoli e della componente longitudinale sui nodi.