CAPITOLO 5 ANALISI DEL SEGNALE DIGITALE

CAPITOLO 5

5.1 INTRODUZIONE

Il primo passo nell’analisi delle misure rilevate è la conversione del segnale, che è naturalmente analogico, in forma digitale in modo tale che le quantità che devono essere processate siano sotto forma di valori discreti e non di funzioni continue. Si osserva che un segnale può essere definito analogico o digitale nella maniera seguente:

- segnale analogico: un segnale rappresentato da una funzione continua del tempo; esso è analogo al segnale fisico che rappresenta;

- segnale digitale: un segnale rappresentato da una sequenza di numeri, ognuno dei quali rappresenta il valore del segnale in un determinato istante.

In questa prima fase di conversione si individuano diversi tipi di problematiche insite nella modalità d’acquisizione dei dati ed in quella di trasformazione: aliasing, leakage, windowing, averaging e overlapping.

5.2 ANALISI DI FOURIER

Data una registrazione stazionaria

x

(t

)

periodica, di periodo T e frequenza fondamentale f=1/T, allora

x

(t

)

può essere scritta in serie di Fourier:

(

)

(

)

[

]

∑

+

+

=

∞ =1 0

_cos

₂

_sin

₂

2

)

(

q q q

ft

b

ft

a

a

t

x

π

π

(5.1) dove:

∫

⋅

=

T q

_T

x

t

qft

dt

a

0

)

2

cos(

)

(

2

_π

q=0,1,2,… (5.2)

∫

⋅

=

T q

x

t

qft

dt

T

b

0

)

2

sin(

)

(

2

_π

q=0,1,2,… (5.3)

Si assume inoltre che la registrazione venga campionata in un numero N di punti egualmente spaziati, a distanza ∆t tale da produrre la frequenza di taglio (detta

anche frequenza di Nyquist):

t

f

_c

∆

=

2

1

(5.4)

Si procede quindi a calcolare la forma della serie di Fourier che passi attraverso questi N valori; per ogni punto t dell’intervallo (0,T) risulta:

∑













+

∑













+

=

− = = 1 2 1 2 1 0

cos

2

sin

2

)

(

N q q N q q

T

qt

B

T

qt

A

A

t

x

π

π

(5.5)

In particolare nei punti in cui t=n∆t con n=1,2,…,N e T=N∆t

∑













+

∑













+

=

∆

=

− = = 1 2 1 2 1 0

cos

2

sin

2

)

(

N q q N q q

N

qn

B

N

qn

A

A

t

n

x

xn

π

π

(5.6) dove :

0

1

1 0

=

∑

=

=

=

x

x

N

A

N n n (5.7)













⋅

∑

=

=

N

qn

x

N

A

N n n q

2

cos

2

π

1

1

2

,...,

2

,

1

−

=

N

q

(5.8)













⋅

∑

=

=

N

qn

x

N

B

N n n q

2

sin

2

π

1

1

2

,...,

2

,

1

−

=

N

q

(5.9) 5.2.1 Trasformata di Fourier

La trasformata di Fourier (FT) in un intervallo infinito di una grandezza di valori

)

(t

x

è definita dalla quantità complessa:

dt

e

t

x

X

=

∞

_∫

⋅

i t ∞ − −ω

ω

)

(

)

(

(5.10) Le condizioni per l’esistenza della trasformata di Fourier sono le condizioni di Dirichelet:

- se la funzione presenta discontinuità, il loro numero deve essere finito; - la funzione deve contenere un numero finito di massimi e minimi; - la funzione deve essere assolutamente integrabile.

∫

<

∞

∞ ∞ −

dt

t

x )

(

(5.11) La funzione X(ω) può essere scritta in notazione complessa nella forma:

) (

)

(

)

(

)

(

)

(

ω

=

R

ω

+

i

⋅

I

ω

=

C

ω

⋅

e

iΦ ω

X

(5.12)

dove

C

(

ω

)

è detto spettro di Fourier di

x

(t

)

,

_C

2

(

_ω

)

_{è il suo modulo, ovvero}

l’energia spettrale, e

Φ

(

ω

)

è la fase. Una volta che sia nota la trasformata è possibile risalire alla

x

(t

)

mediante:

∫

⋅

=

∞ ∞ −

ω

ω

π

X

e

ω

d

t

x

(

)

i t

2

1

)

(

(5.13) Tale equazione è nota come trasformata inversa di Fourier di

X

(

ω

)

. Il legame tra

)

(t

x

e

X

(

ω

)

è espresso dalla notazione

x

(

t

)

↔

X

(

ω

)

. Se

x

(t

)

è una funzione reale, si ottiene:

∫

=

∞ ∞ −

dt

t

t

x

R

(

ω

)

(

)

cos(

ω

)

(5.14)

∫

=

∞ ∞ −

dt

t

t

x

I

(

ω

)

(

)

sin(

ω

)

(5.15)

)

(

)

(

)

(

)

(

ω

ω

ω

ω

I

I

R

R

−

=

−

=

−

(5.16)

Qualora la funzione

X

(

ω

)

sia riferita ad una funzione

x

(t

)

che rappresenti la risposta del sistema ad una forzante, questa prende il nome di spettro di risposta in frequenza della forzante.

In generale, restringendo i limiti ad un intervallo di tempo finito (0,T), la trasformata di Fourier è data dalla relazione:

∫

⋅

=

T

_x

_t

_e

−i t

_dt

T

f

X

0 2

)

(

)

,

(

π (5.17) Si assuma ora che x(t) sia campionata in N intervalli di ampiezza ∆t:

∑

⋅

=

− = ∆ − 1 0 2

)

,

(

N n t fn i n

e

x

T

f

X

π

x

n

=

x

(

n

∆

t

)

(5.18)

dove la frequenze vengono selezionate al modo seguente:

t

N

k

T

k

f

k

f

_k

∆

=

=

⋅

=

k=0,1,2,…,N-1 (5.19) A queste frequenze, i valori trasformati forniscono le componenti di Fourier date da:

N k i N n n k k

_T

x

e

T

f

X

X

π 2 1 0

)

,

(

− − =

⋅

∑

=

∆

=

k=0,1,2,…,N-1 (5.20)

5.3 ALIASING

Nella digitalizzazione di un segnale continuo, il campionamento del segnale è usualmente effettuato ad intervalli di tempo uguali. Il problema è determinare un appropriato intervallo di campionamento ∆t. Infatti, se il campionamento è effettuato

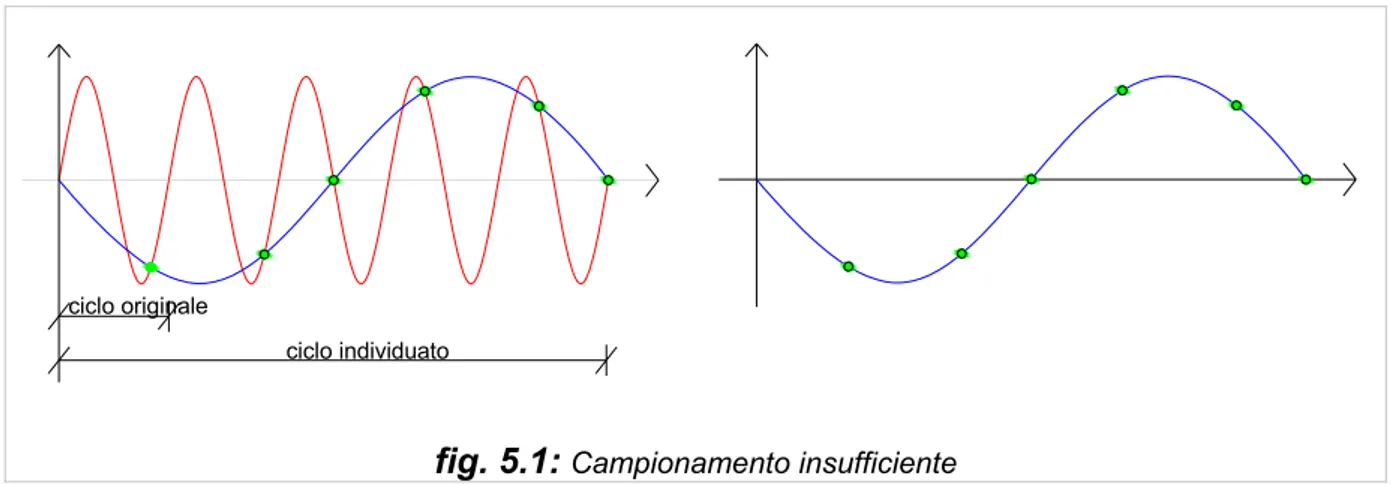
in punti molto vicini, si avrà una sovrabbondanza di dati ed un aumento inutile dell’onere computazionale. Se invece il campionamento è effettuato in punti distanti tra loro si può avere confusione tra le alte e le basse frequenze nei dati originari. Questo problema è definito aliasing e costituisce una potenziale sorgente di errore che interessa qualsiasi processo che sia preceduto da una conversione del segnale da analogico a digitale (figura 5.1).

ciclo individuato ciclo originale

fig. 5.1: Campionamento insufficiente

Dato un segnale continuo, supponiamo di campionarlo ad un intervallo di tempo ∆t; il

rapporto di campionamento è 1/T campioni al secondo. E’ importante osservare che almeno due campioni per ciclo sono richiesti per individuare una componente di frequenza nel segnale originario (figura 5.2):

ciclo originale = ciclo individuato

Quindi la frequenza più alta che può essere definita mediante un rapporto di campionamento di 1/∆t campioni al secondo è 1/2∆t. Le frequenze nel segnale

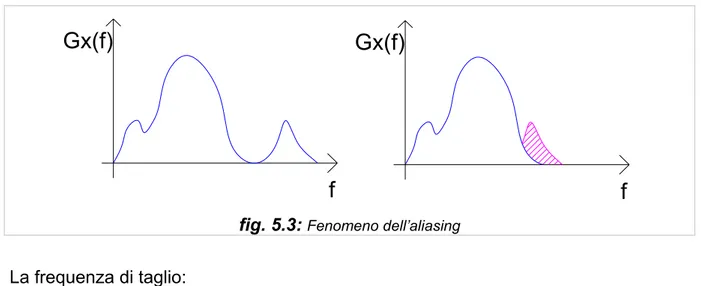
originale al di sopra 1/2∆t saranno ripiegate indietro nell’intervallo di frequenze tra 0 e 1/2∆t e confuse con i dati già presenti in questo intervallo (figura 5.3).

f

Gx(f)

Gx(f)

f

fig. 5.3: Fenomeno dell’aliasing

La frequenza di taglio:

t

f

_c

∆

=

2

1

(5.21)

è chiamata anche frequenza di Nyquist o frequenza ripiegata. Per ogni frequenza f compresa nell’intervallo

0

≤

f

≤

f

c ci sono delle frequenze alte che vengono

confuse con esse:

),...

2

(

),...,

4

(

),

2

(

f

c

±

f

f

c

±

f

nf

c

±

f

(5.22) Questo problema può essere trattato in due modi: il primo è quello di avere un campionamento più fitto; il secondo è quello di filtrare il segnale prima di campionarlo rispetto ad una frequenza massima d’interesse. Allora scegliendo la frequenza di Nyquist pari alla massima frequenza d’interesse, si otterranno dei risultati privi di aliasing per frequenze inferiori a quella di taglio.

5.4 LEAKAGE

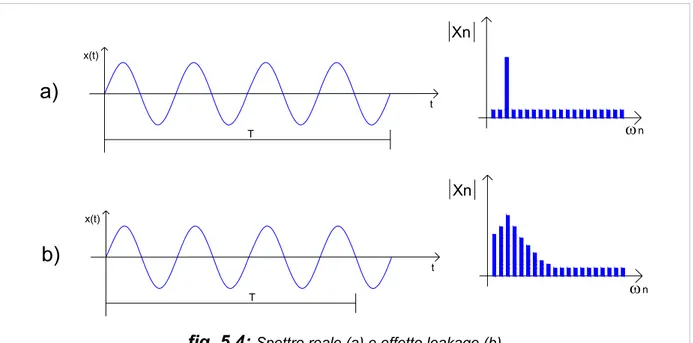
E’ un problema legato alla lunghezza della time-history che è di dimensione finita, associato all’assunzione di periodicità del segnale. Se si considera un tratto di segnale di lunghezza T pari ad un multiplo intero del segnale stesso, non c’è alcun tipo di problema; in caso contrario l’assunzione di periodicità non è strettamente

valida, in particolare in prossimità dell’estremità dell’intervallo, perché ciò provoca una dispersione dell’energia spettrale (figura 5.4).

x(t) t T T t x(t) Xn ω Xn n n ω

a)

b)

fig. 5.4: Spettro reale (a) e effetto leakage (b)

5.5 WINDOWING

E’ un metodo impiegato per risolvere il problema del leakage e consiste nel filtrare il segnale x(t) iniziale attraverso una funzione filtro W(t). L’operazione di finestramento nel dominio del tempo restituisce un segnale x’(t) = x(t) W(t) in cui la dispersione di energia spettrale è contenuta.

I tipi di finestre utilizzate nell’analisi dei segnali sono (figura 5.5): a) box window;

b) hanning window;

c) cosine taper window; d) exponential window.

Ciascuna finestra è generalmente riferita ad un tipo di segnale, infatti i filtri b) e c) sono utilizzati per segnali periodici o per vibrazioni random, mentre il filtro d) viene utilizzato per vibrazioni in transitorio in cui le informazioni più importanti sono concentrate in un tratto dell’intero segnale.

a) t x(t) W1(t) t x1(t) t t x2(t) t W2(t) x(t) t b) d) t x(t) W4(t) t x4(t) t t x3(t) t W3(t) x(t) t c)

fig. 5.5: Tipi di finestre per l’analisi dei segnali

5.6 OVERLAP AVERAGING

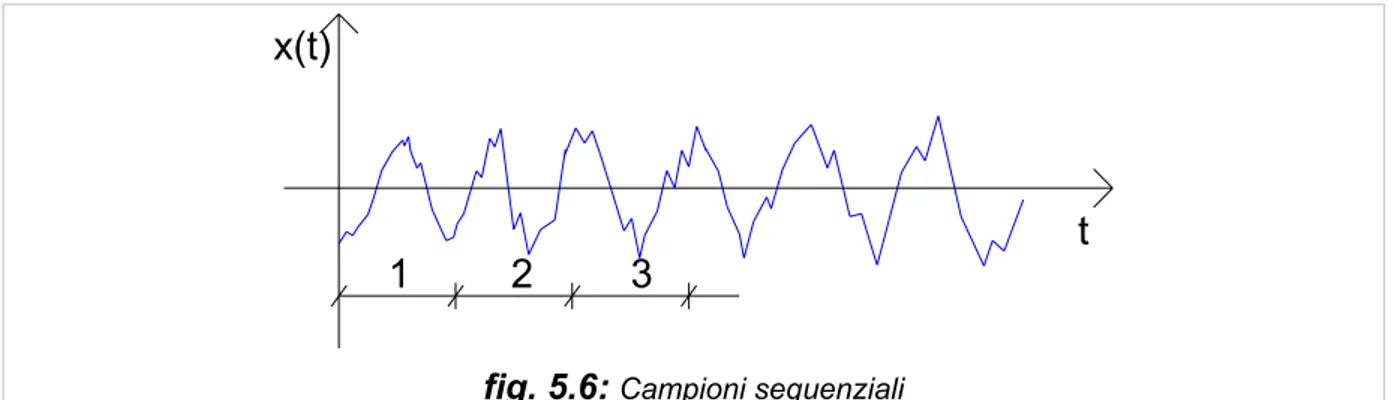
Nell’analisi dei segnali casuali non è sufficiente calcolare la trasformata di Fourier perché in senso stretto questa non esiste per un segnale casuale; bisogna invece ottenere una stima della densità spettrale e della funzione d’autocorrelazione impiegate per caratterizzare questo tipo di segnale che viene suddiviso in campioni. Tuttavia, essendo queste quantità ottenute tramite la trasformata di Fourier, è necessario effettuare una operazione di media tra le trasformate ottenute dai singoli campioni estratti dal segnale.

Per un segnale casuale l’operazione di media può essere effettuata su dei campioni sequenziali o sovrapposti (figure 5.6 e 5.7):

t

x(t)

1

2

3

3 2 1 x(t)

t

fig. 5.7: Campioni sovrapposti

5.7 ANALISI DI MULTIRESOLUTION

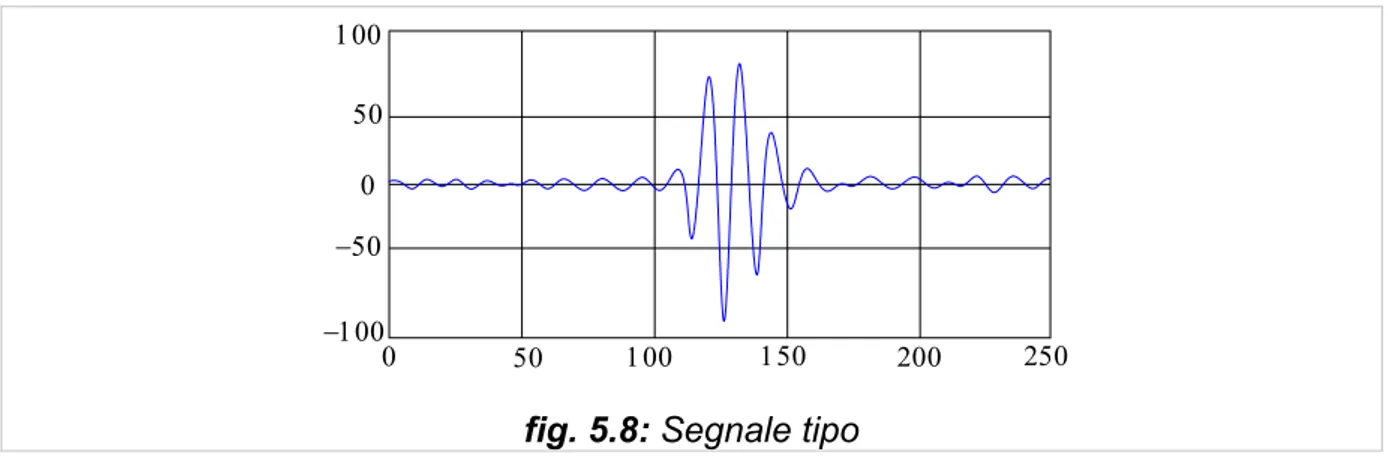
E’ possibile analizzare un segnale usando un approccio alternativo chiamato l'analisi di multiresolution (MRA) per cercare di ovviare ai problemi di risoluzione in frequenza anche se questi permangono nonostante il tipo di trasformata utilizzata in quanto sono risultati di un fenomeno fisico (il principio d’incertezza di Heisemberg). L’analisi MRA, come indicato dal suo nome, analizza il segnale a frequenze diverse con differenti risoluzioni: ogni componente spettrale non è ugualmente risolta, come è nel caso della trasformata corta nel tempo di Fourier (STFT) dove il segnale viene suddiviso in molti piccoli intervalli nei quali il segnale è considerato stazionario. L’approccio MRA è progettato per dare una buona risoluzione nel tempo e una mediocre risoluzione in frequenza per le frequenze alte e una buona risoluzione in frequenza e una mediocre risoluzione nel tempo per le frequenze basse. Questo approccio ha senso specialmente quando il segnale ha componenti di frequenza alte per brevi durate e componenti di frequenza basse per lunghe durate. I segnali che si incontrano nelle applicazioni pratiche sono spesso di questo tipo ed un esempio è riportato nella figura 5.8.

0 50 100 150 200 250 0 50 100 −50 −100

5.8 LA TEORIA DELLE WAVELET

La FT definita da Fourier usa delle funzioni base per analizzare e poi ricostruire una funzione. Ogni vettore in uno spazio vettoriale può essere scritto come una combinazione lineare dei vettori base dello stesso spazio vettoriale, cioè moltiplicando i vettori per dei numeri e poi prendendo la sommatoria dei prodotti. L'analisi del segnale comporta la stima di questi numeri (i coefficienti della trasformata, i coefficienti di Fourier, i coefficienti delle wavelet ecc). La sintesi, o la ricostruzione, corrisponde a calcolare l'equazione risultante dalla combinazione lineare.

Una base di un vettore spaziale

V

è un set di vettori linearmente indipendenti tale che ogni vettore

v

in

V

può essere scritto come una combinazione lineare di questi vettori di base.

∑

=

k k k

_b

V

v

(5.23) dove

_b

_k è la base e

_V

k sono i coefficienti corrispondenti.

Ci possono essere più basi per uno spazio vettoriale, comunque tutte le basi hanno lo stesso numero di vettori e questo è noto come la dimensione dello spazio vettoriale. Questo concetto, espresso attraverso i vettori, può essere generalizzato facilmente alle funzioni sostituendo la base del vettore

_b

_k con quella della funzione

)

(

t

k

Φ

ed il vettore

v

con la funzione

f

(

t

)

. L’equazione (5.23) diventa quindi:

)

(

)

(

t

t

f

k k k

∑

Φ

=

µ

(5.24) Il complesso esponenziale (funzioni seno e coseno) è la base per la FT; queste funzioni sono ortogonali e questa loro caratteristica comporta delle proprietà auspicabili per la ricostruzione della funzione originaria.

Supponiamo che

f

(t

)

e

g

(t

)

siano due funzioni in L2 [a,b], ciò denota che le funzioni quadrate siano integrabili nell'intervallo [a,b]; Il prodotto interno di due funzioni è definito come:

∫

⋅

>=

<

b a

dt

t

g

t

f

t

g

t

f

(

),

(

)

(

)

*

(

)

(5.25)

dove

g

*

indica la coniugata e quindi la CWT (vedi par 5.8.1) può essere pensata come il prodotto interno del segnale con la funzione base

_Ψ

_τ,s

(

t

)

:

∫

⋅

=

Ψ

=

s

x

t

t

dt

s

CWT

ψx

(

τ

,

)

ψx

(

τ

,

)

(

)

ψ

τ*_,s

(

)

(5.26) dove











 −

=

s

t

s

s

τ

ψ

ψ

_τ,

1

(5.27) Questa definizione della CWT mostra che l'analisi con le wavelet è una misura della somiglianza tra la funzione base (la wavelet) ed il segnale stesso: la somiglianza è nel senso del contenuto di frequenza simile. I coefficienti della CWT calcolati si riferiscono alla larghezza del segnale e alla wavelet alla scala corrente: se il segnale ha una notevole componente della frequenza che corrisponde alla scala corrente, allora la funzione base (la wavelet) a tale scala sarà simile o vicina al segnale nella particolare ubicazione dove si trova questo componente di frequenza. Perciò il coefficiente della CWT calcolato a questo punto nel grafico tempo-scala sarà un numero relativamente grande. Due vettori

v

e

w

si dicono ortogonali se il loro prodotto interno uguaglia zero:

0

,

_>=

_∑

*

₌

<

v

w

v

w

n

n n

(5.28)

Similmente, due funzioni

f

(t

)

e

g

(t

)

si dicono ortogonali se il loro prodotto interno è zero:

0

)

(

*

)

(

)

(

),

(

>=

_∫

⋅

=

<

b a

dt

t

g

t

f

t

g

t

f

(5.29) Un set di vettori

{

_v

₁

,

_v

₂

,...,

_v

_n

}

si dice ortonormale se i vettori sono ortogonali due a due e se tutti hanno lunghezza unitaria. Questo può essere espresso come:

δ

mn n

m

v

v

>=

<

,

(5.30) Similmente un set di funzioni si dice che sia ortonormale se:

0

)

(

)

(

_⋅

_Φ

*

₌

∫ Φ

t

_l

t

dt

b a k con

k

≠

l

e

k

=

1

,

2

,...

(5.31) e

[

]

∫

Φ

=

b a k

dx

t

)

1

(

2 (5.32)

o

δ

_kl

dt

t

t

_l b a k

=

Φ

⋅

∫ Φ

(

)

*

(

)

_(5.33) dove

δ

_kl è la funzione di delta di Kronecker definito come:







=

0

1

δ

kl

_se

se

l

k

l

k

≠

=

(5.34)

Come già detto, ci possono essere più di un set di funzioni (o vettori) base. La base di funzioni (o vettori) ortonormali è particolarmente importante perché possono avere delle buone proprietà per trovare questi coefficienti di analisi. Le basi ortonormali permettono il calcolo di questi coefficienti in un modo molto semplice basato appunto sulla loro ortonormalità. Per queste basi, i coefficienti

µ

_k possono essere calcolati come segue:

∫

⋅

Φ

>=

Φ

=<

f

_k

f

t

_k

t

dt

k

,

(

)

*

(

)

µ

(5.35) dove

∑

<

Φ

>

Φ

=

Φ

∑

=

k k k k k k

t

f

t

t

f

(

)

µ

(

)

,

(

)

(5.36) Le basi Ortonormali non possono essere disponibili per ogni tipo di applicazione dove una versione generalizzata, le basi biortogonali, possono essere usate. Il termine biortogonale si riferisce a due basi diverse che sono ortogonali fra loro, ma ognuna non forma un set ortogonale.

In alcune applicazioni, comunque, le basi biortogonali possono anche non essere disponibili ed in questi casi possono essere usate le cornici [7].

Riportiamo ora due esempi di wavelet madre usati comunemente nell’analisi con le wavelet. La wavelet di Cappello Messicano è definita come la derivata seconda della funzione gaussiana:

e

t

t _σ

σ

π

ω

₂ 2 2

2

1

)

(

=

− (5.37) che è













−

⋅













=

−

₁

2

1

)

(

₂ 2 2₂ 2

σ

σ

π

ψ

t

e

t _σ

t

(5.38) La Morlet wavelet è definita come:

e

e

t

iat t _σ

ω

2 2

)

(

=

⋅

− (5.39)

dove

a

è un parametro di modulazione e

σ

è un parametro di misurazione in scala che influenza l'ampiezza della finestra.

5.8.1 Le wavelet transform continue

Le wavelet transforms continue (CWT) furono sviluppate come un approccio alternativo alle STFT (Short Time Fourier Transform) per superare il problema di risoluzione. L'analisi con le wavelet è fatta in un modo simile all'analisi con le STFT, nel senso che il segnale è moltiplicato per una funzione (la wavelet appunto) simile alla funzione di finestra nel STFT e la trasformata è calcolata separatamente per intervalli diversi nel dominio del tempo del segnale.

Ci sono comunque, due differenze principali tra le STFT e le CWT:

1. le trasformate di Fourier del segnale “finestrato” non sono prese, e perciò sarà vista la sola vetta che corrisponde ad una sinusoide, cioè i valori negativi del segnale non sono presi in considerazione;

2. l'ampiezza della finestra viene cambiata e la trasformata è calcolata per ogni singolo componente spettrale e questa probabilmente è la caratteristica più significativa delle wavelet trasforms che sono definite come segue:

dt

s

t

t

x

s

s

s

CWT

x _x

∫











 −

=

=

ψ

τ

ψ

τ

τ

ψ ψ

₍

_,

₎

₍

_,

₎

1

₍

₎

_(5.40)

dove

τ

è la traslazione,

s

è il parametro di scala e

ψ

(

t

)

è la funzione di trasformazione che si chiama wavelet madre.

Il termine wavelet madre deriva da due importanti proprietà dell'analisi con le wavelet:

1) il termine wavelet intende una piccola onda, cioè una funzione-finestra oscillatoria di lunghezza limitata;

2) il termine madre implica che le funzioni con regione diversa di appoggio che sono usate nel processo di trasformazione sono dedotte da una funzione principale, la madre appunto.

In altre parole, la wavelet madre è un prototipo per generare le altre funzioni di finestra.

Il termine traslazione è riferito all'ubicazione della finestra, poichè la finestra viene spostata attraverso il segnale. Questo termine corrisponde a calcolare informazioni

del tempo nel dominio di trasformazione. Tuttavia ora non c’è un parametro di frequenza, come nel caso delle STFT, ma uno di scala che è definito come 1/frequenza.

5.8.1.1 La Scala

Il parametro di scala nell'analisi con le wavelet è simile alla scala usata nelle mappe: le scale alte corrispondono ad una vista globale e non particolareggiata del segnale e le scale basse corrispondono, invece, ad una vista particolareggiata dello stesso. Similmente, in termini di frequenza, le frequenze basse ,cioè le scale alte, corrispondono ad informazioni globali di un segnale che di solito durano per tutto il tempo, mentre le frequenze alte , cioè le scale basse, corrispondono ad informazioni particolareggiate di un modello ignoto nel segnale che di solito dura un tempo relativamente corto.

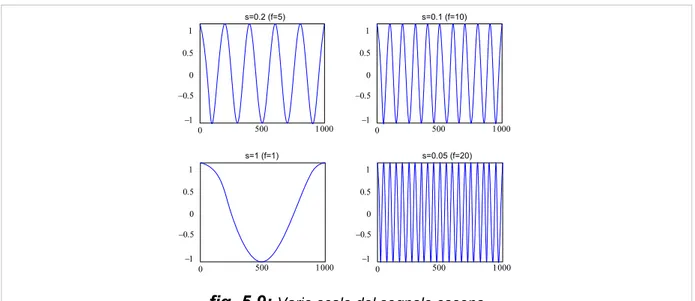
I segnali del coseno, alle scale s=0.05, s=0.1, s=0.2 e s=1, sono riportati come esempi nella figura 5.9.

−1 −0.5 1 0.5 0 1000 500 0 s=0.2 (f=5) s=0.1 (f=10) 0 500 1000 0 0.5 1 −0.5 −1 s=1 (f=1) 0 500 1000 0 0.5 1 −0.5 −1 s=0.05 (f=20) 0 500 1000 0 0.5 1 −0.5 −1

fig. 5.9: Varie scale del segnale coseno

Come un'operazione matematica, il segnale si può regolare, cioè si può dilatare o comprimere: le scale grandi corrispondono ad un segnale dilatato, mentre le scale piccole corrispondono ad un segnale compresso. Tutti i segnali dati nella figura 5.9 sono dedotti dallo stesso segnale di coseno, dilatando o comprimendo la stessa funzione: s=0.05 è la scala più piccola e s=1 è la scala più grande.

Nella definizione delle wavelet trasforms, il termine di misurazione in scala è usato al denominatore e perciò una scala s> 1 dilata il segnale, mentre una scala s <1 lo comprime.

5.8.1.2 Il calcolo della CWT

Supponiamo che x(t) sia il segnale da analizzare; la wavelet madre è scelta per servire come prototipo per tutte le finestre nel processo: tutte le finestre che sono usate sono dilatazioni, compressioni o versioni spostate della wavelet madre.

Esistono molte funzioni usate come wavelet madre; una volta che essa è stata scelta si inizia il calcolo con s=1 e la wavelet trasform continua è calcolata per tutti i valori di s, sia più piccoli che più grandi di “1''.

Comunque, dipendendo dal segnale, una trasformata completa non è di solito necessaria; per tutti gli scopi pratici, i segnali sono band limited e perciò il calcolo delle trasformate per un intervallo limitato di scale è di solito più adeguato.

Per convenienza, la procedura sarà cominciata da s=1 della scala e continuerà per i valori in aumento di s, cioè l'analisi comincerà da frequenze alte e procederà verso quelle basse. Questo primo valore di s corrisponde alla wavelet più compressa e, come il valore di s verrà aumentato, le wavelet si dilateranno.

La wavelet è messa all'inizio del segnale al punto che corrisponde a time=0. La funzione wavelet alla scala “1'' è moltiplicata per il segnale e poi integrata; il risultato dell'integrazione è moltiplicato poi per il numero costante

1

s

per normalizzare l’energia in modo che il segnale trasformato abbia la stessa energia ad ogni scala. Il risultato finale è il valore della trasformazione, cioè il valore della wavelet transform continua a tempo zero e valore s=1 della scala: in altre parole, è il valore che corrisponde al punto

τ

=

0

e s=1 nel grafico tempo-scala.

La wavelet a s=1 della scala viene poi spostata verso destra della quantità

τ

per giungere a

t

=

τ

e l'equazione (5.40) viene calcolata per ottenere il valore della trasformata a

t

=

τ

e s=1 nel grafico tempo-frequenza.

Questa procedura è ripetuta fino a che la wavelet non raggiunge la fine del segnale. Una fila di punti sul grafico tempo-scala per s=1 della scala ora è completata e s viene aumentato di un piccolo valore e la procedura viene ripetuta.

Si noti che questo processo è una continua trasformazione e quindi sia

τ

che s devono essere continuamente incrementate.

Ogni calcolo per un valore determinato di s riempie la sola fila corrispondente del grafico tempo-scala. Quando il processo è completato per tutti i valori voluti di s, la CWT del segnale è stato calcolata (figura 5.10).

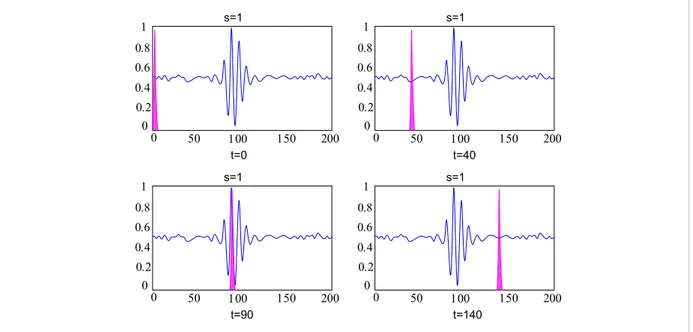
200 150 100 50 0 0 0.2 0.4 0.6 0.8 1 s=1 t=90 t=0 s=1 1 0.8 0.6 0.4 0.2 0 0 50 100 150 200 t=140 s=1 1 0.8 0.6 0.4 0.2 0 0 50 100 150 200 t=40 s=1 1 0.8 0.6 0.4 0.2 0 0 50 100 150 200

fig. 5.10: Il segnale e la funzione wavelet con s=1

Nella figura 5.10 il segnale e la funzione wavelet sono mostrati per quattro valori diversi di

τ

. Il valore di scala è 1 (scala più bassa, frequenza più alta). Si nota come è compatta la funzione wavelet (finestra rosa) che deve essere stretta come la componente di frequenza più alta che esiste nel segnale. Il prodotto è diverso da zero soltanto dove il segnale cade nella regione di supporto della wavelet ed è zero altrove.

Spostando la wavelet nel tempo, il segnale è localizzato nel tempo e, cambiando il valore di s, il segnale è localizzato in scala (la frequenza).

Se il segnale ha una componente spettrale che corrisponde al valore corrente di s (1 in questo caso), il prodotto della wavelet col segnale all'ubicazione dove questa componente spettrale esiste dà un valore relativamente grande e viceversa. Il segnale in figura 5.10 ha componenti spettrali comparabili all'ampiezza della finestra a s=1 intorno alla spettrografia di massa t=100.

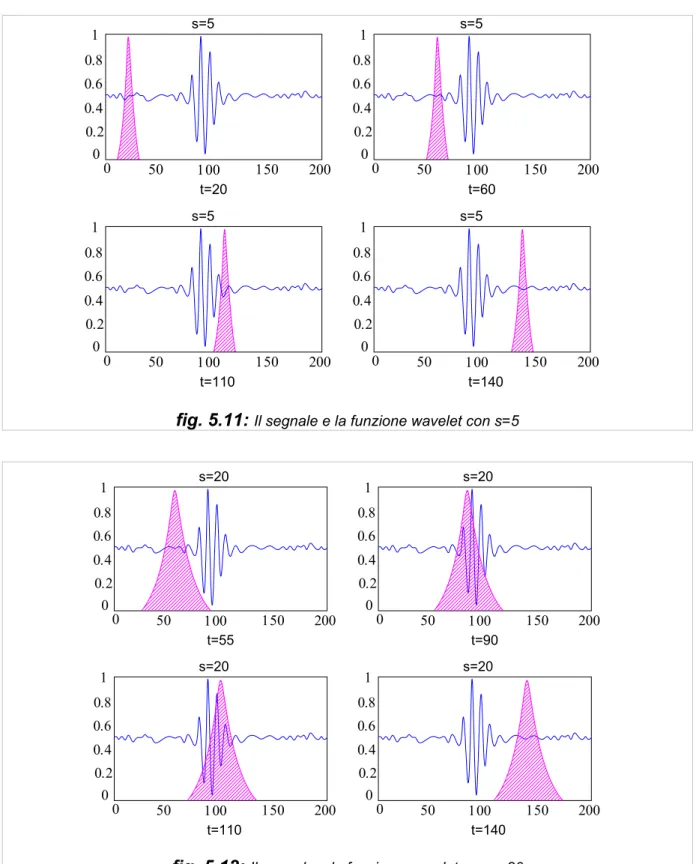
200 150 100 50 0 0 0.2 0.4 0.6 0.8 1 s=5 t=60 200 150 100 50 0 0 0.2 0.4 0.6 0.8 1 s=5 t=140 200 150 100 50 0 0 0.2 0.4 0.6 0.8 1 s=5 t=20 t=110 s=5 1 0.8 0.6 0.4 0.2 0 0 50 100 150 200

fig. 5.11: Il segnale e la funzione wavelet con s=5

200 150 100 50 0 0 0.2 0.4 0.6 0.8 1 s=20 t=90 200 150 100 50 0 0 0.2 0.4 0.6 0.8 1 s=20 t=140 200 150 100 50 0 0 0.2 0.4 0.6 0.8 1 s=20 t=55 t=110 s=20 1 0.8 0.6 0.4 0.2 0 0 50 100 150 200

fig. 5.12: Il segnale e la funzione wavelet con s=20

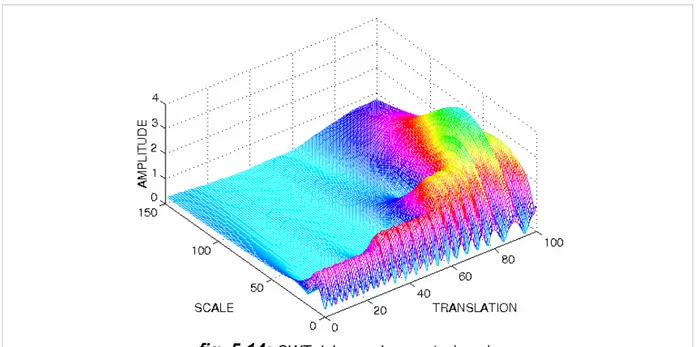
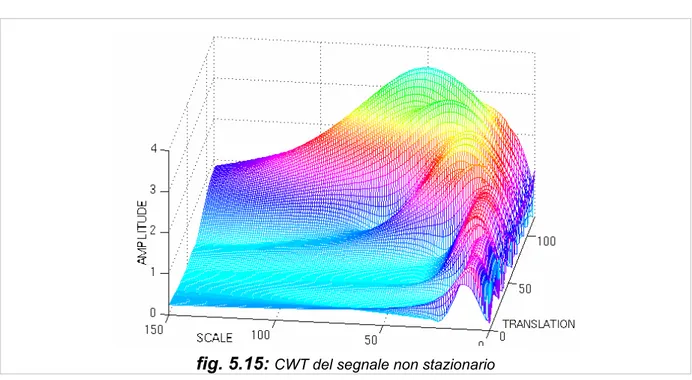
Si nota come l'ampiezza della finestra cambia con la scala in aumento (frequenza decrescente): se l'ampiezza della finestra aumenta, la trasformata comincia a raccogliere le componenti di frequenza più basse. I calcoli ad una scala costruiscono le file del grafico tempo-scala e quelli a scale diverse ne costruiscono le colonne. Consideriamo ora un segnale non stazionario composto da quattro componenti di frequenza a 30Hz, 20Hz, 10Hz, 5HZ (figura 5.13).

0 200 400 600 800 1000 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 30Hz 20Hz 10Hz 5Hz

fig. 5.13: segnale non stazionario

La wavelet transform continua (CWT) di questo segnale è rappresentata nelle figure 5.14 e 5.15: si nota che gli assi sono la traslazione e la scala, non il tempo e la frequenza.

fig. 5.15: CWT del segnale non stazionario

Gli assi sono normalizzati e quindi i 100 punti nell'asse di traslazione corrispondono a 1000 ms ed i 150 punti sull'asse di scala corrispondono ad un nastro di frequenza di 40Hz (i numeri sull’asse della traslazione e su quello della scala non corrispondono a secondi e Hz rispettivamente, loro sono solo il numero di esemplari nel calcolo). Si riscontrano nel grafico le diverse componenti del segnale: 30Hz appare nella scala più bassa ai valori 0-30 della traslazione; ugualmente si nota la componente a 20Hz tra 30 e 60, quella a 10Hz tra 60 e 80 e quella a 5Hz alla fine dell’asse della traslazione ed a scale più alte (frequenze più basse).

Come detto, diversamente dalla STFT che ha una risoluzione costante per ogni tempo e frequenza, la WT ha una buona risoluzione nel tempo e mediocre nella frequenza a frequenze alte, e viceversa a frequenze basse.

5.8.1.3 Risoluzioni del tempo e della frequenza

Il problema della risoluzione è la ragione principale per cui sono state introdotte le WT al posto delle STFT.

Time

Freque

ncy

fig. 5.16: Risoluzione del tempo e della frequenza

La figura 5.16 è usata comunemente per spiegare come devono essere interpretate le risoluzioni del tempo e della frequenza: ogni scatola corrisponde ad un valore della wavelet trasform nel grafico tempo-frequenza; le scatole hanno una certa area non nulla che implica che il valore di un particolare punto nel grafico tempo-frequenza non può essere conosciuto. Tutti i punti del suddetto grafico che precipitano in una scatola sono rappresentati da un valore della WT.

Si nota che anche se le larghezze e le altezze delle scatole variano, l'area è continua. Ogni scatola rappresenta una porzione uguale del grafico tempo-frequenza, ma hanno proporzioni diverse per il tempo e la frequenza. L'altezza delle scatole alle frequenze basse è minore (che corrisponde alle migliori risoluzioni di frequenza in quanto l'ambiguità riguardo al valore della frequenza esatta è minore in queste zone), ma le loro larghezze sono maggiori (che corrispondono a risoluzioni di tempo mediocri in quanto l'ambiguità riguardo al valore del tempo esatto è maggiore in queste zone). Alle frequenze alte si ha l’opposto.

Nel caso delle STFT la risoluzione del tempo e della frequenza sono determinate dall'ampiezza della finestra di analisi che viene scelta e perciò sono continue; il grafico tempo-frequenza risulta quindi formato da quadrati.

Nonostante le dimensioni delle scatole, la somma delle loro aree, sia nelle STFT che nelle WT, sono uguali e determinate dall'ineguaglianza di Heisenberg.

5.8.2 La Serie delle Wavelet

Per poter eseguire il calcolo delle wavelet queste devono essere discretizzate: solo apparentemente le FT, le STFT e le CWT vengono calcolate usando equazioni analitiche, integrali etc. Come nel caso delle FT e STFT, il modo più intuitivo per farlo è campionando il grafico tempo-frequenza (scala) con un range percentuale uniforme. Comunque, nel caso delle WT, il cambiamento della scala può essere usato per ridurre la percentuale di campionatura.

A scale più alte (frequenze più basse), la percentuale di campionatura può essere diminuita secondo la regola di Nyquist; in altre parole, se il grafico tempo-scala ha bisogno di essere campionato con una percentuale di campionatura di N1 alla scala

s1, lo stesso grafico può essere campionato con una percentuale di campionatura di

N2 alla scala s2 ,dove s1<s2 (che corrisponde alle frequenze f1>f2) e N2<N1. Valgono

le seguenti relazioni tra N1 e N2:

_N

s

s

N

1 2 1 2

=

o

N

f

f

N

1 1 2 2

=

(5.41)

In altre parole, la percentuale di campionatura può essere diminuita alle frequenze più basse risparmiando un tempo considerevole di calcolo.

La discretizzazione può essere fatta senza alcuna restrizione come per quanto riguarda l'analisi del segnale: se la sintesi non è richiesta, non occorre che il criterio di Nyquist venga soddisfatto. Le restrizioni sulla discretizzazione e la campionatura diventano importanti se, e solamente se, viene richiesta la ricostruzione del segnale. Il campionamento di Nyquist è la minima percentuale di campionatura che permette di ricostruire il segnale originario a partire dai suoi esemplari distinti. I vettori base che sono stati menzionati precedentemente sono particolarmente importanti per questa ragione.

La CWT è una trasformata reversibile se sono soddisfatte le seguenti relazioni:

dtds

s

t

s

s

c

t

x

_{s x}

_









 −

∫ ∫ Ψ

=

_τ ψ

τ

ψ

τ

ψ2 2

1

)

,

(

1

)

(

(5.42)

∞

<

















∫

=

∞ ∞ − 2 1 2

)

(

2

ξ

ξ

ξ

ψ

π

ψ

d

c

(5.43)

dove

ψ

(

ξ

)

è la FT di

ψ

(

t

)

. Dall’equazione (5.43) segue che:

∫

ψ

( dt

t

)

= 0

(5.44) Questa condizione non è molto restrittiva ed implica che la wavelet sia oscillatoria. La ricostruzione del segnale è quindi possibile attraverso la funzione riportata in (5.42): questo è però vero solo per le trasformate continue.

Per poter ricostruire un segnale con i parametri tempo e scala discretizzati si devono porre delle condizioni:

1) prima il parametro di scala s è discretizzato su una griglia logaritmica; 2) poi il parametro di tempo è discretizzato riguardo al parametro di scala.

In questo modo viene usata una percentuale di campionatura diversa per ogni scala. In altre parole, la campionatura è fatta sulla griglia bivalente mostrata in figura 5.17.

Time

log s

fig. 5.17: Griglia di campionatura

Pensiamo l'area coperta dagli assi come l’intero grafico tempo-scala; la CWT assegna un valore al continuo di punti su questo grafico e perciò c'è un numero infinito dei coefficienti della CWT. Prima consideriamo la discretizzazione dell'asse di scala: da un numero infinito di punti ne vengono presi solamente un numero limitato usando una regola logaritmica. La base del logaritmo viene scelta di volta in volta: il valore più comune è 2 perché è quello che risulta essere più conveniente; se viene scelto 2 come base, solamente le scale 2, 4, 8, 16, 32, 64... ecc. vengono calcolate. L'asse del tempo è poi discretizzato secondo la discretizzazione dell'asse di scala. I cambi di scala distinti dal fattore 2 comportano, per l’asse del tempo, una riduzione della percentuale di campionatura di un fattore 2 ad ogni scala. Noti quelli alla scala più bassa (s=2), solamente 32 punti dell'asse del tempo sono campionati (per il

particolare caso dato in figura 5.16). Al valore successivo della scala, s=4, la percentuale di campionatura dell’asse del tempo è ridotta da un fattore 2 perché la scala è aumentata da un fattore 2 e perciò solamente 16 valori vengono presi. Al passo successivo, s=8, solo 8 valori sono presi nel tempo e così via.

E’ quindi più appropriato chiamarlo grafico traslazione-scala piuttosto che tempo-scala perché il tempo nel dominio trasformato corrisponde al cambiamento della wavelet nel tempo. Per la serie delle wavelet, il tempo è ancora continuo.

Come esiste una relazione tra la trasformata continua di Fourier, la serie di Fourier e la trasformate discrete di Fourier, ne esiste anche una tra la trasformata continua della wavelet, la trasformata semi-discreta della wavelet (anche nota come serie delle wavelet) e la trasformata discreta della wavelet.

Esprimendo la procedura di discretizzazione in termini matematici, quella della scala è

s

=

_s

₀j e quella della traslazione è

τ

=

k

⋅

_s

₀j

⋅

τ

₀ dove

s

₀

>

1

e

_τ

₀

>

0

; si vede quindi come la discretizzazione della traslazione sia dipendente da quella della scala attraverso il parametro

_s

₀.

La funzione continua della wavelet è:











 −

=

s

t

s

s

τ

ψ

ψ

_τ,

1

(5.45) e sostituendo

s

_s

j 0

=

e

τ

=

k

⋅

_s

₀j

⋅

τ

_{0 l’equazione diventa:}

(

τ

)

ψ

ψ

2 _{0 0} 0 ,k

(

t

)

s

j

s

j

t

k

j

=

− −

−

(5.46)

Se

ψ

_j,k costituisce una base ortonormale, la serie delle trasformate della wavelet diviene:

∫

=

Ψ

ψ_x

(

j

,

k

)

x

(

t

)

ψ

*_j,k

(

t

)

dt

(5.47) oppure

)

(

)

,

(

)

(

t

c

j

k

_,

t

x

_{j k} j k x

ψ

ψ ψ

_Ψ

⋅

=

_{∑ ∑} (5.48)

Una serie della wavelet richiede che

ψ

_j,k siano entrambi ortonormali, biortogonali o cornici. Se

ψ

_j,k non è ortonormale, l’equazione 5.47 diviene:

∫

=

dove

ψ

*_j,k

(

t

)

è o la base biortogonale duplice o la cornice duplice (l’ * denota l'asse coniugato).

Se

ψ

_j,k è ortonormale o biortogonale, la trasformata sarà non-ridondante e, se loro formano una cornice, la trasformata sarà ridondante. D'altra parte è molto più facile trovare cornici che trovare basi ortonormali o basi biortogonali.

L'analogia seguente può chiarire questo concetto. Consideriamo l’intero processo come se stessimo guardando un particolare oggetto: gli occhi umani adattano la vista in base alla distanza degli stessi dall'oggetto; questo corrisponde ad aggiustare il parametro di scala

_s

−₀j. Quando si guarda un oggetto da molto vicino, con grande dettaglio, j è negativo e grande (scala bassa, frequenza alta si analizza nel dettaglio il segnale). Gli spostamenti della testa (o degli occhi) molto lenti e con incrementi molto piccoli (di angolo, di distanza in base all'oggetto che si sta vedendo), corrispondono ai piccoli valori di

τ

=

k

⋅

_s

₀j

⋅

τ

₀; j negativo e grande corrisponde a piccoli cambi nel tempo (

τ

) e quindi ad una percentuale di campionatura alta e a grandi cambi in

_s

−₀j e quindi ad una scala bassa (frequenze alte) dove è alta la percentuale di campionatura. Il parametro di scala può essere anche pensato come ingrandimento.

Per ottimizzare la procedura il valore più conveniente (in termini di programmazzione) è stato trovato essere 2 per

_s

₀ e 1 per

τ

; quando la percentuale di campionatura deve essere quanto più possibile bassa, anche il numero delle wavelet ortonormali disponibile è ridotto.

5.8.3 La trasformata discreta delle wavelet (DWT)

Anche se la discretizzazione delle trasformate continue delle wavelet vista in precedenza abilita il calcolo delle stesse per mezzo del computer, queste non sono delle vere trasformate discrete. La serie delle wavelet è semplicemente una versione campionata delle CWT e le informazioni che fornisce sono altamente ridondanti per quanto riguarda la ricostruzione del segnale e questa ridondanza richiede una quantità significativa di tempo e di risorse di calcolo. Le trasformate discrete delle wavelet (DWT), d'altra parte, forniscono le informazioni sufficienti sia per l’analisi che

per la sintesi del segnale originale con una riduzione significativa del tempo di calcolo.

5.8.3.1 La codifica Subband e L'Analisi di Multiresolution

L'idea principale è la stessa delle CWT. Una rappresentazione tempo-scala di un segnale digitale è ottenuta usando tecniche di filtrazione digitali. Ricordiamo che la CWT è una correlazione tra una wavelet a scale diverse ed il segnale e viene usata come misura di somiglianza. Le CWT sono calcolate cambiando la scala della finestra di analisi, spostando la finestra nel tempo, moltiplicando per il segnale ed integrando. Nel caso discreto, sono utilizzati diversi filtri delle frequenze di taglio per analizzare il segnale a scale diverse: il segnale viene passato attraverso una serie di filtri di passaggio alti per analizzare le frequenze alte e una serie di filtri di passaggio bassi per analizzare le frequenze basse.

La risoluzione del segnale, che è una misura della quantità di informazioni sul segnale, viene cambiata dalle operazioni di filtrazione, e la scala viene cambiata dalle operazioni di upsampling e downsampling (il subsampling). Eseguire il subsampling di un segnale corrisponde a ridurre la percentuale di campionatura rimuovendo alcuni dei campioni del segnale; viceversa eseguire l’upsampling di un segnali corrisponde ad aumentare la percentuale di campionatura del segnali aggiungendo esemplari nuovi al segnale stesso. Anche se non è l'unica scelta possibile, i coefficienti della DWT sono di solito campionati dalla CWT su una griglia bivalente, cioè

s

₀

=

2

e

_τ

₀

=

1

rendendo

s 2

=

j e

τ

=

k 2

⋅

j. Poichè il segnale è una funzione nel tempo discreta, i termini della funzione e della sequenza saranno usati intercambiabilmente nella presentazione seguente. Questa sequenza sarà denotata da

x

[n

]

, dove n è un numero intero.

La procedura comincia col passare questo segnale (sequenza) attraverso un mezzo filtro digitale lowpass con risposta impulsiva

h

[

n

]

. Filtrare un segnale corrisponde all'operazione matematica della convoluzione del segnale con la risposta impulsiva del filtro. L'operazione di convoluzione nel tempo discreto è definita come segue:

⋅

=

∑

∞

⋅

−

−∞ = k

k

n

h

k

x

n

h

n

x

[

]

[

]

[

]

[

]

(5.50)

Un mezzo filtro di lowpass rimuove tutte le frequenze che sono sopra la metà della frequenza più alta nel segnale. Per esempio, se un segnale ha un massimo di una componente a 1000Hz, con un mezzo filtro di lowpass si rimuovono tutte le frequenze sopra 500 Hz.

L'unità della frequenza è, a questo punto particolarmente importante. Nei segnali discreti la frequenza è espressa in termini di radianti, quindi la frequenza di campionamento del segnale è uguale a 2π radianti in termini di frequenza radiale. La componente di frequenza più alta che esiste in un segnale sarà quindi π radianti, se il segnale è campionato alla percentuale di Nyquist (che è due volte la frequenza massima che esiste nel segnale), cioè la percentuale di Nyquist corrisponde a π rad/s nel dominio discreto della frequenza. Usare perciò gli Hz come unità di misura nei segnali discreti non è appropriato. Gli Hz sono tuttavia usati ogni qualvolta che c’è bisogno di chiarificare una discussione in quanto è molto più pratico pensare alla frequenza in termini di Hz.

Dopo aver fatto passare il segnale attraverso un filtro di mezza banda lowpass , la metà dei campioni può essere eliminata secondo la regola di Nyquist, poiché il segnale ora ha una frequenza più alta pari a π/2 radianti invece di π radianti. Scartando semplicemente tutti i campioni compresi entro due sottocampioni del segnale, avremo un segnale con la metà del numero di punti: la scala del segnale è ora raddoppiata.

Si noti che il filtrare con un lowpass rimuove le informazioni di frequenza alte, ma lascia la scala immutata. Solamente il processo di subsampling cambia la scala. La risoluzione, d'altra parte, è riferita alla quantità di informazioni nel segnale e quindi è influenzata dalle operazioni di filtrazione. Un filtro di mezza banda lowpass rimuove la metà delle frequenze e questo può essere interpretato come la perdita della metà delle informazioni: la risoluzione è dimezzata dopo l'operazione di filtrazione. Comunque, si deve far notare che filtrare il segnale con l'operazione di subsampling non influenza la risoluzione, rimuovendo la metà delle componenti spettrali dal segnale e rendendo comunque dimezzato il numero di campioni ridondanti: la metà dei campioni possono essere scartati senza alcuna perdita di informazioni.

Il segnale è poi sottocampionato in 2 poiché la metà del numero di campioni è ridondante: questo raddoppia la scala.

∑

⋅

−

=

∞ −∞ = k

h

k

x

n

k

n

y

[

]

[

]

[

2

]

(5.51) La DWT analizza il segnale a frequenze diverse con risoluzioni diverse decomponendo il segnale in un'approssimazione grossolana ed in informazioni di dettaglio. La DWT assume due set di funzioni, chiamate funzione di scala e funzione wavelet alle quali sono associati rispettivamente i filtri lowpass e highpass. La decomposizione del segnale in bande di frequenza diverse è ottenuta semplicemente filtrando il segnale nel dominio del tempo con gli highpass e i lowpass. Il segnale originario

x

[n

]

viene prima passato attraverso un filtro di mezza banda highpass

]

[

n

g

e un filtro lowpass

h

[

n

]

, poi, dopo la filtrazione, la metà degli esemplari può essere eliminata secondo la regola di Nyquist, così, come già detto, il segnale avrà una frequenza più alta pari a π/2 radianti invece di π. Il segnale può essere perciò sottocampionato in 2, semplicemente scartando ogni altro campione. Questo costituisce un livello della decomposizione e matematicamente può essere espresso come segue:

∑

⋅

−

=

∑

⋅

−

=

n low n high

n

k

h

n

x

k

y

n

k

g

n

x

k

y

]

2

[

]

[

]

[

]

2

[

]

[

]

[

(4.52)

dove

y

_high

[k

]

e

y

_low

[k

]

sono le uscite dopo il sottocampionamento di 2 dei filtri highpass e lowpass rispettivamente.

Questa decomposizione dimezza la risoluzione del tempo poichè solamente la metà del numero di campioni caratterizza l’intero segnale, ma raddoppia quella della frequenza dimezzando la banda del segnale, dimezzando quindi efficacemente l'incertezza nella frequenza. La procedura suddetta, nota come “codifica subband” può essere ripetuta per una ulteriore decomposizione: ad ogni passo, la filtrazione e il subsampling daranno luogo alla metà del numero di campioni (e quindi dimezza la risoluzione nel tempo) e alla metà della banda di frequenza (e quindi raddoppia la risoluzione nella frequenza).

Nella figura 5.18 viene illustrata questa procedura dove

x

[n

]

è il segnale originale che deve essere decomposto,

h

[n

]

e

g

[n

]

sono rispettivamente i filtri lowpass e highpass e f indica la larghezza di banda ad ogni livello.

fig. 5.18: Procedura di codifica subband

La DWT del segnale originale è ottenuta concatenando tutti i coefficienti a partire dall'ultimo livello della decomposizione e avrà quindi lo stesso numero di coefficienti del segnale originario.

Le frequenze che sono molto sporgenti nel segnale originario appariranno con ampiezze alte in quella regione della DWT del segnale che include quelle particolari frequenze. La differenza di questa trasformata da quella di Fourier è che la localizzazione nel tempo di queste frequenze non sarà persa, comunque tale localizzazione avrà una risoluzione che dipende dal livello al quale appaiono. Se le informazioni principali del segnale giacciono nelle frequenze alte, la localizzazione nel tempo di queste frequenze sarà più precisa in quanto sono caratterizzate da un numero maggiore di campioni. Invece, se le informazioni principali del segnale giacciono solamente nelle frequenze molto basse, la localizzazione nel tempo non sarà molto precisa in quanto solo pochi esemplari sono usati per esprimere il segnale a queste frequenze. Questa procedura in effetti offre una buona risoluzione nel tempo a frequenze alte e una buona risoluzione nelle frequenze a frequenze basse. Le bande di frequenza che non sono molto sporgenti nel segnale originario avranno ampiezze molto basse e quella parte della DWT del segnale può essere scartata senza alcuna ulteriore perdita di informazioni, permettendo comunque una riduzione di dati.

Nelle figure 5.19 viene illustrato un esempio di come la DWT del segnale fornisce una riduzione dei dati. La figura 5.19a mostra un tipico segnale a 512 campioni

normalizzato all’unità dell’ampiezza: l'asse orizzontale è il numero di campioni e l'asse verticale è l'ampiezza normalizzata. La figura 5.19b mostra l’ottavo livello della DWT del segnale in figura 5.19a.

fig. 5.19: Esempio di una DWT

Un'importante proprietà delle trasformate discrete delle wavelet è la relazione tra le risposte ad un impulso dei filtri di highpass e di lowpass. Questi filtri non sono indipendenti l'uno dall'altro, come si può notare dalla relazione seguente:

]

[

)

1

(

]

1

[

L

n

h

n

g

−

−

=

−

n

⋅

(5.53) dove

g

[n

]

è il filtro di highpass,

h

[n

]

è il filtro di lowpass e

L

è la lunghezza del filtro in numero di punti. Si nota che, quando l’indice è dispari, i due filtri sono versioni invertite l'uno dell'altro: la conversione da filtro di lowpass a quello di highpass è ottenuta attraverso il termine

(−

1

)

n. I filtri che soddisfano questa condizione sono usati comunemente nella lavorazione dei segnali e sono noti come i filtri dello specchio della quadratura (QMF).

Come visto in precedenza le due operazioni di filtrazione e sottocampionamento possono essere espresse dalle relazioni:

∑

⋅

−

+

=

∑

⋅

−

+

=

n low n high

k

n

h

n

x

k

y

k

n

g

n

x

k

y

]

2

[

]

[

]

[

]

2

[

]

[

]

[

(5.54)

In questo caso la ricostruzione è molto facile in quanto i filtri di mezza banda formano una base ortonormale. La ricostruzione viene eseguita percorrendo la procedura precedentemente vista in ordine rovescio. I segnali ad ogni livello sono

sopracampionati di due, passati attraverso i filtri di sintesi

g

'

[

n

]

e

_h

'

[

n

]

(highpass e lowpass, rispettivamente) e poi addizionati. E’ interessante notare che in questa fase dell'analisi i filtri di sintesi sono identici l'uno all'altro, ad eccezione di un'inversione del tempo.

La formula di ricostruzione per ogni strato diviene:

(

)

(

)

∑

⋅

−

+

+

⋅

−

+

=

∞ −∞ = k high low

k

n

h

k

y

k

n

g

k

y

n

x

[

]

[

]

[

2

]

[

]

[

2

]

(5.55)

Comunque, se i filtri non sono ideali di mezza banda, la ricostruzione perfetta non può essere realizzata. Anche se non è possibile realizzare filtri ideali, sotto certe condizioni è possibile trovare filtri che offrono la ricostruzione perfetta; i più famosi sono gli quelli sviluppati da Ingrid Daubechies che sono noti come la wavelets di Daubechies.

Si noti che per via del sottocampionamento di 2 successivo la lunghezza del segnale deve essere una potenza di 2 o almeno un multiplo di una potenza di 2 per rendere questo schema efficiente. La lunghezza del segnale determina il numero di livelli nei quali il segnale può essere decomposto. Per esempio, se la lunghezza del segnale è 1024, allora sono possibili dieci livelli della decomposizione.

Interpretare i coefficienti delle DWT qualche volta può essere piuttosto difficile perché il modo in cui i coefficienti delle DWT sono presentati è piuttosto particolare. Infatti tali coefficienti di ogni livello sono concatenati per rendere corta una storia lunga cominciando con l'ultimo livello.

Si noti che un numero sempre minore di campioni è usato alle frequenze più basse, perciò la risoluzione sia nel tempo che nella frequenza diminuisce, ma se decresce anche l'intervallo di frequenza alle frequenze basse, la risoluzione nella frequenza aumenta. Evidentemente, i primi coefficienti non porterebbero tutte le informazioni, semplicemente a causa di una risoluzione nel tempo grandemente ridotta.

La tecnica delle trasformate delle wavelet sta riscontrando molto successo in svariate applicazioni dove viene richiesta una elaborazione di un segnale contenente una grande quantità di dati, come ad esempio nel trattamento informatico delle immagini.

Riferimenti Bibliografici

[1] J. S. Bendat, A. G. Piersol, Engineering applications of correlation and spectral analysis, John Wiley & Sons, 1980.

[2] R. Brincker, L. Zhang, P. Andersen, Damping Estimation by frequency domain decomposition.

[3] R. Brincker, L. Zhang, P. Andersen, Output-only modal analysis by frequency domain decomposition, Proceedings of ISMA25, Volume 2, 2000.

[4] M. L. Beconcini, Elementi di dinamica delle strutture, Pisa, 2000.

[5] L. Meirovitch, Elements of vibration analysis, McGraw-Hill, second edition, 1986.

[6] J. M. Keiser, A friendly guide to wavelets, Birkhäuser, Boston, 1994.

[7] R. Polikar, The wavelets tutorial, Ames, Iowa, 1996.