Capitolo 2

Capitolo 2

Struttura e metodi di caratterizzazione

del microspecchio

Gli scopi della presente tesi di laurea sono:

1) la progettazione e la realizzazione di opportuni circuiti elettronici per la stimolazione di un microspecchio torsionale;

2) la misura della risposta alle sollecitazioni di tale microspecchio.

Il dispositivo che ci interessa in tal modo caratterizzare è stato già studiato, analiticamente e tramite metodi di calcolo numerico e di simulazione ad elementi finiti (con il software FEMLAB), in un nostro precedente lavoro [1]. Ci riferiamo dunque ad esso per i dettagli, mentre presentiamo in questa sede solo gli aspetti fondamentali, necessari alla comprensione del seguito.

Nel presente capitolo, quindi, illustriamo la struttura in analisi ed alcune delle sue proprietà meccaniche ed elettriche; dopodicché descriviamo i metodi di misura che intendiamo applicare sul dispositivo; infine presentiamo un metodo di pilotaggio alternativo a quello classico, che permette di migliorare le prestazioni del microspecchio.

2.1 Analisi di un microspecchio torsionale a

veneziana

Il dispositivo preso in analisi è un microspecchio torsionale in configurazione a veneziana, realizzato con la tecnologia del surface micromachining, tramite il processo THELMA di STMicroelectronics.

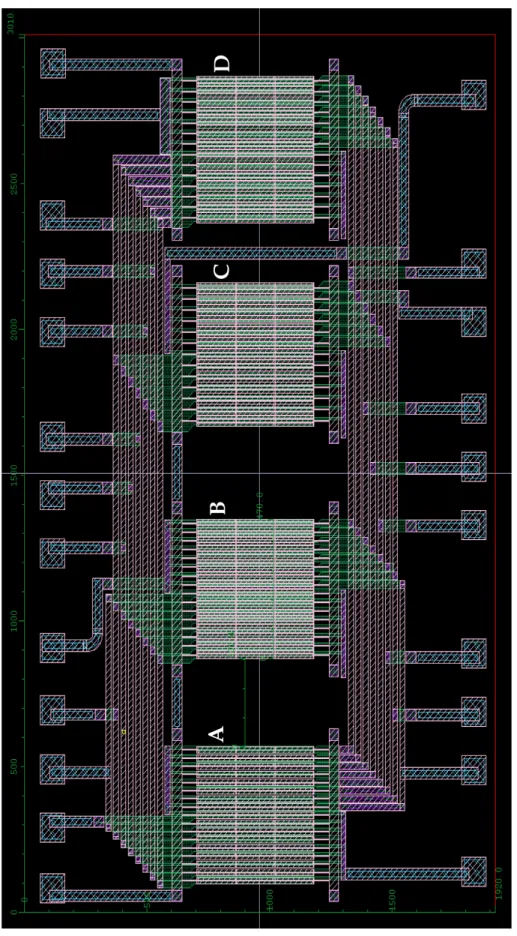
Su ciascun die sono presenti quattro dispositivi, di geometria leggermente differente, che indichiamo con le lettere A, B, C e D, come visibile nel layout riportato in fig.2.1. Nel descriverne la struttura, ci riferiamo in particolare allo specchio C (fig.2.2).

La superficie riflettente è costituita da un array di dieci elementi in polisilicio cresciuto tramite epitassia, ciascuno di dimensioni

49

×480

×15

, i quali sono attuati elettrostaticamente tramite la tensione applicata tra essi e gli elettrodi sottostanti; la rotazione angolare è concessa in una sola dimensione (si tratta cioè di specchi 1D).

Figura 2.2 Layout di un microspecchio a veneziana composto di dieci elementi (specchio C)

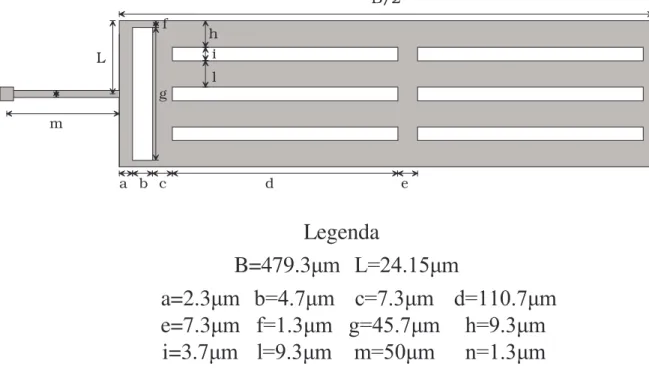
Nella fig.2.3 è rappresentata la struttura semplificata di un array di specchi in fase e nella fig.2.4 la vista in pianta della metà destra del singolo microspecchio: su tale schema sono riportate le dimensioni di maggior interesse.

La lastra di polisilicio spesso di ciascun elemento dell’array presenta delle fessure, che permettono alla soluzione chimica di attaccare lo strato sacrificale sottostante e liberare la struttura: si sono realizzati dei fori a fessura, anziché quadrati, perché tale scelta è risultata preferibile dal punto di vista ottico. Queste fessure sono 12 (

3 nel senso della larghezza

× 4

nella direzione della lunghezza), di dimensioni

3

×110

.

Figura 2.3 Struttura semplificata di un array di microspecchi in fase (ed elettrodi sottostanti)

Gli elettrodi di attuazione sono realizzati anch’essi in polisilicio (si tratta di poly1, nome dello specifico layer del processo THELMA) e hanno uno spessore di

1

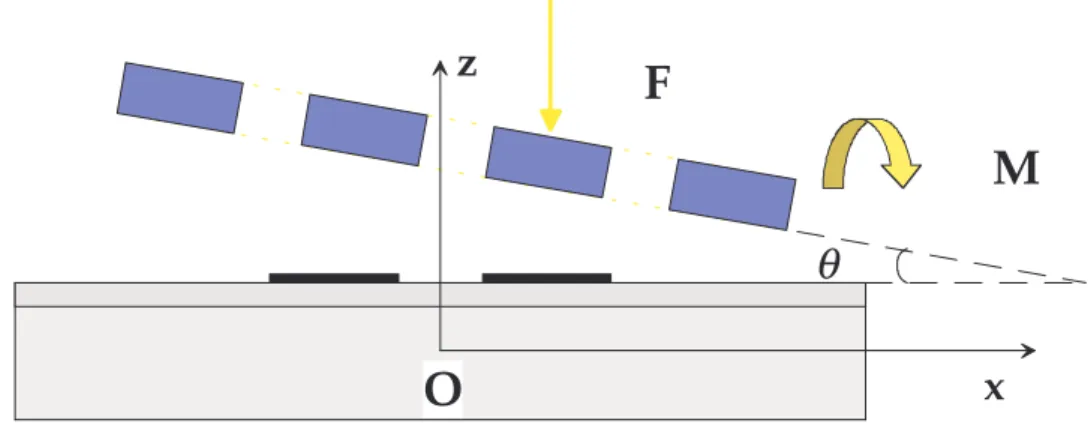
; sono due per ciascun elemento della veneziana, al di sotto del quale si estendono come lunghe strisce, in senso longitudinale. Nella fig.2.6 è rappresentata una sezione dello specchio (ruotato di un angolo

θ

): in essa l’origine degli assi è posta in O, l’asse

x

direzione della lunghezza e l’asse

z

in quella dello spessore. La lastra riflettente è colorata di azzurro (non è continua perché ci sono le fessure per l’attacco, di cui si è parlato in precedenza); il substrato e l’ossido di silicio sono in grigio (rispettivamente chiaro e scuro) e gli elettrodi di attuazione in nero. B/2 L a b c d e f g h i l m

a=2.3

e=7.3

i=3.7

B=479.3

Legenda

Figura 2.4 Vista in pianta della metà destra del singolo microspecchio (i dati forniti tengono conto del sottoattacco)

Poiché si è verificato che la larghezza degli elettrodi incide significativamente sulla dinamica angolare dello specchio (in quanto più sono grandi gli elettrodi minore è l’angolo di pull-in - di cui si parlerà nel seguito -), si è ritenuto opportuno mantenere tale dimensione su un valore piuttosto basso, vale a dire

10

. Questa scelta comporta, però, un problema realizzativo, in quanto il processo di fabbricazione prevede per le strutture in poly1 una larghezza di circa

40

, in modo da impedire che durante l’attacco dell’ossido sottostante vengano liberate anche le strutture realizzate con tale layer. Affinché, dunque, gli elettrodi restino ancorati al substrato, nonostante le dimensioni ridotte, si è pensato di allargarli in alcuni tratti: in pratica il layout prevede una sorta di piazzole quadrate, poste a distanze regolari, in cui la larghezza raggiunge i

34

(a tal proposito, si veda la fig.2.6). Ovviamente, in seguito a tale disomogeneità, si hanno comportamenti differenti del dispositivo nelle zone in cui l’elettrodo è stretto e in quelle in cui esso è largo, pertanto se ne è tenuto conto nel calcolo delle varie grandezze di interesse.

θ

x

z

_F

M

O

Figura 2.5 Vista in sezione del singolo microspecchio (in corrispondenza delle fessure) ruotato di un angolo θθθθ

La distanza tra la lastra riflettente e gli elettrodi è data dallo spessore dello strato sacrificale realizzabile che, con il processo da noi usato, è di

16

. Ciascun microspecchio che compone la veneziana è sospeso sugli elettrodi ed è ancorato al substrato tramite due molle torsionali, collegate agli estremi (ovviamente in direzione longitudinale). Le molle, di dimensioni 1.3

×50

×15

, sono anch’esse realizzate in polisilicio.

Nella figura 2.4 è ritratto il singolo specchio in pianta (in corrispondenza di una piazzola degli elettrodi): le grandezze indicate saranno utilizzate nello sviluppo dei calcoli analitici e nelle simulazioni per le caratterizzazioni statica e dinamica del dispositivo, che presentiamo qui di seguito.

2.1.1 Caratterizzazione statica

In questo paragrafo presentiamo in breve la caratterizzazione statica del dispositivo, che è stata effettuata nel precedente – già citato – lavoro: [1]. Ci riferiamo, dunque, ad esso per i dettagli.

Quando si applica una differenza di potenziale tra lo specchio e uno dei due elettrodi sottostanti, sulla lastra riflettente vengono ad agire una

forza, che la induce ad abbassarsi, e un momento, che la porta a ruotare

intorno all’asse delle molle (nel nostro caso l’asse

y

). Se

θ

è l’angolo di rotazione,

α

lo spostamento verso il basso dello specchio (considerato come un corpo rigido),

di

la distanza iniziale tra esso e l’elettrodo (cioè a

0

θ =

), per

θ ≠

0

la distanza tra le armature è data da:

( )

,

tan .

d

α θ

= − − ⋅

di

α

x

θ

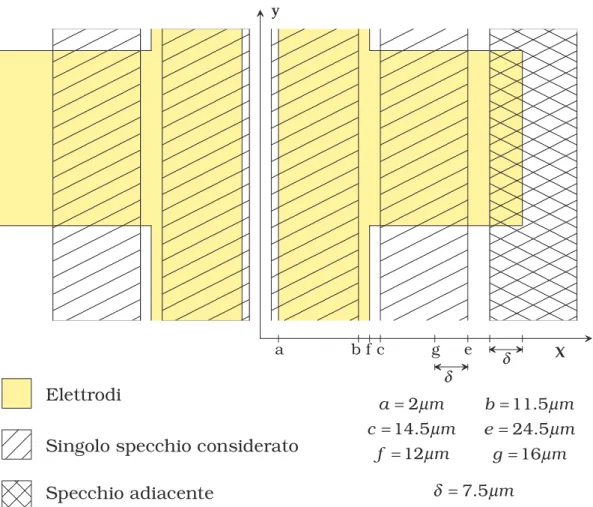
(2.1) y X a b cf g e _δ δ Elettrodi

Singolo specchio considerato Specchio adiacente µ µ µ = = = 2 14.5 12 a m c m f m µ µ µ = = = 11.5 24.5 16 b m e m g m δ = 7.5 mµ

Figura 2.6 Vista in pianta dello specchio in corrispondenza di una piazzola dell'elettrodo

La forza elettrostatica e il momento agenti sul dispositivo sono espressi dalle seguenti relazioni:

2

1

2

E

C

F

V

d

∂

= ⋅

⋅

∂

(2.2) 2

1

2

E

C

M

V

θ

∂

= ⋅

⋅

∂

(2.3)

in cui

C

è la capacità tra la lastra e l’elettrodo (che rappresentano, rispettivamente, l’armatura superiore e quella inferiore del condensatore) e

V

la tensione di tra essi applicata.

Per calcolare la succitata capacità occorre tenere presente che, come spiegato nel paragrafo 2.1, il microspecchio non ha una conformazione costante lungo la direzione y (cioè lungo il suo asse principale). Si procede - pertanto - al calcolo della capacità per unità di lunghezza, distinguendo quattro casi differenti, in corrispondenza delle varie sezioni possibili della struttura. Ciò che si ottiene è espresso dalle formule qui di seguito (per le lettere indicate ci si riferisce alla fig.2.6).

1° caso - Sezione in corrispondenza delle fessure nello specchio e di elettrodo stretto: 0 1

ln

.

di

a

C

di

b

ε

α

θ

θ

α

θ

− − ⋅

=

⋅

− − ⋅

(2.4)

2° caso - Sezione in corrispondenza delle fessure nello specchio e di elettrodo largo: 0 2

ln

ln

.

di

a

di

c

C

di

b

di

e

ε

α

θ

α

θ

θ

α

θ

α

θ

− − ⋅

− − ⋅





=

⋅

_

+

_

− − ⋅

− − ⋅





(2.5)

3° caso - Sezione con specchio intero (in corrispondenza delle zone in cui non vi sono fessure) ed elettrodo stretto:

0 3

ln

.

di

a

C

di

f

ε

α

θ

θ

α

θ

− − ⋅

=

⋅

− − ⋅

(2.6)

4° caso - Sezione con specchio intero ed elettrodo largo: 0 3

ln

.

di

a

C

di

e

ε

α

θ

θ

α

θ

− − ⋅

=

⋅

− − ⋅

(2.7)

Le lettere

a

, b,

c

,

e

, f presenti nelle (2.4)-(2.7) si riferiscono alle dimensioni delle varie parti della lastra riflettente, come riportato in fig.2.7.

0

ε

è la costante dielettrica del vuoto (si osservi che siamo nell’aria, quindi si dovrebbe porre

ε ε

₀

⋅

_r, ma la

ε

_r dell’aria è pari ad 1).

Per verificare se queste formule siano o meno adatte a descrivere l’effettivo andamento della capacità tra specchio ed elettrodo (in funzione di

θ

e

α

), si è realizzata una simulazione accoppiata elettro-meccanica con il metodo degli elementi finiti (ricorrendo al software FEMLAB). In essa il calcolatore ha tenuto conto anche dei fenomeni secondari che si erano trascurati nel calcolo analitico, vale a dire: gli effetti di bordo, gli accoppiamenti tra i due elettrodi (uno portato a tensione

V

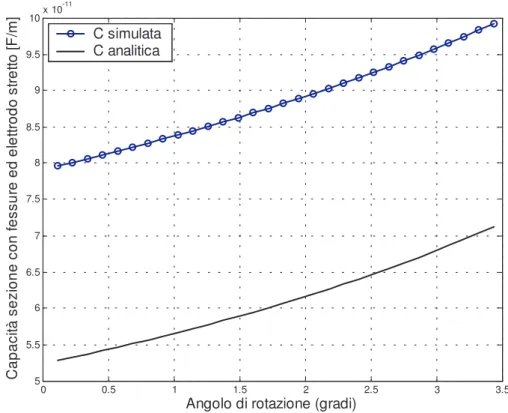
e l’altro tenuto a massa) e quelli tra essi e la lastra riflettente.

0 0.5 1 1.5 2 2.5 3 3.5 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10x 10 -11

Angolo di rotazione (gradi)

C ap ac ità s ez io ne c on fe ss ur e ed e le ttr od o st re tto [F /m ] C simulata C analitica

Nella fig.2.7 è rappresentato il grafico comparativo di due curve di capacità (in corrispondenza di una dei quattro tipi di sezioni del dispositivo) ottenute, rispettivamente, tramite calcolo analitico e per mezzo di simulazione FEMLAB. Dal confronto tra esse, rilevato che l’andamento è il medesimo, si evince che le equazioni analitiche da noi ricavate sono adeguate a descrivere il sistema. Vi è però, tra le due curve, uno scarto pressappoco costante (per le quattro sezioni e per tutti gli angoli), che indica la presenza di un termine aggiuntivo da sommare alle capacità per unità di lunghezza ottenute tramite calcolo analitico. Esso è dovuto proprio al fatto che in tale calcolo si sono trascurati gli effetti secondari, i quali si manifestano invece sotto forma di una capacità (che potremmo definire parassita) in parallelo a quella espressa analiticamente.

Dato che ai fini nei nostri studi ciò che conta sono le derivate della capacità (rispetto allo spostamento e all’angolo di rotazione), è evidente che una componente costante aggiuntiva non ha alcuna rilevanza. L’unico effetto che essa produce è quello di richiedere carica aggiuntiva, cioè rendere necessaria una tensione di pilotaggio più alta, rispetto a quella considerata nel modello analitico, a parità di angolo di rotazione. Ma anche in relazione alla tensione possiamo affermare che trascurandola non si incorre in un grosso errore, in quanto essa è di entità molto ridotta. Infatti, a fronte di una capacità propria del dispositivo pari a 10÷100pF per unità di lunghezza, quella parassita di cui stiamo parlando vale:

-10 par

C =0.27×10 F m

per unità di lunghezza.

A partire dalle (2.2) e (2.3), tramite opportuni calcoli (riportati dettagliatamente nel lavoro già menzionato [1]) è possibile ricavare la forza elettrostatica e il momento agenti sul microspecchio, tenendo conto della particolare struttura del nostro dispositivo. Le espressioni di tali grandezze sono le seguenti:

( )

0 2 1 2

1

1

,

2

1

1

1

1

1

1

E

V

F

B

di

b

di

a

B

di

b

di

a

di

e

di

c

di

e

di

g

ε

θ α

θ

α

θ

α

θ

α

θ

α

θ

α

θ

α

θ

α

θ

α

θ

⋅







=

⋅

_

⋅

_

−

_

+

⋅





− − ⋅

− − ⋅





+ ⋅

_{ − − ⋅}

−

+

− − ⋅







+

−

+

−

_

_

⋅

− − ⋅

− − ⋅

− − ⋅

_{− − ⋅ }

(2.8)

( )

0 2 1 2

,

ln

2

ln

ln

.

E

V

di

b

b

a

M

B

di

a

di

b

di

a

di

b

b

a

B

di

a

di

b

di

a

di

g

g

c

di

c

di

g

di

c

ε

α

θ

θ

θ

θ α

θ

α

θ

α

θ

α

θ

α

θ

θ

θ

α

θ

α

θ

α

θ

α

θ

θ

θ

α

θ

α

θ

α

θ



⋅



− − ⋅

⋅

⋅



=

⋅

_

⋅

_

+

−

_

+

⋅

_

_

− − ⋅

− − ⋅

_{− − ⋅ }

− − ⋅

⋅

⋅



+

_

+

−

− − ⋅

− − ⋅

− − ⋅







− − ⋅

⋅

⋅

+

+

−

_

_

− − ⋅

− − ⋅

_{− − ⋅ }

(2.9) 1

B

e

B

₂ indicano, rispettivamente, la lunghezza della somma dei tratti in cui il singolo elettrodo è corto (cioè di 10 di larghezza) e quella della somma dei tratti in cui il singolo elettrodo è largo (cioè di

34

);

V

è la tensione applicata all’elettrodo - ponendo il substrato e quindi anche lo specchio, che è ad esso collegato, a massa. Per la geometria da noi presa in considerazione, ossia quella dello specchio C, si ha:

B =140

₁ e

B =340

₂ .

La forza e il momento qui espressi sono già opportunamente corrette per tener conto del contributo dovuto alla presenza degli elettrodi adiacenti, ossia al fatto che le piazzole (cioè le zone larghe) degli elettrodi eccedono la larghezza del singolo elemento di specchio. Ciò comporta, infatti, che una parte dell’attuazione agisca sul lato contrario a quello desiderato, così da produrre una componente di forza che si somma e una componente di momento che si sottrae rispettivamente alla forza e al momento dati dalla parte di elettrodo destro sottostante lo specchio. La lettera

g

presente nelle (2.8) e (2.9) (v. fig. 2.7) è la coordinata in corrispondenza della quale si ha l’estremo sinistro dell’elettrodo adiacente,

ossia quest’ultimo si estende sotto lo specchio preso in considerazione tra

e

e

g

.

Scritte le espressioni della forza e del momento, si calcolano quella dello spostamento dello specchio verso il basso (dovuto alla forza) e quella della costante elastica torsionale delle molle che reggono la lastra riflettente (torsione dovuta al momento). La prima si ottiene tramite l’applicazione della relativa equazione differenziale della linea elastica ed è pari a: 3 3 3 3 4 12 z z z x x x l F l F l F E I E I E I α = ⋅ − ⋅ = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ (2.10)

con Fz forza elastica agente sull’estremo non vincolato della molla, data

da:

( )

,

2

E z

F

F = θ α , dove la FE

( )

θ α, è quella sopra indicata. Ix è il

momento d’inerzia della sezione della molla rispetto all’asse

x

, l è la lunghezza della stessa (l

=50

) ed E il modulo elastico (o di Young) del polisilicio, pari a 150Gpa.

Per quanto riguarda la costante elastica torsionale, invece, definita

t

K la costante di ciascuna molla, all’equilibrio si ha la relazione:

( )

, 2 . E t M θ α = ⋅K ⋅ = ⋅θ K θ (2.11) dove: 2 t p . G J K K l ⋅ = ⋅ = (2.12)

Nella (2.12)

G

è il modulo di elasticità tangenziale, detto anche

shear modulus, ed è espresso come segue:

(

)

2 1 E G ν = ⋅ + , con E=modulo

di Young e

ν

=coefficiente di Poisson=

0.3

;

J

_p è il momento di inerzia polare equivalente che, per una trave a sezione rettangolare, è dato dalla

formula:

(

)

3 0.6 . 3 p t w w J = − ⋅ ⋅

Note, quindi, l’espressione del momento torcente (2.9) e quella della costante elastica K (2.12), si ricava, dall’uguaglianza espressa nella (2.11), una relazione che lega la tensione di attuazione all’angolo di inclinazione e all’abbassamento del microspecchio:

( )

3

_{( )}

0 2 1 , , K V f θ θ α ε θ α ⋅ ⋅ = ⋅ ⋅ (2.13) nella quale è:

( )

1 2

,

ln

ln

ln

.

di

b

b

a

f

B

di

a

di

b

di

a

di

b

b

a

B

di

a

di

b

di

a

di

g

g

c

di

c

di

g

di

c

α

θ

θ

θ

θ α

α

θ

α

θ

α

θ

α

θ

θ

θ

α

θ

α

θ

α

θ

α

θ

θ

θ

α

θ

α

θ

α

θ



− − ⋅

⋅

⋅



= ⋅

_

+

−

_

+

− − ⋅

− − ⋅

_{− − ⋅ }



− − ⋅

⋅

⋅



+

_

+

−

− − ⋅

− − ⋅

− − ⋅





− − ⋅

⋅

⋅

+

+

−

_

− − ⋅

− − ⋅

_{− − ⋅ }

(2.14)

Dall’esame delle (2.13) e (2.14) è evidente che la tensione applicata al dispositivo dipende dall’abbassamento

α

dello specchio, il quale, a sua volta, varia a seconda della forza esercitata, cioè della tensione stessa. Si tratta evidentemente di un problema non risolvibile analiticamente; pertanto si è effettuato uno studio tramite iterazione numerica, impiegando il software MATLAB.

Nella figura 2.8 è rappresentato l’andamento della tensione di attuazione in funzione dell’angolo di rotazione, ricostruito tramite i risultati di tale iterazione numerica; sono inoltre evidenziati i valori dell’angolo e della tensione ad esso corrispondente per cui si verifica il pull-in, ossia

pin

θ

e

V

_pin.

Il fenomeno del pull-in rappresenta un limite per il pilotaggio dello specchio. Il dispositivo, infatti, funziona correttamente quando lavora in

condizione di equilibrio, stato nel quale la forza e il momento elettrostatici sono eguagliati dalla forza e dal momento meccanici. Accrescendo la tensione di attuazione, però, si giunge ad un punto in cui non riesce più a stabilirsi un equilibrio tra le due componenti (ci si trova cioè in uno stato instabile), cosicché lo specchio collassa sull’elettrodo.

Figura 2.8 Tensione di attuazione in funzione dell'angolo di rotazione

E’ dunque fondamentale conoscere i parametri di pull-in, ossia la tensione di attuazione e l’angolo di rotazione per cui si incorre in tale fenomeno. I calcoli analitici, effettuati trascurando - per semplicità – l’abbassamento dello specchio, hanno fornito i seguenti valori:

0.059

3.4

pin

rad

θ

e

V

_pin

=

105.3

V

. Il calcolo tramite iterazione numerica, in cui si è tenuto conto della struttura effettiva e dell’abbassamento, fornisce invece per tali parametri i valori:

0.042

2.4

pin

rad

θ

e

V

_pin

=

93

V

(fig. 2.5).

Il confronto delle due coppie di risultati dimostra che la dinamica del microspecchio viene ridotta dal fenomeno dell’abbassamento. Si continua

specifica minima per una buona applicabilità del nostro dispositivo come commutatore ottico.

2.1.2 Caratterizzazione dinamica

Si procede con uno studio in frequenza del comportamento del dispositivo. In particolare, occorre prendere in considerazione il fenomeno della risonanza meccanica, in quanto esso determina la velocità massima di pilotaggio, ossia di variazione della tensione applicata, per cui la struttura risponde con uno spostamento meccanico.

Tramite il software FEMLAB abbiamo calcolato, per il nostro microspecchio, le frequenze di risonanza (delle varie forme modali presenti, ciascuna delle quali provoca un diverso tipo di deformazione e oscillazione della struttura) e simulato il suo comportamento in corrispondenza di esse. Le prime quattro sono le seguenti:

• 1° modo – alla frequenza di

55.1kHz

, il dispositivo vibra sul piano dello specchio (cioè

x y

−

); le molle si flettono nella stessa direzione rispetto all’asse centrale della struttura;

• 2° modo – alla frequenza di

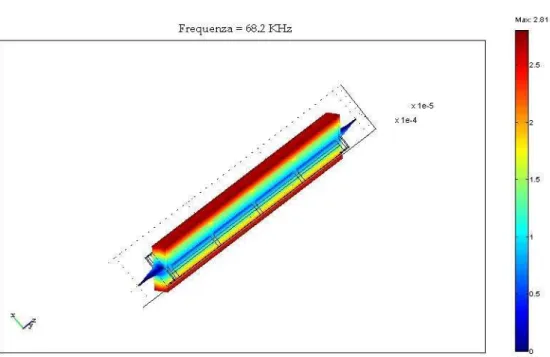
68.2kHz

, il dispositivo subisce una torsione intorno al proprio asse longitudinale;

• 3° modo – alla frequenza di

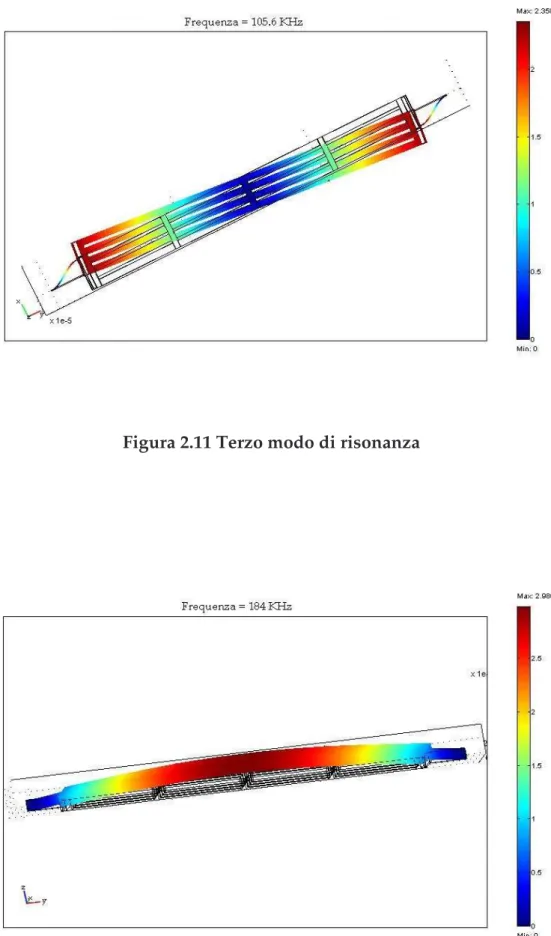
105.6kHz

, la struttura oscilla sul piano dello specchio (cioè

x y

−

); le molle si flettono in direzione opposta rispetto all’asse centrale del dispositivo;

• 4° modo – alla frequenza di

184kHz

, la struttura vibra fuori dal piano dello specchio, incurvandosi.

Nella figure 2.9-2.12 è possibile vedere lo schema del dispositivo alle frequenze di risonanza sopra presentate. I colori indicano, secondo le scale riportate a fianco, il grado di deformazione dello specchio rispetto alla struttura di partenza.

Figura 2.9 Primo modo di risonanza

Figura 2.11 Terzo modo di risonanza

Poiché intendiamo pilotare il dispositivo in modo che esso ruoti rispetto al proprio asse longitudinale, siamo interessati alla seconda frequenza di risonanza, che - per l’appunto - è legata ad un movimento torsionale. In realtà, però, non possiamo prescindere dalla prima frequenza: infatti se facciamo lavorare il sistema in corrispondenza di essa, incorriamo comunque nell’oscillazione, anche se nel piano dello specchio e non in torsione.

Ricordiamo che, per tutti i procedimenti con cui si perviene ai risultati presentati in questo paragrafo e per le considerazioni relative, si può fare riferimento al testo [1].

2.2 Metodi di misura

Per caratterizzare il comportamento, sotto l’effetto dell’attuazione, di dispositivi quali i microspecchi si ricorre principalmente a metodi di tipo elettrico [38] [39] [40] [41] e di tipo ottico [42] [43]. I primi risultano particolamente comodi in quanto possono essere automatizzati e si basano sull’uso di strumentazione comunemente utilizzata in ambito elettronico. Essi però sono spesso affetti da disturbi e fenomeni elettrici parassiti (generalmente di tipo capacitivo): ciò implica la necessità di separare in qualche modo le grandezze che si desidera misurare da quelle di natura parassita. Questo obiettivo si può raggiungere scindendo temporalmente la fase di stimolazione da quella di rilevamento, cioè effettuando in un primo tempo la sollecitazione e in un secondo la misura (in assenza di stimolo) [40] [41]; oppure realizzando una separazione frequenziale tra il segnale utile e quello indesiderato [38] [39].

I metodi ottici di misura non incorrono invece in effetti parassiti e disturbi, in quanto non si rileva il segnale elettrico in uscita al dispositivo, ma risultano poco pratici e necessitano sempre l’intervento di un operatore umano. Essi si basano generalmente sull’illuminazione del dispositivo sotto test tramite un fascio laser e della conseguente misura del

movimento dell’oggetto, rilevabile tramite osservazione diretta della deflessione apportata da esso al fascio ottico.

Abbiamo sottoposto i nostri microspecchi torsionali ad entrambi i tipi di indagine, che spieghiamo in dettaglio nel seguito.

2.3 Il metodo della seconda armonica

Il metodo di misura della seconda armonica [38] [39] sfrutta il legame quadratico esistente tra il momento torcente agente sullo specchio e la tensione applicata all’elettrodo di pilotaggio per separare in frequenza la componente utile da quella indesiderata del segnale raccolto in uscita.

Consideriamo un singolo microspecchio (ossia un singolo elemento della veneziana) e i due elettrodi ad esso sottostanti. Poniamo – come sempre – la lastra riflettente a massa e applichiamo: al primo elettrodo (sia quello sinistro) una tensione di attuazione fatta di una componente continua,

E

₁, ed una sinusoidale, di ampiezza

V

_M e pulsazione ; al secondo (sia quello destro) una tensione continua

E

₂. Cioè:

( )

( )

1 1 2 2

sin

.

M

V t

E V

t

V t

E

ω

=

+

⋅

=

(2.15)

Per comodità di caratterizzazione,

E

₁ è scelto molto più grande di

M

V

. Questo consente alcune semplificazioni nella trattazione analitica che segue.

Le tensioni applicate tra gli elettrodi, a causa della capacità tra specchio ed elettrodi destro e sinistro (siano dette rispettivamente

C

₁ e

2

C

) generano una forza ed un momento torcente. La corrente di uscita

i

₂, viene prelevata sull’elettrodo destro. Essa può essere espressa dalla formula:

(

2 2

)

2 2 2

d C V

dC d

i

E

dt

d

dt

θ

θ

⋅

= −

= − ⋅

⋅

. (2.16)

Utilizzeremo il valore della corrente

i

₂ per risalire alla misura della derivata della capacità rispetto all’angolo di rotazione e da qui, tramite l’equazione del momento del sistema meccanico, alla misura dello stesso angolo

θ

.

Vediamo pertanto come si possa esprimere la

i

₂, date le tensioni imposte - indicate nella (2.15) -, e in cosa consiste il metodo di misura della seconda armonica.

Il sistema non è di immediata modellazione, in quanto tra l’angolo di torsione

θ

, le capacità

C

₁ e

C

₂ ed il momento torcente sussistono relazioni non lineari. Effettuiamo, quindi, alcune semplificazioni.

In primo luogo, anticipiamo che siamo interessati alla sollecitazione meccanica in corrispondenza della seconda armonica del segnale d’ingresso, che è comunque presente a causa della non-linearità della relazione tensione/momento. Questa frequenza verrà fatta coincidere con la frequenza di risonanza meccanica dello specchio. È noto dalla letteratura su MEMS capacitivi di tipo analogo che è lecito aspettarsi unfattore di qualità meccanico

Q

molto elevato (dell’ordine del centinaio o superiore). Ciò significa che il sistema è fortemente selettivo in frequenza. Come conseguenza, lo spostamento angolare dello specchio sarà apprezzabile solo in coincidenza della frequenza di risonanza. D’altra parte, non si può trascurare la deflessione angolare statica, in quanto la tensione continua di ingresso che la provoca è almeno un ordine di grandezza superiore a quella della componente sinusoidale della tensione stessa.

Date queste ipotesi, possiamo scrivere l’espressione dell’angolo di torsione come somma di un termine in continua ed uno di seconda armonica, cioè:

(

)

0 2

sin 2 t

θ

θ θ θ

= +

ω ϕ

+

(2.17)

nella quale

θ

₀ rappresenta l’angolo raggiunto per effetto della tensione costante di pilotaggio,

θ

l’ampiezza della componente in seconda

armonica e

ϕ

_θ lo sfasamento di quest’ultima rispetto al segnale alternato d’ingresso.

Procediamo quindi linearizzando le capacità (in funzione di

θ

), con uno sviluppo in serie di Taylor arrestato al primo ordine, intorno all’angolo

0

θ

:

( )

(

)

(

)

( )

(

)

(

)

0 0 1 1 10 0 10 11 0 2 2 20 0 20 21 0

C

C

C

C

C

C

C

C

C

C

θ θ θ θ

θ

θ θ

θ θ

θ

θ

θ θ

θ θ

θ

= =

∂

=

+

⋅ −

=

+

⋅ −

∂

∂

=

+

⋅ −

=

+

⋅ −

∂

(2.18) 10

C

e

C

₂₀ indicano il valore delle capacità in corrispondenza di

0

θ θ

=

; per

θ ≠

₀

0

è

C

₁₀

≠

C

₂₀ e

C

₁₁

≠

C

₂₁.

Andiamo ora a scrivere l’espressione del momento torcente agente sul dispositivo; esso è dato dall’equazione:

( )

1 2

( )

2 2

( )

1 2

1

,

.

2

C

C

M t

θ

V t

V t

θ

θ

∂

∂





= ⋅

_

⋅

+

⋅

_

∂

∂





(2.19)

Sostituendo in quest’ultima le espressioni delle tensioni

V

₁ e

V

₂ e delle derivate delle capacità

C

₁ e

C

₂, si ottiene la seguente espressione:

( )

2 2 2 11 1 1 2 21 2 2 2 2 11 1 21 2 11 1 2 11 0 1 2

1

,

2

sin

cos 2

2

2

2

1

2

1

1

_sin

2

2

2

1

_{cos 2}

4

sin

cos 2

M M M M M M

V

V

M t

C

E

E V

t

t

C

E

V

C

E

C

E

C E V

t

C V

t

M

M

t M

t

θ

ω

ω

ω

ω

ω

ω









= ⋅

⋅

_

_

+

_

+ ⋅ ⋅

⋅

−

⋅

_









+ ⋅

⋅





= ⋅

_

+

_

+ ⋅

⋅

+

⋅ ⋅

⋅





− ⋅

⋅

⋅

=

+

+

(2.20)

con: 2 2 2 0 11 1 21 2 1 11 1 2 2 11

1

1

2

2

2

1

_.

4

M M M

V

M

C

E

C

E

M

C E V

M

C V





= ⋅

⋅

_

+

_

+ ⋅

⋅





=

⋅ ⋅

= − ⋅

⋅

(2.21)

Osserviamo che il momento, in virtù del fatto che nella sua espressione le tensioni di pilotaggio compaiono elevate al quadrato, risulta composto da tre termini: una componente costante, una componente sinusoidale alla frequenza del segnale alternato in ingresso (prima armonica) e una, cosinusoidale, ad una frequenza doppia rispetto a quella della tensione di pilotaggio (seconda armonica). E’ proprio quest’ultima la componente interessante ai fini della nostra misura, come vedremo fra breve.

M

₀,

M

₁ ed

M

₂ sono le ampiezze delle tre componenti suddette del momento; è evidente che

M

₀ è molto maggiore rispetto alle altre due, essendo legata quadraticamente all’ampiezza delle tensioni costanti di pilotaggio

E

₁ ed

E

₂.

Ricordiamo ora le equazioni differenziali che esprimono l’equilibrio dinamico di un sistema meccanico, quale è il nostro dispositivo:

F f

F

= ⋅ +

m z b z K z

⋅ +

⋅

(2.22)

M t

M

= ⋅ +

I

θ

b

⋅ +

θ

K

⋅

θ

(2.23) (dove

m

è la massa,

I

il momento di inerzia,

b

_F e

b

_M gli smorzamenti,

t

K

e

K

_f le costanti elastiche torsionale e flessionale,

z

,

z

e

z

lo spostamento e le sue derivate rispetto al tempo,

θ

,

θ

e

θ

l’angolo di rotazione e le derivate rispetto al tempo) e prendiamo in considerazione la seconda, ossia quella del momento torcente. L’equazione dinamica dello specchio è dunque la seguente:

( )

( )

2 2 1 2 1 2

1

2

M t

C

C

I

θ

b

θ

K

θ

V t

V t

θ

θ

∂

∂





⋅ +

⋅ +

⋅ = ⋅

_

⋅

+

⋅

_

∂

∂





(2.24)

Trasferiamo ora la (2.23) dal dominio del tempo a quello della frequenza:

( )

(

)

2 2

_.

M t M t

M

I

j

b

K

I

j

b

K

ω

ω θ

ω

θ

θ

ω

ω

θ

= − ⋅

⋅ +

⋅

⋅ +

⋅ =

= − ⋅

+

⋅

+

⋅

(2.25)

Sulla base di quest’ultima possiamo scrivere la risposta in frequenza del dispositivo (relativa al momento) come segue:

( )

( )

_{( )}

2 1 2

1

.

1

M t t r r

H

M

I

j

b

K

K

j

Q

θ ω

ω

ω

ω

ω

ω

ω

ω

ω

−

=

=

− ⋅

+

⋅

+

=



 



+

_

_{ }

−

_

⋅



 



(2.26) dove: t r

K

I

ω =

(2.27) t M

K I

Q

b

⋅

=

(2.28)

sono, rispettivamente, la frequenza di risonanza e il fattore di qualità del sistema elettromeccanico.

Abbiamo, dunque, tutti gli elementi per esprimere il valore dell’angolo di torsione dello specchio, il quale è dato istantaneamente dalla seguente relazione:

( )

( )

₍

( )

₎

( )

(

( )

)

( )

(

( )

)

0 1 1 2 0 2

sin

arg

2

cos 2

arg

2

2

cos 2

arg

2

.

t t

M

t

H

M

t

H

K

H

M

t

H

M

_H

_M

_t

_H

K

θ θ

θ

ω

ω ϕ

ω

ω

ω ϕ

ω

ω

ω ϕ

ω





=

+

⋅

⋅

_

+ +

_





+

⋅

⋅

_

+

+

_





+

⋅

⋅

_

+

+

_

(2.29)

In quest’ultima abbiamo trascurato la componente di prima armonica di

θ

, coerentemente con la (2.17) (

ϕ

₁ è lo sfasamento relativo a tale armonica). Si osservi che si sono in tal modo trovate le espressioni di

θ

₀ e

2

θ

, ossia:

( )

0 0 2

2

2 t

M

K

H

M

θ

θ

ω

=

=

⋅

(2.30)

La derivata prima rispetto al tempo di

θ

( )

t

è, di conseguenza (ricordando le espressioni (2.21)):

( )

_{( )}

₍

_{( )}

₎

( )

₍

( )

₎

2 2 2 11 1 2

2

2

sin 2

arg

2

2

M

2

sin 2

arg

2

.

d t

H

M

t

H

dt

C E V

H

t

H

θ

ω

ω

ω ϕ

ω

ω

ω

ω ϕ

ω





= − ⋅ ⋅

⋅

⋅

_

+

+

_





= − ⋅ ⋅

⋅ ⋅

⋅

⋅

_

+

+

_

(2.31)

A questo punto abbiamo quanto necessario per esplicitare l’espressione della corrente

i

₂. Essa assume quindi la forma seguente:

(

)

( )

₍

( )

₎

2 2 2 2 2 2 11 21 1 2 2

2

M

2

sin 2

arg

2

d C V

dC d

i

E

dt

d

dt

C C

E E V

H

t

H

θ

θ

ω

ω

ω ϕ

ω

⋅

= −

= − ⋅

⋅





= ⋅ ⋅

⋅

⋅ ⋅

⋅

⋅

⋅

_

+

+

_

(2.32)

Si osserva ora che la corrente di uscita

i

₂, cioè il segnale elettrico che andremo a misurare, è una sinusoide a frequenza doppia rispetto alla

tensione alternata di pilotaggio posta in ingresso. Il metodo della seconda armonica consiste nella misurazione proprio di questa seconda componente e consente di evitare che i disturbi rendano indistinguibile il segnale utile. Infatti è presumibile che il nostro dispositivo manifesti effetti elettrici parassiti, in particolare una capacità tra i due elettrodi, che diventerebbe un percorso parallelo a quello desiderato (cioè a quello “attraverso” lo specchio) per il passaggio del segnale dalla porta d’ingresso a quella di uscita. Tale segnale parassita si manifesterebbe sull’uscita sotto forma di una tensione sinusoidale a frequenza

ω

, cioè pari a quella dello stimolo in ingresso. E’ dunque evidente come, andando a misurare la componente di

i

₂ a frequenza doppia (

2

ω

), si realizza una separazione tra segnale utile e disturbo, che è quanto ci si è prefissi.

Sottolineamo ora che, come già anticipato, la misura viene effettuata alla frequenza di risonanza, ossia pilotando il dispositivo con un segnale sinusoidale di pulsazione pari alla metà di essa:

2

r

ω

ω =

. Infatti, in corrispondenza di

ω

_r la funzione di trasferimento

H

( )

ω

ha modulo massimo e, di conseguenza, è massima anche l’ampiezza della componente in seconda armonica di

i

₂. La componente di segnale d’uscita in prima armonica risulta, invece, notevolmente smorzata, si può pertanto trascurare: ciò è esattamente quello che si è fatto nella (2.32) e rappresenta il discorso a valle della semplificazione apportata all’espressione dell’angolo di rotazione (2.17).

In conclusione, essendo

( )

r t

Q

H

j

K

ω = −

(2.33) e quindi:

( )

( )

(

)

arg

,

2

r t r

Q

H

K

H

ω

π

ω

=

= −

(2.34) in

2

req

ω

ω =

la (2.32) assume la forma seguente:

2

2

11 21 1 2

sin 2

2

2

2

r M t

Q

i

C C

E E V

t

K

ω

_ω

_{ω ϕ}

π





_{= ⋅ ⋅}

_⋅

_{⋅ ⋅}

_⋅

_⋅

_⋅



₊

₋









_



_





(2.35)

Si osservi che, dalla misura dell’ampiezza di

i

₂ si può risalire al valore dell’angolo

θ

₀ intorno cui si è linearizzato il sistema, dato il legame esistente tra esso e le derivate delle capacità

C

₁ e

C

₂ calcolate proprio in

0

θ

, cioè

C

₁₁ e

C

₂₁ (cnfr. (2.30)).

Come già detto, la corrente che eventualmente si aggiunge alla

i

₂

sopra espressa, a causa della presenza di un collegamento parassita tra ingresso e uscita - rappresentato da una capacità indesiderata tra i due elettrodi -, ha forma sinusoidale e frequenza pari alla tensione di ingresso, cioè alla metà di

ω

_r, per cui non influenza la nostra misura. Ciò perché effettuiamo il rilevamento della corrente d’uscita agganciandoci alla frequenza desiderata per mezzo di un amplificatore lock-in (v.par.3.2).

2.4 Pilotaggio di tensione in regime

dinamico

La caratterizzazione del microspecchio proposto è propedeutica alla implementazione di un sistema innovativo di attuazione in regime dinamico, proposto in letteratura per dispositivi diversi, ma che arrecherebbe grandi vantaggi anche per la nostra applicazione. Per chiarire questo aspetto, accenniamo ai problemi connessi al pilotaggio

statico del microspecchio, e di come questi possano essere superati dall’attuazione dinamica. Presentiamo poi la teoria che è alla base del pilotaggio dinamico, sebbene la sua implementazione per il nostro dispositivo non sia scopo del presente lavoro, in quanto rappresenta un obiettivo futuro di questo studio.

Si è detto che la dinamica angolare del microspecchio è limitata dal

fenomeno del pull-in: aumentando la tensione di pilotaggio si giunge ad

una situzione di non equilibro, in cui forza e momento elettrostatici non riescono a bilanciare forza e momento meccanici, per cui lo specchio collassa sugli elettrodi sottostanti. Si ha, dunque, una tensione massima applicabile

V

_pin, a cui corrisponde una rotazione massima di un angolo

pin

θ

.

Questa osservazione, però, non è sempre valida. Essa, infatti, si basa sul presupposto che si analizzi il comportamento del dispositivo in un

regime quasi-statico, ossia in una condizione in cui la velocità di

variazione della tensione in ingresso è sufficientemente contenuta da permettere al microspecchio di assestarsi di volta in volta in uno stato di equilibrio. Se, invece, pilotiamo il dispositivo meccanico in modo da mantenerlo sempre in regime dinamico, le analisi fatte sul fenomeno del pull-in non sono più applicabili.

La ridotta dinamica angolare rappresenta un grande ostacolo ad un ampio impiego dei microspecchi torsionali, ne segue che la possibilità di pilotarli in modo da abbattere tale vincolo risulta di grandissima importanza.

Il problema è stato affrontato e discusso da L.A.Rocha, E.Cretu,

R.F.Wolffenbuttel [44], i quali hanno – però - preso in considerazione un

dispositivo MEMS differente da quello proposto in questa tesi (in particolare con spostamento lineare anzicché rotazionale). L’analisi risulta comunque valida e adattabile a dispositivi quali i nostri microspecchi torsionali; del resto la loro caratterizzazione, oggetto di questa tesi, rappresenta una fase preliminare all’utilizzo degli stessi in regime dinamico esteso. Presentiamo pertanto qui di seguito lo studio teorico e i risultati pratici ottenuti da Rocha e i suoi collaboratori.

2.5 Pilotaggio dinamico in un attuatore

elettrostatico a piatti piani e paralleli: studio di

L.A.Rocha et al.

2.5.1 Modello dinamico

Il dispositivo micromeccanico cui si fa riferimento è costituito da una trave planare, lungo la cui estensione sono connessi i piatti mobili di una struttura a condensatori interdigitati. La parte statica degli stessi è invece collegata al substrato. La trave è sospesa tramite molle a serpentina collocate ai due estremi. I condensatori interdigitati sono raccolti in tre gruppi: quello centrale costituisce l’elemento di attuazione; quelli laterali sono impiegati per la rilevazione della posizione. La presenza di questi elementi di sensing sarà spiegata meglio in seguito. Ovviamente la trave e gli elettrodi mobili costituiscono nel complesso il rotore della struttura, mentre gli elettrodi connessi al substrato costituiscono i due statori, rispettivamente sul lato sinistro e destro del rotore. In fig.2.13 è possibile vedere lo schema del dispositivo adottato.

Tutti i sistemi elettromeccanici, come già visto, sono descritti tramite equazioni differenziali che prendono in considerazione le varie forze agenti e stabiliscono un equilibrio tra esse. Si ha, quindi (trascurando l’effetto della temperatura, che si può supporre costante):

m b k elec

F

+

F

+

F

=

F

(2.36) cioè 2

1

2

F f

C

m x b x K x

V

x

∂

⋅ + ⋅ +

⋅ = ⋅

⋅

∂

(2.37)

dove

m

è la massa,

b

_F lo smorzamento,

K

_f la costante elastica flessionale,

x

,

x

e

x

lo spostamento e le sue derivate temporali.

Figura 2.13 Schema del microattuatore elettrostatico a piatti piani e paralleli

Nel sistema di pilotaggio che andremo ad illustrare riveste un ruolo importante il fenomeno dello smorzamento. Osserviamo, infatti, che tra i piatti dei condensatori è presente un isolante (nel nostro caso l’aria), quindi, fuorché non si adoperi il dispositivo sempre e solo nel vuoto, occorre considerare la resistenza che il gas oppone al movimento della microstruttura. Per descrivere tale fenomeno si fa ricorso all’equazione di Reynold [45]. Senza scendere troppo nel dettaglio riguardo alla modellazione di tale smorzamento, riportiamo solo la soluzione proposta da T.Veijola, A.Kuisuma, J.Lahdenpera [46]. Il loro modello comporta che si calcoli la forza di smorzamento complessivo come il risultato degli effetti di una rete di smorzatori a molla indipendenti dalla frequenza. Ciascuno di questi elementi è stato poi rappresentato dal suo equivalente elettrico, cosicché la forza di smorzamento per ampi spostamenti risulta modellata come una serie di induttanze non lineari e di resistenze, controllate dallo spostamento

x

. Ovviamente, anche la distanza tra le armature è espressa

in funzione di

x

:

d x

( )

=

d

₀

−

x

, con

d

₀ distanza iniziale. Poiché ciascuno di tali gruppi R-L si comporta come un sistema del primo ordine con guadagno variabile e una certa costante di tempo, la forza di smorzamento totale può essere espressa some la somma di varie componenti chiamate

F

_{m n,} , dove

m

ed

n

sono numeri dispari.

L’equazione (2.36) acquisisce quindi la forma:

, ,

.

m m n k elec m n

F

+

∑

F

+

F

=

F

(2.38) Di conseguenza si ha:

( )

2 , ,

1

1

2

m n m n

x y

y

F

k x

C x V

m

=





= − ⋅

_

+ ⋅ − ⋅

⋅

_



∑



(2.39)

Per le espressioni delle resistenze e induttanze equivalenti dei vari elementi smorzatori, delle relative componenti di forza

F

_{m n,} , nonché degli altri paramentri di interesse, si rimanda al testo di riferimento [].

2.5.2 Diagrammi dello spazio delle fasi

Una volta realizzato il modello come sopra descritto, si passa a tracciare i diagrammi dello spazio delle fasi: in essi vengono graficate le

traiettorie in termini di variabili di stato, distinte sulla base delle condizioni iniziali. Per le microstrutture le variabili di stato prese in considerazione

sono lo spostamento

x

e la velocità

y

. Lo spazio delle fasi è dunque bidimensionale, con le

x

sull’asse delle ascisse e le

y

su quello delle ordinate. Per tracciare tali diagrammi è necessaria l’equazione non lineare del moto, ossia la (2.39), la quale, in seguito ad alcune semplificazioni che non riferiamo in questa sede, può essere riscritta nella forma seguente:

(

0 0

)

2 2

( )

0 02 0

1

2

x y

C d

y

V

y

x

Q x

m d

x

ω

_ω

=

⋅

= ⋅

⋅

−

⋅ −

⋅

⋅

−

(2.40)

dove:

C

₀ è la capacità iniziale, ossia per spostamento nullo; ₀

k

m

ω =

è la frequenza di risonanza naturale del sistema,

( )

( )

k m

Q x

b x

⋅

=

è il fattore di qualità. Il coefficiente di smorzamento

b x

( )

è calcolato tenendo conto che il braccio mobile, ossia il piatto facente parte del rotore, è collocato tra due elettrodi fissi, connessi ai due statori, per cui si devono considerare due distinti strati di gas. In particolare si avranno uno spostamento destro e uno sinistro, definiti come segue:

( )

( )

00

,

,

s d

d x

d

x

d x

d

x

=

−

=

+

(2.41)

(dove

d

₀ è la distanza iniziale tra le armature) e, di conseguenza, un coefficiente di smorzamento non lineare composto di due termini ad essi relativi:

( )

_s

( )

_d

( )

.

b x

=

b x

+

b x

(2.42)

Normalizzando poi

x

,

y

e

V

, si ottiene una forma più generale della (2.40), cioè:

(

)

( )

2 0 2 0 2 0 2 0

1

2

n n pin n n n n

x

y

C V

y

V

y

x

Q x

m d

x

ω

_ω

=

⋅

= ⋅

⋅

−

⋅ −

⋅

⋅

−

(2.43)

I parametri importanti sono il fattore di qualità,

Q

, e la tensione applicata (normalizzata rispetto alla

V

_pin),

V

_n, per cui si tracciano i

diagrammi di fase per differenti valori di tali parametri, in modo da descrivere il comportamento dinamico non-lineare del generico dispositivo micromeccanico. Si osservi a tal proposito che la derivata di

y

_n dipende quadraticamente dalla tensione

V

_n e inversamente dal fattore di qualità.

Nella fig.2.14 sono riportati alcuni di tali diagrammi dello spazio delle fasi. La curva nera spessa rappresenta la linea di pull-in, ossia il confine tra la regione in cui il sistema si trova in una condizione di stabilità e quella in cui, invece, si ha instabilità. Le traiettorie rappresentano le possibili evoluzioni del sistema in funzione delle due variabili di stato

x

_n ed

y

_n, a partire da determinate condizioni iniziali. Si rileva che tutte le traiettorie per le quali tali valori di partenza si trovano nel cosiddetto bacino di attrazione (evidenziato nei grafici con il colore grigio) tendono a convergere verso il punto di equilibrio, mentre le altre divergono e portano, di conseguenza, al collasso dell’armatura mobile sul contro-elettrodo.

Sottolineamo che, mentre nella convenzionale analisi di pull-in statico i parametri di interesse sono la tensione per la quale si verifica la perdita della condizione di stabilità (

V

_pin) e il massino spostamento possibile (

x

_pin), nell’analisi di pull-in dinamico sono tre gli elementi importanti: 1) il moto descritto dalla parte mobile del dispositivo; 2) il tempo che essa impiega per scontrarsi con l’elettrodo statico; 3) le condizioni dinamiche che inducono la perdita della stabilità.

Dall’ispezione dei diagrammi in fig.2.2 risulta che si può verificare il collasso della struttura anche per valori di tensione inferiori a

V

_pin; ma anche che, allo spostamento pari al valore del pull-in statico (

1

3

n

x

=

), il sistema può trovarsi ancora nel bacino di attrazione: ciò dipende dai valori di

y

_n,

Q

e

V

_n. Ci si trova, dunque, in una situazione molto diversa rispetto a quella dello studio classico del pull-in statico.

In generale, come si può anche osservare dal confronto dei diagrammi riportati, per valori bassi del fattore di qualità (

Q

<

0.5

) il bacino di attrazione è più grande rispetto ai casi di

Q

elevati, circostanze nelle quali le oscillazioni che si vengono ad avere contribuiscono alla perdita

Figura 2.14 Diagrammi dello spazio delle fasi per un generico dispositivo MEMS a piatti piani e paralleli: (a) Q=0.5, Vn=0.5; (b) Q=0.5,

Vn=1.2; (c) Q=5, Vn=0.5; (d) Q=5, Vn=0.95

Il fatto che il diagramma dello spazio delle fasi vari con la tensione di pilotaggio indica che la struttura può spostarsi dinamicamente da una traiettoria stabile ad una instabile (o viceversa) semplicemente cambiando (nel tempo) la tensione applicata.

2.5.3 Spostamento con pilotaggio dinamico

Dall’analisi dei diagrammi dello spazio delle fasi condotta nel paragrafo precedente, si conclude che un punto di tale spazio collocato nella regione di instabilità può essere raggiunto senza incorrere nella perdita della stabilità da parte del sistema. Affinché ciò avvenga è necessario che il dispositivo sia pilotato in maniera dinamica con una tensione alternata avente:

o un’ampiezza sufficiente affinché, quando essa raggiunge il punto

di massimo, il sistema possa uscire dal bacino di attrazione;

o una velocità di variazione (quindi una frequenza) maggiore dei tempi di reazione della struttura, in modo che la traiettoria possa rientrare nella zona di attrazione prima che il dispositivo percepisca la variazione dello stato (da stabile ad instabile).

Gli autori dello studio che stiamo qui esponendo hanno realizzato delle simulazioni per verificare la validità dell’analisi teorica. Ad esempio, è stata presa in considerazione una tensione di pilotaggio sinusoidale di ampiezza pari a

5.04V

e frequenza di

400Hz

. I risultati sono mostrati nel grafico in fig.2.15 e indicano che, in effetti, sebbene la tensione e lo spostamento di pull-in statico siano stati superati, la struttura non è incorsa nel fenomeno del pull-in.

In conclusione, nel lavoro qui esposto, Rocha sostiene la tesi (avvalorata da opportune simulazioni) che sia possibile realizzare un dispositivo attuato elettricamente a piatti piani e paralleli, pilotato con una tensione alternata di ampiezza e frequenza opportune, che realizzi un movimento che includa la regione dello spazio tra le armature usualmente considerato inaccessibile a causa del fenomeno del pull-in. Si tratta però di un sistema in catena aperta, il quale consente sì di effettuare uno spostamento oltre il limite imposto dal pull-in statico, ma non di trovarvi una posizione di stabilità.

Figura 2.15 Risultati della simulazione per una tensione sinusoidale a 400Hz

Un risultato migliore può essere raggiunto tramite un sistema ad anello chiuso, che raccolga informazioni circa la posizione.

2.5.4 Attuazione dinamica in anello chiuso

Dati i risultati ottenuti è auspicabile realizzare un sistema tale non solo che lo spostamento dell’armatura mobile del condensatore possa aver luogo fin nella zona proibita dalla teoria del pull-in statico, bensì anche che – pur con un pilotaggio quale quello spiegato - si trovi in una condizione di stabilità (che possiamo definire stabilità dinamica). Rocha e i suoi collaboratori hanno indagato anche questa possibilità: vediamone i concetti salienti.

L’idea di base è quella di confrontare la posizione istantanea della struttura mobile, misurata, con una di riferimento, che rappresenta quella desiderata. La tensione di attuazione applicata si fa variare – in accordo con il risultato del suddetto confronto - tra due valori: un livello alto (superiore alla tensione di pull-in statico

V

_pin), se la distanza istantanea tra le armature è inferiore a quella voluta; un livello basso (inferiore a

V

_pin), se

tale distanza supera quella posta come riferimento. (In fig.2.16 è rappresentato uno schema a blocchi del sistema ad anello chiuso che stiamo illustrando.) Per implementare questa tecnica è, dunque, necessario che la misura della posizione dell’armatura mobile sia effettuata piuttosto rapidamente. Il dispositivo presentato nel lavoro cui ci stiamo riferendo (descritto nel paragrafo 2.5.1) è dotato di due blocchi di capacitori interdigitati impiegati, per l’appunto, nel rilevamento di tale posizione.

Figura 2.16 Diagramma a blocchi del sistema ad anello chiuso

Appena si mette in funzione il dispositivo si impone una tensione di ampiezza superiore a quella per cui si ha il pull-in statico: ciò fa sì che la microstruttura raggiunga la posizione desiderata. Giunta in tale condizione, poiché la tensione è ancora applicata, l’armatura tende ad avvicinarsi ulteriormente al controelettrodo. A tal punto il sistema di misura rileva l’eccesso di spostamento e induce il circuito di controllo a commutare, cioè a posizionarsi sul livello basso di tensione. Ne segue che la struttura mobile reagisce allontanandosi dall’elettrodo statico, fino a tornare nella posizione desiderata e superarla: questo comporta che il circuito di controllo, in seguito al rilevamento effettuato dal sistema di misura, commuti nuovamente sul livello alto di tensione. Tale ciclo si ripete così ininterrottamente. E’ quindi evidente come un pilotaggio che comporta un continuo processo di uscita e rientro da una situazione di

stabilità (secondo la teoria del pull-in statico) permetta di determinare uno stato di equilibrio dinamico.

Naturalmente, per un sistema siffatto sono particolarmente critici i tempi di ritardo che, inevitabilmente, si hanno nella commutazione e nel rilevamento dello spostamento. La commutazione infatti, come è noto, non avviene istantaneamente (come si assume a livello teorico-ideale), bensì in un tempo nonnullo; durante tale processo la struttura prosegue nel suo movimento, cosicché si viene ad avere uno spostamento aggiuntivo rispetto a quello di riferimento. Ciò provoca un’oscillazione intorno alla posizione desiderata, la cui entità è ovviamente proporzionale al tempo impiegato dal circuito per effettuare la commutazione. Analogo problema si ha nella catena di reazione; è, infatti, abbastanza probabile che si accumuli un ritardo tra l’istante in cui il blocco di condensatori di sensing rilevano il superamento della posizione impostata e quello in cui viene disposta la commutazione. Si tratta chiaramente di ritardi dovuti alla struttura fisica dei componenti del circuito, che hanno tempi di reazione non sempre trascurabili nell’ambito di applicazioni quali quella qui descritta, in cui la velocità di azione è determinante.

In fig.2.17 è possibile vedere l’andamento simulato dello spostamento, intorno alla posizione desiderata, in seguito all’azione del controllo ad anello chiuso sopra spiegato, nel caso di ritardo del sistema di

15

. Il riferimento di posizione è configurato al valore 1.5 (esso indica la distanza dal controelettrodo alla quale si vuole che l’armatura mobile del condensatore si collochi); i livelli di tensione imposti sono :

V = 4V

_high e

low

V = 2V

; la tensione teorica di pull-in statico per il dispositivo simulato è

pin

V =3.820V

. A

2

dalla posizione di partenza dell’elettrodo superiore (in una distanza complessiva tra le armature di

2.25

) sono collocate delle strutture di blocco. Esse svolgono la funzione di frenare il movimento dell’armatura dopo il raggiungimento del pull-in, per impedire il verificarsi di un corto-circuito elettrico.