Meccanica Capitolo4

Meccanica

In questo capitolo verranno trattati gli aspetti meccanici dell’azionamento. Nella prima sezione si presenta l’impianto meccanico e le relative criticit´a. La successiva sezione sar´a dedicata al calcolo dell’inerzia dove si ipotizza di non conoscere la geometria e la massa del carico meccanico posto in rotazione dalle due macchine, perci´o nel calcolo sar´a inclusa solo la quota relativa al rotore di una macchina.

4.1

Stress meccanici

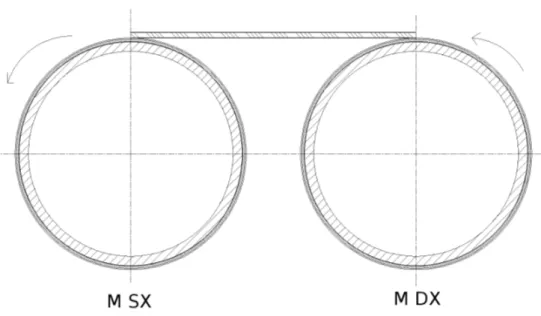
L’azionamento ´e composto da un complesso di due macchine le quali si trovano con i rotori connessi per mezzo di parti meccaniche. Risulta de-terminante evitare che ci siano asincronismi nella rotazione pena l’aumento di tensioni nelle connessioni. In figura 4.1 si riporta lo schema meccani-co dell’azionamento. In questa fase si vuol dare un’indicazione di massima sull’applicazione. Non si entra nel merito delle specifiche meccaniche. Per quanto riguarda le connessioni, sono comunque da ritenere ragionevolmente elastiche, ma ´e vietato qualunque stress che porti a deformazioni plastiche.

Sotto le ipotesi di:

1. Materiale in campo elastico. 2. Materiale duttile.

3. Connessioni con dimensione longitudinale molto maggiore delle tra-sversali.

4. Mancato slittamento delle connessioni rispetto alla superficie cilindrica di rotore.

5. Stato di tensione monoassiale.

La tensione che si svilupper´a nelle connessioni meccaniche sar´a correlabile alla differenza tra le due coppie motrici, quindi della posizione.

CAPITOLO 4. MECCANICA

Figura 4.1: Schema meccanico di principio dell’azionamento

Per quantificare lo stato di stress si introduce la grandezza riportata nella 4.1:

Δθm= θmSX − θmDX (4.1)

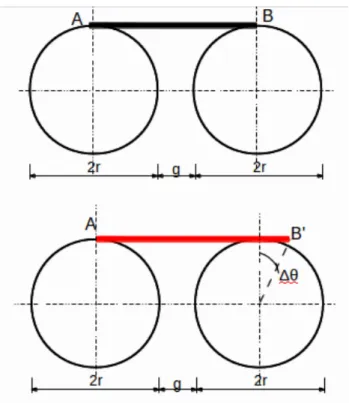
Si ipotizza di trovarsi in presenza di un disturbo tale da far rallentare il motore di destra. In figura 4.2 si rappresenta l’azionamento che risulta essere sincrono al tempo t=0, ma dopo l’azione del disturbo si genera un Δθm.

Data la geometria in figura 4.3 si pu´o calcolare l’allungamento Δl a partire dai dati sulla distanza fra gli assi.

La soluzione rigorosa ´e riportata nella 4.2 e 4.3. tan γ = r l −rlcos(Δθm) 1 +r_lsin(Δθm) = 1_l− cos(Δθm) r + sin(Δθm) (4.2) AB� ₌ 1 cos γ(l + r sin Δθm) (4.3)

Sotto l’ipotesi (frequentemente verificata nelle simulazioni) che γ sia piccolo si pu´o considerare la proiezione ortogonale al posto che riportare il segmento AB� _{con un arco di cerchio, giungendo alla soluzione approssimata riportata}

nella 4.4. Δl = r_{· sin Δθ}m =⇒ Δl l = r_{· sin Δθ}m 2r + g (4.4)

Uno degli obiettivi richiesti all’azionamento ´e quello di muovere le macchine in maniera sincrona, perci´o risulteranno dei Δθm relativamente piccoli, tali

Figura 4.2: Scenario ipotizzato per la valutazione dello stress

CAPITOLO 4. MECCANICA da poter dire: Δl l ≈ rΔθm 2r + g (4.5)

Per ottenere il massimo Δl_l tollerabile dalla connessione si introducono le relative caratteristiche meccaniche:

� Sezione S = 520mm2 � Tensione di rottura Fb = 160000N � Modulo di elasticit´a E = 105000 N mm2 rΔθm 2r + g ≈ Δl l = Fb E_{· S} = 160_{· 10}3 1.2_{· 105000 · 520} = 2.5· 10 −3 _{= 0.25% (4.6)}

N.B Nella 4.6 si ´e introdotto un coefficiente di sicurezza del 20% per distan-ziarsi dalla regione di deformazione plastica.

Dalla 4.6 si mette in evidenza la necessit´a di avere un controllo accurato e puntuale che limiti l’allungamento, causa principe di eventuali deformazioni plastiche.

In generale i materiali duttili sono simmetrici, in quanto presentano un com-portamento in compressione molto simile a quello di trazione. Di conseguen-za l’analisi fatta in precedenconseguen-za, dalla quale si ottengono i criteri per evitare di uscire dalla regione elastica, si applica anche agli stati compressi.

4.2

Calcolo momento d’inerzia

Nota la geometria della macchina dal dimensionamento statico si provvede al calcolo del momento di inerzia. Il calcolo ´e stato condotto assumendo le seguenti ipotesi:

1. Macchina funzionante in condizioni di temperatura costante, pari alle condizioni standard alle quali sono note le densit´a dei materiali. 2. Si adottano le dimensioni geometriche di progetto trascurando

even-tuali dilatazioni termiche radiali. 3. Corpo rigido

Per il calcolo, si utilizza la formula per ricavare il momento di inerzia di cilindri cavi che ruotano attorno al proprio asse.

J = 1 8M

�

D_e2+ D_i2� (4.7)

Per primo si procede alla determinazione delle masse rotanti per poi passare alle grandezze geometriche.

La parte in movimento ´e un cilindro cavo con spessore sottile. Il complesso rotore ´e composto da:

Figura 4.4: Disegno di massima della sezione assiale della macchina � Magneti permanenti (descrizione materiale in appendice)

� Giogo di rotore ( Descrizione materiale in appendice) � Supporto

Dal dimensionamento statico, non ´e nota la massa del supporto. Quest’ul-timo non ´e necessario che sia realizzato con materiali ferromagnetici, non facendo parte del circuito magnetico. In prima battuta verr´a trascurato e successivamente confrontato, con l’ipotesi che tale supporto venga realizzato con acciaio da costruzioni. 1

La massa in movimento vale:

M_r∗ = Mlamr+ Mmag= 75 + 72 = 147kg (4.8)

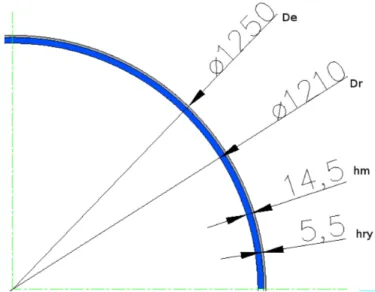
Dalla figura 4.4 si ricavano le grandezze geometriche rilevanti:

Dr= De+ 2hm+ 2hry = (1250− 29 − 11) = 1210mm. (4.9)

Infine si calcola il momento di inerzia di un cilindro cavo. J_r∗ = 1 8 · M ∗ r � De2+ Dr2 � = 55.61· 106kg· mm2= = 55.61_{· 10}6kg_·�m_{· 10}−3�2 = 55.61kg_{· m}2 (4.10) Si confronta questo risultato con quello che si avrebbe ipotizzando un sup-porto di acciaio.

Nota la geometria, si calcola il volume e successivamente la massa.

Dis = (De− 2 · hry) = 1239mm. (4.11)

1_{Densit´a acciaio in condizioni standard ρ = 7900}kg m3

CAPITOLO 4. MECCANICA Vs = � D2_{e− D}is2 � π 4 · la= � 12502_{− 1239}2� π 4360 = 7.741· 10 6_mm3 _(4.12)

Moltiplicando la densit´a per il risultato della 4.12 si ottiene: Ms = Vs· ρacciaio = 7.741· 106· (m · 10−3)3· 7900

kg m3 =

= 7.741_{· 10}−3_{· 7900 = 61kg (4.13)} A questo punto si pu´o calcolare la nuova massa

Mr= Mr+ Ms= 208kg (4.14)

Utilizzando la 4.10 si calcola il nuovo valore del momento di inerzia Jr= 1 8 · Mr � De2+ Dr2 � = 78.69· 106kg· mm2 = 78.69_{· 10}6kg_·�m_{· 10}−3�2 = 78.69kg_{· m}2 (4.15) Confrontando i due valori si conclude che la differenza tra i due ´e :

J_r∗− Jr

J∗ r

=−0.415 (4.16)

ovvero circa il 42 % .

Si assume come momento di inerzia Jr = 78.7kg· m2.

Parole chiave