IMAGING IN RISONANZA MAGNETICA

Capitolo 1

IMAGING IN RISONANZA

MAGNETICA

1.1

La Tecnica di Imaging in Risonanza Magnetica

L’Imaging in Risonanza Magnetica (MRI –Magnetic Resonance Imaging) è una moderna1 e potente tecnica diagnostica per immagini, la quale offre notevoli vantaggi rispetto ad altre tecniche (radiografia, ecografia, TAC). Infatti:

• non richiede l’esposizione del paziente a radiazioni ionizzanti, ed è per questo che può essere considerata una tecnica sicura2;

• consente di ottenere immagini ad elevata risoluzione non solo del piano trasversale del corpo (come avviene per la Tomografia Assiale Computerizzata, TAC), ma anche relativamente a sezioni posizionate su un qualunque piano ( ad esempio sezione sagittale e frontale) ottimizzando così la visualizzazione dell’area corporea.

1 _{Le prime applicazioni cliniche sull’uomo risalgono al 1981,in Italia al 1985.}

2 _{Ci sono, però, considerazioni importanti in merito alla sicurezza che riguardano, in particolar modo, i} forti campi magnetici utilizzati (esistono misure cautelative a cui lo staff medico deve attenersi) e l’energia di radiofrequenza (esistono valori limite di riferimento indicati dalla USFDA sull’esposizione a un’energia di RF. Viene considerato, a riguardo, un coefficiente detto SAR, rate di assorbimento specifico misurato in [Watt/Kg], diverso a seconda del distretto anatomico in esame e tale da non far alterare la temperatura corporea di più di un grado Celsius) [11].

Questa tecnica svolge dunque un ruolo importante in ambito medico, pertanto si può presupporre che in futuro subisca ulteriori sviluppi, per lo più mirati alla progettazione di apparecchiature per organi specifici [1,2,3,5,6].

L’MRI si basa sul fenomeno della risonanza magnetica nucleare (NMR –

Nuclear Magnetic Resonance), attraverso il quale è possibile ricostruire

l’immagine diagnostica desiderata (essenzialmente una mappa rappresentativa della distribuzione di densità dei nuclei di idrogeno e dei parametri che riflettono il loro movimento nei liquidi cellulari e nei grassi) valutando l’effetto, o più in particolare i tempi necessari per ripristinare lo stato iniziale, della perturbazione indotta da onde elettromagnetiche della gamma delle radiofrequenze (RF) su di un sistema i cui nuclei atomici siano immersi in un campo magnetico statico notevolmente intenso.

Un limite della MRI, le cui unità presenti nel mondo sono comunque stimate essere circa 10000 (stima effettuata nel 2003), è il costo ancora elevato unito al fatto che questa tecnica richiede un personale specializzato in più discipline nonché una continua ed accurata manutenzione delle apparecchiature. Inoltre la NMR è controindicata per pazienti portatori di pace-maker cardiaci o di protesi dotate di circuiti elettronici, di clips vascolari o schegge di materiale ferromagnetico [4,6,11].

1.2

Principi della Risonanza Magnetica Nucleare

Il fenomeno fisico della risonanza magnetica nucleare fu scoperto nel 1946 da Bloch e Purcell e consiste, quando siano verificate certe condizioni, nell’emissione, da parte del sistema di nuclei di un dato campione biologico, di segnali elettromagnetici a una frequenza pari alla frequenza di risonanza per il sistema di nuclei stesso. Esso si verifica quando il

campione, posto in un campo magnetico statico sufficientemente intenso ed omogeneo B0, viene irradiato mediante un campo magnetico a

radiofrequenza B1, che giace su di un piano perpendicolare al primo, e che

ha una frequenza pari a quella di risonanza per il sistema di nuclei.

Tale fenomeno fisico si basa sul fatto che certi nuclei, quando vengono posti in un campo magnetico statico, possono assumere uno fra due possibili stati caratterizzati rispettivamente da un alto ed un basso livello energetico; la differenza di energia fra i due stati è linearmente proporzionale all’intensità del campo magnetico applicato (effetto Zeeman). All’equilibrio termico il numero di nuclei nello stato ad alta energia è lievemente inferiore al numero di nuclei che si trovano nello stato a bassa energia. Quando questi vengono irradiati con campi elettromagnetici (fotoni) ad una specifica frequenza, generati da bobine a radiofrequenza (RF), una frazione dei nuclei che si trovano a bassa energia assorbono energia fornita dal campo RF e saltano allo stato ad alta energia; questo fa sì che l’equilibrio termico venga distrutto. Pertanto, non appena terminata l’irradiazione, i nuclei in eccesso nello stato ad alta energia tendono a tornare in quello a bassa energia per ripristinare l’equilibrio del sistema emettendo, sotto forma di campo elettromagnetico RF, l’energia che avevano acquisito.

In particolare, come rivela la moderna meccanica quantistica, certi3 nuclei atomici possiedono una proprietà conosciuta come spin, la quale è definita come momento angolare intrinseco delle particelle che costituiscono il nucleo, e nel modello classico viene visualizzata come una rotazione fisica simile alla rotazione attorno al proprio asse [10]. I nuclei, infatti, sono

3 _{Quei nuclei caratterizzati da un numero atomico o da un numero di neutroni dispari, come dimostra il} principio di esclusione di Pauli (il momento angolare di ciascun protone, quando il loro numero è pari, deve assumere stato di spin opposto a quello dell’altro protone per evitare che ci siano degenerazioni).

costituiti da protoni e neutroni, che possono essere pensati come piccole sfere elettricamente cariche ruotanti a grande velocità attorno al proprio asse. Poiché cariche elettriche in movimento generano campi magnetici, intorno a tali nuclei è presente un campo magnetico. Questi nuclei si comportano quindi come piccoli magneti, ed i deboli campi magnetici che generano originano dei momenti magnetici. Il rapporto tra il momento magnetico e il momento angolare della rotazione viene detto rapporto giromagnetico ed assume valori caratteristici per ogni tipo di nucleo [1]. Attualmente la quasi totalità dell’imaging RM (imaging di Risonanza Magnetica) è impostata sul segnale proveniente dai nuclei di idrogeno, anche se è allo studio l’impiego di altri nuclei atomici. Il nucleo dell’idrogeno non ha neutroni ed è costituito da un solo protone; fra i vari nuclei questo è il più adatto ad essere preso in considerazione per uno studio di risonanza magnetica poiché è presente in grande abbondanza nel corpo umano, sotto forma di acqua (il corpo è costituito per il 70% da acqua) e legato chimicamente a formare zuccheri, grassi e proteine, ed inoltre è dotato di un rapporto giromagnetico ottimale (42,58 MHz/T).

Prima che venga applicato il campo magnetico statico B0 i nuclei del

materiale campione sono orientati casualmente, avendo così un momento magnetico risultante netto pari a zero. Non appena viene applicato questo campo magnetico (generalmente orientato secondo la direzione longitudinale, indicata dall’asse z) ogni singolo momento magnetico si orienta secondo la direzione del campo principale con verso ad esso parallelo (up) o antiparallelo (down), in dipendenza dei due livelli energetici menzionati [1,7]. Essendo la popolazione dei nuclei up superiore a quella dei nuclei down, otteniamo una risultante nel verso del campo magnetico principale detta magnetizzazione longitudinale M0.

In realtà i nuclei non sono esattamente allineati secondo la direzione dell’asse z; infatti, oltre al moto intrinseco di rotazione intorno all’asse nucleare, i nuclei sono soggetti ad un movimento di precessione intorno alla direzione del campo magnetico principale, intendendo con questo termine il movimento relativamente lento compiuto dall’asse di un corpo in rotazione attorno alla superficie di un cono ideale, come descritto in fig. 1.1

Fig.1.1 - Precessione dei nuclei

La velocità e la frequenza di precessione sono proporzionali all’intensità del campo magnetico principale B0 (costante della particolare macchina)

secondo l’equazione di Larmor: ω0 =γB0.

L’energia di eccitazione da fornire ad un nucleo per portarlo dalla configurazione energetica minima a quella massima è fornita dall’equazione di Planck: E= hω0 dove h è la costante di Planck divisa per

2π . Fornendo ai nuclei questa energia, mediante un campo magnetico a radiofrequenza (RF), i protoni vengono eccitati, dopo di che tendono a tornare nello stato di minima energia (magnetizzazione netta con direzione parallela al campo statico B0) emettendo un segnale a radiofrequenza alla

frequenza ω0 (segnale FID – Free Induction Decay) che viene captato

mediante un’antenna posta perpendicolarmente alla direzione del campo statico (bobina RF di ricezione).

Come conseguenza di ciò abbiamo la possibilità di perturbare i nuclei mediante un campo magnetico a radiofrequenza B1, trasversale rispetto

all'asse longitudinale e oscillante ad una frequenza esattamente corrispondente a quella di precessione dei nuclei di idrogeno [1].

In funzione della durata dell’applicazione del campo a radiofrequenza, avremo un maggiore o minore assorbimento di energia da parte dei nuclei e una conseguente variazione della magnetizzazione longitudinale e trasversa. Una volta esaurita la fase di eccitazione a RF la magnetizzazione totale tende ad orientarsi lungo l’asse z, come evidenziato in fig. 1.2, per ripristinare il valore di equilibrio M0, e la componente del momento

magnetico nel piano x-y decade esponenzialmente (decadimento trasversale) con un tempo di “rilassamento” T2; simultaneamente anche la

componente lungo l’asse z del momento totale tende ad allinearsi alla posizione di equilibrio lungo quest’asse, subendo anch’essa un decadimento esponenziale (decadimento longitudinale) con tempo di “rilassamento” T1.

Quindi, i tempi di rilassamento T2 e T1 rappresentano, rispettivamente, il

tempo che regola l’annullarsi della magnetizzazione traversa creata da un un impulso a RF (esprimibile matematicamente come tempo necessario all’annullamento del 63% di tale magnetizzazione), e il tempo che regola il ripristino della magnetizzazione longitudinale dopo un impulso RF, che matematicamente è il tempo necessario al recupero del 63% del valore globale di tale magnetizzazione. A prima vista i due fenomeni potrebbero sembrare legati da una proporzionalità inversa, in realtà il recupero della

magnetizzaione longitudinale è generalmente più lungo del decadimento di quella trasversa e quindi in generale T1 è maggiore di T2; ciò dipende

principalmente dalla struttura molecolare nella quale si trovano i protoni (T1

e T2 risultano uguali solo nei liquidi puri).

Fig. 1.2 - Effetto dell'eccitazione ad RF

Riassumendo, al cessare dell’impulso RF di interrogazione il sistema protonico si trova in situazione di instabilità e l’energia in sovrappiù viene ceduta attraverso i tessuti circostanti, che la riemettono sottoforma di un segnale detto FID (Free Induction Decay), il quale ha un’ampiezza determinata dalla cosiddetta densità protonica (quantità di protoni di idrogeno risonanti per unità di volume di tessuto, che aumenta con l’aumentare dell’intensità del campo magnetico B0, poiché in tal caso la

probabilità di allineamento dei protoni nella direzione del campo sarà più elevata) ed una durata regolata da T2 e T1.

I processi di rilassamento svolgono quindi un ruolo fondamentale in questo genere di tecnica. Infatti, variazioni nei tempi di rilassamento tra tessuti

biologicamente diversi forniscono la chiave per evidenziare i contrasti per discriminazioni anatomiche, in quanto il decadimento del segnale nel tempo dipende dall’ambiente molecolare in cui i nuclei si trovano.

Inoltre, la differenza tra i tempi di rilassamento misurati e quelli di riferimento fornisce un potente meccanismo per la rivelazione di patologie; per esempio, i tempi di rilassamento magnetici nucleari dei tessuti sani sono differenti da quelli dei tumori (come dimostrato nel 1971 da Raymond Damadian).

1.3

L’Hardware in MRI

I componenti fondamentali di un sistema di imaging a Risonanza Magnetica Nucleare sono mostrati in fig. 1.3, in cui sono evidenziate le parti principali [1].

Il magnete viene utilizzato per fornire il campo magnetico statico uniforme

0

B . Tale condizione di uniformità è di fondamentale4 importanza, in quanto consente di allineare parallelamente tutti i magneti nucleari presenti nel volume da esaminare. In realtà, raramente il magnete principale produce un campo sufficientemente uniforme da solo. Per questo motivo spesso, nella pratica, viene utilizzato un set di bobine, dette shim-coils, progettate per produrre un campo, polarizzato nella stessa direzione del campo principale e di note dipendenze spaziali, in modo che , note le disomogeneità del campo prodotto dal magnete principale, siano in grado di compensare queste non uniformità attraverso appositi gradienti. Le disomogeneità del campo principale sono, però, generalmente difficili da caratterizzare e

4 _{se tale condizione venisse meno, i protoni del campione in esame, non trovandosi sottoposti alla stessa} intensità di campo magnetico, non risentirebbero tutti dell’impulso RF applicato (non precedendo così tutti alla stessa frequenza di risonanza), dando come risultato un’immagine di scarsa qualità.

quindi spesso vengono usate procedure empiriche dirette per aggiustare le shim-coils.

I magneti rappresentano il componente più costoso del sistema di imaging a risonanza magnetica e possono essere: resistivi (in grado di fornire campi con un’intensità che va da 0.05T a circa 0.4T) o a superconduttore (in grado di fornire campi con intensità maggiori di 0.5T). E’ quasi sempre nell’interesse del progettista che il campo principale sia alto e quanto più possibile ”economicamente realizzabile”. Oggi vengono per lo più impiegati magneti a superconduttore che producono un campo magnetico di 1T o 1.5T.

I gradienti modificano il campo magnetico B0, facendo oscillare le regioni

del volume in esame ciascuna ad una propria frequenza. In questo modo il segnale emesso da un punto dipende in modo univoco dalla sua posizione nello spazio e pertanto si possono ottenere informazioni sulla localizzazione spaziale.

Vengono utilizzati tre gradienti, uno per ogni direzione del sistema di coordinate e sono ottenuti con apposite bobine. Inoltre il gradiente di campo magnetico utilizzato è lineare in modo che il campo e la frequenza risultante siano variabili linearmente con la distanza lungo l’oggetto in esame. Con l’utilizzo del gradiente di campo magnetico si ottiene che la frequenza di risonanza nei piani perpendicolari alla direzione del gradiente è costante: in questo modo, nell’analisi dello spettro del segnale ricevuto l’ampiezza spettrale di una particolare frequenza corrisponde direttamente al contributo nel segnale di tutti i nuclei giacenti in un piano perpendicolare alla direzione del gradiente di campo applicato.

PAZIENTE BOBINE RF BOBINE RF BOBINE GRADIENTI BOBINE GRADIENTI MAGNETE MAGNETE AMPLIFICATORI

GRADIENTI AMPLIFICATORIRF RICEVITORERF

GENERATORE IMPULSI GRADIENTI GENERATORE IMPULSI RF CONVERTITORE A/D COMPUTER STANZA SCHERMATA

Fig. 1.3 - Schema di un sistema di imaging NMR

Il segnale FID ricevuto viene quindi analizzato mediante la Trasformata di Fourier per ottenere la mappa della distribuzione spaziale dei momenti magnetici. I valori dei gradienti variano secondo gli apparecchi tra 0.05 e 1 gauss/cm (1 tesla = 1Wb₂

m = 10.000 gauss) e ciò condiziona lo spessore

minimo dello strato e la risoluzione spaziale. Inoltre non funzionano di continuo ma vengono commutati rapidamente durante le sequenze di acquisizione.

Il sistema di trasmissione RF: fornisce il campo magnetico a radiofrequenza ed è costituito da un trasmettitore RF (oscillatore accordato alla frequenza di Larmor), da un amplificatore di potenza a RF e da una bobina, che genera un campo magnetico ortogonale al campo magnetico statico.

Il sistema di ricezione RF: rivela la magnetizzazione nucleare e genera un segnale di uscita che deve essere trattato dal computer; sarà analizzato più in dettaglio nel § 1.4.2.

Il computer: rappresenta il cervello del sistema e controlla, tramite opportune interfacce, tutte le operazioni eseguite, dalla sintonia delle bobine, alla digitalizzazione dei segnali analogici ricevuti, alla trasformata di Fourier, alla ricostruzione e la visualizzazione dell’immagine, a tutte le operazioni di di post-processing, come il calcolo di distanze, superfici, intensità di segnale. Proprio per questo deve possedere un elevata capacità di calcolo oltre ad un’alta velocità di acquisizione dei dati.

1.4

Analisi delle relazioni fra campo magnetico e

magnetizzazione e fra magnetizzazione e segnale NMR

Si premette che, per condurre l’analisi svolta in questo paragrafo, verranno introdotti concetti relativi alle bobine a radiofrequenza che rappresentano una componente fondamentale per i sistemi di MRI nonché l’oggetto di studio di questo lavoro di tesi, e saranno trattate più approfonditamente nel capitolo 2.

1.4.1 Equazione di Bloch

Considerando il campione in esame come un sistema avente in ingresso il campo magnetico B(t) e in uscita la magnetizzazione nucleare M(t), la descrizione fenomenologica della dipendenza della magnetizzazione nucleare M(t) dal campo magnetico applicato B(t) è data dall’equazione di Bloch. Questa equazione fornisce uno dei modelli più semplici per il comportamento di spin nucleare dopo l’eccitazione tramite impulsi, e assume la forma: ∧ ∧ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ₊ − ∧ = M B x y z M 1 0 2 T M M T M M dt d γ x y _z (1.1) in cui M M_x, _y,M_z sono le componenti della magnetizzazione M,avente come valore di equilibrio M z0

∧

e dove B è composto da un campo statico omogeneo B0 orientato secondo l’asse z, da un campo perpendicolare a

radiofrequenza B t1

( )

e da un gradiente di campo magnetico lineare

(

, ,

)

g

B x y z (in B t

( )

non sono inclusi i contributi al campo magnetico dovuti

ad interazioni e collisioni locali dei nuclei in quanto gli effetti di questi campi “interni” sono inclusi nei parametri T1 e T2).

La direzione di z∧ , parallela al campo statico B0, è detta “longitudinale”,

mentre il piano che contiene i versori x,∧ y∧, è detto “trasverso” [1].

Per la risoluzione dell’equazione di Bloch si consideri inizialmente l’applicazione del solo campo statico B0.

Il termine M∧B descrive il moto di precessione dei nuclei atomici ed assumendo come valori iniziali per le componenti della magnetizzazione i termini 0 0

, _y

x M

M ed 0

z

) cos ( ) (_{t e} 2 _M 0 _{0t M} 0_{sin 0t} M T _{x y} t x = ω − ω − (1.2) ) cos ( ) ( 0 0 0 0 2 _{M sin t M t} e t M x y T t y = ω + ω − (1.3) ) 1 ( ) ( 1 1 0 0 T t T t z z t M e M e M − − − + = (1.4)

La componente longitudinale decade dal suo valore iniziale 0

z

M verso il suo valore di equilibrio M0, mentre la componente trasversa ruota a frequenza

0

ω e decade a zero.

Una forma compatta dell’espressione della componente trasversa della magnetizzazione si ottiene definendo:

y x jM

M

M = +

(1.5) con la quale si ha:

) 2 / exp( ) ( 0 0 T t t j M t M = ω − _(1.6) dove 0 0 0 y x jM M M = + (1.7)

Per ricondurre lo studio a casi di interesse fisico, si supponga eterogeneo il campione in esame, per cui la magnetizzazione totale diventa M

( )

t r, , dove r, vettore di componenti x y z, , , rappresenta la posizione nel volume in esame.

Si procede con l’analisi dell’equazione di Bloch considerando adesso anche l’applicazione del campo gradiente, il cui effetto è quello di far precessare a frequenze diverse protoni localizzati in differenti punti dello spazio.

Il campo gradiente è composto da tre componenti chiamate G tx

( )

, G ty

( )

e

( )

z

G t , generate da tre bobine indipendenti, ed il campo magnetico diviene:

∧ ∧ + + + = z z B(t,x) B₀ [G_x(t) x G_y(t)y G_z(t)z] (1.8)

I tre gradienti possono essere raggruppati in un vettore gradiente G

( )

t di componenti G tx

( )

, Gy

( )

t e G tz

( )

, per cui si può scrivere:

∧

• +

= G r z

B(t,x) [B0 (t) ] _(1.9) La localizzazione spaziale è dovuta al campo gradiente G

( )

t rt : infatti, considerando il caso particolare in cui il gradiente sia statico, G

( )

t = G, la frequenza di Larmor ω'

del campione nella posizione r è:

) ( ) ( ' r =γ B₀+G•r ω _(1.10)

Da questa relazione si evince che variando il segnale di stimolo di ingresso mediante diversi campi gradiente, ogni punto del campione può essere reso distinguibile tramite la rivelazione della frequenza di Larmor.

La soluzione dell’equazione di Bloch in notazione complessa diventa adesso: )] ( / ) ( ' exp[ ) ( ) , (t r M0 r j r t t T₂ r M = ω − _(1.11)

dove, rispetto alla (1.6), si è aggiunta la dipendenza da r e si è sostituito

( )

'

ω r al posto di ω0.

Ricapitolando, se un gradiente statico G viene applicato al campione, la frequenza di oscillazione della magnetizzazione rivelata ω'

diviene dipendente da r e questa dipendenza spaziale si riflette sul segnale di uscita.

Si consideri adesso anche il campo a radiofrequenza, che serve per eccitare i nuclei in modo che possano emettere il segnale utile; la bobina che trasmette questo segnale al campione genera un campo magnetico a RF

( )

1 B t descritto da: ∧ = x B₁(t) 2B₁(t)cos(ωt) _(1.12)

Un campo così descritto è detto “polarizzato linearmente”, poiché oscilla in una singola direzione (

∧

x_); ω _{è chiamata frequenza di irradiazione ed un} valore tipico è di 8

1.0 10⋅ rad/ sec.

Il fenomeno della risonanza si verifica quando la frequenza di irradiazione

ω uguaglia la frequenza naturale di precessione dei protoni ω0, con il

risultato fisico della rotazione degli spin nucleari ad una velocità proporzionale all’intensità del campo applicato.

Gli impulsi RF applicati sono caratterizzati da un parametro α dato da:

∫

= T dt t B 0 1( ) γ α (1.13) dove T rappresenta la durata dell’impulso applicato ed α è l’angolo del quale ruota la magnetizzazione. Risulta quindi evidente che possiamo ruotare il vettore magnetizzazione,allontanandolo dalla sua posizione di equilibrio di un qualunque angolo desiderato,attraverso l’applicazione di un campo magnetico oscillante sul piano traverso.

Gli impulsi più utilizzati nella MRI sono quello a 90°, che ruota la magnetizzazione dalla posizione di allineamento con il campo principale

0

B verso il piano trasverso, e quello a 180°, che inverte la magnetizzazione, ruotandola dall’allineamento parallelo a quello antiparallelo col campo principale.

1.4.2 Sistema di Rivelazione

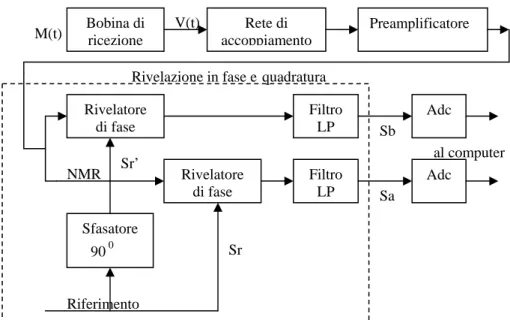
Fig. 1.6 - Schema a blocchi di un sistema rivelazione NMR

• Bobina di ricezione: La bobina di ricezione circonda il campione e si comporta da antenna captando la magnetizzazione nucleare del campione stesso e convertendola in una tensione fluttuante V t

( )

.

La relazione che lega queste due grandezze è la seguente:

∫

• − = M t r B_c r dr dt d t V( ) ( , ) ( ) (1.18) dove B r_c( ) descrive la sensibilità della bobina di ricezione in differenti punti dello spazio ed è calcolabile come rapporto tra il campo magnetico generato dalla stessa bobina e la corrente che vi scorre.

La geometria della bobina e la sua posizione devono essere tali che il valore della componente trasversale di B r_c( ) sia la più grande possibile, mentre la componente longitudinale dia un contributo minimo alla tensione di uscita e quindi possa essere trascurata: questo è una conseguenza del

al computer Bobina di ricezione Rete di accoppiamento Preamplificatore Rivelatore di fase Rivelatore di fase Sfasatore 900 Filtro LP Filtro LP Adc Adc Riferimento Sr Sr’ NMR Sa Sb V(t) M(t)

fatto che la componente M_z

( )

t r, decade lentamente con costante di tempo

1

T, tipicamente da 0.1 s ad 1s, mentre la componente trasversale oscilla con un periodo da 0.05µs a 0.2 µs.

Per la sensibilità della bobina si assuma:

∧ ∧ + = x y r Bc( ) a b _(1.19)

in cui a e b sono delle costanti.

Questa equazione descrive una bobina che ha sensibilità uniforme verso il campione, ma la cui direzione di massima sensibilità non coincide con la direzione del campo RF applicato: queste assunzioni sono ambedue realistiche, in quanto una bobina progettata correttamente avrà una piccola deviazione rispetto ad una uniformità ideale ma la direzione di massima sensibilità può essere difficile da controllare.

Vedremo comunque che questa indeterminazione nella direzione sarà tenuta in conto nella fase del segnale di uscita e sarà causa di difficoltà ridotte.

Sostituendo la (1.19) nella (1.18) e ricordando la (1.5) si ottiene:

∫

+ − = aM t r bM t r dr dt d t V( ) [ _x( , ) _y( , )] =−

∫

a− jb M t r dr dt d )] , ( ) Re[( (1.20) Con l’espressione (1.11), scrivendo 0

( )

M r in forma polare: )] ( exp[ ) ( ) ( 0 r r r A jθ M = _(1.21)

e con le seguenti sostituzioni:

' cos a=k φ e ' b= −ksenφ si ottiene: r r r r e r k t d A dt d t V T t ] ' ) ( ) ( ' cos[ ) ( ) ( =−

∫

2( ) ω +θ +φ − (1.22)

Si può notare che l’effetto della bobina di ricezione su M_x

( )

t x, è quello di una moltiplicazione per un fattore k (guadagno che dipende dalla struttura della bobina) e di introdurre uno sfasamento φ'

.

Per la linearità degli operatori di derivazione ed integrazione si ha:

+ + + ⎩ ⎨ ⎧ + =

∫

( ) − [1 ( )]*sen[ '( ) ( ) '] ) ( 0 ) ( 0 2 ω θ φ ω ω ω A r e r r r t r k t V T h t r r r r t d T _⎭⎬ ⎫ + + + cos[ '( ) ( ) '] ) ( 1 2 0 φ θ ω ω _(1.23)

dove ωh

( )

r =γh

( )

r , in cui h r

( )

è il contributo dei gradienti al campo totale.

Essendo i termini

( )

0 h ω ω r ed

( )

0 2 1 T

ω r trascurabili rispetto all’unità e

definendo ' / 2 φ φ π= + , si ottiene: r r r r e r t d A k t V h T t ] ) ( )) ( cos[( * ) ( ) ( 0 ) ( ' 2 ω +ω +θ +φ =

∫

− (1.24)

in cui tutte le costanti moltiplicative sono incluse in '

k .

Riassumendo, la magnetizzazione nucleare M

( )

t,r induce una tensione di uscita V t

( )

nella bobina di ricezione, chiamata segnale NMR.

• Rete di accoppiamento: La rete di accoppiamento trasferisce il segnale dalla bobina al preamplificatore ed ha lo scopo di realizzare l’adattamento di impedenza fra il carico rappresentato dalla bobina di ricezione ed il cavo di collegamento con gli stadi a valle. Essendo questa lineare, gli unici effetti introdotti sul segnale NMR sono una variazione del guadagno '

k e

della fase φ del segnale.

• Preamplificatore: E’ un amplificatore a radiofrequenza a basso livello di rumore, e quindi ha il compito di rendere sufficientemente bassa la cifra di rumore complessiva della catena di ricezione: il fattore di rumore del

primo stadio contribuisce direttamente a quello della catena di ricezione, ed il suo guadagno di potenza disponibile riduce l’effetto della cifra di rumore degli stadi a valle.

• Rivelazione in fase e quadratura: Il rivelatore di fase ha in ingresso il segnale a radiofrequenza NMR il cui spettro è centrato sulla pulsazione di irradiazione ω, ed opera una conversione di frequenza attraverso una frequenza angolare di riferimento pari anch’essa ad ω5: se attraverso un filtro passa basso preleviamo la componente in banda base possiamo inviare il segnale così ottenuto ad un convertitore analogico digitale. Il principio descritto è quindi quello del classico ricevitore supereterodina. Si consideri inizialmente un singolo rivelatore, in particolare quello presente sul canale A. Il rivelatore in esame ha in ingresso due segnali, il segnale NMR V t

( )

(1.24) ed un segnale di riferimento che oscilla ad una frequenza uguale alla frequenza del segnale di irradiazione ω, detto ad esempio Sr =acos

( )

ωt .

Effettuando la moltiplicazione di questi due segnali e ricordando che i valori delle frequenze ω ed ω0sono molto simili, all’uscita del singolo

rivelatore è presente la somma di due componenti, una centrata in zero ed una centrata in 2ω0. Il filtro passa basso rimuove tutte le componenti del

segnale eccetto quella centrata in zero, così che il segnale Sa t

( )

presente dopo il filtro è : r r e r t d A k t Sa T t ] ) cos[( * ) ( ) ( = '

∫

2( ) ω₀−ω +β − (1.25) dove β ω= h

( )

r t+θ

( )

r +φ.

5 _{Il segnale trasmesso e quello utilizzato per la rivelazione saranno tratti dal solito oscillatore di} riferimento.

Il circuito sfasatore ha in ingresso il segnale di riferimento Sr t

( )

ed in uscita il segnale '

( )

Sr t : ) sen( ) ( ' t a t Sr = ω

Seguendo lo stesso ragionamento per il canale B, in uscita al filtro passa basso si ottiene : r r e r t d A k t Sb T t ] ) sen[( * ) ( ) ( = '

∫

2( ) ω₀ −ω +β − (1.26) Considerando il segnale complesso tale che S t

( )

=Sa t

( )

− jSb t

( )

, si ottiene:

[ ] [ ] { } r r r r r d e A k t S t j T t h

∫

− + − + + + = ' _{( )} 2( ) ω0 ω ω ( ) θ( ) φ ) ( (1.27) Ricordando la (1.11), si può legare S t

( )

alla magnetizzazione ottenendo :

r r e d t M K t S j t

∫

− = (, ) ) ( ω (1.28) dove ' j

K =k eφ è una costante arbitraria complessa e

) , ( ) , ( ) , (t r M t r jM t r M = _x + _y . • Convertitori analogico-digitali: La conversione del segnale complesso costituito dai due canali in una doppia stringa di numeri digitali {Sn}

fornisce : r r e d t M K Sn=

∫

( , ) −jωn∆t (1.29)

dove ∆t è l’intervallo di campionamento. Questa relazione lega il segnale di uscita campionato Sn alla magnetizzazione del campione M t

( )

,r .