L'analisi sismica di spinta

(1)

L'analisi sismica di spinta

Il DM 14 gennaio 2008 prevede quattro diversi tipi di analisi sismiche: lineare statica, lineare dinamica, non lineare statica, non lineare dinamica56_.

Indubbiamente l'analisi non lineare dinamica è quella più completa ed efficace, trattandosi di integrazioni al passo delle equazioni del moto, ma risulta piuttosto difficoltosa a livello pratico e poco diffusa in ambito professionale. A questa si preferiscono, dunque, delle analisi più semplici ed approssimate, ma che comunque consentano stime realistiche ed affidabili della risposta strutturale.

Delle analisi disponibili nel presente lavoro di tesi si sceglie quella di pushover: la risposta globale di una struttura in muratura è più significativamente rappresentata dall'analisi statica non lineare, avendo questa comportamento ultimo spiccatamente non lineare57_.

7.1 Cenni di dinamica delle strutture

7.1.1 Le equazioni del moto SDOF

Le forze sismiche sono forze dinamiche che hanno la capacità di interagire dinamicamente con le strutture inducendo delle vibrazioni.

Si definisce telaio shear type l'oscillatore semplice ad un grado di libertà composto da una trave e due pilastri in cui il contributo in massa dei pilastri è trascurabile e la rigidezza estensionale e flessionale dei pilastri si avvicina all'infinito.

56 NTC 2008, §7.3 57 CE 2009, §C7.8.1.5.4.

(2)

Quando il telaio viene investito da una forza esterna dinamica F(t), questo reagisce con una forza di richiamo elastico (Fel) ed una smorzante (Fdis).

Scrivendo l'equazione del moto si ottiene:

m

⋅¨x  t=F t−F

el

−F

dis

F

t=m⋅¨x tF

el

F

dis

F

t=m⋅¨x tk⋅x tC⋅˙x t

dove

m è la massa del telaio, corrispondente a quella della trave k è la rigidezza dei pilastri

C è il coefficiente di smorzamento

L'equazione che si ottiene è una equazione differenziale del II ordine lineare e completa ed ammette soluzioni solo se accompagnata da due condizioni a contorno.

7.1.1.1 Vibrazioni libere non smorzate

Si ottengono vibrazioni libere non smorzate per F(t)=0 ; C=0. Ponendo ω2 _{= k/m si ottiene:}

m

⋅¨x  tk⋅x t =0

¨x  t

2

⋅x  t=0

x

 t=A

₁

⋅e

 i⋅⋅t

A

₂

⋅e

−i⋅⋅t 

x

 t=A⋅sin ⋅t

Il moto risulta sinusoidale e dipendente da ω, la pulsazione naturale, a sua volta legata al periodo proprio (T) dalla relazione: ω2 _{= 2π/T.}

(3)

7.1.1.2 Vibrazioni forzate non smorzate

Si ottengono vibrazioni forzate non smorzate per C=0. In questo caso la soluzione è la somma dell'integrale dell'omogenea associata, già risolta nel paragrafo precedente, ed una soluzione particolare che dipende dall'espressione della F(t). Se si considera che F(t) = F0 sin(ωF t), si

ricava che la soluzione particolare è pari a xp = AF sin(ωF t). Sostituendo:

−m⋅A

F



F

2

sin



F

⋅t A

F

⋅k⋅sin 

F

⋅t=F

0

⋅sin 

F

⋅t 

A

_F

=

F

0

k

⋅1−



F 2



2



x

t =A⋅sin ⋅t

F

0

k

⋅1−



F 2



2



⋅sin 

F

⋅t

Si nota che per ω → ωF l'ampiezza del contributo della forzante tende ad infinito (fenomeno

della risonanza).

7.1.1.3 Vibrazioni libere smorzate

Si ottengono vibrazioni libere smorzate per F(t)=0. Si introduce il rapporto di smorzamento ξ tale che C/m = 2 ω ξ. Si ottiene:

¨x t 

C

m

⋅˙xt

k

m

⋅x t =0

¨x t 2⋅⋅⋅˙x t 

2

⋅x t=0

x

t =A

₁

⋅e

−⋅⋅2−1 

A

₂

⋅e

−⋅−⋅2−1

Il moto del sistema è periodico decrescente, l'effetto smorzante cresce al tendere del fattore di smorzamento all'unità.

Le vibrazioni smorzate si dicono sovrasmorzate per ε = ξ2_{-1 > 0: il moto non assume più la}

(4)

forma periodica e tende a fermarsi con rapidità.

Le vibrazioni si dicono sottosmorzate per ε = ξ2_{-1 < 0: gli esponenziali rimangono complessi e}

la forma del moto torna ad essere periodica.

7.1.1.4 Vibrazioni forzate e smorzate

L'equazione del moto diventa la seguente:

m

⋅¨x  tC⋅˙x tk⋅x  t=F

0

sin



F

⋅t

, si

nota che l'equazione omogenea è la medesima del paragrafo precedente. Alla soluzione già esaminata va dunque sommata la soluzione dell'integrale particolare dipendente dalla forzante, in questo caso pari a

x

_p

=A

F

⋅sin

F

⋅t−

.

L'equazione che si ottiene infine sarà:

A

_F

=

F

0

k

⋅



1−



F





2

4⋅

2

⋅



F





2

x

 t=A⋅sin ⋅tA

F

⋅sin 

F

⋅t

La quantità

1



1−



F





2

4⋅

2

⋅



F





2 _{si chiama rapporto di amplificazione dinamica e}

dipende sia dal rapporto α = ωF/ω sia da ξ nella seguente maniera:

(5)

Per uno smorzamento piuttosto limitato, al limite nullo, il fattore di amplificazione cresce notevolmente quando α = 1, ovvero quando il periodo proprio dell'oscillatore si avvicina a quello della forzante. Al crescere dello smorzamento, questo effetto è sempre meno evidente: la risposta statica (F/k) tende ad essere più attutita quanto più è grande ξ.

7.1.2 Le equazioni del moto MDOF

Le equazioni del moto per i corpi a più gradi di libertà si possono scrivere in forma matriciale nel seguente modo:

[M]⋅{ ¨x}[C]⋅{ ˙x }[k ]⋅{x}={F}

Suppongo che il moto, per semplicità, sia libero non smorzato, si avrà:

[M]⋅{ ¨x}[k ]⋅{x}=0

Si pone

{x t}={}⋅qt   { ¨x t }={}⋅¨q t

, dove

{}

rappresenta il vettore delle ampiezze costanti e q(t) la funzione armonica che descrive il moto del corpo. Si ottiene:

−

_n2

_{⋅[M ]⋅{}⋅qt [ k ]⋅{}⋅qt =0}

−

n

2

_{⋅[ M ][k ]⋅{}⋅qt =0}

L'equazione risulta verificata quando: • q(t)=0, soluzione banale

•

{}

= {0}, la forma dello spostamento è nulla

(6)

•

det

−

_n2

_{⋅[M ][k ]=0}



_n2

_{⋅[M ]⋅{}=[k ]⋅{}}



n 2

⋅{}=[M]

−1

⋅[k ]⋅{}

det

−

n 2

⋅[M ][k ]=0  det[M]

−1

⋅[k ]−

n 2

⋅I =0

Risolvendo l'equazione si trovano gli autovalori e gli autovettori della matrice

−

_n2

_{⋅[M ][ k ]}

rispettivamente le pulsazioni proprie del corpo ed i modi normali di vibrare relativi ad ogni pulsazione.

Per semplificazione, si definiscono la matrice modale e la matrice spettrale per corpi a due gradi di libertà. Si ottiene: [ ]=

[

11 21 ₁₂ ₂₂

]

Matrice modale []=

[

1 2 0 0 ₂2

]

Matrice spettrale

Ricordando che il vettore d'influenza {R} indica quali siano i gradi di libertà attivati dall'azione sismica per una data direzione, si definiscono γr, il coefficiente di partecipazione modale, e



m

_r , la massa modale partecipante: •



r

=

{

_r

}

t

_{⋅[M ]⋅{R }}

{

r

}

t

⋅[M ]⋅{

r

}

Coefficiente di partecipazione modale; indica di quanto il singolo modo partecipa alla risposta globale della struttura per una data direzione r dell'azione sismica; •

m



_r

=

{

r

}

t

_{⋅[M ]⋅{R}}

2

{

r

}

t

⋅[M ]⋅{

r

}

Massa modale partecipante; percentuale della massa complessiva che il generico modo attiva quando la struttura è soggetta al sisma in direzione r.

(7)

7.2 L'analisi statica non lineare

L'analisi statica non lineare consiste nella valutazione del comportamento sismico della struttura (legame forza-spostamento generalizzato) da confrontarsi con lo spostamento richiesto dal terremoto, valutato in termini spettrali.

Operativamente si procede applicando alla struttura per ogni direzione dell'azione sismica, oltre ai carichi gravitazionali, un sistema di forze orizzontali (F1, F2, F3, …) distribuite ad ogni livello

della costruzione, proporzionali alle forze d'inerzia ed aventi come risultante il taglio alla base Fb = Σ Fi.

Le forze sono scalate monotonamente sia in verso positivo che negativo sino al raggiungimento dello spostamento (dc) di un un punto di controllo, corrispondente alla condizione di collasso

globale o locale58_{. Il risultato dell'analisi sarà una curva che pone in relazione le grandezze F} b e

dc denominata curva di capacità.

58 NTC 2008, §7.3.4.1

92. Distribuzione delle forze nell'analisi pushover, elaborazione personale

(8)

Questo tipo di analisi è utilizzabile qualora l'edificio in esame abbia comportamento sotto sisma governato da un modo di vibrare principale, caratterizzato da una notevole massa modale partecipante. Ciò è dovuto al fatto che si ha l'esigenza di associare al sistema strutturale reale (MDOF) un sistema equivalente SDOF.

Le strutture in muratura, avendo comportamento non lineare, risultano significativamente rappresentate da un'analisi statica non lineare; pertanto tale metodo è applicabile anche nei casi in cui la massa modale partecipante del primo modo sia inferiore al 75% della massa totale, ma comunque superiore al 60%59_.

La corrispondenza tra F*_{e F}

b, nonché tra d* e dc è data dalle seguenti relazioni:

F*_{= F} b / γr

d* _{= d} c / γr

Alla curva di capacità ottenuta per il sistema SDOF va poi associata una curva bilineare equivalente, composta da un primo tratto elastico ed un secondo tratto perfettamente plastico (si veda la fig. 94)60_.

Detta Fbu la resistenza massima della struttura reale e F*bu = Fbu / γr quella del sistema SDOF, si

può calcolare la quota 0,6 F*

bu e collegare l'origine degli assi con il punto corrispondente

all'intersezione tra la curva di capacità e la retta y = 0,6 F*

bu , ottenendo l'inclinazione del tratto

elastico. Inoltre, il punto di inizio del tratto plastico è collocato all'altezza di F*

y , la forza di

plasticizzazione, che si ottiene imponendo l'uguaglianza tra l'area sottesa alla curva di capacità e 59 CE 2009, §C7.8.1.5.1 e NTC 2008, §7.8.1.4.5

60 CE 2009, §C7.3.4.1

(9)

quella sottesa al diagramma bilineare equivalente per lo spostamento massimo d* u

corrispondente ad una riduzione della resistenza del 15%.

Il grafico si interrompe a dmax , lo spostamento massimo che la struttura può sopportare.

Quest'ultimo dipende dal rapporto tra il periodo elastico del sistema bilineare ed il periodo TC

dello spettro di risposta elastico.

Il periodo elastico del sistema bilineare si ottiene per:

T=2 ⋅



m



k

dove



m

è la massa modale partecipante

k è la rigidezza del tratto elastico della bilineare

Se accade che

TT

_C la domanda in spostamento del sistema anelastico è assunta uguale a quella di un sistema elastico di uguale periodo:

d*

max =de max = SDe( T ).

Se invece

TT

_C la domanda in spostamento del sistema anelastico è maggiore di quella di un sistema elastico, per cui si deve ricorrere alla relazione:

d*

max = de max / q* [1+(q*-1) TC/T*]

q*_=S

e(T*)

m



/ F*y

Nell'esecuzione dell'analisi statica non lineare si devono considerare almeno due distribuzioni di

95: CE 2009, fig. C7.3.2: Spostamenti di riferimento per T*_>T

(10)

forze d'inerzia, una ricadente nel gruppo 1 e l'altra nel gruppo 261_.

Gruppo 1

• Distribuzione proporzionale alle forze statiche applicabile solo se al modo di vibrare principale corrisponde una massa modale partecipante di almeno il 75% ed a condizione di usare quale distribuzione secondaria la 2a;

• distribuzione corrispondente ad una distribuzione di accelerazioni proporzionale alla forma del modo di vibrare, sempre nell'ipotesi che al modo di vibrare fondamentale corrisponda una massa modale partecipante del 75%;

• distribuzione corrispondente alla distribuzione dei tagli di piano calcolati in un'analisi lineare dinamica, nell'ipotesi che T*_>T

C .

Gruppo 2

• Distribuzione uniforme di forze, da intendersi come derivata da una distribuzione di accelerazioni lungo l'altezza della costruzione;

• Distribuzione adattiva, che cambia al crescere dello spostamento di controllo al crescere della plasticizzazione nella struttura.

Nel caso delle costruzioni esistenti è possibile utilizzare l'analisi statica non lineare assegnando come distribuzioni principale e secondaria rispettivamente la prima distribuzione del gruppo 1e la prima del gruppo 2, indipendentemente dalla massa partecipante sul primo modo62_.

61 NTC 2008, §7.3.4.1 62 CE 2009, §C8.7.1.4

(11)

7.3 Risultati dell'analisi sul modello dello stato di fatto

Il modello dello stato di fatto dell'edificio in questione è stato sottoposto ad analisi pushover ed ha evidenziato delle carenze notevoli.

Mediante l'utilizzo del software SismiCad è stato possibile calcolare le curve di capacità relative alle otto combinazioni di carico per ogni distribuzione scelta. Il programma richiede all'utente di definire alcune caratteristiche di tali curve: lo spostamento iniziale corrispondente al primo punto sulla curva di capacità, quindi lo spostamento finale, ed infine il numero di punti totali per descrivere la curva, ad esclusione dell'origine. In questo caso si scelgono i seguenti dati: lo spostamento iniziale, pari al default di 0,5cm, quello finale pari a 4cm, il numero di iterazioni pari a cinque data la complessità della struttura ed i limiti di calcolo del pc utilizzato.

Prima di procedere con il calcolo delle curve suddette è anche possibile definire il punto di controllo, per normativa il centro di massa del sistema. Il punto scelto si trova al terzo piano dell'edificio con la torretta, in prossimità del reale centro di massa relativo a quel piano (nodo 4916). A questo corrispondono le forze sismiche elastiche 2312daN per il gruppo 1 e 1496daN per il gruppo 2 sia in direzione x che in direzione y.

Dalle curve seguenti si può notare che nella totalità dei casi analizzati, il drift imposto è eccessivo, la crisi avviene per spostamenti interpiano molto minori di quello scelto. Si può inoltre osservare che al sistema di forze agente una volta in direzione x ed una volta in direzione

(12)

y corrispondono spostamenti tali da imporre un moto torsionale alla struttura: maggiormente rigido è infatti il corpo orientato in direzione est-ovest che ospita la Chiesa, di recente consolidato con il metodo dell'Intonaco armato, mentre l'impianto di base è fortemente irregolare. Tali moti di rotazione principalmente concentrano la crisi nella torretta. Inoltre l'edificio risponde in modo diverso a forze lungo l'asse x e lungo l'asse y: in generale risulta più rigido e resistente ad azioni sismiche lungo l'asse x piuttosto che lungo l'asse y.

Si indica con x la direzione nord-sud, mentre con y quella est-ovest.

Nei paragrafi seguenti si riportano le sedici curve di capacità (calcolate come rapporto tra il moltiplicatore del carico e lo spostamento in cm) in output dal programma, accompagnate dai dati relativi all'oscillatore ad un grado di libertà corrispondente e dal confronto tra il grafico bilineare equivalente e gli spettri di risposta (elastico e plastico).

(13)

7.3.1 Gruppo 1 7.3.1.1 Combinazione 1

Grafico 7. SismiCad: curva di capacità relativa alla prima combinazione del gruppo 1

(14)

7.3.1.2 Combinazione 2

Grafico 9. SismiCad: curva di capiacità relativa alla seconda combinazione del gruppo 1

(15)

Grafico 11. SismiCad: curva di capacità relativa alla combinazione 3 del gruppo 1

(16)

Grafico 13. SismiCad: curva di capacità per la combinazione 4 del gruppo 1

(17)

(18)

(19)

(20)

(21)

7.3.2 Gruppo 2 7.3.2.1 Combinazione 1

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

7.3.3 Verifiche e risultati sintetici

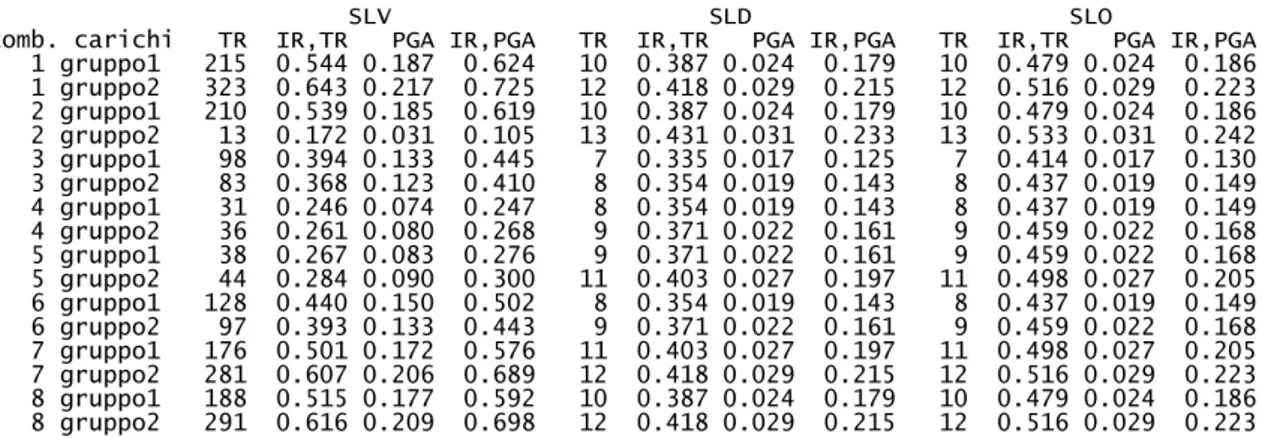
Dai risultati delle analisi si evince che nessun elemento murario verifica per le combinazioni studiate. Tali risultati sono riportati in forma sintetica nella seguente tabella, in cui per ogni combinazione considerata e per ogni Stato Limite sono indicati: la domanda e la capacità in termini di spostamenti, il fattore di struttura q*, che dovrebbe attenersi a valori inferiori a 3, e l'indicazione di avvenuta verifica, sempre negativa.

Per ogni curva di capacità il software restituisce i periodi di ritorno (TR) ed i livelli di PGA

corrispondenti al raggiungimento dei diversi Stati Limite; nella tabella 20 questi sono messi a confronto con periodi di ritorno (TR rif) e PGA (PGA rif) richiesti dalla attuale normativa in

corrispondenza degli stessi Stati Limite. Si indica con IR,TR il rapporto (TR / TR rif)^0,41, che

rappresenta il coefficiente di vulnerabilità denominato anche indicatore di rischio sismico, e con IR,PGA il rapporto tra PGA e PGA rif.

Valori prossimi all’unità degli indicatori di rischio sismico caratterizzano edifici con resistenza

Tabella 19. SismiCad, riepilogo dei risultati dell'analisi pushover nel modello dello stato di fatto

(30)

sismica paragonabile a quella richiesta dalla norma, ma nel caso specifico si allontanano notevolmente da questo valore. Si nota inoltre che tutti i valori di TR relativi alle varie

combinazioni per SLV sono notevolmente lontani dal valore di riferimento circa pari a 949anni, il minimo tempo di ritorno è pari a 13anni, ovvero l' 1,4% di TR, rif .