Modellazione ed analisi strutturale

CAPITOLO IV

Modellazione ed analisi strutturale

Si descrive, dal punto di vista teorico, come svolgere l’analisi statica e dinamica di un’antenna strallata, facendo riferimento anche a strutture più semplici per chiarire gli aspetti del comportamento. Si illustrano poi i criteri con cui il programma di calcolo SAP 2000 svolge i vari tipi di analisi affinchè sia possibile la corretta impostazione del modello e l’interpretazione dei risultati forniti. In chiusura si propone un criterio specifico per il dimensionamento e l’analisi delle antenne strallate.

4.1 L’analisi delle antenne strallate

In questo capitolo si fa una descrizione semplice dei metodi usati per analizzare il comportamento della struttura antenna strallata. In primo luogo si considerano i passi da condurre per l’analisi statica, successivamente si descrive il comportamento sotto azioni dinamiche e si tenta di spiegare, almeno da un punto di vista teorico, come i moderni programmi di calcolo riescono a fornirci dei risultati molto accurati.

L’azione principale cui un’antenna strallata è sottoposta è il vento: data la snellezza e le notevoli altezze raggiunte, difficilmente questa azione potrà essere assunta con un modello statico equivalente, salvo per un predimensionamento delle membrature.

Come specificato nel Cap. III le fluttuazioni della velocità del vento possono interagire pericolosamente con le caratteristiche dinamiche proprie dell’antenna.

L’altra azione difficile da modellare è il sisma che, d’altro canto, non può più essere esclusa dall’analisi per la definizione di zone sismiche su tutto il territorio nazionale.

L’analisi dinamica andrà effettuata sotto vibrazioni libere per caratterizzare le frequenze proprie e i modi di vibrare della struttura. Ma, se si vuole definire con precisione la risposta strutturale, dovrà condursi l’analisi sotto vibrazioni forzate, siano esse indotte da una storia temporale della velocità del vento o dall’accelerogramma relativo ad un terremoto di progetto. Si avranno quindi delle deformazioni e delle sollecitazioni variabili nel tempo (con valori di picco) e legate all’eccitazione, da parte della forzante, delle masse strutturali in gioco.

L’analisi dinamica potrà altresì essere effettuata alle oscillazioni libere: si ricaveranno le forme modali ed i periodi propri di vibrazione della struttura. Per definire l’azione si utilizzeranno degli spettri di progetto che, in funzione del periodo considerato, forniranno solo la risposta massima del sistema per un certo modo di vibrare. Dalla composizione delle risposte dei modi di vibrare

considerati, si avranno le corrispondenti azioni da applicare in certi punti alla struttura.

Per avere una panoramica sui metodi di indagine del comportamento dinamico che venivano usati in passato si rimanda al già citato Cap. III.

4.2 L’analisi statica lineare

Questo tipo di analisi è valido per eseguire un predimensionamento di massima dell’antenna strallata. Si assume un modello bi-dimensionale ipotizzando che i carichi agiscano nel piano che contiene due stralli simmetricamente opposti. La struttura viene scomposta in due elementi:

1) il traliccio, considerato come un’asta verticale appoggiata alla base; 2) il complesso degli stralli, vincolato al suolo e ai vari livelli sull’asta. Il comportamento di entrambi è assunto elastico lineare trascurando, e questo non è accettabile in generale, sia la deformabilità dello strallo che gli effetti del secondo ordine legati alla deformata dell’asta.

L’azione di ritegno degli stralli sull’asta è schematizzata con una serie di appoggi in modo da ottenere uno schema a trave continua su più appoggi. Si suppone la congruenza fra gli spostamenti dell’asta e quelli del sistema di stralli nei punti di ancoraggio, e che tali punti rimangano allineati.

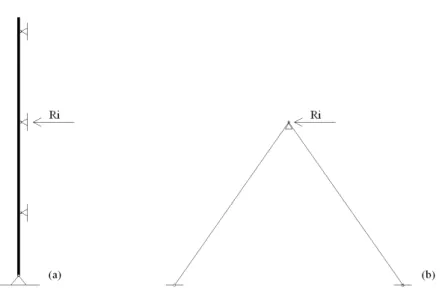
Nonostante le notevoli ipotesi semplificative, ne risulta comunque un modello facilmente risolvibile “a mano” utile nelle prime fasi della progettazione (fig. 1).

Tutte le azioni si considerano agenti in maniera statica: - peso proprio;

- permanenti portati (le antenne e gli accessori);

- il vento è modellato tramite la pressione media alle varie altezze (costante a tratti).

Figura 1 - Schema per l'analisi statica lineare: asta (a); stralli dell'ordine i-esimo (b)

Di solito, in un modello così semplice non si considera l’azione sismica: qualora se ne voglia tener conto si potranno applicare delle azioni orizzontali agli appoggi o nei punti dove si pensano concentrate le masse (mezzeria delle campate): queste azioni saranno proporzionali alle masse, all’altezza e all’accelerazione al suolo considerata.

Per gli stralli va prevista una certa pretensione: orientativamente il 20 % della reazione Ri che compete ad un certo ordine.

Risolvendo la trave continua si ottiene:

- le caratteristiche della sollecitazione di taglio e momento flettente lungo l’asse dell’asta;

- le reazioni agli appoggi e alla base.

Con le prime è possibile dimensionare, ipotizzando una certa resistenza di calcolo, l’ area e le caratteristiche di inerzia che la sezione dovrà avere globalmente: è quindi agevole definire una configurazione della sezione del traliccio posizionando i montanti in modo da soddisfare la resistenza richiesta. Il taglio permette anche di dimensionare le aste di parete, diagonali e calastrelli, elementi atti ad evitare lo scostamento dei montanti.

Con le reazioni di appoggio, riportate all’asse dello strallo, si ricava lo sforzo medio che esso deve sopportare, quindi la sezione trasversale necessaria e la reazione trasmessa ai blocchi di ancoraggio.

A causa dello schema adottato risulta privo di significato il calcolo della deformata dell’asta; solo per avere un’idea dell’ordine di grandezza della freccia per lo strallo sopravento (sottovento) è possibile utilizzare la formula 2, ampiamente discussa nel Cap. III, par. 3.1.1 al quale si rimanda.

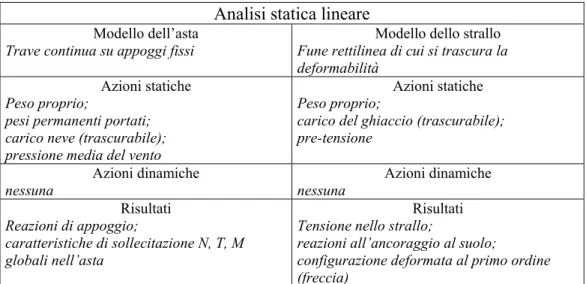
Nella tabella seguente si ricapitolano le ipotesi ed il modo di procedere quando si voglia compiere il predimensionamento di una antenna strallata mediante analisi statica lineare:

Analisi statica lineare

Modello dell’asta

Trave continua su appoggi fissi

Modello dello strallo

Fune rettilinea di cui si trascura la deformabilità

Azioni statiche

Peso proprio;

pesi permanenti portati; carico neve (trascurabile); pressione media del vento

Azioni statiche

Peso proprio;

carico del ghiaccio (trascurabile); pre-tensione

Azioni dinamiche

nessuna nessuna Azioni dinamiche

Risultati

Reazioni di appoggio;

caratteristiche di sollecitazione N, T, M globali nell’asta

Risultati

Tensione nello strallo;

reazioni all’ancoraggio al suolo;

configurazione deformata al primo ordine (freccia)

Tabella 1 – Modello, azioni e risultati per l’analisi statica lineare, utile per un predimensionamento di massima.

Il modulo di elasticità dello strallo può essere assunto alla Dischinger, per tener conto della maggior attitudine ad allungarsi di un cavo inclinato soggetto al peso proprio che si dispone secondo la funicolare, rispetto al caso ideale del cavo rettilineo. La sua espressione è:

E st E 1 γ 2 l2 ⋅ σ3 E ⋅ + dove:

E è il modulo effettivo della fune;

γ il peso specifico;

l la lunghezza della fune;

4.3 L’analisi statica non lineare

Come detto poco sopra, trascurare la deformabilità dello strallo è una semplificazione accettabile solo ed esclusivamente per avere un modello della struttura facilmente risolvibile a mano ed in grado di fornire, in pochi passaggi, un dimensionamento di massima delle membrature.

Rimanendo nell’ambito delle azioni statiche, lo spostamento dei punti di ancoraggio degli stralli all’asta dipende dalla deformabilità dello strallo e, dunque, dallo sforzo che lo sollecita.

Lo strallo non ha rigidezza verso le azioni flettenti ed il legame sforzo S – deformazione δ è fortemente non lineare. Come è stato discusso nel Cap. III par. 3.1.1, si ha: δ Q 2 a ⋅ 24 1 So2 1 S2 −     ⋅ l Est A⋅ cos θ⋅

( )

(

)

δ è lo spostamento orizzontale dell’ancoraggio;

a è la proiezione orizzontale dello strallo;

θ l’inclinazione sull’orizzontale;

A la sezione;

Q la risultante dei carichi verticali (peso proprio, eventuale ghiaccio) sullo strallo.

So lo sforzo nello strallo prima della deformazione;

S lo sforzo nello strallo dopo la deformazione.

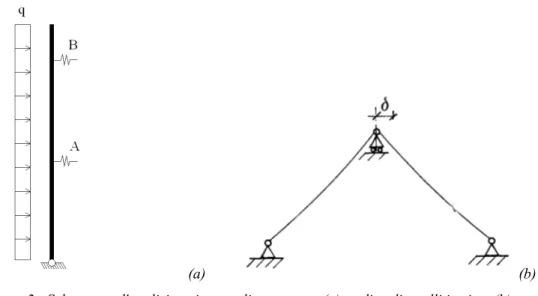
L’analisi di questa formula mostra un diverso comportamento della fune sotto lo stesso spostamento δ: a seconda del verso di questo, si hanno incrementi (decrementi) di tensione S differenti. E’ questa la situazione tipica, per un certo ordine, fra lo strallo sopravento e quello sottovento di un’antenna strallata. Il modello del traliccio è quello di un’asta con rigidezza equivalente su più appoggi, questa volta cedevoli elasticamente: la costante elastica delle molle dipende appunto dalla deformabilità dello strallo (fig. 2).

Per i due schemi si impone la congruenza degli spostamenti δi all’attacco degli

stralli.

Le azioni da prendere in considerazione sono le stesse del punto precedente.

(a) (b)

Figura 2 - Schema per l'analisi statica non lineare: asta (a), ordine di stralli i-esimo (b).

Questo modello fornisce risultati più verosimili nei riguardi del comportamento globale della struttura sotto l’azione del vento: anche in questo caso si considera l’equivalente azione statica media, costante a tratti o su tutta l’altezza.

Il procedimento di risoluzione, di tipo iterativo, è stato discusso nel capitolo precedente al par. 3.2.1; se ne riportano i punti salienti:

a) si fissa un valore di tentativo alla pre-tensione degli stralli (20% della reazione che compete a ciascun ordine);

b) con il valore della pre-tensione si calcolano i valori di partenza della cedevolezza degli appoggi elastici (L/F) da aggiornare nei passaggi successivi;

c) si risolve la trave su appoggi elastici e si ricavano le reazioni vincolari; d) con queste è possibile calcolare i nuovi sforzi negli stralli e quindi lo

spostamento δ della loro sommità con la formula (1);

e) poiché, per uno stesso ordine, si ottengono spostamenti δ diversi per gli stralli sopravento e sottovento, si impone la congruenza degli spostamenti

nel nodo in esame e ciò porta la calcolo di una variazione di sforzo ∆Si

negli stralli.

f) questa, sommata o sottratta agli sforzi calcolati al punto d), ci fornisce lo sforzo che rende congruenti gli spostamenti δ della sommità di ogni strallo (facenti capo ad uno stesso ordine);

g) lo sforzo calcolato al punto precedente, permette di aggiornare la cedevolezza di partenza per l’iterazione successiva;

h) con la nuova cedevolezza si risolve la trave su appoggi elastici e si ripercorrono i punti d) ed e).

Il punto e) può essere risolto in due modi, uno più speditivo e l’altro che richiede la risoluzione di un sistema di equazioni. Il modello della struttura, rappresentato in fig. 2, può essere ipotizzato bi-dimensionale: ad uno stesso ordine fanno capo due soli stralli perciò è sufficiente ipotizzare una perdita di tensione nello strallo sottovento e farla variare finchè l’espressione (1) non fornisce uguali risultati per i due stralli.

Qualora si voglia tener conto che la configurazione degli stralli è tri-dimensionale, si dovrà scrivere l’equilibrio del nodo nelle due direzioni ortogonali e alla traslazione verticale (che per semplicità viene considerata nulla, vedi par. 3.2.1).

Il processo converge velocemente: quando si ottengono, in due passi successivi, valori delle reazioni vincolari poco diversi fra loro, si arresta.

I risultati sono le caratteristiche della sollecitazione globali nell’asta, le reazioni di appoggio e alla base, gli sforzi negli stralli, la configurazione deformata dell’intera struttura (spostamento degli ancoraggi e freccia dello strallo).

Rispetto all’analisi statica lineare di primo approccio, si ottengono differenze notevoli sui valori del momento flettente lungo l’asta (nonostante le reazioni di appoggio differiscano di poco) e, questa volta, la configurazione deformata ha senso. A tal proposito c’è da sottolineare il fatto che per lo strallo, elemento non lineare per geometria, le deformazioni al secondo ordine sono di entità superiore rispetto a quelle di prima analisi.

Eseguire l’analisi statica non lineare correttamente (anche “a mano”) significa ottenere un ottimo dimensionamento delle membrature; allora, con l’ausilio del calcolo automatico, si potranno affrontare i problemi legati alla dinamica strutturale, oscillazioni libere e vibrazioni forzate, senza aspettarsi sostanziali modifiche delle sezioni così predimensionate.

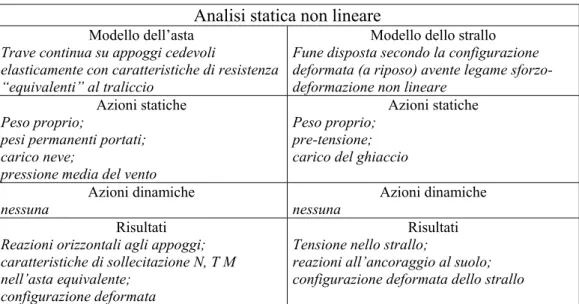
Nella tabella seguente si ricapitolano le ipotesi ed il modo di procedere quando si voglia compiere il dimensionamento di una antenna strallata mediante analisi statica non lineare:

Analisi statica non lineare

Modello dell’asta

Trave continua su appoggi cedevoli

elasticamente con caratteristiche di resistenza “equivalenti” al traliccio

Modello dello strallo

Fune disposta secondo la configurazione deformata (a riposo) avente legame sforzo-deformazione non lineare

Azioni statiche

Peso proprio;

pesi permanenti portati; carico neve;

pressione media del vento

Azioni statiche

Peso proprio; pre-tensione; carico del ghiaccio

Azioni dinamiche

nessuna nessuna Azioni dinamiche

Risultati

Reazioni orizzontali agli appoggi; caratteristiche di sollecitazione N, T M nell’asta equivalente;

configurazione deformata

Risultati

Tensione nello strallo;

reazioni all’ancoraggio al suolo; configurazione deformata dello strallo Tabella 2 - Modello, azioni e risultati per l’analisi statica non lineare, utile per il predimensionamento della struttura.

4.4 L’analisi dinamica

All’inizio del paragrafo 4.1 si è detto che, per un’antenna strallata, l’azione del vento e quella sismica non possono, in generale, essere considerate a carattere statico, data l’elevata snellezza e le grandi altezze raggiunte. Per cogliere l’effettivo comportamento sotto l’azione del vento, predominante per queste strutture, si dovrà applicare una storia di carico variabile. Inoltre sarà utile trovare le caratteristiche dinamiche proprie della struttura (frequenze proprie) in modo da capire quali azioni generano amplificazione del moto. Nei paragrafi che seguono si tratta il problema della dinamica strutturale facendo esempi su

semplici strutture; i risultati ottenuti verranno estesi alle antenne strallate. Infine si descrive come operano i moderni programmi di calcolo.

4.4.1 L’analisi dinamica alle oscillazioni libere

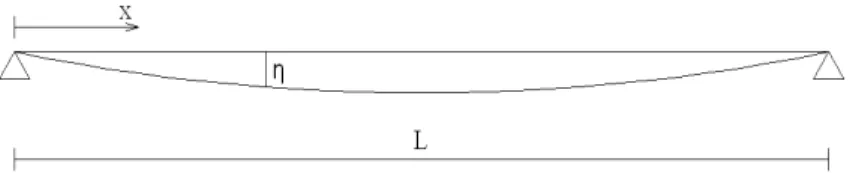
Se una struttura è sottoposta ad un’azione variabile nel tempo, anche la sua risposta in termini di deformazioni e sollecitazioni varierà nel tempo. Ogni struttura è dotata di massa propria e l’eccitazione di tale massa porta alla nascita di forze di inerzia che si oppongono al moto. L’equazione di equilibrio della struttura dovrà tener conto delle forze di inerzia che dipendono a loro volta dalla deformazione: si otterrà un’equazione di equilibrio differenziale che dovrà essere integrata. Per chiarire questo concetto consideriamo una semplice trave appoggiata:

Figura 3 – Schema di trave semplicemente appoggiata.

Fissiamo le seguenti ipotesi:

- sia η(x) la deformata della trave nel piano verticale che la contiene,

- EJ siano costanti con x,

- si trascuri la deformabilità dovuta al taglio;

in ogni sezione le caratteristiche della sollecitazione si ricavano dalle formule: E J⋅ ₂ x η d d 2 M − E J⋅ ₃ x η d d 3 ⋅ −T E J⋅ ₄ x η d d 4 ⋅ q (2)

Affrontando il problema dinamico, si deve sostituire a q la forza di inerzia per unità di lunghezza: q −m ₂ t η d d 2 ⋅

in cui m è la massa per unità di lunghezza della trave. La terza delle 2 diventa: E J⋅ ₄ x η d d 4 ⋅ −m ₂ t η d d 2 ⋅ da cui: m ₂ t η d d 2 ⋅ E J⋅ ₄ x η d d 4 ⋅ + 0 2 t η d d 2 α2 ₄ x η d d 4 ⋅ + 0 (3) α 2 EJ m

Questa è l’equazione differenziale di Eulero la cui soluzione è una funzione sia del tempo t che dell’ascissa x considerata:

η x t( , ) f x( ) sin⋅

( )

Per ricavare la funzione incognita f(x), si sostituisce la 4 nella 3 e si impongono le condizioni di vincolo:

η(0) = 0 ossia f(0) = 0 M(0) = 0 ossia f ′′(0) = 0 η(L) = 0 ossia f(L) = 0 M(L) = 0 ossia f ′′(L) = 0

Come si vede dal secondo membro della 3, è nullo, cioè non ci sono azioni forzanti, il problema è alle oscillazioni libere quindi si possono ricavare le pulsazioni, le frequenze ed i periodi propri della struttura.

Per la trave di figura 3 si ottengono questi risultati: η x t( , ) C sin n⋅π

l ⋅x 

 

⋅ ⋅sin

( )

dove, al variare di n (n = 1, 2, 3..), si ottengono le deformate per i vari modi di vibrazione (quella rappresentata in fig. 3 è la fondamentale, n = 1).

La costante C, che rappresenta l’ampiezza del moto, rimane indeterminata ma per il momento non ci interessa.

Le altre grandezze da considerare, in generale per qualsiasi struttura, ma riportate per la trave appoggiata, sono:

ω n _n⋅_lπ_

2

E J⋅ m ⋅

(pulsazione del modo n-esimo) f n _n_l_ 2 π 2 ⋅ E J⋅ m ⋅

(frequenza propria del modo n-esimo) T n 1

f n _{(periodo proprio del modo n-esimo)}

Lo studio delle vibrazioni libere ci permette di determinare delle caratteristiche proprie della struttura in esame. Confrontando le frequenze proprie dei vari modi di vibrazione con la frequenza del disturbo (vento, sisma, carichi in movimento) ci si può accorgere se alcuni modi possono venire esaltati: in questo caso le due frequenze saranno simili o uguali (risonanza). Dunque si dovranno adottare delle contromisure per cambiare o la frequenza del disturbo o la frequenza propria della struttura.

4.4.2 L’analisi dinamica sotto vibrazione forzata

Il nostro fine però è quello di determinare le massime sollecitazioni cui la struttura è sottoposta durante una storia di carico temporale: per le antenne strallate, questa può essere la storia delle velocità del vento o l’accelerogramma per il terremoto considerato.

Supponiamo dunque che la trave della figura 3 sia sottoposta ad un carico

pulsante q(x,t) variabile, in generale, sia lungo l’ascissa che nel tempo.

L’equazione di equilibrio del sistema differisce dalla 3 per la presenza al secondo termine della funzione q(x,t):

m ₂ t η d d 2 ⋅ E J⋅ ₄ x η d d 4 ⋅ + q x t( , ) (4)

Spesso il carico q(x,t) è rappresentato come somma di funzioni sinusoidali in x e

t di ampiezza qmax e pulsazione ω nota, ad esempio:

q x t( , ) _{q maxsin} n⋅ xπ⋅ l 

 

⋅ ⋅sin

( )

La soluzione è data dall’integrale generale nel caso dell’equazione omogenea, più la soluzione particolare (anch’essa una funzione sinusoidale di x e t):

η x t( , ) _{C n sin} n⋅ xπ⋅ l     ⋅ ⋅sin

( )

Imponendo le condizioni iniziali e quelle di vincolo, si ricavano tutte le costanti di integrazione, compresa l’ampiezza della deformazione (indeterminata nel caso delle vibrazioni libere):

η x t( , ) q max m⋅_{ω n}2−ω2_ sin n⋅ xπ⋅ l    ⋅ sin

( )

( )

La soluzione η(x,t), funzione di n, qmax e del rapporto ω/ωn, è composta dalla

sovrapposizione della vibrazione forzata e di quella naturale.

A causa delle resistenze passive (attrito) la vibrazione naturale tende a scomparire dopo un certo lasso di tempo e la deformazione segue l’andamento della vibrazione forzata. Nella prima fase però le due vibrazioni possono manifestarsi in fase e quindi produrre notevoli deformazioni aggravando le sollecitazioni nelle membrature.

Lo scopo dello studio di una struttura sotto vibrazioni forzate è quello di determinare l’ampiezza massima della deformata e delle sollecitazioni che ne conseguono, funzioni che dipendono dall’ampiezza della vibrazione impressa. Se poi si vuole quantificare l’effetto dinamico con un coefficiente numerico (come si faceva in passato), una volta determinata la risposta massima (picco), si calcola il fattore di risposta dividendo questa per la deformazione media durante la storia di carico. Questo coefficiente, di solito adimensionale, permette di amplificare l’azione media (statica) in modo che fornisca gli stessi effetti della storia di carico:

fr = δpicco/δmedio

Notiamo che, negli esempi fin qui proposti, non si è fatto riferimento alle caratteristiche smorzanti della struttura quali attriti interni, scorrimenti e deformazioni plastiche. Nel seguito verrà introdotto lo smorzamento strutturale, peraltro caratteristica di difficile valutazione analitica, ma che influenza il comportamento di una struttura sotto azioni dinamiche.

4.4.3 I sistemi elastici discreti a più gradi di libertà: oscillazioni libere

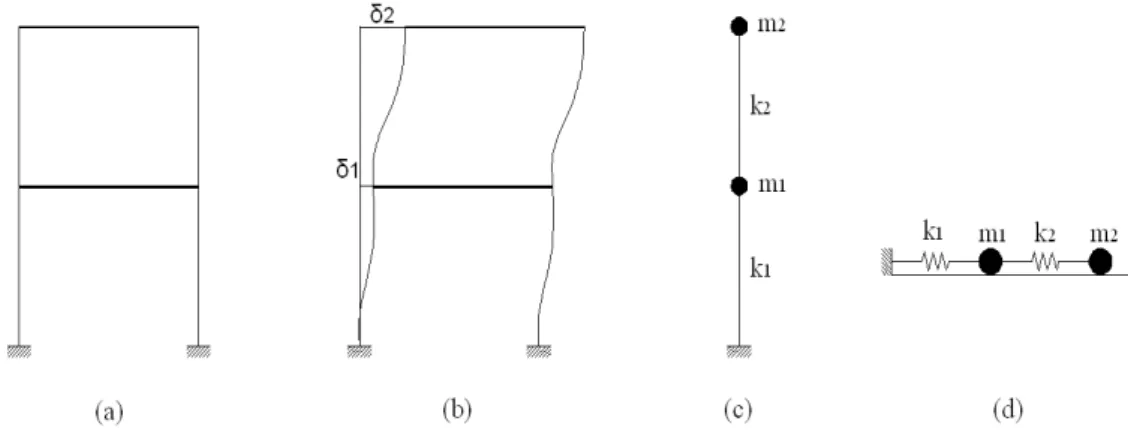
Quando, per un certo sistema strutturale, è lecito concentrare la massa in alcuni punti ed è possibile calcolare le caratteristiche di rigidezza per i gradi di libertà considerati, si può applicare l’analisi dinamica riferendosi a questi punti anziché alla struttura continua (come abbiamo fatto finora). Il tipico esempio è quello di un telaio piano in cui i traversi si considerano infinitamente rigidi e la loro massa viene concentrata nel baricentro:

Figura 4 – Schematizzazione di un telaio come sistema a due gradi di libertà dinamici.

Per gradi di libertà dinamici si intende il numero di spostamenti indipendenti che sono necessari per definire la posizione nello spazio di tutte le masse considerate, in ogni istante. Nel caso della fig. 4 si hanno due gradi di libertà: le traslazioni δ1 e δ2.

Per determinare la rigidezza ki dei piedritti è sufficiente applicare un carico

unitario in direzione di δi e calcolare il corrispondente spostamento: k è il

Se vogliamo studiare il moto sotto oscillazioni libere si può pensare che ad un certo istante t agisca, sulla massa m1, una forza perturbatrice che ne modifichi

la posizione di equilibrio. In questo caso si scrivono due equazioni del moto (una per ogni massa):

m1 2 t δ1 d d 2 ⋅ + _{k1 δ1}⋅ +_{k2 δ1 δ2}⋅

(

)

(

)

(

)

e scrivendo in forma matriciale: [m] {δ′′} + [k] {δ} = 0 (6)

nella quale:

[m] è la matrice delle masse (diagonale); [k] è la matrice di rigidezza del sistema; {δ′′} il vettore delle accelerazioni;

{δ} il vettore degli spostamenti.

La generica soluzione del sistema si può esprimere come il prodotto di una costante u per una funzione del tempo:

δ i t() u i sin ω t⋅⋅

( )

i =1,2 (nel nostro caso) (7)

Derivando e sostituendo questa funzione nel sistema 5/6, se ne ottiene un altro in cui le incognite sono u1 ed u2.

m1 − ⋅ω2+

(

)

Una soluzione diversa da quella banale si ha quando il determinante del sistema 8 è nullo: si ottiene un’equazione di secondo grado in ω2 _{la quale ci}

fornisce i due autovalori ω1 e ω2. Queste sono le pulsazioni naturali del

sistema.

Sostituendo, una alla volta, ω1 e ω2 nel sistema 8 si ottengono gli autovettori

che rappresentano la configurazione deformata della struttura attorno alla quale avvengono le vibrazioni:

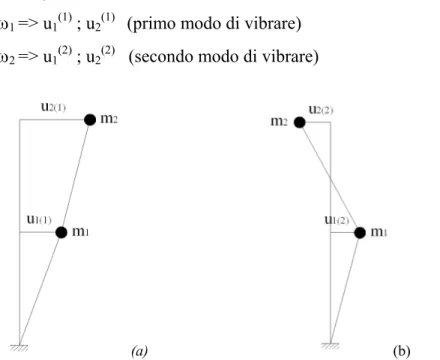
ω1 => u1(1) ; u2(1) (primo modo di vibrare)

ω2 => u1(2) ; u2(2) (secondo modo di vibrare)

(a) (b)

Figura 5 - Forme modali per il telaio di fig. 4: primo modo (a), secondo modo (b).

Agli autovettori si da’ il nome di “forme modali”; il metodo di analisi è detto “analisi modale”.

Anche in questo caso, problema delle vibrazioni libere, non si riesce a calcolare l’ampiezza ui dei modi ma solo il rapporto che c’è fra u1 ed u2.

4.4.4 Lo smorzamento strutturale

Abbiamo detto che le oscillazioni libere si esauriscono dopo un certo tempo (la struttura smette di oscillare) a causa di attriti interni. Bisogna introdurre il concetto di smorzamento strutturale e crearne un modello da poter inserire nell’analisi fino a qui svolta.

Per simulare il comportamento della struttura, si ipotizza che lo smorzamento vari in funzione della velocità assunta dalle masse durante la vibrazione: si introduce il rapporto di smorzamento c che genera un’azione proporzionale al prodotto c⋅δ′(t), indicando con δ′ la velocità delle masse. Il sistema 6 assume la

forma:

[m] {δ′′} + [c] {δ′} + [k] {δ} = 0 (9)

nel quale, oltre ai simboli visti:

[c] è la matrice di smorzamento

{δ′} il vettore delle velocità a livello delle varie masse.

Purtroppo, anche attuando il cambio di variabile 7, questa matrice non è diagonale e non rende possibile la scomposizione del sistema in equazioni indipendenti.

Dal punto di vista sperimentale, si è constatato che c è direttamente proporzionale ad ω quindi i modi di vibrare superiori risultano tanto più smorzati quanto più sono lontani dal modo fondamentale. In altre parole, i modi superiori risultano talmente smorzati che non portano contributo alla soluzione complessiva. E’ per questo che si trascurano i termini fuori della diagonale della matrice [c] senza commettere gravi errori oppure si arresta l’analisi ai primi tre o quattro modi di vibrare.

Un modo per rendere la matrice [c] diagonale è quello di esprimere lo smorzamento come combinazione lineare della matrice delle masse e quella delle rigidezze:

[c] = α ⋅ [m] + β ⋅ [k]

E’ questo il sistema adottato dai moderni programmi di calcolo per poter risolvere le equazioni del sistema. I valori dei coefficienti α e β sono incogniti a priori e di solito si assume per entrambi il valore di 0.05. Se si suppone nullo α allora, come detto poco sopra, lo smorzamento è proporzionale a ω ed i modi superiori risultano più smorzati. Se invece si suppone β = 0 allora lo smorzamento è proporzionale alle masse quindi inversamente proporzionale ad ω e i modi superiori risultano meno smorzati dei primi.

4.4.5 I sistemi elastici discreti a più gradi di libertà: vibrazioni forzate

Anche l’analisi modale deve essere condotta sotto vibrazioni forzate per determinare la massima risposta strutturale: in questo caso infatti si determinano i modi di vibrare, compresa la loro ampiezza (che, come abbiamo visto più sopra, dipenderà dall’ampiezza della perturbazione).

In generale il sistema di equazioni 9 assume la forma: [m] {δ′′} + [c] {δ′} + [k] {δ} = {T} {q(t)} (10)

dove, oltre ai simboli noti:

{T} è il vettore di trascinamento (composto da 0 e 1 a seconda che la causa perturbatrice agisca o meno nel grado di libertà considerato);

{q(t)} è il vettore della causa perturbatrice (forza o spostamento).

Al solito q(t) può essere una funzione qualsiasi che descrive per esempio,

l’andamento della accelerazione del suolo o la fluttuazione della velocità del vento.

Allo stesso modo si opera la sostituzione in coordinate modali 7: δ i t() u i sin ω t⋅⋅

( )

(i =1, 2…, n) ottenendo

[m] {u}{-ω2_{} + [c] {u} {ω}+ [k] {u} = {T} {q}

(t)} (11)

da cui si ricavano tanti modi {u}i _{quanti sono i gradi di libertà considerati.}

Il sistema delle equazioni 11 può essere integrato con metodi numerici e fornisce la risposta strutturale istante per istante mentre viene applicata la forzante. Questo modo di procedere, anche se laborioso dal punto di vista del calcolo, è indispensabile per le antenne strallate e, in generale, per tutte le strutture strallate dove la deformabilità dello strallo sotto vibrazione può interagire pericolosamente con quella del resto della struttura.

I procedimenti analizzati in questo paragrafo hanno finora riguardato quella che viene chiamata “analisi dinamica non lineare”. Questa permette di trovare la risposta della struttura istante per istante e di capirne quindi l’effettivo comportamento. Tutto ciò a discapito del tempo necessario per definire il modello e svolgere l’analisi.

Poiché spesso, almeno per strutture di importanza ordinaria, ci interessa sapere quale è la massima deformazione o le massime sollecitazioni sotto carico pulsante, si può compiere “l’analisi dinamica lineare”.

Il primo passo è quello di risolvere il problema delle vibrazioni libere della struttura determinando, o con lo schema continuo o con l’analisi modale, i modi di vibrare con le relative frequenze e periodi propri.

Per l’azione del vento è sufficiente prendere in considerazione la frequenza del primo modo di vibrare (frequenza fondamentale); in funzione di questa, della velocità di riferimento del vento e di altri parametri strutturali è possibile calcolare il fattore di picco della risposta. Questo andrà ad aumentare il coefficiente dinamico per il calcolo della pressione del vento. In tale modo l’azione media (applicabile staticamente alla struttura) viene amplificata per tener conto dei fenomeni oscillatori dovuti all’interazione fra vento e struttura. La procedura è specificata in un’appendice informativa (Annesso B) dell’Eurocodice 1 parte 2-4.

Per l’azione del sisma si definisce uno spettro di risposta di progetto: le espressioni analitiche sono in funzione della zona sismica (accelerazione al suolo), della stratigrafia del terreno di fondazione, del coefficiente di smorzamento e del fattore di duttilità della struttura. Di solito gli spettri di risposta forniscono la massima accelerazione al suolo Sa(T) oppure la massima

velocità Sv(T) o il massimo spostamento Sd(T).

Si entra nello spettro con il periodo Tn del modo considerato e si legge la

massima risposta nel termine voluto. E’ dunque necessario combinare i massimi per ogni modo secondo la combinazione quadratica poiché difficilmente si manifesteranno tutti nello stesso istante. Il numero di modi da considerare dipende dalla massa partecipante di ogni modo. La procedura dettagliata per compiere questo tipo di analisi è illustrata nell’attuale D.M 14 Gennaio 2008.

4.5 L’analisi dinamica relativamente alle antenne strallate

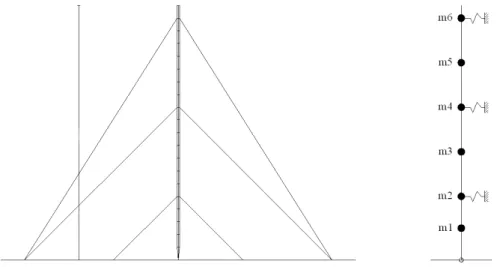
Tornando all’oggetto della tesi, le antenne strallate, in passato l’analisi dinamica modale veniva condotta concentrando le masse in corrispondenza dei punti di attacco degli stralli al traliccio e nella mezzeria delle campate:

Figura 6 - Schema per condurre l'analisi modale di un'antenna strallata.

Per simulare il comportamento sotto l’azione del vento, al livello di ogni massa veniva fatta agire una storia temporale di velocità, della durata di qualche minuto, generata numericamente con svariati modelli (vedi Cap. III, par. 3.5) oppure rilevata nella zona dove sorgeva la costruzione.

Questo modello molto semplice e con pochi gradi di libertà veniva studiato per calcolare i valori massimi dello spostamento δ di un punto di controllo, generalmente la sommità dell’antenna.

Elaborando statisticamente i valori della risposta, si determinava il valore medio δm ed il valore massimo δmax più probabile durante la storia di carico.

Il rapporto δmax / δm forniva il fattore di risposta della struttura: questo

rappresentava il coefficiente dinamico che, moltiplicato per l’azione media del vento (statica), produceva gli stessi effetti.

Veniva svolta l’analisi statica non lineare amplificando l’azione media del vento con il fattore di risposta.

Per l’azione sismica si utilizzava invece lo spettro di risposta, poiché gli effetti del sisma erano di entità minore rispetto a quelli del vento date le basse masse in gioco.

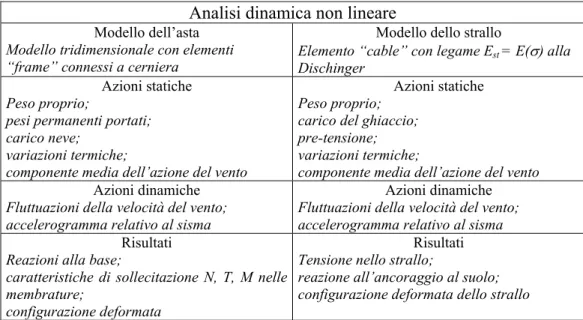
Oggigiorno, sul modello di un’antenna strallata, l’analisi dinamica sarà condotta per l’azione del vento e per l’azione sismica: si fornirà al programma di calcolo la storia temporale della velocità del vento e l’accelerogramma del terremoto di progetto; il software considererà l’effettiva distribuzione delle masse e, tramite integrazione numerica, fornirà i risultati in termini di deformazioni e sollecitazioni (vedi par. 4.8).

Analisi dinamica non lineare

Modello dell’asta

Modello tridimensionale con elementi “frame” connessi a cerniera

Modello dello strallo

Elemento “cable” con legame Est = E(σ) alla

Dischinger

Azioni statiche

Peso proprio;

pesi permanenti portati; carico neve;

variazioni termiche;

componente media dell’azione del vento

Azioni statiche

Peso proprio; carico del ghiaccio; pre-tensione; variazioni termiche;

componente media dell’azione del vento

Azioni dinamiche

Fluttuazioni della velocità del vento; accelerogramma relativo al sisma

Azioni dinamiche

Fluttuazioni della velocità del vento; accelerogramma relativo al sisma

Risultati

Reazioni alla base;

caratteristiche di sollecitazione N, T, M nelle membrature;

configurazione deformata

Risultati

Tensione nello strallo;

reazione all’ancoraggio al suolo; configurazione deformata dello strallo Tabella 3 - Modello, azioni e risultati per l’analisi dinamica non lineare da svolgere con codice di calcolo.

4.6 L’analisi statica non lineare con il programma agli elementi finiti SAP 2000

L’esempio di analisi strutturale di un’antenna strallata che verrà presentato nel prossimo capitolo, è stato risolto con il programma di calcolo SAP 2000 v. 11.0.4©. Il modello della struttura è stato così impostato:

- le aste del traliccio reticolare sono elementi “frame”; - gli stralli sono elementi “cable”.

La presenza di elementi cables impone di eseguire un’analisi non lineare sotto la sola azione del peso proprio per definire un’unica configurazione deformata dell’elemento. Questo perché i cables sono non resistenti a flessione e, alle loro estremità, vengono creati automaticamente dei nodi a cerniera sferica. L’analisi non lineare sotto peso proprio fa disporre l’elemento secondo la catenaria che viene assunta come configurazione a riposo.

L’analisi statica non lineare avviene per step di carico ∆P successivi applicati alla struttura considerando, di volta in volta, la configurazione deformata δi al

termine dello step i-esimo.

In ogni step, opportunamente piccolo, si esegue un’analisi lineare.

Alla fine del primo step si trova la configurazione deformata δ1: considerando

le sollecitazioni nella struttura si scrivono le equazioni di equilibrio nei nodi. Queste, in generale, non risultano verificate: si ottiene lo squilibrio nodale ∆P1.

Alla configurazione (∆P; δ1) si applica lo squilibrio nodale ∆P1, ricercando una

nuova configurazione deformata che sarà più prossima a quella effettiva.

Si troverà un nuovo squilibrio nodale ∆P2, che verrà applicato alla

configurazione (∆P + ∆P1 ; δ1) e così via finchè, nei passi sucessivi lo

squilibrio nodale è minore della tolleranza considerata.

A tal punto si applica un nuovo step ∆P e si ripete il procedimento.

Quando si applica lo squilibrio nodale è possibile considerare la matrice di rigidezza:

- della struttura di partenza: si ha convergenza di tipo lineare (metodo di Newton-Raphson modificato);

- della struttura al termine dello step considerato: si ha convergenza di tipo quadratico (metodo di Newton- Raphson).

In SAP 2000 è possibile impostare il numero massimo di iterazioni all’interno di uno stesso step per entrambi i metodi.

Il programma permette di considerare due tipi di non linearità: • non linearità materiale;

Per ciò che riguarda la non linearità materiale, è possibile immettere, per punti, il legame costitutivo tensione – deformazione: ciò è molto utile per gli stralli che hanno il modulo elastico tangente variabile in funzione della tensione nella fune (modulo elastico alla Dishinger).

La non linearità geometrica può essere impostata secondo due criteri:

1) effetto “P-delta”: quando, a causa di tensioni elevate negli elementi (dovute a forze o coppie) le equazioni di equilibrio scritte nella configurazione indeformata e in quella deformata danno risultati molto diversi, anche se le due configurazioni differiscono di poco. Gli sforzi di trazione tendono a diminuire questo effetto mentre quelli di compressione lo favoriscono; 2) effetto “P-delta con grandi spostamenti”: tutte le equazioni di equilibrio

vengono scritte nella configurazione deformata che differisce di molto da quella indeformata anche se gli sforzi presenti sono bassi. E’ questo il caso tipico dello strallo.

Quando si prevede di impostare un caso di analisi non lineare, partendo dalla configurazione deformata al termine di un precedente caso non lineare, è opportuno scegliere lo stesso tipo di non linearità per non influenzare la soluzione. In questo modo, inoltre, le azioni presenti nel caso percedente sono incluse anche in quello seguente.

E’ indispensabile predisporre gli elementi cables con una mesh abbastanza fitta per fare in modo che le rotazioni e le tensioni relative, fra elementi della mesh consecutivi, siano piccole.

Quando nel modello sono presenti elementi cables, per essi viene automaticamente impostata la non linearità P-delta con grandi spostamenti: il tipo di non linearità che vogliamo considerare dipende perciò da come è fatto il resto della struttura.

E’ possibile inoltre impostare i parametri per il controllo della soluzione: • numero massimo di step: permette di impostare il numero di step di carico

da salvare durante l’analisi e quindi di controllare la durata del processo. Qualora il risultato dell’analisi non converga nel numero di step considerati, è indispensabile aumentare tale numero;

• numero massimo di step nulli: se durante l’analisi viene raggiunto tale valore il processo si arresta. Il fatto che si verifichino troppi step nulli è indice di errori nell’impostazione del modello o nel basso numero di iterazioni permesse in uno stesso step;

• numero massimo di iterazioni per step: se in uno step di carico la soluzione non converge nel numero massimo di iterazioni consentite, il programma dimezza lo step di carico e riprova. Di solito valori compresi fra 10 e 25 vanno bene per la gran parte delle strutture ma per strutture strallate è consigliato un numero maggiore di 100;

• tolleranza di convergenza: questo valore è lo scarto fra la forza agente sulla struttura e quella determinata durante il processo di convergenza. Quanto più questo valore è piccolo, tanto più l’analisi è accurata: per strutture strallate è consigliato il valore 10-4 N.

I risultati del processo di analisi sono le caratteristiche della sollecitazione nei vari elementi, le reazioni vincolari e la deformata della struttura. E’ possibile salvare i risultati non solo nello stato finale ma anche ad ogni step di carico. Ciò è utile per valutare comportamenti anomali del modello che possono pregiudicare la soluzione finale.

Si sottolinea l’importanza dell’ordine con cui vengono applicate le azioni alla struttura: se questo viene cambiato, cambierà anche la soluzione poiché le azioni vengono applicate successivamente, una alla volta, sulla configurazione deformata che si ottiene dall’azione precedente. E’ opportuno prevedere quindi alcune possibili “gerarchie” fra i casi di analisi secondo la logica “main – dependent”.

4.7 L’analisi dinamica non lineare alle oscillazioni libere con il programma agli elementi finiti SAP 2000

Con il codice di calcolo SAP 2000 l’analisi dinamica alle oscillazioni libere viene definita “analisi modale”.

1) agli autovalori: vengono determinate le forme modali e le frequenze proprie del sistema strutturale sotto oscillazione libera non smorzata;

2) ai vettori di Ritz: vengono ricercati quei modi che sono eccitati da carichi particolari.

Per l’antenna strallata oggetto di tesi si è performato l’analisi modale agli autovalori, poiché permette di individuare i comportamenti dinamici propri della struttura: si capisce per quali frequenze vengono eccitati gli stralli inferiori, per quali altre gli stralli superiori e ancora per quali frequenze è il traliccio che governa la deformazione.

L’analisi ai vettori di Ritz è utile, ad esempio, quando sulla struttura sono collocate delle macchine con masse in movimento, aventi una certa frequenza operativa che può interagire con le frequenze proprie della struttura.

L’analisi modale in SAP 2000 è sempre di tipo lineare: questo non significa che sia impossibile valutare il comportamento di strutture “non lineari” come le antenne strallate. E’ sufficiente impostare come configurazione di partenza, per la ricerca dei modi, quella ottenuta al termine di un caso di analisi non lineare (ad esempio sotto il peso proprio). Così facendo si valutano i modi nella condizione P-delta o nel caso di non linearità materiale.

L’analisi agli autovalori prevede la risoluzione del sequente sistema (vedi Par. 4.4.1 e 4.4.3):

[m] {u}{-ω2_{} + [k] {u} = 0}

in cui:

[m] è la matrice delle masse;

[k] è la matrice delle rigidezze;

{-ω2_{} è il vettore degli autovalori;}

{u} è il vettore delle corrispondenti forme modali.

Una volta ricavati gli autovalori ω2 _{si conosce la frequenza angolare ω e quindi}

la frequenza ciclica ed il periodo del modo considerato sono: f = ω/2π e T = 1/f

istante per istante, la posizione delle masse con cui si è discretizzato la struttura. In un qualsiasi modello strutturale le masse vengono automaticamente concentrate nei nodi fra gli elementi, inoltre l’utente può assegnare altri punti dove concentrare la massa.

Si comprende che una struttura avente molti nodi (l’antenna strallata analizzata nel prossimo capitolo ne ha 2094) fornisce altrettanti autovalori; i modi superiori, che hanno frequenza bassa, non condizionano il comportamento della struttura sotto vibrazione: è inutile quindi tenerli in conto. Ecco allora che è possibile specificare il numero minimo e massimo di modi che il programma deve ricercare. Sempre per la struttura analizzata si è impostato tale valore massimo a 100, risultato più che sufficiente.

Il processo di risoluzione dell’equazione dinamica agli autovalori avviene in una subroutine ed è di tipo iterativo: si può impostare la tolleranza sul valore della frequenza calcolata, per ciascun modo, in due passaggi successivi. Un valore ottimale è 10-9:

(fi+1 – fi)/fi+1 ≤ toll (i: iterazione i-esima)

Per ogni modo di vibrare che è stato trovato il programma fornisce i seguenti risultati:

- periodo proprio T in secondi; - frequenza propria f in Hz;

- frequenza angolare ω in radianti/secondi; - autovalore ω2 _{in radianti}2_/secondi2_.

Altri fattori di output che è possibile far stampare al programma sono i seguenti, descriviamoli uno ad uno.

“Fattore di partecipazione modale”: è dato dal prodotto scalare fra il vettore della forma modale e le componenti del carico di accelerazione nelle tre direzioni X, Y, Z. Per il modo n-esimo si ha:

fxn = unT ⋅ ax

fyn = unT ⋅ ay

dove unT è il vettore della forma modale trasposto ed ax, ay, az, i vettori con le

componenti unitarie delle accelerazioni rispettivamente lungo X, Y e Z.

Le componenti del vettore un sono normalizzate rispetto alla matrice diagonale

delle masse secondo il seguente criterio: unT [m] un = 1

“Rapporto di massa partecipante”: fornisce una misura di quanto il modo n-esimo è importante nella risposta alle accelerazioni nelle tre direzioni spaziali. Ad esempio, per la direzione X, è dato da:

rxn = (fxn)2 / Mx

dove Mx è la somma della massa non vincolata che è libera di muoversi in

direzione X.

Il rapporto di massa patecipante è dato in percentuale e tanto più è grande, tanto più il modo considerato contribuisce ad aumentare l’accelerazione globale sulla struttura. Si riesce così a capire quanti e quali modi considerare nell’analisi dinamica con spettro di progetto, ad esempio per l’azione sismica. “Rapporto di massa partecipante per carichi assegnati”: fornisce una misura di quanto il modo n-esimo contribuisce alla risposta strutturale per un certo carico statico o dinamico assegnato. Per ciò che riguarda i carichi dinamici questo indice non tiene conto della variazione temporale ma solo di quella spaziale. Analiticamente è dato da:

rnS = (fn / ωn)2 / uT ⋅ P (nel caso di azioni statiche)

rnD = (fn)2 / aT ⋅ P (nel caso di azioni dinamiche)

dove:

fn = unT ⋅ P fattore di partecipazione modale per l’azione considerata;

u soluzione del sistema [k] u = P nel caso di azione statica;

a soluzione del sistema [m] a = P nel caso di azione dinamica;

P vettore dell’azione statica o dinamica applicata;

Anche in questo caso maggiore è il rapporto e maggiore è il contributo del modo considerato nei confronti dell’azione applicata.

4.8 Lanalisi dinamica non lineare sotto vibrazioni forzate con il programma agli elementi finiti SAP 2000.

In generale l’analisi “time-history” permette di simulare il comportamento dinamico di una qualsiasi struttura sottoposta ad una storia di carico arbitraria. Come detto in precedenza, il modello di un’antenna strallata è costituito da elementi “frame” per le aste del traliccio reticolare e da elementi “cable” per gli stralli. La presenza di questi ultimi, caratterizzati dalla incapacità di resistenza flessionale, impone di dover eseguire l’analisi di tipo non lineare. Anche per l’analisi time history è possibile considerare la non linearità materiale e/o la non linearità geometrica (P-delta o P-delta con grandi spostamenti).

Affinchè l’analisi abbia luogo devono essere specificate le condizioni iniziali in cui la struttura si trova al momento dell’applicazione della storia di carico: - condizione iniziale nulla: la struttura ha spostamenti, velocità e

sollecitazioni nulle; non ci sono deformazioni dovute a carichi applicati in modo non lineare;

- condizione di una precedente analisi non lineare: gli spostamenti, velocità, sollecitazioni e deformazioni iniziali sono quelle ottenute al termine del precedente caso di analisi non lineare. Questo si verifica tipicamente nelle antenne strallate: la storia di carico è fatta agire sulla struttura nella configurazione dovuta al peso proprio e alla pretensione negli stralli.

Il programma permette di impostare una grande varietà di funzioni variabili nel tempo: sinusoidali, triangolari, spezzate (in generale periodiche), oppure definite dall’utente (transitorie).

L’ immissione della time history avviene per punti; nell’esempio applicativo del prossimo capitolo sono state utilizzate delle funzioni casuali definite nell’arco di 120 secondi che rappresentano l’andamento della fluttuazione di velocità del vento. Allo stesso modo si può immettere l’accelerogramma relativo ad un evento sismico.

Appare dunque evidente che il programma permette di legare la time history o ad una condizione di carico o ad un valore dell’accelerazione.

Il programma discretizza la struttura concentrando le masse nei punti che definiscono la mesh degli elementi cable e frame: quanto più questa è fitta, tanto più la risposta sarà accurata ma, di contro, più lungo sarà il tempo necessario ad eseguire l’analisi.

L’analisi si sviluppa mediante la risoluzione, con procedimento iterativo, delle equazioni di equilibrio dinamico (vedi Cap. IV, par. 4.4.2 e 4.4.5):

[m] {δ′′} + [c] {δ′} + [k] {δ} = {q(t)}

in cui:

[m] è la matrice delle masse;

[c] è la matrice di smorzamento;

[k] è la matrice di rigidezza;

{δ′′}, {δ′}, {δ} sono i vettori accelerazione, velocità e spostamento della

struttura;

{q(t)} il vettore delle azioni applicate (carichi o accelerazioni).

Il programma risolve il sistema ad ogni step temporale con il quale è stata definita la time history; l’utente può specificare uno step temporale più piccolo ottenendo i seguenti vantaggi:

- ridurre il numero di iterazioni non lineari;

- aumentare il grado di accuratezza dell’integrazione.

Qualora la soluzione avesse convergenza lenta, automaticamente lo step temporale viene diminuito.

E’ sempre bene performare l’analisi non lineare alle oscillazioni forzate impostando step temporali sempre più piccoli finchè la soluzione finale non è più influenzata dalla dimensione dello step.

L’integrazione delle equazioni del moto può essere fatta con diversi algoritmi: è consigliato, per avere un primo risultato in modo veloce, utilizzare l’algoritmo HHT con parametro α = -1/3 e successivamente aumentare α fino a 0. Bisogna infatti tenere in conto che l’analisi time history non lineare richiede un vasto numero di iterazioni e, anche con sturtture semplici, il tempo necessario a ricavare la soluzione è alto. Per fare un esempio, il modello

dettagliato dell’antenna strallata del prossimo capitolo impiega circa 3 ore per fornire la soluzione.

La matrice di smorzamento è calcolata dal programma come combinazione lineare della matrice di rigidezza e della matrice delle masse secondo due coefficienti specificati dall’utente. Si deve tener presente che:

- la quota di smorzamento dovuta alla matrice di rigidezza è direttamente proporzionale alla frequenza della vibrazione: le alte frequenze risultano più smorzate; inoltre lo smorzamento è maggiore per gli elementi strutturali con comportamento lineare;

- la quota di smorzamento dovuto alla matrice delle masse è direttamente proporzionale al periodo della vibrazione: i lunghi periodi risultano più smorzati.

Il software permette di evere il controllo del procedimento risolutivo mediante i seguenti parametri:

• dimensione massima dello step temporale: impostando questo valore si permette al programma di salvare la soluzione non solo in corrispondenza dello step che definisce la funzione time history, ma anche nel sotto-step impostato. Ad esempio se lo step della time history è 1 secondo e si imposta la dimensione massima al valore 0.1 secondi, il programma ricerca la soluzione su 10 step temporali da 0.1 secondi. Ciò permette di avere risultati più accurati ed è consigliato diminuire questo parametro man mano che si affina l’analisi;

• dimensione minima dello step temporale: se la soluzione non converge, il programma dimezza autonomamante lo step temporale finchè non raggiunge la convergenza. L’impostazione di questo valore permette di evitare che l’analisi non richieda step temporali troppo piccoli (fino a 10-10 secondi), indice di presenza di errori nel modello;

• numero massimo di iterazioni per step: è possibile impostare il numero di iterazioni che il programma esegue all’interno di uno step prima di dimezzarlo, nel caso la soluzione non converga. Per le strutture strallate è

consigliato impostare questo valore a 100 o più, affinchè lo step temporale non venga diminuito troppo;

• tolleranza di convergenza: questo valore è lo scarto fra la forza agente sulla struttura e quella determinata durante il processo di convergenza. Per ottenere buoni risultati nell’analisi non lineare P-delta con grandi spostamenti è opportuno diminuire questo valore più che negli altri casi (consigliato 10-4 N).

Al termine del processo risolutivo vengono fornite le caratteristiche della sollecitazione, le reazioni vincolari e la configurazione deformata della struttura ad ogni step temporale che è stato impostato. Inoltre è possibile visualizzare l’inviluppo dei vari effetti durante la storia di carico: con essi ci si può rendere conto dell’amplificazione dinamica generata dalla storia di carico rispetto al caso in cui l’azione è applicata in modo statico.

4.9 Il criterio di analisi proposto per le antenne strallate

Nei paragrafi precedenti abbiamo visto come condurre vari tipi di analisi su strutture a comportamento non lineare. Il nostro obbiettivo è però quello di fornire una procedura semplice che porti al corretto dimensionamento di un’antenna strallata. Si suggerisce pertanto il seguente criterio:

1) si stabilisca l’altezza da raggiungere ed il numero di stralli da impiegare per l’equilibrio della struttura in funzione della copertura voluta per il segnale e della disponibilità di spazi in situ;

2) si scelga la forma della sezione trasversale: per altezze inferiori ai 150/200 m va bene quella quadrata; per altezze superiori è economicamente migliore quella triangolare equilatera (risparmio di materiale);

3) si esegua l’analisi statica lineare o non lineare:

a. lo schema statico dell’antenna sarà una trave continua verticale su più appoggi fissi o cedevoli;

b. la sola azione considerata sarà quella del vento, secondo il modello statico con legge di variazione logaritmica;

c. con i momenti flettenti ed i tagli lungo l’asta si dimensionano le sezioni dei montanti e delle aste di parete (diagonali e calastrelli); con le reazioni agli appoggi si dimensiona la sezione dello strallo; NOTA: questa analisi può essere condotta con semplici calcoli “a mano”; si può dire che l’analisi statica non lineare, anche se poco più laboriosa, permette di eseguire un migliore predimensionamento e di valutare la deformabilità della struttura;

4) si crei il modello dell’antenna strallata con il codice di calcolo agli elementi finiti e si esegua l’analisi statica non lineare considerando, insieme all’azione del vento, tutte le altre a carattere statico (peso proprio, peso delle antenne, carico neve, variazioni termiche, pretensione, ecc.): in questo modo si affina il dimensionamento, si controlla il rispetto dei limiti di deformabilità e si verifica che gli stralli sottovento rimangano comunque tesi (si stabilisce la pretensione corretta);

NOTA: è meglio che le verifiche di resistenza e deformabilità siano rispettate con un buon margine in questa fase; ciò eviterà di dover fare onerose modifiche sul modello nelle fasi successive;

5) sempre con il codice di calcolo si esegua l’analisi alle oscillazioni libere che sarà indispensabile nel caso che l’analisi sismica venga fatta con spettro di progetto;

6) infine si esegua l’analisi dinamica non lineare alle oscillazioni forzate: a. l’azione del vento verrà modellata con una time history (generata

numericamente o ricavata da elaborazioni statistiche);

b. l’azione sismica verrà modellata con l’accelerogramma relativo ad un evento sismico;

c. si eseguiranno le combinazioni delle azioni tenendo in debito conto il comportamento non lineare (gerarchia fra i casi di analisi);

d. con l’inviluppo delle sollecitazioni e delle deformazioni durante la storia di carico si eseguiranno le verifiche definitive.