3 INTRODUZIONE ALL’ASTRODINAMICA 3

3

3

INTRODUZIONE ALL’ASTRODINAMICA

3.1 Introduzione

Questo capitolo introduce i principi fondamentali dell’astrodinamica ed alcu-ne chiarimenti circa i concetti meccanici utilizzati durante l’analisi orbitale sviluppa-ta nel capitolo quarto.

L’astrodinamica è lo studio della traiettoria di un satellite, del suo cammino nello spazio; quando questo cammino è una curva chiusa si parla di orbita.

Il punto di partenza per lo studio del moto di un satellite è la scelta di un si-stema di riferimento, a cui fa seguito la necessità di una teoria analitica che permetta di conoscere in prima approssimazione la situazione reale della traiettoria. Il mezzo più potente e veloce per arrivare ad una prima comprensione del moto è la teoria ana-litica delle orbite Kepleriane. Questa approssimazione deve essere adeguatamente modificata al maturare del disegno. E’ necessario, infatti, introdurre altri effetti che alterano la forma classica definite dalle Leggi di Keplero per raggiungere la traietto-ria reale del satellite. Forze non desiderate che agiscono sul satellite e ne disturbano il moto, portandolo fuori dall’orbita nominale, sono normalmente chiamate perturba-zioni. Spiegheremo brevemente le tipiche sorgenti di perturbazione e noteremo le cause più importanti di perturbazione relative alle orbite terrestri a bassa quota.

3.2 Moto Kepleriano

Isaac Newton, nelle celebrate Philosophiae Naturalis Principia Mathematica, ha consolidato le basi della Meccanica Celeste. Partendo dalle Leggi di Keplero, pas-sando attraverso le considerazioni di geni universali come Galileo, Copernico e

Tycho Brahe, è arrivato all’impossibile: rendere fattibile, in un futuro che oggi è or-mai storia, i viaggi spaziali. Il Principia Mathematica, pubblicato nel 1687, è consi-derato largamente il più grande lavoro scientifico creato da un’unica persona e, forse, il più importante contributo allo sviluppo delle conoscenze dell’umanità. In tale lavo-ro sono stabilite le Leggi di Moto chiamate di Newton in onore dall’autore e le for-mulazioni matematiche di una forza particolare: la forza di gravità. Con questa pub-blicazione fu spiegato, finalmente, il moto dei pianeti e dei satelliti. Basandosi sulle opere dei grandi del passato, “over giant’s shoulders”, come egli stesso ha definito la base del proprio lavoro, Newton ha sviluppato la meccanica celeste, partendo da os-servazioni empiriche, fino a produrre una solida struttura matematica con cui è pos-sibile identificare e conoscere il moto dei corpi celesti. Con il moto dei pianeti cono-sciuto attraverso le Leggi di Keplero, egli ha risolto il problema inverso, trovare le forze che producessero questo moto, giustificando le leggi empiriche di Keplero. Fi-nalmente, attraverso questa “nuova” forza, si è reso possibile risolvere il problema diretto, scoprire il moto di un qualunque corpo ne sia affetto.

Un’intuitiva presentazione geometrica delle Leggi di Keplero è:

Prima Legge: L’orbita di ciascun pianeta è un ellisse, con il Sole in uno dei due fuo-chi.

Seconda Legge: La linea che unisce il pianeta al Sole spazza aree uguali in tempi uguali.

Terza Legge: Il quadrato del periodo di rotazione di un pianeta è proporzionale al cubo della sua distanza media dal Sole.

In più, è qui presentata la più generale formulazione della forza di gravità, r

r GMm Fr =− ₃ ⋅r

3.2-1 dove Fr è la forza tra due oggetti di massa m ed M, rr è il vettore tra loro e G è la co-stante di gravitazione di Newton. E’ notazione comune raggruppare G ed M nel ter-mine µ (µ = G·M) definito come costante di gravitazione planetaria. Per la Terra µ (costante di gravitazione geocentrica) ha il valore di _{3.986005⋅10}14_m3 _s2_.

3.2.1 Equazione di moto di un Satellite

Usando la teoria gravitazionale e le sue leggi della meccanica, Newton fu abi-le a derivare abi-le Leggi di Kepabi-lero ed ad applicarabi-le a qualunque coppia di masse punti-formi (ipotesi di corpi a simmetria sferica) che si muovono sotto la loro mutua

attra-zione gravitazionale. Viene assunto che la gravità sia l’unica forza e che le due masse puntiformi siano gli unici corpi nel sistema.

Il problema kepleriano di due masse mutuamente attratte si riduce allo studio di un unico corpo grazie alla supposizione che uno dei due corpi, detto primario, sia piazzato nell’origine di un sistema di coordinate inerziali. Questa ipotesi risulta tanto migliore quanto più il primario sia di massa maggiore rispetto all’altro corpo, detto secondario. Questo è il caso di tutti i satelliti artificiali rispetto al corpo centrale di attrazione. Se, invece, le due masse sono comparabili si parla di problema dei due corpi ed il centro di massa del sistema si troverà tra i baricentri dei due corpi. Due masse a simmetria sferica che interagiscono gravitazionalmente devono rimanere nel piano definito dalle loro velocità e dalle loro posizioni relative, perché le forze sono centrali e non esistono forze che possano muoverli fuori da questo piano. Di conse-guenza, quando la gravità è l’unica forza, l’orbita definita da due oggetti interagenti è completamente determinata dalle loro relative posizioni e velocità.

Combinando la seconda legge di Newton con la sua legge di gravitazione (per esempio vedere [3]) otteniamo un’equazione per il vettore accelerazione del satellite:

(

r

)

r 0 dt r d 3 2 2 = ⋅ + − r r µ 3.2-2 dove rr è il vettore tra il Satellite e la Terra e µ la costante di gravitazione terrestre. Moltiplicando vettorialmente l’equazione 3.2-2 con rr si ottiene:

( )

0 0 × = = × r r dt d o r rr &&r r &r 3.2-3 ed integrando: h r r &r r r_{× = .} 3.2-4 Come risultato, il momento angolare per unità di massa del Satellite, hr, ri-mane costante e perpendicolare al piano dell’orbita (poiché perpendicolare sia ad rr che ad r&r ). Ne segue che il piano orbitale rimane fissato in un riferimento inerziale come notato in precedenza.

Una soluzione dell’equazione 3.2-2 è un’equazione polare di una sezione co-nica che fornisce la grandezza del vettore posizione in funzione della posizione nell’orbita, del tipo

(

)

ν cos e 1 e 1 a r 2 + − = 3.2-5 dove a è il semiasse maggiore, e l’eccentricità e ν è l’anomalia vera. Questo concetto sarà spiegato più approfonditamente nel prossimo paragrafo.

3.2.2 Elementi orbitali classici

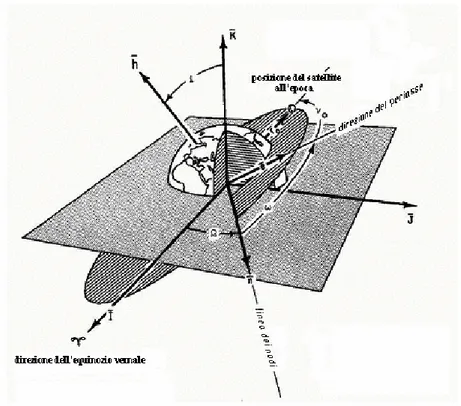
L’equazione 3.2-2 rappresenta un sistema di tre equazioni differenziali scalari del secondo ordine. Per integrare il sistema sono necessarie sei condizioni di integra-zione. Ci sono parecchi modi alternativi per selezionare questo gruppo di condizioni, una prima possibilità è quella di utilizzare la posizione e la velocità all’istante inizia-le, ma la scelta più utilizzata è di utilizzare un gruppo di parametri chiamati elementi orbitali classici, che hanno il vantaggio di fornire una percezione veloce ed intuitiva della geometria dell’orbita. Gli elementi orbitali classici sono formati dai parametri: a, e, ω, i, Ω e υ (vedere figura 3.2.1, estratta da [4], per ω, i, Ω, υ e figura 3.3.2 per a, e e υ).

Il semiasse maggiore, a, e l’eccentricità, e, definiscono la forma e la taglia dell’orbita. La rotazione dell’orbita nel proprio piano è definite dall’argomento del perigeo, ω. L’inclinazione, i, e l’ascensione retta del nodo ascendente (RAAN), Ω, definiscono il piano dell’orbita. In fine l’anomalia media specifica la posizione del satellite nell’orbita al tempo dell’epoca.

L’intersezione del piano dell’orbita e del piano di riferimento attraverso il centro di massa del corpo principale è chiamata linea dei nodi, dove i nodi sono i punti di intersezione della traiettoria dell’orbita sul piano di riferimento. In un satelli-te in orbita satelli-terrestre il piano di riferimento è quello equatoriale. Il nodo discendensatelli-te è il punto dove il satellite attraversa il piano di riferimento da nord a sud, il nodo a-scendente dove l’attraversamento avviene da sud a nord. La linea congiungente il pe-rigeo con baricentro del corpo principale è chiamata, invece, linea degli apsidi.

figura 3.2.1 Elementi orbitali classici.

i: L’inclinazione è l’angolo tra il vettore normale al piano di riferimento ed il vettore momento angolare. Quando l’inclinazione è 0 o 180°, si parla di orbite equatoriali. Con l’inclinazione di 90° l’orbita è cono-sciuta come polare.

Ω: L’ ascensione retta del nodo ascendente (RAAN in seguito) è l’angolo sul piano equatoriale misurato in direzione est tra l’equinozio vernale ed il nodo ascendente. Risulta indefinito nelle orbite equato-riali. L’equinozio vernale è il nodo ascendente dell’orbita della Terra intorno al Sole.

ω: La rotazione dell’orbita sul piano è definite dall’argomento del peri-geo o angolo al baricentro, misurato sul piano orbitale nella direzione del moto del satellite dal nodo ascendente al perigeo4.

a: Il semiasse maggiore è il parametro che da la grandezza della conica. Nel caso ellittico, per un satellite in orbita terrestre, rappresenta la se-mi distanza tra l’apogeo ed il perigeo, rispettivamente il più lontano ed il più vicino punto dell’orbita dalla Terra.

e: L’eccentricità è un parametro non dimensionale che definisce il tipo di conica e, conseguentemente, la forma. E’ uguale a 0 nelle

4 _{Un satellite che ruota attorno alla Terra nella stessa direzione in cui essa ruota attorno al proprio asse è su un}

renze, tra 0 ed 1 per le ellissi, uguale ad 1 per le parabole ed è mag-giore di 1 per le iperboli, l’eccentricità è un parametro classico nella geometria delle coniche che mette in relazione l’asse maggiore con la distanza tra i fuochi della conica.

υ: In fine, per specificare dove il satellite si trovi nella sua orbita si usa l’ anomalia vera, l’angolo al baricentro, misurato sul piano orbitale tra il perigeo e la posizione del satellite al tempo dell’epoca.

Come grandezze alternative per misurare la posizione del satellite al tempo dell’epoca si usano l’anomalia media, M, o l’anomalia eccentrica, E, come mostrato in figura 3.2.2.

figura 3.2.2 Elementi orbitali classici sul piano.

L’anomalia media è 360⋅t Pdeg, dove P è il periodo orbitale e t il tempo a partire dal passaggio del satellite al perigeo. E, introdotta come una variabile inter-media tra υ ed M, è l’angolo, misurato al centro dell’orbita, tra il perigeo e la proie-zione della posiproie-zione del satellite su un’orbita circolare di uguale semiasse maggiore. Ovviamente, per un’orbita circolare, υ, M ed E sono equivalenti. Da un’altra canto, queste variabili sono legate dalle equazioni di Keplero e di Gauss,

E e E M = − ⋅sin 3.2-6       ⋅       − + =       2 tan 1 1 2 tan 2 1 E e e υ 3.2-7 Come esempio sono riportate, in tabella 3.2-1, alcune proprietà delle orbite kepleriane. Tabelle più esaustive e dettagliate circa le proprietà di questo tipo di orbi-te possono essere trovaorbi-te in letorbi-teratura, come, ad esempio, in [1] e [2].

tabella 3.2-1 Alcune proprietà ed equazioni di uso comune per orbite ellittiche.

Raggio di Perigeo rp =a⋅

(

1−e

)

Velocità 

     − ⋅ = a r V µ 2 1

Raggio di Apogeo r_a =a⋅

(

1+e

)

Velocità media

a V_m = µ Semiasse maggio-re b=a⋅

(

1 e− 2

)

Velocità al Perigeo _      − ⋅ = a r V p p 1 2 µ Eccentricità p a p a r r r r e + − = _{Velocità all’Apogeo }      − ⋅ = a r V a a 1 2 µ Periodo orbitale µ π 3 2 a

P= ⋅ ⋅ Velocità angolare

me-dia n _a3

µ =

3.3 Moto non Kepleriano

I satelliti terrestri sono dominati dalla forza centrale gravitazionale della Ter-ra, ma sono affetti anche da altre forze, come l’attrazione gravitazionale di altri pia-neti più lontani (Sole e Luna prevalentemente) e forze non gravitazionali come la re-sistenza atmosferica e la pressione di radiazione solare. Poiché tali forze sono molto minori di quella gravitazionale possiamo supporre che l’orbita reale sia un’ellisse Kepleriana perturbata da poche forze addizionali, chiamate perturbazioni. Conse-guentemente, se nel modello di Keplero gli elementi geometrici rimanevano costanti, considerando le perturbazioni essi variano nel tempo.

Analiticamente l’equazione 3.2-2 deve essere modificata come segue, per contemplare gli effetti di perturbazione:

(

)

p 3 2 2 f r r dt r d r _r r ⋅ + ⋅ − = _µ − _{ε .} 3.3-1 In fr_p sono inglobate tutte le accelerazioni di perturbazione. Il parametro ε è una grandezza infinitesima che definisce la grandezza delle perturbazioni. Ponendo ε uguale a zero porta alla soluzione di ordine zero, di nuovo la soluzione di Keplero.

E’ in uso di studiare la variazione degli elementi orbitali ellittici come varia-zione delle coordinate del satellite. Chiamando λr il vettore che ingloba i sei elementi

ellittici a, e, ω, i, Ω e τ (espressione temporale di υ), una soluzione al primo ordine si ottiene da 1 0 f r r r ⋅ + =λ ε λ 3.3-2 dove λr₀ è il gruppo di elementi costanti del moto di Keplero raggruppati vettorial-mente. La soluzione del moto perturbato è in relazione con gli elementi ellittici attra-verso l’integrazione della derivazione degli elementi stessi,

∫

= ⋅f₁ λdt

ε r &r

3.3-3 note come Equazioni Planetarie di Lagrange, nella formulazione di Gauss.

Lagrange, sviluppando le equazioni di moto, ha ottenuto l’espressione forma-le della variazione degli eforma-lementi orbitali classici a cause di forze esterne perturbati-ve. Si suppone l’esistenza di una funzione potenziale delle perturbazioni, Up, che può essere derivata parzialmente rispetto ad ogni elemento orbitale ellittico. Uno svi-luppo matematico delle Equazioni Planetarie di Lagrange (LPEs) e degli sviluppi successivi dovuti a Gauss possono essere, ancora una volta, trovati in letteratura spe-cializzata.

(

)

(

)

(

)

(

)

(

)

(

)

e Up e e a a Up a i Up i e a e Up a e e i Up i e a Up i e a Up i e a dt di Up a e e Up e e a e Up a a ∂ ∂ − + ∂ ∂ = ∂ ∂ ⋅ − ⋅ ⋅ − ∂ ∂ ⋅ ⋅ − ⋅ = ∂ ∂ ⋅ ⋅ − ⋅ ⋅ = Ω ∂ ∂ ⋅ − ⋅ ⋅ + Ω ∂ ∂ − ⋅ ⋅ − = ∂ ∂ ⋅ ⋅ − ⋅ − ∂ ∂ ⋅ ⋅ − ⋅ − = ∂ ∂ ⋅ ⋅ − = µ µ τ µ µ ω µ ω µ µ ω µ τ µ τ µ 2 2 2 2 2 2 2 2 2 2 1 2 tan 1 1 1 1 1 sin 1 1 1 tan 1 1 1 sin 1 1 1 1 1 1 2 & & & & & 3.3-4 Queste equazioni sono l’espressione matematica delle LPEs. Sono di grande aiuto nel caso di perturbazioni che possano essere espresse come risultato di funzioni

potenziali e, al contrario, di nessun aiuto quando le forze siano non conservative. In-fatti le forze non conservative non possono venir espresse come funzioni potenziali ed è necessario, in questo caso, trovare un’altra formulazione. La forma di Gauss del-le LPEs fornisce la soluzione di questo probdel-lema.

Questa nuova formulazione è legata alla velocità di cambiamento nel tempo degli elementi orbitali classici. In questo caso le perturbazioni appaiono direttamente in forma di accelerazioni. Più precisamente ar è la componente radiale delle

accele-razioni di perturbazione, aθ è la componente normale al raggio vettore nella direzione

del moto ed ah è la componente perpendicolare al piano orbitale, in maniera da

for-mare una terna levogira con ar ed ah.

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

            − + +       − − − = + − = Ω + − −             + + − − = − + =             − − + − =     _{+ −} − = ν ν µ τ ω ν µ ω ν µ ν ν µ ω µ ω ν ν µ ν µ θ θ θ θ sin 1 1 cos 1 2 1 sin sin 1 1 sin 1 cot sin 1 cos 1 1 1 cos 1 sin 1 1 sin 1 2 2 2 2 2 2 2 2 2 2 2 2 2 3 e a r e a a e e a r e a i r a e a r a e a gi a p r a a a a e e e a r a dt di ea r er e a a a e a e e r a a e a e a a r h h r h r r & & & & & 3.3-5 Integrando le equazioni 3.3-4 o 3.3-5 come mostrato attraverso la 3.3-4, e co-noscendo un gruppo di parametri all’istante iniziale, è finalmente possibile ottenere l’evoluzione temporale degli elementi ellittici attraverso l’equazione 3.3-3.

3.3.1 Variazioni secolari e periodiche.

Si chiamano variazioni secolari quelle variazioni negli elementi che sono prodotte in maniera lineare. Gli elementi affetti da variazioni secolari continuamente tendono ad aumentare o diminuire il loro valore, potendo portare l’orbita, in tempi

più o meno lunghi, al collasso o all’incontrollabilità del satellite. Quando, invece, un elemento è perturbato in maniera periodica, con variazioni di corto o lungo periodo, rispettivamente più piccole o più grandi del periodo orbitale, soffre una deviazione oscillante dal suo valore nominale. Per questo si può vedere figura 3.3.1 , dove λi

rappresenta un generico elemento orbitale.

E’ essenziale identificare le componenti cicliche e secolari, e ciò può essere fatto graficamente o analiticamente; nel primo caso disegnando e tirando fuori le per-turbazioni di diversa natura, nel secondo attraverso l’integrazione della variazione degli elementi durante un appropriato numero di orbite, in maniera che si annullino gli effetti periodici.

figura 3.3.1 Variazione periodica e secolare di un parametro orbitale.

3.3.2 Perturbazioni.

Effetto della non sfericità terrestre.

La separazione tra il campo gravitazionale centrale di Newton e quello reale terrestre rappresenta la perturbazione principale per satelliti vicini alla Terra. In real-tà la Terra non è una sfera omogenea e simmetrica, ma risulta schiacciata ai poli con un profilo leggermente a pera, forma comunque distante da quella ideale sferica. L’accelerazione del satellite si ottiene attraverso il gradiente di una nuova funzione potenziale del campo gravitazionale terrestre. Una forma ampiamente usata è la fun-zione geopotenziale

              − = Φ

∑

n n E n n sinL r R P J 1 r µ 3.3-6 in cui RE è il raggio equatoriale terrestre, µ ancora la costante di gravitazione della

Terra, Pn i polinomi di Legendre e Jn dei coefficienti geopotenziali adimensionali

chiamati coefficienti zonali.

Attraverso l’espressione precedente della funzione potenziale, dividiamo la Terra in zone comprese tra due paralleli, regioni che, alternativamente, aggiungono o sottraggono qualcosa al potenziale della simmetria sferica.

Un’altra possibilità è dividere la Terra in spicchi (termini settoriali) o in una mosaico di regioni (termini tesserali) che modificano il potenziale del corpo singolo alla stessa maniera dei termini zonali. Informazioni addizionali possono essere trova-te in [2], [3] e [6].

I primi Jn, quelli che hanno un’importanza quantitativa maggiore, hanno i

se-guenti valori, ottenuti da [1]

6 4 6 3 3 2 10 61 . 1 J 10 54 . 2 J 10 08263 . 1 J − − − ⋅ − = ⋅ − = ⋅ =

J2 rappresenta matematicamente lo schiacciamento terrestre ed è,

chiaramen-te, il termine predominante nella funzione di perturbazione geopotenziale. Concet-tualmente si può supporre che questo effetto sia analogo a quello che si avrebbe ag-giungendo una cintura di massa equatoriale alla sfera omogenea terrestre come rap-presentato in figura 3.3.2, presa da [4].

figura 3.3.2 Effetto di J2.

Dato che J2 risulta essere, come minimo, di circa tre ordini di grandezza

funzione geopotenziale che include una correzione al primo ordine, assumendo una simmetria azimutale e misurando solo gli effetti di J2. Questa può essere scritto come

(

)

        −       + = Φ 1 3sin L r R J 2 1 1 r 2 2 E 2 µ 3.3-7 in cui il primo termine della somma rappresenta il potenziale del moto Kepleriano.

Come risultato possiamo conoscere la funzione potenziale della perturbazione ed usare le LPEs 3.3-5 per conoscere le variazioni dei parametri orbitali dovuti alla non sfericità della Terra. Funzione potenziale che può essere scritta come

(

)

2

[

2

(

₃

₍

)

₂2

₎

₃

]

(

)

3 E 2 2 3 2 E 2 p e 1 a cos e 1 i sin sin 3 1 2 R J L sin 3 1 r 2 R J U − + + − = − = µ µ ω ν ν . 3.3-8 La prima conclusione che si può trarre è che l’effetto di J2 non modifica il

va-lore del semiasse maggiore _∂Up_∂τ =0_. Quindi lo schiacciamento terrestre non può aggiungere o sottrarre energia all’orbita. Ci sono variazioni periodiche in tutti gli e-lementi orbitali, ma solo la RAAN e l’argomento del perigeo sperimentano variazio-ni secolari.

Le velocità di cambiamento dovute a J2, come spiegato in [1] sono:

(

)

(

₂

)

2 2 7 14 J2 2.06474 10 a cosi 1 e − − − ⋅ − ≅ Ω& 3.3-9

(

₂

)(

₂

)

2 2 7 14 J2 1.03237 10 a 4 5sin i 1 e − − − − ⋅ ≅ ω_& 3.3-10 dove, con le solite notazioni, a, è il semiasse maggiore in km, e, l’eccentricità, i, l’inclinazione e Ω&_J2 e ω& sono riportati in gradi al giorno. _J2

La 3.3-9 descrive matematicamente la regressione dei nodi, che causa una precessione del piano orbitale nello spazio inerziale; l’orbita ha una rivoluzione (re-trograda per orbite dirette) attorno all’asse terrestre. Per un’orbita polare (i = 90°) non esiste regressione nodale, per cui l’orbita polare è fissata nello spazio inerziale.

L’equazione 3.3-10 fornisce la precessione della linea degli apsidi: l’orbita ruota attorno al baricentro del sistema nel suo proprio piano. Questa rotazione è di-retta per valori di inclinazione minori di 63.4˚ e maggiori di 116.6˚, è retrograda per

le inclinazioni comprese tra questi due valori, chiamate inclinazioni critiche. Per i = 63.4˚ o i = 116.6˚ il perigeo rimane fissato sullo stesso parallelo terrestre.

Effetto della presenza di un terzo corpo.

Quando un satellite si trovi sotto l’influenza di un altro campo gravitazionale in aggiunta a quello terrestre, il moto kepleriano può essere perturbato in maniera importante. Le principali perturbazioni dovute ad un terzo corpo, per un satellite in orbita terrestre, sono a causa del Sole e della Luna, dovute, nel primo caso, alla sua grande massa e , nel secondo, alla sua vicinanza.

Non ci sono variazioni periodiche di tutti gli elementi, ma solo variazioni se-colari nel RAAN, nell’argomento del perigeo e nell’anomalia media. Comunque, la variazione secolare del moto medio può non essere considerata, in quanto trascurabi-le rispetto al moto medio stesso ed in conseguenza praticamente non ha influenza sull’orbita. Per quanto riguarda il RAAN e l’argomento del perigeo, le variazioni se-colari possono avere importanti ripercussioni solo nel caso di orbite a basso moto medio, quindi di più grande semiasse maggiore. Infatti, una distanza dalla Terra maggiore significa una maggiore influenza del campo gravitazionale di un eventuale terzo corpo. Concettualmente queste perturbazioni causano delle precessioni del pia-no orbitale simili a quelle prodotte dallo schiacciamento terrestre.

Una prima approssimazione delle variazioni di RAAN prodotte su orbite cir-colari o quasi circir-colari è data dalle equazioni seguenti, estratte da [1]:

(

cosi

)

n 00338 . 0 MOON ≅− ⋅ Ω& 3.3-11

(

cosi

)

n 00154 . 0 SUN ≅− ⋅ Ω& . 3.3-12 Per le variazioni sull’argomento del perigeo abbiamo

(

4 5sin i

)

/n 00169 . 0 2 MOON ≅ ⋅ − ω_& 3.3-13

(

4 5sin i

)

/n 00077 . 0 2 SUN ≅ ⋅ − ω_& 3.3-14 dove n è il numero di rivoluzioni al giorno (minore quando il moto medio diminui-sce), i è l’inclinazione dell’orbita, Ω& ed ω&, come sempre, sono in deg/giorno.

Notiamo che la Luna esercita un’influenza circa il doppio di quella data dal Sole.

Per misurare l’influenza di un altro terzo corpo, possiamo usare un metodo approssimato al primo ordine per determinare l’ordine di grandezza dell’accelerazione di perturbazione, come espresso in dettaglio in [3]. Questa stima deve considerare la perturbazione applicata sul satellite e oltre la Terra a causa del terzo corpo sotto studio

3 body 3 body 3 body 3 th th th r r Gm a = ⋅ 3.3-15 essendo m₃th_body la massa del terzo corpo, r₃th_body la minima distanza dalla Terra, ed r

il valore assoluto del vettore posizione rispetto alla Terra del satellite.

La relazione tra questa accelerazione di perturbazione e l’accelerazione pro-dotta dalla Terra nel moto kepleriano (riferita in questo caso ad un satellite in orbita terrestre e chiamata a_⊕) ci fornisce l’ordine di grandezza delle perturbazioni.

Di seguito è presentata un’applicazione di questo metodo per una stima delle accelerazioni prodotte dai principali pianeti del sistema solare per un satellite geosta-zionario5. Questi valori sono stati estratti da [3] e [6]. Come già visto, la Luna eserci-ta una forza doppia rispetto al Sole in accordo con le equazioni dalla 3.3-11 alla 3.3-14.

tabella 3.3-1 Principali perturbazioni prodotte su un GEOs da altri corpi celesti.

Terzo Corpo m₃th_body m⊕

body 3th r (km) a₃th_bodt a_⊕ Luna 1,20·10-2 3,90·105 1,50·10-5 Sole 3,30·105 1,50·108 7,20·10-6 Venere 8,10·10-1 4,30·107 7,50·10-10 Giove 3,20·10-2 6,30·108 9,00·10-11 Marte 1,07·10-1 _5,54·107 _4,65·10-11

Effetto della pressione di radiazione solare.

Ogni area esposta ad una radiazione elettromagnetica è soggetto ad una de-terminate pressione di radiazione, il rapporto tra la potenza ricevuta per unità di area sulla velocità della luce. In concreto, un satellite in orbita terrestre riceve radiazione dal Sole e dalla Terra, dovuta alla riflessione di una parte della radiazione solare

5 _{Un satellite Geostazionario, conosciuto come GEOs, rimane approssimativamente stazionario sopra} una precisa locazione sull’equatore terrestre. Questo accade ad una quota di 33786 km, per cui il pe-riodo orbitale del satellite è di 1436 min, eguagliando il pepe-riodo di rotazione siderale della Terra ri-spetto alle stele fisse.

(chiamata albedo) ed alla radiazione direttamente emessa sotto forma di infrarosso. Il contributo più importante, se il satellite non si trova in condizioni di eclissi, è la pres-sione di radiazione solare, con valore

2 6 8 4.5 10 N/m 10 3 1358 c I p = ⋅ − ⋅ = = 3.3-16 dove viene preso un valore dell’intensità di potenza ricevuta di 1358 W/m2 _{ed una}

velocità della luce di _3⋅108_{m/s, entrambi in [3]. Questa radiazione produce} un’accelerazione espressa da

(

)

s m A 1 10 5 . 4 ar_{=− ⋅} −6 _{⋅ +ε ⋅}r 3.3-17 dove A è l’area su cui agisce la pressione in m2, ε è il coefficiente di riflessione (0 <

ε < 1), m è la massa in kg del satellite, ed sr rappresenta il vettore col Sole. La ra-diazione di pressione solare causa una variazione periodica in tutti gli elementi orbi-tali, ma è rilevante solo in satelliti con un basso coefficiente balistico, termine notato attraverso la lettera B, proporzionale a m/A, ciò si ha con una bassa massa ed un’elevata superficie esposta al Sole. Spesso questa perturbazione non costituisce un problema per satelliti in volo a quote inferiori agli 800 km, dove è più critica la resi-stenza atmosferica.

Effetto della resistenza atmosferica.

Nelle orbite molto vicine a Terra e molto eccentriche, con bassa quota di pe-rigeo, la resistenza atmosferica rappresenta la più importante origine di perturbazio-ne. Quantitativamente è difficile sviluppare un accurato modello della resistenza at-mosferica, perché è difficile determinare con precisione la densità atat-mosferica, come anche il coefficiente di resistenza del satellite. In effetti la resistenza atmosferica, ρ, è una funzione della quota atmosferica e dell’attività solare, dovuta all’espansione del-la termosfera bassa (~90 km) a causa dell’eccitazione termica data daldel-la radiazione ultravioletta estrema (di frequenza fino a 0.2 µm).

L’accelerazione di perturbazione originata dalla resistenza può essere espres-sa come rel rel rel rel D D V V B 2 1 V V m A C 2 1 m D a r r r r _{= =− ρ =−} ρ 3.3-18

dove ρ è la densità atmosferica, A la superficie frontale del satellite, m la massa, Cd il

coefficiente di resistenza, Vr_rel la velocità del satellite relativa all’atmosfera e A

C m B

D

= , quello che abbiamo definito coefficiente balistico, parametro usato nell’analisi della resistenza.

Tenendo conto del moto dell’atmosfera abbiamo che Vrrel e fornita da r

V rel

Vr = r −Ωr ×r

3.3-19 conVr la velocità del satellite espressa in coordinate geocentriche equatoriali (vedere allegato A), rr è il vettore posizione nello stesso sistema di riferimento, ed Ωr la ve-locità angolare atmosferica. E’ veramente difficile sviluppare un modello matematico per Ωr , allora, usualmente, si studia un’atmosfera che ruota rigidamente con la Terra ( 7.282116 10−5 rad s

⊕ = ⋅

Ωr ). Benché l’atmosfera non sia neanche considerata in una prima approssimazione.

Applicando la forma di Gauss delle LPEs 3.3-11, all’accelerazione di resi-stenza 3.3-18 è possibile conoscere un’altra volta la variazione dei parametri orbitali. Come risultato, si trova che esiste una variazione periodica in tutti gli elementi, ma non variazioni secolari per il RAAN o per l’inclinazione. Quindi la resistenza atmo-sferica non modifica il piano orbitale. Al contrario viene rimossa energia al moto e quindi si ha una variazione secolare nel semiasse maggiore e nell’eccentricità nell’argomento del perigeo e nell’anomalia media. Le più importanti diminuzioni si hanno sull’eccentricità e sul semiasse maggiore. Possiamo approssimare questi cam-biamenti per rivoluzione usando le seguenti equazioni, da [1]

(

_{0 1}

)

C p 2 rev a exp I 2 e I B 2 a =− ⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ ∆ π _ρ − 3.3-20

(

)

      + ⋅ + ⋅ ⋅ ⋅ ⋅ − = ∆ − 2 I I e I exp a B 2 e 0 2 1 C p rev ρ π 3.3-21 in cui H e a

c = ⋅ , H è un fattore di scala della densità, ρp è la densità al perigeo, ed

( )

c I

I_i = _i sono le funzioni di Bessel modificate di ordine i e di argomento c.

Astrattamente l’effetto della resistenza atmosferica è di ridurre l’energia tota-le, o, in alter parotota-le, di ridurre il semiasse maggiore. La densità decresce

all’aumentare della quota, come risultato la resistenza massima si ha al perigeo, ridu-cendo in tale punto l’energia cinetica. La quota di apogeo decresce più velocemente della quota di perigeo, a causa di questa diminuzione di energia cinetica, portando una diminuzione anche dell’eccentricità. In figura 3.3.3 , estratta da [4], illustra un esempio di decadimento per resistenza atmosferica di un’orbita non controllata.

Per le orbite circolari, ogni nuova orbita è leggermente più piccola della pre-cedente. La resistenza porta ad una lenta spirale, con un aumento della velocità orbi-tale e, quindi, della resistenza, fenomeno conosciuto come paradosso dello Sputnik.

figura 3.3.3 Esempio di decadimento orbitale.

La quota di apogeo diminuisce più della quota di perigeo, finché non compare una in-controllabilità ed il satellite collassa.

3.4 Manovre orbitali a bassa spinta

Nella storia di ogni veicolo spaziale c’è un momento in cui non si trova alla posizione richiesta, per effetto di perturbazioni orbitali o a causa della richiesta di un cambiamento orbitale. Si necessita allora di una capacità di manovra del satellite per cambiare uno o più parametri orbitali. Per esempio dopo il lancio possono essere ri-chieste manovre di stabilizzazione, ed usualmente un movimento dall’orbita di par-cheggio all’orbita finale attraverso una traiettoria di trasferimento.

Tipicamente, il sistema di propulsione, se chimico, opera per un periodo limi-tato rispetto al periodo orbitale. Questo rende possibile uno studio analitico dove si considera che la propulsione crea un cambiamento impulsivo della velocità, mentre

la posizione rimane fissata. Quindi le manovre per il cambio di orbita avviene nei punti di intersezione della nuova e della vecchia orbita, o dove si ha l’intersezione di un’orbita intermedia con le due se queste non hanno punti di intersezione.

Invece, la propulsione elettrica, avendo una spinta molto bassa, opera per un periodo molto più lungo se paragonato a quello della propulsione chimica. Si ha la richiesta, allora, di sviluppare una nuova teoria di manovra ed una nuova strategia di cambiamento orbitale.

In questo paragrafo, cerchiamo di presentare brevemente la teoria delle ma-novre orbitali effettuate tramite la propulsione elettrica. Per quanto riguarda la classi-ca teoria impulsiva, informazioni possono essere ottenute in ogni libro di mecclassi-caniclassi-ca celeste come [2] e [5].

Le manovre possono essere divise in complanari ed in non complanari. Ma-novre complanari sono quelle maMa-novre in cui possono essere cambiati, in combina-zione o separatamente il semiasse maggiore, l’eccentricità, l’anomalia vera e l’argomento del perigeo, e quindi il piano orbitale rimane fissato. In manovre non complanari viene modificato il piano orbitale attraverso il cambiamento di inclina-zione e/o di ascensione retta del nodo ascendente.

3.4.1 Complanari

Le ragioni per utilizzare questo tipo di manovre sono qui elencate:

• Quando è richiesto di piazzare il satellite su una nuova orbita. Per esempio nel trasferimento da LEO a GEO, o per portare al rientro in atmosfera alla fi-ne della vita.

• Mantenimento orbitale, per contrastare le perturbazioni viste in 3.3.2.

• Correzione orbitale, per contrastare errori sull’orbita nominale. Situazione normale nella fase successiva al lancio.

• Per costruire una costellazione di satelliti sullo stesso piano o per rimpiazzar-ne alcuni. E’ rimpiazzar-necessario produrre un cambiamento di anomalia vera.

• Per cambiare l’ascensione retta del nodo ascendente usando una regressione nodale (eq. 3.3-9). E’ usato per costruire costellazioni di satelliti su più piani Dopo il cambiamento di piano è necessario ridurre il semiasse maggiore per ritornare alle dimensioni originarie.

La manovra complanare più comune è quella effettuata per cambiare la taglia e l’energia dell’orbita, attraverso un cambiamento del semiasse maggiore.

V T dt dE ₌ r_⋅r . 3.4-1 Ovviamente la strategia energetica di ottimo è di applicare la spinta tangen-zialmente o anti-tangentangen-zialmente all’orbita

(

Tr//Vr

)

.

Per un satellite a propulsione elettrica, applicando la spinta continuamente in direzione tangenziale od anti-tangenziale, per un appropriato intervallo di tempo, porta ad movimento a spirale fino all’orbita finale. Usando la ( 3.3-11), abbiamo un’espressione della variazione di semiasse maggiore, informazioni più dettagliate sono riportate in [5], θ θ µ mVT a 2 m T V a 2 dt da 2 = = 3.4-2 dove V è la velocità circolare, m la massa del satellite e Tθ la spinta diretta

tangen-zialmente.

3.4.2 Cambiamento di piano

Questa manovra ha la finalità di cambiare l’orientamento del piano orbitale nel sistema di riferimento inerziale senza cambiarne la taglia. Normalmente si utiliz-za una combinazione di manovre complanari e non. Quando la taglia dell’orbita ri-mane costante si parla di cambiamento di piano semplice.

Di nuovo si possono elencare una serie di ragioni di utilizzo di questo tipo di manovre.

• Il lanciatore ha portato ad un errore maggiore alla tolleranza ed è ne-cessario compiere una manovra di cambiamento di piano correttiva. • Quando la stazione di lancio ha una latitudine superiore

all’inclinazione dell’orbita, in quanto il veicolo spaziale non può arri-vare all’inclinazione opportuna senza avere un sistema di propulsione autonomo. Problema classico per i GEOs.

• Mantenimento orbitale, per contrastare le perturbazioni orbitali viste in 3.3.2.

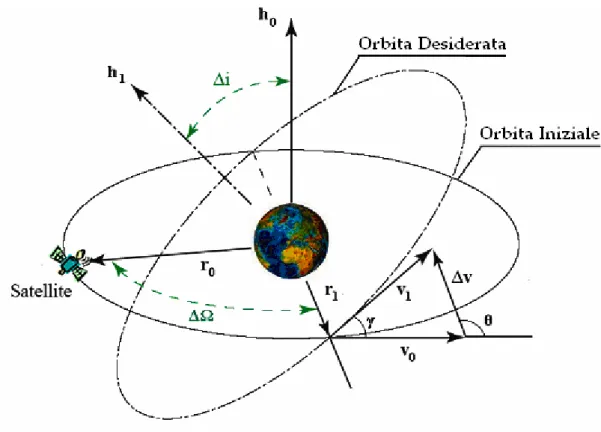
Qui sono analizzate matematicamente le manovre di cambiamento di piano semplice. In figura 3.4.1 è rappresentata questa situazione. Per mantenere le dimen-sioni dell’orbita è necessario che la velocità dopo la manovra sia uguale, in modulo,

alla velocità iniziale. Utilizzando la legge dei coseni, si arriva all’equazione 3.4-3 che mette in relazione la velocità iniziale e l’incremento di velocità.

figura 3.4.1 Cambiamento di piano orbitale.

2 sin V 2 V V V Vr₁ = r₀ = ₀ ⇒∆ = ₀ γ 3.4-3 con γ l’angolo compreso tra Vr₀ e Vr₁.

L’angolo tra V e ₀ ∆V si definisce θ, ed è uguale a

2 2 γ π θ = + . 3.4-4 Questa tesi comprende il caso di propulsione elettrica. Possiamo in questo ca-so imporre una nuova ipotesi: ∆V→0, giustificato dal basso impulso specifico.

0 V→

∆ implica che γ →0, Ω→0 ed i→0, come dimostrato in [5] o [6].

Con queste approssimazioni si possono trovare i risultati seguenti, che ci for-niscono la variazione temporale di inclinazione e di RAAN (per maggiori informa-zione vedere ancora [5] o [6])

mV T cos dt di ⋅ _h = υ 3.4-5 mV T i sin sin dt d υ _h = Ω 3.4-6 dove V è la velocità per l’orbita circolare, m ancora una volta la massa del satellite e Th è la componente perpendicolare al piano dell’orbita della spinta.

Come visto nelle equazioni 3.4-2 e 3.4-3 la variazione in inclinazione e nel RAAN dono proporzionali al rapporto tra la spinta prodotta dal satellite e la quantità di moto. Evidentemente, poiché si ha una grande quantità di moto e bassa spinta do-vuta alla propulsione elettrica, è necessaria una grande quantità di tempo per portare a termine la manovra e, conseguentemente, una grande quantità di propellente. Per tutte queste ragioni è meglio evitare, quanto più possibile, le manovre non complana-ri. Il cambiamento di piano non è una manovra economica, questo ci da la ragione per cui tali manovre siano spesso sostituite da altre. Per esempio per variare RAAN la strategia normalmente usata è quella di aumentare le dimensioni dell’orbita e la-sciar lavorare la regressione nodale al posto del propulsore.

Da ultimo, ritornando alla strategia diretta, il caso di ottimo si ha fornendo spinta intorno alla linea degli apsidi, per il cambio di inclinazione, e intorno a

2

π

υ =± , per cambiare l’ascensione retta del nodo ascendente, come si può desu-mere da 3.4-5 e 3.4-6.