Capitolo 2 Analisi del sistema Motoveicolo

(1)

Capitolo 2

Analisi del sistema Motoveicolo

2.1 Introduzione

In questo capitolo verrà analizzato il motoveicolo, considerando la geome-tria e la cinematica del sistema. Verranno introdotti sistemi di riferimento, che saranno utilizzati anche nei capitoli successivi.

2.2 Definizione cinematica

2.2.1 Parti costituenti il motoveicolo

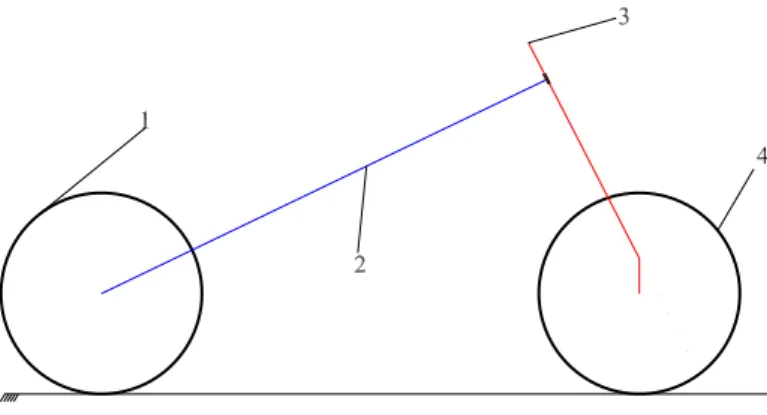
Un motoveicolo completamente assemblato è composto da molti organi distinti. Tuttavia, per un’analisi cinematica si può schematizzare il sistema come composto da quattro gruppi di parti assemblate (corpi rigidi), come si può vedere in Fig. 2.1. Per mantenere compattezza nell’esposizione, si assegnano dei nomi a questi corpi rigidi; essi sono:

1. Posteriore: fanno parte di questo corpo il pneumatico, l’apparato frenante ed il cerchio posteriori, assieme alla corona della trasmissione (in altre parole la ruota posteriore completa).

2. Mainframe: è questo il corpo costituito da più componenti; infat-ti è l’assieme di telaio, serbatoio, sovrastrutture, motore completo1

, trasmissione,. . .

1

Con motore completo si intende dotato di tutto ciò che serve per funzionare.

(2)

2.2 Definizione cinematica 11

Figura 2.1: Schema cinematico del motoveicolo

3. Avantreno: fanno parte di questo corpo la forcella completa ed il manubrio assemblato (comandi, cavi,. . . ).

4. Anteriore: esso è costituito da pneumatico, cerchio e dischi freno anteriori (in altri termini è la ruota anteriore completa).

Questa schematizzazione è valida solo se si considerano le sospensioni rigide; altrimenti si dovrebbero introdurre due sconnessioni:

• L’ avantreno dovrebbe essere suddiviso in due parti, una superiore ed una inferiore collegate da una guida prismatica, in modo da schematiz-zare la forcella.

• Il posteriore non sarebbe direttamente collegato al mainframe, bensì sarebbe opportuno introdurre tra di essi il forcellone, collegato con una due coppie cilindriche.

2.2.2 Vincoli

Trascurando per il momento le sospensioni si può ritenere di descrivere i vincoli fra i corpi precedentemente descritti come facenti parte di due categorie:

• Coppie rotoidali che inibiscono 5 g.d.l., lasciando la possibilità di rotazione attorno ad un asse.

(3)

2.3 Definizione del baricentro 12

• Vincoli pneumatico-strada che inibiscono 3 g.d.l., le tre traslazioni, se si ipotizza che il pneumatico rotoli senza strisciare sulla strada (vd. Fig. 2.2).

Figura 2.2: Possibili rotazioni della ruota

Considerando nullo lo scorrimento longitudinale, che interviene nel contatto pneumatico/strada, i g.d.l. risultano essere 5; essi saranno definiti nella sezione (2.5).

2.3 Definizione del baricentro

Il motoveicolo precedentemente schematizzato, può essere visto come un insieme di masse principali, a loro volta costituite da corpi rigidi colle-gati rigidamente. Con riferimento alla Fig. 2.3, si sono fatte le seguenti assunzioni:

• P rappresenta il baricentro della parte posteriore della moto, definita come in (2.2).

• R rappresenta il baricentro della parte superiore del corpo del pilota (dorso, braccia, testa,. . . ).

• M rappresenta il baricentro del mainframe, definito come in (2.2), con l’aggiunta della parte inferiore del pilota (bacino e gambe).

• B rappresenta il baricentro di un ballast, zavorra mobile utilizzata nelle moto sportive, grazie alla quale nelle competizioni è possibile

(4)

raggiun-2.3 Definizione del baricentro 13

Figura 2.3: Schematizzazione delle masse principali del motoveicolo

gere il peso limite e variare la posizione del baricentro complessivo G.

• F rappresenta il baricentro della parte anteriore del motoveicolo, defini-ta come in (2.2).

Se si assume che la configurazione in Fig. 2.3 sia rigida, si ottiene:            h = mPhP + mRhR+ mMhM + mBhB+ mFhF m b = mPbP + mRbR+ mMbM + mBbB+ mFbF m a = l − b (2.1) Dove: • m = mP + mR+ mM + mB+ mF

• l è il passo del veicolo

• a e b sono rispettivamente i semipassi anteriore e posteriore

Se si considerano P, B, R collegati rigidamente ad M, si ha una situazione come quella descritta in (2.2); questa ipotesi porta a trascurare i moti rela-tivi fra pilota e veicolo (principalmente tipo rollio) e, soprattutto elimina la

(5)

2.4 Geometria del motociclo 14

presenza cinematica della sospensione posteriore.

ef rappresenta la distanza del baricentro dell’anteriore F dall’asse di

ster-zo (vd. Fig. 2.3). Se ef ≈ 02, significa che il baricentro dell’anteriore è

posizionato sull’asse di sterzo; questo ha come conseguenza il fatto che la posizione relativa del baricentro complessivo del veicolo è invariante rispetto al moto di rotazione dello sterzo.

2.4 Geometria del motociclo

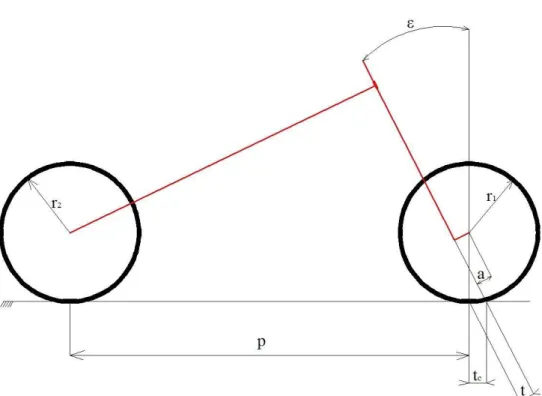
Figura 2.4: Geometria del motociclo

Le grandezze geometriche riportate in Fig. 2.4 sono comunemente uti-lizzate per descrivere la configurazione ciclistica del motociclo; esse sono misurate con il veicolo in posizione verticale3

, con angolo di sterzata nullo.

• p è il passo, definito come la distanza fra i punti di contatto delle ruote a terra.

2

Nel capitolo (4) si vedrà che, per gli scopi del presente lavoro, questa ipotesi può ritenersi valida.

3

(6)

2.4 Geometria del motociclo 15

• r1 e r2 sono rispettivamente i raggi esterni delle ruote anteriore e

posteriore, in configurazione indeformata.

• a è l’avanzamento , distanza fra l’asse di sterzo e la parallela ad esso passante per il centro ruota.

• ǫ è l’angolo di inclinazione dell’asse di sterzo, definito come l’angolo che esiste fra la verticale al suolo e l’asse di sterzo (rappresentato in Fig. 2.4).

• tc è l’avancorsa, definita come la distanza fra l’intersezione dell’asse di

sterzo con il piano stradale ed il punto di contatto della ruota anteriore, misurata sul piano stradale, definita in Fig. 2.4.

• t è l’avancorsa normale.

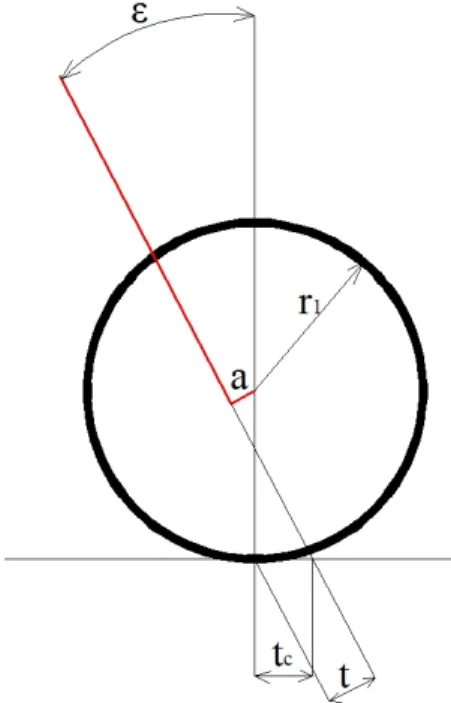
Figura 2.5: Quote ciclistiche anteriori

In Fig. 2.5 è rappresentato il dettaglio dell’anteriore, con una configurazione comune. Valgono le seguenti relazioni:

t = r1sin ǫ − a (2.2)

tc =

t

(7)

2.5 Sistemi di riferimento 16

2.5 Sistemi di riferimento

In questo capitolo verranno definiti i sistemi di riferimento, che saranno utilizzati per le successive considerazioni e per la formulazione delle equazioni dei modelli analitici di motociclo. In Fig. 2.6 è visibile il sistema di rife-rimento solidale alla strada (xO, yO, zO), con l’asse verticale zO diretto verso

l’alto, di versori (iO, jO, kO). La direzione verticale è determinata da quella

della forza peso; ai fini dell’analisi che seguirà, questo sistema di riferimento può essere considerato inerziale (per chiarimenti vd. [1]).

Figura 2.6: Definizione deli assi suolo

2.5.1 Sistemi solidali al motoveicolo

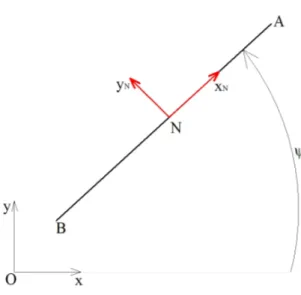
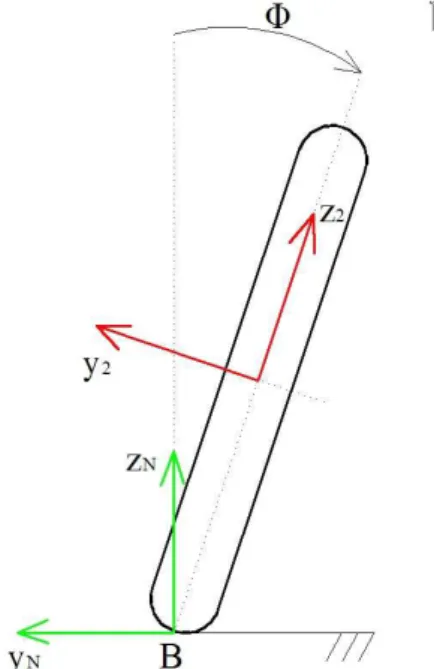
Si introduce un sistema di riferimento (xN, yN, zN) (Fig. 2.7) con

ori-gine nel punto N, che rappresenta la proiezione a terra del baricentro G del motoveicolo quando l’angolo di rollio e quello di sterzo assumono valore nullo (Fig. 2.8). Il piano su cui giacciono gli assi xN− yN coincide con quello degli

assi xO− yO; di conseguenza l’asse zN è diretto come zO. Questo sistema di

riferimento può essere ottenuto mediante una rotazione attorno all’asse zO

del sistema (xO, yO, zO), dell’angolo ψ, detto angolo d’imbardata:

(iO, jO, kO) ψ

(8)

Figura 2.7: Definizione del sistema N

Supponendo di poter ritenere valida l’ipotesi che ef ≈ 0, si introduce

un sistema di riferimento di assi corpo (xG, yG, zG) (Fig. 2.8) con origine

nel baricentro G del motoveicolo. Questo può essere ottenuto mediante una rotazione attorno all’asse xN del sistema (xN, yN, zN), dell’angolo φ, detto

angolo di rollio:

(iN, jN, kN) φ

→ (iG, jG, kG) (2.5)

Questo sistema di riferimento non è la terna centrale d’inerzia del motoveico-lo; tuttavia, se si assume che la moto si simmetrica rispetto al piano xG− zG,

si ha che Ixy = Iyz = 0, mentre Ixz 6= 0. Rispetto a questo sistema i momenti

ed i prodotti d’inerzia sono costanti durante il moto.

Figura 2.8: Definizione del sistema G

(9)

per il calcolo dell’energia cinetica nel capitolo 4.

Si introduce un sistema di riferimento di (x2, y2, z2) con origine nel centro

della ruota posteriore (Fig. 2.9). Questo sistema possiede gli stessi versori di (xG, yG, zG):

(iN, jN, kN) φ

→ (iG, jG, kG) (2.6)

Questo non è un sistema di assi corpo per la ruota posteriore, infatti, per

Figura 2.9: Definizione del sistema posteriore

essere tale dovrebbe rimanere solidale alla ruota in tutti i suoi movimenti. Il sistema (x2, y2, z2), invece non segue la ruota durante la rotazione attorno

all’asse y2 (assimilabile ad un moto di beccheggio). Tuttavia, sfruttando le

proprietà di simmetria della ruota, si può asserire che il sistema di riferimen-to introdotriferimen-to conserva la proprietà precedentemente enunciata per gli assi corpo.

Si introduce un sistema di riferimento di (xE, yE, zE) con origine sul

nel-l’intersezione tra il piano di simmetria del veicolo e l’albero motore (Fig. 2.10). Questo sistema possiede gli stessi versori di (xG, yG, zG):

(iN, jN, kN) φ

(10)

Figura 2.10: Definizione del sistema propulsore

Questo è un sistema di assi corpo; possiede quindi le proprietà precedente-mente elencate.

2.5.2 Anteriore

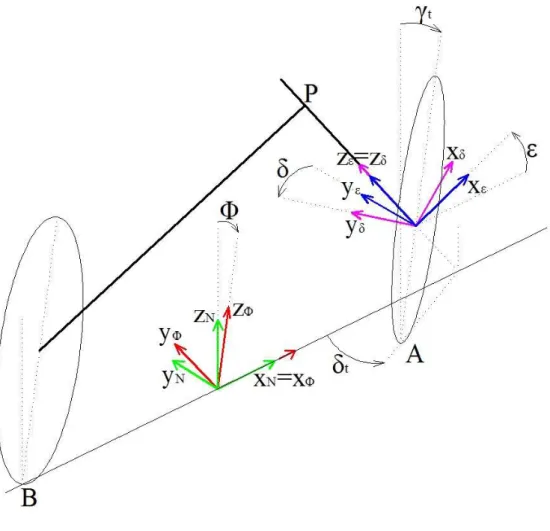
Per descrivere quantità cinematiche riguardanti l’anteriore del motovei-colo si indica una serie di rotazioni con i rispettivi sistemi di riferimento (Fig. 2.11): (iN, jN, kN) φ →¡iφ, jφ, kφ ¢ ǫ → (iǫ, jǫ, kǫ) δ → (iδ, jδ, kδ) (2.8)

Il sistema (xφ, yφ, zφ) può essere ottenuto mediante una rotazione attorno

all’asse xN del sistema (xN, yN, zN), dell’angolo φ, detto angolo di rollio. Il

sistema (xǫ, yǫ, zǫ) può essere ottenuto mediante una rotazione attorno

al-l’asse yΦ del sistema (x_φ, y_φ, z_φ), dell’angolo ǫ, detto angolo di inclinazione

dell’asse di sterzo. Il sistema (xδ, yδ, zδ) può essere ottenuto mediante una

rotazione attorno all’asse zǫdel sistema (xǫ, yǫ, zǫ), dell’angolo δ, detto angolo

di rotazione di sterzo.

Il sistema (xδ, yδ, zδ) non può essere considerato un sistema di assi corpo per

la ruota anteriore, ma lo è per l’avantreno, definito nella sezione (2.2). Qualora servissero altri sistemi di riferimento, saranno definiti all’occorrenza.

(11)

2.6 Cinematica dell’anteriore 20

Figura 2.11: Sistemi di utilizzati per l’anteriore

2.6 Cinematica dell’anteriore

Per descrivere il comportamento cinematico dell’anteriore durante il moto si farà riferimento alla Fig. 2.11. Con un approccio simile a quello proposto in [2], si considera un vettore s diretto come l’asse di rotazione della ruota anteriore. Nel sistema di riferimento (xδ, yδ, zδ) questo vettore si esprime

come:

(12)

Mediante tre rotazioni semplici4

successive si determinano le componenti di snel sistema (xN, yN, zN): s=     0 1 0         cos δ − sin δ 0 sin δ cos δ 0 0 0 1         cos ǫ 0 sin ǫ 0 1 0 − sin ǫ 0 cos ǫ         1 0 0 0 cos φ − sin φ 0 sin φ cos φ     Si ottiene: s= (− sin δ cos ǫ) iN+

+ (cos φ cos δ − sin φ sin δ sin ǫ) jN+

+ (sin φ cos δ + cos φ sin δ sin ǫ) kN =

= sxiN + syjN + szkN

(2.10)

Se si può ipotizzare che gli angoli di sterzo rimangano piccoli5

: s= (δ cos ǫ) iN+

+ (cos φ − δ sin φ sin ǫ) jN+

+ (sin φ + δ cos φ sin ǫ) kN

(2.11)

2.6.1 Angolo di sterzo effettivo

Per come è stato definito in precedenza, l’angolo di sterzo6

, rappresenta l’angolo del quale ruotare il sistema di riferimento (xǫ, yǫ, zǫ) attorno all’asse

zǫ, per passare al sistema (xδ, yδ, zδ). L’angolo di sterzo a terra,o effettivo,

viene definito come l’angolo esistente fra l’asse xN e l’intersezione fra il piano

xδ− zδ e quello xN− yN; con altre parole, l’angolo di sterzo effettivo è quello

formato dalle intersezioni del piano mediano della ruota anteriore e di quello del mainframe con il piano stradale.

Se si ipotizza che le ruote siano lenticolari, cioè assimilabili a dischi di spessore trascurabile, la relazione che esprime l’angolo di sterzo a terra si può ricavare da (2.10), infatti (Fig. 2.11): δt = arctan µ −sx sy ¶ = = arctan µ sin δ cos ǫ

cos φ cos δ − sin φ sin δ sin ǫ

¶ (2.12)

4

La rotazione semplice è rispetto ad un asse coordinato; così facendo, due terne successive hanno sempre una direzione in comune.

5

sin_δ_{≈ δ e cos δ ≈ 1.}

6

(13)

Nel caso di piccoli angoli di sterzo si ha che:

δt=

δ cos ǫ

cos φ − δ sin φ sin ǫ (2.13) è opportuno osservare che l’angolo di sterzo δ è l’unico fra quelli che com-paiono nella relazione (2.12) che si presta all’uso dell’ipotesi dei piccoli angoli (sin δ ≈ δ, cos δ ≈ 1). Infatti, l’angolo di inclinazione dell’asse di sterzo ǫ è un parametro, che di norma assume valori compresi fra −20◦_{e −30}◦_{. L’angolo di}

rollio può assumere valori prossimi a ±50◦_{, soprattutto in manovre}

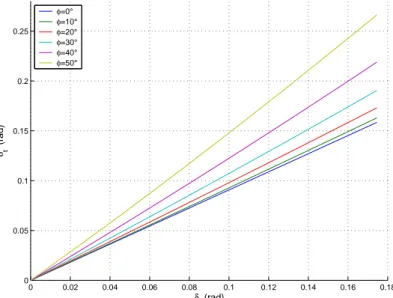
impegna-tive. Nelle Fig. 2.12 e 2.13, sono rappresentati gli andamenti dell’angolo di sterzo effettivo δt, al variare rispettivamente dell’angolo di sterzo imposto δ

e dell’angolo di rollio φ, tenendo di volta in volta gli altri valori costanti. É stato scelto un angolo di inclinazione dell’asse di sterzo ǫ = −25◦_{, valore}

ac-cettabile per molti motoveicoli stradali in produzione. Nella Fig. 2.14, sono rappresentati gli andamenti della differenza fra angolo di sterzo effettivo δt e

quello di sterzo δ al variare rispettivamente dell’angolo di sterzo imposto δ e dell’angolo di rollio φ, tenendo di volta in volta gli altri valori costanti. In Fig. 2.14 si può osservare come il valore di φ influenzi l’andamento di δt al

variare di δ; a parità di angolo di sterzo imposto, all’aumentare dell’angolo di rollio, la differenza (δt− δ) passa da negativa a positiva. In Fig. 2.15 è

rappresentata la differenza fra i valori di δt ricavati dalla relazione (2.12) e

quelli ottenuti per piccoli angoli di sterzo (relazione (2.13)). É opportuno mettere in evidenza come, anche in condizioni che vanno oltre quelle di un utilizzo sportivo del motoveicolo (δ = 10◦ e φ > 50◦), l’errore commesso

con-siderando piccolo l’angolo di sterzo risulti nell’ordine del decimo di grado; pertanto, nella formulazione di modelli che necesssitano dell’angolo di sterzo effettivo, si utilizzerà la (2.13).

In seguito sarà utilizzata la derivata temporale dell’angolo di sterzo effet-tivo; risulta opportuno calcolarla:

˙δt=

˙δ cos ǫ(cos φ − δ sin φ sin ǫ) (cos φ − δ sin φ sin ǫ)2 +

+ δ cos ǫ( ˙φ sin φ + ˙δ sin φ sin ǫ + δ ˙φ cos φ sin ǫ) (cos φ − δ sin φ sin ǫ)2 =

= Aδ˙δ + Bδφ˙

(14)

2.6 Cinematica dell’anteriore 23 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0 0.05 0.1 0.15 0.2 0.25 δt (rad) δ (rad) φ=0° φ=10° φ=20° φ=30° φ=40° φ=50°

Figura 2.12: δt in funzione di δ, per ǫ = −25◦

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.05 0.1 0.15 0.2 0.25 δt (rad) φ (rad) δ=10° δ=5° δ=0°

Figura 2.13: δt in funzione di φ, per ǫ = −25◦

Dove:

Aδ =

cos φ cos ǫ (cos φ − δ sin φ sin ǫ)2

Bδ =

δ sin φ cos ǫ + δ2

cos φ sin ǫ cos ǫ (cos φ − δ sin φ sin ǫ)2

(15)

2.6 Cinematica dell’anteriore 24 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 −0.02 0 0.02 0.04 0.06 0.08 0.1 δt − δ (rad) δ (rad) φ=0° φ=10° φ=20° φ=30° φ=40° φ=50° 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 −0.02 −0.01 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 ( δt − δ ) (rad) φ (rad) δ=5° δ=10° δ=0° Figura 2.14: (δt− δ), per ǫ = −25◦ 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 −3.5 −3 −2.5 −2 −1.5 −1 −0.5 0 0.5x 10 −3 (rad) δ (rad) φ=0° φ=10° φ=20° φ=30° φ=40° φ=50° 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 −2.5 −2 −1.5 −1 −0.5 0 0.5x 10 −3 (rad) φ (rad) δ=10° δ=5° δ=0°

Figura 2.15: Differenza fra δt completo e quello ricavato per piccoli δ, per

ǫ = −25◦

2.6.2 Angolo di rollio dell’anteriore

Si definisce angolo di rollio anteriore γt quello fra il piano xδ− zδ ed il

piano xN − yN. Se si ipotizza che le ruote siano lenticolari, cioè assimilabili

a dischi di spessore trascurabile, la relazione che esprime l’angolo di rollio dell’anteriore si può ricavare da (2.10), infatti (Fig. 2.11):

γt = arcsin (sz) =

= arcsin (sin φ cos δ + cos φ sin δ sin ǫ) (2.15) Nel caso di piccoli angoli di sterzo si ha che:

γt = sin φ + δ cos φ sin ǫ (2.16)

Nelle Fig. 2.16 e 2.17, sono rappresentati gli andamenti dell’angolo di rol-lio anteriore γt, al variare rispettivamente dell’angolo di sterzo imposto δ e

(16)

dell’angolo di rollio φ, tenendo di volta in volta gli altri valori costanti.

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 −0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 γt (rad) δ (rad) φ=0° φ=10° φ=20° φ=30° φ=40° φ=50°

Figura 2.16: γt in funzione di δ, per ǫ = −25◦

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 −0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 γt (rad) φ (rad) δ=0° δ=5° δ=10°

Figura 2.17: γt in funzione di φ, per ǫ = −25◦

Nella Fig. 2.18, sono rappresentati gli andamenti della differenza fra angolo di rollio anteriore γt e quello di rollio φ al variare rispettivamente dell’angolo

di sterzo imposto δ e dell’angolo di rollio φ, tenendo di volta in volta gli altri valori costanti.

(17)

relazione (2.15) e quelli ottenuti considerando piccoli gli angoli di sterzo (relazione (2.16)). 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 −0.09 −0.08 −0.07 −0.06 −0.05 −0.04 −0.03 −0.02 −0.01 0 γt − φ (rad) δ (rad) φ=0° φ=10° φ=20° φ=30° φ=40° φ=50° 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 −0.09 −0.08 −0.07 −0.06 −0.05 −0.04 −0.03 −0.02 −0.01 0 γt − φ (rad) φ (rad) δ=0° δ=5° δ=10° Figura 2.18: (γt− φ), per ǫ = −25◦ 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 −0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 (rad) δ (rad) φ=0° φ=10° φ=20° φ=30° φ=40° φ=50° 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 −0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 (rad) φ (rad) δ=0° δ=5° δ=10°

Figura 2.19: Differenza fra γt completo e quello ricavato per piccoli δ, per

(18)

2.7 Le ruote 27

2.7 Le ruote

Nelle sezioni (2.6.1) e (2.6.2) sono state considerate le ruote come dischi rigidi di spessore trascurabile con raggio esterno pari al raggio di rotolamen-to7

; è invalso l’uso della definizione di lenticolari per questo tipo di schema-tizzazione di ruote. Tuttavia, questa ipotesi porta a trascurare alcuni effetti che la reale forma del pneumatico genera.

In questa sezione verranno schematizzate le ruote come toroidi di raggio medio R e raggio della sezione r. Verrà trascurata l’elasticità della gomma e si studieranno due effetti dovuti al moto di rollio. La situazione è rappre-sentata nelle Fig. 2.20 e 2.21.

Figura 2.20: Vista posteriore

Se il veicolo assume un angolo di rollio φ, definito come in (2.5), il punto di contatto a terra si sposta della quantità |CC′′_{| (Fig. 2.21). Si ha che:}

|C′′_C′_{| = 2r sin}µ φ 2 ¶ |C′′_{K| = r sin φ} |C′_{K| = r(1 − cos φ)} |C′_{C| =} r(1 − cos φ) cos φ |CK| = r(1 − cos φ) tan φ (2.17) 7

In condizioni di puro rotolamento, poiché la ruota viene considerata rigida, esso è il raggio della ruota stessa.

(19)

2.7 Le ruote 28

Figura 2.21: Ruota posteriore in dettaglio

2.7.1 Variazione del punto di contatto a terra dovuta al

moto di rollio

Con riferimento alle relazioni (2.17), si ottiene che lo spostamento del punto di contatto a terra della ruota, dovuto ad un angolo di rollio φ vale:

|CC′′_{| = |CK| + |KC}′′_{| = r tan φ} _(2.18)

In Fig. 2.22 è mostrato l’andamento della variazione del punto di contatto a terra per entrambe le ruote.

E’ opportuno mettere in evidenza che, soprattutto per angoli di rollio φ elevati, lo spostamento della ruota con minor raggio della sezione, a parità del raggio medio del toroide, sia inferiore rispetto a quella di maggior sezione8

. In queste condizioni insorge il fenomeno di imbardata dovuto alle diverse dimensioni delle sezioni dei toroidi.

8

(20)

2.8 Analisi cinematica 29 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 10 20 30 40 50 60 CC’’ (mm) φ (rad) Posteriore Anteriore

Figura 2.22: Variazione del punto di contatto a terra per entrambe le ruote

2.7.2 Variazione dell’altezza del baricentro dovuta al

moto di rollio

Con riferimento alle relazioni (2.17), si ottiene che la variazione dell’al-tezza del baricentro G del veicolo, misurata sul piano xG− zG9, dovuta ad

un angolo di rollio φ vale:

|CC′_{| = r}1 − cos φ

cos φ (2.19)

Con r si è indicato il raggio medio delle due sezioni dei toroidi, ottenuto come media pesata sui semipassi:

r = r1 b l + r2 a l (2.20)

2.8 Analisi cinematica

Tenendo presenti i sistemi di riferimento introdotti nella sezione (2.5), verrà svolta di seguito l’analisi delle velocità dei corpi introdotti in (2.2) ed

9

Si intende la differenza fra l’altezza del baricentro del veicolo nel caso di ruote toroidali e lenticolari, misurata sul piano mediano longitudinale del veicolo stesso.

(21)

2.8 Analisi cinematica 30 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 5 10 15 20 25 ∆ h (mm) φ (rad)

Figura 2.23: Variazione dell’altezza del baricentro dovuta al rollio

in (2.3).

La velocità del punto N vale:

vN = u0i0+ v0j0 = u_NiN+ v_NjN

La relazione fra le due espressioni della velocità del punto N è quella fra i due sistemi di versori in cui è stata espressa:

" uN vN # = " cos ψ sin ψ − sin ψ cos ψ # " uO vO # (2.21)

La rotazione dell’angolo ψ attorno all’asse suolo kO, viene chiamato

imbar-data ed è stato definito in (2.5).

2.8.1 Velocità del baricentro

Volendo conoscere la velocità del baricentro G, è opportuno ricordare la formula fondamentale della cinematica piana:

vG = vN + Ω ∧ ~N G (2.22)

Dove:

(22)

2.8 Analisi cinematica 31

• ~N G = (−h sin φ)j_N + (h cos φ)kN

• vN = uNiN + vNjN

Tenendo presente che iN0 = i0, la velocità angolare Ω si esprime come:

Ω = ˙φiN + ˙ψkN (2.23)

Dalla relazione (2.22) si ricava quindi la velocità del baricentro G:

vG= ³ uN + ˙ψh sin φ ´ iN+ +³vN − ˙φh cos φ ´ jN+ −³ ˙φh sin φ´kN (2.24)

La velocità angolare Ω può essere espressa nel sistema di riferimento bari-centrale (xG, yG, zG) dalle componenti (p, q, r), tenendo presenti le rotazioni

elementari10

per passare attraverso i vari sistemi, in cui si sono trovate le singole componenti.     p q r     =     1 0 0 0 cos φ sin φ 0 − sin φ cos φ         ˙ φ 0 ˙ ψ     =     ˙ φ ˙ ψ sin φ ˙ ψ cos φ     (2.25) Si ottiene:

Ω = ˙φiG+ ( ˙ψ sin φ)jG+ ( ˙ψ cos φ)kG

In [6] si forniscono le seguenti definizioni: • p è la velocità di rollio

• q è la velocità di beccheggio • r è la velocità di imbardata

2.8.2 Velocità di rotazione della ruota posteriore

Considerando la Fig. 2.9, si vuole esprimere la velocità di rotazione Ω2 della ruota posteriore nel sistema di riferimento (x2, y2, z2). Per far

questo si possono considerare separatamente due effetti ed unirli per ottenere l’espressione finale:

10

(23)

• Ω2_t rappresenta il vettore di velocità di rotazione della ruota

poste-riore, considerata solidale rispetto al mainframe; essa è la velocità di trascinamento.

• Ω2_r rappresenta il vettore di velocità di rotazione relativa fra ruota

posteriore e motoveicolo.

Con ragionamenti analoghi a quelli svolti nella sezione precedente si ha che:

Ω2_t = ˙φiG+ ( ˙ψ sin φ)jG+ ( ˙ψ cos φ)kG (2.26)

Ω2_r= µ uN r2 ¶ jG (2.27) Si ottiene quindi: Ω2 = Ω2_t+ Ω2_r = = p2iG+ q2jG+ r2kG= = ˙φiG+ µ ˙ ψ sin φ +uN r2 ¶ jG+ ( ˙ψ cos φ)kG (2.28)

2.8.3 Velocità di rotazione del sistema motore

Considerando la Fig. 2.10, si vuole esprimere la velocità di rotazione ΩE

del sistema motore, schematizzato come un volano, nel sistema di riferimento (xE, yE, zE). Per far questo si possono considerare separatamente due effetti

ed unirli per ottenere l’espressione finale:

• ΩEt rappresenta il vettore di velocità di rotazione del motore,

conside-rato solidale rispetto al mainframe; essa è la velocità di trascinamento.

• ΩEr rappresenta il vettore di velocità di rotazione relativa fra motore

e motoveicolo.

Con ragionamenti analoghi a quelli svolti nella sezione (2.8.1) si ha che:

ΩEt = ˙φiG+ ( ˙ψ sin φ)jG+ ( ˙ψ cos φ)kG (2.29)

(24)

Dove τ rappresenta il rapporto fra il regime di rotazione del motore ed uN.

Si ottiene quindi: ΩE = ΩEt+ ΩEr = = pEiG+ qEjG+ rEkG= = ˙φiG+³ ˙ψ sin φ + uNτ ´ jG+ ( ˙ψ cos φ)kG (2.31)

2.8.4 Velocità dell’anteriore

Considerando la Fig. 2.11, si vuole trovare la velocità di rotazione dell’ante-riore, definito nella sezione (2.2). Si ricorda che il sistema di riferimento (xδ, yδ, zδ), è stato ottenuto dalla (2.8), mediante le rotazioni semplici:

(iN, jN, kN) φ →¡iφ, jφ, kφ ¢ ǫ → (iǫ, jǫ, kǫ) δ → (iδ, jδ, kδ)

Per far questo si possono considerare separatamente due effetti ed unirli per ottenere l’espressione finale:

• ΩP t rappresenta il vettore di velocità di rotazione del punto P,

conside-rato solidale al mainframe.

• ΩP rrappresenta il vettore di velocità di rotazione relativa fra l’anteriore

ed il mainframe. ΩP t = pP tiδ+ qP tjδ+ rP tkδ     pP t qP t rP t     =     cos δ sin δ 0 − sin δ cos δ 0 0 0 1         cos ǫ 0 − sin ǫ 0 1 0 sin ǫ 0 cos ǫ         1 0 0 0 cos φ sin φ 0 − sin φ cos φ         ˙ φ 0 ˙ ψ     Si ottiene:     pP t qP t rP t     =     ˙

φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ − ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ

˙

φ sin ǫ + ˙ψ cos φ cos ǫ

    (2.32) ΩP r = ˙δiδ (2.33)

Sommando i due contributi:

(25)

2.8 Analisi cinematica 34     pP qP rP     =     ˙

φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ − ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ

˙

φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ

   

(2.34)

Se si ipotizza di poter ritenere piccoli gli angoli di sterzo11

, si può ritenere valida la seguente espressione:

    pP qP rP     ≈     ˙

φ cos ǫ − ˙ψ cos φ sin ǫ + ˙ψ sin φδ − ˙φ cos ǫδ + ˙φ cos φ sin ǫδ + ˙ψ sin φ

˙

φ sin ǫ + ˙ψ cos φ cos ǫ + ˙δ    

(2.35)

2.8.5 Velocità angolare della ruota anteriore

Considerando la Fig. 2.11, si vuole esprimere la velocità di rotazione Ω1

della ruota anteriore. Per far questo si possono considerare separatamente due effetti ed unirli per ottenere l’espressione finale:

• Ω1trappresenta il vettore di velocità di rotazione della ruota anteriore,

considerata solidale rispetto all’anteriore.

• Ω1_r rappresenta il vettore di velocità di rotazione relativa fra ruota

anteriore e l’anteriore.

La velocità Ω1t è analoga alla (2.32). La velocità Ω1r vale:

Ω1_r=

µ uN

r1

¶

jδ (2.36)

Sommando i due conributi:

Ω1 = Ω1t+ Ω1r = p1iδ+ q1jδ+ r1kδ     p1 q1 r1     =     ˙

φ cos ǫ cos δ − ˙ψ cos φ sin ǫ cos δ + ˙ψ sin φ sin δ − ˙φ cos ǫ sin δ + ˙φ cos φ sin ǫ sin δ + ˙ψ sin φ cos δ + uN/r1

˙

   

(2.37)

Anche in questo caso, se si ipotizzano piccoli angoli di sterzo:     p1 q1 r1     ≈     ˙

φ cos ǫ − ˙ψ cos φ sin ǫ + ˙ψ sin φδ − ˙φ cos ǫδ + ˙φ cos φ sin ǫδ + ˙ψ sin φ + uN/r1

˙

    (2.38) 11_sin δ≈ δ, cos δ ≈ 1.

(26)

2.9 Angoli di deriva 35

2.9 Angoli di deriva

Figura 2.24: Convenzione sul segno dell’angolo di deriva

Con riferimento alla Fig. 2.24, si definisce angolo di deriva l’angolo fra l’asse x12

e la velocità di avanzamento. Per gli angoli di deriva, si è scelto di seguire la convenzione ISO, in quanto non necessita di introdurre eccezioni ai segni ed è coerente con i sistemi di riferimento introdotti in (2.5).

2.9.1 Angolo di deriva posteriore

Per la ruota posteriore (Fig. 2.25), la velocità di avanzamento v2 può

essere trovata sfruttando la formula fondamentale della cinematica piana:

v2 = v_N + ˙ψk_N ∧ ~N 2 = u2iN+ v2jN (2.39) Si ottiene: " u2 v2 # = " uN vN − b ˙ψ # (2.40)

L’angolo di deriva posteriore è il seguente:

α2 = arctan Ã vn− b ˙ψ uN ! ≈ vn− b ˙ψ uN (2.41)

Dove l’ultima uguaglianza può essere considerata valida solo nel caso di piccoli angoli.

12

(27)

Figura 2.25: Angoli di deriva nel caso di avancorsa nulla

2.9.2 Angolo di deriva anteriore

Se si ipotizza che il punto di contatto a terra della ruota anteriore coincida con l’intersezione fra l’asse di sterzo ed il piano stradale (avancorsa nulla), il calcolo dell’angolo di deriva anteriore può essere svolto in maniera simile a quello per il posteriore, facendo attenzione ad inserire l’angolo di sterzo (Fig. 2.25): v1 = v_N + ˙ψk_N ∧ ~N 1 = u1i1+ v1j1 (2.42) " u1 v1 # = " uN vN + a ˙ψ # (2.43) α1 = −δ + arctan Ã vn+ a ˙ψ uN ! (2.44)

Dove δ è l’angolo di sterzo. Volendo essere più precisi, al posto di δ sarebbe opportuno inserire l’angolo di sterzo effettivo δt (sezione (2.6.1)).

In realtà, se si considera la presenza dell’avancorsa, l’approccio da seguire per calcolare l’angolo di deriva anteriore è un altro. Infatti, come si può osservare in Fig. 2.26, il punto di contatto a terra del pneumatico non coincide con l’intersezione fra l’asse di sterzo ed il piano stradale. La velocità di avanzamento del punto di contatto si calcola applicando due volte la formula

(28)

fondamentale della cinematica piana:

v3 = vN + ˙ψkN ∧ ~N 3

v1 = v3+ ˙δ_tk_N ∧ ~31

Dove:

• ~N 3 = aiN è l’espressione vettoriale del semipasso anteriore;

• ~31 = −tccos δtiN − tcsin δtjN;

• 3 è l’intersezione fra l’asse di sterzo ed il piano stradale; • 1 è il punto di contatto a terra del pneumatico anteriore. Si ottiene: " u1 v1 # = " uN − ˙δttcsin δt vN + a ˙ψ + ˙δttccos δt # (2.45) α1 = −δt+ arctan Ã vn+ a ˙ψ + ˙δttccos δt uN − ˙δttcsin δt ! ≈ ≈ −δt+ vn+ a ˙ψ + ˙δttccos δt uN − ˙δttcsin δt (2.46)

Dove l’ultima uguaglianza può essere considerata valida solo nel caso di pic-coli angoli. Considerando la differenza fra punto di contatto a terra

del-Figura 2.26: Angolo di deriva anteriore completo

la ruota ed intersezione dell’asse di sterzo con il piano stradale, si calcola con maggior precisione l’angolo di deriva anteriore, a spese di una modes-ta complicazione. Permodes-tanto, nel modello più complesso di motoveicolo, sarà utilizzata la relazione (2.46).