Capitolo 2 Misure per stimare la dimensione di linguaggi regolari

Capitolo 2

Misure per stimare la dimensione di

linguaggi regolari

La risoluzione del problema di determinare un insieme di espressioni regolari che soddisfano una data stringa in ingresso consiste, in generale, nella scansione di un insieme R di espressioni più grande e, per ciascuna espressione r ∈ R

incontrata, si procede col verificare se la stringa in ingresso appartiene al linguaggio definito dall’espressione r. Naturalmente, l’uso di una struttura dati indice eviterebbe la completa scansione (sequenziale) di R (analogamente a quanto succede per i B-alberi, che facilitano la ricerca di chiavi ordinate).

L’idea di considerare un indice che memorizzi oggetti che sono espressioni regolari, in modo tale che, data una stringa in ingresso, vengono velocemente restituite le espressioni che la soddisfano (problema del RE-retrieval), comporta l’introduzione del concetto di dimensione (o misura o taglia) di un linguaggio regolare, visto che le espressioni, a differenza di altri tipi di dati indicizzabili, possono rappresentare insiemi infiniti di stringhe. E’ importante stabilire la taglia

di un linguaggio poiché il corrispondente automa ha taglia variabile che può influenzare il fan-out della struttura.

Prima di definire le misure utilizzate per stabilire la dimensione di un linguaggio regolare (che può essere sia finito che infinito), descriviamo, nel corso di questo capitolo, due algoritmi fondamentali per il “counting” (conteggio) ed il “sampling” (campionamento) delle stringhe appartenenti ad un linguaggio L(r) definito da un’espressione regolare r ∈ R. Quindi, proseguiremo con

l’esposizione delle caratteristiche che contraddistinguono i tre tipi di misure presentati.

2.1 Algoritmi di “counting” e “sampling” per automi

deterministici

Il primo algoritmo conta il numero di stringhe di lunghezza n accettate da un automa M (quantità che indicheremo con |Ln(M)| ), mentre il secondo algoritmo

genera un campione casuale appartenente all’insieme Ln(M), cioè l’insieme delle

stringhe di lunghezza n accettate dall’automa M.

Presentiamo gli algoritmi, proposti in [13], per il caso più semplice, cioè quello in cui M è un automa deterministico con un numero finito di stati. Rimandiamo all’articolo [13], il lettore interessato all’estensione di tali algoritmi al caso di automi a stati finiti non deterministici.

In generale, indichiamo con (s, n) il numero di cammini distinti di lunghezza n che possono essere generati, utilizzando un automa M il cui stato iniziale è indicato con s0, a partire dallo stato s, attraversando qualsiasi stato accettante. Algoritmo di counting. Dato un automa M si noti che la quantità |Ln(M)| è uguale

Per n=0, abbiamo che (s, 0) = 1, se s è uno stato accettante, 0 altrimenti. Per n ≥

1, la quantità (s, n) può essere calcolata ricorsivamente come segue: (s, n) = x∈ , t = (s, x) (t, n-1).

Calcoliamo la quantità (s, i) per tutti gli stati s, partendo da un valore di i uguale a zero e proseguendo con valori crescenti di i (fino ad i = n). Ad ogni passo utilizziamo i risultati ottenuti al passo precedente (cioè, i risultati ottenuti considerando i-1). Poiché ciascun (s, i) è calcolato considerando tutti gli stati raggiungibili dallo stato s con una singola transizione, ogni valore di ( ) può essere calcolato in tempo O(min {| |, |M|}). Visto che nel calcolo di ( ) sono

coinvolti |M| n valori, segue che esiste un algoritmo che in O(n|M| min {| |, |M|})

calcola | Li(M) | per tutti gli 1≤ i ≤ n .

Spieghiamo ora come generare una stringa casuale appartenente all’insieme Ln(M). Si procede prendendo in considerazione i valori (•) che abbiamo

calcolato precedentemente.

Algoritmo di sampling. Consideriamo la collezione di tutte le stringhe di

lunghezza n che possono essere generate a partire da uno stato s, attraversando qualsiasi stato accettante. La probabilità, che una stringa selezionata casualmente da questa collezione abbia il simbolo x ∈ come primo simbolo, risulta essere

(t, n-1)/ (s, n) (cioè, casi favorevoli su casi possibili), dove t = (s, x).

Sostanzialmente, un campione uniforme di stringa casuale, appartenente all’insieme Ln(M), può essere generato iterativamente partendo da uno stato

iniziale s e scegliendo una transizione, che porta in un determinato stato, ad ogni passo.

L’algoritmo

G

R

S

Algoritmo

G

R

S

Input: M, l’automa deterministico a stati finiti;

s, uno stato di M, che inizialmente coincide con lo stato s0 ;

n, parametro di lunghezza, scelto maggiore o uguale ad uno.

Output: Una stringa casuale di Ln(M).

1. for i := n downto 1 do

2. Seleziona transizione etichettata col simbolo x ∈ , fuori dallo stato s, con probabilità (t, i-1)/ (s, i), dove t = (s, x);

3.

4. s := (s, yi );

5. return yn· yn-1 ··· y1 ;

E’ giusto mostrare che se s0, sn, sn-1,…, s1 denota la sequenza di stati visitati

dall’algoritmo, allora la probabilità che una stringa w ∈ Ln(M) sia restituita

dall’algoritmo è:

Notiamo che la complessità temporale dell’algoritmo è pari ad O(n) nel caso in cui la funzione ( ) sia stata già calcolata. Inoltre, un campione uniforme casuale di Ln(M) di dimensione k può essere generato invocando ripetutamente

l’algoritmo

G

R

S

Fig. 2.1 Algoritmo che genera una stringa casuale appartenente all’insieme Ln(M)

(sn, n-1) (sn-1, n-2) (s1, 0) 1 1

× ×……× = =

2.2 Stime per la misura di un linguaggio regolare

Stimare la dimensione di un linguaggio regolare L(M) risulta più difficile che calcolare la quantità |Ln(M)| poiché L(M) può essere un insieme infinito.

Nel resto del capitolo sono descritte tre differenti metriche che non solo provano a “catturare” la dimensione di linguaggi regolari infiniti, ma consentono anche di confrontare le dimensioni di due linguaggi regolari.

Le tecniche che vengono presentate di seguito risultano molto utili soprattutto per quelle applicazioni alla cui base c’è il concetto di indicizzazione di espressioni regolari ed inoltre possono essere utilizzate anche per stimare la selettività di un insieme di espressioni, il clustering di espressioni, ecc.

Prima di procedere con la definizione delle misure per stabilire la dimensione di L(M) è possibile identificare alcune caratteristiche di tali misure.

Innanzitutto è da notare che non ha senso contare il numero di stringhe in un linguaggio regolare infinito. Inoltre bisogna sapere che, mentre risulta arduo assegnare una dimensione precisa ed intera ad un linguaggio infinito, non tutti i linguaggi regolari infiniti sono uguali rispetto alla dimensione. Ad esempio, il linguaggio definito dall’espressione regolare r = (a | b)* è “più grande” del

linguaggio definito dall’espressione regolare r1 = a(a | b)*, in quanto

quest’ultimo è un sottoinsieme proprio del primo, anche se entrambi sono infiniti. E’ necessario individuare e definire una misura che rifletta l’intuizione della relazione “più grande di” valida per insiemi che sono linguaggi regolari. Denotiamo questa misura della dimensione di L(M) con |L(M)| e formalizziamo la relazione “più grande di” nel seguente modo:

Definizione 2.1: Presa una coppia di automi Mi ed Mj diciamo che L(Mi ) è più

grande di L(Mj) se e solo se esiste un intero positivo N t. c. per tutti i k ≥ N ,

k k

s = 1 | Ls (Mi )| > s = 1 | Ls (Mj )| .

Quindi questo vuol dire che presa una coppia di automi Mi ed Mj , se L(Mi) è

più grande di L(Mj) allora | L(Mi)| > | L(Mj)| .

2.3 Max-Count Measure

Una misura abbastanza semplice ed intuitiva utilizzata per stabilire |L(M)| è quella di sommare tutte le quantità |Ls (M)| per 1≤ s ≤ , dove il parametro intero

rappresenta la lunghezza massima di una stringa appartenente ad L(M). La quantità |L(M)|, applicando questa misura, è stimata nel seguente modo:

|L(M)| = | L1 (M)| + | L2 (M)| +…+ | L (M)|

Chiaramente, più grande scegliamo e maggiori saranno l’efficienza e la precisione con cui la misura Max-Count riflette la relazione “più grande di”, anche se per valori molto grandi di questo tipo di approccio potrebbe risultare poco pratico. Quindi, un buon compromesso è quello di assegnare a un valore uguale o leggermente più grande della dimensione di M, cioè |M|, che corrisponde al numero di stati dell’automa M. Questo assicurerebbe che la maggior parte delle stringhe accettate da L(M) venga conteggiata in |L(M)| .

La misura Max-Count risulta particolarmente utile per quelle applicazioni in cui è conosciuta a priori la massima lunghezza della query string in ingresso. Quindi è possibile, se questo valore non risulta troppo grande, assegnare a questa quantità.

Utilizzare la misura Max-Count, in applicazioni in cui l’informazione riguardante la massima lunghezza della query string non è conosciuta a priori, può essere davvero problematico a causa del fatto che la precisione di tale misura dipende sensibilmente dal parametro , che il più delle volte rappresenta proprio la massima lunghezza della query string. Nell’esempio seguente mostriamo come la misura Max-Count conduca ad un risultato diverso a seconda dell’intervallo in cui è compreso il valore del parametro . Infatti, stabilire che il parametro assuma un valore al di sotto di una certa soglia può comportare non solo un

risultato diverso rispetto ad un’altra scelta, ma anche un risultato finale totalmente errato.

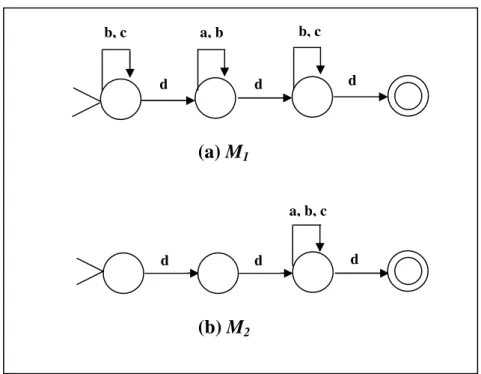
Esempio 2.1 Consideriamo due automi M1 ed M2 riportati in fig. 2.2. Il

linguaggio accettato dall’automa M1 è il linguaggio denotato dall’espressione

regolare (b|c)*d(a|b)*d(b|c)*d; il linguaggio accettato da M2 è il linguaggio

denotato dall’espressione dd(a | b| c)*d.

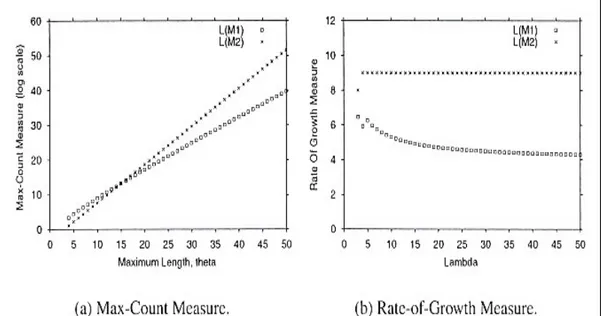
La fig. 2.3(a) confronta le due quantità |L(M1)| e |L(M2)| utilizzando la misura

Max-Count per 30 ≤ ≤ 50. Chiaramente, l’insieme L(M2) è più grande di L(M1),

poiché la quantità |Ln(M2)| cresce più velocemente di |Ln(M1)| al crescere di n.

Infatti, la quantità |Ln+3(M1)| = (n+1)(n+2)2(n-1) e |Ln+3(M2)| = 3n per n > 0.

b, c a, b b, c d d a, b, c d d d (a) M1 (b) M2

Fig. 2.2 Esempi di automi

Il punto (crossover point) a partire dal quale la funzione |L(M2)| è più grande

di |L(M1)| si trova in corrispondenza di = 16; infatti, si ottiene che

s=1 | Ls(M2)| > s=1 | Ls(M1)| per ≥ 16 . Questo vuol dire che se il valore di ,

utilizzando la misura Max-Count, è fissato minore o uguale al valore 16, L(M1)

viene considerato, in modo scorretto, più grande di L(M2).

2.4 Rate-of-Growth Measure

Per ottenere una misura più robusta che permetta di stabilire con maggiore esattezza la dimensione di linguaggi regolari infiniti, si propone una seconda metrica che cattura il “rate-of-growth” (ovvero tasso di crescita) di linguaggi infiniti.

L’idea è la seguente: presa una coppia di automi Mi ed Mj, se la quantità

|Ln(Mi)| cresce ad un tasso più veloce di |Ln(Mj)| (questo sarà stabilito usando la

Fig. 2.3 Confronto della dimensione di L(M2 ) ed L(M1 ) usando due

nozione di derivata prima di una funzione lineare), allora L(Mi) risulta più grande

di L(Mj), in quanto esiste un N t.c. per tutti i valori di k ≥ N

k k

s=1 | Ls(Mi)| > s=1 | Ls(Mj)| .

Intuitivamente, alla luce di questa affermazione, il “rate-of-growth” di un linguaggio può essere considerato una buona misura della sua dimensione.

In generale, data una funzione f(•) non negativa e non conosciuta, possiamo determinare quanto velocemente la funzione f(•) sta crescendo attraverso il calcolo della derivata della sua funzione primitiva; in particolare, possiamo considerare il calcolo di F′( , ) nel seguente modo:

[F( + ) − F( )]

k

dove la funzione F(k) = s=1 f(s) è una funzione crescente.

Applicando l’idea appena enunciata al calcolo del “rate-of-growth” di L(M) otteniamo il seguente risultato: | L(M)| = F′( , ), dove f(s) = | Ls(M)|; quindi,

+

[ s = +1 | Ls(M)| ]

Comunque, similmente alla misura Max-Count, la sommatoria s = +1 | Ls(M)| può essere sensibile ai valori che assumono le variabili e θ.

L’approccio che utilizza il calcolo della derivata, basato sulla funzione F′,

risulta valido per funzioni f con tassi di crescita lineari. Però, visto che il tasso di crescita di un linguaggio regolare infinito è generalmente non lineare, proponiamo una misura approssimata della dimensione di un linguaggio come il tasso di cambio della sua dimensione considerato a partire da una “finestra” (intervallo) di lunghezze alla successiva (consecutiva) “finestra” di lunghezze;

F′( , ) =

| L(M)| =

ossia, la misura Rate-of-Growth per stabilire la dimensione di un linguaggio regolare L (M) è calcolata come segue:

dove rappresenta il parametro di lunghezza che denota l’inizio della prima “finestra” e il parametro di grandezza della “finestra”.

In buona sostanza, l’equazione (1) dà un’indicazione del tasso di crescita di L(M) e, nel seguente esempio, mostriamo come la misura Rate-of-Growth rimpiazzi alcuni degli svantaggi introdotti con la misura Max-Count.

Esempio 2.2 Consideriamo nuovamente gli automi M1 ed M2 riportati in fig. 2.2.

Nella fig. 2.3(b) vengono rappresentate le funzioni |L(M1)| e |L(M2)| utilizzando la

misura Rate-of-Growth, per 3 ≤ ≤ 50 e =2 (è da notare che l’andamento di

queste funzioni è ottenuto per valori di molto grandi). Il grafico indica in modo corretto che L(M2) è più grande di L(M1) a prescindere dal valore assunto da .

In modo simile a come si procede nella misura Max-Count, al fine di assicurare che le stringhe che coinvolgono una porzione sostanziale di cammini, cicli e stati accettanti siano conteggiate in ogni “finestra”, i parametri e potrebbero essere scelti leggermente più grandi di |M|.

Come abbiamo avuto modo di vedere, la misura Rate-of-Growth è più robusta della misura Max-Count. Sono stati individuati però alcuni casi in cui anche la prima metrica fallisce e non cattura in modo corretto il concetto della relazione “più grande di” tra linguaggi regolari. La prova lampante di questa affermazione è il seguente esempio: + 2( )-1 s = + |Ls(M)| |L(M)| = ₍₁₎ + -1 s = |Ls(M)|

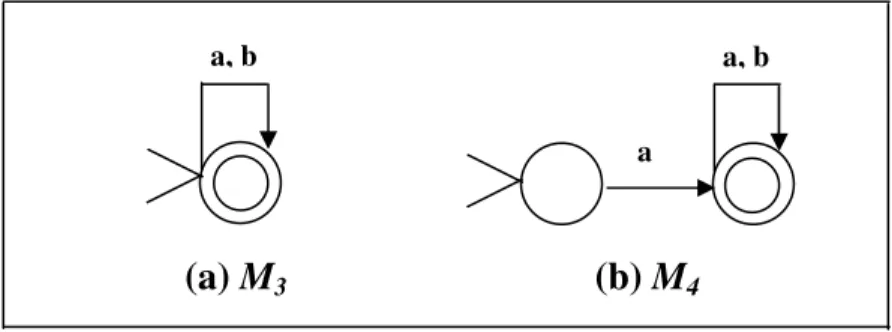
Esempio 2.3 Consideriamo i due automi M3 ed M4 riportati in fig. 2.4.

I linguaggi accettati rispettivamente dall’automa M3 e dall’automa M4

risultano simili. La differenza che c’è tra i due insiemi di stringhe è caratterizzata dal fatto che il linguaggio accettato dal secondo automa è costituito da tutte quelle stringhe che cominciano per ‘a’ e possono terminare con un numero

imprecisato di ‘a’ o di ‘b’, invece il linguaggio accettato dal primo automa è costituito da tutte quelle stringhe che cominciano per ‘a’ o per ‘b’.

Si può osservare che |Ln(M3)| = 2n e |Ln(M4)| = 2n-1 in quanto, come accennato

in precedenza, L(M4) è un insieme che contiene solo stringhe che iniziano con a,

mentre l’insieme L(M3) contiene oltre alle stringhe che iniziano con a, anche

quelle che cominciano con b. Quindi, per tutti i k ≥ 1, si ha che

k k

s =1 | Ls (M3 )| > s=1 | Ls (M4 )|

e L(M3) risulta essere più grande di L(M4).

Utilizzando la misura Rate-of-Growth non è possibile determinare quale tra L(M3) ed L(M4) sia più grande. Questo accade perché per qualunque valore di

e , con la misura Rate-of-Growth, |L(M3)| e |L(M4)| sono entrambi uguali a 2 .

2.5 Minimum Description Lenght (MDL) Measure

Al fine di ottenere una misura più robusta e precisa della dimensione di linguaggi regolari infiniti, presentiamo ora un tipo di misura alternativa, basata

a, b a, b

a

Fig. 2.4 Esempi di automi

sull’uso del principio Minimum Description Lenght (MDL) di Rissanen [14], che pone rimedio ad alcune delle insufficienze riscontrate utilizzando le misure precedenti.

Il principio MDL si basa essenzialmente sulla seguente idea: partendo da un insieme di dati ed un insieme di teorie, che possono spiegare tali dati, si effettui la scelta della teoria che permette di rappresentare i dati nella maniera più compatta possibile. In pratica, ciò significa individuare il rapporto ottimale “theory/model” che può essere desunto da un insieme di dati. Il principio MDL viene applicato ad una varietà di problemi, ad esempio è stato utilizzato per la costruzione di alberi di decisione [15], per la ricerca dei pattern comuni in un insieme di stringhe [16], per la desunzione dei DTD (Document Type Descriptor) da una collezione di dati XML [17]. Un’osservazione importante fatta in [17] è la seguente: date due espressioni regolari Ri e Rj, se Ri definisce un linguaggio più

grande di Rj (cioè, Ri è meno preciso di Rj rispetto alla stessa collezione di

sequenze di dati in ingresso) allora il costo di decodifica di una sequenza di dati in ingresso utilizzando Ri è probabilmente più alto di quello che si sosterrebbe

utilizzando Rj. Questa osservazione è consistente con la teoria dell’informazione,

che, in generale, afferma che occorrono più bit per specificare un elemento che proviene da una collezione di elementi più grande rispetto ad un’altra.

L’uso del principio MDL per definire una misura della dimensione di un linguaggio regolare si ispira all’osservazione appena fatta e si basa sulla seguente intuizione: dati due automi deterministici a stati finiti Mi ed Mj, se L(Mi) è più

grande di L(Mj) allora il “per-symbol-cost” di decodifica di una stringa casuale

appartenente a L(Mi), utilizzando Mi, è probabilmente più alto di quello che si

sosterrebbe decodificando una stringa appartenente a L(Mj), utilizzando Mj.

Il “per-symbol-cost” di decodifica di una stringa w ∈ L(M) è dato dal rapporto

tra il costo di decodifica di w, ottenuto sfruttando il principio MDL, e la lunghezza di w. Quindi, una misura ragionevole della dimensione di un

linguaggio regolare L(M) è il “per-symbol-cost” della decodifica, basata sul principio MDL, di un campione casuale di stringhe appartenenti ad L(M).

Denotiamo con MDL(M, w) il costo di decodifica di una stringa w ∈ L(M),

utilizzando l’automa M, e con c un campione casuale di L(M). La misura per stabilire la dimensione del linguaggio L(M), basata sul principio MDL, viene calcolata nel seguente modo:

dove |w| denota la lunghezza della stringa w.

A questo punto ciò che ci rimane da definire è il costo di decodifica di w ottenuto considerando l’automa M (ossia, MDL(M, w)): supponiamo di considerare w nella seguente forma w = w1. w2.…. wn ∈ L(M) e la sequenza s0, s1,

s2,…, sn l’unica sequenza di stati in M visitati dalla stringa w, allora il valore di

MDL(M, w) viene calcolato nel seguente modo:

dove ciascun ni denota il numero di transizioni fuori dallo stato si, e log2(ni) è il

numero di bit richiesti per specificare la transizione fuori dallo stato si. Poiché la

formula (3) è basata sul conteggio del numero delle transizioni, per ottenere una misura accurata della dimensione di un linguaggio infinito è importante che M non contenga transizioni “non-essential” (cioè, transizioni che non sono parte di un cammino accettante che coinvolge almeno un ciclo). Per questo motivo, si considera l’automa M come un automa deterministico col minor numero di stati [1], senza transizioni “non-essential”.

|L (M)| = 1 | c | w ∈ c

Illustriamo con un esempio come calcolare i costi di una decodifica basata sul principio MDL.

Esempio 2.4 Consideriamo due automi M1 ed M2 riportati in fig. 2.2 e due

stringhe di lunghezza dieci della forma w1= bbbdbbdbbd ∈ L(M1) e w2=

ddbbbbbbbd ∈ L(M2) .

Il “per-symbol-cost” di decodifica di w1 e w2 , utilizzando rispettivamente gli

automi M1 ed M2, è calcolato nel seguente modo:

e

dove, per il primo automa, il valore ni , cioè il numero di transizioni fuori dallo

stato si, è sempre uguale a 3, mentre per il secondo automa il valore di ni è uguale

a 1 nel caso degli stati s0 e s1, e a 4 nel caso degli stati rimanenti.

I costi calcolati mostrano, in modo corretto, che L(M2) è più grande di L(M1).

Per completare il calcolo, generiamo un campione casuale c, di stringhe appartenenti all’insieme L(M), utilizzando l’algoritmo

G

R

S

ovviamente calcolati per ciascuna stringa w appartenente al campione c. La somma totale andrà moltiplicata per l’inverso della dimensione di c.

MDL(M1, w1) |w1| = 10 × log2(3) 10 ≈ 1.5850 MDL(M2, w2) |w2| = (2×0) + (8 × log2(4)) 10 ≈ 1.6000 MDL(M, w) |w|