CAPITOLO II

CAPITOLO II

CRITERIO DEL CERCHIO PER LA STIMA DI

PARAMETRI DEL SISTEMA

1.1

INTRODUZIONE

1.2

CRITERIO DEL CERCHIO

1.1 Introduzione

In questo capitolo viene esposto un metodo che permette di individuare alcuni parametri caratteristici di un processo come: margine di ampiezza, margine di fase, banda passante, sensibilità e picco di risonanza a ciclo chiuso.

Data una funzione di trasferimento G(s), per il teorema di Nyquist, si è in condizione limite di stabilità se:

G(s)=-1 (II.1.1)

In tale situazione l’uscita y presenta una oscillazione stabile con pulsazione ω (rad/s) tale per cui

π ω =−

∠G( j ) (II.1.2)

Tale ω (rad/s) può essere individuata in vari modi:

1. tramite la tecnica ATV, sfruttando la teoria della funzione descrittiva

2. attraverso il luogo delle radici in corrispondenza dei punti di attraversamento da

parte dei rami del luogo sull’asse delle ordinate 3. attraverso la tecnica SATV

1.2 Criterio del cerchio

L’idea di base [8],[12] consiste nella ricerca dei punti di intersezione sul piano di Nyquist tra la funzione di trasferimento G(s) e una generica circonferenza di raggio R e centro C ( C ,0).

Si consideri il caso di una semicirconferenza di centro C (C ,0) e raggio R descritta dalla seguente espressione parametrica:

C s s R s C + + − = 1 1 ) ( (II.2.1)

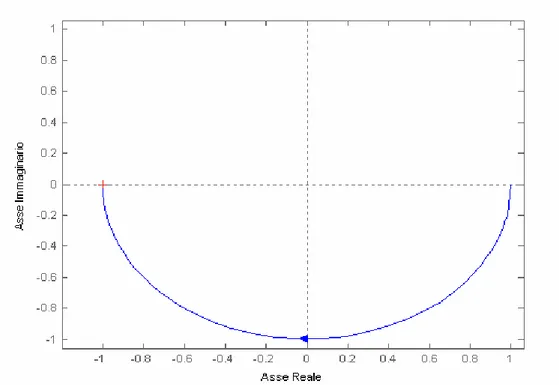
L’equazione parametrica del semicerchio (ad esempio di centro l’origine e raggio unitario) nel piano di Nyquist è mostrata in figura II.2.1. La (II.2.1) ha modulo unitario e fase per s=j pari a:

) ( tan 2 1 1 _{+ =−} −1 _ω + − ∠ C s s R (II.2.2)

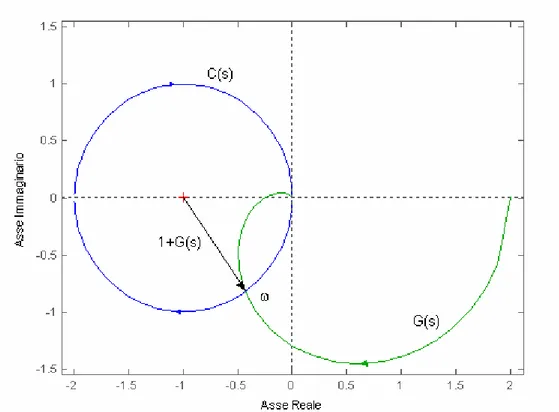
Il punto di intersezione tra la generica funzione di trasferimento G(s) e il semicerchio C(s) individua la pulsazione ω (rad/s) come si può vedere dalla figura II.2.2. Dal punto di vista matematico l’intesezione tra la generica f.d.t. G(s) e il semicerchio C(s) si ottiene imponendo la seguente uguaglianza:

Figura II.2.1 – Equazione del semicrechio di raggio R=1 e centro C=(0,0) nel piano di Nyquist

Inserendo la (II.2.1) nella (II.2.3) e sviluppando si ottiene la seguente relazione: ) ) ( ( ) ( ) (s R C s G s R C G − + =− + − (II.2.4) Posto − = + = C R k C R h (II.2.5)

dalla (II.2.4) si arriva alla seguente espressione:

1 1 ) ( ) ( 1 ₌₋ + − k s G k h k s G s (II.2.6) Posto: 1 ) ( ) ( 1 ) ( ) ( + − = = k s G k h k s G s s G s P (II.2.7)

La (II.2.6) coincide con G(s)=-1.

Quindi l’individuazione della (rad/s) per cui si ha l’intersezione tra la f.d.t. G(s) e il semicerchio C(s) si è ricondotto all’individuazione della ω (rad/s) per cui ∠P(s)=−π.

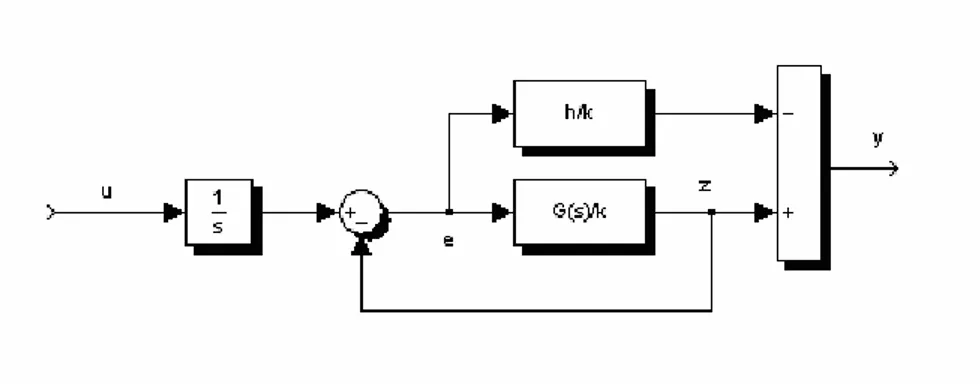
L’individuazione della pulsazione ω (rad/s) relativa all’individuazione dell’intersezione della funzione di trasferimento con un particolare cerchio avviene, per la tecnica ATV e SATV, applicando fisicamente lo schema di figura II.2.3 al processo G(s).

Figura II.2.3 – Diagramma a blocchi della (II.2.6) Si verifica infatti che lo schema di figura II.2.3 rappresenta la G(s). Si ha: ) ( ) ( ) ( z s s s u s e = − (II.2.8) e ) ( ) ( ) ( e s k s G s z = (II.2.9)

dalla (II.2.8) sostituendo la (II.2.9) si ottiene:

+ = 1 ) ( ) ( ) ( k s G s s u s e (II.2.10)

inoltre posto − = + − = + − = k h k s G s e s e k s G k h s e s z k h s e s y( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (II.2.11) si ottiene k h k s G s y s e − = ₍ (₎ ) ) ( (II.2.12)

Mettendo insieme la (II.2.10) con la (II.2.12) si può verificare l’uguaglianza con la (II.2.7). 1 ) ( ) ( 1 ) ( ) ( ) ( + − = = k s G h k s G s s u s y s G (II.2.13)

La P(s) di (II.2.7), è un sistema di tipo 1 per la presenza dell’integratore. Per questo motivo, se l’ingresso ha un valor medio non nullo, anche l’uscita avrà un bias. Questa situazione poteva creare problemi di misura di frequenza e fase nella realizzazione della tesi Di Moia [9]. Con l’utilizzo dell’algoritmo FFT questo problema viene eliminato in quanto tale algoritmo e indifferente ad eventuali bias sul segnale da stimare

Diversamente al metodo ATV e SATV , per trovare la pulsazione ω (rad/s) relativa all’intersezione tra il cerchio e la funzione di trasferimento G(s) non viene applicato al sistema lo schema di figura II.2.3, ma tale schema viene solamente calcolato matematicamente. Nella realizzazione di questo progetto infatti la stima del modulo e fase che viene effettuata tramite l’algoritmo FFT, viene sempre applicata al sitema G(s).

Senza dover creare fisicamente il circuito che realizza la formula (II.2.7) (come avveniva per la tesi di Di Moia), si può calcolare direttamente il modulo e la fase del sistema P(s) conoscendo il modulo e la fase di G(s).

Si può infatti riscrivere la (II.2.7) come:

k s G h s G s s P + − = ) ( ) ( 1 ) ( (II.2.14)

Dato che h e k sono numeri reali conosciuti e visto che:

) ( ) ( ) ( ) (s G jω R ω jI ω G = = + (II.2.15)

posso riscrivere la (II.2.7) come:

(

)

(

)

Quindi se si conosce, per una data frequenza di G(j ) la sua parte reale e la sua parte immaginaria (cosa che restituisce l’algoritmo di FFT in forma polare), allora si può calcolare con la (II.2.16) la parte reale e la parte immaginaria e quindi anche modulo e fase del processo P(s) a quella data frequenza.

Per calcolare quindi i vari parametri da stimare con il criterio del cerchio, basta porre il giusto valore di h e k calcolato attraverso la (II.2.5) nella (II.2.16) dove R( ) e I( ) sono la parte reale e la parte complessa che restituisce l’algoritmo FFT relativo alla frequenza del sistema G(s). In questo modo posso conoscere contemporaneamente la funzione di trasferimento dei vari processi P(s) creati a seconda delle stime effettuate ( e quidi al variare dei valori di h e k) conoscendo funzione di trasferimento del sistema G(s).

CALCOLO DEL MARGINE DI FASE

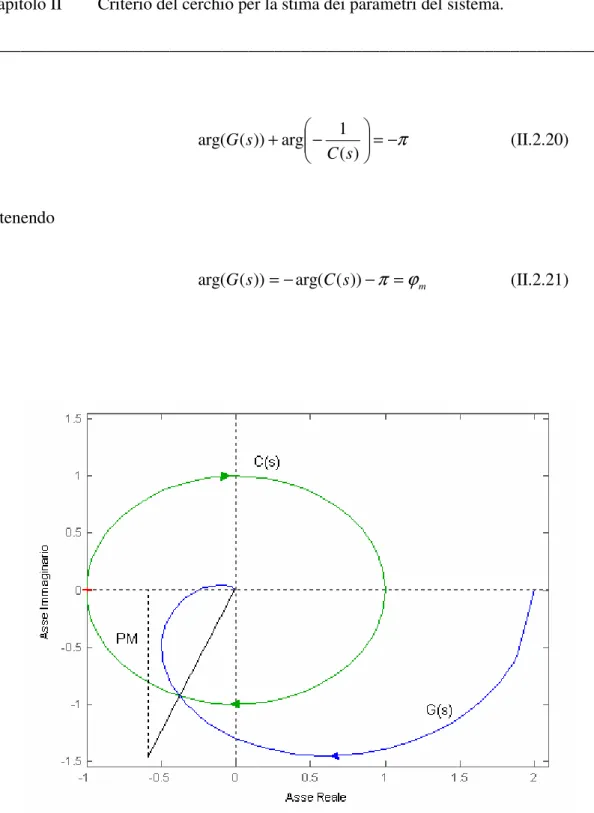
Il calcolo del margine di fase PM [8] (gradi) si ottiene intersecando il cerchio di centro l’origine C=(0,0) e raggio unitario (R=1) con la funzione di trasferimento G(s), come mostrato in figura II.2.4 . Se si pone C=0 e R=1 nella (II.2.1), sfruttando (II.2.5) la trasformazione (II.2.7) si traduce nella seguente relazione:

1 ) ( 1 ) ( 1 ) ( + − = s G s G s s G (II.2.17)

Considerando l’espressione iniziale (II.2.3) si ha che

1 ) ( 1 ₌₋ − s C G (II.2.18) in termini di fase π − = − ) ( 1 arg s C G (II.2.19) da cui segue

π − = − + ) ( 1 arg )) ( arg( s C s G (II.2.20) ottenendo m s C s G( ))=−arg( ( ))−π =ϕ arg( (II.2.21)

Figura II.2.4 – Diagramma di Nyquist di G(s) e C(s) per il calcolo del margine di fase PM

Lo sfasamento tra l’uscita z(t) di figura II.2.3 e l’ingresso e(t) del processo avente funzione di trasferimento G(s)/k è proprio il margine di fase.

Nello sviluppo del presente progetto però non è stato realizzato il blocco fisico di figura II.2.3 ma viene calcolato solo matematicamente con la formula (II.2.16). Quindi controllando i valori della fase che vengono calcolati tramite la (II.2.16), quando questi valgono – , il valore della fase stimato dall’algoritmo FFT del processo G(s) è proprio il valore del margine di fase cercato. Questo comporta una maggiore semplicità di realizzazione in quanto non è necessario aggiungere ulteriori moduli per la stima dello sfasamento del segnale di ingresso al sistema G(s) rispetto al segnale in uscita.

CALCOLO DEL MARGINE DI AMPIEZZA

Il calcolo del margine di ampiezza GM [8] (db) può essere facilmente ottenuto senza dover applicare alcuna trasformazione. Se G(s) rappresenta la funzione di trasferimento del processo, calcolando la pulsazione c (rad/s) corrispondente alla fase –

nel diagramma di Bode, il margine di ampiezza GM si ottiene dalla seguente relazione:

db c

db G j

GM =− ( ω ) (II.2.21)

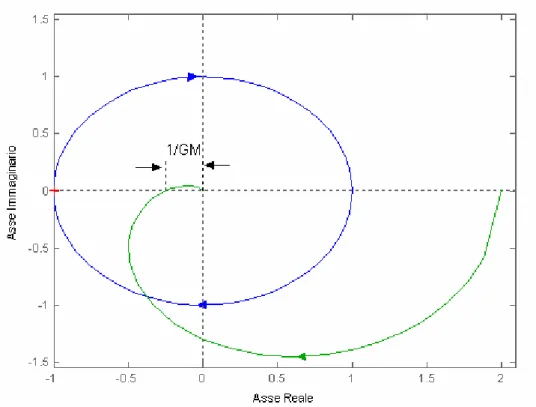
Nel piano di Nyquist, dal punto di vista grafico il margine di ampiezza si calcola considerando la lunghezza del segmento che parte dall’origine degli assi e termina sul punto di intersezione tra la G(s) e l’asse reale negativo ( vedi figura II.2.5).

Il reciproco della lunghezza di tale segmento rappresenta il margine di ampiezza.

Nel presente progetto infatti non viene fatto alcun calcolo per trovare il valore della funzione di trasferimento relativa al calcolo del Margine di ampiezza; tale valore infatti coincide con il valore della fase del sistema G(s). Quindi per questo calcolo basterà controllare i valori della fase del sistema G(s) e quando questi valgono – , il valore del modulo e fase stimati dall’algoritmo FFT del processo G(s) calcolati con la (II.2.21) è proprio il valore del margine di fase cercato.

Anche in questo caso si può notare che non è necessario nessun altro modulo aggiuntivo per la stima della frequenza o dell’ampiezza in quanto tali valori vengono restituiti dall’algoritmo FFT.

Figura II.2.5 – Diagramma di Nyquist di G(s) e C(s) per il calcolo del margine di ampiezza GM.

CALCOLO DELLA SENSIBILITA’

Nel caso di sistema SISO la funzione sensibilità [8] è definita come:

) ( 1 1 ) ( ω ω j G j S + = (II.2.21)

dove G(s) è la funzione di trasferimento ad anello aperto. Assumendo ) ( 1 ) ( ) ( s G s G s W + = la funzione di trasferimento di G(s) ad anello con retroazione negativa, la funzione sensibilità S(j ) caratterizza il comportamento del sistema ad anello chiuso rispetto al sistema ad anello aperto, in presenza di piccole variazioni nei parametri della funzione di trasferimento G(s) ad anello aperto.

Il vettore 1+G(s) a meno dell’inversione rappresenta la funzione sensibilità. Affinchè 1

) (jω <

S , deve essere 1+G(jω) >1. La relazione 1+G(jω) =1 descrive proprio un cerchio di raggio unitario centrato in C=(-1,0) (cerchio per calcolare la sensibilità) come è mostrato in figura II.2.6. La pulsazione rappresenta il limite per il quale il sistema funziona ancora bene in termini di sensibilità; infatti occorre lavorare a frequenze esterne a tale cerchio.

Imponendo C=(-1,0) e R=1 nella (II.2.1) e sfruttando la (II.2.5) la trasformazione (II.2.7) si traduce nella seguente relazione:

1 2 ) (2 ) ( 1 ) ( + = _{G s} s G s s G (II.2.21)

Dato che il seguente valore da ricercare è solamente una frequenza, nel progetto viene effettuato il calcolo relativo alla formula (II.2.21) dato il valore di G(j ) stimato con l’algoritmo FFT e quando la fase del processo G(s) raggiunge il valore di – viene ottenuto il valore (rad/s) relativo alla frequenza limite di sensibilità.

CALCOLO DELLA BANDA PASSANTE A CICLO CHIUSO

Nel caso di processi di tipo 1, la banda passante del processo ad anello chiuso si ottiene dalla stima dell’intersezione della G(s) con un cerchio di raggio R= 2 e centro C=(1,0).

In questo modo si riesce a trovare la frequenza di banda passante che indica la pulsazione alla quale il modulo della risposta armonica è inferiore di 3 db ( corrispondenti ad un rapporto di 1 ad

2

1 _{) al valore statico G}

Lavorare a frequenze esterne a tale cerchio significa lavorare nella zona della funzione di trasferimento del sistema G(s) in cui la risposta in ampiezza è maggiore di 3 db rispetto al valore statico.

Come si può notare dalla figura II.2.7 abbiamo 2 valori validi di banda passante. In questo caso infatti per le frequenze all’interno del cerchio si hanno valori del modulo della risposta armonica di G(s) minore di 3 db al valore statico.

Figura II.2.7 – Diagramma di Nyquist di G(s) e C(s) per il calcolo della banda passante

Imponendo C=(1,0) e R= 2 nella (II.2.1) e sfruttando la (II.2.5) la trasformazione (II.2.7) si traduce nella seguente relazione:

) 1 2 ( ) ( ) 1 2 ( ) ( 1 ) ( − + + − = s G s G s s G (II.2.22)

Anche in questo caso il valore da ricercare è solamente una frequenza, quindi nel progetto viene innanzitutto ricercato il valore del guadagno statico G0(0) immettendo nel sistema

G(s) a ciclo chiuso con reazione unitaria una costante (unitaria). In tale modo si riesce ad ottenere il valore M del guadagno statico del sistema.

A questo punto posso calcolare il raggio R ed il centro C del cerchio con le formule (II.2.24) e (II.2.25). con tali parametri è quindi possibile calcolare i valori di h e k:

− = + = C R k C R h (II.2.22b)

in modo da poter applicare l’equazione (II.2.16). Effettuato il calcolo relativo al dato valore di G(j ) stimato con l’algoritmo FFT e quando la fase del processo G(s) raggiunge il valore di – viene ottenuto il valore (rad/s) relativo alla frequenza della banda passante per il sistema rappresentato in figura II.2.7 si avranno quindi 2 punti in cui il processo G(s) raggiunge il valore di – .

Dalle simulazioni si può verificare che il valore di M nel caso di sistemi di tipo 1, è circa unitario ( errore 1/1000).

CALCOLO DELLA PULSAZIONE DI RISONANZA

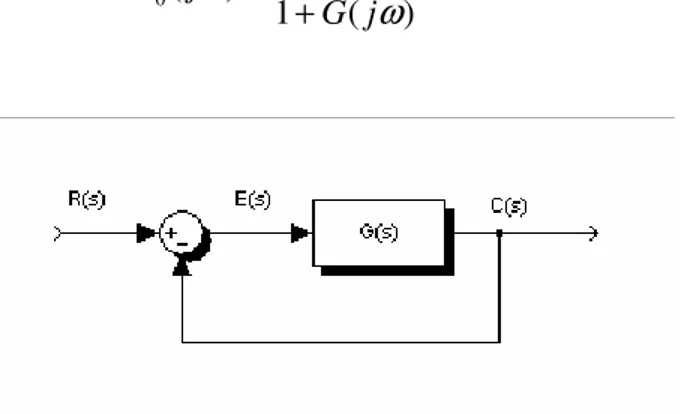
Si supponga di avere un processo avente una funzione di trasferimento G(s). Se si effettua una retroazione negativa unitaria come mostrato in figura II.2.8 si ottiene la seguente funzione di traferimento:

) ( 1 ) ( ) ( 0 _ω ω ω j G j G j G + = (II.2.23)

Figura II.2.8 – Sistema con retroazione unitaria negative

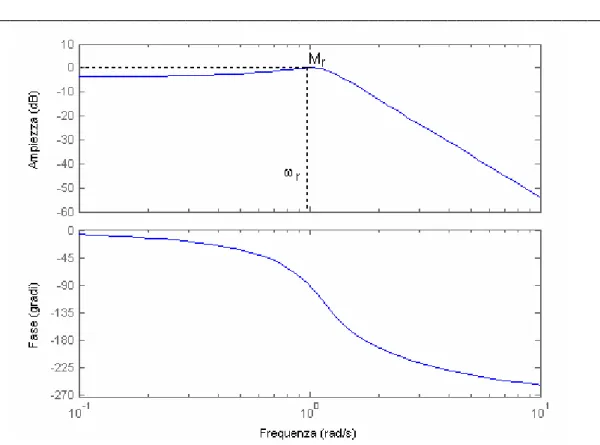
Attraverso il diagramma di Bode è possibile determinare per via grafica la pulsazione di risonanza r (rad/s) e il picco di risonanza Mr (vedi figura II.2.9).

Pulsazione di risonanza r (rad/s): Pulsazione in corrispondenza della quale il modulo di

G0(j ) assume il valore massimo.

Figura II.2.9 – Diagramma di Bode di un sistema ad anello con retroazione unitaria

Sfruttando la teoria del cerchio [8],[12], il meccanismo per determinare la pulsazione di risonanza del processo è quello di considerare il cerchio (cerchi di Hall) tangente alla funzione di trasferimento G(s). I cerchi di Hall nel piano di Nyquist sono caratterizzati dall’avere il centro e il raggio espressi dalle seguenti relazioni:

2 2 1 M M C − = (II.2.24) 2 1 M M R − = (II.2.25) dove M = G0(jω)

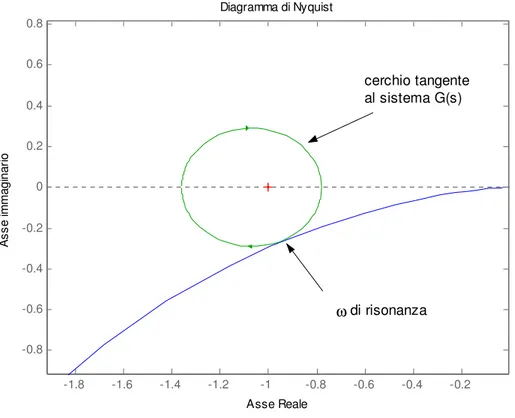
nell’ipotesi di reazione unitaria, si cerca il raggio e il centro del cerchio tangente alla curva della G(s) nel piano di Nyquist (figura II.2.10). Il punto di intersezione determina una pulsazione rappresentante la pulsazione di risonanza r (rad/s) del sistema ad anello

chiuso (II.2.23). Diagramma di Nyquist Asse Reale A ss e im m ag in ar io -1.8 -1.6 -1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 cerchio tangente al sistema G(s) ω di risonanza