Capitolo 2: Analisi del metodo di sintesi scelto

Capitolo 2: Analisi del metodo di sintesi scelto

2-1 Generalità

In questo capitolo ci proponiamo di descrivere i diversi metodi di deformazione che sono stati implementati.

Come detto in precedenza i metodi di sintesi diretta sono i più utilizzati nel caso in cui si debbano realizzare antenne a riflettore sagomato, di conseguenza abbiamo utilizzato tali metodi per la realizzazione del nostro progetto.

Prima di passare all’analisi delle specifiche del progetto vediamo in dettaglio i vari metodi di sintesi diretta che si sono utilizzati.

Il metodo di sintesi diretta da noi utilizzato consiste nella ricerca di una Superficie di Deformazione da sommare ad una superficie base (paraboloide) in modo da ottenere il diagramma di irradiazione richiesto:

Z

( )

x,y = Z_b

( ) ( )

x,y +δ x,y (2.1) dove

• Z(x,y) è la superficie del riflettore finale, cioè quella deformata

• Z_b

(

x,y

)

è la superficie base

Cioè partendo inizialmente da una superficie base la quale dà origine ad un certo diagramma di irradiazione, si vuole perturbare tale diagramma di irradiazione effettuando delle deformazioni sulla superficie che lo ha generato.

Questo modo di procedere consente di inizializzare il metodo di sintesi da antenne aventi un diagramma di irradiazione con caratteristiche simili a quelle richieste (si veda capitolo 3).

La superficie di deformazione sarà caratterizzata da alcuni coefficienti che rappresentano le incognite del problema, e che verranno determinati mediante un procedimento iterativo basato su un Algoritmo Genetico. In questo lavoro vengono analizzati tre metodi che ci consentono di costruire la superficie di deformazione ottimale:

• DEFORMAZIONE MEDIANTE POLINOMI RETTANGOLARI • DEFORMAZIONE MEDIANTE POLINOMI DI ZERNIKE • DEFORMAZIONE MEDIANTE FUNZIONI B-SPLINES

Di seguito analizziamo in dettaglio i tre metodi menzionati in precedenza.

2.2 Deformazione mediante polinomi rettangolari

In questo caso la superficie di deformazione viene descritta mediante polinomi rettangolari del tipo:

∑

∑

= = ⎟⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = n ij m B y y A x x c y x 0 j 2j i 0 i ) ( , 0 0 δ

(2.2)

in cui

• x e 0 y individuano il centro dell’apertura; 0

• A e B indicano i semiassi dell’apertura;

• m e n fissano il grado massimo del polinomio

• c costituiscono l’insieme dei coefficienti incogniti da ij

determinare mediante il metodo iterativo.

La funzione δ nella (2.2) determina il tipo di deformazione della superficie del riflettore, e di conseguenza l’andamento del diagramma di irradiazione dell’antenna.

Osserviamo che nella (2.2) il polinomio presenta una struttura di funzione pari rispetto alla variabile y. Questo al fine di ottenere una deformazione simmetrica della superficie rispetto al piano YZ, che è condizione necessaria affinchè il diagramma di irradiazione sia simmetrico sul piano azimutale.

Nel caso in cui si fosse interessati ad avere un diagramma di irradiazione simmetrico sia sul piano di elevazione e sia sul piano di azimuth, allora dovremo utilizzare anche un esponente 2i in corrispondenza della variabile x. In tal caso il polinomio prende la forma sguente:

∑

∑

= = ⎟⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = n ij m B y y A x x c y x 0 j 2j i 0 i ) ( 0 2 0 , δ

(2.3)

Di conseguenza note le specifiche dovremo fissare i termini all’esponente nel polinomio di deformazione a seconda degli andamenti dei diagrammi di irradiazione richiesti.

La continuità e la derivabilità dei polinomi rettangolari assicura la regolarità della superficie finale.

Queste condizioni sono necessarie nel caso si utilizzino metodi di sintesi basati sulla Ottica Fisica (PO) [5].

2.3 Deformazione mediante polinomi di Zernike

Una classe di funzioni utilizzate in molte applicazioni è rappresentata dai polinomi di Zernike [12].

In questa sezione diamo la descrizione del metodo perturbativo attraverso l’uso di questi polinomi, richiamando alcune proprietà importanti.

Iniziamo con la definizione dei polinomi di Zernike, a tal fine denoteremo con x! e con [x] rispettivamente il fattoriale di x, qualora x sia un numero intero non negativo, e la parte intera del numero reale x. Definizione 1. Il polinomio di Zernike di ordine p è definito nel modo seguente: ⎪ ⎩ ⎪ ⎨ ⎧ = ≠ ≠ = 0 ) ( (2.4) 0 , dispari ) sin( ) ( 0 pari, ) cos( ) ( ) , ( 0 _m R m p m R m p m R Zer n m n m n p ρ ϕ ρ ϕ ρ ϕ ρ per m ≤ n1, dove (2.5) , ) , ( ) ( n i m i i m n c n m R ρ

∑

ρ = =

in cui i coefficienti c_i = c_i( mn, ) sono dati dalle seguenti relazioni:

[

]

[

]

(2.7) 0 (2.6) ! ! 2 / ) ( ! 2 / ) ( ) 1 ( 1 ] 2 / ) [( = − + − = + − m m n m c m m n n m c Sia quindi (2.8) dispari 2 1 pari 2 ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ + = i i i i a_i allora

(

)

(2.9) 1 2 2 2 i i i i i i a m a a m n a m n c c + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{− −} ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⎥⎦ ⎤ ⎢⎣ ⎡ + − = +

per ogni i=m,………..,n.

Osservazione 1. Gli interi n ed m nella Definizione 1 rappresentano rispettivamente il grado radiale e la frequenza azimutale. In particolare il numero n può essere dedotto dall’ ordine p usando la relazione

[ ]

(

1 8 7

)

. (2.10) 2 1 , 1 ₁ 1 − = + − = q q p n

Il numero m si ricava dalla n nel modo seguente:

(

)

(

₂ mod2 mod2

)

, ₂

[

(

1

)(

₁ 1

)

]

. (2.11) 2 + + = + − − = q n q q n q n m

In seguito consideriamo gli interi m ed n come assegnati, slegandoli dal loro legame con l’ordine p. Tuttavia osserviamo che data una coppia di interi m ed n è sempre possibile determinare un intero p per cui m ed n soddisfano le equazioni (2.10) e (2.11).

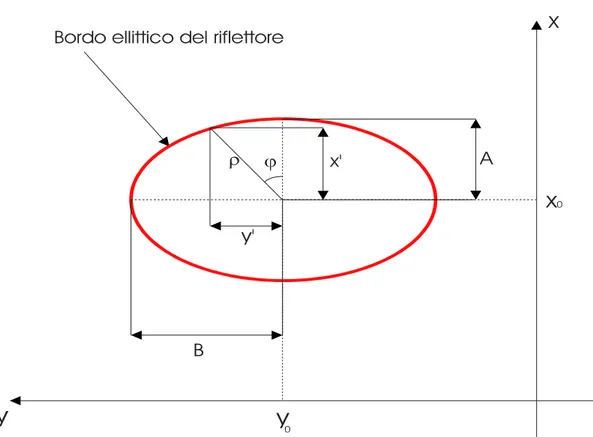
Le variabili ρ eϕ sono legate alle variabili cartesiane dalla seguente

trasformazione polare generalizzata, relativa ad un fissato centro

(

x₀, y₀

)

ed alle lunghezze A, B >0 dei semiassi ellittici:

( )

( ) ( )

(2.12) ' ' arctan ' ' , 2 2 ⎪ ⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = + = = x y y x y x T ϕ ρ essendo (2.13) . -' , ' 0 0 B y y y A x x x = − =

Per chiarezza riportiamo in figura 2.1 un disegno della relazione che

Figura 2.1: Disegno della relazione che intercorre tra

( ) (

x, y e ρ,ϕ

)

.

Richiamiamo ora alcune proprietà dei polinomi di Zernike.

• I polinomi di Zernike sono funzioni ortogonali nelle variabili x, y, nel dominio _x2 + y2 <1_.

• Essi sono invarianti rispetto ad una rotazione degli assi, cioè

Zerp(ρ,ϕ) = g_p

( )

ϑ Zer_p

(

ρ,ϕ +ϑ

)

, (2.14)

dove g è una funzione continua e 2_p π -periodica e ϑ è l’angolo di

• I polinomi radiali soddisfano la relazione di ortogonalità: ₀1

( ) ( )

m_' d _{n n,n'} (2.15) n m n R r R ρ ρ ρ = δ

∫

dove r_n è un coefficiente positivo e δ_n,n' è il simbolo di

Kronecker.

• I polinomi di Zernike normalizzati formano un sistema ortogonale completo.

Tornando al nostro problema di descrivere la deformazione ottimale da

aggiungere al paraboloide Z_b, noi consideriamo la rappresentazione

( )

( )

(

(

)

)

(

∑

)∈ − = S m n nm m n nmR m A w y x , (2.16) , cos , ρ ϕ ϕ δ

in cui w>0 è un fattore di scala, S definisce un insieme finito e prefissato di coppie di indici interi (n,m) non negativi con m≤n, e le variabili

nm

A (Ampiezza del modo di Zernike m,n) e ϕ_nm (Fase del modo di

Zernike m,n) rappresentano i coefficienti rispetto ai quali ottimizzare la forma della superficie Z.

Osserviamo che nella relazione (2.16), il generico termine può essere sviluppato nel seguente modo:

_A(1)_R

( ) ( )

ρ cos _mϕ _A(2)_Rm

( ) ( )

ρ sin _mϕ , (2.17) n nm m n nm + dove

(1) cos

(

)

(2.18) nm nm nm A m A = ϕ (2) sin

(

)

. (2.19) nm nm nm A m A = ϕ

Quindi dalla (2.17) segue che il generico termine della somma si scrive come una combinazione di due polinomi di Zernike.

La modulazione del fattore di scala w offre un ulteriore grado di libertà rispetto alla scelta della deformazione δ.

2.4 Deformazione mediante funzioni B-Splines

In questa sezione introduciamo l’approccio con B-Splines alla deformazione della superficie. A tal fine richiamiamo alcune proprietà fondamentali di questa classe di approssimanti.

Definizione 2. Sia t =

{ }

t_{i i≥0} ⊂ I , dove I ⊂ è un intervallo, una ℜ

successione (eventualmente infinita) non decrescente. La i-esima

B-Spline di ordine k per la sequenza t è indicata con B_i,k e si ottiene per

ricorrenza secondo il seguente algoritmo:

( )

(2.20) altrimenti 0 1 ₁ 1 , ⎩ ⎨ ⎧ ≤ < = i i+ i t x t x B

( )

( )

_{1, 1}

( )

(2.21) 1 1 , 1 , B x t t x t x B t t t x x B _{i k} i k i k i k i i k i i k i + − + + + − + + − − + − − = per ogni x I∈ .

Osservazione 2. In seguito assumeremo che la successione t sia formata da un numero finito di nodi dell’intervallo [0,1], detto intervallo dei

parametri, cioè t =

{

0 = t₀ ≤ t₁ ≤...≤ t_m =1

}

.

In tal caso è sottointeso che le B-Splines saranno poste uguali a zero al di fuori dell’intervallo dei parametri.

Riportiamo alcune proprietà delle B-Splines:

• La generica B-Spline B_i,k, k≥1, è una funzione a supporto

compatto contenuto nell’intervallo

[

t_i,,t_i+k+1

)

.

• Dalla (2.21) ciascuna Bi,k è calcolata a partire da due B-Splines

di ordine k-1, ciascuna delle quali è a sua volta calcolata da due

B-Splines di ordine k-2, etc. Quindi B_i,k è costruita

ricorsivamente da una base di funzioni di grado 1.

• Notiamo che B_i,k ≥0 e che la somma di tali funzioni sull’indice

i è 1. Questo richiama la ben nota proprietà di partizione dell’unità di cui gode questa classe di funzioni.

La superficie di deformazione che considereremo per le simulazioni prende in questo contesto la seguente forma:

( )

, 0 (2.22) , 0 0 0 , 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − =

_{∑ ∑}

= = B y y B A x x B c y x q k j m i m j q k i ij δ

in cui l’ordine k≥1 è fissato, i coefficienti c descrivono, come al solito, _ij

del riflettore mentre A e B sono le lunghezze dei semiassi del bordo ellittico del riflettore.

Le funzioni q

k i

B_, , con q∈

{ }

d,p , sono definite di seguito:

( )

( )

_{( )}

(2.23) 0 , 0 , , , , ⎩ ⎨ ⎧ < − ≥ = x x B x x B x B k i k i p k i e

( )

( )

_{( )}

(2.24) 0 , 0 , , , , ⎩ ⎨ ⎧ < − − ≥ = x x B x x B x B k i k i d k i Quindi p k i B_, e d k i

B_, rappresentano rispettivamente le estensioni pari e

dispari della i-esima B-Spline B_i,k .

Le motivazioni principali per questa scelta della rappresentazione della superficie di deformazione δ sono riassunte nei successivi punti:

• Fissare il centro del riflettore al fine di non modificare in quel

punto la superficie di base Z_b.

• Data la struttura a supporto compatto delle B-Splines su [0,1], prolunghiamo per x<0 tali funzioni, al fine di produrre una

deformazione anche nel dominio x < x₀ ,y < y₀ .

• Con la scelta di q = p nella dipendenza dalla variabile x in (2.22) possiamo replicare il comportamento simmetrico che si ottiene nel caso della deformazione mediante polinomi rettangolari, si veda la sezione 2.2.

L’uso del simulatore necessita, nel caso si faccia utilizzo di una superficie diversa da quelle già previste dal simulatore stesso,

l’introduzione delle derivate prime e seconde della superficie che si intende utilizzare.

Poiché la forma funzionale (2.22) non è prevista all’interno del simulatore, nell’implementazione della deformazione con B-Splines, avremo bisogno di introdurre le espressioni delle derivate di (2.22). Dunque riportiamo il seguente Teorema di derivabilità per la cui dimostrazione rimandiamo al libro di Carl de Boor [8].

Teorema 1. Dato k≥2 intero e una sequenza non decrescente e finita t=

{ }

t_{i 0≤i≤m} di numeri reali, sia

{ }

B_{i,k 0≤i≤m} la relativa successione

B-Splines di ordine k. Allora per ogni α₀,α₁,....,α_m∈ ℜla funzione

( )

∑

( )

= = Φ m i i ik x B x 0 , (2.25) , α

ammette derivate di ogni ordine 0 ≤ j ≤ k-1, e vale la seguente formula per la derivata di ordine j:

( )

1

( )

, (2.26) 0 , ) 1 (

∑

+ = − + = Φ m i ik j j i j j x B x dx d _α

con

(

)

/

(

)

0 (2.27) 0 ) ( 1 ) ( ) 1 ( ⎪ ⎩ ⎪ ⎨ ⎧ > − − − = = − + − + j j k t t j r j k r j r j r r j r α α α α

per ogni r=0,….,m+1, essendo ( ) 0

1 ) ( 1 = + = − j m j α α , per ogni j.

Applicando il teorema 1, otteniamo il seguente Corollario.

Corollario 1. Sia k ≥ 2 e sia assegnata la successione di B-Splines di

ordine k corrispondente alla sequenza 0 = t₀ ≤ t₁ ≤ ....≤ t_m =1.

Allora per ogni coppia di interi 0 ≤ r, s ≤ k-1, la funzione (2.22) ammette la derivata di ordine r+s. Inoltre vale la formula:

( )

, 1 , 0 , (2.28) , 0 0 0 , , 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ∂ ∂ ∂

∑ ∑

= = + B y y B A x x B B A c y x y x s q k j m i m j r q k i s r ij s r s r δ

dove per ogni 0 ≤ µ≤ k-1, q∈

{ }

p,d ,ξ ∈ℜ ,i = 0,...,m, si ha:

( )

( )

1

( )

0 (2.29) 0 ) ( , , , , , ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ < − − ≥ = + _{ξ ξ} ξ ξ ξ ξ ξ µ µ δ µ µ µ µ k i k i q k i B d d B d d B d q

Dimostrazione del corollario 1. La dimostrazione segue

immediatamente se si osserva che B_i,k, con k ≥ 2 e 0 ≤ i ≤ m, ha

supporto strettamente contenuto in (0,1], quindi le estensioni pari e dispari (2.23) e (2.24) sono funzioni derivabili fino all’ordine j ≤ k-1. Poiché la funzione (2.22) è una combinazione lineare di tali funzioni, essa è differenziabile rispetto ad entrambe le variabili x ed y fino all’ordine j ≤ k-1.

Osservazione 3. Chiaramente nella scrittura del gradiente e della matrice Hessiana di (2.22), in vista del precedente corollario e della (2.29) introdurremo la relazione ricorsiva (2.27) per calcolare le

derivate della funzione B_i,k, ponendo α_i =1eα_r = 0 ,per r ≠i nella