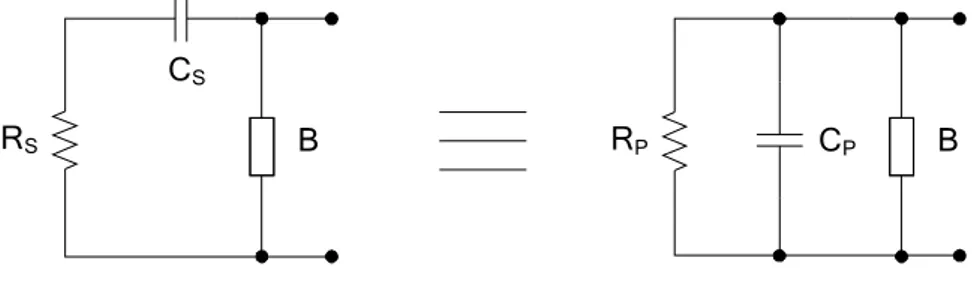Capitolo 3 RETE DI ADATTAMENTO E DISTANZA MASSIMA DI FUNZIONAMENTO

103

Capitolo 3

RETE DI ADATTAMENTO E

DISTANZA MASSIMA DI FUNZIONAMENTO

Nel capitolo precedente abbiamo visto che l’impedenza equivalente di ingresso del moltiplicatore di tensione è rappresentata dal parallelo di una resistenza Req e di una capacità Ceq. La parte resistiva tiene di conto del consumo di potenza del moltiplicatore di tensione, mentre quella capacitiva è data dal parallelo delle capacità dei diodi presenti nel circuito.

Per sistemi RFID che utilizzano la procedura sequenziale, l’ottimizzazione del circuito consiste nel dimensionare i componenti in modo tale da permettere la carica della capacità C, utilizzata come batteria, alla tensione necessaria al funzionamento del tag, nel tempo a disposizione per questa fase.

Risulta quindi ovvio che la rete di adattamento, in quanto utilizzata durante un transitorio e non con il circuito a regime, non viene realizzata con il criterio del massimo trasferimento di potenza, adattando il carico in uscita all’impedenza della sorgente, ma partendo dall’impedenza in ingresso al duplicatore che ottimizza la carica si dimensiona la rete di adattamento.

Questa procedura ha lo svantaggio che non risulta ottimizzata dal punto di vista del trasferimento della potenza e ciò si traduce in un range di funzionamento inferiore.

In questo capitolo viene introdotta la procedura per la progettazione della rete di adattamento partendo dalla rete che ottimizza il funzionamento del duplicatore, calcolata nel capitolo precedente. Viene inoltre spiegato il criterio

104 per determinare il range di funzionamento del tag, introducendo alcuni concetti della teoria delle onde elettromagnetiche.

3.1 Dimensionamento della rete di adattamento

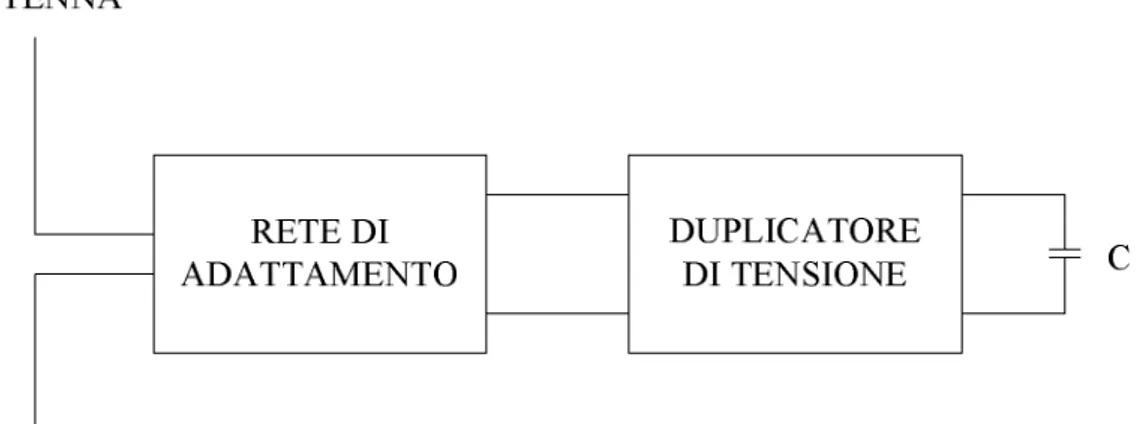
Senza considerare gli altri blocchi che compongono il tag, ma focalizzando l’attenzione su antenna, rete di adattamento e duplicatore di tensione (fig. 3.1), occorre capire come procedere nel dimensionamento del circuito, perché si abbiamo le prestazioni ottenute nel capitolo precedente.

Figura 3.1 Sezione di ingresso del transponder

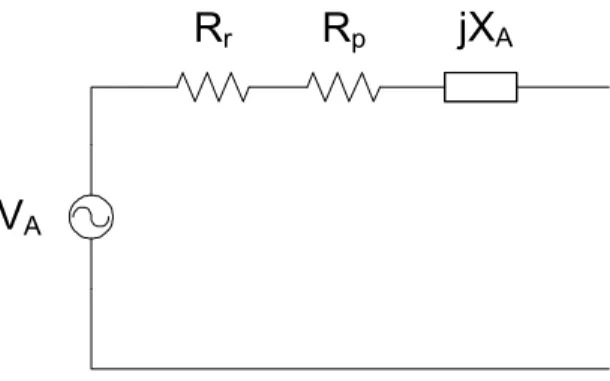
Il circuito equivalente dell’antenna (fig. 3.2) è composto da una impedenza ZA e da un generatore VA, la cui ampiezza corrisponde alla tensione a vuoto indotta dal campo elettromagnetico incidente, ai capi dell’antenna stessa.

L’impedenza di ingresso dell’antenna è composta da una resistenza di perdita Rp, da una resistenza di radiazione Rr e da una reattanza XA:

A r p A

105 VA

Rp jXA

Rr

Figura 3.2 Circuito equivalente dell’antenna

La resistenza di perdita Rp è una resistenza vera e propria e serve a descrivere tulle le perdite che si hanno nell’antenna e nella connessione della stessa al resto del circuito. La potenza ai capi di questa resistenza è dissipata per effetto Joule.

La resistenza di radiazione Rr anche se assume le dimensioni di una resistenza vera e propria, è un elemento circuitale equivalente introdotto per valutare la potenza emessa dall’antenna nello spazio circostante sotto forma di onde elettromagnetiche.

Alla frequenza di lavoro dell’antenna, la parte reattiva XA tende a zero, per cui se ipotizziamo che l’antenna sia priva di perdite (ipotesi che consideriamo valida), possiamo assumere che:

( )

A r

Z

f

;

R

La resistenza di radiazione Rr è una caratteristica tipica del tipo di antenna utilizzata. Un dipolo a mezz’onda, comunemente chiamato dipolo a λ/2, è un pezzo diritto di linea di lunghezza inversamente proporzionale alla frequenza del segnale incidente e pari appunto a l = λ/2, interrotto a metà, dove viene prelevato o inviato il segnale da trasmettere. Un dipolo a λ/2 presenta una resistenza di radiazione Rr = 73 Ω.

La rete di adattamento deve essere dimensionata in modo tale che la sua impedenza di uscita ZU, alla frequenza di lavoro dell’antenna, sia pari a

106 l’impedenza che ottimizza la carica di C, permettendo al circuito di sfruttare gli effetti della risonanza serie:

U

Z = +R j L

w

Il valore di ZU, come visto nel capitolo precedente, dipende dal tipo di componenti utilizzati per il duplicatore di tensione e dalle caratteristiche elettriche del circuito che la capacità C dovrà alimentare.

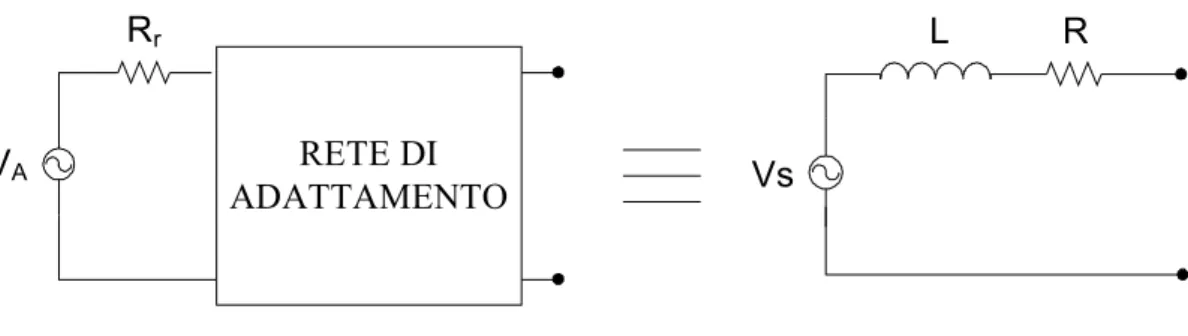
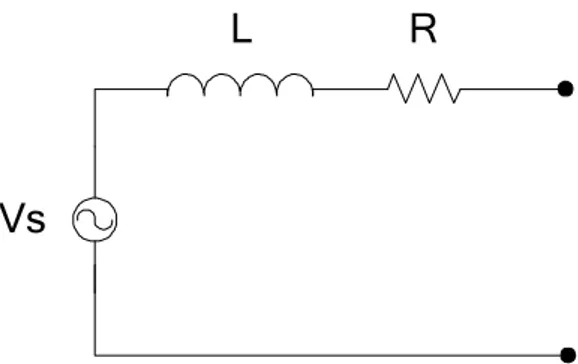
VA Rr RETE DI ADATTAMENTO Vs R L

Figura 3.3 Circuito equivalente visto dall’uscita della rete di adattamento

Per valutare che tipo trasformazione deve realizzare la rete di adattamento, occorre confrontare l’inverso della conduttanza presente in uscita alla rete stessa con l’inverso della conduttanza che deve essere trasformata.

Per fare questo occorre calcolare l’ammettenza che si vede dai terminali della rete di adattamento:

( )

( )

Nell’ipotesi che la resistenza di perdita sia nulla e che l’antenna lavori alla frequenza per la quale è stata realizzata, la conduttanza che si vede ai morsetti dell’antenna stessa è pari all’inverso della resistenza di radiazione Rr.

1 r A R G = (3.5)

107 Nel nostro caso specifico risulta sempre verifica la relazione:

( )

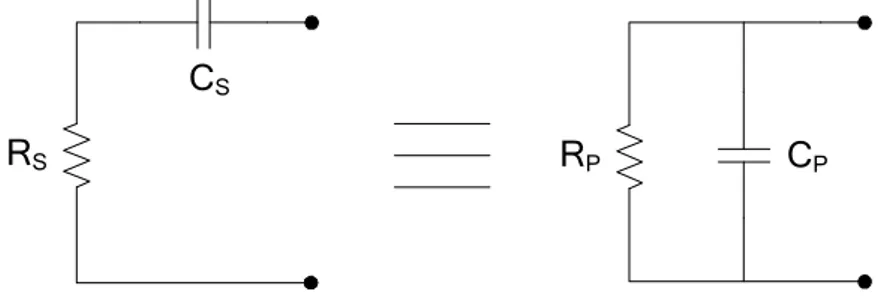
La (3.6) ci dice che la rete di adattamento deve essere dimensionata facendo una trasformazione da serie a parallelo.

RS

CS

RP CP

Figura 3.4 Trasformazione serie-parallelo

La resistenza serie RS corrisponde alla resistenza di radiazione Rr, mentre la resistenza parallelo RP all’inverso della conduttanza GU.

Il primo passo consiste nel calcolare il fattore di qualità QS della rete serie e da questo il valore della capacita CS da porre in serie alla resistenza Rr da trasformare. Il fattore di qualità QS può essere ricavato dall’uguaglianza:

( )

₍

₎

w

Per il corretto dimensionamento della rete, QS non deve superare il valore di 20-30 unità.

( )

w

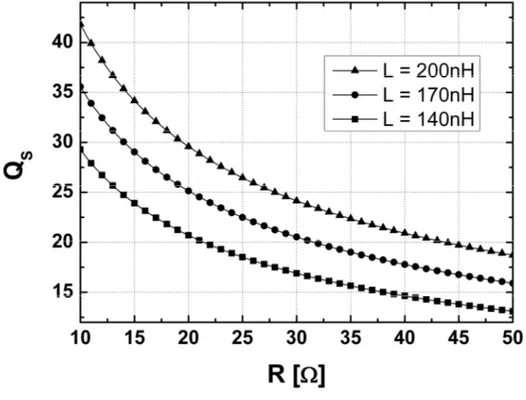
108 La (3.8) permette di tracciare il fattore di qualità al variare di R e L, utili per verificare se la scelta dei componenti, che ottimizzano la carica della capacità in uscita, verificano la condizione su QS.

Figura 3.5 Fattore di qualità QS al variare di R e L

Dalla fig. 3.5 si vede che i valori di ZU utilizzati nel capitolo precedente verificano la condizione su QS, che risulta circa 20.

Il fattore di qualità, oltre che dalla (3.8), può anche essere espresso in funzione dei componenti della rete serie che andiamo a trasformare:

1 S S r Q C R w = (3.9)

Dalla relazione (3.9) è possibile ottenere il valore della capacità serie CS che insieme alla resistenza di radiazione Rr, nella trasformazione da serie a parallelo, aggiustano il valore della conduttanza GU.

109 1 S S r C Q wR = (3.10)

Sostituendo la (3.8) relativa al fattore di qualità QS nell’espressione sopra, è possibile ottenere una relazione tra la capacità CS e il valore dell’impedenza che voglio ottenere in uscita dalla rete di adattamento.

( )

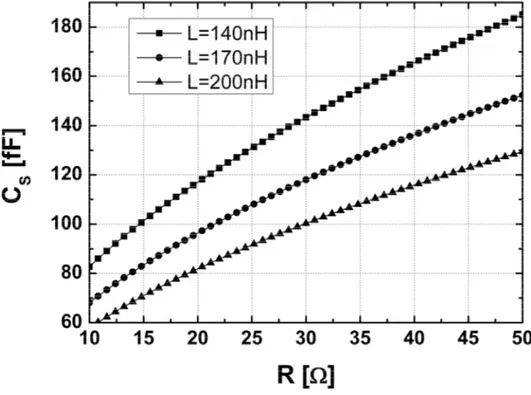
In fig. 3.6 è possibile osservare come varia la capacita CS al variare della resistenza R e dell’induttanza L che vogliamo ottenere dalla trasformazione di Rr.

110 La capacità parallelo CP, come è possibile vedere dalla (3.12), per valori del fattore di qualità QS sufficientemente elevati, è approssimabile con la capacità serie CS. 2 2 1 S P S S Q C C Q = + (3.12)

Se nell’espressione sopra sostituiamo la (3.8) e la (3.11), otteniamo il legame tra la capacità parallelo CP e i parametri circuitali iniziali.

(

)

( )

Figura 3.7 Capacità CP al variare di R e L

A questo punto della trasformazione la resistenza serie Rr è stata trasformata nella resistenza parallelo RP, ma occorre inserire una suscettanza B in parallelo a CP per ottenere in uscita la suscettanza BU.

111

RS

CS

RP CP

B B

Figura 3.8 Inserimento della suscettanza B

Deve quindi essere verificata l’uguaglianza:

( )

Dalla precedente relazione si vede che la suscettanza B risulta negativa, ciò vuol dire che è realizzabile mediante un’induttanza di valore LP.

( )

Dall’espressione sopra si ottiene il valore dell’induttanza da porre in parallelo all’uscita della rete di adattamento.

( )

Anche in questo caso è possibile, sostituendo la (3.13) nella relazione sopra, ottenere un’espressione funzione dei parametri circuitali di partenza.

112

( )

Figura 3.9 Induttanza LP al variare di R e L

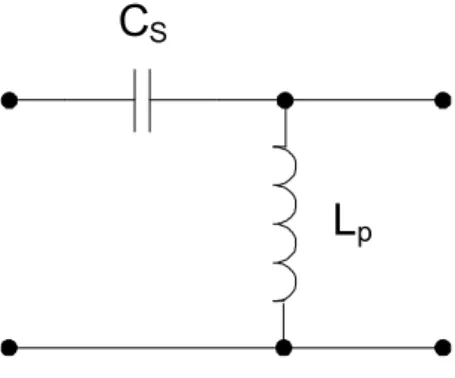
Una volta determinati il valore della capacità serie CS e dell’induttanza LP, è completamente determinata la rete di adattamento (fig. 3.10).

C

L

113 Il circuito complessivo che si trova a monte del duplicatore di tensione, antenna più rete di adattamento, è rappresentato in fig. 3.11.

VA Rr CS Lp + -VS0

Figura 3.11 Antenna e rete di adattamento

3.2 Distanza massima di funzionamento

Il generatore VA (fig. 3.11) rappresenta la tensione a vuoto indotta nell’antenna dal campo elettromagnetico incidente ed è proporzionale all’intensità del campo elettrico E.

( )

0cos

A A

V =V wt (3.18)

Nel capitolo precedente è sempre stato fatto riferimento al circuito equivalente che si vede dall’uscita della rete di adattamento, dove compare il generatore di tensione VS (fig. 3.12).

Vs

R L

114 Il generatore VS rappresenta la tensione a vuoto in uscita dalla rete di adattamento (fig. 3.11) e può essere espressa come partitore della tensione VA indotta ai capi dell’antenna:

1 P S A r P S j L V V R j L j C w w w = + + (3.19)

Purtroppo questo comporta l’attenuazione della tensione che ritroviamo in ingresso al circuito risonante serie RLC, diminuendo la distanza massima di funzionamento tra tag e reader. Passando al modulo di VS:

0 ₂ 0 2 1 P S S A r P S L V V V R L C w w w = = æ ö +_ç - _÷ è ø (3.20)

Sostituendo nella (3.20) le espressioni di LP (3.17) e di CS (3.11), è possibile tracciare le curve relative all’attenuazione introdotta dalla rete di adattamento in funzione dei parametri R e L che ottimizzano la carica della capacità in uscita. In realtà dalla fig. 3.13 è possibile vedere che le curve relative all’attenuazione introdotta dalla rete di adattamento, al variare dell’induttanza L, sono indistinguibili tra loro.

Dalla (3.20), nota la VS0 minima che permette al duplicatore di raggiungere la tensione voluta nel tempo a disposizione per la carica, è possibile ricavare il valore della tensione a vuoto VA0 minima, necessaria ai capi dell’antenna.

min 2 2 0 0min 1 r P S A S P R L C V V L w w w æ ö +_ç - _÷ è ø = (3.21)

115 Occorre adesso capire come la tensione VA0 è legata alla distanza tra tag e reader, facendo riferimento ad alcuni concetti di base delle teoria delle onde elettromagnetiche.

Figura 3.13 Attenuazione introdotta dalla rete di adattamento

3.2.1 Concetti di base sulla teoria delle onde elettromagnetiche

Prendiamo in esame un’antenna isotropica, ovvero un’antenna che irradia la stessa quantità di energia in tutte le direzioni (omnidirezionale).

Un’onda elettromagnetica si propaga dall’antenna che l’ha generata nello spazio sferico circostante trasportando con se energia e man mano che la distanza dalla sorgente aumenta, l’energia irradiata è divisa su una superficie sferica di valore sempre maggiore. Viene definita densità di radiazione S, il rapporto tra la potenza PEIRP trasmessa dalla sorgente e la superficie della sfera avente raggio r.

2 4 EIRP P S r p = (3.22)

116 Con il termine PEIRP (Effective Isotropic Radiated Power) si indica la potenza effettiva irradiata nello spazio da un’antenna isotropica e può essere espressa come il prodotto tra la potenza P fornita all’antenna e il guadagno d’antenna G.

EIRP

P = ×P G (3.23)

L’energia trasportata nello spazio dalle onde elettromagnetiche è immagazzinata nel campo elettrico e nel campo magnetico, quindi esiste una relazione tra l’intensità E del campo elettrico, l’intensità H del campo magnetico e la densità di radiazione S.

Viene definito vettore di Poynting S il vettore risultante dal prodotto vettoriale tra il campo elettrico E ed il campo magnetico H, campi che risultano ortogonali tra loro (fig. 3.14).

S =E ´ H (3.24)

Figura 3.14 Vettore di Poynting

La grandezza λ rappresenta la lunghezza d’onda del campo elettromagnetico ed è data dal rapporto tra la velocità della luce c e la frequenza della radiazione.

c f

117 L’intensità E del campo elettrico e l’intensità H del campo magnetico, sono legate tra loro attraverso la permittività magnetica e la costante dielettrica del mezzo in cui avviene la propagazione. Nel caso di propagazione in aria:

0 0 F

E=H× m e = H Z× (3.26)

ZF rappresenta l’impedenza caratteristica dell’onda, che nel vuoto:

120 377

F

Z = p W = W (3.27)

Sostituendo la (3.26) nell’espressione (3.24) del vettore di Poynting e utilizzando la (3.22) per la densità di radiazione S, è possibile ottenere una relazione che lega l’ampiezza E del campo elettrico alla distanza dalla sorgente ed alla potenza emessa dalla sorgente stessa:

2 4 EIRP F F P Z E S Z r p × = × = (3.28)

La tensione VA0 indotta a vuoto ai capi dell’antenna è legata all’ampiezza E del campo elettrico incidente, mediante un coefficiente di proporzionalità l0 che ha le dimensioni di una lunghezza e viene definito lunghezza effettiva:

0 0 ₂ 0 4 EIRP F A P Z V E l l r p × = × = × (3.29)

Il coefficiente di proporzionalità l0 è un parametro caratteristico dell’antenna che viene utilizzata in trasmissione o in ricezione e può essere espresso in funzione di altre grandezze note:

0 r F G R l Z l p × = × (3.30)

118 Un dipolo a λ/2 presenta un guadagno d’antenna G = 1.64 e di conseguenza ha una lunghezza effettiva l0 = 0.32 λ.

3.2.2 Calcolo distanza massima di funzionamento

Introdotti alcuni concetti fondamentali nel paragrafo precedente, occorre determinare la massima distanza tra tag e reader che permette il corretto funzionamento del sistema.

Sostituendo la (3.30) nell’espressione (3.29) della tensione VA0 indotta a vuoto ai capi dell’antenna, si trova una relazione che è funzione della distanza e di tutti gli altri parametri che caratterizzano il sistema:

(

)

La tensione VA0 è inversamente proporzionale alla distanza tra tag e reader e alla frequenza dell’onda elettromagnetica incidente, dipende inoltre dalla potenza emessa dalla sorgente (PEIRP) e dal tipo di antenna utilizzata, da cui dipendono il guadagno d’antenna G e la resistenza di radiazione Rr.

Nella banda UHF la potenza PEIRP emessa dalla sorgente è limitata dalle vigenti normative ad un valore massimo di 500 mW, quindi fissata la frequenza dell’onda elettromagnetica trasmessa, l’unico parametro libero rimane la scelta del tipo di antenna da utilizzare in ricezione.

Uguagliando la relazione (3.31), valutata alla distanza massima rmax in cui il sistema continua a funzionare correttamente, alla (3.21), che esprime la medesima grandezza ma in funzione della rete di adattamento e di VS0min si ottiene:

119 min 2 2 0 0min max 1 2 r P S EIRP r A S P R L C P G R c V V f r L w w p w æ ö +_ç - _÷ × × _{è ø} = = (3.32)

Indicando con H l’attenuazione introdotta dalla rete di adattamento, è possibile ottenere un’espressione di rmax funzione di soli parametri noti:

max 0min 2 EIRP r S P G R H c r V f p × × = (3.33)

Utilizzando un dipolo a λ/2 che presenta un guadagno d’antenna G = 1.64 e una resistenza di radiazione Rr = 73 Ω, sfruttando per la sorgente la massima potenza possibile alla frequenza f = 900 MHz:

min max 0min 0 -3 -3 S A H 410.17×10 r 410.17×10 V V = = (3.34)

Dalla precedente relazione, una volta nota la rete di adattamento che mi permette di ricavare l’attenuazione H, e la tensione minima VS0min che consente alla capacità di caricarsi nel tempo a disposizione, è possibile ottenere la distanza massima di funzionamento del sistema.

3.3 Duplicatore con diodo integrato

Nel capitolo precedente è stato analizzato il duplicatore di tensione in cui grazie alla rete di adattamento e sfruttando il circuito equivalente del duplicatore stesso, si viene a creare un circuito risonante serie RLC, che permette di ottenere una tensione d’uscita superiore a quella che si avrebbe senza sfruttare la risonanza.

120 + -Vin C C Vs _D1 D2 I_D2 I_D1 R I_in V -+ L

Figura 3.15 Duplicatore con circuito equivalente della rete di adattamento

Scelto il valore della capacità C in base alle caratteristiche elettriche e alla potenza assorbita dal circuito che deve alimentare, una volta esaurita la fase di carica, viene fatta una stima delle grandezze Req e Ceq che costituiscono il circuito equivalente del duplicatore. Il passo successivo è il dimensionamento di R e L, che rappresentano l’impedenza d’uscita della rete di adattamento, in modo da ottenere, nel tempo a disposizione, la massima tensione di uscita.

Per un valore della capacità C = 3 nF, fissata la resistenza R = 35 Ω in modo da avere un fattore di qualità QS accettabile, la massima tensione di uscita V si ottiene per L = 170 nH. L [nH] V (t = 5 ms) [V] V (t = 30 ms) [V] 160 1.314 1.480 165 1.495 1.515 170 1.700 1.707 175 0.019 0.217

Tabella 3.1 Tensione di uscita al variare di L con R = 35 Ω e VSO = 100 mV

Noto il valore di R e L occorre determinare il valore della capacità serie CS e dell’induttanza LP che costituiscono la rete di adattamento, valori che possono essere determinati anche graficamente.

122

Figura 3.16 Dimensionamento della rete di adattamento

Dai grafici sopra si vede che noti i valori di R e L, la rete di adattamento ha un fattore di qualità QS = 19, ed occorrono una capacità CS = 127.5 fF ed una induttanza LP = 100.6 nH.

Dall’ultimo grafico si legge inoltre l’attenuazione H = 0.6924 introdotta dalla rete di adattamento, che sostituita nella (3.34) insieme al valore VS0min = 100 mV, permette di ottenere la distanza massima di funzionamento rmax = 2.84 m.

C C VA _D1 D2 Rr LP CS

123 Simulando il circuito completo (fig. 3.17), possiamo osservare che per valori di VA0 inferiori a 175 mV, la capacità in uscita non riesce a caricarsi nei 30 ms a disposizione, ma si ottiene una tensione di pochi mV. Per VA0 = 175 mV, dopo un tempo t = 5.5 ms, l’uscita ha già raggiunto una tensione V = 2.12 V ed praticamente a regime, in quanto dopo 30 ms assume un valore V = 2.26 V.

La differenza tra la VA0min ottenuta simulando il circuito ed il valore teorico calcolato partendo dalla VS0min e dividendolo per il guadagno introdotto dalla rete di adattamento, è probabilmente dovuto al fatto che si hanno delle perdite lungo il circuito, perdite che fanno si che la tensione necessaria al corretto funzionamento del sistema sia maggiore di quella preventivata.

C’è da osservare però che la tensione in uscita dal duplicatore di tensione è sensibilmente aumentata, passando da 1.7 V senza rete di adattamento a 2.26 V con la rete di adattamento.

La distanza massima di funzionamento rmax che era stata stimata in 2.84 m subisce una drastica riduzione, attestandosi sui 1.62 m.

VA0 [mV] t [ms] V [V] 160 30 1.4·10-3 165 30 2.78·10-3 170 30 6.46·10-3 175 5 733·10-3 175 5.37 1.60 175 5.5 2.12 175 30 2.26 200 5 2.45 250 5 2.62 400 5 3.2

Tabella 3.2 Tensione di uscita al variare della tensione indotta ai capi dell’antenna

Dalla tabella sopra si vede che se il tag si avvicina al reader, ovvero la tensione VA0 indotta dal campo elettromagnetico E ai capi dell’antenna è maggiore, anche il valore della tensione in uscita al duplicatore aumenta.

124 Il sistema nel suo complesso ha un comportamento a soglia nei confronti della tensione indotta ai capi dell’antenna dal campo elettromagnetico, in quanto per valori di VA0 inferiori ai 175 mV, la capacità in uscita non riesce a caricarsi.

Aumentando la capacità C utilizzata come batteria al valore di 30 nF, ovvero facendo l’ipotesi che il circuito che deve essere alimentato assorba una potenza maggiore rispetto al caso precedente in cui C = 3 nF, c’è da aspettarsi un aumento della costante di tempo e quindi tempi maggiori per la carica di C.

Effettuando una serie di simulazioni, è possibile vedere che la rete di adattamento che ottimizza la carica della capacità in uscita è la stessa del caso precedente, quindi ci sarà da aspettarsi un comportamento analogo.

VA0 [mV] t [ms] V [V] 175 30 225·10-3 185 30 715·10-3 190 13.36 1.6 190 14 1.83 190 15 2.06 190 20 2.17 190 30 2.19 195 30 2.21 400 30 3.22

Tabella 3.3 Tensione di uscita al variare della tensione indotta ai capi dell’antenna

Come era prevedibile, occorre avere in ingresso una tensione maggiore rispetto al caso precedente e questo influisce, anche se di poco, sulla massima distanza di funzionamento, che risulta essere in questo caso rmax = 1.49 m.

Dalla tabella sopra si vede che anche in questo caso, avvicinando il tag al reader, il valore della tensione in uscita al duplicatore aumenta, inoltre il sistema nel suo complesso continua ad avere comportamento a soglia nei confronti della tensione indotta ai capi dell’antenna dal campo elettromagnetico, in quanto per valori di VA0 inferiori ai 190 mV, la capacità in uscita non riesce a caricarsi.