Capitolo 1 Definizione del modello

Definizione del modello

Prima di iniziare l’analisi occorre definire, in modo dettagliato, il modello matematico impiegato per lo studio del comportamento dinamico di un veicolo con differenziale bloccato. Per un’analisi preliminare, si utilizzer`a un modello di veicolo dotato di pneu-matici linearizzati, per passare successivamente ad uno con pneupneu-matici non lineari, capace di fornire risposte pi`u vicine alla realt`a fisica dei fenomeni in gioco.

1.1

Ipotesi semplificative

Per poter cominciare la descrizione del modello, si rende necessario specificare le ipotesi semplificative utilizzate per lo sviluppo dello stesso; questo permetter`a di conoscerne i limiti di validit`a ed applicabilit`a, evitando che possa essere impiegato al di fuori di tali condizioni.

Per prima cosa occorre dire che verr`a analizzato il comportamento del veicolo a

regi-me, non studiando ci`o che accade durante il transitorio, ed analizzando il moto come

una successione di stati di equilibrio. Questo permetter`a una notevole semplificazione nel calcolo, svincolando quest’ultimo dal tempo. Si suppone, inoltre, che il veicolo si muova su strada piana ed orizzontale, assimilabile, cio`e, ad un piano geometrico.

1.1 Ipotesi semplificative 8

Interessandoci solamente il comportamento direzionale a regime del modello, possia-mo considerare la velocit`a di avanzamento (indicata successivamente con il simbolo u) variabile solo attraverso stati di equilibrio. Questo vuol dire evitare sia brusche accele-razioni che frenature. Anche se il modello si riferisce a veicoli provvisti di sospensioni, si suppone che i moti di beccheggio e di scuotimento della carrozzeria siano trascura-bili, ipotizzando quest’ultima come perfettamente rigida. Il moto di rollio `e supposto molto piccolo, tale cio`e da non poter essere completamente trascurato e da dar origine ad un trasferimento di carico tra le ruote di un assale (il valore del rollio dipender`a dall’accelerazione laterale e dalla rigidezza al rollio del veicolo in esame). Conseguenza dell’aver supposto basso il rollio e trascurabili lo scuotimento ed il beccheggio, `e che il veicolo assumer`a un moto piano, dove ogni punto della carrozzeria avr`a la stessa distanza da terra.

Per maggior semplicit`a nella realizzazione del modello, si considerano sterzanti sola-mente le ruote anteriori, mentre si ipotizzano motrici le ruote posteriori.

Per quanto riguarda la sterzatura possiamo dire che l’angolo di sterzo alle ruote an-teriori risulta essere univocamente determinato dalla posizione del volante, bench`e la tiranteria dello sterzo ed i braccetti delle sospensioni siano provvisti di una certa ela-sticit`a; in tal modo la posizione angolare delle ruote sterzanti risulta assegnata e non costituisce una variabile. Per mantenere piana la cinematica del modello, `e stata fatta un’ultima approssimazione, sempre sulle ruote anteriori, ed in particolar modo sull’asse di sterzo, che viene assunto ortogonale alla strada e passante per il centro dell’impron-ta a terra del pneumatico. Questo ovviamente non `e vero, in quanto l’asse di sterzo, nella realt`a, `e un asse sghembo, che genera, a seguito della sua intersezione con il piano stradale, le due distanze caratteristiche, l’avancorsa in senso longitudinale ed il braccio

a terra in senso trasversale, rispetto al centro dell’impronta a terra del pneumatico.

Essendo per`o, queste due grandezze, piccole qualche centimetro `e possibile trascurarle nella nostra trattazione e considerare l’asse di sterzo di ciascuna ruota come passante per il centro dell’impronta a terra.

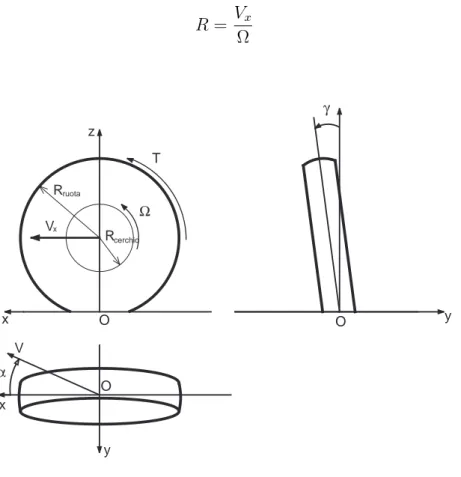
i j _v u r G α11 α₁₂ δ δ a₁ a2 t2 l Vg α₂₁ α₂₂

Figura 1.1: modello di veicolo

Quindi, l’effetto complessivo di tutte queste ipotesi, `e un modello con tre soli gradi di libert`a, dove il veicolo `e schematizzato come un unico corpo rigido in moto piano.

1.2

Modello e grandezze di riferimento

Per poter definire matematicamente il modello, sulla base anche delle precedenti ipo-tesi, si rende necessaria una sintetica rappresentazione delle principali grandezze, che verranno richiamate in seguito. Il disegno riportato in Fig 1.1 schematizza un veicolo rigido a 3 gradi di libert`a, di massa m e baricentro in G. Per poterne definire uni-vocamente il moto, si definisce un sistema di riferimento cartesiano solidale al veicolo (x, y, z, G) di versori i, j,k. Gli assi sono cos`ı disposti: l’asse x `e diretto nella direzione

1.2 Modello e grandezze di riferimento 10

di avanzamento del veicolo, l’asse y `e ortogonale all’asse x e diretto verso la sinistra del veicolo, mentre l’asse z `e ortogonale al piano stradale e passante, ovviamente, per il baricentro. In generale questo sistema di riferimento non coincide con la terna centrale d’inerzia, ma se si assume che il veicolo sia simmetrico rispetto al piano medio longi-tudinale, contenente gli assi x e z, otterremo che almeno l’asse y sia centrale d’inerzia. Da questo discende che i prodotti d’inerzia Jxy e Jyz si annullino, mentre in generale

non sar`a nullo il prodotto d’inerzia Jzx cos`ı come saranno ovviamente diversi da zero

i tre momenti d’inerzia Jx, Jy, Jz. Si indica con Ω = rk la velocit`a d’imbardata del

veicolo (yaw rate), con k ortogonale al piano stradale e diretta verso l’alto; si assume pertanto r positiva se il veicolo ruota in senso antiorario. La velocit`a assoluta del baricentro `e indicata con Vg, mentre le distanze dello stesso dagli assali anteriore e

posteriore sono indicate rispettivamente dalle lettere a1, a2 . Il passo `e indicato con la

lettera l = a1+a2 , mentre la carreggiata, misurata dai centri delle ruote, con la lettera

t, specificando con t1 e t2 rispettivamente la carreggiata anteriore e quella posteriore.

Per quanto riguarda la sterzatura cinematica, ovvero con angoli di deriva1 _{tutti nulli,}

occorre precisare che gli angoli di sterzo delle ruote sono diversi tra loro e che l’angolo della ruota interna alla curva risulta pi`u grande di quello della ruota esterna; `e possibile ipotizzare per`o, valendo la seguente relazione2_:

δe = δi−

t lδ

2

i + O(δi3)

che per piccoli valori degli angoli di sterzo si abbia l’uguaglianza tra i due. Possia-mo procedere adesso alla formulazione matematica del Possia-modello mediante i seguenti tre gruppi di equazioni: equazioni di congruenza, equazioni di equilibrio ed equazioni costitutive.

1_{Per la definizione vedere [6] Cap.1, §1.1, pag.5} 2_{Vedere [6] Cap.4, Fig. 4.3 pag.5}

1.3

Equazioni di congruenza

Anche se la definizione delle equazioni di congruenza, fornita dalla teoria classica3_,

α1 = δ − v + ra1 u α2 = − v − ra2 u (1.1)

continua a valere ancora, `e pi`u corretto assumere come grandezza di riferimento per la nostra trattazione, il vettore scorrimento teorico, il quale, oltre a tener conto della velocit`a angolare della ruota, caratterizza il moto del punto di contatto tra pneumatico e strada, permettendo, insieme al trasferimento di carico di definire completamente ciascuna forza a terra.

1.3.1

Definizione dello scorrimento teorico

Consideriamo che l’asse della ruota sia in moto con velocit`a assegnata V parallela alla strada, costante in modulo e direzione, ed inclinata, in generale, dell’angolo di deriva

α; l’asse avr`a quindi un moto traslatorio uniforme di componenti Vx = V cos α

Vy = V sin α

il cui sistema di riferimento `e mostrato in Fig 1.2. Il cerchio della ruota si muover`a, inol-tre, di moto rotatorio attorno al proprio asse, con una velocit`a angolare Ω = (0, Ω, 0) dipendente, non solo dalla velocit`a V, ma anche dalla coppia T (wheel drive torque) applicata all’asse ruota ( motrice se T > 0, frenante se T < 0), dall’angolo di deriva

α, dal carico verticale, nonch`e dal tipo di pneumatico etc. Normalmente per le prove

si considera solamente l’effetto della variazione di T e di α.

3_{Per classica si intende la teoria esposta in [6] cap.4, §4.3 dove, per esprimere le equazioni di} congruenza, necessarie per la definizione del modello matematico di veicolo, si `e utilizzato l’angolo di deriva come grandezza cinematica di riferimento.

1.3 Equazioni di congruenza 12

Noti V = (Vx, Vy, 0) e Ω = (0, Ω, 0) `e possibile, in ogni istante, individuare l’asse

eli-coidale (o asse di Mozzi) dell’atto di moto del cerchio. Come noto i punti dell’asse

elicoidale hanno velocit`a parallela al vettore velocit`a angolare, pertanto, nel caso in esame, l’asse elicoidale risulta sempre parallelo all’asse y, ed i suoi punti hanno velocit`a pari a (0, −V sin α, 0). Indicando con R la distanza con segno fra l’asse del cerchio e l’asse elicoidale, si ottiene subito la seguente espressione

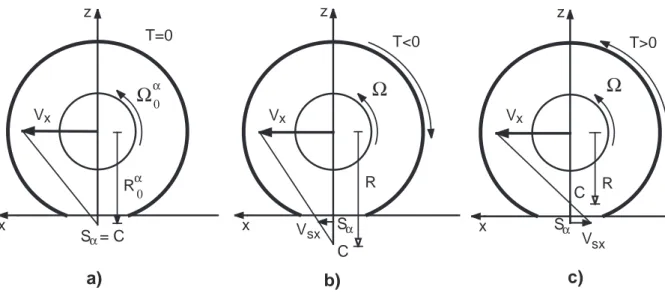
R = Vx Ω (1.2) x z T Vx R y O O x V O cerchio ruota R y α γ Ω

Figura 1.2: Rappresentazione del sistema di riferimento e del verso positivo adottato per la descrizione delle caratteristiche della ruota

`

E evidente che l’asse elicoidale si trova sempre al di sotto dell’asse del cerchio, come illustrato in Fig 1.3, dove `e si `e indicata con la lettera C la traccia dell’asse elicoidale nel piano coordinato x − z.

Vy = 0, l’asse elicoidale diventa asse d’istantanea rotazione e tutti i suoi punti assumono velocit`a nulla. x x z z T=0 _T<0 R V S = C S C V R x z T>0 S C R a) b) c) x Vx Vx sx _V sx

Ω

Ω

Ω

Figura 1.3: Effetto di una coppia sulla posizione della traccia C dell’asse elicoidale del cerchio; a) caso con coppia nulla T = 0, b) caso con coppia frenante T < 0, c) caso con coppia motrice T > 0

Convenzionalmente si parla di puro rotolamento quando la ruota rotola in direzione perfettamente longitudinale (α = 0) e senza coppia applicata all’asse (T = 0). In que-ste particolari condizioni, il cerchio ruoter`a con una certa velocit`a angolare, indicata con Ω0, mentre la distanza fra l’asse d’istantanea rotazione dello stesso e l’asse della

ruota, verr`a indicata con R0; le grandezze sono legate dalla seguente relazione:

R0 = V

Ω0

(1.3)

Se, a parit`a di tutti gli altri parametri, la ruota risulta ancora folle (T = 0), ma con un angolo di deriva non nullo (α 6= 0), il cerchio ruoter`a con una velocit`a di rotazione minore di Ω0, che verr`a indicata con Ωα0. Inoltre, dato che il cerchio non ha pi`u un

1.3 Equazioni di congruenza 14

alla (1.2), anche in queste nuove condizioni, si pu`o calcolare la distanza (questa vol-ta indicavol-ta con Rα

0) fra l’asse della ruota e l’asse elicoidale dell’atto di moto del cerchio,

Rα 0 = V cos α Ωα 0 (1.4)

mentre la traccia dell’asse di Mozzi sul piano x − z verr`a indicata con Sα, come

mo-strato in Fig. 1.3 a).

L’applicazione all’asse del cerchio di una coppia T 6= 0, come mostrato in Fig. 1.3 b), determina un nuovo valore Ω (con Ω 6= Ωα

0) della velocit`a angolare del cerchio stesso e

quindi un riposizionamento dell’asse elicoidale, che verr`a a trovarsi ad una distanza R dal centro ruota:

R = V cos α

Ω (1.5)

In queste nuove condizioni di funzionamento il punto, definito in precedenza, assume rispetto alla strada una velocit`a Vs, normalmente definita velocit`a di scorrimento, le

cui componenti sono date da

Vs=

  

Vsx = V cos α − ΩRα0 = (Ωα0 − Ω)Rα0

Vsy = −V sin α = −V tan α = −Ωα0R0αtan α

(1.6)

La velocit`a di scorrimento Vs `e, quindi, diretta come l’asse x se α = 0, e come l’asse y

se T = 0, ovvero se Ω = Ωα 0.

`

E utile definire un vettore velocit`a ausiliario

Vr = (ΩRα0, 0, 0) (1.7)

che rappresenta la velocit`a di rotolamento, ovvero la parte della velocit`a del centro ruota che non comporta scorrimento con il piano stradale; si ha infatti la seguente

relazione

V = Vr+ Vs

Dato che le velocit`a V, Vr , e Vs hanno sempre la terza componente nulla, si

conside-rano per semplicit`a, come vettori a due componenti.

Per caratterizzare completamente il moto del cerchio, sono sufficienti i valori di V , α, ed Ω, tuttavia `e conveniente introdurre dei parametri adimensionali, che meglio espri-mano lo scostamento dalle condizioni di funzionamento con T = 0 . Si definisce, quindi, il vettore scorrimento teorico definito come il rapporto tra la velocit`a di scorrimento Vs ed il modulo della velocit`a di rotolamento Vr:

σ = Vs Vr = µ Ωα 0 Ω − 1, Ωα 0 Ω tan α ¶ (1.8)

1.3.2

Scorrimento teorico di ciascuna ruota

Dalla definizione di scorrimento teorico (1.8) `e possibile ottenere, adesso, l’espressione degli scorrimenti per le quattro ruote del veicolo considerando, come da ipotesi, un veicolo sterzante solamente all’anteriore (δ1 6= 0 e δ2 = 0) e con trazione al posteriore :

• Scorrimenti longitudinali σx11 = (u − rt1/2) + (v + ra1)δ1 − Ω11R1 Ω11R1 σx12 = (u + rt1/2) + (v + ra1)δ1− Ω12R1 Ω12R1 σx21 = (u − rt2/2) − Ω21R2 Ω21R2 σx22 = (u + rt2/2) − Ω22R2 Ω22R2 (1.9) • Scorrimenti laterali

1.3 Equazioni di congruenza 16 σy11 = − (u − rt1/2)δ1+ (v + ra1) Ω11R1 σy12 = − (u + rt1/2)δ1+ (v + ra1) Ω12R1 σy21 = (v − ra2) Ω21R2 σy22 = (v − ra2) Ω22R2 (1.10)

dove sono state indicate con i termini Ωij le velocit`a angolari dei cerchi delle singole

ruote, mentre con R1 ed R2 i raggi di rotolamento, rispettivamente delle ruote anteriori

e posteriori. Occorre precisare che, sperimentalmente, si nota una scarsa dipendenza del raggio di rotolamento dal carico verticale agente sul pneumatico, basti osservare che la lunghezza della cintura rimane praticamente costante.

Per rendere pi`u chiara la notazione, si osserva che le ruote anteriori si trovano in condi-zione di puro rotolamento, e quindi , per definicondi-zione, hanno scorrimento longitudinale nullo e velocit`a pari a

Ω11R1 = µ u − rt1 2 ¶ + (v + ra1)δ1 Ω12R1 = µ u + rt1 2 ¶ + (v + ra1)δ1.

Di conseguenza lo scorrimento laterale assume la forma

σy11 = −(u − rt1/2)δ1+ (v + ra1) (u − rt1/2) + (v + ra1)δ1 ' −(u − rt1/2)δ1+ (v + ra1) (u − rt1/2) ' −δ1+ v + ra1 u = −α1 σy12 = −(u + rt1/2)δ1+ (v + ra1) (u + rt1/2) + (v + ra1)δ1 ' −(u + rt1/2)δ1+ (v + ra1) (u + rt1/2) ' −δ1+ v + ra1 u = −α1. (1.11)

Quindi gli scorrimenti teorici per le quattro ruote risulteranno: σx11 = σx12 = σx1 = 0 σy11 = σy12 = σy1 = −α1 σx21 = − µ 1 −u − rt/2 Ω2R2 ¶ σx22 = − µ 1 −u + rt/2 Ω2R2 ¶ σy21 = σy22 = σy2 = v − ra2 Ω2R2 (1.12)

dove con Ω2 = Ω21 = Ω22 si `e indicata la velocit`a angolare dei cerchi delle ruote

po-steriori (essendo il differenziale bloccato), e con R2 il loro raggio di rotolamento; di

conseguenza, con il prodotto Ω2R2, si indicher`a la velocit`a di rotolamento delle ruote

motrici. `E importante sottolineare come la presenza di uno slittamento longitudinale anche piccolo, purch`e diverso da zero, determini il passaggio immediato dall’espressio-ne dello scorrimento laterale (e longitudinale) delle ruote anteriori a quello delle ruote posteriori. Infatti, mentre i primi sono legati solamente all’angolo di deriva, che `e una grandezza cinematica dipendente dalle condizioni globali del veicolo, i secondi sono legati, oltre che alle velocit`a caratteristiche (v, r), anche alla velocit`a angolare della ruota, che `e influenzata da fattori non strettamente cinematici, come ad esempio la coppia applicata alla ruota, quella erogata dal motore etc..

Rispetto a quanto scritto precedentemente, si osserva che nelle normali condizioni di marcia, Ω2R2 ed u sono poco diversi tra loro, tanto da poter porre

1.3 Equazioni di congruenza 18 ossia Ω2R2 u = 1 + q u (1.14) con q u ¿ 1. `

E evidente che ci`o che accade alle ruote posteriori non accade invece a quelle anteriori, dove, la mancanza di un’azione motrice alla ruota, determina scorrimenti longitudinali nulli, con conseguente uguaglianza tra la velocit`a longitudinale del veicolo e la velocit`a di rotolamento delle ruote anteriori

Ω1R1 = u

Avvalendosi delle ultime espressioni, `e possibile scrivere nuovamente gli scorrimenti teorici delle ruote posteriori linearizzati rispetto al termine q/u :

σx21 ' − · q u+ rt2 2u ³ 1 − q u ´¸ σx22 ' − · q u− rt2 2u ³ 1 − q u ´¸ σy2 ' −α2 ³ 1 − q u ´ = µ v − ra2 u ¶ ³ 1 − q u ´ (1.15)

Si noti, quindi, come non sia pi`u sufficiente l’angolo di deriva a caratterizzare il com-portamento dei pneumatici posteriori, basti pensare che in marcia rettilinea, essendo

del fatto che quest’ultimi saranno piccoli, ma non rigorosamente nulli.

Appare quindi pi`u corretto utilizzare lo scorrimento teorico come grandezza di riferi-mento invece dell’angolo di deriva della teoria classica.

1.4

Equazioni di equilibrio

Per poter esprimere le equazioni di equilibrio, occorre calcolare le espressioni delle accelerazioni e valutare, successivamente, le forze ed i momenti agenti sul veicolo.

1.4.1

Accelerazioni

Per quanto riguarda la determinazione delle accelerazioni, possiamo dire che nulla cam-bia rispetto alla teoria classica; infatti possiamo definire:

• L’accelerazione del baricentro come la derivata della velocit`a VG = ui + vj

ri-spetto al tempo

aG = dVG

dt = ˙ui + urj + ˙vj − vri

= ( ˙u − vr)i + ( ˙v + ur)j (1.16) = axi + ayj

ottenendo cos`ı una scomposizione dell’accelerazione baricentrale in accelerazione

longitudinale

ax = ˙u − vr (1.17)

1.4 Equazioni di equilibrio 20

ay = ˙v + ur = ˙v +

u2

R (1.18)

rispetto all’asse del veicolo.

• L’accelerazione laterale a regime

˜ay = ur =

u2

R (1.19)

che espressa in questa forma permette di scrivere l’accelerazione laterale nel mo-do seguente ay = ˙v + ˜ay.

`

E possibile inoltre rapportare l’accelerazione laterale ay all’accelerazione

gravi-tazionale g ottenendo

k = ˜ay

g (1.20)

il cui valore massimo `e detto tenuta in curva.

• L’accelerazione angolare come data semplicemente da ˙r.

1.4.2

Forze e momenti agenti sul veicolo

Per la valutazione delle forze e dei momenti agenti sul veicolo, occorre precisare che, rispetto alla teoria classica, compare un termine supplementare rappresentato dal mo-mento d’imbardata, che agisce sul veicolo a seguito del bloccaggio del differenziale. Per convenzione si indicano con Fxij le componenti longitudinali e con Fyij le

compo-nenti trasversali delle forze trasmesse dalla strada alle ruote. Occorre precisare che i termini longitudinale e trasversale sono relativi ad un sistema di riferimento solidale

alla ruota e non all’intero veicolo. Si considerano nulli, per semplicit`a, tutti i momenti di autoallineamento Mzij , in quanto lo spostamento di qualche centimetro della retta

di applicazione delle forze laterali, rispetto al piano medio trasversale della ruota, non avrebbe significativi effetti sulla dinamica globale dell’intero veicolo.

Tenendo presente che per angoli di sterzo fino a 15◦ _{' 0.26 rad `e lecito}4 _{porre cos δ ' 1}

e sin δ ' δ e, considerando le forze agenti sul veicolo, otteniamo le tre equazioni di equilibrio ( longitudinale, laterale e a momento) :

m( ˙u − vr) = (Fx11 + Fx12) − (Fy11+ Fy12)δ1 + (Fx21+ Fx22) − Fa

m( ˙v + ur) = (Fx11 + Fx12)δ1+ (Fy11+ Fy12) + (Fy21 + Fy22)

J ˙r = [(Fx11+ Fx12)δ1+ (Fy11 + Fy12)]a1− (Fy21 + Fy22)a2+ − (Fx11− Fx12)t1/2 − (Fx21− Fx22)t2/2 + (Fy11 − Fy12)δ1t1/2

(1.21)

all’interno della quale si indica con Fa la forza aerodinamica

Fa= 1 2ρSCxu 2 dove: • ρ = densit`a dell’aria

• S = superficie della proiezione frontale del veicolo • Cx = coefficiente di resistenza aerodinamica

4<sub>La linearizzazione trigonometrica dell’angolo di sterzo pu`o ritenersi valida anche nell’analisi</sub> di-namica del veicolo con pneumatici non lineari; questo perch`e, anche in condizioni limite di perdita di aderenza, gli angoli di deriva non superano i 15◦_{− 20}◦_{, cos`ı come quelli di sterzo e quindi restano} valide le precedenti linearizzazioni.

1.4 Equazioni di equilibrio 22

• u = velocit`a longitudinale del veicolo

Per rendere pi`u compatta la notazione si sommano i contributi delle due ruote di uno stesso assale Fx1 = Fx11 + Fx12 Fx2 = Fx21 + Fx22 Fy1 = Fy11+ Fy12 Fy2 = Fy21+ Fy22 (1.22)

Restringendo l’analisi ai veicoli a due ruote motrici, ed in particolar modo a quelli a trazione posteriore e sterzatura all’anteriore, si ottiene una semplificazione, trascuran-do la resistenza a rotolamento dei pneumatici anteriori e ponentrascuran-do Fx11 = Fx12 = 0 .

Rimane ancora il termine (Fy11 + Fy12)δ1t1/2 il quale non `e rigorosamente nullo, visto

che Fy11 6= Fy12 ; infatti, anche se le ruote di uno stesso assale lavorano con angoli

di deriva simili, non hanno necessariamente simili forze laterali. Questo deriva prin-cipalmente dal diverso carico verticale gravante sulle ruote dell’assale, a seguito del trasferimento di carico generato, durante la percorrenza di una curva, dall’azione del-l’accelerazione laterale. Occorre osservare, per`o, che il prodotto della differenza delle forze laterali dell’assale anteriore per l’angolo di sterzo, espresso in radianti, risulta pic-colo e, poich`e il valore di quest’ultimo non supera, nella nostra analisi, i 15◦_{, possiamo}

trascurare quest’ultimo termine senza compiere un grossolano errore, con il vantaggio di una notevole semplificazione matematica oltre che formale.

In base a quanto detto possiamo riscrivere le equazioni di equilibrio nella forma se-guente:

m( ˙u − vr) = Fx2 + Fy1δ1− Fa m( ˙v + ur) = Fy1 + Fy2

J ˙r = Fy1a1− Fy2a2+ Mz2

(1.23)

compare anche un’altra grandezza:

• Il momento d’imbardata

Mz2 = (Fx22− Fx21) t2

2. (1.24)

Occorre precisare che l’intera analisi verr`a svolta considerando il sistema a regime, trascurando quindi il transitorio che intercorre tra un’ eventuale manovra e l’attimo in cui il veicolo si stabilisce su una particolare traiettoria. Questo, ovviamente, determina un’ulteriore variazione nell’espressione delle equazioni di equilibrio, dove scompare la dipendenza dal tempo, dovuta alle derivate della velocit`a longitudinale, trasversale e d’imbardata ( ˙u = ˙v = ˙r = 0) −mvr = Fx2+ Fy1δ1− Fa mur = Fy1+ Fy2 0 = Fy1a1− Fy2a2+ Mz2. (1.25)

1.5

Equazioni costitutive

Per completare il modello di veicolo, necessario per l’analisi dinamica, restano da defini-re le caratteristiche di ciascun pneumatico. Questo `e possibile enunciando le equazioni costitutive che possono essere considerate le discriminanti dei vari casi in cui `e suddi-visa l’analisi, a seconda della tipologia di pneumatico modellato.

A differenza di ci`o che accade nella teoria classica, le forze tangenziali, esercitate dalla strada su ciascun pneumatico, dipendono sia dal corrispondente scorrimento teorico

1.6 Modello monotraccia 24

σij che dal carico verticale Fzij gravante su ciascuna ruota

F = −

− →_σ

σ f (σ, ±∆Fzij).

In analogia con ci`o che avviene nella teoria classica, si trascura l’influenza dell’angolo di camber sulla forza laterale Fyij, in quanto, avendo considerato trascurabili gli angoli

di caster e di kingpin, ed assumendo basso il valore del rollio, risultano trascurabili le variazioni dell’angolo di camber delle singole ruote. Le equazioni costitutive saranno enunciate con le opportune espressioni a seconda del caso in esame, all’interno del ca-pitolo corrispondente.

1.6

Modello monotraccia

Per completare il modello matematico, necessario per lo studio della dinamica di un veicolo con differenziale bloccato, conviene, a questo punto, mettere insieme i tre gruppi di equazioni (congruenza, equilibrio e costitutive), ottenendo un sistema che `e alla base del modello monotraccia5 _{(single track model). Questa volta, a differenza della teoria}

classica, il sistema `e costituito solo da equazioni valide a regime, ossia durante uno steering pad, risultando quindi indipendente dalla variabile tempo. Una volta fissato

il modello, prima di procedere con l’analisi e quindi con la risoluzione del sistema, non resta che stabilire cosa considerare noto e cosa incognito. Una scelta naturale `e supporre assegnate sia la velocit`a longitudinale del veicolo u, che l’angolo di sterzo

δ, lasciando come incognite la velocit`a laterale v e quella d’imbardata r, che risultano

essere le uniche variabili di stato del sistema. Occorre dire che, oltre a v ed r, il sistema ha una nuova incognita, costituita dal termine q/u (introdotto per tener conto della presenza di piccoli slittamenti alle ruote posteriori motrici). Quest’ultimo, pur non

essendo una nuova variabile di stato, impedisce il disaccoppiamento delle equazioni del sistema dinamico (come avviene, invece, nella teoria classica), e, cosa pi`u importante, trasforma il sistema in un sistema non lineare, indipendentemente dal tipo di modello di pneumatico scelto per l’analisi.