Capitolo III

Capitolo III

MODELLI LONG-RANGE

DEPENDENCE (LRD) PER LA

SUPERFICIE DEL MARE

In questo capitolo viene affrontato il problema della stima della densità spettrale di potenza (DSP) di un’immagine SAR del mare e l’analisi delle sue proprietà caratteristiche.

Nella prima parte si illustrano alcune tecniche di stima della DSP di processi aleatori bidimensionali, la cui applicazione alle immagini SAR del mare, interpretate come singole realizzazioni di processi aleatori stazionari bidimensionali, restituisce una stima dello spettro direzionale dell’immagine.

Successivamente si richiamano le definizioni dei modelli Long-Range

Dependence (LRD) 1-D e 2-D principalmente utilizzati nella letteratura scientifica

per la rappresentazione della DSP radiale media (DSPRM), ponendo particolare attenzione ai modelli Fractionally EXPonential (FEXP). Il loro impiego, infatti, permette di implementare, tramite l’applicazione della trasformazione diretta di Hasselmann, una tecnica d’inversione spettrale di tipo parametrico che, dall’analisi della DSP stimata dell’immagine SAR, permette la ricostruzione dello spettro direzionale del mare.

3.1 - Metodi di stima della DSP di immagini

Il problema della stima spettrale può essere affrontato in due modi [15]: applicando i metodi classici, che consistono nello stimare lo spettro direttamente dai dati osservati, oppure con un approccio di tipo parametrico, che consiste nell’ipotizzare un modello, stimarne i parametri dai dati e verificare a posteriori la validità del modello adottato.

I metodi classici di stima dello spettro si basano sul calcolo della trasformata di Fourier dei dati osservati o della loro funzione di autocorrelazione [16]. Queste tecniche di stima assicurano buone prestazioni nel caso in cui i campioni disponibili siano numerosi e richiedono la sola ipotesi di stazionarietà dei dati osservati.

I metodi che dipendono dalla scelta di un modello assicurano stime migliori di quelle ottenibili con i metodi classici nel caso in cui i dati disponibili siano pochi (purché il modello assunto sia corretto).

I metodi classici sono da preferire per lo studio delle immagini SAR. In queste applicazioni, infatti, si ha a disposizione un elevato numero di pixel e non si possono utilizzare modelli che descrivano il processo di generazione dei campioni e che risultino, al contempo, semplici ed accurati.

3.1.1 - Il periodogramma

Questo metodo di stima, nel caso 1-D, richiede il calcolo della trasformata di Fourier della sequenza dei dati osservati. Quando si lavora con processi stocastici bidimensionali, le cui funzioni campione sono delle immagini [17], in luogo di una sequenza x n

[ ]

si considera una matrice di dati x m,n

[ ]

con m=0,...,M − e 1

0 1

n= ,...,N−

Si utilizza, in questi casi, la versione bidimensionale del periodogramma:

(

)

[ ]

(1 2 ) 2 1 1 2 1 2 0 0 1 M N j f m f n PER m n ˆP f , f x m,n e MN π − − − + = = =

∑∑

(3.1) Osservando che

(

)

[ ]

(1 2 ) 1 1 2 1 2 0 0 M N j f m f n m n X f , f − − x m,n e− π + = = =

∑∑

(3.2)

è la trasformata discreta di Fourier bidimensionale della sequenza dei dati, si può riscrivere la (3.1) nella forma

(

)

(

)

2 1 2 1 2 1 PER ˆP f , f X f , f MN = (3.3)

Si può dimostrare che lo stimatore in (3.3) è asintoticamente non polarizzato (il valor medio dello stimatore tende, al limite per N → ∞ e M → ∞, alla DSP dei dati), ma anche non consistente (la varianza dello stimatore non tende a zero nel limite per

N → ∞ e M → ∞). La tecnica di stima tramite il periodogramma resta comunque di grande interesse pratico: dalla relazione (3.3) si intuisce la semplicità computazionale raggiungibile tramite un’implementazione di calcolo veloce della trasformata di Fourier (FFT).

3.1.2 - Metodo di Bartlett

Una semplice strategia adottata per ridurre la varianza dello stimatore (3.3) consiste nel calcolare la media di più stime indipendenti. Poiché la varianza non migliora all’aumentare della lunghezza dei dati, si può pensare di suddividere la matrice dei dati osservati in sottoinsiemi disgiunti, calcolare il periodogramma di ogni sottoinsieme ed eseguire la media di tutti i periodogrammi.

La Fig. 3.1 mostra un’immagine di N M× pixel (una matrice di N M×

elementi) suddivisa in _{K sottofinestre non sovrapposte ciascuna di} 2 _{R S× elementi}

[ ]

x y l l x y x m,n = x m l K ,n l K_ + + _ 0 1

₍

(

1

₎

)

0 1 1 m , ,..., R n , ,..., S  = −  = −  (3.4) con

(

)

(

)

0 1 1 0 1 1 x y M R K N S K l , ,..., K l , ,..., K = ×   = ×   = −   = −  (3.5)

La stima secondo il procedimento di Bartlett risulta:

(

1 2

)

2 1 1 ( )

(

1 2

)

0 0 1 x y x y K K l l BART PER l l ˆ ˆ P f , f P f , f K − − = = =

∑∑

(3.6) Nella (3.6) ˆP( )l lx y

(

)

identificata dalla coppia

( )

l ,l e definito dalla relazione _{x y} ( )

₍

₎

_{[ ]}

( 1 2 ) 2 1 1 2 1 2 0 0 1 x y x y R S l l j f m f n PER l l m n ˆP f , f x m,n e RS π − − − + = = =

∑∑

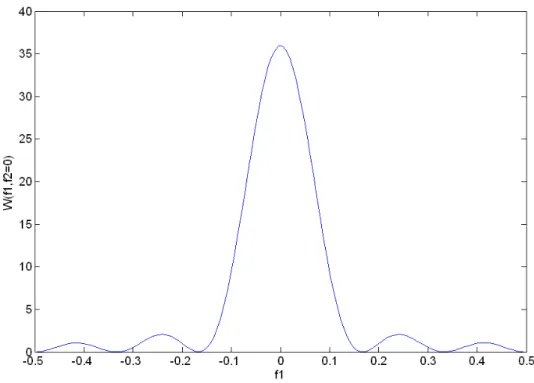
(3.7)

Ad una riduzione delle dimensioni delle finestre contenenti i dati sotto analisi corrisponde una perdita di risoluzione per lo spettro stimato.

1 2 3 K 2 3 K M campioni N cam p ioni R S ly lx

Fig. 3.1 - Calcolo del periodogramma di un’immagine con il metodo di Bartlett

Si consideri infatti il valor medio dello stimatore modificato secondo Bartlett:

(

)

{

}

1 1

{

( )

₍

₎

}

{

( )

₍

₎

}

1 2 2 1 2 1 2 0 0 1 x y x y x y K K l l l l

BART PER PER

l l ˆ ˆ ˆ E P f , f E P f , f E P f , f K − − = = =

∑∑

= (3.8)

Tramite alcuni passaggi aritmetici si può giungere all’espressione:

(

)

{

ˆBART 1 2

}

B

(

1 2

)

x

(

1 2

)

E P f , f =W f , f ⊗ ⊗S f , f (3.9)

Dalla precedente relazione si osserva che il valor medio dello stimatore può essere visto come la doppia convoluzione periodica tra la funzione W_B

(

f , f_{1 2}

)

e la densità spettrale di potenza S_x

(

f , f_{1 2}

)

relativa alla matrice dei dati; la relazione (3.6) definisce quindi uno stimatore polarizzato. Attraverso una diretta estensione della teoria monodimensionale della stima spettrale è possibile interpretare la funzione

(

1 2

)

B

W f , f come trasformata di 2D di Fourier della finestra:

( )

1 1 0 k R k l per w k ,l R S l S altrove     ≤_ − −     =_{   } ≤   (3.10)

dal momento che la finestra è separabile, la trasformata di Fourier sarà il prodotto delle trasformate 1-D:

(

)

(

_{( )}

)

(

₍

₎

)

2 2 1 2 1 2 1 2 1 1 B sin f R sin f S W f , f R S sin f sin f

π

π

π

π

    = _{    }     (3.11)

L’applicazione del metodo di Bartlett ha come controindicazione l’allargamento (smearing) dello spettro stimato, che è di scarsa rilevanza solo se W_B

(

f , f_{1 2}

)

è molto stretta nei confronti di X f , f

(

_{1 2}

)

, cioè se la finestra utilizzata è sufficientemente lunga. Dalla Fig. 3.2 relativa al profilo, per R S= =6, si vede che la banda a -3dB del lobo principale di W_B

(

f , f_{1 2}

)

è all’incirca pari a 1 1

6

R = : non possiamo risolvere

dettagli inferiori a questo valore.

A tale svantaggio fa riscontro una riduzione della varianza di un fattore proporzionale a _{K [18], di conseguenza si ha:} 2

(

)

{

}

{

( )

₍

₎

}

1 2 2 1 2 1 l BART PER ˆ ˆ var P f , f var P f , f K = (3.12)

Tale risultato è corretto nel caso in cui i periodogrammi costituiscono stime indipendenti. Quando i sottoinsiemi di dati vengono scelti come i blocchi contigui di una stessa realizzazione, come mostrato in Fig. 3.1, le finestre di dati non risultano incorrelate tra loro e si deve accettare una riduzione della varianza di un fattore inferiore a _{K .} 2

Fig 3.3 - Trasformata di Fourier della finestra di Bartlett 2-D (R=6 S=6)

In conclusione, il periodogramma è uno stimatore non consistente e asintoticamente non polarizzato della DSP di una sequenza bidimensionale. La polarizzazione dello stimatore è matematicamente descrivibile in forma di doppia convoluzione dello spettro vero con una finestra spettrale del tipo

(

)

(

_{( )}

)

(

₍

₎

)

2 2 1 2 1 2 1 2 1 1 Btot sin f M sin f N W f , f M N sin f sin f

π

π

π

π

    = _{    }    

considerata.

Se si opera una media dei periodogrammi calcolati su più sottosequenze adiacenti (metodo di Bartlett), ciascuna di R S× campioni, come in Fig. 3.1, la polarizzazione dello stimatore è ancora rappresentabile dalla doppia convoluzione (vedi relazione (3.9)) dello spettro vero con la finestra spettrale (3.11):

(

)

(

_{( )}

)

(

₍

₎

)

2 2 1 2 1 2 1 2 1 1 B sin f R sin f S W f , f R S sin f sin f

π

π

π

π

    = _{    }     (3.13) con M R K N S K  =    = 

La polarizzazione dello stimatore ˆP_BART

(

f , f è maggiore di quella di _{1 2}

)

ˆP_PER

(

f , f , _{1 2}

)

a causa della maggiore larghezza del lobo principale della corrispondente finestra spettrale. La polarizzazione può quindi essere interpretata in relazione ai suoi effetti sulla risoluzione dello spettro. Per una dimensione fissata della sequenza da analizzare, M righe ed N colonne, la varianza dello stimatore diminuisce al crescere del numero dei periodogrammi, ma diminuiscono anche R ed S e quindi la risoluzione dello spettro stimato.

Occorre perciò raggiungere un compromesso, nel metodo di Bartlett, tra la polarizzazione o risoluzione dello spettro da un lato e la varianza dello stimatore dall’altro. La scelta effettiva dei parametri M , N, R ed S in una situazione reale è orientata dalle conoscenze a priori sul segnale da analizzare. Per esempio, se sappiamo che lo spettro ha un picco molto stretto, e se è importante risolverlo,

dobbiamo scegliere R ed S abbastanza grandi per ottenere la risoluzione in

frequenza desiderata. È poi necessario utilizzare una coppia di valori M ed N sufficientemente elevati per ottenere una varianza convenientemente bassa per lo stimatore di Bartlett.

3.2 - Definizione di processi stocastici auto-simili

I processi auto-simili vennero introdotti da Kolmogorov nel 1941 [19] ed utilizzati in statistica da Mandelbrot ed altri a partire dal 1968 (ad esempio in [20]-[23]).

L’idea di base della auto-similarità è molto semplice:

una forma geometrica è detta auto-simile, in senso deterministico, se in essa vengono osservate le stesse strutture geometriche indipendentemente dalla distanza dalla quale la si esamina.

La definizione di auto-similarità di un processo stocastico è riferita alla sua distribuzione.

Definizione 1: Sia Y un processo aleatorio dipendente dalla variabile continua t . _t t

Y è detto auto-simile con parametro di auto-similarità H , se, per ogni fattore di scala positivo c, il processo scalato con fattore di scala ct t, H

ct

c Y− _{, è equivalente in}

distribuzione al processo Y . _t

Questo implica che, per ogni sequenza di punti t ,...,t e per ogni costante positiva _{1 k}

c, H

(

₁, , _k

)

ct ct

c− Y … Y ha la stessa distribuzione di

(

Y_t1, ,… Y_tk

)

. Diverse realizzazioni di un processo auto-simile appaiono qualitativamente le stesse, indipendentemente dalla

distanza dalla quale le si esamina.

Definizioni più utili per le applicazioni che seguono sono quelle di processi auto-simili del secondo ordine; esse impongono una condizione sulla struttura della funzione di correlazione di processi stazionari.

Sia X =

(

X ,t_t =0 1 2, , ,...

)

un processo aleatorio stazionario in covarianza, con media

µ, varianza _σ2 _{e funzione di autocorrelazione ρ}

( )

_{k , k≥0. Si assuma che, per} k→ ∞, X abbia una funzione di autocorrelazione della forma [24]-[25]

( )

k c k_ρ α

dove 0< <α 1 e c_ρ è una costante. Per ogni m=1, 2,... si indichi con

( )m

(

( )m _{, 1, 2,3...}

)

k

X = X k = la serie ottenuta mediando la serie originale X su

blocchi non sovrapposti di lunghezza m

( ) ( )

(

1 1

)

1 ... , 1 m k k m km X X X k m − − = + + ≥ (3.15)

Definizione 2: Un processo X è detto (esattamente) auto-simile del secondo ordine, con parametro di auto-similitudine H = −1 α 2, se per tutti gli m=1, 2,...

( )

{ }

m 2 var X =σ m−α e ( )

_{( )}

_{( )}

1

(

₍

₎

2 ₂ 2

)

1 2 1 , 0 2 H H m H k k k k k k ρ =ρ = + − + − ≥ (3.16)

dove _ρ( )m _{rappresenta la funzione di autocorrelazione di X}( )m _.

Definizione 3: Un processo X è detto (asintoticamente) auto-simile del secondo ordine, con parametro di auto-similitudine H = −1 α 2, se per ogni k abbastanza grande

( )

_{( )}

(

m

)

( )

mlim→∞

ρ

k →

ρ

k (3.17)

In altri termini, X è un processo stazionario auto-simile del secondo ordine se i corrispondenti processi aggregati, _X( )m _{, sono statisticamente equivalenti ad X o}

divengono indistinguibili da esso almeno relativamente alle loro funzioni di autocorrelazione.

Un risultato particolarmente interessante che evidenzia il significato matematico della auto-similarità di processi stocastici è dovuto a Lamperti (1962) [26]. Il teorema di Lamperti dimostra che l’auto-similarità è una conseguenza dei teoremi sul limite della somma di variabili aleatorie [27]. L’enunciato del teorema richiede la seguente definizione.

Definizione 4: Sia Y un processo aleatorio dipendente dalla variabile continua t . _t Se per ogni k≥1 ed ogni insieme di k punti t₁, ,… t_k, la distribuzione delle variabili

aleatorie (v.a.)

(

)

1 1 1, , k k 1

t c t c t c t c

Y ₊ −Y_{+ −} … Y ₊ −Y _{+ −} non dipende da c R∈ , allora si dice che il processo Y ha incrementi stazionari. _t

TEOREMA DI LAMPERTI

1. Sia Y un processo stocastico tale che _t P Y

(

₁≠0

)

>0 e Y è il limite in _t distribuzione della sequenza delle somme parziali normalizzate

1 1 1 nt n nt n i i a S a X     − − = =

∑

n=1,2,… (3.18)

Nella (3.18)  _{ }nt indica la parte intera di nt , X X … è una sequenza ₁, ₂,

stazionaria di variabili aleatorie e a a … è una sequenza di costanti di ₁, ,₂

normalizzazione positive e tali che

(

( )

_n

)

n

lim log a

→∞ = ∞. Allora esiste un H >0

tale che, per ogni u>0. a. nu H n n a lim u a →∞ = .

b. Y è auto-simile con parametro di auto-similarità H . _t c. Y ha incrementi stazionari. _t

2. Tutti i processi auto-simili con incrementi stazionari ed H >0 possono essere ottenuti per mezzo di somme parziali come nella (3.18).

La prima parte del teorema di Lamperti stabilisce che quando un processo è il limite di somme parziali normalizzate di v.a. esso è necessariamente auto-simile.

3.2.1 - Incrementi stazionari di processi aleatori auto-simili

Sia Y un processo auto-simile con parametro di auto-similarità H . La _t

proprietà

1 0

H t d

Y = t Y ∀ >t (3.19)

dove il simbolo = indica l’uguaglianza in distribuzione, implica il seguente _d comportamento al limite di Y per t tendente all’infinito [27]. _t

distribuzione).

2. Se H =0, allora Y_t =_d Y₁.

3. Se H >0 e Y_t ≠ , allora 0 Y_t → ∞_d . Analogamente, se t tende a zero, si ha:

1. Se H <0 e Y_t ≠ , allora 0 Y_t → ∞_d . 2. Se H =0, allora Y_t =_d Y₁.

3. Se H >0, allora Y_t →_d 0.

Se si esclude il caso Y_t = , le relazioni precedenti implicano che 0 Y è un processo _t

non stazionario, a meno che risulti H =0. L’eccezione H =0 è di scarso interesse pratico perché implica che, per ogni t>0, Y uguaglia _t Y con probabilità unitaria. ₁

Allo scopo di modellare dati che appaiono stazionari, si utilizzano soltanto quei processi auto-simili che hanno incrementi stazionari ed un parametro H >0.

Se per un processo auto-simile con incrementi stazionari si utilizzano valori negativi del parametro H , il processo risulta matematicamente patologico ovvero non è un processo misurabile. L’unica eccezione è il caso Y_t = = con probabilità Y₁ 0 1 [27]-[28]. Nel seguito si farà riferimento esclusivamente al caso H >0 e, in particolare, alla sottoclasse di processi auto-simili e ad incrementi stazionari per i quali Y₀ = con probabilità 1. 0

La forma della funzione di covarianza γ_y

( )

t,s =cov Y ,Y

(

_{t s}

)

di un processo auto-simile Y con incrementi stazionari segue dalle due proprietà precedenti. Per _t

semplificare la notazione si assuma E Y

( )

_t =0. Sia s t< e si indichi con

(

)

2

2 2

1 1

t t

E Y Y E Y

σ = _ − ₋ _{=  }  la varianza del processo degli incrementi

1 t t t X = −Y Y₋ . Allora risulta:

(

)

2

(

)

2 ₂

(

)

2 0 H t s t s E Y Y_ − _=E Y_{ −} −Y _=

σ

t s− (3.20) Si ha anche che

(

)

2 _{2 2}

[ ]

_{2 2 2 2}

( )

2 H H 2 , t s t s t s y E Y Y_ − _=E Y_{ } +E Y_{ } − E YY =

σ

t +

σ

s −

γ

t s (3.21) Quindi

( )

1 _{2 2}

(

)

2 ₂ , 2 H H H y t s t t s s

γ

₌

σ

 _{− − +}    (3.22)

Allo stesso modo può essere calcolata la covarianza della sequenza degli incrementi

(

)

1 1, 2,3,

i i i

X = −Y Y₋ i= … . La covarianza tra X e _i X_{i k+}

(

k >0

)

è espressa dalla relazione

( )

(

)

(

)

(

)

(

)

(

)

(

)

{

}

1 1 2 2 2 2 1 1 1 2 1 2 2 2 2 2 1 0 1 0 0 0 1 2 1 2 i i k k k k k k j j j j j j j j k k k k k cov X ,X cov X ,X E X X X X E Y Y E Y Y E Y Y E Y Y

γ

_{+ +} + + = = = = + − = = _{       }    = _{ } +_{ } −_{ } −_{  }                     = _ − _+ _ − _− _ − _− _ − _

∑

∑

∑

∑

(3.23)

Utilizzando la proprietà di auto-similarità si ottiene la formula

( )

(

)

(

)

( )

( )

2 2 2 2 1 1 2 1 , 0 2 , 0 H _H H k k k k k k k k

γ

σ

γ

γ

 _{=  + − + −  ≥}  _{ }   _{= − <}  (3.24) Le correlazioni sono date da

( )

(

)

(

)

( )

( )

2 2 2 1 1 2 1 , 0 2 , 0 H H H k k k k k k k k

ρ

ρ

ρ

 _{=  + − + −  ≥}  _{ }   _{= − <}  (3.25)

Il comportamento asintotico di ρ

( )

k si può ottenere dal suo sviluppo in serie

di Taylor nell’intorno dell’origine. Si osservi che

( )

1 2

( )

1

2 H k k g k ρ ₌ − _{, dove}

( ) (

)

2

(

)

2 1 H 2 1 H g x = +x − + −x . Se 0<H <1 e 1 2

H ≠ , il primo termine non nullo

nello sviluppo in serie di Taylor di g x

( )

nell’origine è _2H

(

_2H−1

)

_x2_{. Vale quindi} la relazione

( )

(

_{2 1}

)

2H 2 1 k k lim H H k

ρ

− →∞ − = (3.26) Per 1 1

2<H < , questo implica che le correlazioni tendono a zero così lentamente che

( )

k k

ρ

∞ =−∞ = ∞

∑

(3.27)

Il processo X_i con i=1 2, ,... ha lunga memoria. Per 1 2

H = , tutte le correlazioni che corrispondono ad intervalli non nulli (k≠0) sono nulle e le osservazioni X_i sono

incorrelate. Se 0 1

2

H

< < , le correlazioni sono sommabili e vale la relazione seguente

( )

0 k k

ρ

∞ =−∞ =

∑

(3.28)

In pratica questo caso si presenta di rado, principalmente perché la condizione (3.28) è molto instabile. Si ipotizzi che la (3.28) valga per il processo Y_t e sia δ_t un processo di rumore, indipendente da Y_t, con una varianza arbitrariamente piccola e con autocorrelazioni la cui somma, per k→ ∞, tende ad una costante positiva c (finita o infinita). Si ipotizzi di osservare il processo Y_t+ invece di δ_t Y_t; in questo caso la somma delle correlazioni del processo Y_t+ è uguale a δ_t c≠0. Dunque, un disturbo di ampiezza arbitrariamente piccola modifica la proprietà (3.28).

Fino ad ora si sono considerati i tre casi 0 1

2 H < < , 1 2 H = e 1 1 2<H < . Cosa accade se H ≥ ? 1

Per H = la (3.26) implica che 1 ρ

( )

k =1, ∀k: tutte le correlazioni valgono 1 indipendentemente dalla distanza tra le osservazioni considerate. Questo caso non ha alcun interesse pratico.

Per 1H > ,

(

( )

)

k

lim ρ k

→∞ = ∞. Questo risultato contraddice il fatto che le correlazioni debbano sempre assumere valori compresi tra -1 e 1.

Si può quindi affermare che se le covarianze esistono ed il

(

( )

)

0

k

lim ρ k

→∞ = , allora

0<H <1.

In conclusione, si ha che:

1. Un processo auto-simile Y_t per il quale vale la proprietà (3.19) è non stazionario.

2. La rappresentazione, mediante processi auto-simili, di dati che appaiono stazionari può essere ottenuta utilizzando processi auto-simili con incrementi

stazionari.

3. Dall’analisi delle correlazioni delle sequenze degli incrementi X_i, risulta che:

a. Per 1 1

2<H < il processo è a lunga memoria (LRD).

b. Per 1

2

H = le osservazioni X_i sono incorrelate.

c. Per 0 1

2

H

< < il processo è a breve memoria (SRD) e la somma delle correlazioni tende a zero.

Se non diversamente specificato, si considerano nel seguito processi con momenti

del secondo ordine finiti,

(

( )

)

0

k

lim ρ k

→∞ = e quindi 0<H <1.

Con queste ipotesi, la DSP del processo degli incrementi X_i può essere calcolata nella forma seguente [29].

( )

(

)

2 1 2 _f 1 2 H j f

λ

c cos

λ

∞

π

j

λ

− − =−∞ = −

∑

+

λ

∈ −

[

π π

,

]

(3.29) con

(

2

)

2

( )

₂ 1

(

) (

_{2 1}

)

2

( )

f f i c =c H ,

σ

=

σ

π

− sin

π

H Γ H + ,

σ

=var X

Il comportamento di f in prossimità dell’origine può essere valutato analizzando il suo sviluppo in serie di Taylor in zero.

Dalla (3.29) segue che

( )

1 2H

(

min(3 2H ,2)

)

f

f

λ

=c

λ

− +o

λ

− (3.30)

L’approssimazione di f con c_f λ1 2H− risulta sperimentalmente molto buona anche per frequenze relativamente alte e non solo per λ→0. Si osserva che la funzione

(

1 2

)

( )

(

) ( )

1 2

H

f f

log c λ − =log c + − H log λ rappresentata rispetto al log

( )

λ è una

retta con pendenza negativa per ogni 1

2

H > , cioè per ogni processo a lunga

memoria.

Si consideri infine la relazione seguente

(

)

(

)

1 1 1 0 1 0 1 n H i n d i X n− X n− Y Y n n Y Y− = =

∑

= − = − (3.31)

( )

2 2H 2

var X =

σ

n − (3.32)

Per 1

2

H = le v.a. X_i sono incorrelate e quindi _{var X}

( )

_=σ2_n−1_{. Inoltre, se}

i X è un

processo Gaussiano con media µ e varianza _σ2_{, allora}

(

)

1 H n X µ σ − ₋ è una v.a. gaussiana standard.

Nel paragrafo che segue si enunciano le principali proprietà dei processi stocastici stazionari a lunga memoria e se ne forniscono definizioni matematicamente rigorose in funzione delle loro correlazioni e DSP.

3.3 - Processi stocastici a lunga memoria

Siano X X₁, ₂,...X_n variabili aleatorie con la stessa distribuzione marginale

F, che rappresentano i campioni di un processo aleatorio discreto 1-D nei punti 1, 2,...

i= n [30]. L’autocovarianza tra X_i e X_j è γ

( )

i j, =E X

{

(

_i−µ

)

(

X_j−µ

)

}

e la funzione di autocorrelazione risulta ρ

( )

i j, γ

( )

i j,₂

σ = . La DSP è definita dalla relazione [31]

( )

2

( )

2 ik k S

λ

σ

ρ

k e λ

π

∞ =−∞ =

∑

(3.33)

Per un processo stazionario a lunga memoria valgono le relazioni seguenti:

1) La varianza della media campionaria var X

( )

_n decade a zero con una pendenza minore di _n−1 _{ed è della forma}

var

c _⋅n−α _{per una qualche costante} var

c e per

0< <α 1.

2) I coefficienti ρ

( )

k tendono asintoticamente ad una espressione della forma

c_ρ⋅k−α per una qualche costante c_ρ e per 0< <α 1.

3) La DSP S

( )

λ ha un polo nell’origine e tende a zero come c_{f ⋅}λ−β _{per una} qualche costante c_f e per 0< < . β 1

4) In prossimità dell’origine il logaritmo del periodogramma I

( )

λ , rappresentato in funzione del logaritmo di λ, oscilla in modo casuale intorno ad una linea retta con pendenza negativa.

Definizione 5: Sia X un processo stazionario per il quale esistono un numero reale _t

( )

0,1

α∈ ed una costante cρ > tali che 0

( )

(

)

1 k k lim c k_ρ α

ρ

− →∞ = (3.34)

(il parametro H = −1 α 2, noto come parametro di Hurst, è spesso utilizzato al posto di α ). Allora X è un processo stazionario a lunga memoria (long-memory) o _t

con Long-Range Dependence, o strong dependence, o anche con correlazione lentamente tendente a zero (slowly decaying o long-range correlations).

In altre parole, processi stazionari con correlazioni tendenti iperbolicamente a zero

( )

k c k_ρ α

ρ

= − (3.35)

(correlazioni tendenti a zero così lentamente che la loro somma diverge

( )

k k

ρ

∞ =−∞ = ∞

∑

) sono detti processi stazionari di tipo LRD. Al contrario, i processi

stazionari con correlazioni esponenzialmente tendenti a zero

( )

k bak, 0 b , 0 a 1

ρ ≤ < < ∞ < < (3.36)

(per i quali la somma delle correlazioni tende ad un valore finito

( )

costante k k

ρ

∞ =−∞ = < ∞

∑

) sono chiamati processi stazionari con breve memoria

(short-memory) o Short-Range Dependence (SRD) o weak dependence.

La LRD può anche essere definita imponendo una condizione sulla DSP di un processo.

Definizione 6: Sia X un processo stazionario per il quale esistono un numero reale _t

( )

0,1

β∈ ed una costante c_f > tali che 0

( )

(

)

0 1 f S lim c β λ λ λ− → = (3.37)

Allora X è un processo stazionario a lunga memoria (long-memory) o con Long-_t Range Dependence.

Con questa definizione S

( )

λ ha un polo nell’origine.

È importante osservare che le definizioni di LRD di cui sopra sono di tipo asintotico. La LRD dipende dal comportamento delle correlazioni al tendere dell’intervallo k all’infinito e dal comportamento delle DSP al tendere della frequenza a zero.

3.3.1 - Il modello fractional Brownian motion

Il modello stocastico fractional Brownian motion (fBm) è tra i più largamente usati in letteratura per la rappresentazione delle immagini. Si tratta di un processo non stazionario ma con incrementi stazionari. Tra i processi 1-D l’fBm è l’unico processo Gaussiano auto-simile con incrementi stazionari.

Un processo

{

B t_H

( )

, t R∈

}

è un fBm 1-D se è Gaussiano, a media nulla e se la sua funzione di autocorrelazione è data da

( )

{

( ) ( )

}

2 2 2 2 , 2 H H H H B H H R t s =E B t B s =

σ

_t + s − −t s _ (3.38) dove 0<H <1. Se 1 2

H = si ottiene il ben noto processo di Wiener o moto Browniano, indicato con

( )

B t , che ha incrementi indipendenti.

Il processo degli incrementi del primo ordine di un modello fBm campionato è il fractional Gaussian noise (fGn) [32]:

( )

( )

;1

( )

(

1 ,

)

H H H H

G k = ∆B k =B k −B k− k Z∈ (3.39)

L’fGn è un processo stocastico discreto e stazionario la cui funzione di autocorrelazione decresce iperbolicamente come k2H−2 per ogni 1

2

H ≠ . Per quanto

affermato nel paragrafo precedente, il processo discreto G_H

( )

k presenta SRD per 1 0 2 H < < , indipendenza per 1 2 H = e LRD per 1 1

2<H < . Inoltre, poiché tutti i processi auto-simili del secondo ordine e con incrementi stazionari hanno le stesse statistiche del secondo ordine del processo fBm, segue che i loro incrementi hanno la stessa funzione di autocorrelazione del processo fGn.

La DSP del processo fGn è data da

( )

2 1 1 fGn H S

λ

λ

− ∝ (3.40)

Un'altra importante proprietà del modello fBm è la sua regolarità locale misurata per mezzo dell’esponente di Holder α che risulta pari ad H ovunque con probabilità 1

{

}

1

esponente α nel punto x₀ se, intorno a x₀, il grafico “appare” come la curva

( )

0 0

f x +c x x− α nel senso descritto di seguito:

Per ogni ε positivo esiste un intorno di x₀ tale che i valori assunti da f x

( )

in questo intorno appartengono all’inviluppo definito dalle due curve

( )

0 0

f x +c x x− α ε− e f x

( )

₀ −c x x− ₀α ε− . Questa proprietà non vale per ε negativi. Un valore grande del parametro α implica che f x

( )

è lentamente variabile in x₀, mentre un comportamento irregolare di f x

( )

in x₀ è dovuto a valori di α prossimi a zero.

Per un fBm α

( )

x₀ =H per ogni x₀ con probabilità 1 e quindi maggiore è il valore di

H e maggiore è la regolarità evidenziata dal processo.

Una possibile estensione al caso 2-D del modello fBm, detta isotropic

fractional Brownian field o Lévi fractional Brownian field è il campo Gaussiano a media nulla B_H con funzione di autocorrelazione

( )

(

2 2 2

)

, H H H H B R x y ∝ x + y − −x y 2 x e y R∈ (3.41)

Nella (3.41) 0<H <1 ed il simbolo i rappresenta la norma euclidea in _R2_.

Si osserva che il processo 1-D ottenuto “tagliando” il campo isotropo fBm 2-D con una linea passante per l’origine degli assi è un processo fBm 1-D con lo stesso indice

H. Come affermato in precedenza, il valore del parametro H determina la rugosità dell’immagine: più H è prossimo a zero e maggiore è la rugosità dell’immagine (per

0

H → l’immagine appare come una realizzazione di rumore bianco 2-D), più il

(a) (b)

Fig. 3.4 - Superfici fBm generate per diversi valori del parametro di Hurst H=0.2 (a) H=0.9 (b)

Un modello fBm bidimensionale o in dimensione n

(

n≥2

)

può anche essere

definito come un integrale stocastico che esiste nel senso dei minimi quadrati [33]. Con questa costruzione gli incrementi del processo fBm vengono generati eccitando un filtro frazionario bidimensionale con un processo di rumore bianco 2-D. Per un campo isotropo, il filtro frazionario ha risposta in frequenza

( )

1 H N2

G

λ

=

λ

− − (3.42)

dove N è la dimensione dello spazio (N =2 per le immagini). Usando questa

tecnica Reed definì uno spettro di potenza generalizzato per un fBm n-dimensionale [33] nella forma

( )

2 H H N B

λ

λ

− − Φ = (3.43)

Un’ulteriore possibilità per costruire estensioni n-dimensionali del modello fBm consiste nel definire campi auto-simili con incrementi 2-D stazionari. La definizione di auto-similarità n-dimensionale è analoga a quella 1-D: sia _{F x}

( )

_{, x R∈} 2 _un campo stocastico continuo nello spazio, esso è detto auto-simile con parametro di

auto-similarità H se per ogni a>0 si ha che

( )

H

( )

_, 2

d

F ax = a F x x R∈ , dove il

simbolo = indica l’uguaglianza in distribuzione. Questo implica che le statistiche _d del processo sono invarianti (a meno di una costante moltiplicativa) ad un cambiamento di scala. L’estensione della nozione di “incrementi stazionari” può essere ottenuta in modi diversi introducendo campi con differenti proprietà. Ad

esempio, nel caso 1-D si può definire la stazionarietà in senso stretto del processo degli incrementi come l’invarianza della loro d.d.p. alle traslazioni (l’unico spostamento possibile di un corpo rigido in uno spazio con un’unica dimensione). In uno spazio bidimensionale questa proprietà può essere definita come l’invarianza della funzione di distribuzione degli incrementi F x

( )

−F

( )

0 rispetto a qualunque spostamento rigido (traslazioni e rotazioni rigide e qualsiasi loro combinazione). Con questa definizione il modello fBm isotropo è l’unico campo Gaussiano auto-simile 2-D con incrementi stazionari.

L’estensione del modello fBm 2-D isotropo per la rappresentazione di immagini frattali anisotrope può essere realizzata in diversi modi; è ad esempio possibile costruire campi intrinsecamente anisotropi mediante un’opportuna definizione degli incrementi in _R2_{. Assumendo incrementi di dimensioni diverse} lungo due direzioni ortogonali, si introduce l’anisotropia del campo considerato. Questa procedura permette la costruzione di campi Gaussiani, auto-simili e con incrementi stazionari, diversi dal modello fBm isotropo 2-D precedentemente introdotto.

Si consideri una direzione arbitraria sul piano

( )

x y, individuata dagli incrementi

(

∆ ∆ . Gli incrementi _x, _y

)

∆(D D, ')F x y

(

, ;∆ ∆_x, _y

)

di ordine frazionario,

(

_{D D,} '

)

_∈R2_{, di un campo aleatorio bidimensionale, F x y}

( )

_{, , vengono ottenuti} filtrando F x y

( )

, con un filtro lineare la cui funzione di trasferimento è

(

)

(

)

'

( )

2 1 x 1 y , , D D _s p e− ∆ e− ∆ p s C − − ∀ ∈ (3.44)

In questo contesto, un campo F x y

( )

, a media nulla ha incrementi stazionari (in senso stretto), di ordine

(

_{D D,} '

)

_{, se esso ha varianza finita e, per ogni}

(

_{, ,} ' _, '

)

x y x y

∆ ∆ ∆ ∆ , la funzione di cross-correlazione tra ∆(D D, ')F x y

(

, ;∆ ∆_x, _y

)

e

( _, ')

₍

₎

'_{, ;}' ' _, ' D D x y F x y ∆ ∆ ∆ dipende solo da

(

_{x x−} '

)

_,

(

_{y y−} '

)

_{, e} x ∆ , ∆ , _y ' x ∆ , ' y ∆ . Questi campi sono analizzati in maggiore dettaglio in [34] e [35]. Il campo isotropo fBm

2-D, con parametro 0<H <1, ha incrementi stazionari di ordine

(

D,0 / 0,

) (

D

)

∀ ∈D R D H, > .

Un processo F x y

( )

, , con incrementi stazionari di ordine

( ) ( )

1,0 / 0,1 , è completamente descritto dalla sua funzione struttura, ϕ

(

∆ ∆ , che rappresenta la _x, _y

)

varianza di F x y

( )

, −F x

(

− ∆_x,y− ∆_y

) (

, ∀ ∆ ∆ . La funzione struttura è stata _x, _y

)

impiegata anche per la risoluzione di problemi di geostatistica [36] e per la caratterizzazione della rugosità di superfici meccaniche, che sono, per loro natura, anisotrope e non stazionarie. Essa risulta di notevole interesse perché può essere usata per esprimere la funzione di autocorrelazione di campi con incrementi stazionari (questo dimostra che i campi Gaussiani con incrementi stazionari risultano completamente descritti da questa funzione).

Inoltre l’espressione della funzione struttura di campi auto-simili può essere determinata in forma esplicita con espressione _ϕ

( )

_{x y, =ρ}2H_f

( )

_{ϑ , dove 0<H <1,}

2 2

x y

ρ = + , ϑ =arctg y x

(

)

, ed f

( )

ϑ è una funzione periodica con periodo π.

Ad esempio, la funzione f

( )

ϑ si riduce ad una costante nel caso di un modello fBm 2-D isotropo.

3.4 - Modelli Fractionally EXPonential

I modelli Fractionally EXPonential (FEXP) furono introdotti da Beran nel 1993 [37].

Definizione 7: Sia g:

[

−π π,

]

→R₊ una funzione positiva tale che

( )

0 1 g lim λ λ λ →   =     e

( )

( )

g λ =g −λ . Si definisca f₀ ≡ e siano 1 f f₁, , ,₂ … f_p funzioni lentamente variabili nell’intervallo

[

−π π,

]

. Si assuma che f_k

( )

λ = f_k

( )

−λ e, per ogni n, la matrice

( 1) 1 , 2 n p n n parteintera ∗_{× +} ∗ −   = _{ }  

H , con vettori colonna

(

)

1 2 3 2 , 2 , 2 , , 2 , 0,1, , t k k k k n f f f f k p n n n n π π π π ∗            ₌  _ _ _ _ _ _       …  … sia non singolare.

Sia θ =

(

η₀, , , ,H η₁ …η_p

)

un vettore reale con 1 1

2<H < . Si dice che X è un t processo FEXP con componenti SRD f f₁, , ,₂ … f_p e componente LRD g , se la sua DSP è data da

(

)

( )

1 2

( )

0 p H FEXP j j j S

λ θ

; g

λ

− exp

η

f

λ

=   = _{ } 

∑

 (3.45)

Per diverse scelte della funzione g

( )

λ e delle funzioni f₁

( ) ( )

λ , f₂ λ , ,… f_p

( )

λ , si ottengono diverse classi di modelli FEXP.

Si consideri allora la classe di modelli FEXP per i quali vale

( )

( )

( )

1 0 1 k k g exp j f , k , ,..., p

λ

λ

λ

λ

 = −   = =  (3.46)

Il logaritmo della DSP è la somma del logaritmo della componente LRD

(

1 2

)

(

1

)

(

1 2

)

2 2

j

H log e λ H log sin λ

− − = − _{ }

Si osserva che

(

)

(

)

(

)

0 0 0 1 2 2 2 1 2 1 2

lim H log sin

lim H log lim H log

λ λ λ

λ

λ

₊

λ

→ → →  _{ } −          = _ − _=  −_ _ (3.47)

Dalla (3.47) si rileva che la DSP rappresentata in funzione di λ in scala logaritmica è, in prossimità dell’origine, una retta con pendenza negativa e pari a

1 2− H = −2d, dove d indica il fractional differencing parameter. Quindi, per

0

d > , la DSP del processo ha un polo nell’origine (LRD).

Per la stima del parametro d si applica una tecnica di regressione lineare al logaritmo del periodogramma radiale medio I_mr

( )

λ_{j n,} rispetto al log

( )

λ_{j ,n} e si calcola d dalla pendenza della retta risultante, secondo quanto esposto da Bertacca in [38]. Il periodogramma radiale medio, I_mr

( )

λ_{j n,} , è definito dalla relazione

( )

1

(

,

)

, , n j n k k mr j n I I n λ ϑ λ ₌

∑

= _(3.48)

dove I

(

λ ϑ_{j n,} , _k

)

è il risultato della trasformazione da coordinate cartesiane a polari dei campioni del periodogramma 2-D, I

(

λ λ_x, _y

)

.

3.4.1 - Modelli FEXP Frattali

I modelli LRD 2-D, introdotti nei paragrafi precedenti permettono la rappresentazione di campi omogenei ed isotropi [32], [39]. È possibile dimostrare che le forme anisotrope degli stessi modelli non possono essere direttamente applicate alla rappresentazione di DSP 2-D di immagini SAR della superficie marina. Per stimare la DSP S

(

λ λ_x, _y

)

di un’immagine SAR, si calcola il periodogramma 2-D, I

(

λ λ_x, _y

)

, come descritto nel paragrafo 3.1. Supponiamo che le finestre utilizzate, di forma quadrata, abbiano dimensioni pari a 256 256× pixel e che l’immagine considerata sia di 2048 2048× pixel. La riduzione della varianza della stima spettrale

viene quindi ottenuta mediando 64 stime calcolate su blocchi adiacenti e non

in azimuth sia in (ground) range, si ha che:

( )

( )

1 max , , , max 128, 128, 128, 128, 12.5 1 0.08 2 , 1, ,128, 256 j n j n j n n x n n y n risoluzione m f m risoluzione j j n n s f s s s s

π

λ

λ

λ

λ

λ

λ

λ

λ

λ

−  =   _{= =}    _{= = =}   =  − ≤ <  − ≤ <  … _(3.49)

La trasformazione da coordinate cartesiane a coordinate polari restituisce una matrice

n n∗×

I i cui elementi sono i campioni del periodogramma su griglia polare

(

j n, , k

)

I λs ϑ , dove _k 2 k, k 1, ,n

n

π

ϑ = = … e n∗ _{rappresenta la parte intera di} 1

2

n− . In questo caso si ha: n=256, 128n∗ _{= .}

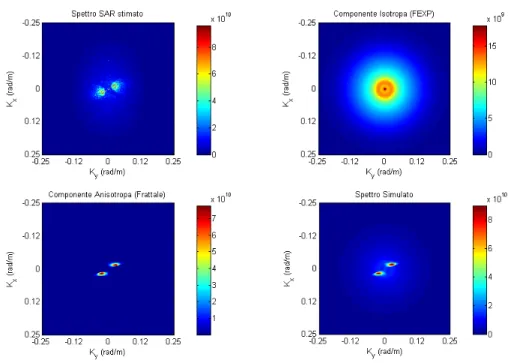
In Fig. 3.5 è mostrato, a titolo di esempio, lo spettro di potenza in forma polare di un’immagine SAR: le regioni “A” e “B” corrispondono rispettivamente al settore angolare che contiene i due lobi della DSP 2-D e al settore angolare che contiene una componente della DSP pressoché indipendente dalla direzione angolare

k

θ (gradi) k (ra d/ m) Regioni A e B 0 50 100 150 200 250 300 350 0 0.05 0.1 0.15 0.2 0.25 0 1 2 3 4 5 6 7 8 9 x 1010

B

_B

A

A

Fig. 3.5 - DSP 2-D in coordinate polari

Dall’analisi della DSP 2-D si ottiene che il 70% della potenza complessiva è associato alla regione “A”, mentre il rimanente 30% è associato alla regione “B”. Si consideri ora, ad esempio, la funzione di anisotropia proposta da Pesquet-Popescu e Lévy Véhel [32] per rendere anisotropo il campo FD 2-D:

(

)

(

)

(

)

2 2 1 2 1 1 2 2 x , x y y x y A , cos sin

cos sin sin sin sin

α ϕ

λ

λ λ

α

ϕ

λ

α

ϕ

α

ϕ

λ

λ

  = − _{ }+     + + _{ }−   (3.50) Si osserva che:

1) Nella (3.50) non è possibile separare la componente della DSP nella regione “A” da quella rappresentata nella regione “B”. In altri termini, modificando i parametri della (3.50) siamo in grado di modellare la sola componente anisotropa nella regione “A”, oppure di far tendere lo spettro di potenza all’isotropia (per α →0).

2) Nella (3.50) non è possibile modificare indipendentemente il coefficiente di

anisotropia α e la posizione del massimo dello spettro di potenza

K (rad/m)

Regioni A e B

(

λx_ max,λy_ max

)

. La relazione tra anisotropia e massimo della DSP 2-D andrebbe quindi modificata in modo da adattarla alle caratteristiche dello spettro di potenza di un’immagine SAR del mare. La relazione introdotta dovrebbe essere sostituita non solo per adattarla alle trasformazioni della DSP prodotte dalla variazione della velocità del vento, ma anche per tener conto dell’eventuale presenza di macchie d’olio sulla superficie.

3) Data la suddivisione della potenza complessiva tra le due regioni di Fig. 3.5, un modello, anche accurato, in grado di rappresentare una sola delle due regioni introduce un’approssimazione eccessiva, con la sola eccezione della rappresentazione di immagini SAR isotrope.

Il modello FEXP viene utilizzato per la rappresentazione di campi 2-D isotropi e omogenei. Per campi statisticamente omogenei ed isotropi, infatti, è facile derivare un modello D da un modello 1-D: per caratterizzare la DSP radiale del modello

2-D basta sostituire la variabile λs_{j n,} della DSP 1-D con il modulo

2 2

,

j n x y

s

λ = λ = λ +λ . La DSP 2-D di un modello isotropo e omogeneo gode della

proprietà di isotropia ed è completamente caratterizzata dalla sua DSP radiale. Il modello FEXP 2-D viene utilizzato per rappresentare la componente isotropa,

(

,

)

FEXP j n

S λs , della DSP dell’immagine. I parametri da cui dipende la S_FEXP

(

λs_{j n,}

)

vengono stimati dalla DSPRM calcolata sulla sola regione “B” di Fig. 3.5:

( )

(

)

(

,

)

1 _ , , B n j n k k mr mr B j n B I s I I s n

λ

ϑ

λ

₌

λ

₌

∑

= _(3.51)

Nella relazione (3.51) n_B indica il numero delle colonne della matrice I_{n n}∗_× che

appartengono alla regione “B”. Sulla regione “B” la componente isotropa,

(

,

)

FEXP j n

S λs , è l’unica componente della DSP 2-D dell’immagine SAR,

(

j n, , k

)

I λs ϑ .

Nella regione “A” la funzione I

(

λs_{j n,} ,ϑ_k

)

è modellata come la somma della stessa

componente isotropa, S_FEXP

(

λs_{j n,}

)

, con una componente anisotropa,

(

, ,

)

FRATT j n k

vengono stimati dallo spettro omnidirezionale, S_{omni SAR_}

(

λs_{j n,}

)

, calcolato in funzione della DSPRM sulla regione “A” dopo aver sottratto la componente isotropa

(

,

)

FEXP j n

S λs . Il procedimento è riassunto dalla relazione seguente:

(

)

(

)

(

)

(

)

{

}

_ , , _ , , , , 1 , A

omni SAR j n j n mr fratt j n n j n j n k FEXP j n k A S s s I s s I s S s n

λ

λ

λ

λ

λ

ϑ

λ

= = ⋅ =  −    =

∑

(3.52)

Nella (3.52) n_A indica il numero delle colonne della matrice I_{n n}∗_× che appartengono

alla regione “A”. Vale inoltre la relazione

(

) (

)

(

)

(

)

_ , , , _ , , , , 1, , 0, sulla regione B mr fratt j n k j n k FEXP j n A mr fratt j n k I s I s S s k n I s λ ϑ λ ϑ λ λ ϑ  = − =   =  … (3.53) Si stimano ora i parametri del modello frattale, σ , N_f, b_f , s, ε, K₀, che

minimizzano l’errore quadratico medio tra tutti i possibili spettri omnidirezionali,

(

,

)

omni j n

S λs , del modello frattale del mare ed il vettore S_{omni SAR_}

(

λs_{j n,}

)

. Sia

(

,

)

omni _{j n}

S λs la stima così ottenuta.

La relazione tra la funzione 2-D S_FRATT

(

λs_{j n,} ,ϑ_k

)

e lo spettro 1-D Somni

(

λs_{j n,}

)

è

espressa dalla relazione

(

,

)

omni

( ) ( )

FRATT

S λ ϑ λs s d s dλ ϑ=S λs G ϑ d s dλ ϑ (3.54)

che considera le variabili continue λs e ϑ.

Utilizzando le variabili discrete λs_{j n,} e ϑ_k si ottiene

(

,

)

(

,

)

( )

, 1 , omni FRATT j n k j n k j n S s S s G s λ ϑ λ ϑ λ = (3.55)

Nelle (3.54) e (3.55) si indicano con S_FRATT

(

λ ϑs,

)

e S_FRATT

(

λs_{j n,} ,ϑ_k

)

, e con G

( )

ϑ e G

( )

ϑ_k , rispettivamente la componente anisotropa del modello FEXP Frattale (FEXPF) e una funzione di spreading che descrive la distribuzione angolare dello spettro omnidirezionali.

seguenti [40]:

( )

( )

( )

2 0 2 0 sulla regione A 0 sulla regione B G d G G π ϑ ϑ π ϑ ϑ  =    _≠   ₌  

∫

(3.56)

Il motivo per il quale si utilizza il modello frattale dello spettro omnidirezionale è che la sua espressione dipende dai valori assunti da ben cinque parametri. Modificando tali valori, è possibile adattare la forma dello spettro S_omni

(

λs_{j n,}

)

a quelle degli spettri omnidirezionali delle immagini, che risultano dalle distorsioni non lineari introdotte dall’elaborazione SAR sullo spettro direzionale del mare.

La funzione di spreading, generalmente indicata come G K

(

,ϑ

)

, definisce le modalità secondo le quali la potenza complessiva del segnale h x y

( )

, , che rappresenta l’altezza della superficie marina, si distribuisce in funzione delle variabili

K e ϑ. Nelle espressioni più semplici proposte in letteratura, per evitare le complicazioni di calcolo che derivano dall’utilizzare una funzione di distribuzione angolare dipendente dal numero d’onda K , si considerano funzioni della sola variabile ϑ. È questo il caso della funzione proposta da Pierson (1955)

( )

₄ 2

(

)

2

W W

G

ϑ

= cos

ϑ ϑ

− ,

ϑ ϑ

− ≤

π

(3.57)

(dove con ϑ_W si indica la direzione media del vento), Kitaigorodskii (1973) e Cotè et al. (1960) [41], [14]. Tutte quante risultano definite sullo stesso insieme di direzioni angolari:

2

W

π ϑ ϑ− ≤ .

Si può pensare di estendere la definizione di funzione di spreading per caratterizzare la relazione intercorrente tra lo spettro omnidirezionale, S_{omni SAR_}

(

λs_{j n,}

)

, e la DSP dell’immagine SAR.

Dall’analisi d’immagini reali risulta che la trasformazione non lineare del SAR produce immagini con lobi della DSP 2-D non troppo dispersi nell’intorno di una direzione media. Il contributo delle componenti d’onda con direzioni angolari ortogonali alla direzione del vento è poco significativo nell’immagine SAR, perché

le dispersioni maggiori nelle direzioni angolari sono associate alle onde capillari. Onde gravitazionali, interne alla banda delle frequenze spaziali risolvibili dal sensore, con direzioni fortemente diverse da quella media del vento (la (3.57) si annulla soltanto per

2

W

π

ϑ ϑ− = ) non sono solitamente presenti sulla superficie

marina.

Sull’immagine SAR, il modello FEXPF introduce una netta separazione in angolo tra le due regioni “A” e “B”. La larghezza delle due regioni è una funzione della velocità e della direzione del vento sulla superficie (si consideri il fenomeno del cut-off azimuthale prodotto dalla trasformazione introdotta dal sensore). È allora necessario definire una funzione di spreading, G

( )

ϑ , la cui dispersione angolare sia un parametro modificabile in funzione della velocità del vento e dell’angolo tra la direzione di moto del satellite e la direzione media di propagazione delle onde. Si definisce quindi la seguente classe di funzioni di dispersione angolare:

( )

(

)

(

)

(

)

(

)

2 2 2 2 W W W W n G z cos n rect n z cos n rect , z R

ϑ ϑ

ϑ

ϑ ϑ

π

ϑ ϑ

π

ϑ ϑ

π

π

 −    = _ − _{  }+    − −    + _ − − _{  } ∈   (3.58)

La stessa classe di funzioni di spreading, come sarà meglio precisato nel paragrafo 3.5, viene utilizzata per simulare gli spettri direzionali del mare utilizzati come segnali d’ingresso nella procedura di trasformazione diretta (approssimazione quasi-lineare di Hasselmann [6]) dallo spettro direzionale del mare alla DSP 2-D della corrispondente immagine SAR. Il parametro z delle funzioni di spreading (3.58)

viene scelto pari al valore minimo per il quale non si verifica il fenomeno dello sdoppiamento del picco dello spettro SAR nella direzione dell’azimuth, in accordo con quanto dimostrato sperimentalmente da Alpers e Bruening in [42].

3.5 - Generazione di spettri SAR simulati con il metodo di

Hasselmann

In questo paragrafo si riportano i risultati ottenuti applicando la procedura, proposta da Hasselmann [6], per la trasformazione dello spettro direzionale della superficie marina nella DSP 2-D della corrispondente immagine SAR.

Gli spettri direzionali del mare sono stati ottenuti per diverse velocità e direzioni del vento utilizzando

1. il modello frattale per la simulazione degli spettri omnidirezionali

(

,

)

omni j n S λs ;

2. la classe delle funzioni di spreading G

( )

ϑ (3.58) valutate per ϑ ϑ= _k. La simulazione degli spettri direzionali del mare si ottiene dalla relazione

(

,

)

(

,

)

( )

, 1 , DIR j n k omni j n k j n S s S s G s

λ

ϑ

λ

ϑ

λ

= (3.59)

Nel seguito le DSP 2-D delle immagini SAR vengono rappresentate in funzione dei numeri d’onda spaziali K e _x K . Le direzioni medie di propagazione delle onde _y

sono espresse in gradi e contate in senso antiorario dall’asse K positivo. _x

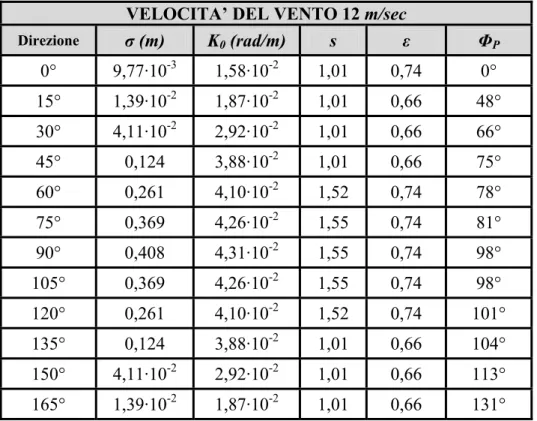
I parametri frattali utilizzati per il calcolo degli spettri omnidirezionali del mare sono riferiti alle velocità del vento 6 m/sec, 7,5 m/sec, 9,5 m/sec, 12 m/sec e 15 m/sec. I valori di tutti i parametri frattali sono stati scelti come i valori medi ottenuti

dall’elaborazione di più insiemi di dati misurati dalla rete ondametrica nazionale (RON). I valori scelti per il parametro σ per le diverse velocità del vento risultano anche consistenti con quelli ricavabili dall’altezza significativa d’onda, h , riportati _s

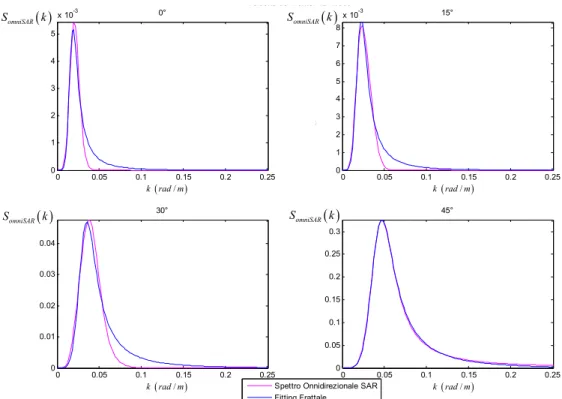
nella scala Beaufort, universalmente riconosciuta per la classificazione delle varie categorie di vento. Si ricorda che tra le due grandezze vale la relazione h_s =4σ . Nel seguito si fa uso del modello frattale costruito sulle funzioni di Weierstrass, descritto in Appendice I, per rappresentare lo spettro omnidirezionale, S_{omni SAR_}

(

λs_{j n,}

)

, dell’immagine SAR della superficie marina. Si ricorda che per questo modello lo spettro omnidirezionale assume la forma:

(

)

(

)

2 2 2 1 2 2 ₂ 2( 2) 2 2 0 0 0 ( ) 2 n n f R K K N s n n W n n n C S K

σ

K b R e I R b K K  +    − − _{ }   −   = =

∑

(3.60)

Il processo di stima inizia scegliendo N_f =50. I parametri K , ₀ ε ed s vengono calcolati applicando una procedura iterativa. In particolare il valore di K decresce ₀

da K_max fino a 0 9. K⋅ _max con passo ∆K₀ =K_max 100. I valori dei parametri s e ε si assumono appartenenti ad intervalli dedotti sperimentalmente per le immagini SAR:

(

0.1,5

)

ε∈ , ∆ =ε 4.9 100 e s∈

(

1.01,1.9

)

, ∆ =s 1.89 100. Il valore della deviazione

standard σ viene calcolato per ultimo: per ogni insieme di valori dei parametri K , ₀

s e ε, il valore del σ è quello che rende minimo l’errore quadratico medio tra lo spettro omnidirezionale frattale e la funzione S_{omni SAR_}

(

λs_{j n,}

)

. Di seguito si riportano i risultati ottenuti applicando la procedura seguente:

1. Si simula lo spettro direzionale del mare (vedi relazione (3.59)).

2. Si applica la tecnica di trasformazione diretta di Hasselmann, approssimazione quasi-lineare.

3. Si calcola lo spettro omnidirezionale dalla DSP 2-D dell’immagine SAR,

(

)

_ ,

omni SAR j n

S λs .

4. Si stimano i parametri frattali della funzione S_{omni SAR_}

(

λs_{j n,}

)

come descritto in precedenza.

La Tab. 3.1 mostra i valori dei parametri frattali utilizzati, per diverse velocità del vento, nella simulazione degli spettri direzionali del mare.

Velocità del vento Nf σ (m) K0 (rad/m) s ε z

6 m/sec 350 0,21 18,2·10-2 1,16 1,17 2,54 7,5 m/sec 380 0,4 10·10-2 1,20 1,05 2,54 9,5 m/sec 430 0,55 7,3·10-2 1,24 0,9 2,21

12 m/sec 500 0,875 3,97·10-2 1,30 0,68 1,77 15 m/sec 600 1,06 2,99·10-2 1,33 0,5 1,32