Capitolo 3 Aspetti implementativi

Capitolo 3

Aspetti implementativi

In questo capitolo vengono descritte le principali scelte implementative effettuate nella realizzazione del software e comuni a tutte le varianti dell’approccio euristico proposte.

3.1 Struttura del software

Il software prodotto durante il lavoro di tesi è stato sviluppato in C++ e ad esso è asso-ciata una documentazione, generata con Doxygen [17], a cui l’utente può fare riferimen-to per avere indicazioni accurate su classi, meriferimen-todi, variabili e loro utilizzo. Nel seguiriferimen-to riportiamo la struttura della libreria e le principali scelte effettuate durante la progetta-zione e realizzaprogetta-zione del software.

Nel software si possono individuare quattro moduli principali:

• Interfaccia Utente. Questo modulo contiene una classe che realizza una semplice interfaccia utente; nella classe sono presenti un metodo per acquisire il grafo di input su cui eseguire l’approccio euristico, un metodo per avviare l’esecuzione dell’algoritmo e un metodo per leggere la soluzione calcolata.

• Cammino Minimo Vincolato. Il modulo contiene classi per risolvere problemi di tipo “cammino minimo vincolato”; nel caso in esame, si tratta dell’individuazione di un cammino colorful.

• Classi d’Utilità. Qui sono presenti le classi che definiscono e implementano tutte le strutture dati di supporto per l’implementazione dell’approccio euristico. Ad esempio, le classi utilizzate per implementare la verifica dell’equivalenza di due colorazioni e le classi che descrivono i sottografi da analizzare sono contenute in questo modulo.

• Implementazione Euristica. Questo modulo contiene l’implementazione dell’approccio euristico.

In Figura 6 riportiamo in forma grafica la struttura del software, le classi che fanno parte di ogni modulo e le interazioni tra esse intercorrenti.

La descrizione degli aspetti fondamentali di ogni classe, e l’utilizzo che si fa di ognuna di esse, vengono messi in evidenza nei paragrafi successivi, in cui si descrivono le fasi di progettazione e realizzazione del software. Per ogni scelta effettuata durante la pro-gettazione, infatti, verranno descritte le classi che poi sono state utilizzate a livello im-plementativo e le caratteristiche fondamentali di tali classi.

Figura 6

Interfaccia Utente Implementazione Euristica

Classi d’Utilità Cammino Minimo Vincolato

Class Solver Class DSManager Class CnstSPC olor Class MCFClass Class CnstSP Class Label Altro software Class PartitionE-lement Class Coloring Class subGraph Class ExpandedNde Class Cheked usa eredita da implementa l’interfaccia

3.2 Individuazione di un cammino colorful

Per individuare un cammino colorful nel grafo espanso si fa uso delle classi contenute nel modulo “Cammino Minimo Vincolato”. Tali classi implementano un algoritmo di programmazione dinamica per la risoluzione del problema del cammino minimo vinco-lato. Il problema del cammino minimo vincolato è così definito. Sia un gra-fo ed R una risorsa; ad ogni arco

(

,

G= N E

)

( )

i j, ∈E siano associati un costo ed un valore che indichi quanta risorsa di tipo R consuma l’arco; siano inoltre dati due nodi ed una quantità massima di risorsa utilizzabile lungo ogni cammino da a t in , sia essa 0 ij c ≥ 0 ij r ≥ , s t∈N s

G Max . Si vuole determinare un cammino di costo minimo tra tutti i cammi-_R

ni da a t che consumino una quantità di risorsa R non superiore a s Max . _R

Si osservi che il problema del cammino minimo vincolato generalizza il problema dell’individuazione di un cammino colorful. In questo ultimo caso, infatti, il tipo di ri-sorsa da considerare è il colore, la quantità di riri-sorsa a disposizione è data dall’insieme dei colori Co e il vincolo è che, lungo ogni cammino da s a t in , ogni colore può essere utilizzato al più una volta.

l G

L’algoritmo utilizzato per risolvere il problema è il seguente. Si effettua una visita del grafo a partire dal nodo . Quando si raggiunge un nodo si trova, associato ad esso, un insieme di etichette

{

s i

}

1,..., p

e e . Le etichette indicano i modi di arrivare da s ad e i rispettivi consumi della risorsa fino ad i , siano essi

i

1,..., p

i e

r r_ei . Più precisamente, ogni e-tichetta indica il costo minimo dei cammini analizzati, da s ad i , aventi un consumo

di risorsa pari a . Quando il nodo viene analizzato, l’algoritmo verifica, per ogni e-tichetta ad esso associata e per ogni arco

l e l i e r i l e

( )

i j, , se il vincolo è

verifi-cato o meno. Se il vincolo è verifiverifi-cato si aggiorna l’insieme delle etichette del nodo

l

i e ij

r + ≤r Max_R

j ,

altrimenti il cammino considerato da a s j non è ammissibile e può essere scartato.

Quando si aggiorna l’insieme delle etichette di un nodo si deve effettuare il seguente controllo: se due etichette e_l ed e sono associate ad uno stesso consumo di risorsa _f

(cioè ), una delle due deve essere eliminata e tra le due si elimina quella maggio-re (corrispondente, cioè, al cammino di costo maggiomaggio-re).

l

e e

r =r

f

Le classi in cui è implementato l’algoritmo di programmazione dinamica descritto non sono state sviluppate durante il lavoro di tesi, ma sono parte di un codice sviluppato dal Gruppo di Ricerca Operativa del Dipartimento di Informatica dell’Università di Pisa. Ciò che è stato fatto nella tesi è stato includere le classi nella nostra libreria e, sfruttando l’ereditarietà, derivare da esse un’altra classe (CnstSPColor) che gestisca opportuna-mente tutto ciò che riguarda la colorazione. La tecnica per il controllo del consumo del-la “risorsa colore” e del-la tecnica di aggiornamento delle etichette, implementate neldel-la nuova classe, sono descritte nel prossimo paragrafo. Si noti che, nel nostro caso, il con-sumo della risorsa è associato ad ogni nodo del grafo anziché ad ogni arco.

3.3 Rappresentazione dei colori e verifica della proprietà

co-lorful

Supponiamo di aver stabilito che l’insieme di colori Co utilizzati nell’algoritmo debba contenere

l

γ colori. L’idea utilizzata nell’implementazione dell’approccio euristico è la seguente. Si utilizzano gli interi 1,...,γ per rappresentare i colori e, nell’algoritmo di programmazione dinamica, si usa un array di bit C di dimensione γ per rappresentare il consumo della risorsa colore lungo un cammino da s ad un certo nodo i. Nell’array C,

alla k-esima posizione si trova un 1 se e solo se, lungo il cammino da s a i, c’è un nodo

con colore k. Vediamo a questo punto come, nell’algoritmo di programmazione

dinami-ca, si effettua il controllo del vincolo relativo al colore. Si supponga di avere selezionato il nodo i , siano le sue etichette e i rispettivi valori di consumo del co-lore. Si supponga inoltre di analizzare la q-esima etichetta del nodo i , l’arco

1,..., p

e e C₁,...,C_p

q

e

( )

i j, ,

e che col j

( )

sia il colore del nodo j . Per controllare se è già stato usato nel cammino da a i corrispondente ad , si analizza il valore di . Se

, è già stato usato e quindi il cammino non può essere esteso

uti-( )

col j s e_q C col j_q[ ( )] [ ( )] 1 q C col j = col

(

j

)

lizzando l’arco

(

i j,

)

; se invece C col j_q[ ( )]= , il colore del nodo j non è ancora stato 0 usato. Si può aggiornare quindi l’insieme delle etichette di j aggiungendo l’etichetta associata al consumo di risorsa , dove denota un array di bit tale che

se e solo se e dove ∨ indica l’operatore logico di OR.

( ) col j q C ∨ C Ccol j( ) ( ) [ ] 1 col j C h = h=col j( )

Alla superorigine s e alla superdestinazione t deve essere assegnato un colore “neutro”, in quanto sono gli unici nodi che saranno comuni ai cammini node-disjoint cercati. Nell’implementazione si è scelto di usare lo zero per rappresentare il colore neutro, in particolare quindi col s

( )

=col t

( )

=0, e gli archi

( )

i j, per i quali non con-sumano la risorsa colore. Questa scelta rende possibile l’utilizzo dell’euristica anche nel caso in cui si cerchino cammini parzialmente disgiunti.

( )

0

col j =

In una prima fase di sviluppo del software per rappresentare il consumo di risorsa asso-ciato ad un’etichetta e per effettuare la verifica della proprietà colorful erano state effet-tuate scelte implementative diverse da quelle appena descritte. La prima implementa-zione realizzata era la seguente. Si usa un intero C per rappresentare il consumo della risorsa colore lungo un cammino da s ad un certo nodo i. C è l’intero nella cui rappre-sentazione binaria (su γ bit) il k-esimo bit è 1 se lungo il cammino da s a i c’è un nodo con colore k. Nell’algoritmo di programmazione dinamica, il controllo del vincolo rela-tivo al colore si effettua nel seguente modo. Si supponga ancora una volta di avere sele-zionato il nodo i , siano le sue etichette e i rispettivi valori di consu-mo del colore. Si supponga inoltre di analizzare l’arco

1,..., p

e e C₁,...,C_p

( )

i j, , la q-esima etichetta e che sia il colore del nodo

q

e

( )

col j j . Per controllare se col j

( )

è già stato usato nel

cammino da a corrispondente ad s i e_q, si effettua la divisione intera _{( )} 2

q col j

C

e si controlla se si ottiene un numero pari o dispari. Se il numero ottenuto è dispari vuol dire che è già stato usato e quindi il cammino non può essere esteso utilizzando l’arco ; se invece il numero ottenuto è pari il colore del nodo

( )

col j

(

i j,

)

j non è ancora stato

usato. Si può aggiornare quindi l’insieme delle etichette di j aggiungendo un’etichetta con associato un consumo di risorsa pari a C_q +2col j( ).

La limitazione di questa scelta implementativa è nel massimo numero di colori utilizza-bili per colorare i nodi del grafo. Con tale implementazione, infatti, non si possono uti-lizzare più di trentuno colori. Si è quindi preferito passare all’implementazione con l’array di bit per non limitare l’utilizzabilità del software e l’applicabilità dell’approccio euristico proposto.

3.4 Scelte implementative per un miglioramento delle

perfor-mance

Descriviamo ora alcune scelte effettuate a livello implementativo allo scopo di ottenere, quando possibile, dei miglioramenti nell’esecuzione dell’approccio euristico. Tali scelte riguardano, ad esempio, le approssimazioni di alcuni parametri utilizzati o l’ordine di analisi di alcune strutture, e possono portare ad una riduzione del numero di iterazioni da effettuare. Poiché i miglioramenti ottenibili sono strettamente dipendenti dall’istanza del problema che si sta analizzando, nel capitolo relativo all’indagine sperimentale si metterà di volta in volta in evidenza in quali casi la scelta ha portato ad un effettivo guadagno e quando invece si è rivelata inutile, senza comunque portare ad una perdita di efficienza computazionale.

3.4.1 Approssimazione di U e ricerca binaria

Nel capitolo precedente è stato spiegato che la costruzione del grafo espanso viene effettuata usando un’approssimazione di U pari a , con

(

, U U U G = V E

)

(

n−2k+1

)

c_max

( )

{

}

max max ij| ,

c = c i j ∈E . Un’operazione che si può effettuare, prima di aggiunge-re la superorigine s e la superdestinazione t e prima di calcolaaggiunge-re , è l’eliminazione da di tutti gli archi appartenenti alla stella entrante di ogni nodo origine (sia essa

max

c

E s_i

( )

i

BS s ) e di tutti quelli appartenenti alla stella uscente di ogni nodo destinazione (sia essa ). Chiaramente un’operazione del genere non porta alcun vantaggio se

i

t

( )

i

FS t

( )

i

( )

i

una riduzione delle dimensioni di , e la riduzione è tanto maggiore quanto maggiore è la differenza tra i costi degli archi delle

U

G

( )

i

BS s eFS t

( )

i , i=1,..,k, e i restanti archi

di E.

In precedenza si è fatto osservare che la ricerca binaria descritta in 1.3.1 può essere ef-fettuata nell’intervallo ⎡_⎣0,U−cmin⎤⎦ anziché in

[

0,U

]

. Facciamo ora notare che non è necessario effettuare il calcolo esplicito di . Infatti una volta costruito il grafo , se indichiamo con

min

c G_U

{

1_,..., p

}

T%= tα tα l’insieme delle copie del nodo t in G_U, si ha che

{

}

min

1

min ,..., _p

c = α α .

L’intervallo in cui effettuare la ricerca binaria può essere ridotto ulteriormente. L’estremo superiore dell’intervallo rappresenta la massima differenza in costo che può esserci tra il cammino più costoso e quello meno costoso dell’insieme dei k cammini

node-disjoint cercati, e questa differenza può essere al più αmax−cmin, dove

{

}

max

1

max ,..., _p

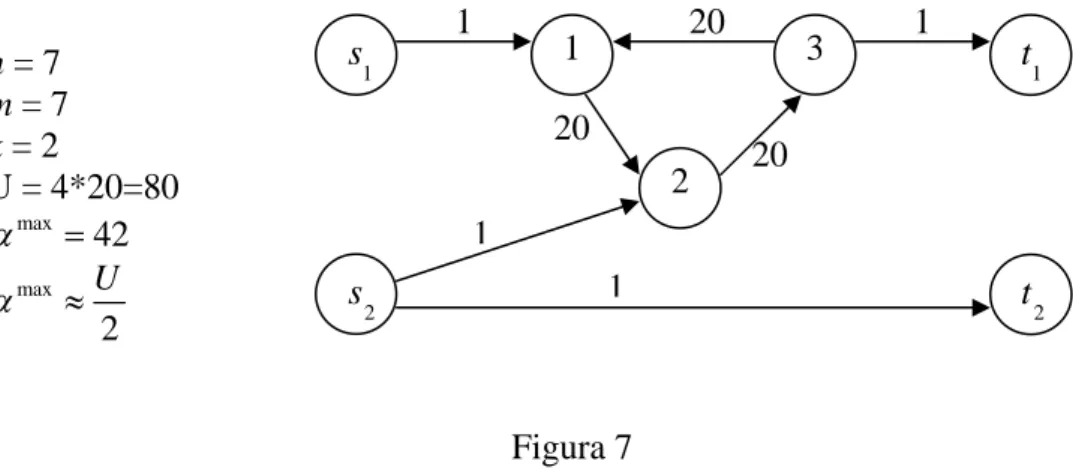
α = α α . Ci sono istanze del problema, e un esempio è riportato in Figura 7, in cui U è molto maggiore di αmax, e quindi l’intervallo della ricerca binaria è sensi-bilmente ridotto.

Nel software l’insieme T% è rappresentato mediante un vettore detto copiesT. Il vettore

copiesT viene riempito durante la costruzione del grafo espanso, che avviene “per

livel-li”. Le copie j

tα del nodo t vengono quindi create, e inserite in copiesT, in ordine di α_j crescente. Si ha quindi che cmin = copiesT[0] e αmax= copiesT[l-1] dove l è la lunghezza del vettore copiesT.

Figura 7 1 s 2 s 2 t 1 t 1 2 3 1 20 20 1 20 n = 7 m = 7 k = 2 U = 4*20=80 max 42 α = max 2 U α ≈ 1 1

Un’ulteriore riduzione dell’intervallo della ricerca binaria si può ottenere quando si cambia colorazione dei vertici del grafo. Nell’implementazione dell’approccio euristico, infatti, quando si analizza una nuova colorazione, se con le colorazioni precedenti è sta-ta trovasta-ta almeno una soluzione ammissibile e δ è il miglior valore ottenuto della fun-zione obiettivo, allora la ricerca binaria viene effettuata in 0,⎡_⎣ δ −1⎤_{⎦ . Qualora non sia} ancora stata trovata alcuna soluzione, invece, si procede come descritto sopra.

3.4.2 Calcolo di una soluzione iniziale: caso coppie origini-destinazione

non date

Se in input si ha un’istanza del problema in cui i nodi origine e destinazione possono es-sere connessi in modo qualsiasi, l’intervallo iniziale della ricerca binaria può eses-sere ul-teriormente ridotto effettuando la seguente operazione. Si trasforma il problema di input

node-disjoint in un equivalente problema arc-disjoint come descritto in 1.4.1. Sul grafo

così trasformato si risolve un problema di flusso di costo minimo con i seguenti dati di input: ogni arco ha capacità superiore uguale ad 1; i nodi origine sono le sorgenti di flusso del problema e ad essi è associata un’offerta pari a -1; i nodi destinazione sono i nodi pozzo del problema di flusso e ad essi è associata una domanda uguale ad 1 unità di flusso; tutti gli altri nodi del grafo sono nodi di trasferimento. I costi degli archi sono

quelli definiti nella trasformazione del problema da node-disjoint ad arc-disjoint. Una volta risolto il problema di flusso di costo minimo, si riporta la soluzione in termini del grafo iniziale e si calcola la differenza in costo tra il cammino più costoso e quello meno costoso tra quelli individuati, sia esso δ . La ricerca binaria può dunque essere effettuata nell’intervallo

[

0,δ −1

]

.

Se il problema di flusso di costo minimo risultasse inammissibile allora anche il pro-blema dei cammini bilanciati sarebbe inammissibile.

3.4.3 Calcolo di una soluzione iniziale: caso coppie origini-destinazione

date

Nel caso in cui nel problema di input sono fornite k coppie di nodi origine-destinazione , invece, e i cammini devono connettere ogni origine con la rispettiva destinazione, si può tentare di ridurre l’intervallo iniziale della ricerca binaria, senza a-vere però la garanzia di riuscirci come nel caso precedente. Nel caso di coppie date si procede nel modo seguente. Si effettua la trasformazione del problema da node-disjoint ad arc-disjoint e si stabilisce un ordinamento delle coppie di input. Si cercano quindi, uno alla volta e seguendo l’ordinamento definito, k cammini minimi che connettano l’origine e la destinazione delle coppie, eliminando di volta in volta gli archi utilizzati da una coppia per le coppie successive nell’ordinamento. Se si riescono ad individuare k cammini, si calcola la differenza in costo tra il cammino più costoso e quello meno co-stoso e si utilizza tale valore per fissare l’estremo superiore dell’intervallo in cui iniziare la ricerca binaria. Si può effettuare l’operazione appena descritta anche per più ordina-menti delle coppie di input e scegliere la soluzione migliore tra quelle ottenute. Il sof-tware è stato implementato in modo da poter specificare da riga di comando per quanti ordinamenti si vuole effettuare l’operazione appena descritta. Gli ordinamenti da testare vengono scelti in modo random. In particolare per le istanze usate nella fase di testing sono stati analizzati tutti gli ordinamenti delle coppie di input in quanto analizzarli tutti non ha mai richiesto un tempo che influisse negativamente sulla valutazione dell’approccio euristico.

3.4.4 Scelta delle famiglie di sottografi di

GU

da analizzare

Ad ogni passo della ricerca binaria dell’algoritmo, in corrispondenza del valore δ in esame, si costruisce la famiglia di sottografi di contenente tutti i cammini di che vanno da s ai nodi in

{

U G G_U

}

,..., p p

t t +δ per ogni intero p≤ − . Poiché in U δ non neces-sariamente esiste un nodo per ogni intero

U

G

p

t p≤ , possono esistere due interi U p e ₁

2

p per cui

{

1 1

}

{

2 2

}

1 ,..., 2 ,...,

p p p p

T = t t +δ ⊆T = t t +δ . Se il sottografo corrispondente a contiene k cammini node-disjoint, questi sono contenuti anche nel sottografo corrispon-dente a e quindi saranno trovati analizzando . In una situazione del genere sarebbe quindi inutile analizzare sia che . Sulla base di questa osservazione, nella scelta dei sottoinsiemi del tipo

{

1 T 2 T T₂ 1 T T₂

}

,..., p p

t t +δ da analizzare si è proceduto come segue. Sia come

prima

{

1_,..., p

}

T%= tα tα . Fissato δ , la famiglia di sottoinsiemi di T% da analizzare si co-struisce in modo che :

• ogni elemento di T% appartenga ad almeno uno dei sottoinsiemi; • nessun sottoinsieme sia contenuto in (o uguale ad) un altro; • gli elementi in uno stesso sottoinsieme distino al più δ .

Vediamo un esempio: sia T%=

{

t t t t t t1, , , , ,2 7 8 9 11,t12,t17,t18,t19

}

e δ =4. I sottoinsiemi di

T% analizzati sono allora T₁ =

{ }

t t1, 2 , T₂ =

{

t t t t7, , ,8 9 11

}

, T₃ =

{

t t t8, ,9 11,t12

}

e

{

17 18 19

}

4 , ,

T = t t t .

Si osservi che alcuni sottoinsiemi

{

tp,...,tp+δ

}

vengono generati più volte in corrispon-denza di valori diversi di δ e che, ovviamente, basta analizzarli solo la prima volta che vengono generati. Nell’esempio precedente un insieme di questo tipo è che viene ge-nerato per i valori 1,2,3, 4 e 5 di

1

T

δ .

Sempre nell’ambito della scelta dei sottografi da analizzare, un’ulteriore ottimizzazione che si può effettuare è l’esclusione di tutti quei sottoinsiemi

{

tp,...,tp+δ

}

il cui sottogra-fo associato non contiene almeno una copia pi di un dato nodo destinazione . Nella

i

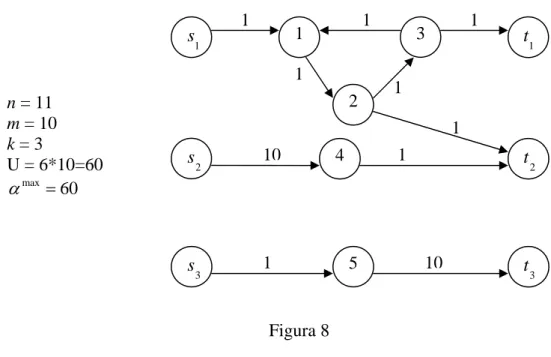
Figura 8 è riportato l’esempio di un grafo per cui, nel grafo , tutti i sottografi corri-spondenti a sottoinsiemi

{

U G

}

,..., p p

t t +δ con p >11 possono non essere analizzati in quan-to non contengono alcuna copia del nodo destinazione . t₃

Si osservi che l’istanza in Figura 8 è un esempio in cui U =αmax; si tratta quindi di un’istanza per cui non esiste alcuna differenza nell’usare U o αmax per fissare l’estremo superiore dell’intervallo della ricerca binaria.

Figura 8 1 s 2 s 2 t 1 t 1 2 3 1 1 1 1 1 n = 11 m = 10 k = 3 U = 6*10=60 max 60 α = 1 10 1 10 4 5 3 s 3 t 1

Altri sottoinsiemi

{

_tp_,...,tp+δ1

}

_{di T% di cui si può evitare l’analisi sono quelli per cui sia} nota, dalle iterazioni precedenti, l’esistenza di un altro sottoinsieme

{

_tq_,...,tq+δ2

}

_che non contiene alcuna soluzione ammissibile e tale che

{

_tp_,...,tp+δ1

} {

⊆ _tq_,...,tq+δ2

}

_.

Tutte le strategie descritte sono implementate nella classe DSManager facendo uso delle classi subGraph e Checked che ora descriviamo.

Ogni istanza di tale classe descrive un insieme

{

jmin_,..., jmax

}

j

T = t t e alcune proprietà del corrispondente sottografo del grafo espanso. Le variabili utilizzate per descrivere

{

jmin_,..., jmax

}

j

T = t t sono:

• due interi min e max i cui valori sono, rispettivamente, jmin e jmax;

• due interi imin e imax tali che copiesT[imin]= _tjmin e copiesT[imax]= _tjmax; • una variabile booleana containsKPaths che indica se il corrispondente sottografo

di GU contiene o meno un insieme colorful di k;

• una variabile booleana isValidIstance il cui valore è true se e solo se il sottogra-fo associato contiene almeno una copia di ogni nodo destinazione , per

. i p i t t_i 1,..., i= k

Per poter inizializzare la variabile isValidIstance, quando nella classe DSManager si co-struisce il grafo espanso, si coco-struisce una matrice M di booleani di dimensione

k×copiesT.size() tale che M[i][h]=true se e solo se in esiste il nodo destinazione . U G [ ] copiesT h i t

La variabile containsKPaths viene invece inizializzata a false, e poi viene modificata dopo la verifica dell’esistenza o meno di k cammini node-disjoint nel sottografo di associato a .

U

G

j

T

Si osservi che, dati due insiemi

{

jmin_,..., jmax

}

j

T = t t e

{

lmin_,..., lmax

}

l

T = t t , per verificare se è sufficiente verificare che valgano le due disuguaglianze

j

T ⊆T_l l_min ≤ j_min e

max max

j ≤l .

La classe Checked

La classe contiene un array ordinato di elementi di tipo subGraph. E’ utilizzata in DSManager per rappresentare l’insieme dei sottografi di per i quali è già stata effet-tuata la verifica dell’esistenza di un insieme colorful di k cammini.

U

G

L’ordinamento utilizzato è il seguente. Dati

{

jmin_,..., jmax

}

j

T = t t e

{

lmin_,..., lmax

}

l

T = t t ,

3.4.5 Ordine di analisi dei sottografi

Si supponga che, durante la ricerca binaria, l’intervallo corrente dei costi sia

[ ]

a b, e che si stia quindi analizzando il valore di

2

a b δ _{= ⎢}⎢ + ⎥_⎥

⎣ ⎦. Supponiamo che sia già stata scelta la famiglia di sottografi di in cui effettuare la ricerca dei cammini

node-disjoint, e siano i sottoinsiemi di

U

G

1,..., l

T T T% selezionati. Per ogni j∈

{

1,...,l

}

sia

{

jmin_,..., jmax

}

j

T = t t . Nell’implementazione dell’approccio euristico, gli insiemi vengono analizzati in ordine di

1,..., l

T T

max min

j − j non decrescente. Non appena si trova un nel cui sottografo associato esiste una soluzione ammissibile del problema, si interrom-pe l’analisi dei sottoinsiemi relativi a

j

T

δ e si procede con la ricerca binaria nell’intervallo

[

a, (j_max− j_min) 1−

]

anziché nell’intervallo

[

a,δ −1

]

. L’intervallo della ricerca binaria può essere ridotto ulteriormente utilizzando il valore della funzione o-biettivo corrispondente alla soluzione associata a T_j; se indichiamo tale valore con δ , la ricerca binaria può essere proseguita in ⎡_⎣a,δ −1⎤_{⎦ . Anche in questo caso, possono} es-serci istanze del problema per cui j_max− j_min = = e non si ottiene quindi alcuna ri-δ δ

duzione del numero di iterazioni da effettuare. Se nessun contiene una soluzione si procede normalmente con la ricerca binaria in

j

T

[

δ+1, b

]

senza aver avuto alcun guada-gno dall’aver analizzato gli insiemi nell’ordine descritto.

3.4.6 Verifica dell’equivalenza di due colorazioni

Descriviamo ora come, nel software prodotto, vengono rappresentate le colorazioni e come si verifichi se due colorazioni sono equivalenti.

Ogni colorazione viene rappresentata, tramite la partizione di V che essa induce, nel seguente modo. Sia

:

r V →Col

ν il numero di colori utilizzati da ; r ∀ ∈j

{

1,...,ν

}

indi-chiamo con V j

[ ]

l’insieme dei vertici in V colorati con il j -esimo colore. Si ordinino

ora i nodi di ogni sottoinsieme V j

[ ]

in ordine di indice crescente, e sia pivot il primo _j

elemento dell’insieme ordinato. Infine, si ordini la famiglia

{

V j

[ ]

,j=1,...,ν

}

sulla ba-se dei pivot : _j

[ ]

V j < V i

[ ]

se e solo se pivot < _j pivot , _i

cioè si ordinino per pivot crescenti. j

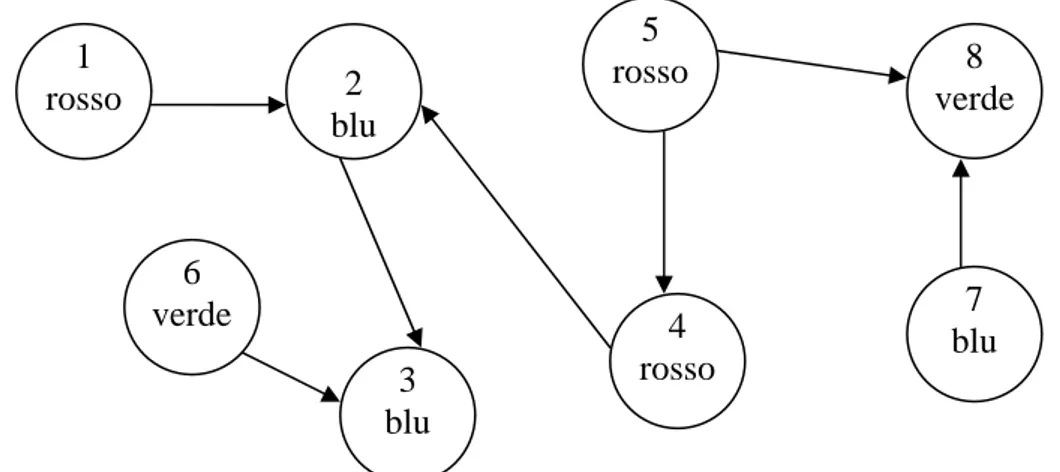
In Figura 9 è riportato l’esempio della rappresentazione di una colorazione.

Figura 9 1 rosso 6 verde 3 blu 4 rosso 7 blu 8 verde 5 rosso 2 blu

r: V[blu]= {3,2,7}, V[rosso]= {1,5,4}, V[verde]= {6,8}.

Si ordinano i nodi in ogni V[j]:

V[blu]= {2,3,7}, V[rosso]= {1,4,5}, V[verde]= {6,8}

2, 1, 6.

pivot_blu = pivot_rosso = pivot_verde = Si ordinano i sottoinsiemi V[j]:

V[rosso] < V[blu] < V[verde].

La colorazione r viene quindi rappresentata come segue:

1 4 5 2 3 7 6 8

Nella nostra implementazione, la rappresentazione di una colorazione appena generata è effettuata in modo tale che gli elementi vengano inseriti in ogni V j

[ ]

già ordinati; è quindi necessario effettuare solo l’ordinamento basato sui pivot. Nel software, per

rap-presentare ogni insieme V j

[ ]

si usa la classe PartitionElement, mentre per rappresenta-re una colorazione si usa la classe Coloring.

Per controllare se due colorazioni ed sono equivalenti si usa la rappresentazione appena descritta nel seguente modo. Innanzitutto si confrontano ed se e solo se u-sano lo stesso numero di colori; supponiamo dunque che sia così e sia

1

r r₂

1

r r₂

ν il numero di colori comuni ad ed . Nel primo passo della verifica si confrontano ordinatamente i pivot delle due colorazioni, cioè si effettua un ciclo per

1

r r₂

1,...,

j= ν in cui al j -esimo passo si confrontano il j -esimo pivot di e il r₁ j -esimo pivot di . Non appena si tro-va un pivot su cui le due colorazioni non coincidono, si può interrompere la verifica e concludere che le due colorazioni non sono equivalenti. Se invece le due colorazioni coincidono su tutti i pivot, si confrontano, sempre seguendo l’ordine, le dimensioni de-gli insiemi delle partizioni generate. Anche in questo caso quindi si effettua un ciclo per

2

r

1,...,

j= ν in cui al j -esimo passo si confrontano la dimensione del j -esimo sottoin-sieme di e la dimensione del r₁ j -esimo sottoinsieme di e non appena si trovano due sottoinsiemi di dimensione diversa si può concludere che ed non sono equivalenti. Se ciò non accade bisogna procedere con il confronto dei singoli elementi dei sottoin-siemi effettuando il solito ciclo per

2

r

1

r r₂

1,...,

j= ν , in cui al j -esimo passo si confrontano gli elementi del j -esimo sottoinsieme di con quelli del r₁ j -esimo sottoinsieme di . Poiché tali elementi sono ordinati, fissato

2

r j , basta confrontare l’ i -esimo elemento del

sottoinsieme j di con l’ -esimo elemento del sottoinsieme r₁ i j di e concludere che le due colorazioni non sono equivalenti appena si trova un elemento i su cui non coin-cidono. Chiaramente, se ed coincidono su tutti gli elementi di ogni sottoinsieme allora le due colorazioni sono equivalenti. La tecnica di rappresentazione e confronto delle colorazioni appena descritta è simile alla tecnica delle postings list, descritta in [2], utilizzata in alcuni motori di ricerca per indicizzare i documenti e per risolvere alcuni tipi di interrogazioni.

2

r

1

r r₂

Qualora l’occupazione di memoria delle strutture dati sopra descritte dovesse risultare troppo onerosa, una migliore rappresentazione delle colorazioni si potrebbe ottenere

ap-plicando agli elementi degli insiemi V j

[ ]

algoritmi di compressione, migliorando in tal modo l’occupazione in spazio. Se si usa una algoritmo di compressione come il gamma

code [2], che permette una codifica a lunghezza variabile degli interi e che risulta

esse-re più efficiente su interi “piccoli”, può esseesse-re pesse-referibile sostituiesse-re gli elementi conte-nuti in ogni V j

[ ]

con la differenza rispetto al precedente elemento nell’insieme. Ad e-sempio, la rappresentazione della colorazione riportata in Figura 9 sarebbe (prima di es-sere compressa):

1 3 1 2 1 4 6 2

Tali tecniche di compressione, tuttavia, non sono state utilizzate in questo lavoro di tesi, non essendo risultata critica l’occupazione di memoria richiesta dalle strutture dati pre-cedentemente descritte.